Công thức giải nhanh Hình học lớp 12 đầy đủ, dễ hiểu nhất

Công thức giải nhanh Hình học lớp 12 đầy đủ, dễ hiểu nhất
1. Tổng hợp công thức toán hình 12 khối đa diện
Đến với chương đầu tiên - khối đa diện, bạn được học về hình chóp tam giác,
chóp tứ giác, hình hộp,.. Chúng ta có thể hiểu rằng khối đa diện là phần
không gian được giới hạn bởi hình đa diện, bao gồm cả hình đa diện đó. Ta
sẽ có những công thức như sau:
1.1. Công thức toán hình 12 khối đa diện
Thể tích khối chóp áp dụng cho chóp tam giác và chóp tứ giác:
Công thức tính thể tích hình chóp được hiểu là một phần ba diện tích mặt đáy
nhân với chiều cao. Thể tích khối chóp tứ giác đều và tam giác đều có cùng chung công thức.
Ta có thể tích khối chóp: V= Sđáy . h Trong đó:
• S đáy: Diện tích mặt đáy • h: Độ dài chiều cao
Thể tích khối chóp S.ABCD là:
1.2. Công thức toán hình 12 khối lăng trụ
Hình lăng trụ có vài đặc điểm giống nhau, đó là:
• Nằm trên 2 mặt phẳng song song với nhau và có hai đáy giống nhau.
• Cạnh bên đôi một bằng nhau và song song với nhau, các mặt bên là hình bình hành
Thể tích khối lăng trụ được tính bằng công thức như sau: V= S.h Trong đó: • S là diện tích đáy. • h là chiều cao.
Lưu ý: Hình lăng trụ đứng có chiều cao chính là cạnh bên.
Ngoài ra, các em có thể tham khảo thêm công thức tính thể tích khối lăng trụ
tam giác đều để giải các bài tập về hình lăng trụ.
1.3. Thể tích hình hộp chữ nhật lớp 12
Hình hộp chữ nhật có các cạnh đáy lần lượt là a, b và chiều cao c, khi đó thể
tích hình hộp chữ nhật là V= a.b.c (a, b, c có cùng đơn vị).
Hình lập phương là dạng đặc biệt của hình hộp chữ nhật có a = b = c. Do vậy
thể tích hình lập phương được tính theo công thức: V =
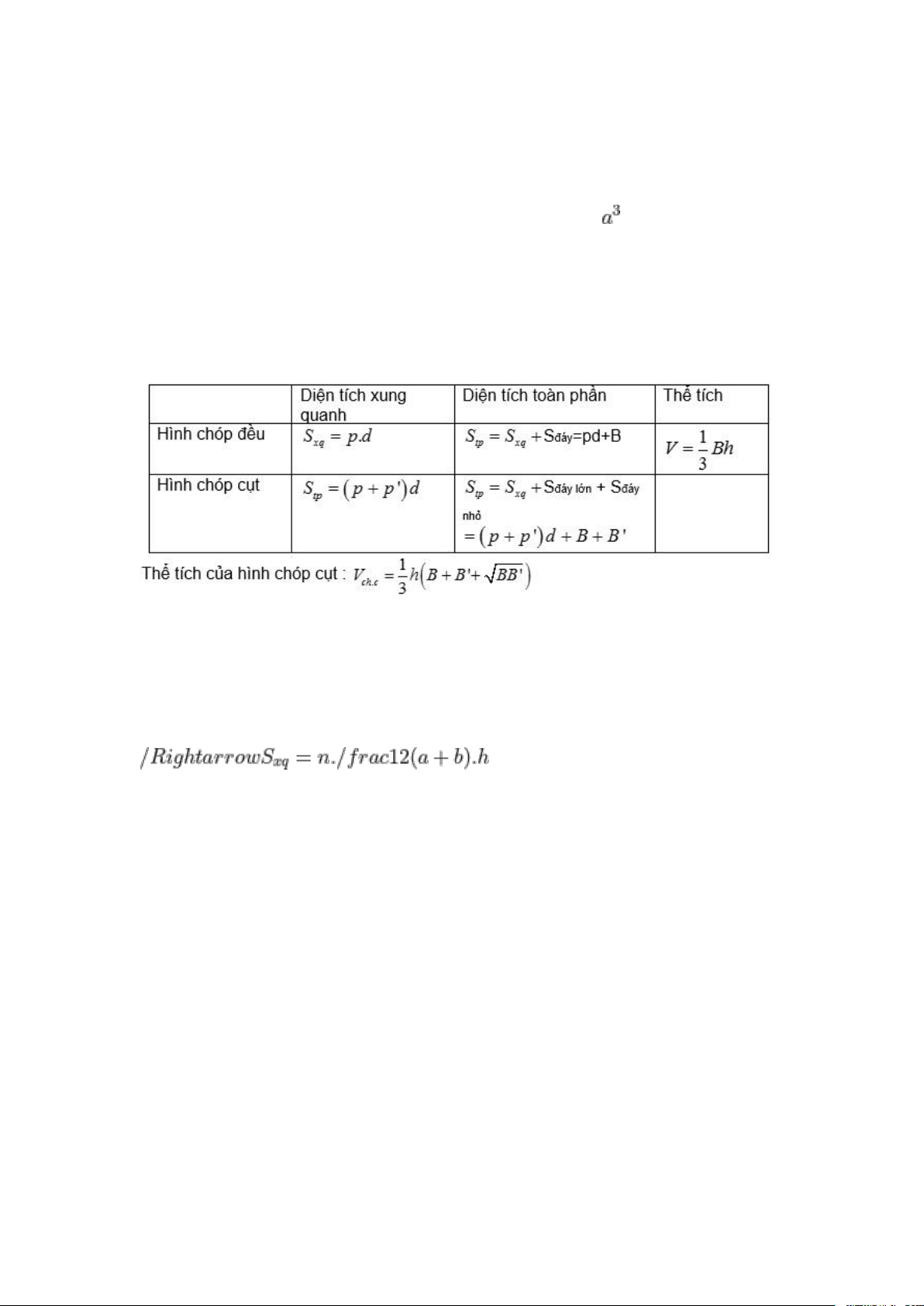
1.4. Công thức toán hình 12 khối chóp cụt
Hình chóp cụt được định nghĩa là một phần của khối đa diện nằm giữa mặt
đáy và thiết diện cắt bởi đáy của hình chóp và một mặt phẳng song song với đáy.
a) Diện tích xung quanh hình chóp cụt
Diện tích xung quanh của hình chóp cụt là diện tích các mặt xung quanh,
phần bao quanh hình chóp cụt không bao gồm diện tích hai đáy.
Diện tích hình chóp cụt đều được tính bằng công thức dưới đây: Sxq = n . Smặt bên Trong đó:
• Sxq: diện tích xung quanh.
• n: số lượng mặt bên.
• a, b: chiều dài cạnh của 2 đáy trên và dưới của hình chóp cụt. • h: chiều cao mặt bên.
Công thức tính diện tích xung quanh của hình chóp cụt là tính diện tích từng
mặt bên của hình chóp cụt theo công thức tính diện tích hình thang bình
thường, sau đó tính tổng diện tích của tất cả các hình cấu thành hình chóp cụt.
b) Công thức tính diện tích toàn phần
Diện tích toàn phần của hình chóp cụt được tính bằng tổng diện tích 2 mặt
đáy và diện tích xung quanh của hình chóp cụt đó. Công thức:
Stp = Sxq + Sđáy lớn + Sđáy nhỏ Trong đó:
• Stp: Diện tích toàn phần
• Sxq: Diện tích xung quanh
• Sđáy lớn: Diện tích đáy lớn
• Sđáy nhỏ: Diện tích đáy nhỏ
c) Thể tích hình chóp cụt được tính bằng công thức Công thức: Trong đó:
• V: thể tích hình chóp cụt.
• S, S’ lần lượt là diện tích mặt đáy lớn và đáy nhỏ của hình chóp cụt.
• h: chiều cao (khoảng cách giữa 2 mặt đáy lớn và đáy nhỏ)
2. Công thức toán hình 12 hình nón
Có thể hiểu đơn giản, hình học có không gian ba chiều mà bề mặt phẳng và
bề mặt cong hướng lên phía trên là hình nón. Đầu nhọn của hình nón được
gọi là đỉnh và bề mặt phẳng được gọi là đáy. Ta có thể dễ dàng bắt gặp
những vật dụng có hình nón như chiếc nón lá, mũ sinh nhật,..
a) Diện tích xung quanh hình nón được tính bằng tích của số Pi (π) nhân với
bán kính đáy hình nón (r) rồi nhân với đường sinh hình nón (l). Ta có công thức: Trong đó:
• Sxq: là diện tích xung quanh. • π: là hằng số
• r: là bán kính mặt đáy hình nón
• l: đường sinh của hình nón.
b) Diện tích toàn phần hình nón được tính bằng diện tích xung quanh hình
nón cộng với diện tích mặt đáy của hình nón.
Vì diện tích của mặt đáy là hình tròn nên ta áp dụng công thức tính diện tích hình tròn:
c) Để tính thể tích khối nón, ta áp dụng công thức sau: Trong đó:
• V: Ký hiệu thể tích hình nón • π: = 3,14
• r: Bán kính hình tròn đáy.
• h: là đường cao tính từ đỉnh hình nón xuống tâm đường tròn
d) Tổng hợp một vài công thức mặt nón:
• Đường cao: h = SO (hay còn gọi là trục của hình nón)
• Bán kính đáy: r = OA = OB = OM
• Đường sinh: l = SA = SB = SM • Góc ở đỉnh: ASB
• Thiết diện qua trục SAB cân tại S
• Góc giữa mặt đáy và đường sinh: SAO = SBO = SMO • Chu vi đáy: • Diện tích đáy: Sđáy
3. Bài tập luyện tập liên quan
Bài 1: Các đỉnh, cạnh, mặt của một đa diện phải thỏa mãn những tính chất nào? Lời giải:
Các đỉnh, cạnh, mặt của một đa diện phải thỏa mãn những tính chất:
- Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh, ba mặt;
- Mỗi cạnh là cạnh chung của đúng hai mặt;
- Hai mặt bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có đúng một cạnh chung.
Bài 2: Cho hình chóp tam giác S.ABC có AB = 5a, BC = 6a, CA = 7a. Các
mặt bên SAB, SBC, SCA tạo với đáy một góc 60 độ. Tính thể tích của khối chóp đó. Lời giải:
Từ S dựng SH vuông góc (ABC), H thuộc mặt phẳng (ABC), dựng HE vuông
góc AB, HF vuông góc BC. HI vuông góc AC với E thuộc AB, F thuộc BC, I thuộc AC.
Ta có: AB vuông góc SH (SH vuông góc với mặt phẳng ABC) và AB vuông
góc HE => AB vuông góc mặt phẳng SHE.
(Với r là bán kính đường tròn nội tiếp tam giác ABC)
Chu vi tam giác ABC là: 5a + 6a + 7a = 18a
Suy ra nửa chu vi tam giác ABC là: p = 18a : 2 = 9a
Theo công thức Hê – rông, diện tích tam giác ABC là: HE = HF = HI = r
(Với r là bán kính đường tròn nội tiếp tam giác ABC)
Chu vi tam giác ABC là: 5a + 6a + 7a = 18a
Suy ra nửa chu vi tam giác ABC là: p = 18a : 2 = 9a
Theo công thức Hê – rông, diện tích tam giác ABC là: SH =
Vậy thể tích của S.ABC là:
Bài 3: Cho tứ diện ABCD cạnh AD vuông góc với mặt phẳng (ABC) và
cạnh BD vuông góc với cạnh BC. Khi quay các cạnh của tứ diện đó
xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành? A) 1 B) 2 C) 3 D) 4 Lời giải: Chọn B. 2
Ta có: DA vuông góc với mặt phẳng ABC vuông tại A và góc ABD nhỏ hơn 90
độ. Vậy khi tam giác ABD quãyung quanh AB ta được một hình nón có đỉnh là
B, trục AB, bán kính bằng AD, đường sinh BD. Ta lại có:
+ BC vuông góc với BD (giả thiết)
+ BC vuông góc với DA (vì DA vuông góc với mặt phẳng ABC)
Suy ra BC vuông góc với mặt phẳng ABD => BC vuông góc với AB.
Nghĩa là tam giác ABC quay xung quanh AB ta được hình nón có đỉnh A, trục
là AB và bán kính bằng BC, đường sinh AC. Ta được hai hình nón khi quay tứ diện ABCD quanh AB.
Bài 4: Các đa diện sau đây, đa diện nào không luôn luôn nội tiếp được trong mặt cầu:
A) Hình chóp tam giác (tứ diện)
B) Hình chóp đều ngũ giác C) Hình chóp tứ giác D) Hình hộp chữ nhật Lời giải:
Chọn đáp án C. Hình chóp tứ giác có các đỉnh có thể không ở trên cùng một mặt cầu.
Bài 5: Cho hai điểm cố định A, B và một điểm M di động trong không
gian thỏa mãn điều kiện góc MAB = α với 0 < α < 90 độ. Khi đó điểm M
thuộc mặt nào trong các mặt sau: A) Mặt nón B) Mặt trụ C) Mặt cầu D) Mặt phẳng Lời giải: Chọn đáp án A
Ta có: góc MAB = α (0 < α < 90o)
Vậy M thuộc mặt nón đỉnh là A, trục là đường thẳng AB và góc ở đỉnh bằng 2α
Document Outline

• Công thức giải nhanh Hình học lớp 12 đầy đủ, dễ hi
  • 1. Tổng hợp công thức toán hình 12 khối đa diện
    • 1.1. Công thức toán hình 12 khối đa diện
    • 1.2. Công thức toán hình 12 khối lăng trụ
    • 1.3. Thể tích hình hộp chữ nhật lớp 12
    • 1.4. Công thức toán hình 12 khối chóp cụt
  • 2. Công thức toán hình 12 hình nón
  • 3. Bài tập luyện tập liên quan