Công thức tính diện tích hình tam giác chính xác nhất
1. Khái niệm hình tam giác?
Hình tam giác là một trong những loại hình học rất cơ bản trong hệ thống hình học phẳng. Đây là
một loại đa giác lồi với các góc được tạo thành luôn nhỏ hơn 180o. Đây là loại hình học có ba đỉnh
là ba điểm không thẳng hàng với nhau. Đoạn thẳng nối ba điểm với nhau được gọi là ba cạnh của hình tam giác.
2. Công thức tính diện tích hình tam giác
Đơn vị đo diện tích tam giác được xác định là: cm2; m2; dm2;...
2.1 Công thức tính diện tích tam giác thường
Tam giác thường có đặc điểm như sau:
- Độ dài của ba cạnh trong tam giác khác nhau;
- Số đo của mỗi góc trong tam giác khác nhau.
* Công thức tính diện tích tam giác thường    
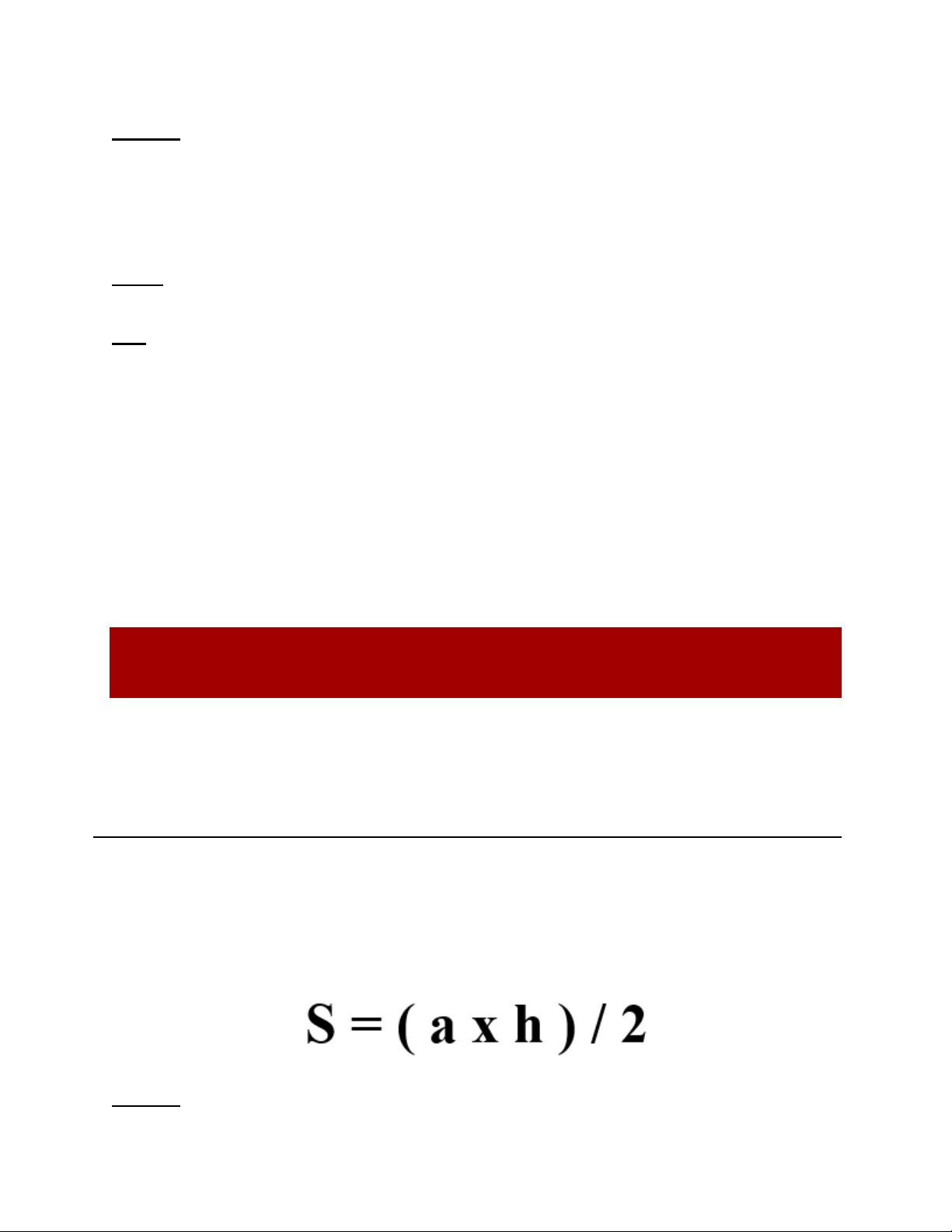
Diện tích của tam giác thường được xác định bằng công thức lấy chiều cao của tam giác nhân với
độ dài cạnh đáy của tam giác, sau đó chia hai (bằng một phần hai tích giữa chiều cao và chiều dài
cạnh đáy). Cụ thể được mô tả bởi công thức sau đây: Quy ước:
- h: được xác định là chiều cao của tam giác (chiều cao của tam giác được xác định là đoạn thẳng
nối giữa đỉnh của tam giác xuống cạnh đáy đối diện với đỉnh của tam giác, chiều cao phải được hạ
vuông góc với đáy của tam giác);
- a = BC: được xác định là cạnh đáy của tam giác
Ví dụ: Cho tam giác ABC (như hình trên), với chiều cao của tam giác là h = 8cm và độ dài đáy
của tam giác là BC = 20cm. Xác định diện hình tam giác ABC? Giải
Diện tích tam giác ABC được xác định là:
SABC = ( a x h ) / 2 = ( BC x h ) / 2 = ( 20 x 8 ) / 2 = 80cm2
2.2 Công thức tính diện tích tam giác cân
Tam giác cân có các đặc điểm như sau:
- Hai cạnh bên của tam giác này có độ dài bằng nhau;
- Hai góc đáy của tam giác cân có số đo góc bằng nhau;
* Công thức tính diện tích tam giác cân    
Cũng giống như diện tích tam giác thường, diện tích tam giác cân cũng được xác định theo công
thức là bằng một phần hai tích của chiều cao tam giác (đoạn thẳng nối từ đỉnh của tam giác xuống
cạnh đáy của tam giác, đoạn thẳng này phải hạ vuông góc với đáy của tam giác), cụ thể được mô tả bởi công thức sau: Quy ước:
- h: được quy ước là chiều cao của hình tam giác;
- a = BC: được quy ước là chiều dài cạnh đáy của hình tam giác.
Ví dụ: Cho tam giác cân ABC (như hình trên) với chiều dài các cạnh như sau: Các cạnh bên AB
= AC = b = 8cm; cạnh đáy BC = a = 14cm và chiều cao hạ từ điểm A xuống cạnh đáy BC là h =
10cm. Xác định tính diện tích hình tam giác ABC? Giải
Diện tích tam giác cân ABC được xác định như sau:
SABC = ( a x h ) / 2 = ( BC x h ) / 2 = ( 14 x 10 ) / 2 = 70cm2
2.3 Công thức tính diện tích tam giác vuông
Tam giác vuông có những đặc điểm như sau:
- Tam giác này có một góc vuông (góc có số đo góc là 90o )
- Trong tam giác vuông thì nguyên tắc xác định các cạnh như sau:
+ Cạnh đối diện với góc vuông (góc 90o) được xác định là cạnh huyền - cạnh này là cạnh có độ
dài lớn nhất trong ba cạnh của tam giác vuông;
+ Hai cạnh còn lại của tam giác được gọi là cạnh góc vuông của tam giác.
- Đối với các dạng bài tập thì định lý Pythagoras là một định lý rất phổ biến được áp dụng để giải
quyết các bài toàn về tam giác vuông trong đấy có các dạng bài về tính diện tích tam giác vuông.
* Công thức tính diện tích tam giác vuông
Vì tam giác vuông có đặc điểm khác biệt so với tam giác thường ở chỗ chiều cao của tam giác
vuông trùng với một cạnh góc vuông trong tam giác, còn cạnh góc vuông còn lại sẽ là cạnh đáy
của tam giác. Do đó công thức tính diện tích tam giác vuông được xác định bằng một phần hai tích
hai cạnh góc vuông của tam giác vuông (1/2 tích chiều cao nhân với chiều dài của cạnh đáy tam
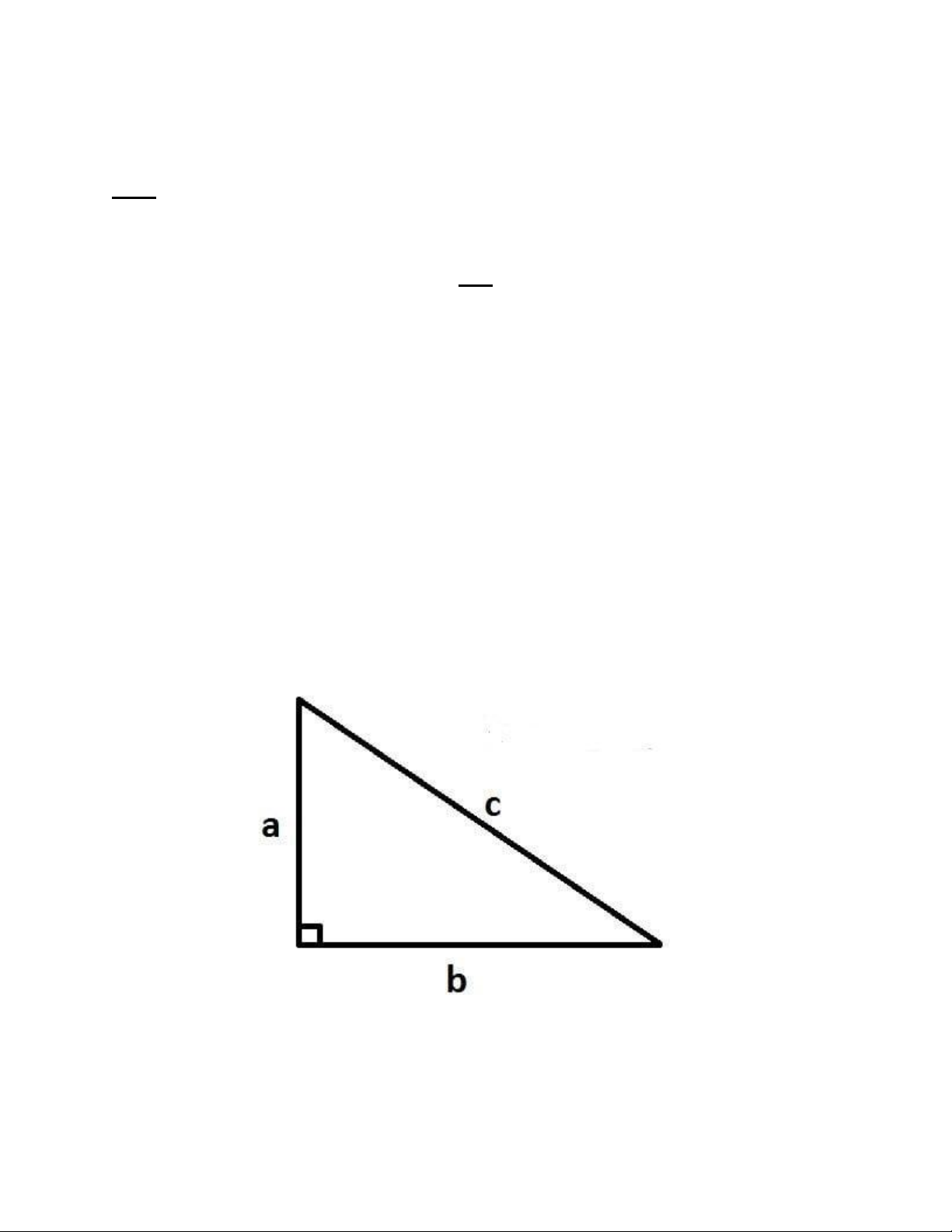
giác), cụ thể công thức tính diện tích tam giác vuông được mô tả như sau: Quy ước:
- a: được xác định là chiều cao của tam giác vuông (trường với chiều dài của một cạnh góc vuông)
- b: được xác định là một cạch của góc vuông.
Ví dụ: Cho tam giác vuông (như hình trên) với độ chiều dài các cạnh của góc vuông được xác định
như sau: a = 5cm và b = 15cm. Hãy xác định diện tích của tam giác vuông nêu trên? Giải
Diện tích tam giác vuông được xác định là:
S = ( a x b ) / 2 = ( 5 x 15 ) /2 = 37,5cm2
2.4 Công thức tính diện tích tam giác đều
Tam giác đều cũng có đặc điểm giống như tất cả các loại tam giác khác. Tuy nhiên ngoài những
điểm chung thì tam giác đều cũng có những đặc điểm khác biệt như sau:
- Ba cạnh của tam giác thường có kích thước bằng nhau;
- Ba góc của tam giác thường có số đo góc bằng nhau và đều có số đo là 60o
* Công thức tính diện tích tam giác đều
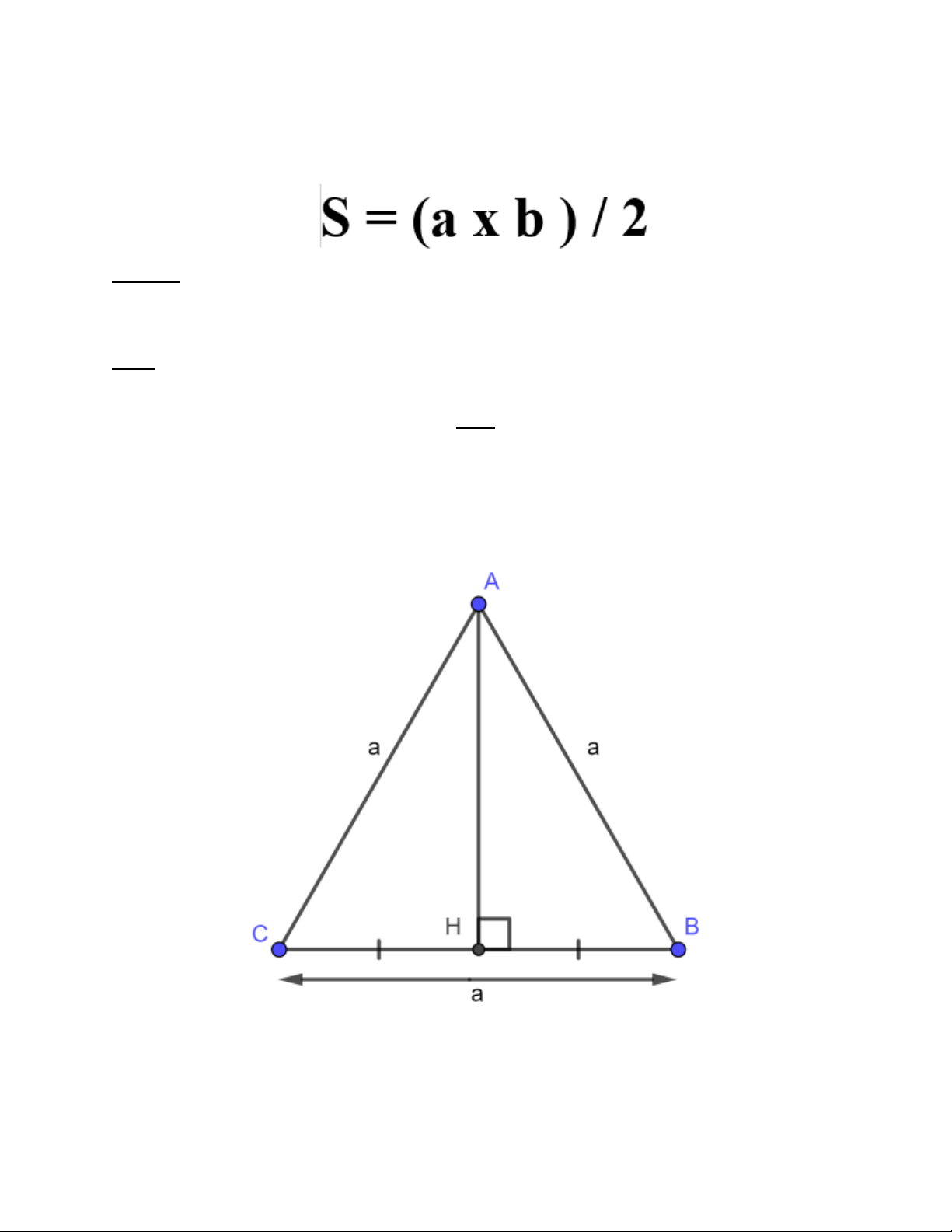
Cũng giống như tam giác thường diện tích tam giác đều cũng được xác định dựa trên công thức
bằng một phần hai tích giữa chiều cao của tam giác nhân với chiều dài của cạnh đáy tam giác, được mô tả như sau: Quy ước:
- S: được xác định là diện tích hình tam giác;
- a: được xác định là kích thước cạnh đáy của hình tam giác;
- h: được xác định là chiều cao của hình tam giác.
Ví dụ: Cho tam giác đều ABC (như hình ở trên), chiều dài các cạnh của tam giác là: AB = BC =
AC = a = 12cm; chiều cao của tam giác là AH = h = 8cm. Hãy xác định diện tích của tam giác ABC? Giải
Diện tích của tam giác ABC được xác định như sau:
SABC = ( AH x BC ) / 2 = ( a x h ) / 2 = ( 12 x 8 ) / 2 = 48cm2
Trên đây là những công thức cơ bản nhất để tính diện tích hình tam giác, dựa vào dạng bài tập cơ
bản này thì căn cứ theo khung chương trình học thì có thể biến dạng thành nhiều dạng bài toán
trong khung chương trình học của mỗi học sinh.