Công thức tính khoảng cách giữa đường thẳng và mặt phẳng song song mới nhất

Công thức tính khoảng cách giữa đường thẳng
và mặt phẳng song song mới nhất 1. Đường thẳng là gì?
Đường thẳng được hiểu là một đường dài vô hạn, mỏng vô cùng, thẳng tuyệt
đối và không bị giới hạn về hai phía.
Theo đó thì trong hình học, đường thẳng được hiểu là một đường dài vô hạn,
thẳng tuyệt đối và không có bất kỳ chiều rộng nào. Điều này có nghĩa là một
đường thẳng không có điểm cuối và không bị giới hạn về hai phía. Bạn có thể
di chuyển dọc theo một đường thẳng trong cả hai hướng vô hạn mà không
bao giờ đạt được điểm cuối của nó. Mô tả này của đường thẳng thường
được sử dụng trong hình học và toán học để định nghĩa và nghiên cứu tính chất của chúng. 2. Mặt phẳng là gì?
Mặt phẳng là một đối tượng của toán học. Mặt phẳng không có bề dày và
không có giới hạn. Để biểu diễn tả mặt phẳng ta thường dùng hình bình hành
hay một miền góc và ghi tên của mặt phẳng vào một góc của hình biểu diễn.
Để kí hiệu mặt phẳng, ta thường dùng các chữ cái in hoa hoặc chữ cái Hi Lạp
đặt trong dấu ngoặc "( )".
Ví dụ: mặt phẳng (P) hoặc viết tắt mp(P)...
3. Công thức tính khoảng cách giữa đường thẳng và mặt phẳng song song
Trong không gian đường thẳng và mặt phẳng có 3 vị trí tương đối: Cắt nhau;
Đường thẳng nằm trên mặt phẳng; Đường thẳng song song với mặt phẳng.
bình thường một bài toán dạng này sẽ không hỏi về 2 trường hợp đường
thẳng cắt hoặc nằm trên mặt phẳng. Trong các trường hợp này chúng ta có
thể coi khoảng cách giữa đường thẳng và mặt phẳng là bằng 0. Trong trường
hợp đường thẳng d và mặt phẳng (P) song song với nhau. Khoảng cách giữa
d và (P) là khoảng cách từ 1 điểm bất cứ trên d tới mặt phẳng (P). Ký hiệu là d(d,(P)).
Trong không gian Oxyz, cho đường thẳng d và mặt phẳng (P) song song với
nhau. Đường thẳng d có chứa điểm M(α;β;γ). Mặt phẳng (P) có phương trình:
ax+by+cz+d=0. Khi đó khoảng cách giữa d và (P) được tính theo công thức:
Theo đó thì khoảng cách giữa đường thẳng và mặt phẳng đồng thời được
tính hoàn toàn theo công thức khoảng cách giữa điểm và mặt phẳng.
4. Cách giải khoảng cách giữa đường thẳng và mặt phẳng song song
Cho đường thẳng d // (P); để tính khoảng cách giữa d và (P) ta thực hiện các bước:
+ Bước 1: Chọn một điểm A trên d, sao cho khoảng cách từ A đến (P) có thể
được xác định dễ nhất.
+ Bước 2: Kết luận: d(d; (P)) = d(A; (P)).
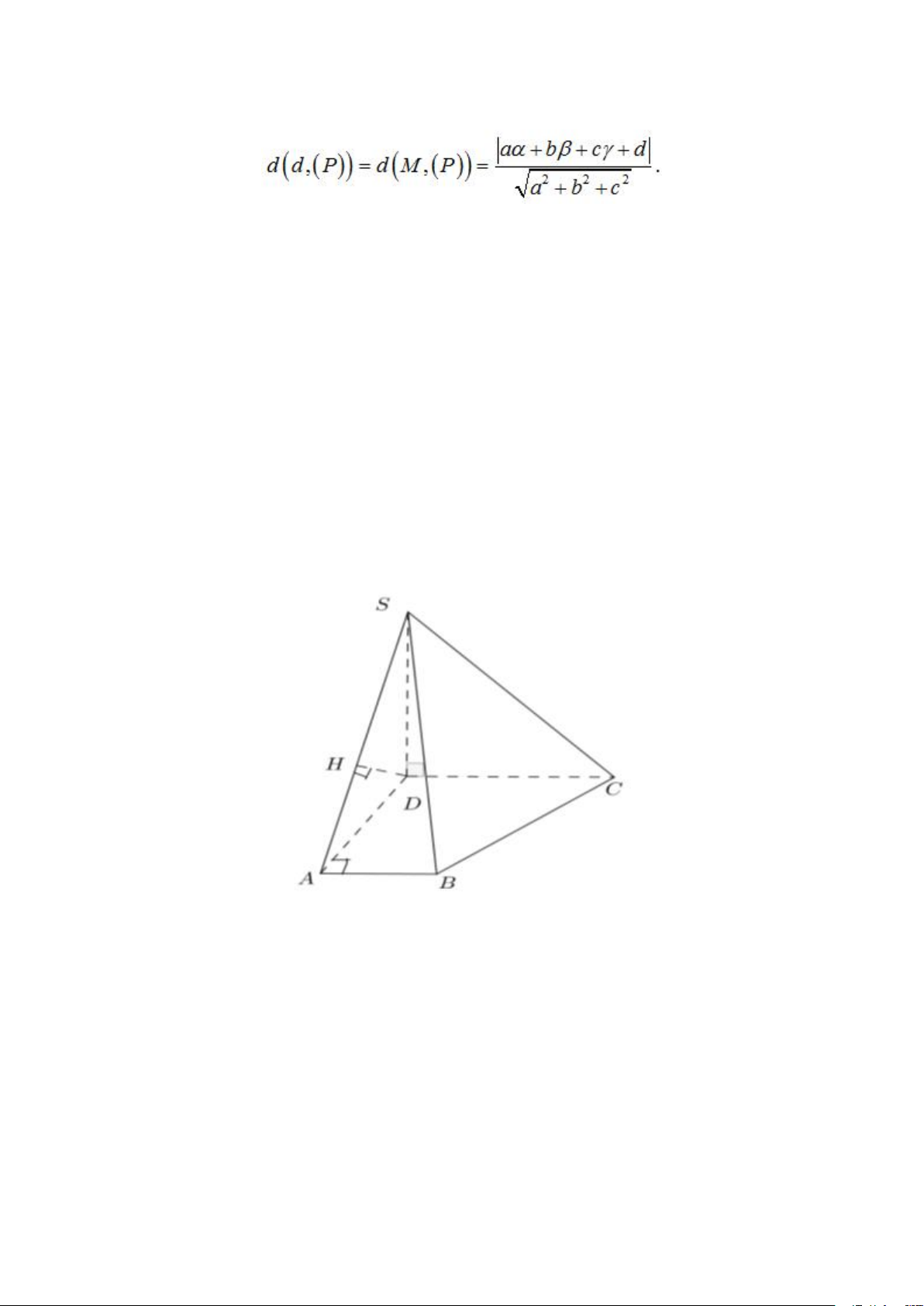
Ví dụ: Cho hình thang vuông ABCD vuông ở A và D; AD = 2a. Trên đường
thẳng vuông góc tại D với (ABCD) lấy điểm S với SD = a√2. Tính khỏang
cách giữa đường thẳng CD và (SAB). Vì DC // AB nên DC // (SAB) ⇒ d(DC; (SAB)) = d(D; (SAB)) Kẻ DH ⊥ SA
Do AB ⊥ AD và AB ⊥ SA nên AB ⊥ (SAD)
⇒ DH ⊥ AB lại có DH ⊥ SA ⇒ DH ⊥ (SAB) Nên d(CD; (SAB)) = DH.
Trong tam giác vuông SAD ta có:
5. Một số bài tập về tính khoảng cách giữa đường thẳng và mặt phẳng song song
Bài 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a.
Biết hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy và SA =
a√2. Gọi E là trung điểm AD. Khoảng cách giữa AB và (SOE) là:
+ Vì hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy . mà
(SAB) ∩ (SAD) = SA ⇒ SA ⊥ (ABCD) .
+ Do E là trung điểm của AD khi đó
Tam giác ABD có EO là đường trung bình ⇒ EO // AB ⇒ AB // (SOE)
⇒ d(AB, (SOE)) = d(A; (SOE)) = AH
với H là hình chiếu của A lên SE.
Bài 2: Cho hình chóp S.ABCD có SA ⊥ (ABCD) đáy ABCD là hình chữ nhật
với AC = a√5 và BC = a√2. Tính khoảng cách giữa (SDA) và BC?
+ Ta có: BC // AD nên BC // (SAD) ⇒ d(BC; (SAD)) = d(B; SAD))
+ Ta chứng minh BA ⊥ (SAD) :
Do BA ⊥ AD (vì ABCD là hình chữ nhật)
Và BA ⊥ SA (vì SA ⊥ (ABCD)) ⇒ BA ⊥ (SAD) ⇒ d(B; (SAD)) = BA
Áp dụng định lí Pytago trong tam giác vuông ABC có:
AB2 = AC2 - BC2 = 5a2 - 2a2 = 3a2 ⇒ AB = √3 a ⇒ d(CB; (SAD)) = AB = √3 a
Bài 3: Cho hình chóp tứ giác đều S.ABCD có đường cao SO = 2, mặt bên
hợp với mặt đáy một góc 60°. Khi đó khoảng cách giữa hai đường thẳng AB và (SCD) bằng
Ta gọi I là trung điểm của CD ta có
⇒ ((SCD), (ABCD)) = (OI, SI) = 60°
+ Ta có: AB // CD nên AB // (SCD)
⇒ d(AB, (SCD)) = d(A, ( SCD)) = 2.d(O, (SCD))
+ Trong mp (SOI) , gọi H là hình chiếu vuông góc của O lên SI
Tam giác SOI vuông tại O có đường cao OH nên
Do đó thì d(AB; (SCD))= 2d( O;(SCD))= 2.OH= 2.1= 2 => Đáp án : 2
6. Làm quen với các bài tập về tính khoảng cách từ đường
thẳng đến mặt phẳng song song như thế nào?
Để làm quen với các bài toán về tính khoảng cách từ đường thẳng đến mặt
phẳng song song, bạn có thể thực hiện các bước sau:
Hiểu rõ cơ bản về đường thẳng và mặt phẳng: Trước hết, hãy đảm bảo bạn
hiểu rõ về phương trình đường thẳng và phương trình mặt phẳng. Hiểu cách
chúng được biểu diễn và làm việc với chúng là quan trọng.
cách tìm điểm giao điểm ảo: Một kỹ năng quan trọng trong các bài toán này là
tìm điểm giao điểm giữa đường thẳng và mặt phẳng. Hãy nắm vững cách làm
điều này bằng cách giải hệ phương trình.
Hiểu rõ công thức khoảng cách: Nắm vững công thức tính khoảng cách từ
một điểm đến một mặt phẳng, như đã được trình bày trong trả lời trước đó.
Luyện tập nhiều bài tập: Hãy tìm và làm nhiều bài toán liên quan đến tính
khoảng cách từ đường thẳng đến mặt phẳng. Các sách giáo trình, tài liệu học
tập, hoặc trang web chuyên về toán học có thể cung cấp nhiều ví dụ và bài tập thực hành.
Tự thực hành và tìm hiểu: Thực hành và tự thực hiện các bài toán là cách tốt
nhất để nắm vững kiến thức và kỹ năng. Hãy thử tự tạo ra các bài toán hoặc
sử dụng phần mềm đồ họa để thấy cách đường thẳng và mặt phẳng tương tác trong không gian.
+ Sử dụng phần mềm đồ họa: Có nhiều phần mềm đồ họa như GeoGebra,
Desmos, hoặc các phần mềm hình học khác có sẵn trực tuyến. Bạn có thể sử
dụng chúng để tạo ra các đường thẳng và mặt phẳng, sau đó tính toán
khoảng cách từ các điểm đến mặt phẳng.
+ Tạo bài toán của riêng bạn: Thử tạo ra các bài toán mới liên quan đến tính
khoảng cách từ đường thẳng đến mặt phẳng. Bạn có thể tạo các tình huống
khác nhau và thử giải quyết chúng. Điều này sẽ giúp bạn hiểu rõ hơn cách áp
dụng kiến thức vào các tình huống thực tế.
+ Tìm hiểu thêm thông qua tài liệu và bài giảng: Ngoài sách giáo trình, có
nhiều tài liệu mở và bài giảng trực tuyến về hình học không gian. Tìm hiểu và
nghiên cứu thêm về chủ đề này để có cái nhìn sâu rộng hơn.
+ Xem ví dụ và hướng dẫn trực tuyến: Có nhiều tài liệu hướng dẫn và ví dụ
trực tuyến liên quan đến tính khoảng cách từ đường thẳng đến mặt phẳng.
Xem các video hướng dẫn và giải quyết các ví dụ để thấy cách các vấn đề
được giải quyết trong thực tế.
Hỏi và thảo luận với người khác: Nếu bạn gặp khó khăn trong việc giải quyết
bài toán, đừng ngần ngại hỏi giáo viên, bạn bè hoặc tham gia các diễn đàn
trực tuyến về toán học để hỏi và thảo luận về các vấn đề liên quan đến
khoảng cách, đường thẳng và mặt phẳng.
Xem các tài liệu tham khảo: Tìm các sách giáo trình, bài giảng trực tuyến
hoặc video hướng dẫn về hình học không gian và các bài toán liên quan đến khoảng cách.
Tạo mô hình thực tế: Cố gắng áp dụng kiến thức vào các vấn đề thực tế, ví
dụ như tính khoảng cách của máy bay đối với mặt đất, tính khoảng cách của
đường ray đối với mặt đường, và các ví dụ khác để thấy rõ ứng dụng của kiến thức.
Từ việc thực hiện các bước này và không ngừng luyện tập, bạn sẽ cảm thấy
tự tin hơn khi giải quyết các bài toán liên quan đến tính khoảng cách từ
đường thẳng đến mặt phẳng song song.
Document Outline

• Công thức tính khoảng cách giữa đường thẳng và mặt
  • 1. Đường thẳng là gì?
  • 2. Mặt phẳng là gì?
  • 3. Công thức tính khoảng cách giữa đường thẳng và
  • 4. Cách giải khoảng cách giữa đường thẳng và mặt p
  • 5. Một số bài tập về tính khoảng cách giữa đường t
  • 6. Làm quen với các bài tập về tính khoảng cách từ