




Preview text:
1 = + +
CÔNG THỨC TÍNH NHANH VẬT LÝ 10
4. Phương trình chuyển động : 2 x x v t at HỌC KỲ I 0 0 2
I. Chuyển động thẳng đều:
1. Vận tốc trung bình Dấu của x0 Dấu của v0 ; a s
x0 > 0 Nếu tại thời điểm ban đầu v0; a > 0 Nếu v;a cùng
a. Trường hợp tổng quát: v = tb
chất điểm ở vị thí thuộc phần 0x t chiều 0x x v t + v t + ... + v t
0 < 0 Nếu tại thời điểm ban đầu v ; a < 0 Nếu
b. Công thức khác: 1 1 2 2 n n v; a v =
chất điểm ở vị thí thuộc phần 0x, tb t + t + ... + t ngược chiều 0x 1 2 n x
0 = 0 Nếu tại thời điểm ban đầu
c. Một số bài toán thường gặp:
chất điểm ở gốc toạ độ.
Bài toán 1: Vật chuyển động trên một đoạn đường thẳng từ địa
Chú ý: Chuyển động thẳng nhanh dần đều a.v > 0.; Chuyển
điểm A đến địa điểm B phải mất khoảng thời gian t. vận tốc của
động thẳng chậm dần đều a.v < 0
vật trong nửa đầu của khoảng thời gian này là v1 trong nửa cuối
5. Bài toán gặp nhau của chuyển động thẳng biến đổi
là v2. vận tốc trung bình cả đoạn đường AB: đều: v + v 1 2 v =
- Lập phương trình toạ độ của mỗi chuyển động : tb 2 2 a t 2 a t
Bài toán 2:Một vật chuyển động thẳng đều, đi một nửa quãng 1 x = x + v t + ; 1 x = x + v t + 1 02 02 2 02 02
đường đầu với vận tốc v 2 2
1, nửa quãng đường còn lại với vận tốc v
- Khi hai chuyển động gặp nhau: x
2 Vận tốc trung bình trên cả quãng đường: 1 = x2 Giải phương trình 2v v
này để đưa ra các ẩn của bài toán. 1 2 v =
Khoảng cách giữa hai chất điểm tại thời điểm t v + v 1 2 d = x − x
2. Phương trình chuyển động của chuyển động thẳng 1 2 đều: x = x
6. Một số bài toán thường gặp: 0 + v.t
Bài toán 1: Một vật chuyển động thẳng nhanh dần đều đi được Dấu của x0 Dấu của v
những đoạn đường s1và s2 trong hai khoảng thời gian liên tiếp
x0 > 0 Nếu tại thời điểm ban đầu v > 0 Nếu v cùng
bằng nhau là t. Xác định vận tốc đầu và gia tốc của vật.
chất điểm ở vị thí thuộc phần 0x chiều 0x Giải hệ phương trình
x0 < 0 Nếu tại thời điểm ban đầu 2 v < 0 Nếu v ngược at
chất điểm ở vị thí thuộc phần 0x, s = v t + v 1 0 0 chiều 0x 2
x0 = 0 Nếu tại thời điểm ban đầu a 2 s + s = 2v t + 2at
chất điểm ở gốc toạ độ. 1 2 0
3. Bài toán chuyển động của hai chất điểm trên cùng
Bài toán 2: Một vật bắt đầu chuyển động thẳng nhanh dần đều. một phương:
Sau khi đi được quãng đường s1 thì vật đạt vận tốc v1. Tính vận
Xác định phương trình chuyển động của chất điểm 1:
tốc của vật khi đi được quãng đường s2 kể từ khi vật bắt đầu x chuyển động. 1 = x01 + v1.t (1)
Xác định phương trình chuyển động của chất điểm 2: s2 v = v x 2 1 2 = x02 + v2.t (2) s1
Lúc hai chất điểm gặp nhau x1 = x2 t thế t vào (1) hoặc
Bài toán 3:Một vật bắt đầu chuyển động nhanh dần đều không
(2) xác định được vị trí gặp nhau vận tốc đầu:
Khoảng cách giữa hai chất điểm tại thời điểm t
- Cho gia tốc a thì quãng đường vật đi được trong giây thứ n: d = x − x + v − v t 01 02 ( 01 02) a = −
II. Chuyển động thẳng biến đổi đều s na 2
1. Vận tốc: v = v0 + at
- Cho quãng đường vật đi được trong giây thứ n thì gia tốc 2 at xác định bởi:
2. Quãng đường : s = v t + 0 2 s a =
3. Hệ thức liên hệ : 1 n − 2 2 v − v = 2as 2 0 2 2 2 2
Bài toán 4: Một vật đang chuyển động với vận tốc v v − v v − v 0 thì 2 0 0 v = v + 2as;a = ;s =
chuyển động chầm dần đều: 0 2s 2a
- Nếu cho gia tốc a thì quãng đường vật đi được cho đến khi g s = 2gh − 2 − dừng hẳn: v 2 0 s = 2a
Bài toán 2: Cho quãng đường vật rơi trong giây cuối cùng: s
- Cho quãng đường vật đi được cho đến khi dừng hẳn s , thì
-Tthời gian rơi xác định bởi: s 1 t = + 2 − g 2 gia tốc: v0 a = 2s = + −
- Vận tốc lúc chạm đất: g v s v 2
- Cho a. thì thời gian chuyển động:t = 0 a 2 g s 1 = +
- Nếu cho gia tốc a, quãng đường vật đi được trong giây cuối
- Độ cao từ đó vật rơi: h . 2 g 2 cùng: a s = v + at −
Bài toán 3: Một vật rơi tự do: 0 2
- Vận tốc trung bình của chất điểm từ thời điểm t1 đến thời
- Nếu cho quãng đường vật đi được trong giây cuối cùng là điểm t 2: s , thì gia tốc : s a = (t + t g 1 2 ) 1 v = t − TB 2 2
Bài toán 5: Một vật chuyển động thẳng biến đổi đều với gia tốc
- Quãng đường vật rơi được từ thời điểm t1 đến thời điểm t2: 2 2 a, vận tốc ban đầu v (t −t g 2 1 ) 0: s =
- Vận tốc trung bình của vật từ thời điểm t1 đến thời điểm t2: 2 (t + t a
IV. Chuyển động ném đứng từ dưới lên từ mặt đất với vận 1 2 ) v = v + TB 0 tốc ban đầu v 2
0: Chọn chiểu dương thẳng đứng hướng lên, gốc thời gian lúc ném vật.
- Quãng đường vật đi được từ thời điểm t 1 đến thời điểm t2: ( 2 2
1. Vận tốc: v = v0 - gt t − t a 2 1 ) s = v t − t + 2 gt 0 ( 2 1 ) 2
2. Quãng đường: s = v t − 0
Bài toán 6: Hai xe chuyển động thẳng đều trên cùng 1 đường 2
thẳng với các vận tốc không đổi. Nếu đi ngược chiều nhau, sau
3. Hệ thức liên hệ: 2 2 v − v = 2 − gs 0
thời gian t khoảng cách giữa 2 xe giảm một lượng a. Nếu đi 2 gt = −
cùng chiều nhau, sau thời gian t khoảng cách giữa 2 xe giảm
4. Phương trình chuyển động : y v t 0 2
một lượng b. Tìm vận tốc mỗi xe:
5. Một số bài toán thường gặp: Giải hệ phương trình:
Bài toán 1: Một vật được ném thẳng đứng lên cao từ mặt đất v + v = a.t a − b t a + b t với vận tốc đầu v 1 2 ( ) ( ) 0 : v = ; v = 1 2 2 v − v = b.t 2 2 v 2 1
- Độ cao cực đại mà vật lên tới: 0 h =
III. Sự rơi tự do:Chọn gốc tọa độ tại vị trí rơi, chiều dương max 2g
hướng xuông, gốc thời gian lúc vật bắt đầu rơi. 2v
- Thời gian chuyển động của vật : 0 t =
1. Vận tốc rơi tại thời điểm t v = gt. g
2. Quãng đường đi được của vật sau thời gian t :
Bài toán 2: Một vật được ném thẳng đứng lên cao từ mặt đất . s = 1 2 gt
Độ cao cực đại mà vật lên tới là h max 2 - Vận tốc ném : v = 2gh 0 max
3. Công thức liên hệ: v2 = 2gs 2 = − gt
- Vận tốc của vật tại độ cao h1 : 2 v v 2gh 0 1
4. Phương trình chuyển động: y = 2
V. Chuyển động ném đứng từ dưới lên từ độ cao h0 với
4. Một số bài toán thường gặp:
vận tốc ban đầu v0 :
Bài toán 1: Một vật rơi tự do từ độ cao h:
Chọn gốc tọa độ tại mặt đất chiểu dương thẳng đứng hướng
lên, gốc thời gian lúc ném vật.
- Thời gian rơi xác định bởi: 2h t =
1. Vận tốc: v = v0 - gt g 2 gt
- Vận tốc lúc chạm đất xác định bởi: v = 2gh
2. Quãng đường: s = v t − 0 2
- Quãng đường vật rơi trong giây cuối cùng:
3. Hệ thức liên hệ: 2 2 v − v = 2 − gs 0 2 gt H − h
4. Phương trình chuyển động : y = h + v t − v = 2gh 0 0 0 2 2h
5. Một số bài toán thường gặp:
VI. Chuyển động ném ngang: Chọn gốc tọa độ tại vị trí ném,
Bài toán 1: Một vật ở độ cao h
Ox theo phương ngang, Oy thẳng đứng hướng xuống.
0 được ném thẳng đứng lên cao với vận tốc đầu v0
1. Các phương trình chuyển động: : 2 v - Theo phương Ox: x = v0t
- Độ cao cực đại mà vật lên tới: 0 h = h + max 0 1 2g - Theo phương Oy: y = 2 gt 2
- Độ lớn vận tốc lúc chạm đất 2 v = v + 2gh 0 0 g
2. Phương trình quỹ đạo: 2 y = x
- Thời gian chuyển động : 2 2v0 2 v + 2gh 0 0 t =
3. Vận tốc: v = v + (gt)2 2 0 g
Bài toán 2: Một vật ở độ cao h 2h
0 được ném thẳng đứng lên cao .
4.Tầm bay xa: L = v0
Độ cao cực đại mà vật lên tới là hmax : g - Vận tốc ném : v = 2g h − h = + 0 ( max 0 )
5. Vận tốc lúc chạm đất: 2 v v 2gh 0
- Vận tốc của vật tại độ cao h 2
IV. Chuyển động của vật ném xiên từ mặt đất: Chọn gốc 1 : v = v + 2g h − h 0 ( 0 1)
tọa độ tại vị trí ném, Ox theo phương ngang, Oy thẳng đứng
- Nếu bài toán chưa cho h0 , cho v0 và hmax thì : hướng lên 2 v0 h = h −
1. Các phương trình chuyển động: 0 max 2g 2 gt
VI. Chuyển động ném đứng từ trên xuống x = v cos . t; y = v sin . t − : Chọn gốc tọa 0 0 2
độ tại vị trí ném ; chiểu dương thẳng đứng hướng vuống, gốc g
thời gian lúc ném vật.
2. Quỹ đạo chuyển động 2 y = tan . x − .x 2 2 2v cos 1. Vận tốc: v = v 0 0 + gt 2 2 2 gt
2. Vận tốc:v = (v cos + v sin − gt 0 ) ( 0 )
2. Quãng đường: s = v t + 0 2 2 2 v sin 0 =
3. Hệ thức liên hệ: 2 2 v − v = 2gs . 3. Tầm bay cao: H 0 2g 2 gt 2
4. Phương trình chuyển động: y = v t + v sin 2 0 0 4. Tầm bay xa: L = 2 g
5. Một số bài toán thường gặp:
VII. Chuyển động tròn đều:
Bài toán 1: Một vật ở độ cao h được ném thẳng đứng hướng
1. Vectơ vận tốc trong chuyển động tròn đều.
xuống với vận tốc đầu v0:
- Điểm đặt: Trên vật tại điểm đang xét trên quỹ đạo.
- Vận tốc lúc chạm đất: 2 v = v + 2gh
- Phương: Trùng với tiếp tuyến và có chiều của chuyển max 0 động. 2 v + 2gh − v
- Thời gian chuyển động của vật 0 0 t = = g - Độ lớn : s v = hằng số. t
- Vận tốc của vật tại độ cao h 2 1: v = v + 2g h − h 0 ( 1 ) 2. Chu kỳ: 2 r T =
Bài toán 2: Một vật ở độ cao h được ném thẳng đứng hướng v
xuống với vận tốc đầu v0 (chưa biết). Biết vận tốc lúc chạm đất 3. Tần số f: 1 f = là vmax: T - Vận tốc ném: 2 v = v − 2gh 0 max 2 2 v − v
4. Tốc độ góc: = - Nếu cho v max 0
0 và vmax chưa cho h thì độ cao: h = t 2g s
Bài toán 3: Một vật rơi tự do từ độ cao h. Cùng lúc đó một vật
5. Tốc độ dài: v = = r = r t t
khác được ném thẳng đứng xuống từ độ cao H (H> h) với vận
6. Liên hệ giữa tốc độ góc với chu kì T hay với tần số f
tốc ban đầu v0. Hai vật tới đất cùng lúc: 2 r 2 v = r = ; = = 2 f c. Khi 1
v ,2 vuông góc với v2,3 : T T 2 2 v = v + v 1,3 1,2 2,3
7. Gia tốc hướng tâm aht
- Điểm đặt: Trên chất điểm tại điểm đang xét trên quỹ đạo 1 v ,3 hớp với 1
v ,2 một góc xác định bởi
- Phương: Đường thẳng nối chất điểm với tâm quỹ đạo. v2,3 tan = - Chiều: Hướng vào tâm v1,2 2 v
3. Một số bài toán thường gặp: - Độ lớn: 2 a = = r ht r
Bài toán 1:Một chiếc ca nô chạy thẳng đều xuôi dòng chảy từ
Chú ý: Khi vật có hình tròn lăn không trượt, độ dài cung
A đến B hết thời gian là t1, và khi chạy ngược lại từ B về A phải
quay của 1 điểm trên vành bằng quãng đường đi mất thời gian t2 .
8. Một số bài toán thường gặp:
Thời gian để ca nô trôi từ A đến B nếu ca nô tắt máy:
Bài toán 1: Một đĩa tròn quay đều quanh một trục đi qua tâm s 2t t 1 2 t = =
đĩa bán kính của đĩa là R. So sánh tốc độ góc ; tốc độ dài v và v t − t 23 2 1
gia tốc hướng tâm aht của một điểm A và của một điểm B nằm
Bài toán 2:Một chiếc ca nô chạy thẳng đều xuôi dòng chảy từ
trên đĩa; điểm A nằm ở mép đĩa, điểm B nằm trên đĩa cách tâm
A đến B hết thời gian là t1, và khi chạy ngược lại từ B về A phải một đoạn R R =
mất t2 giờ. Cho rằng vận tốc của ca nô đối với nước v12 tìm v23; 1 n AB
- Tốc độ góc của điểm A và điểm B bằng nhau = s A B Khi xuôi dòng: v = v + v = = s (1)
- Tỉ số Tốc độ dài của điểm A và điểm B: 13 12 23 t 2 1 v R R A = = = n s Khi ngược dòng: , v = v − v = (2) v R R 13 12 23 B 1 t2 n
Giải hệ (1); (2) suy ra: v23; s
- Tỉ số gia tốc hướng tâm của điểm A và điểm B:
IX. Tổng hợp và phân tích lực. Điều kiện cân bằng của chất 2 a R .v 1 A B A 2 = = điểm .n = n 2 a R .v n = + B A B
1. Tổng hợp lực F F F 1 2
Bài toán 2: Kim phút của một đồng hồ dài gấp n lần kim giờ.
▪ Phương pháp chiếu:
- Tỉ số tốc độ dài của đầu kim phút và kim giờ: Chiếu lên Ox, Oy : v R T p p g = = F = F + F 12n x 1x 2x 2 2 F = F + F v R T x y = + g g p F F F y 1y 2 y
- Tỉ số tốc độ góc của đầu kim phút và kim giờ:
F hợp với trục Ox 1 góc α xác định bởi: T p g = = 12 F + F 1y 2 y T tan = g p F + F 1y 2 y
- Tỉ số gia tốc hướng tâm của đầu kim phút và kim giờ:
▪ Phương pháp hình học: 2 a R p p g = = a. 144n
F cùng hướng với F : 1 2 a R g g p
F cùng hướng với F ; F = F 1 1 + F2
VIII. Tính tương đối của chuyển động:
b. F ngược hướng với F :
1. Công thức vận tốc 1 2 = +
F cùng hướng với vectơ lực có độ lớn lớn hơn 1 v ,3 1 v ,2 v2,3
2. Một số trường hợp đặc biệt: F = F − F 1 2 a. Khi 1
v ,2 cùng hướng với v2,3 :
c. F vuông góc với F : 1 2 1 v ,3 cùng hướng với 1 v ,2 và v2,3 2 2 F = F + F 1 2 v = v + v 1,3 1,2 2,3 F
F hợp với F một góc xác định bởi 2 tan = b. Khi 1 1
v ,2 ngược hướng với v2,3 : F1 1
v ,3 cùng hướng với vec tơ có độ lớn lơn hơn
d. Khi F hợp với F một góc bất kỳ: 1 2 v = v − v 1,3 1,2 2,3 2 2 F = F + F + 2F F cos 1 2 1 2
3. Điều kiện cân băng của chất điểm: 1 1 1 = −
a. Điều kiện cân bằng tổng quát: a a a 1 2 + + + = 1 F F2 ... Fn 0
Bài toán 5: Dưới tác dụng của lực F nằm ngang, xe lăn có khối
b. Khi có 2 lực: Muốn cho chất điểm chịu tác dụng của hai
lượng m chuyển động không vận tốc đầu, đi được quãng
lực ở trạng thái cân bằng thì hai lực phải cùng giá, cùng độ lớn
đường s trong thời gian t. Nếu đặt thêm vật có khối lượng Δm và ngược chiều
lên xe thì xe chỉ đi được quãng đường s, trong thời gian t Bỏ qua + = 1 F F2 0 ma sát.
c. Khi có 3 lực: Muốn cho chất điểm chịu tác dụng của ba m + m s =
lực ở trạng thái cân bằng thì hợp lực của hai lực bất kỳ cân bằng Ta có mối liên hệ: , m s với lực thứ ba
Bài số 6: Có hai quả cầu trên mặt phẳng nằm ngang. Quả cầu 1 + + = 1 F F2 3 F 0
chuyển động với vận tốc v0 đến va chạm với quả cầu 2 đang
X. Các định luật Niu tơn
nằm yên. Sau va chạm hai quả cầu cùng chuyển động theo
1. Định luật 1 Newton Nếu không chịu tác dụng cuả một
hướng cũ của quả cầu 1 với vận tốc v.
lực nào hoặc chịu tác dụng của các lực có hợp lực bằng 0 thì vật m v =
giữ nguyên trạng thái đứng yên hay chuyển động thẳng đều. Ta có mối liên hệ: 1 m v − v 2 0 F Bài số 7:
2. Định luật II Newton a = Hoặc là: F = m.a
Quả bóng A chuyển động với vận tốc v1 đến đập vào m
quả bóng B đang đứng yên (v2 = 0). Sau va chạm bóng A dội
Trong trường hợp vật chịu tác dụng của nhiều lực thì gia tốc
ngược trở lại với vận tốc ,
v , còn bóng B chạy tới với vận tốc 1
của vật được xác định bời ,
v . Ta có hệ thức liên hệ: 2 F + F + .... + = n F m.a 1 2 , m v
3. Định luật III Newton 1 2 = , m v + v
Khi vật A tác dụng lên vật B một lực, thì vật B cũng tác dụng 2 1 1
trở lại vật A một lực .Hai lực này là hai lực trực đối
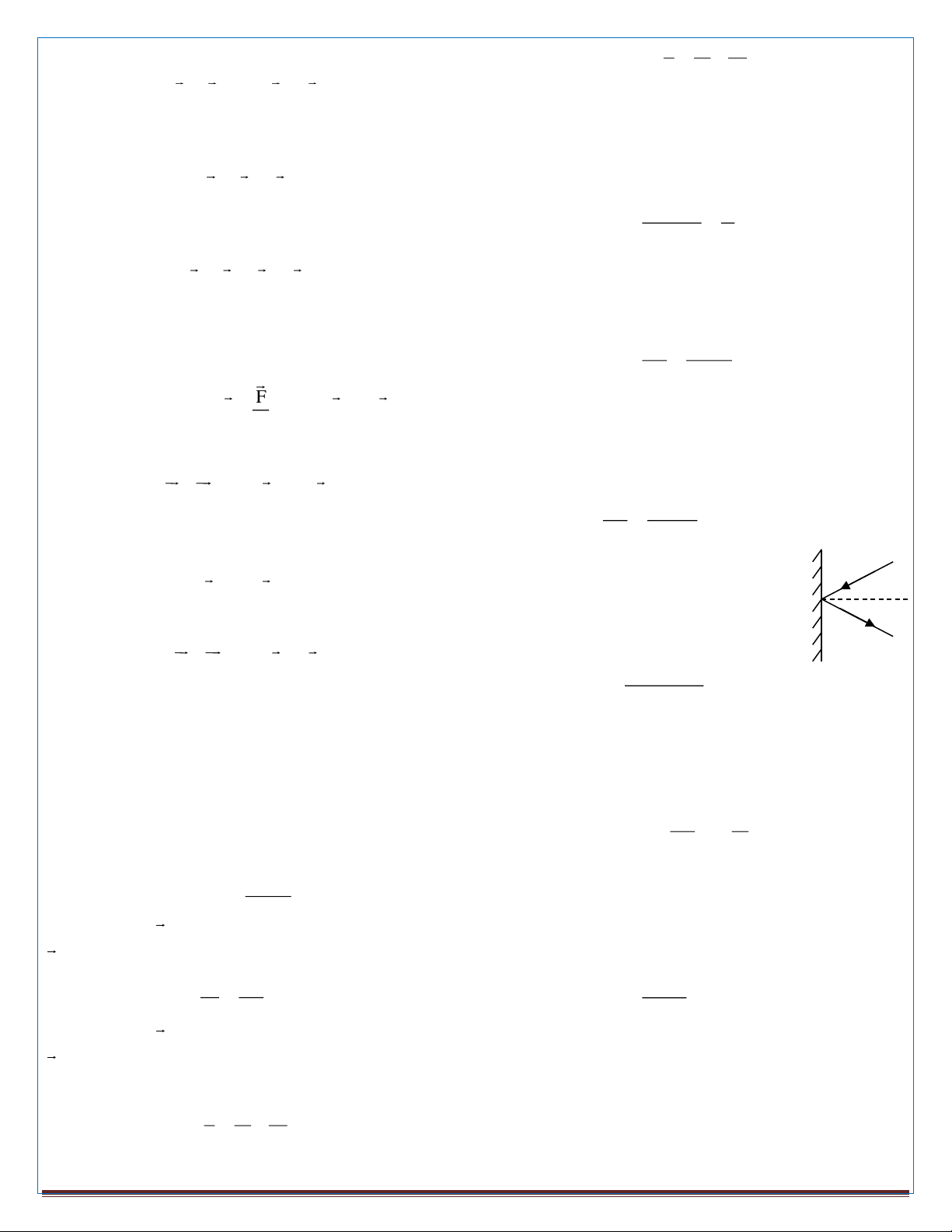
Bài số 8: Quả bóng khối lượng m bay với vận tốc v F = −
0đến đập vào tường và bật trở lại với vận AB FBA
tốc có độ lớn không đổi (hình vẽ). Biết thời α
4. Một số bài toán thường gặp: α gian va chạm là t
. Lực của tường tác dụng
Bài toán 1: Một vật cân bằng chịu tác dụng của n lực: vào bóng có độ lớn: F + F + .... + F = n 0 1 2 2mv cos 0 Chiếu lên Ox; Oy: F = t F + F +...+ F = 0 1x 2x nx Bài số 9:
Hai quả bóng ép sát vào nhau trên mặt phẳng ngang. F + F + ... + F = 0
Khi buông tay, hai quả bóng lăn được những quãng đường s 1x 2x nx 1
Giải hệ suy ra đại lượng vật lý cần tìm.
và s2 rồi dừng lại. Biết sau khi dời nhau, hai quả bóng chuyển
Bài toán 2: Một quả bóng đang chuyển động với vận tốc v
động chậm dần đều với cùng gia tốc. Ta có hệ thức: 0 thì
đập vuông góc vào một bức tường, bóng bật ngược trở lại với 2 m s 2 1
vận tốc v, thời gian va chạm = t
. Lực của tường tác dụng vào m s bóng có độ lớn.: 1 2
XI. Các lực cơ học: v + v0 F = m 1. Lực hấp dẫn t
- Điểm đặt: Tại chất điểm đang xét
Bài toán 3: Lực F truyền cho vật khối lượng m1 gia tốc a1; lực
- Phương: Đường thẳng nối hai chất điểm.
F truyền cho vật khối lượng m2 gia tốc a2: - Chiều: Là lực hút a m m m
Ta có hệ thức liên hệ: 2 1 = - Độ lớn: 1 2 F = G a m hd 2 r 1 2 Bài toán 4: Lực
G = 6,67.10-11N.m2/kg2 : hằng số hấp dẫn
F truyền cho vật khối lượng m1 gia tốc a1; lực 2. Trọng lực:
F truyền cho vật khối lượng m2 gia tốc a2:
- Điểm đặt: Tại trọng tâm của vật.
- Lực F truyền cho vật khối lượng m1 + m2 một gia tốc a: - Phương: Thẳng đứng. 1 1 1 = + - Chiều: Hướng xuống. a a a 1 2 - Độ lớn: P = m.g
- Lực F truyền cho vật khối lượng m1 - m2 một gia tốc a:
3. Biểu thức của gia tốc rơi tự do M
7. Lực hướng tâm - Tại độ cao h:g = G h (R + h)2
- Điểm đặt: Trên chất điểm tại điểm đang xét trên quỹ đạo
- Phương: Dọc theo bán kính nối chất điểm với tâm quỹ đạo M - Gần mặt đất: g = G
- Chiều: Hương vào tâm của quỹ đạo 2 R 2 v 2 2 = = = g R - Độ lớn: F ma m. m r ht ht - Do đó: h = r g R + h
8. Lực quán tính li tâm
4. Lực đàn hồi của lò xo
- Điểm đặt: Trên chất điểm tại điểm đang xét trên quỹ đạo
- Phương: Trùng với phương của trục lò xo.
- Phương: Dọc theo bán kính nối chất điểm với tâm quỹ đạo
- Chiều: Ngược với chiều biến dạng cuả lò xo
- Chiều: Hướng xa tâm của quỹ đạo
- Độlớn: Tỉ lệ thuận với độ biến dạng của lò xo 2 v 2 = = F = k. l - Độ lớn: F m. m r lt đh r
k(N/m) : Hệ số đàn hồi (độ cứng) của lò xo.
XII. Phương pháp động lực học
l : độ biến dạng của lò xo (m).
1 . Bài toán thuận :
2. Lực căng của dây:
Biết các lực tác dụng : 1 F , 1
F ,...Fn Xác định chuyển động :
- Điểm đặt: Là điểm mà đầu dây tiếp xúc với vật. a, v, s, t
- Phương: Trùng với chính sợi dây.
Phương pháp giải :
- Chiều: Hướng từ hai đầu dây vào phần giữa của sợi dây
- Bước 1 : Chọn hệ quy chiếu thích hợp. (chỉ là lực kéo)
- Bước 2 : Vẽ hình – Biểu diễn các lực tác dụng lên vật
3. Lực ma sát nghỉ.
- Bước 3 : Xác định gia tốc từ định luật II Newton
- Giá cuả Fmsn luôn nằm trong mặt phẳng tiếp xúc giữa hai F = F + F + ... = ma (1) vật. hl 1 2 F - F
Chiếu (1) lên các trục toạ độ suy ra gia tốc a hl = ( 2 )
msn ngược chiều với ngoại lực tác dụng vào vật. a m
- Lực ma sát nghỉ luôn cân bằng với ngoại lực tác dụng lên vật. F
- Bước 4 : Từ (2), áp dụng những kiến thức động học, kết mns = F
hợp điều kiện đầu để xác định v, t, s
Khi F tăng dần, Fmsn tăng theo đến một giá trị FM nhất định
thì vật bắt đầu trượt. F
2 . Bài toán ngược: Biết chuyển động : v, t, s Xác định lực
M là giá trị lớn nhất của lực ma sát nghỉ tác dụng F F ; F = N msn M M n
Phương pháp giải :
Với : hệ số ma sát nghỉ n
- Bước 1 : Chọn hệ quy chiếu thích hợp. F F ;F = F
- Bước 2 : Xác định gia tốc a dựa vào chuyển động đã cho msn M msn x F
(áp dụng phần động học )
x thành phần ngoại lực song song với mặt tiếp xúc
4. Lực ma sát trượt
- Bước 3 : Xác định hợp lực tác dụng vào vật theo định luật II Niutơn
- Lực ma sát trượt tác dụng lên một vật luôn cùng phương
và ngược chiều với vận tốc tương đối của vật ấy đối với vật kia. Fhl = ma
- Độ lớn cuả lực ma sát trượt không phụ thuộc vào diện tích
- Bước 4 : Biết hợp lực ta suy ra các lực tác dụng vào vật .
mặt tiếp xúc, không phụ thuộc vào tốc độ của vật mà chỉ phụ
3. Một số bài toán thường gặp:
thuộc vào tính chất của các mặt tiếp xúc
Bài toán 1:(Chuyển động của vật trên mặt phẳng ngang không có lực kéo
- Lực ma sát trượt tỉ lệ với áp lực N:
) Một ô tô đang chuyển động với vận tốc v0 thì
hãm phanh; biết hệ số ma sát trượt giữa ô tô và sàn là μ F = N : mst t
Gia tốc của ô tô là: a = -μg
là hệ số ma sát trượt t
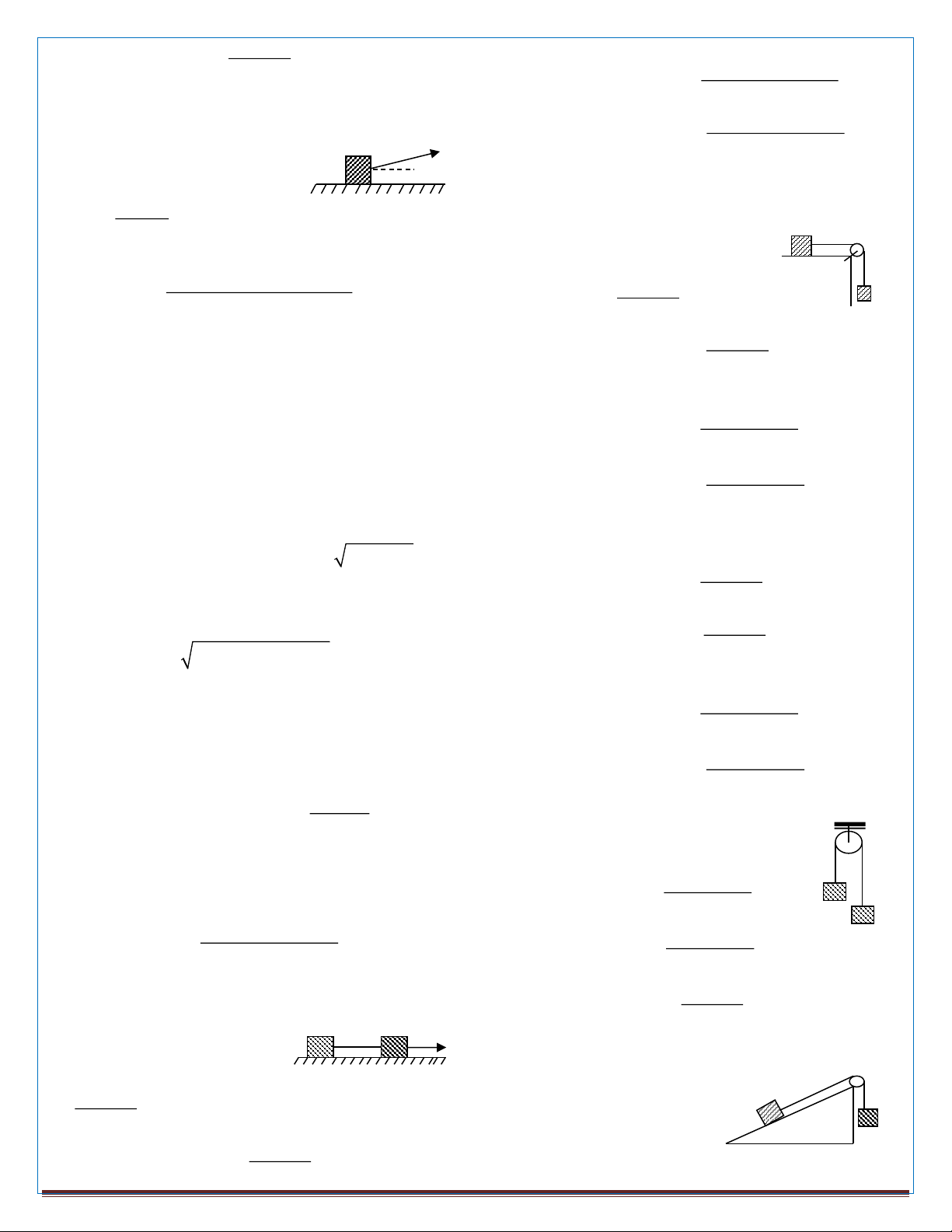
Bài toán 2: :(Chuyển động của vật trên 5. Lực ma sát lăn
mặt phẳng ngang có lực kéo F) Cho cơ hệ F
Lực ma sát lăn cũng tỷ lệ với áp lực N giống như lực ma sát
như hình vẽ. Cho lực kéo F, khối lượng của
trượt, nhưng hệ số ma sát lăn nhỏ hơn hệ số ma sát trượt hàng vật m chục lần.
- Nếu bỏ qua ma sát thì gia tốc của vật là: 6 Lực quán tính F =
- Điểm đặt : Tại trọng tâm của vật a m
- Hướng : Ngược hướng với gia tốc a của hệ quy chiếu
- Nếu hệ số ma sát giữa vật và sàn là thì gia tốc của vật là: - Độ lớn : Fqt = m.a F − m g
▪ Nếu ma sát giữa m1; m2 với sàn lần lượt là μ1 và μ2: a = m F − m g − m g - Gia tốc của m = 1 và m2: 1 1 2 2 a
Bài toán 3:(Chuyển động của vật trên mặt phẳng ngang m + m 1 2
phương của lực kéo hợp với phương ngang một góc α) Cho cơ F − m g − m g
hệ như hình vẽ. Cho lực kéo F, khối - Lực căng dây nối: 1 1 2 2 T = m 2 F m + m
lượng của vật m, góc α. 1 2 α
Bài toán 7:(Chuyển động của hệ vật vắt qua ròng rọc cố định
- Nếu bỏ qua ma sát thì gia tốc của
chuyển động theo hai phương khác nhau) Cho cơ hệ như hình vật là: F cos a =
vẽ. Cho khối lượng m1; m2 m ▪ m2
Nếu bỏ qua ma sát
- Nếu hệ số ma sát giữa vật và sàn là μ thì gia tốc của vật là:
- Gia tốc của m1, m2 là:
F cos − (mg − Fsin ) a = m g 1 a = m1 m m + m
Độc giả có nhu cầu về file word toàn bộ giáo trình vật lý 10 1 2 m g
bao gồm lý thuyết và các bài tập tự luận và bài tập trắc nghiệm - Lực căng dây nối: 1 T = m . 2
có giải chi tiết tham khảo m + m vui lòng email : 1 2
tomhocgioi2006@gmail.com
▪ Nếu hệ số ma sát giữa m2 và sàn là μ (m − m g 1 2 ) - Gia tốc của m = 1, m2 là:a
Bài toán 4 (Vật trượt trên mặt phẳng nghiêng từ trên xuống): m + m 1 2
Một vật bắt đầu trượt từ đỉnh một mặt phẳng nghiêng , góc (m − m g 1 2 )
nghiêng α, chiều dài mặt phẳng nghiêng là l:
- Lực căng dây nối:T = m . 2 ▪ +
Nếu bỏ qua ma sát m m 1 2
- Gia tốc của vật: a = gsinα
Chú ý : nếu m1 đổi chỗ cho m2: ▪
- Vận tốc tại chân mặt phẳng nghiêng:
Nếu bỏ qua ma sát v = 2g sin . l m g
▪ Nếu ma sát giữa vật và mặt phẳng nghiêng là μ - Gia tốc của m = 1, m2 là: 2 a m + m
- Gia tốc của vật: a = g(sinα - μcosα) 1 2
- Vận tốc tại chân mặt phẳng nghiêng: m g - Lực căng dây nối: 2 T = m . 1 + v = 2g (sin − c os).l m m 1 2
▪ Nếu hệ số ma sát giữa m
Bài toán 5 (Vật trượt trên mặt phẳng nghiêng từ dưới lên): Một 1 và sàn là μ
vật đang chuyển động với vận tốc v (m − m g 2 1 ) 0 theo phương ngang thì - Gia tốc của m = 1, m2 là:a
trượt lên một phẳng nghiêng, góc nghiêng α: m + m 1 2
▪ Nếu bỏ qua ma sát (m − m g 2 1 ) =
- Gia tốc của vật là: a = - gsinα - Lực căng dây nối:T m . 2 m + m 2 1 2 v
- Quãng đường đi lên lớn nhất: 0 s =
Bài toán 8: (Chuyển động của hệ vật nối với ròng rọc số định max 2g sin
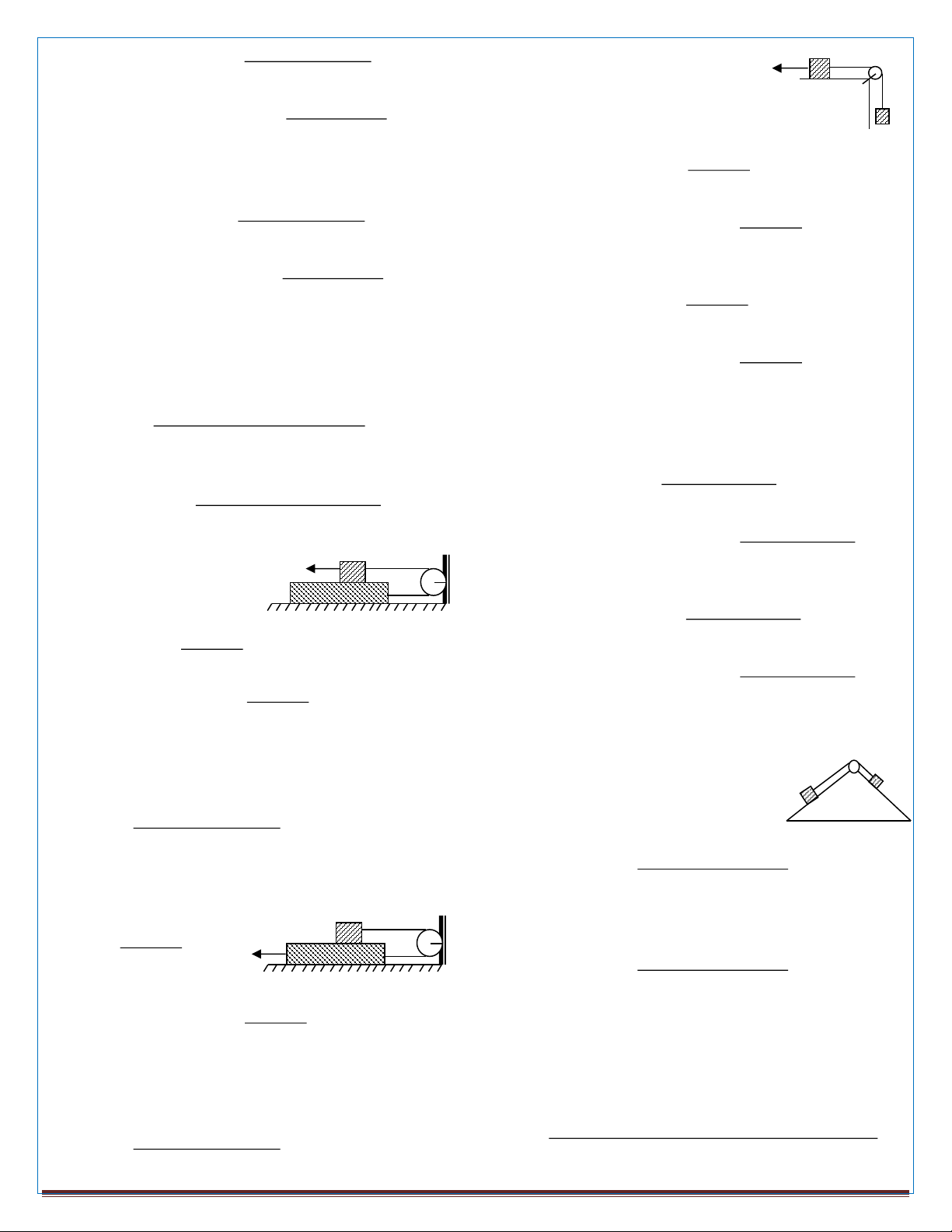
chuyển động cùng phương): Cho cơ hệ
▪ Nếu hệ số ma sát giữa vật và mặt phẳng nghiêng là μ
như hình vẽ. Biết m1, m2.
- Gia tốc của vật là: a = g − (sin + c os) (m − m g 1 2 ) - Gia tốc của m = m 1:a 2
- Quãng đường đi lên lớn nhất: 1 m + m 1 2 m1 2 v (m − m g 2 1 ) 0 s = max - Gia tốc của m a = 2g (sin + c os) 2: 2 m + m 1 2
Bài toán 6 ( Chuyển động của hệ hai vật trên mặt phẳng 2 2m g
ngang):: Cho cơ hệ như hình vẽ. - Lực căng dây nối: 1 T = m + m Cho F, m 1 2 1, m2 m2 m1 F
▪ Nếu bỏ qua ma sát
Bài toán 9: (Hệ hai vật nối với ròng rọc cố định trên mặt phẳng - Gia tốc của vật là: nghiêng) ▪ F
Nếu bỏ qua ma sát: m a = 1
Trường hợp 1: Nếu m m + m 2 1 2
m1gsinα > m2g. khi đó m1 đi F
- Lực căng dây nối: T = m . xuống m2 đi lên 2 m + m 1 2 g (m sin − m
Bài toán 12: Cho cơ hệ như hình vẽ 1 2 ) m - Gia tốc của m = 2 1; m2 là: a F m + m cho F,m1, m2. 1 2 ▪ Bỏ qua ma sát: m sin − m - Lực căng dây nối: 1 2 T = m g 1+
Trường hợp: F>m1g m1 đi lên m1 2 m + m 1 2 - Gia tốc của m1, m2:
Trường hợp 2: Nếu m F − m g
1gsinα < m2g. khi đó m1 đi lên m2 đi 1 a = xuống m + m 1 2 g (m − m sin 2 1 ) − - Gia tốc của m = F m g 1; m2 là:a = + m + m - Lực căng dây nối: 1 T m g 1 1 2 m + m 1 2 m − m sin - Lực căng dây nối: 2 1 T = m g 1−
Trường hợp 2: F < m1g m1 đi xuống 2 m + m m g − F 1 2 - Gia tốc của m = 1, m2: 1 a
▪ Nếu hệ số ma sát giữa m + 1 và sàn là μ m m 1 2
Trường hợp 1: Nếu m1gsinα > m2g. khi đó m1 đi xuống m2 m g − F đi lên - Lực căng dây nối: 1 T = m g + 1 m + m - Gia tốc của m 1 2 1; m2 là: ▪ g (m sin − m cos − m
Hệ số ma sát giữa m2 và sàn là μ 1 2 2 ) a =
Trường hợp: F > m1g m1 có xu hướng đi lên m + m 1 2 - Gia tốc của m1, m2: - Lực căng dây nối: F − m g − m g 1 2 a = m sin − m cos − m 1 2 2 + T = m g 1+ m m 1 2 2 m + m 1 2 F − m g − m g = +
Bài toán 10: Cho cơ hệ như - Lực căng dây nối: 1 2 T m g 1 m1 m + m hình vẽ . Cho m 1 2 F 1; m2,
▪ Bỏ qua mọi ma sát:
Trường hợp 2: F < m1g m1 đi xuống m2 − − - Gia tốc của m m g F m g 1 và m2: - Gia tốc của m = 1, m2: 1 2 a F m + m 1 2 a = (với a1=-a2 =a) m + m m g − F − m g 1 2 - Lực căng dây nối: 1 2 T = m g + F 1 m + m
- Lực căng dây nối: T = m 1 2 2 m + m 1 2
Bài toán 13:(Chuyển động của hệ vật trên hai mặt phẳng
▪ Cho hệ số ma sát giữa m 1 và m2 là , giữa m
nghiêng): Cho cơ hệ như hình vẽ, Biết m1, m2, α, β: 1 2 và sàn μ ▪ Bỏ qua ma sát: 2 m2 Gia tốc của m
Trường hợp 1: m1gsinα > m2gsinβ m1 1 và m2: F − 2 m g − m g m1 đi xuống. α β 1 1 2 2 a = (với a1 = -a2 = a) Gia tốc của m m + m 1; m2 là: 1 2 (m sin − m sin 1 2 )
Bài toán 11: Cho cơ hệ như hình vẽ. Cho m = 1, m2, F a g ▪ +
Nếu bỏ qua ma sát m m 1 2 Gia tốc của m Trường hợp 2: m 1 và m2:
1gsinα < m2gsinβ m2 đi xuống. m1 F m2 Gia tốc của m1; m2 là: a = F (m sin− m sin 2 1 ) m + m 1 2 a = g với a m + m 2= -a1 = a 1 2 F
▪ Hệ số ma sat giữa m1, m2 với mặt phẳng nghiêng là
- Lực căng dây nối: T = m 1 m + m μ1, μ2. 1 2
▪ Cho hệ số ma sát giữa m
Trường hợp 1: m1gsinα > m2gsinβ m1 có xu hướng đi 1 và m2 là , giữa m 1 2 và xuống., m sàn μ 2 đi lên, 2 Gia tốc của m1; m2 là: Gia tốc của m1 và m2:
(m sin − m sin− m cos − m cos 1 2 1 1 2 2 ) F − 2 m g − m g a = g 1 1 2 2 a = (với a2 = -a1 = a) m + m m + m 1 2 1 2
Trường hợp 2: m1gsinα < m2gsinβ m1 có xu hướng đi
Bài toán 17: (Tính áp lực nén lên cầu vồng lên tại điểm cao lên., m2 đi xuống nhất) Gia tốc của m1; m2 là: 2 v ( = −
m sin − m sin − m cos − m cos N m g g 2 1 1 1 2 2 ) a = g R m + m 1 2
m: khối lượng vật nặng; R: bán kính của cầu
Bài số 14:Cho cơ hệ như hình vẽ. Cho m1, m2 α
Bài toán 18: (Tính áp lực nén lên cầu lõm xuống tại điểmthấp
▪ Bỏ qua mọi ma sát: nhất)
Trường hợp 1: m1 > m2 : Thì m1 2 v đi xuống m N = m g + g 2 đi lên m1 R Gia tốc của m1, m2: (m − m sin m2
M: khối lượng vật nặng; R: bán kính của cầu 1 2 ) a = .g
Bài toán 19: (Tính áp lực nén lên cầu vồng lên tại vị trí bán m + m 1 2 α
kính nối vật với tâm hợp với phương thẳng đứng 1 góc α) Với a1 = - a2 = a 2 v Trường hợp 2: m = −
1 < m2: Thì m1 đi lên, m2 đi xuống N m gcos Gia tốc của m R 1, m2: (m −m sin
Bài toán 20: (Tính áp lực nén lên cầu lõm tại vị trí bán kính nối 2 1 ) a = .g
vật với tâm hợp với phương thẳng đứng 1 góc α) m + m 1 2 2 v Với a2 = - a1 = a N = m gcos +
▪ Hệ số ma sát giữa m R
2 và sàn μ1, giữa m1 và m2 μ2
Trường hợp 1: m1 > m2 : Thì m1 đi xuống m2 đi lên
Bài toán 21: Một lò xo có độ cứng k. Đầu trên cố định đầu Gia tốc của m1, m2:
dưới treo vật có khối lượng m:
Ta luôn có a1 = - a2 = a. Với a xác định bởi (
- Cho k, m tìm độ biến dạng của lò xo: mg l = m − m sin − 2 + cos 1 2 ) ( 1 2) k a = .g m + m
- Cho m, k và chiều dài ban đầu. Tìm chiều dài của lò xo khi 1 2 Trường hợp 2: m mg
1 < m2: Thì m1 đi lên, m2 đi xuống cân bằng: l = l + CB 0 Gia tốc của m1, m2: k
(m − m sin − 2 + cos
Bài toán 22: Một lò xo có độ cứng k, chiều dài l cắt thành 2 lo 2 2 ) ( 1 2) a = .g xo có chiều dài l m + m
1, l2. Độ cứng của lò xo cắt: 1 2 l l Với a = = 2 = - a1 = a k k. ; k k. 1 2 Bài số 15: l l
(Chuyển động của hệ vật nối qua ròng rọc động) 1 2
Cho cơ hệ như hình vẽ. cho m
Bài toán 23: (Ghép lò xo). Cho hai lò xo có độ cứng k 1, m2 1, k2 tìm -Gia tốc của m độ cứng tương đương 1, m2: (m − m g
- Ghép nối tiếp: k = k1 + k2. 1 2 ) a = 1 1 1 1 m + 4m - Ghép song song: = + 1 2 k k k 2(m − m g 1 2 2 1 ) a =
Bài toán 24: Vật có khối lượng 2 m + 4m m1 m2 1 2
m gắn vào đầu một lò xo nhẹ. Lò
Bài số 16: (lực tương tác giữa hai vật chuyển động trên mặt
xo có chiều dài ban đầu l0 và độ
phẳng nghiêng) Cho m1, m2, μ1, μ2, α
cứng k. Người ta cho vật và lò xo quay tròn đều trên một mặt
- Gia trị nhỏ nhất của α để cho m
sàn nằm ngang, trục quay đi qua đầu lò xo. Tính tốc độ góc để 1 hai vật trượt xuống:
lò xo dãn ra một đoạn x m + m m2 1 1 2 2 tan = kx = m + m 1 2 m (l + x 0 ) - Lực tương tác giữa m α 1 và m2 khi chuyển động:
Bài toán 25: Lò xo có độ cứng k, chiều dài tự nhiên l0 đầu trên
cố định đầu dưới treo vật có khối lượng m. Quay lò xo quanh m m − g cos 1 2 ( 1 2 ) F =
trục thẳng đứng qua đầu trên của lò xo. Vật vạch một đường m + m
tròn nằm ngang, có trục quay hợp với trục lò xo một góc 1 2 : mg m (g − a )
- Chiều dài của lò xo lúc quay: l = l + = 0 l k cos k g - Tốc độ góc: =
Bài 31: (Áp lực nén lên sàn thang máy). Một vật có khối lượng mg
m đặt trên sàn của thanh máy. l cos + 0 k
Trường hợp 1: Thang máy chuyển động thẳng đều :
Bài toán 26: Hai lò xo: Lò xo 1 dài thêm một đoạn x1 khi treo N = mg
m1, lò xo 2 dài thêm x2 khi treo m1 thì ta luôn có:
Trường hợp 2: Thang máy chuyển động nhanh dần đều đi k m x
lên , hoặc chuyển động chậm dần đều đi xuống với gia tốc a 1 1 2 = . k m x N = m(g + a) 2 2 1
Trường hợp 3: Thang máy chuyển động chậm dần đều đi
Bài toán 27:(Lực quán tính tác dụng vào vật treo trên xe
chuyển động theo phương ngang
lên , hoặc chuyển động nhanh dần đều đi xuống với gia tốc a
) Một vật nặng khối lượng m,
kích thước không đáng kể treo ở đầu một sợi dây trong một N = m(g - a)
chiếc xe đang chuyển động theo phương ngang với gia tốc a.
- Cho gia tốc a. Góc lệch của dây treo so với phương thẳng đứng: a tan = g
- Cho góc lệch α. gia tốc của xe: a = gtanα
Bài toán 28: (Chuyển động trên vòng xiếc). Xét một xe đáp đi
qua điểm cao nhất của vòng xiếc. Điều kiện để xe không rơi: v gR
Bài toán 29: (Lực căng dây khi vật chuyển động tròng trong
mặt phẳng thẳng đứng) Một quả cầu khối lượng m treo ở đầu
A của sợi dây OA dài l. Quay cho quả cầu chuyển động tròn
đều với tốc độ dài v trong mặt phẳng thẳng đứng quanh tâm O. 2 v
- Lực căng dây cực đại:T = m + g max l 2 v
- Lực căng dây cực tiểu: T = m − g min l
- Lực căng dây khi A ở vị trí thấp hơn O. OA hợp với 2
phương thẳng đứng một góc v : T = m + gcos l
- Lực căng dây khi A ở vị trí cao hơn O. OA hợp với 2
phương thẳng đứng một góc v : T = m − gcos l
Bài 30: (Tính độ biến dạng của lò xo treo vào thang máy
chuyển động thẳng đứng).
Treo vật nặng có khối lượng m vào đầu dưới một lò xo có độ
cứng k, đầu trên của lò xo gắn vào thang máy.
Trường hợp 1: Thang máy chuyển động thẳng đều mg l = k
Trường hợp 2: Thang máy chuyển động nhanh dần đều đi
lên , hoặc chuyển động chậm dần đều đi xuống với gia tốc a m (g + a ) l = k
Trường hợp 3: Thang máy chuyển động chậm dần đều đi
lên , hoặc chuyển động nhanh dần đều đi xuống với gia tốc a




