Công thức tính thể tích tứ diện đều cạnh a và bài tập áp dụng

Công thức tính thể tích tứ diện đều cạnh a và bài tập áp dụng
1. Tứ diện là gì? Tứ diện đều là gì?
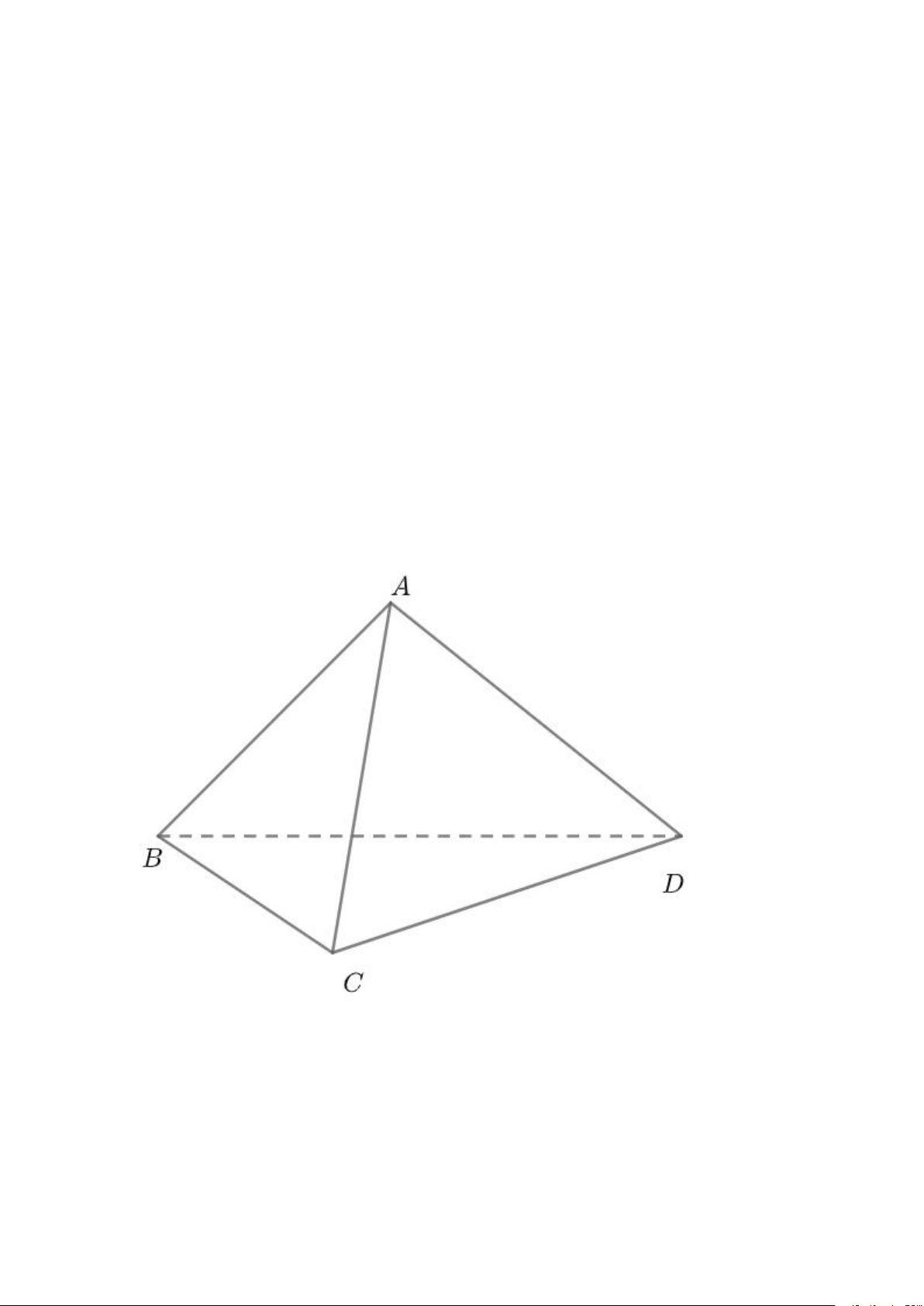
Tứ diện là hình có bốn đỉnh và thường được đặt với ký hiệu là A, B, C,D.
Trong đó thì với bất kỳ điểm nào trong số các điểm A, B, C,D cũng được xem
như đỉnh của tứ diện. Mặt tam giác đối diện với D cũng được xem là đỉnh của
tứ diện. Mặt tam giác đối diện với đỉnh sẽ được gọi là mặt đáy. Ví dụ, nếu
chọn B là đỉnh của tứ diện thì mặt đáy sẽ là ACD
Hay còn được hiểu theo cách ngắn gọn thì trong không gian nếu cho 4 điểm
không đồng phẳng gồm A, B, C,D thì khi đó khối đa diện có 4 đỉnh A, B, C, D
gọi là khối tứ diện. Ký hiệu là ABCD
- Tứ diện đều được hiểu là: Nếu một tứ diện có các mặt bên là các tam giác
đều thì đây được gọi là hình tứ diện đều Và tứ diện đều được xem là một
trong 5 khối đa diện đều.
Các tính chất của tứ diện đều:
Tứ diện đều có các tính chất như sau:
- Bốn mặt xung quanh đều là các tam giác đều bằng nhau
- Các mặt của tứ diện là những tam giác có ba góc đều nhọn
- Tổng các góc tại một đỉnh bất kì của tứ diện là 180
- Hai cặp cạnh đối diện trong một tứ diện có độ dài bằng nhau.
- Các mặt của tứ diện đều tương đường bằng nhau
- Bốn đường cao của tứ diện đều có độ dài bằng nhau
- Tâm của các mặt nối tiếp và ngoại tiếp nhau trùng với tâm của tứ diện
- Hình hộp ngoại tiếp tứ diện là hình họp chữ nhật
- Các góc phẳng nhị diện ứng với mỗi cạnh đối diện của tứ diện bằng nhau
- Đoạn thẳng nối trung điểm của các cạnh đối diện là một đường đứng vuông
góc của cả hai cạnh đó
- Một tứ diện có ba trục đối xứng
- Tổng các cos của các góc phẳng nhị diện chứa cùng một mặt của tứ diện bằng 1
2. Công thức tính thể tích tứ diện đều cạnh a
Tứ diện đều cạnh a là tứ diện có tất cả các cạnh đều bằng a
Khi giải toán liên quan đến tứ diện đều chúng ta cần lưu ý về cách vẽ. Cụ thể
các vẽ tứ diện đều ABCD ta thực hiện theo các bước sau:
- Coi tứ diện đều là hình chóp tam giác đều. Chẳng hạn như A. BCD
- Vẽ mặt là mặt đáy . Chẳng hạn là mặt BCD
- Vẽ một đường trugn tuyến của mặt đáy BCD. Chẳng hạn BM là trung tuyến của tam giác BCD
- Xác định trọng tâm G của tam giác BCD. Và G là chính là tâm của đáy.
Dựng đường cao (đường thẳng đi qua G song song với mép bên vở hoặc tờ
giấy trên của các bạn )
Xác định điểm A trên đường vừa dựng và hoàn thiện hình
bài toán: Tính thể tích khối tứ diện cạnh a Lời giải:
Giả sử ABCD là khối tứ diện đều cạnh a. G là trọng tâm của tam giác BCD như hình trên Ta có: S tam giác BCD = a 3 / 4 AG = AB 2 - BG 2 = a2 - ( a 3/ 3) 2 = a 6 / 3
Vậy thể tích của khối tứ diện đều cạnh a là:
V = 1/3 S tam giác BCD . AG = 1/3 . a2 3/ 4 . a 6/ 3 = a3 2/ 12
Một tứ diện đều có 6 cạnh bằng nhua và 4 mặt tam giác đều sẽ có các công
thức tính thể tích như sau:
- Thể tích tứ diện ABCD: thể tích của một khối tứ diện bằng một phần ba tích
số của diện tích mặt đáy và chiều cao của khối tứ diện tương ứng: V = 1/3 x A (BCD) x AH
- Thể tích tứ diện đều tam giác A. ABC: Thể tích của một khối chóp bằng một
phần ba tích số của diện tích mặt đáy và chiều cao của khối chóp đo: V = 1/3 x B x h
Vậy thể tích của tứ diện đều cạnh a được tính theo công thức:
3. Bài tập vận dụng tự luyện tập
Câu 1: Khối chóp tứ diện đều cạnh a có thể tích bằng: A. a3/3 B. a3 6 / 12 C. a3 2 / 12 D. a3 3 / 12
Câu 2: Số mặt phẳng đối xứng của hình tứ diện đều là A. 4 mặt phẳng B. 6 mặt phẳng C. 8 mặt phẳng D. 10 mặt phẳng
Câu 3: Trung điểm các cạnh của một tứ diện đều tạo thành:
A. các đỉnh của một hình hai mươi mặt đều
B. các đỉnh của một hình mười hai mặt đều
C. các đỉnh của một hình bát diện đều
D. các đỉnh của một hình tứ diện
Câu 4: Cho khối chóp tam giác đều S. ABC có cạnh đáy bằng a, cạnh bên
đáy. Tính theo a thể tích V của khối chóp S.ABC A. V = 11a3 / 4 B. V = 13a3 / 12 C. 11a3 / 12 D. 11a3 / 6
Câu 5: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng a
21 / 6. Tính thể tích khối chóp S. ABC
Câu 6: Cho tứ diện đều ABCD có thể tích bằng 12 và G là trọng tâm của tam
giác. Tính thể tích của khối chóp A. GBC A. V = 4 B. V = 3 C. V = 5 D. V = 6
Câu 7: Hãy tính thể tích khối tứ diện đều ABCD biết: a. cạnh AB = 4 cm b. cạnh CD = 6 cm c. cạnh BD = 3 cm Giải bài toán:
a. Vì tứ diện đều nên có các cạnh có độ dài bằng nhau: BC = CD = BD = AC
= AB = 4 cm nên thể tích là:
Cho hình tứ diện đều ABCD cạnh a = 5cm. Hỏi thể tích bằng bao nhiêu
b. Vì tứ diện đều nên có: AB = DA = BD = AC = CD = 6 cm nên thể tích là:
c. Vì là tứ diện đều nên AB = BC = DA = AC = BD = 3 cm nên thể tích là:
Câu 8: Cho hình chóp đều S> ABCD đáy là hình vuông, đường SA vuông góc
với mặt phẳng ABC. Xác ddunhj hình chóp này có mặt đối xứng nào?
Câu 9: Cho tứ diện đều ABCD cạnh a. Tính góc giữa AB và CD
Câu 10: Cho ABCD là tứ diện đều cạnh a, kéo dài BC một đoạn CE = a, kéo
dài BD 1 đoạn DF = a. M là trung điểm của AB
a. Tìm thiết diện của tứ diện với mặt phẳng (MÈ)
b. Tình diện tích của thiết diện theo a
Câu 11: Cho hìn chóp đều S. ABCD đáy là hình vuông, đường SA vuông góc
với mặt phẳng (ABCD) xác định hình chóp này có mặt đối xứng nào?
Câu 12. Chúng ta có thể biết được điều gì khi hình tứ diện ABCD được viết là D. ABC?
A. Hình tứ diện ABCD có thể coi là hình chóp tam giác D. ABC có đỉnh là D
B. Hình tứ diện ABCD có thể coi là hình chóp tam giác D. ABC có đáy là mặt phẳng (ABC)
C. Hình tứ diện ABCD có thể coi là hình chóp tam giác D. ABC và có thể tích
được tính bằng cách lấy diện tích tam giác ABC nhân với khoảng cách từ
đỉnh D đến mặt phẳng (ABC) rồi chia cho 3 D.A, B, C đều đúng
Câu 13. Hình tứ diện ABCD có thể tích bằng 9a3 và có diện tích tam giác
BCD là 3a2. Trong các phát biểu sau đây, phát biểu đúng là:
A. khoảng cách từ đỉnh A đến mặt phẳng BCD là 3a
B. khoảng cách từ đỉnh A đến mặt phẳng BCD là 9a
C. khoảng cách từ đỉnh A đến mặt phẳng BCD là 6a
D. khoảng cách từ đỉnh A đến mặt phẳng BCD là a
Câu 14: Thể tích hình tứ diện ABCD là bao nhiêu khi khoảng cách từ đỉnh D
đến mặt phẳng (ABC) là 4a và diện tích ABC là 12a2
A. thể tích tứ diện ABCD là 3a3
B. thể tích tứ diện ABCD là 16a3
C. thể tích tứ diện ABCD 48 a3
D. thể tích tứ diện ABCD là 12a3
Câu 15: TRong một tứ diện đều có:
A. tất cả các cạnh có độ dài bằng nhau
B. tất cả các mặt có diện tích bằng nhau C. cả A và B đều sai D. A và B đều đúng
Document Outline

• Công thức tính thể tích tứ diện đều cạnh a và bài
  • 1. Tứ diện là gì? Tứ diện đều là gì?
  • 2. Công thức tính thể tích tứ diện đều cạnh a
  • 3. Bài tập vận dụng tự luyện tập