11/1/2016 Critical Thinking Chapter 10 A Little Propositional Logic
Lecture Notes © 2008 McGraw Hill Higher 1 Education Propositional logic
It is often difficult to determine whether a long and
complex argument is valid or invalid just by reading it. Example:
 If the Democrat loses the Senate race, the
Republicans will have a majority in the Senate.
 If the Republicans have a majority in the Senate, the
Senate will vote down the new bill.
 It is not the case that the Senate will vote down the
new bill or the Democrat will lose the Senate race.
 So, it is not the case that if the Democrat does not
lose, the Senate will not vote down the new bill 2 1 11/1/2016 Symbolization
Propositional logic is the way to symbolize the parts of
arguments so that we can analyze the whole arguments for validity.
When you symbolize an argument, you represent its
simple statements with single letters, and then represent
the relationship between them (that the argument suggests) with symbols. 3 Symbolization
Example: If Bush won we’re all going to die. Bush won.
Therefore we are all going to die.  Where:  b = Bush won  d = We’re all going to die 
The argument gets symbolized like this: 1. b  d 2. b 3.  d
“” means “Therefore” 4 2 11/1/2016 Conjunction and validity
 When two simple statements are conjoined with an
“and,” we call it a “conjunction.”
 We represent each statement as a simple letter, and
represent the “and” with an “&.”  Example:
 “Tina is tall and Sarah is tall.” gets symbolized like this: p & q  p = Tina is tall  q = Sarah is tall 5 Other words for “and”
 If you see any of the following words, treat them like
“and” and symbolize the statement with an “&”:
 but, yet, while, whereas, although, though, however.
 They are different in meanings, but functionally similar.
 Note: What letter you give it really doesn’t matter, just
as long as you are consistent (use the same letter for
that statement every time) and don’t use the same
letter for two different statements in the same argument. 6 3 11/1/2016 Other words for “and”
 Be warned: not every statement with “and” in it is compound.
Example: The Knicks and Bulls are playing each other.
 This is not expressing the facts that each team is playing…
 Mistake: The Knicks are playing and the Bulls are playing (i.e., k & b).
 …it is expressing the single fact that the two teams are playing each other.
 So it would just get a single letter, for instance, “e.” 7 Truth Tables
 When evaluating validity, you don’t worry
about the truth value of the statements you are symbolizing.
 But each statement is either true or false (you just don’t know which).
 Truth Tables allow you to evaluate statements
and arguments without knowing truth values
by representing all possible truth value combinations. 8 4 11/1/2016 Truth Tables
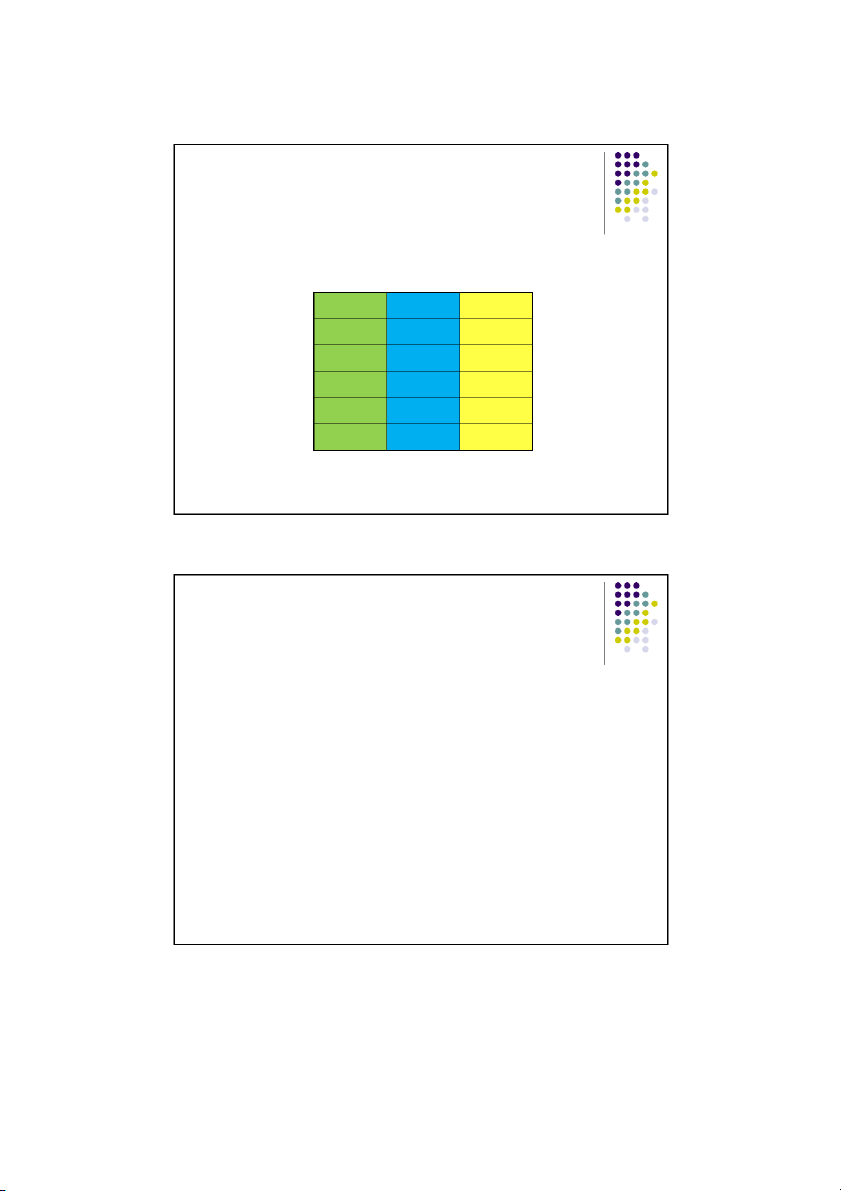
 Recall, we symbolized “Tina is tall and Sarah is tall” as “p&q”.
 We don’t know if they are or not, but we can represent all possibilities this way: p q p&q
---------- ---------- ---------- T T T T F F F T F F F F
Notice: what “p&q” means is “both p and q are true.” This means that, unless both p and
q are true, “p&q” will not be true. That is why, above, p&q has a T only on the row on 9
which both p and q both have a T as well. Using Truth Tables to Examine Validity  Since….
 …an argument is invalid only when it is possible for its
premises to be true and the conclusion false…
 …and since truth tables show us all possible truth values
 …we can use truth tables to evaluate validity.
 We use them to determine all the possible truth
values, and then look for a row where all the
premise are true but the conclusion is false.
 If we find one, the argument is invalid
 If there is no such row, the argument is valid. 10 5 11/1/2016 Example  (1) Tina is tall.  (2) Sarah is tall.
 (3) Therefore, Tina and Sarah are tall. Symbolized: p, q.  q.
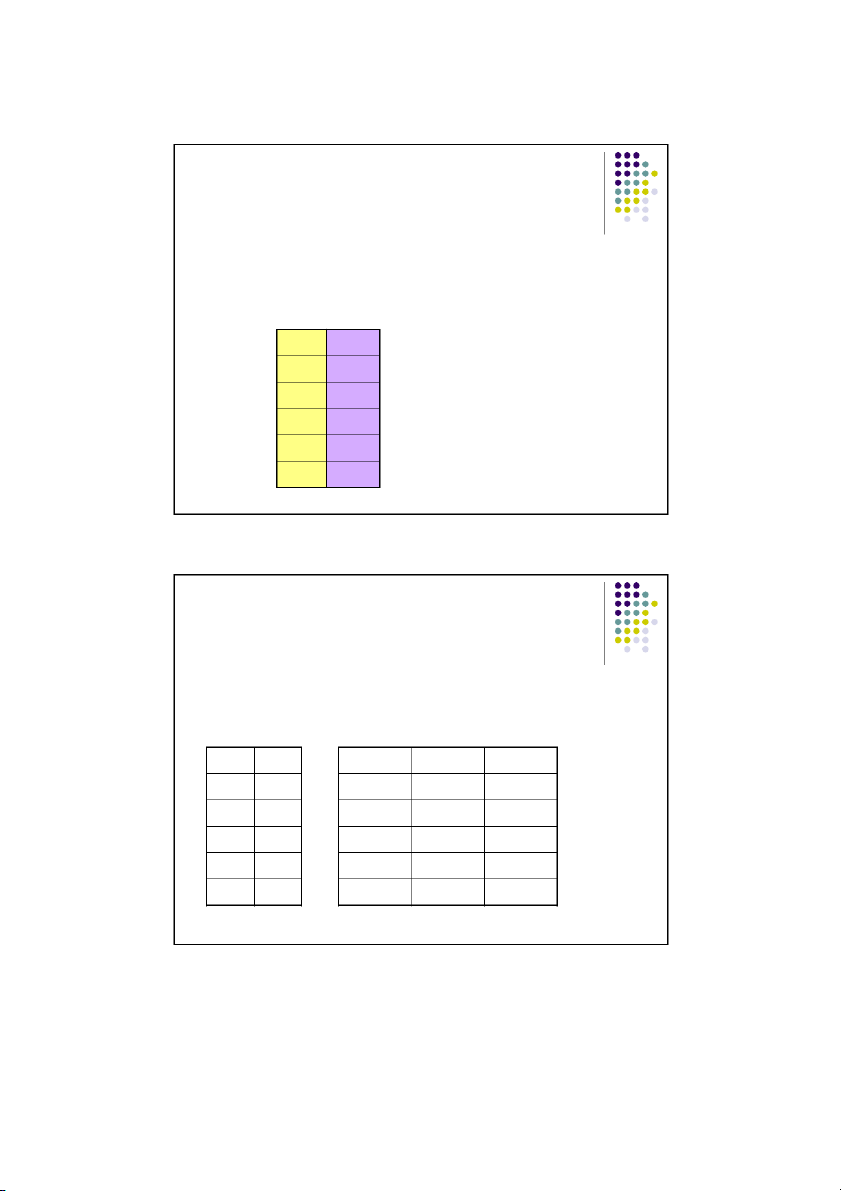
First, represent all the statement letters and their truth values. p q Notice: ------ ------
First row: two T’s, two F’s, T T
Second row: one T, one F (repeat) T F F T F F 11 Example
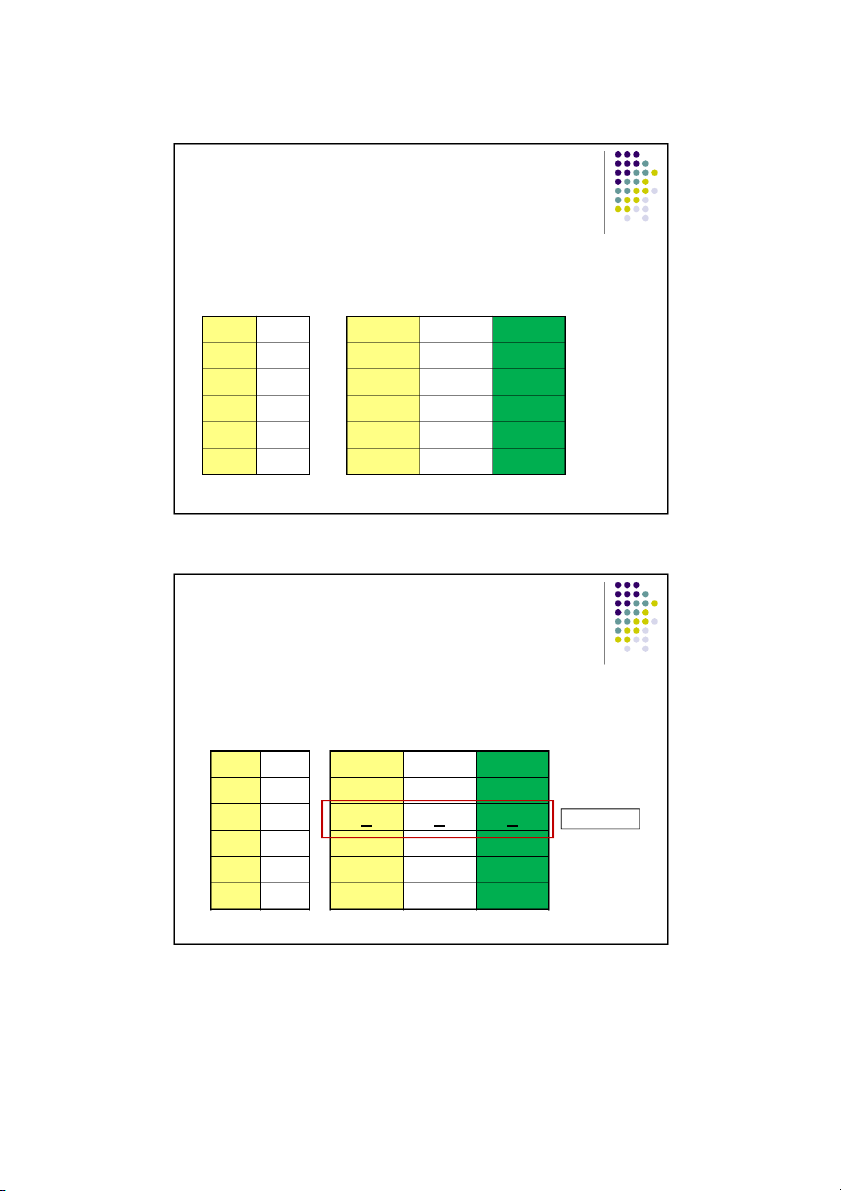
 Then, add the premises and the conclusion. p q p* q* p&q (C) ------ ------
---------- ---------- ---------- T T T F F T F F 12 6 11/1/2016 Example
 Then, add the truth values. p q p* q* p&q (C) ------ ------
---------- ---------- ---------- T T T T T T F T F F F T F T F F F F F F 13 Example
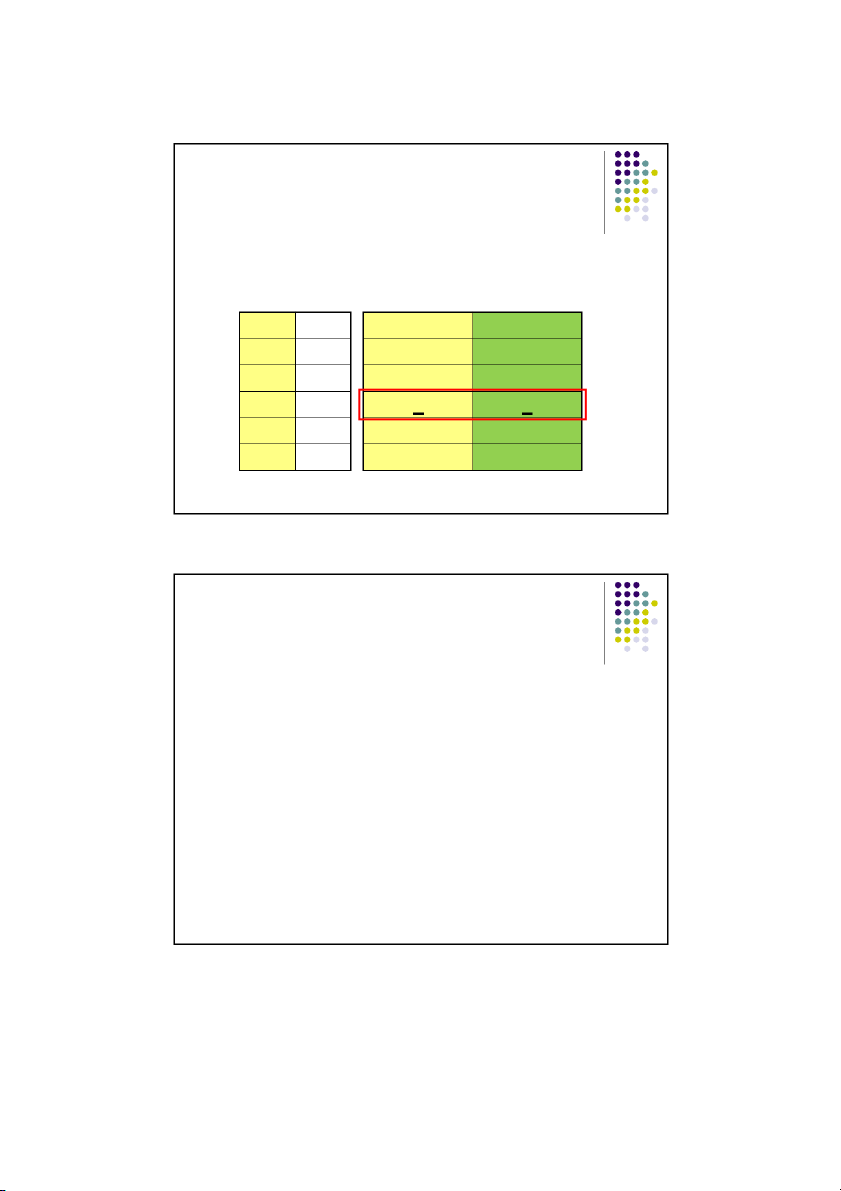
Then look for rows where the premises are all true, and see if the
conclusion is false on those rows. If there is such a row, then the
argument is invalid. In this case, the only row with all true premises
is one in which the conclusion is also true. Thus, the argument is valid. p q p* q* p&q (C) ------ ------
---------- ---------- ---------- T T T T T Valid T F T F F F T F T F F F F F F 14 7 11/1/2016 More Examples 1. Grass is green. 2.
Therefore, grass is green and the sky is blue. Symbolized: g  g & s g s g* g&s (c) ------ ------ ------ ------ T T T T T F T F Shows it to be F T F F invalid F F F F
Since, on the second row, the premise is true but the conclusion is false, the argument is 15 invalid. Negation
We can easily represent “negated
statements” with a “~” (tilde).
If “Sarah is tall” is “p”
“Sarah is not tall” is “~p” On a truth table: anywhere p has a T ~p will have an F 16 8 11/1/2016 Example:
(1) Tina is not Tall, but Sarah is tall. So, Tina is not tall. Symbolized: ~p, q ~p p q ~p* q* ~p (C) ------ ------
---------- ---------- ---------- T T F T F T F F F F F T T T T Valid F F T F T
The argument is valid. The only row on which both premises are true is a row on which the conclusion is also true. 17 Another example
Argument: Frank does not drive a truck. Therefore,
Frank doesn’t drive a truck and Vinny doesn’t drive
a minivan. Symbolized: ~f ~f & ~v f v ~v ~f* (~f & ~v) (c) --- --- --- ---------- ---------- T T F F F f f T F T F F f t F T F T F t f invalid F F T T T t t
Argument is invalid. Row 3 is an example of a row with true premises but a false 18 conclusion. 9 11/1/2016 Whole statement negations
Not only can individual statements be negated: ~p
Compound statements can be too: ~(p&q)
Since “p&q” means “Both p and q are true”
“~(p&q)” means “It is false that both p and q are true.” 19 Whole statement negations
But don’t distribute (like in math):
~(p&q) is not the same as (~p & ~q) Why?
~(p&q) means they are not both true (at least one is false)
(~p & ~q) means they are both false 20 10 11/1/2016
Proof: ~(p&q) ≠ (~p & ~q) p q ~p ~q p&q ~ (p&q) ~p & ~q ---- ---- ---- ---- ---- ---- ----- T T F F T F F T F F T F T F F T T F F T F F F T T F T T 21 Truth tables with 3 variables (set up) p q r Notice: ---- ---- ----
Third column, one T, one F (repeat)
Second column, two T’s, Two F’s (repeat) T T T
First column, four T’s, four F’s T T F T F T T F F F T T F T F F F T 22 F F F 11 11/1/2016 Argument: p, ~q & r, p  & r p q r p* (~q & r)* (p & r) (c) --- --- --- ----------- ---------------- ------------ T T T T F T f t t t T T F T F F f f t f T F T T T T t t t t Valid T F F T F F because the t f t f only row F T T F F F f t f t with true premises F T F F F F f f f f also has a F F T F T F true t t f t conclusion. F F F F F F 23 t f f f
Argument: ~(p&q), (~q&r) ~p p q r ~(p&q)* (~q & r)* ~p (c)
--- --- --- ----------- ---------------- ------------ T T T F F F t f t T T F F F F t f f T F T T T F Shows it f t t is invalid T F F T F F f t f F T T T F T f f t F T F T F T f f f F F T T T T Even f t t though F F F T F T f t f 24 12 11/1/2016 Disjunctions (or statements)
“Frank is angry or Hank is tired.” gets symbolized: a v t
(To make things easier, don’t ever use the letter “v”
to symbolize a simple statement.)
Exclusive and inclusive “or”:
Exclusive or: “a or b” means “a or b, but not both.”
Inclusive or: “a or b” means “at least a or b, but maybe both.”
The convention is to use the inclusive sense. So…. 25 Disjunction truth tables p q pvq --- --- ---- T T T T F T F T T F F F 26 13 11/1/2016 Argument: pvq p  p q pvq* p (C) --- --- ---- ---- T T T T T F T T F T T F Invalid F F F F 27 Be careful with negations of disjunctions
Frank is angry or Hank is tired. a v t
Frank is not angry or Hank is tired. ~a v t
Frank is not angry or Hank is not tired. ~a v ~t
It’s not the case that Frank is angry or Hank is tired. ~(a v t)
Neither is Frank angry nor is Hank tired. ~(a v t)
These last two are the same as “Frank is not angry and Hank is not tired.” (~a & ~t) 28 14 11/1/2016 Proof: ~(pvq)  ~p&~q p q ~(pvq) ~p&~q --- --- -------- --------- T T F F t f f T F F F t f t F T F F t t f F F T T f t t   29 look they match Conditional (if, then) statements
“If it rained then the ground is wet.” Where: r = it rained w = the ground is wet r w “r” is the antecedent “w” is the consequent
Lecture Notes © 2008 McGraw Hill Higher 30 Education 15 11/1/2016 Conditional truth tables
Truth table is tricky. “p q”
means “every time p is true, p q p q q is true.” Or “when p is true, q is --- --- ------ true.” T T T So, only when the antecedent is true and the consequent false, is it the T F F case that the conditional is false. F T T If this confuses you, don’t
worry… It is confusing. Just F F T remember it. 31 Be careful with negation and conditionals
If it did not rain, then the game was played. ~r p
If it did not rain, then the game was not played. ~r ~p
It is not the case that, if it rained then the game was played. ~(r p)
These all have different meanings. 32 16 11/1/2016 Be careful with negation and conditionals p q p q ~p q ~p ~q ~(p q) --- --- ----- -------- --------- ---------- T T T T T F f t f f t T F F T T T f f f t f F T T T F F t t t f t F F T F T F t f t t t 33 Argument: ~(p q), (q v r)  (q p) p q r ~(p q)* (q v r)* (q p) (C) --- --- --- ---------- ------- ------- T T T F T T t t t t t T T F F T T t t f t t T F T T T T Valid f f t f t because the T F F T F T f f f f t only row with true premises F T T F T F t t t t f also has a F T F F T F true t t f t f conclusion F F T F T T t f t f f F F F F F T 34 t f f f f 17