lOMoARcPSD|359 747 69 11/1/2016 Critical Thinking Chapter 9 A Little Categorical Logic
Lecture Notes © 2008 McGraw Hill Higher 1 Education Categorical Statements
 A Categorical Statement makes a claim about the
relationship between two or more categories or classes of things.
 Standard-Form Categorical Statements
 All S are P (e.g., All Democrats are liberals).
 No S are P (e.g., No Democrats are liberals).
 Some S are P (e.g., Some Democrats are liberals).
 Some S are not P (e.g., Some Democrats are not liberals). 2
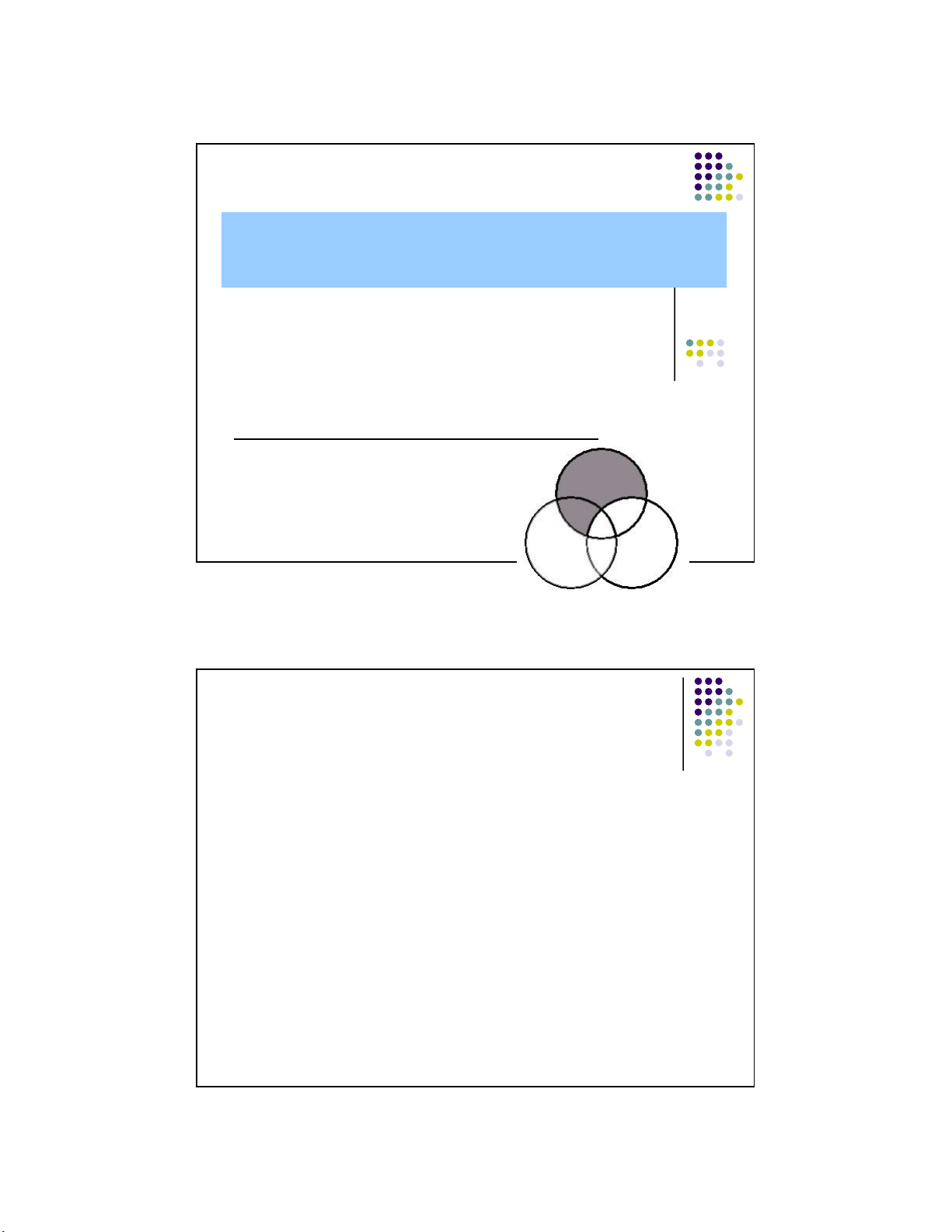
Lecture Notes © 2008 McGraw Hill Higher Education 1 lOMoARcPSD|359 747 69 11/1/2016 Venn diagrams
 Venn diagrams are ways to represent categorical
statements (or test categorical arguments) with a
series of overlapping circles that represent the
suggested groups and their relations.
 Open circles represent groups.
 Overlapping circles suggests that that there are things
which are members of both groups.
 An “X” is a portion of a circle entails that there is at
least one thing within that portion
 Coloring (shading) in a portion entails that there is nothing within that portion.
Lecture Notes © 2008 McGraw Hill Higher 3 Education
Standard-Form Examples All S are P. Some S are P. No S are P. Some S are not P.
Lecture Notes © 2008 McGraw Hill Higher Education 2 lOMoARcPSD|359 747 69 11/1/2016 4
Four Basic Parts of Categorical Statements
Lecture Notes © 2008 McGraw Hill Higher 5 Education
Lecture Notes © 2008 McGraw Hill Higher Education 3 lOMoARcPSD|359 747 69 11/1/2016
Translating into Standard Categorical Form
 Tip 1: Rephrase all nonstandard subject and
predicate terms so that they refer to classes.
 e.g., “All actors are vain” becomes “All actors are vain people.”
 Tip 2: Rephrase all nonstandard verbs.
 e.g., “Some students walk to school” becomes
“Some students are persons who walk to school.” 6
Lecture Notes © 2008 McGraw Hill Higher Education 4 lOMoARcPSD|359 747 69 11/1/2016
Translating into Standard Categorical Form
 Tip 3: Fill in any unexpressed quantifiers.  Examples:
 “Koalas are marsupials” becomes “All Koalas are marsupials.”
 “Californians are health nuts” becomes “Some
Californians are health nuts.” (Be charitable.)
Lecture Notes © 2008 McGraw Hill Higher 7 Education
Translating into Standard Categorical Form
 Tip 4: Translate singular statement as all or no
statements : Singular statement refers to a particular person or thing.
Lecture Notes © 2008 McGraw Hill Higher Education 5 lOMoARcPSD|359 747 69 11/1/2016
Translating into Standard
 e.g., “This flower is blooming” becomes “All things
identical with (that are) this (particular) flower are things that are blooming.”
 This may seem silly, but if we do this Venn
Diagrams can be used on more arguments. 8 Categorical Form
 Tip 5: Translate stylistic variants into the appropriate categorical form.
 e.g., “Only if something is a fish is it a salmon”
becomes “All salmon are fish.”
 See lists on p.234-235 (textbook).
Lecture Notes © 2008 McGraw Hill Higher 9 Education
Lecture Notes © 2008 McGraw Hill Higher Education 6 lOMoARcPSD|359 747 69 11/1/2016
Translating into Standard
Translating into Standard Categorical Form
Common Stylistic Variants of “No S are P”
 No P are S. Example: No vegetables are fruits.
 S are not P. Example: Oaks are not conifers.
 Nothing that is an S is a P. Example: Nothing that is a known fact is a mere opinion.
 No one who is an S is a P. Example: No one who is a Democrat is a Republican. 10 Categorical Form
Common Stylistic Variants of “No S are P”
 None of the S is a P. Example: None of the students is a registered Independent.
 Not a single S is P. Example: Not a single U.S. president is a woman.
 If anything is an S, then it is not a P. Example: If
anything is a plant, then it is not a mineral.
 All S are non-P. Example: All robots are nonhumans.
Lecture Notes © 2008 McGraw Hill Higher 11 Education
Lecture Notes © 2008 McGraw Hill Higher Education 7 lOMoARcPSD|359 747 69 11/1/2016
Translating into Standard
Translating into Standard Categorical Form
Common Stylistic Variants of “Some S are P”
Some P are S. Example: Some Democrats are women.
A few S are P. Example: A few mathematicians are poets.
There are S that are P. Example: There are monkeys that are carnivores.
Several S are P. Example: Several planets in the solar system are gas giants. 12 Categorical Form
Common Stylistic Variants of “Some S are P”
Many S are P. Example: Many billionaires are Internet tycoons.
Most S are P. Example: Most high school principals are men.
Nearly all S are P. Example: Nearly all Hollywood producers are liberals.
Lecture Notes © 2008 McGraw Hill Higher 13 Education
Lecture Notes © 2008 McGraw Hill Higher Education 8 lOMoARcPSD|359 747 69 11/1/2016
Translating into Standard
Translating into Standard Categorical Form
Common Stylistic Variants of “Some S are not P”
 Not all S are P. Example: Not all mammals are quadrupeds.
 Not everyone who is an S is a P. Example: Not
everyone who is a used-car dealer is a crook.
 S are not always P. Example: Sailors are not always swimmers.
 Some S are non-P. Example: Some theologians are nonbelievers. 14 Categorical Form
Common Stylistic Variants of “Some S are not P”
 There are S that are not P. Example: There are bears that are not carnivores.
 A few S are not P. Example: A few logicians are not eccentrics.
 Several S are not P. Example: Several of the world’s
most famous sports celebrities are not good role models.
 Most S are not P. Example: Most students are not binge drinkers.
Lecture Notes © 2008 McGraw Hill Higher Education 9 lOMoARcPSD|359 747 69 11/1/2016
Translating into Standard
 Nearly all S are not P. Example: Nearly all physicists are
not sharp dressers. Lecture Notes © 2008 McGraw Hill Higher 15 Education Categorical Syllogisms 
Syllogism: three-lined deductive argument. 
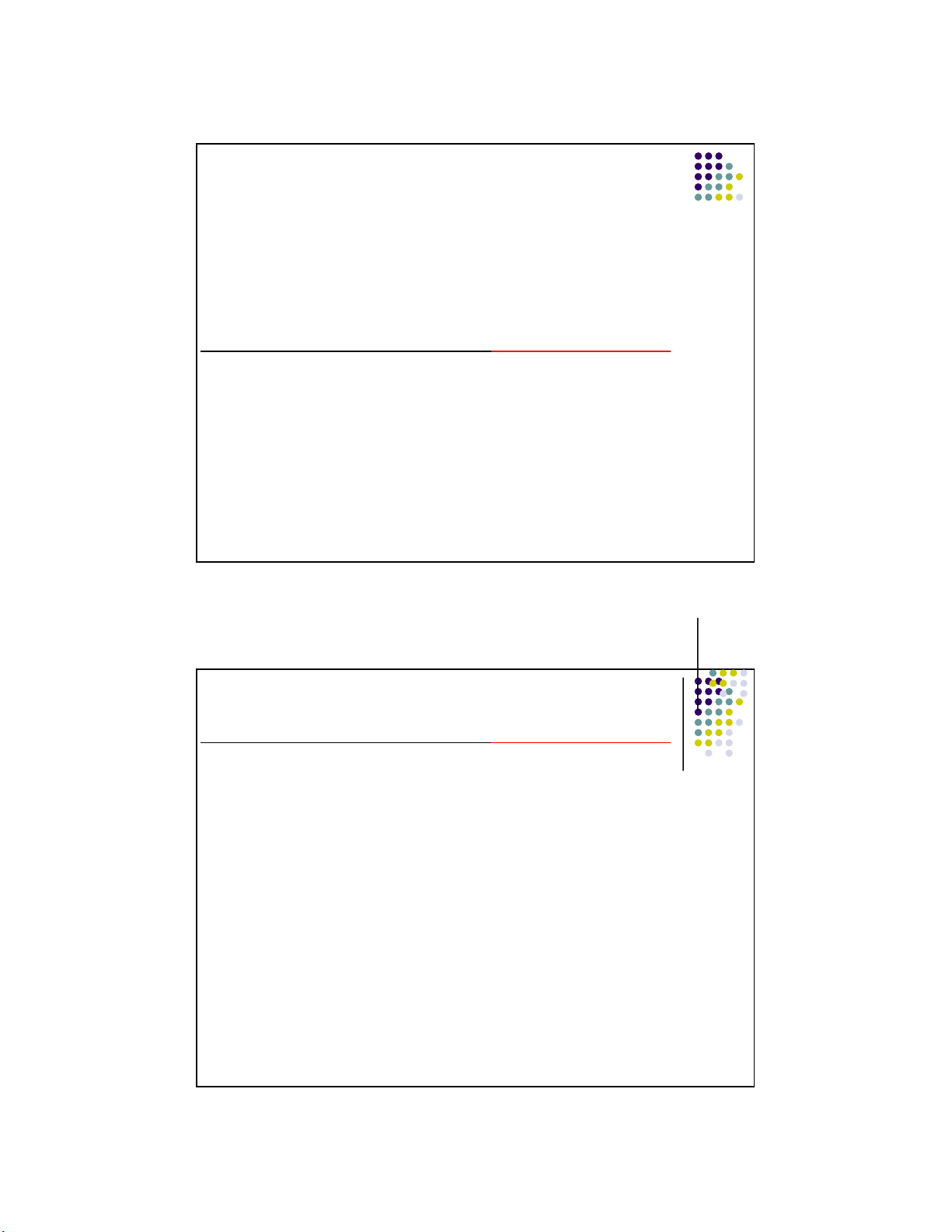
Categorical Syllogism: syllogism made of all categorical statements.  Example: 1.
No doctors are professional wrestlers. 2. All cardiologists are doctors 3.
So, no cardiologists are professional wrestlers.
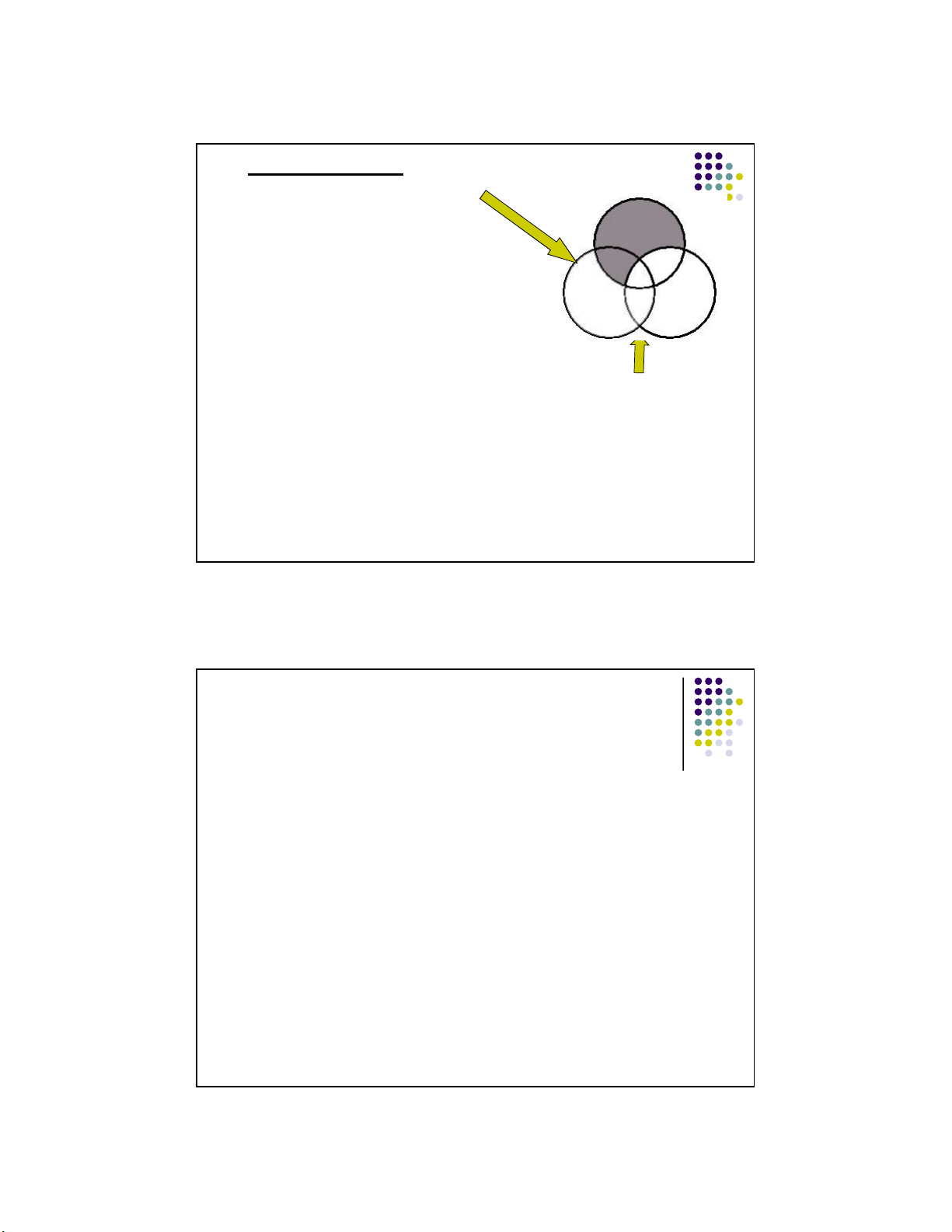
Let’s look at how to evaluate this argument with a Venn Diagram. 16
Lecture Notes © 2008 McGraw Hill Higher Education 10 lOMoARcPSD|359 747 69 11/1/2016 Using Venn Diagrams to Test Validity Since it has three category terms
(Doctor, Cardiologist, and Pro Wrestler) we need three interlocking circles.
Lecture Notes © 2008 McGraw Hill Higher 17 Education
Take it one statement at a time.
1. No doctors are professional wrestlers.
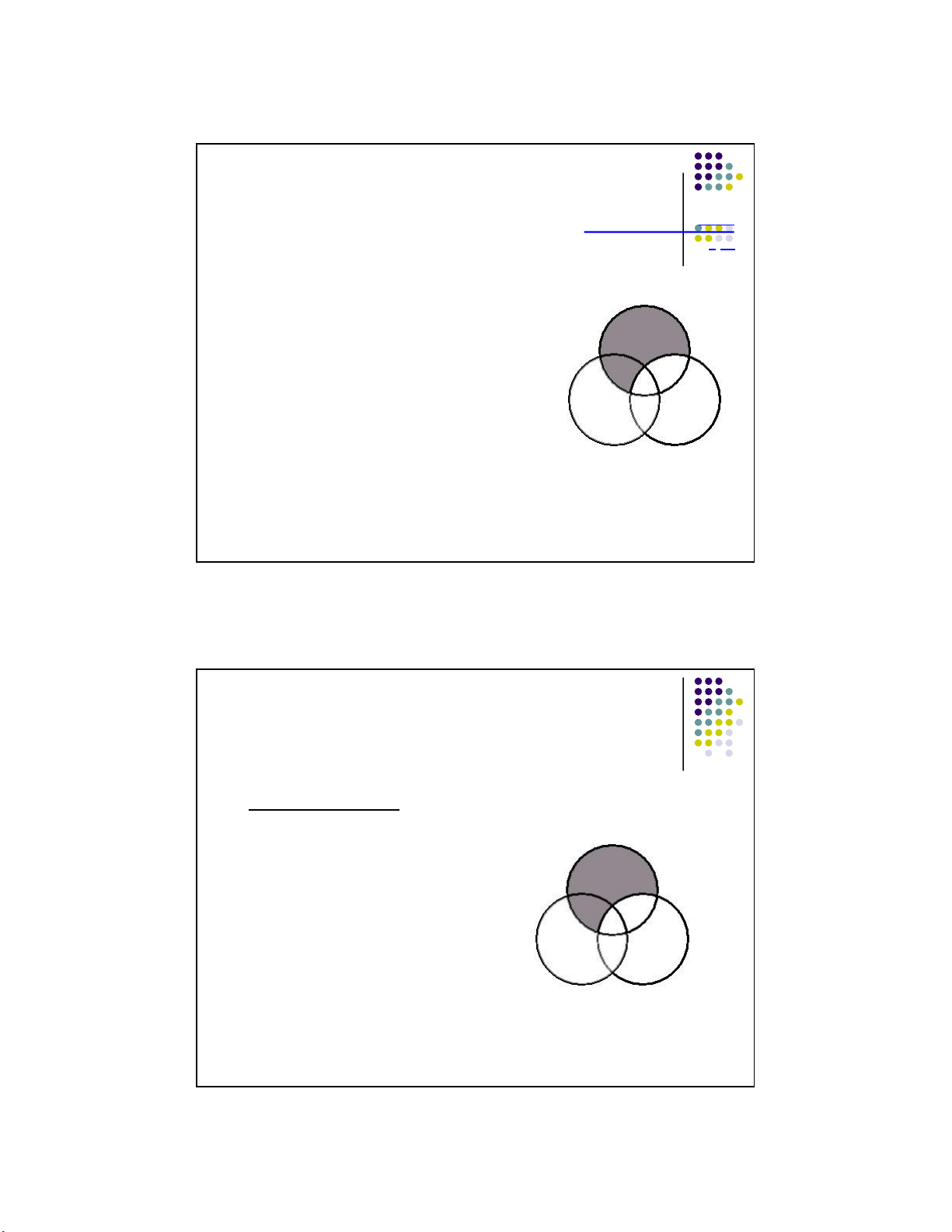
Lecture Notes © 2008 McGraw Hill Higher Education 11 lOMoARcPSD|359 747 69 11/1/2016 18 Take it one statement at a time. 1. No doctors are professional wrestlers. 2. All cardiologists are doctors (i.e., there are no non-doctor cardiologists).
Lecture Notes © 2008 McGraw Hill Higher 19 Education
Take it one statement at a time. 1.
No doctors are professional wrestlers. 2. All cardiologists are doctors (i.e., there are no non-doctor cardiologists). 3. So, no cardiologists are professional
Since the conclusion suggests the shared 12 lOMoARcPSD|359 747 69 11/1/2016
wrestlers. area between Cardiologists and Pro Wrestlers is empty (shaded), and the first two
premises already shaded that area, the argument is valid. 20
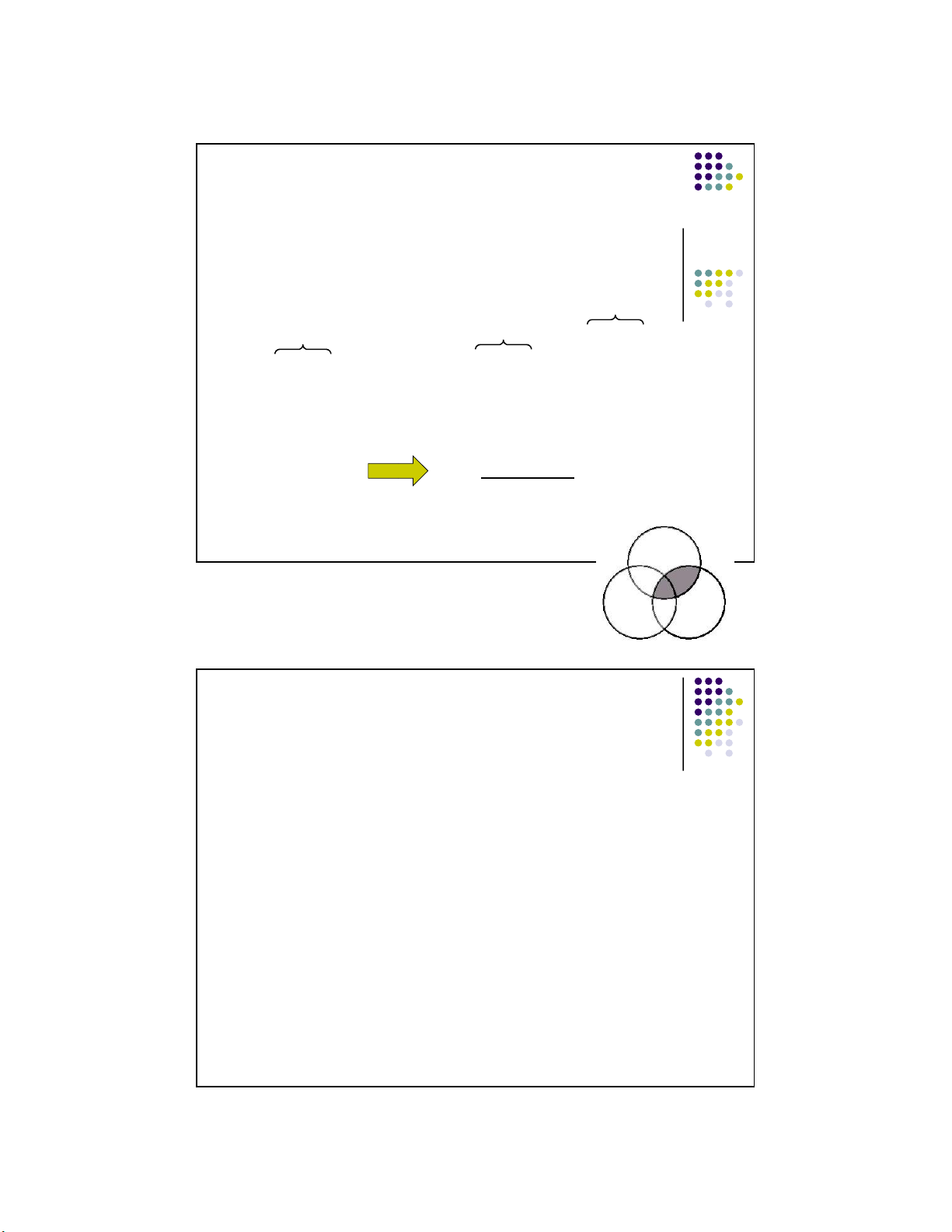
Take it one statement at a time. 1.
No doctors are professional wrestlers. 2.
All cardiologists are doctors (i.e., there are no non-doctor cardiologists). 3. So, no cardiologists are professional
We look at the diagram to see if this area is
wrestlers. shaded, and we see that it is indeed shaded. That means that the conclusion is implicitly
“contained in” (i.e., fol ows logically from) the
premises. Thus, the argument is shown to be 21 valid. 13 lOMoARcPSD|359 747 69 11/1/2016
Some Hints for “some” statements
 They don’t involve shading, but placing an “X” and can be tricky so…
 Always diagram them last (do your shading first).
 If part of the placement area has already been
shaded, place the X in the un-shaded area.
 If neither part of the placement area has been shaded,
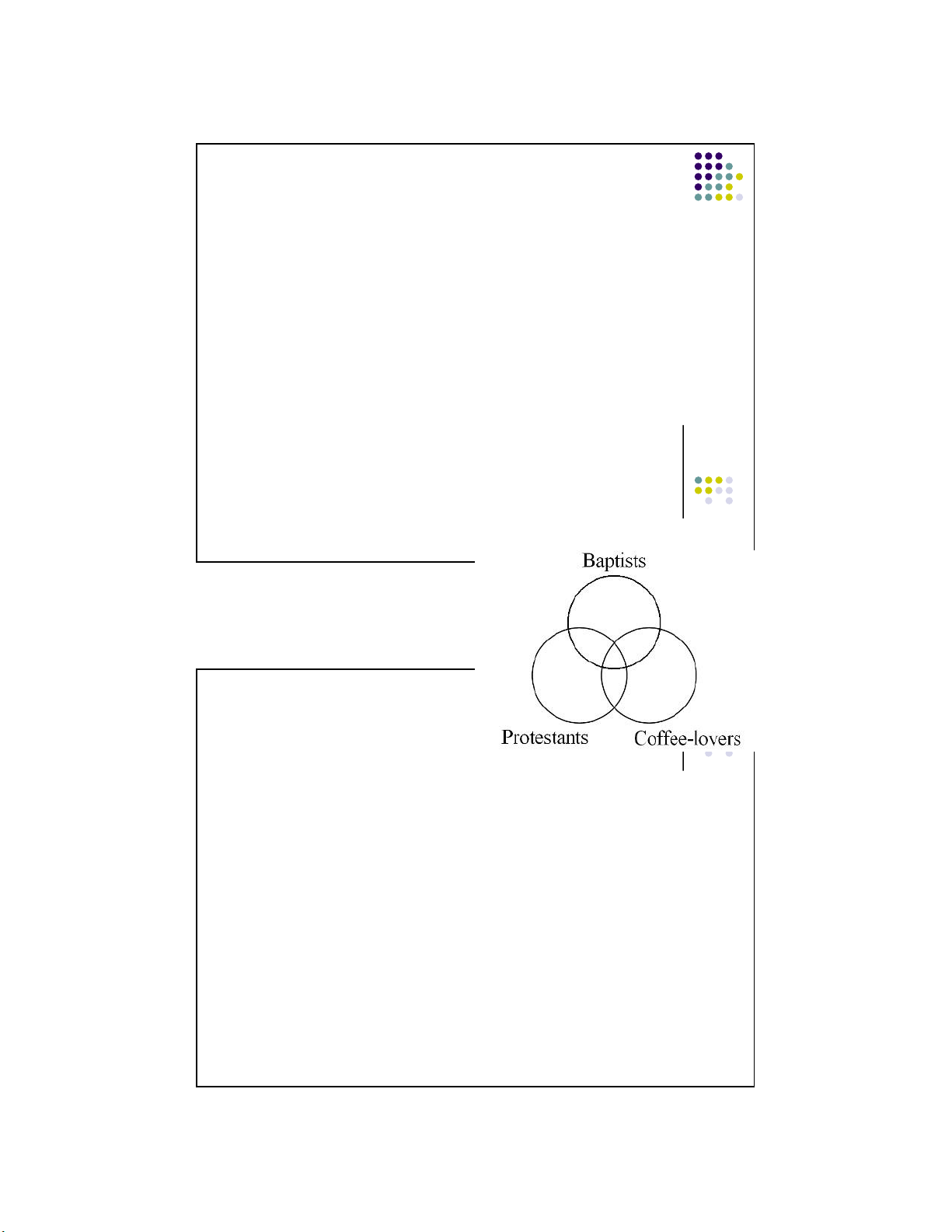
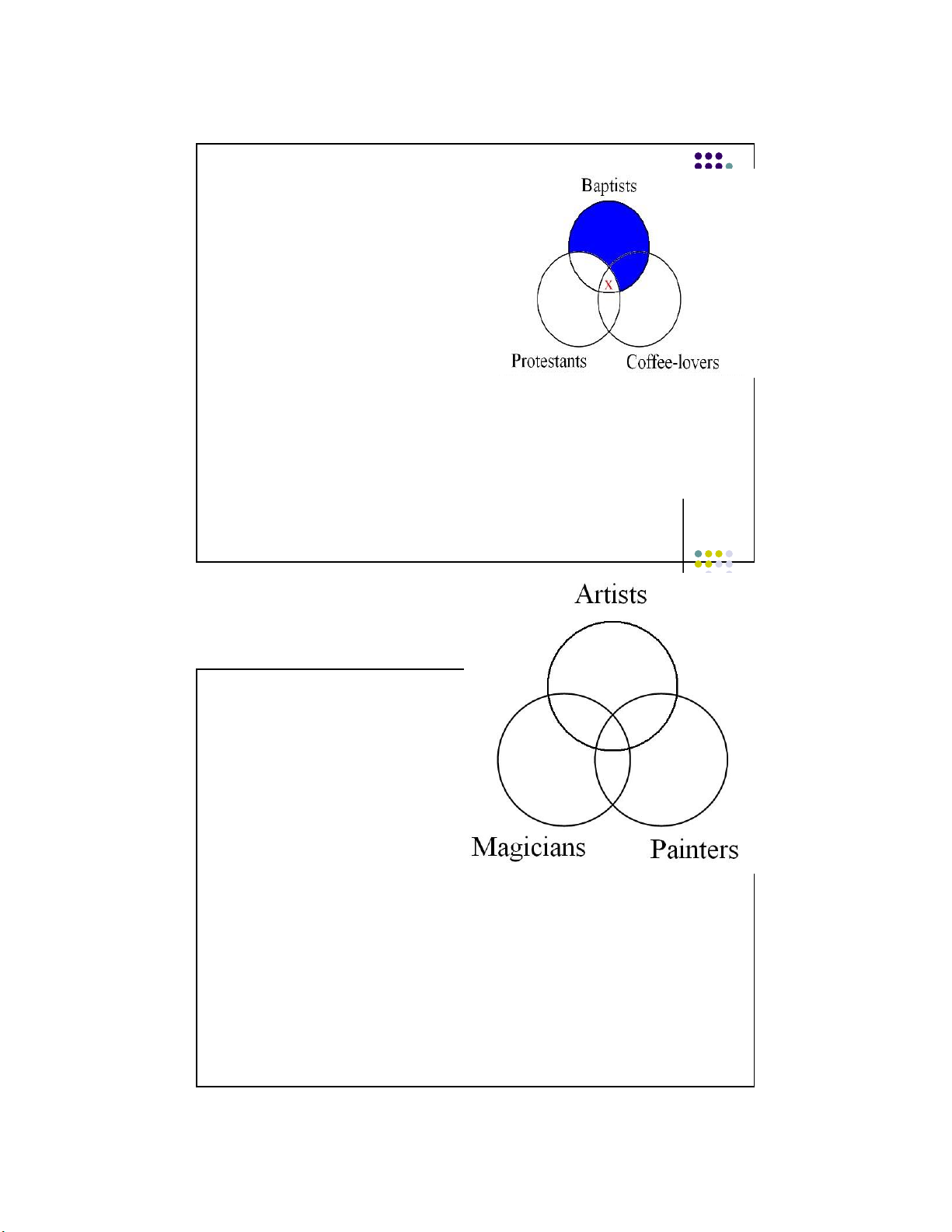
place the X on the line that separates the area. Lecture Notes © 2008 McGraw Hill Higher 22 Education Another example 1. Some Baptists are coffee-lovers. 2. All Baptists are Protestants. 3. So, some Protestants are coffee-lovers.
Lecture Notes © 2008 McGraw Hill Higher 23 Education 14 lOMoARcPSD|359 747 69 11/1/2016 Another example 1. 2. All Baptists are Protestants.
Notice we do the “all” statement first
Lecture Notes © 2008 McGraw Hill Higher because it requires shading. 24 Education Another example 1. Some Baptists are coffee-lovers. 2. All Baptists are Protestants. that Since part of the area represents the overlap of
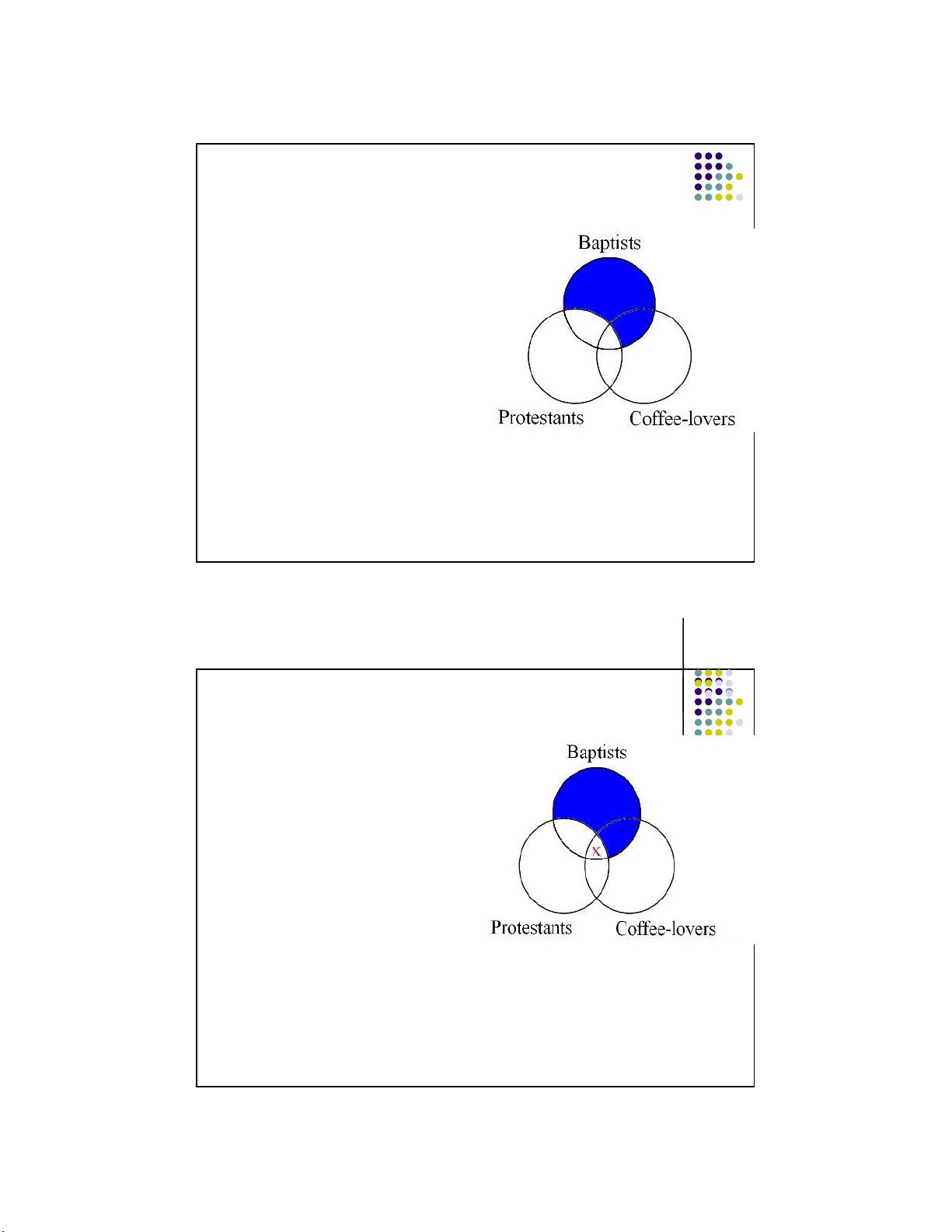
Baptists and Coffee-lovers is already
shaded, we place the “X” in the un- shaded part of that overlap.
Lecture Notes © 2008 McGraw Hill Higher 25 Education 15 lOMoARcPSD|359 747 69 11/1/2016 Another example 1. Some Baptists are coffee-lovers. 2. All Baptists are Protestants. 3. So, some
Protestants are coffee-lovers.
Since the conclusion suggests that there is at least
one individual within the overlap of Protestants and
coffeelovers, and the first two premises place an “X” in that
area, the argument is valid. 26
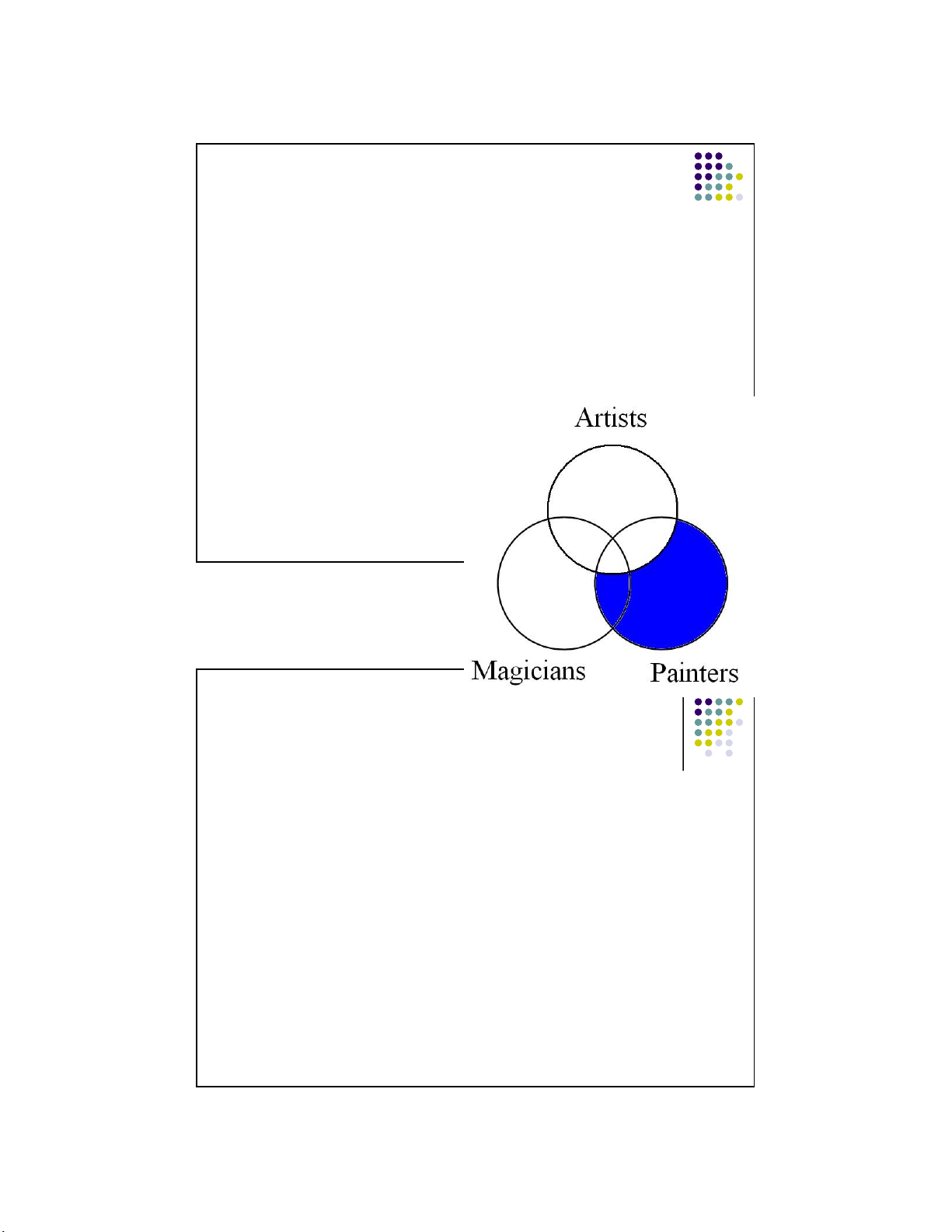
Example with an invalid argument. 1. All painters are artists. 2. Some magicians are artists. 3.
So, some magicians are painters. 16 lOMoARcPSD|359 747 69 11/1/2016
Lecture Notes © 2008 McGraw Hill Higher 27 Education
Example with an invalid argument. 1. All painters are artists.
Notice we start with the first premise
because it is an “al ” statement and thus requires shading. Lecture
Notes © 2008 McGraw Hill Higher 28 Education 17 lOMoARcPSD|359 747 69 11/1/2016 Example with an invalid argument. 1. All painters are artists. 2. Some magicians are artists.
The second premise suggests there is
at least one thing in the overlap of
magicians and artists. Since neither
section of that overlap (the painters vs.
non painters) is shaded, and we don’t
know if that thing would be a painter or
not, we place the X right on the line that divides the overlap.
Lecture Notes © 2008 McGraw Hill Higher 29 Education
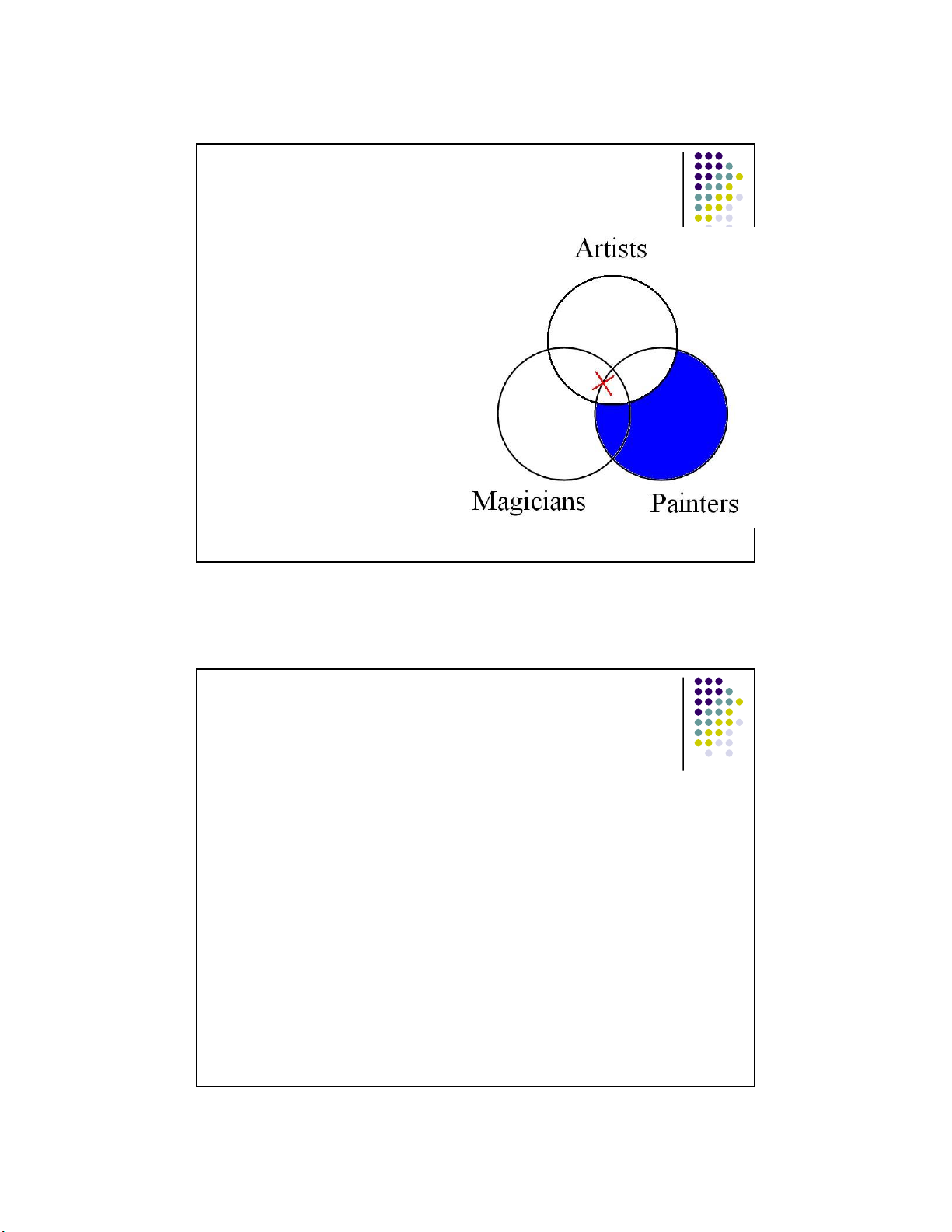
Example with an invalid argument. 18 lOMoARcPSD|359 747 69 11/1/2016 1. All painters are artists. 2. Some magicians are artists. 3. So, some magicians are painters.
Since we already know that the rest of
the overlap between Magicians and
Painters is empty, in order for the
conclusion to be true, there would need
to be an “X” in the middle overlap—
where the “?” is. But the first two
premises don’t give us enough
information to know if the “X” goes there or not. So the argument is invalid.
Lecture Notes © 2008 McGraw Hill Higher 30 Education Step by Step
For step by step instructions on using Venn
Diagrams to Test the Validity of Categorical Syllogisms, see p. 237-247.
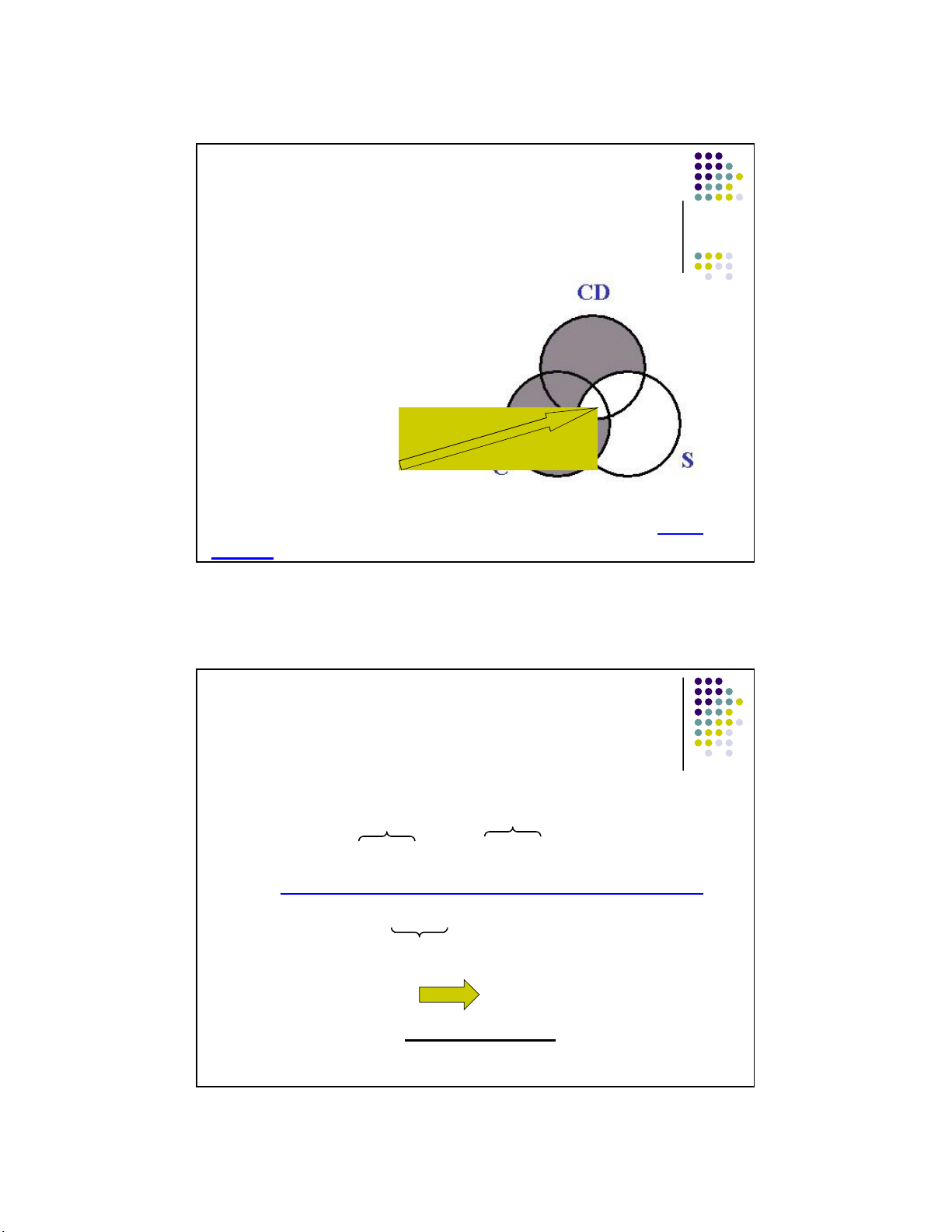
Lecture Notes © 2008 McGraw Hill Higher 31 Education 19 lOMoARcPSD|359 747 69 11/1/2016 Venn Diagram CD are S All C are C CD All C are S
For convenience it is best to be
consistent in assigning terms to
the circles. The subject term of S
the conclusion is assigned the
lower left circle, and the All
predicate term of the conclusion CD
is assigned the lower right circle. Venn Diagram
As you work through this tutorial, realize that what
you draw in the Venn Diagram represents exactly
what is in the premises of the syllogism; nothing more and nothing less.
There are three steps in this process: CD 1. Draw premise one. 2. Draw premise two.
3. Check the validity. CS Venn Diagram CD 20 lOMoARcPSD|359 747 69 11/1/2016
So, to represent “All CD are S”
we focus on the CD and S circles only. Our rule is to shade EMPTY areas.
Imagine that we don’t know C S how many things are inside
these circles, or where exactly
they are inside the circles, but All CD are S
we know that all the things in All C are CD CD are also in S. All C are S Venn Diagram
Look at the first premise and then at the shading. Since
we know all CD are in S, we know the rest of CD is empty. 21 lOMoARcPSD|359 747 69 11/1/2016
Now draw premise 2. All the items in C are also in CD.
Thus the rest of C is empty All CD are S and should be shaded. All C are CD All C are S Venn Diagram All CD are S All C are CD
Now for step 3. We’ve drawn All C are S
each premise exactly and can now
check for validity. If valid, the
conclusion will be shown in the
drawing to be necessarily true.
If the drawing allows for the
possibility of the conclusion
being false then the syllogism is
invalid. What do you think? Valid or Invalid? 22 lOMoARcPSD|359 747 69 11/1/2016 Venn Diagram
This is a valid syllogism . The drawing clearly shows that the conclusion is necessarily true. All
C are indeed S . The only area of C that is not
empty is the part All CD are S that is in S. All C are CD All C are S Venn Diagram - Example E R
All educated people respect books.
Some bookstore personnel are not truly educated.
Some bookstore personnel don’t respect books. B All E are R Translated into
standard form Some B are not E 23 lOMoARcPSD|359 747 69 11/1/2016 Some B are not R Be clear that: E = Educated people
R = People who respect books.
B = Bookstore personnel Venn Diagram - Example All E are R Some B are not E E Some B are not R
Draw the first premise. All E
are inside R, so we know that the rest of E is empty. We
represent this empty area by B R shading it. Venn Diagram - Example All E are R 24 lOMoARcPSD|359 747 69 11/1/2016 Some B are not E Some E B are not R Should the X “X” go here?
Now the second premise.
We read “some” as “at
least one” and represent it X X
with an “X.” So we want to B R put an X
inside the B circle but
outside of the E circle. Or here?
We want to say exactly what the premises say, but no more. 25 lOMoARcPSD|359 747 69 11/1/2016 Venn Diagram - All E are R Example
Some B are n ot E
Some B are no t R
Think about it. If we opt for E the blue X, we are saying
“some B are not R,” but this is not in the premises and we
can’t draw something that is
not in the premises. Likewise the red X? X?
X would say, “Some B are R,” and B R
this is not in the premises either.
What we need is an “X” on the line which will mean that
“some B” are on one side of the line or the other, or both,
but we’re not sure which. Venn Diagram - Example All E are R Some B are not E Some B are not R E
So, having drawn exactly what
is in the two premises and no more, is the conclusion
necessarily true? Is it true that X? some B are not R? B R 26 lOMoARcPSD|359 747 69 11/1/2016
No, this is an invalid argument.
The “X” shows that there may be
some B that are not R, but not necessarily. Venn Diagram - H Example I M
No islands are part of the mainland and Hawaii is an
island. Therefore, Hawaii is not on the mainland. No I are M Translated into All H are I
standard formNo H are M I
Draw the first premise. Nothing that is
an I is inside the M circle. So, all the
things inside I, if there are any, are in the other parts of the circle. H M Venn Diagram - Example I No I are M 27 lOMoARcPSD|359 747 69 11/1/2016 All H are I No H are M
Now draw the second premise. Everything that is in the H
circle is also in the I circle. H M
Thus, the rest of the H circle is empty and should be shaded.
Step 3 asks you to look at what you’ve drawn and see if
the conclusion is necessarily true. Is it necessarily true
from the picture that nothing in the H circle is in the M circle?
Yes, this is a valid argument!
Venn Diagram - Example M C
Some modems are cable connections and some cable
connections are digital. Thus, some modems are digital. D Some M are C Translated into Some C are D
standard formSome M are D C
Draw the first premise. At least one thing
in M is also in C. Where should the “X” X
go? Do you see why the “X” has to go on
the line? From the premise you can’t tell which
side of the line is correct. M D 28 lOMoARcPSD|359 747 69 11/1/2016 C Venn Diagram - Example XX Some M are C Some C are D Some M are D
Now the second premise. Where should M
D the “X” go to represent ‘at least one’ C
that is inside the D circle? Remember you want to draw
just what the premise says, no more and no less.
Again, the “X” must go on the line. Our drawing can
never be more precise than the premise is. Is it Valid?
No this is an invalid argument. There is no guarantee,
from the premises that the conclusion is true. There
may or may not be an M in the D circle. 29
Document Outline

• Categorical Statements
• Venn diagrams
  • Translating into Standard Categorical Form
  • Categorical Form
  • Translating into Standard Categorical Form (1)
  • Categorical Form (1)
  • Translating into Standard Categorical Form (2)
  • Categorical Form (2)
  • Translating into Standard Categorical Form (3)
  • Categorical Form (3)
  • Translating into Standard Categorical Form (4)
  • Categorical Form (4)
• Categorical Syllogisms
  • Using Venn Diagrams to Test Validity
    • 3. So, no cardiologists
    • 3. So, no cardiologists (1)
  • Some Hints for “some” statements
• Another example
• Another example (1)
• Another example (2)
• Another example (3)
• Step by Step
  • Venn Diagram
  • Venn Diagram (1)
  • Venn Diagram (2)
  • Venn Diagram - Example
  • Venn Diagram - Example (1)
    • Some B are not E E
  • Venn Diagram - Example (2)
  • Venn Diagram - Example (3)
  • Venn Diagram - Example (4)
    • Some B are not E
  • Venn Diagram - Example (5)
  • Venn Diagram - Example (6)
    • All H are I
  • Venn Diagram - Example M C
  • Venn Diagram - Example (7)