Cuối kỳ cơ sở dữ liệu | Cơ sở dữ liệu | Trường Đại học Công nghiệp TP.HCM
Cuối kỳ cơ sở dữ liệu môn Cơ sở dữ liệu của Trường Đại học Công nghiệp Thành phố Hồ Chí Minh. Hi vọng tài liệu này sẽ giúp các bạn học tốt, ôn tập hiệu quả, đạt kết quả cao trong các bài thi, bài kiểm tra sắp tới. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.
Môn: Cơ sở dữ liệu (ĐHCN) 19 tài liệu
Trường: Đại học Công nghiệp Thành phố Hồ Chí Minh 405 tài liệu
Tác giả:
Preview text:
Câu 2: Q(A,B,C,D,E,G)
Cho F={AB→C;C→A;BC→D;ACD→B;D→EG;BE→C;CG→BD;CE → AG}
X={B,D}, X+=?
Y={C,G}, Y+=?
Bài làm X={B,D}, X+=?
X+=B,D
D→EG => X+=B,D,E,G
BE→C => X+=B,D,E,G,C
CE → AG => X+=B,D,E,G,C,A
Vậy X+= A,B,C,D,E,G Y={C,G}, Y+=?
Y+ = C,G
C→A => Y+ = C,G,A
CG→BD => Y+ = C,G,A,B,D
D→EG => Y+ = C,G,A,B,D,E
Vậy Y+ = A,B,C,D,E,G
Câu 3: cho lược ồ quan hệ Q và tập phụ thuộc hàm F
- F={AB→E;AG→I;BE→I;E→G;GI→ H} chứng minh rằng AB → GH.
- F={AB→C;B→D;CD→E;CE→GH;G→A}chứng minh rằng AB → E; AB → G
Bài làm
- Ta tìm bao óng của AB AB+ = { ABEGHI} AB → GH là thành viên của F+
Vì GH thuộc {ABEGHI} Vậy nên ta
Chứng minh ược AB → GH
- Ta tìm bao óng của AB AB+ = { ABCDEGH}
AB → E là thành viên của F+ vì E thuộc { ABCDEGH }
AB → G là thành viên của F+ vì G thuộc { ABCDEGH }
Vậy nên ta chứng minh ược AB → E VÀ AB → G
Câu 4: Cho quan hệ r
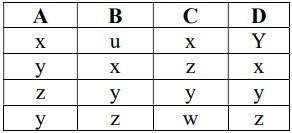
Trong các phụ thuộc hàm sau ây, PTH nào không thỏa A → B; A → C; B → A; C → D; D → C; D → A Bài làm
Xét A → B: ta thấy A2 = A4 = y mà B2 ≠ B4 => Không thoả
Xét A → C: ta thấy A2 = A4 = y mà C2 ≠ C4 => Không thoả
Xét C → D: ta thấy C3 = D3 = y => Thoả
Xét D → C: ta thấy D1 = D3 = y mà C1 ≠ C3 => Không thoả
Xét D → A: ta thấy A2 = A4 = y mà D2 ≠ D4 => Không thoả
Câu 6: Xét lược ồ quan hệ và tập phụ thuộc dữ liệu: Q(C,T,H,R,S,G)
f={ f1: C→ T; f2: HR→ C; f3: HT→ R; f4: CS→ G; f5: HS→ R}
Tìm phủ tối thiểu của F
Bài làm:
Phân tích tập phụ thuộc dữ liệu f:
- f1: C → T: C xác ịnh duy nhất T.
- f2: HR → C: HR xác ịnh duy nhất C.
- f3: HT → R: HT xác ịnh duy nhất R.
- f4: CS → G: CS xác ịnh duy nhất G.
- f5: HS → R: HS xác ịnh duy nhất R. Xác ịnh các thuộc tính phụ thuộc:
- T phụ thuộc vào C (f1: C → T).
- S phụ thuộc vào C (f4: CS → G, suy ra CS → CSG, suy ra CS → C). Loại bỏ các phụ thuộc hàm thừa:
- f2: Do C → T và HR → C, ta có thể suy ra HR → T. Do ó, f2 là phụ thuộc hàm thừa.
- f5: Do HT → R và HS → T, ta có thể suy ra HS → R. Do ó, f5 là phụ thuộc hàm thừa.
Sau khi loại bỏ các phụ thuộc hàm thừa, ta còn lại tập phụ thuộc hàm tối thiểu sau:
- f1: C → T
- f3: HT → R
- f4: CS → G
Kiểm tra tính tối thiểu:
- Loại bỏ f1: Việc loại bỏ f1 sẽ vi phạm phụ thuộc hàm f2 (HR → C).
- Loại bỏ f3: Việc loại bỏ f3 sẽ vi phạm phụ thuộc hàm f5 (HS → R).
- Loại bỏ f4: Việc loại bỏ f4 không vi phạm bất kỳ phụ thuộc hàm nào khác. Do ó, tập phụ thuộc hàm f1, f3, f4 là tối thiểu.
Kết luận: Phủ tối thiểu của F cho lược ồ quan hệ Q và tập phụ thuộc dữ liệu f là {C → T, HT → R, CS → G}.
Câu 8: Q(A,B,C,D) F={AB→C; D→B; C→ABD} Hãy tìm tất cả các khóa của Q
Bài làm
TN: (rỗng) TG: ABCD
Xi | (TN → Xi) | (TN → Xi)+ | Siêu Khoá | Khoá |
→ | → | → |
|
|
A | A | A |
|
|
B | B | B |
|
|
C | C | ABCD | C | C |
D | D | DB |
|
|
AB | AB | ABCD | AB | AB |
AC | AC | ABCD | AC |
|
AD | AD | ABCD | AD | AD |
BC | BC | ABCD | BC |
|
BD | BD | BD |
|
|
CD | CD | ABCD | CD |
|
ABC | ABC | ABCD | ABC |
|
ABD | ABD | ABCD | ABD |
|
BCD | BCD | ABCD | BCD |
|
ACD | ACD | ABCD | ACD |
|
ABCD | ABCD | ABCD | ABCD |
|
BÀI TẬP TỔNG HỢP
Câu 2: Kiểm tra dạng chuẩn Q(C,S,Z) F={CS→Z;Z→C} Bài làm
TN: S TG: CZ
Xi | (TN → Xi) | (TN → Xi)+ | Siêu khoá | Khoá |
| S | S |
|
|
C | SC | SCZ | SC | SC |
Z | SZ | SZC | SZ | SZ |
CZ | SCZ | SCZ | SCZ |
|
=>Chuẩn dạng 3 vì vế trái ều là thuộc tính khoá
Câu 4: Cho lược ồ quan hệ Q(A,B,C,D) và tập phụ thuộc hàm F
F = {A→B;B→C; D→B} C = {Q1(A,C,D); Q2(B,D)}
a) Xác ịnh các Fi (những phụ thuộc hàm F ược bao trong Qi) Bài làm
- Q1 (A,C,D)
A -> B không bao trong Q1 vì B không thuộc lược ồ của Q1 B -> C không bao trong Q1 vì B không thuộc lược ồ của Q1
D -> B không bao trong Q1 vì B không thuộc lược ồ của Q1
F1 = 
vì không có phụ thuộc hàm nào trong F hợp lệ trong Q1
- Q2 (B,D)
- -> B không bao trong Q2 vì A không thuộc lược ồ của Q2
- -> C không bao trong Q2 vì C không thuộc lược ồ của Q2
D -> B bao trong Q2 vì cả D và B ều thuộc lược ồ của Q2
F2 = { D -> B}
Vậy: các phụ thuộc hàm ược bao trong các quan hệ con Q1 và Q2 là :
Q1 (A,C,D): không có phụ thuộc hàm nào
Q2 (B,D): D -> B
Câu 5: Giả sử ta có lược ồ quan hệ Q(C,D,E,G,H,K) và tập phụ thuộc hàm F như sau: F = {CK→ H; C →D;E→C; E →G;CK →E}
- Từ tập F, hãy chứng minh EK → DH
- Tìm tất cả các khóa của Q
- Xác ịnh dạng chuẩn của Q.
Bài làm a) Từ tập F, hãy chứng minh EK → DH
EK+=E,K
E→C => EK+=E,K,C
C →D => EK+=E,K,C,D
CK→ H => EK+=E,K,C,D,H
Ta thấy bao óng EK có chứa DH nên EK->DH(Điều phải chứng minh)
- Tìm tất cả các khóa của Q.
TN=K
TG=C,E
Xy | Xy U TN | (Xy U TN)+ | Siêu khóa | Khóa |
Rỗng | K | K |
|
|
C | CK | C,K,H,E,D,G | CK | CK |
D | DK | D,K |
|
|
E | EK | E,K,C,G,H,D | EK | EK |
G | GK | G,K |
|
|
H | HK | H,K |
|
|
CD | CDK | E,K,C,G,H,D | CDK |
|
CE | CEK | E,K,C,G,H,D | CEK |
|
CG | CGK | E,K,C,G,H,D | CGK |
|
CH | CHK | E,K,C,G,H,D | CHK |
|
DE | DEK | E,K,C,G,H,D | DEK |
|
DG | DGK | D,G,K |
|
|
DH | DHK | D,H,K |
|
|
EG | EGK | E,K,C,G,H,D | EGK |
|
EH | EHK | E,K,C,G,H,D | EHK |
|
GH | GHK | G,H,K |
|
|
CDE | CDEK | E,K,C,G,H,D | CDEK |
|
CDG | CDGK | E,K,C,G,H,D | CDGK |
|
CDH | CDHK | E,K,C,G,H,D | CDHK |
|
DEG | DEGK | E,K,C,G,H,D | DEGK |
|
DEH | DEHK | E,K,C,G,H,D | DEHK |
|
EGH | EGHK | E,K,C,G,H,D | DEHK |
|
CDEG | CDEGK | E,K,C,G,H,D | CDEGK |
|
CDEH | CDEHK | E,K,C,G,H,D | CDEHK |
|
DEGH | DEGHK | E,K,C,G,H,D | DEGHK |
|
CDEGH | CDEGHK | E,K,C,G,H,D | CDEGHK |
|
Tất cả các khóa của Q={EK,CK} Thuộc tính khóa bao gồm E,C,K
- Xác ịnh dạng chuẩn của Q.
-Xét dạng chuẩn BC
Tách F về các phụ thuộc hàm vế phải 1 thuộc tính
Ftt= { CK→ H; C →D; E→C; E →G; CK →E}
Ta thấy CK->H có H không là siêu khóa nên có không ạt chuẩn BC
-Xét chuẩn 3
Ta thấy CK->H có H không là siêu khóa và cũng không là thuộc tính khóa nên không ạt chuẩn 3 -Xét chuẩn 2
+ Xét khóa CK:
C+=C,D
Ta thấy D không là thuộc tính khóa nên không ạt chuẩn 2 + Xét khóa EK:
E+ = E,C,G
Ta thấy C và G không là thuộc tính khóa nên không ạt chuẩn 2
Vậy lược ồ Q ạt chuẩn 1
Câu 6: Cho lược ồ quan hệ Q(S,I,D,M) F = {f1:SI → DM; f2:SD→ M; f3:D→ M} a)
Tính bao óng D+ , SD+ , SI+
- Tính bao óng D+, SD+, SI+
- Tìm tất cả các khóa của Q
- Tìm phủ tối thiểu của F
- Xác ịnh dạng chuẩn cao nhất của Q
Bài làm F = { SI -> DM, SD -> M, D -> M }
- D+ = {DM}
SD+ ={ SDM}
SI+ ={SIDM}
- TN= SIDM – DM= SI
TG= SID ∩ DM= D
XiXi U TN(Xi U TN)+ SIÊU KHÓAKHÓA
SISIDMSISI
DDSISIDMDSI
Khóa SI
c)
- Bước1: tách F thành 1 phụ thuộc hàm vế phải có 1 thuộc tính
SI -> D, SI -> M, SD -> M, D -> M - Bước 2:
SI -> D
Giả sử bỏ S, I+ ={I} không chứa D=>S không dư
Bỏ I, S+ ={S} không chứa D => I không dư
SI -> M
Giả sử bỏ S, I+ ={I} không chứa M => S không dư
Bỏ I, S+ ={S} không chứa M => I không dư - Bước 3:
Giả sử SD -> M thừa
SD+ ={ SDM} có M => SD -> M thừa
Giả sử D -> M thừa
D+ ={D} không chứa M => D -> M không thừa => phủ tối thiểu: F ={ SI -> D, SI -> M, D -> M}
Xác ịnh dạng chuẩn
D -> M, D không là siêu khóa
=> không ạt BCNF
D -> M, D không là siêu khóa, M không phải là thuộc tính khóa -> không ạt 3NF
S+ ={S}
I+ = {I}
=> Đạt 2NF
Câu 7: Kiểm Tra Dang Chuẩn
- Q(A,B,C,D) F={CA→D; A→B}
- Q(S,D,I,M) F={SI→D;SD→M}
- Q(N,G,P,M,GV) F={N,G,P→M;M→GV}
- Q(S,N,D,T,X) F={S→N; S→D; S→T; S→X} Bài làm:
- Q(A,B,C,D), F={CA→D; A→B}:
- CA→D: Không có vấn ề vì CA là khóa chính (tổ hợp của CA duy nhất xác ịnh một giá trị cho D).
- A→B: Không có vấn ề vì A không phải là khóa chính.
=> Đây là dạng chuẩn.
- Q(S,D,I,M), F={SI→D; SD→M}:
- SI→D: Không có vấn ề vì SI là khóa chính.
- SD→M: Có vấn ề vì SD không phải là khóa chính. M không ầy ủ phụ thuộc vào khóa chính. => Không phải dạng chuẩn.
- Q(N,G,P,M,GV), F={NGP→M; M→GV}:
- NGP→M: Không có vấn ề vì NGP là khóa chính.
- M→GV: Không có vấn ề vì M không phải là khóa chính.
=> Đây là dạng chuẩn.
- Q(S,N,D,T,X), F={S→N; S→D; S→T; S→X}:
- S→N, S→D, S→T, S→X: Có vấn ề vì không có một tập con của S nào duy nhất xác ịnh một giá trị duy nhất cho N, D, T, và X. Điều này chỉ xảy ra nếu S là khóa chính và không có phụ thuộc phần bổ sung nào.
- Các phụ thuộc hàm này vi phạm khái niệm về phụ thuộc hàm (một thuộc tính không thể xác ịnh nhiều thuộc tính khác).
=> Không phải dạng chuẩn.