ĐÁP ÁN ĐỀ KTCKI_TOÁN 9_KNTT

ĐỀ KIỂM TRA CUỐI HỌC KÌ I 2025 – 2026 MÔN TOÁN – LỚP 9
Thời gian làm bài: 90 phút
Bài 1. (1,5 điểm) Rút gọn biểu thức 5+√10 8
a) 2√5 − √125 − √80 + √605 b) + √5+√2 1−√5 𝑥−9 c) ( √𝑥 + √𝑥 ) . ; 𝑥 > 0, 𝑥 ≠ 9 √𝑥−3 √𝑥+3 √9𝑥 LỜI GIẢI a)
2√5 − √125 − √80 + √605
= 2√5 − √52. 5 − √42. 5 + √112. 5
= 2√5 − 5√5 − 4√5 + 11√5 = 4√5 5+√10 4 b) + √5+√2 1−√5 √5 (√5+√2) 4(1+√5) = + √5+√2 (1−√5)(1+√5) 4(1+√5) = √5 + 1−5 = √5 − 1 − √5 = −1 c) √𝑥 √𝑥 𝑥 − 9 ( + ) . √𝑥 − 3 √𝑥 + 3 √9𝑥
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn
√𝑥(√𝑥 + 3) + √𝑥(√𝑥 − 3) (√𝑥 + 3)(√𝑥 − 3) = . (√𝑥 + 3)(√𝑥 − 3) √9𝑥
𝑥 + 3√𝑥 + 𝑥 − 3√𝑥 (√𝑥 + 3)(√𝑥 − 3) = . (√𝑥 + 3)(√𝑥 − 3) √9𝑥 2 = √𝑥 3
Bài 2. (1,5 điểm) Giải các phương trình, hệ phương trình sau:
a) (𝑥 + 5)(3𝑥 − 9) = 0 𝑥 − 𝑦 = 1 b) {3𝑥 + 𝑦 = 7 1 1 5𝑥 c) − = 𝑥+5 𝑥−5 𝑥2−25 LỜI GIẢI
a) (𝑥 + 5)(3𝑥 − 9) = 0
𝑥 + 5 = 0 hoặc 3𝑥 − 9 = 0 𝑥 = −5 hoặc x = 3
Vậy phương trình đã cho có nghiệm là 𝑥 = −5 hoặc 𝑥 = 3 𝑥 − 𝑦 = 1 (1) b) { 3𝑥 + 𝑦 = 7 (2)
Cộng hai vế của hai phương trình ta được: 4𝑥 = 8, suy ra 𝑥 = 2 Thay x = 2 vào (1) ta có: 2 − 𝑦 = 1 y = 1
Vậy hệ phương trình đã cho có nghiệm duy nhất (x;y) = (2;1) 1 1 5𝑥 c) − = 𝑥+5 𝑥−5 𝑥2−25
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn
ĐKXĐ: 𝑥 ≠ 5; 𝑥 ≠ −5 𝑥 − 5 𝑥 + 5 5𝑥 − = (𝑥 − 5)(𝑥 + 5) (𝑥 + 5)(𝑥 − 5) (𝑥 − 5)(𝑥 + 5)
𝑥 − 5 − (𝑥 + 5) = 5𝑥 5𝑥 = −10 𝑥 = −2 (nhận) Vậy 𝑥 = −2
Bài 3. (1,5 điểm) Trong tháng thứ nhất, cả hai phân xưởng sản xuất được 800 sản phẩm. So
với tháng thứ nhất, tháng thứ hai phân xưởng 1 sản xuất vượt 16%, phân xưởng 2 sản xuất
vượt 12%, nên trong tháng này cả hai phân xưởng sản xuất được 910 sản phẩm. Hỏi trong
tháng thứ nhất, mỗi phân xưởng sản xuất được bao nhiêu sản phẩm? LỜI GIẢI
Gọi x là số sản phẩm tháng thứ nhất xưởng 1 sản xuất được (𝑥 ∈ ℕ∗, 𝑥 < 800, sản phẩm)
y là số sản phẩm tháng thứ nhất xưởng 2 sản xuất được ( y ∈ ℕ∗, 𝑦 < 800, sản phẩm)
Tổng số sản phẩm cả hai tổ sản xuất được trong tháng một là 800 cái nên ta có: x + y = 800 (1)
Số sản phẩm tháng thứ hai xưởng 1 sản xuất được: 116%.x (sản phẩm)
Số sản phẩm tháng thứ hai xưởng 2 sản xuất được: 112%.y (sản phẩm)
Tổng số sản phẩm cả hai xưởng sản xuất được trong tháng hai là 910 sản phẩm nên ta có phương trình: 116%.x + 112%.y = 910 1,16x + 1,12y = 910 x + y = 800
Ta có hệ phương trình: {1,16x + 1,12y = 910
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn x = 350
Giải hệ phương trình ta được {y = 450 (nhận)
Vậy tháng thứ nhất phân xưởng 1 sản xuất được 350 sản phẩm, phân xưởng 2 sản xuất được 450 sản phẩm.
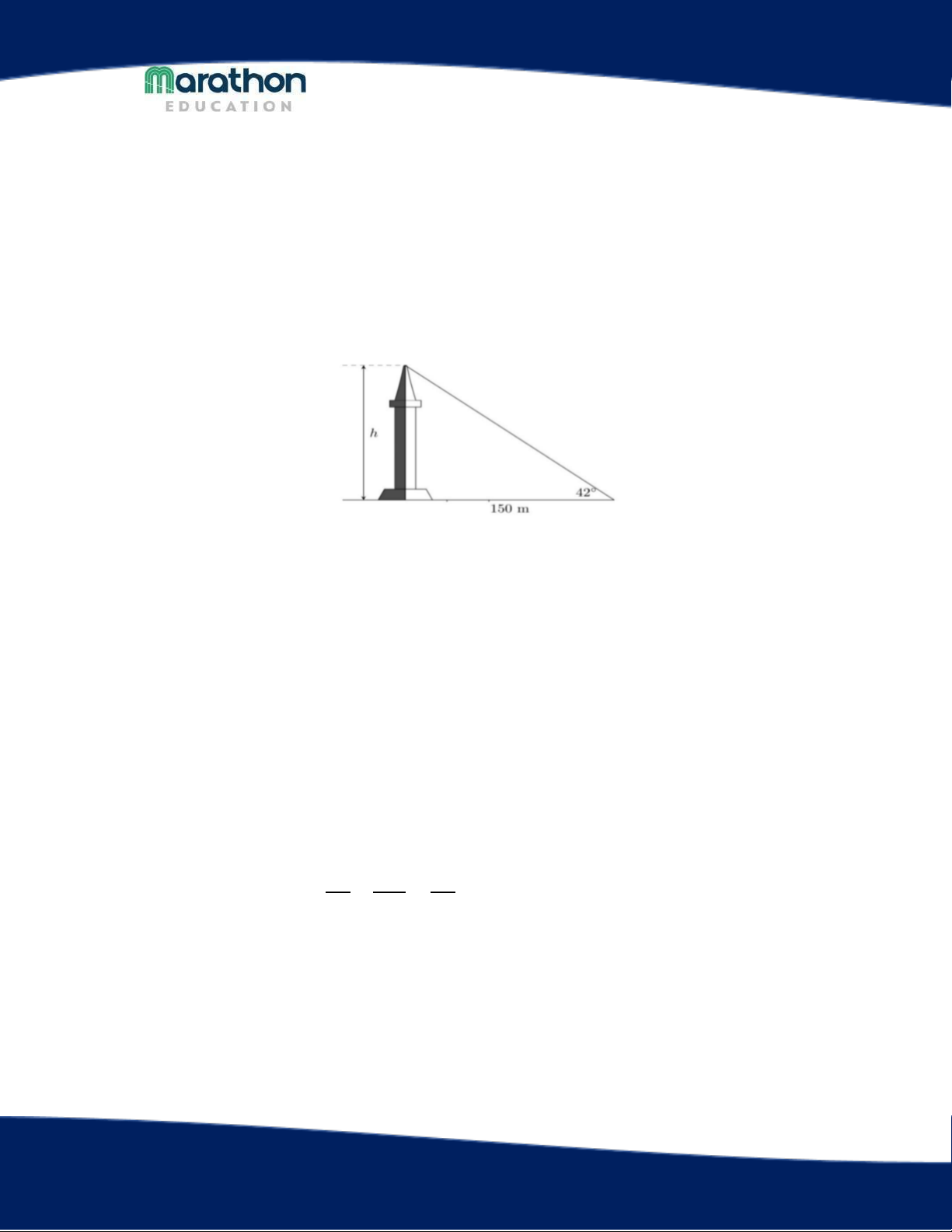
Bài 4. (1,0 điểm) Tính chiều cao của một cái tháp, cho biết khi các tia nắng mặt trời tạo với
mặt đất một góc 42° thì bóng của tháp trên mặt đất có chiều dài 150. LỜI GIẢI
Gọi chiều cao của tháp là AB, AC là bóng của tia nắng đến chân tháp
Xét tam giác ABC vuông tại A, ta có: AB = AC.tanC
AB = 150.tan42° ≈ 135,06 (m)
Vậy chiều cao của tháp là khoảng 135,06 mét
Bài 5. (2,0 điểm) 𝑥+1 4𝑥−3 𝑥−2
1. Giải bất phương trình: − ≤ 3 5 15
2. Một ngân hàng đang áp dụng lãi suất gửi tiết kiệm kỳ hạn 1 tháng là 0,4%/tháng. Hỏi
nếu muốn có số tiền lãi hàng tháng ít nhất là 3 triệu đồng thì số tiền gửi tiết kiệm ít nhất là
bao nhiêu (làm tròn đến hàng triệu đồng). LỜI GIẢI
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn 𝑥+1 4𝑥−3 𝑥−2 1. − ≤ 3 5 15
⇔ 5(𝑥 + 1) − 3(4𝑥 − 3) ≤ 𝑥 − 2
⇔ 5𝑥 + 5 − 12𝑥 + 9 − 𝑥 + 2 ≤ 0 ⇔ −8𝑥 + 16 ≤ 0 ⇔ 𝑥 ≥ 2
2. Gọi x (triệu đồng) là số tiền gửi tiết kiệm (𝑥 > 0)
Khi đó số tiền lãi 1 tháng là 0,4%. 𝑥 = 0,004𝑥 (𝑡𝑟𝑖ệ𝑢 đồ𝑛𝑔)
Để số tiền hàng tháng ít nhất là 3 triệu đồng thì ta phải có: 0,004𝑥 ≥ 3 𝑥 ≥ 750
Vậy số tiền tiết kiệm ít nhất là 750 triệu đồng để có số tiền lãi hàng tháng ít nhất là 3 triệu đồng.
Bài 6. (2,5 điểm)
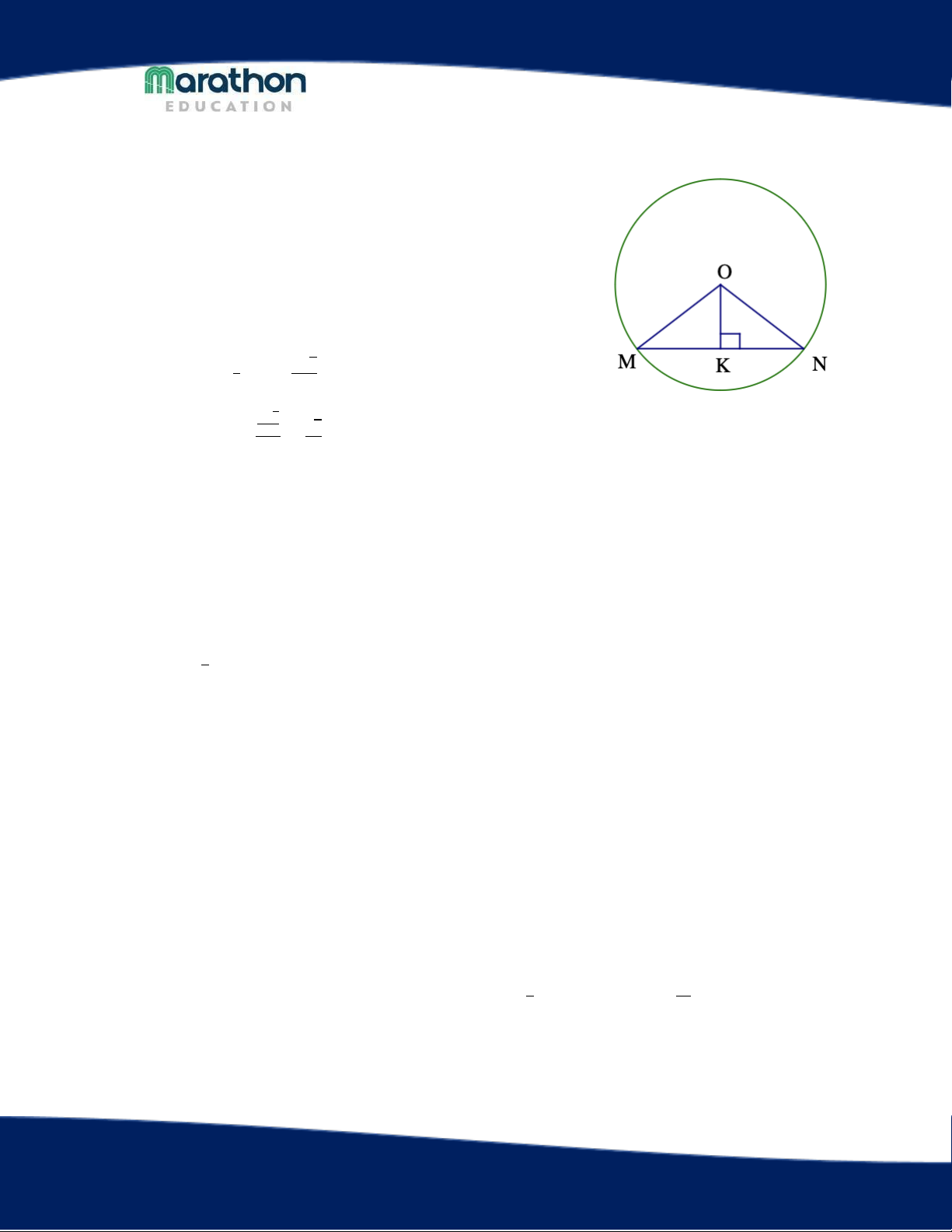
1. Cho (O;R) và dây cung MN = R√3. Kẻ OK vuông góc với MN tại K
a) Tính số đo của 𝑀𝑂𝐾 ̂ , 𝑀𝑂𝑁 ̂
b) Tính số đo cung nhỏ và cung lớn MN
2. Một chiếc quạt giấy khi xoè ra có dạng nửa hình tròn bán kính 18 cm (như hình vẽ). Tính
diện tích phần giấy của chiếc quạt biết rằng khi gấp lại, phần giấy có chiều đài 1,4 dm (làm
tròn kết quả đến hàng phần trăm). LỜI GIẢI
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn
1. a) Xét tam giác OMN ta có: OM = ON = R
=> Tam giác OMN cân tại O
Mà OK là đường cao (𝑂𝐾 ⊥ 𝑀𝑁)
=> OK là đường trung tuyến
=> K là trung điểm của MN 1 𝑅√3 => MK = NK = 𝑀𝑁 = 2 2 𝑅√3
Ta có: 𝑠𝑖𝑛𝑀𝑂𝐾 ̂ = 2 = √3 𝑅 2 => 𝑀𝑂𝐾 ̂ = 60°
Ta có: Tam giác OMN cân tại O Mà OK là đường cao
=> OK là đường phân giác 1 => 𝑀𝑂𝐾 ̂ = 𝑀𝑂𝑁 ̂ 2 => 𝑀𝑂𝑁 ̂ = 2𝑀𝑂𝐾 ̂ = 120°
b) Xét đường tròn (O;R) ta có: 𝑀𝑂𝑁 ̂ = 120° mà 𝑀𝑂𝑁
̂ là góc nội tiếp chắn cung MN => 𝑀𝑂𝑁 ̂ = sđMN = 120°
=> Số đo cung lớn 𝑀𝑁 là 240° 2. Đổi 18 cm = 1,8 dm
Diện tích phần giấy của chiếc quạt là một nửa hình vành khuyên được tạo bởi hai hình tròn 1 16
đồng tâm có bán kính lần lượt 1,8dm và 1,4 dm là 𝜋(1,82 − 1,42) = 𝜋 ≈ 2,01(𝑑𝑚2) 2 25
------------------------------ HẾT ----------------------------
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn
Marathon.edu.vn | Hotline: (028) 7300 3033 | Email: learnwithus@marathon.edu.vn