Đáp án thi hết học phần hè 2023 học phần : giải tích 2 – mat1042 trường đại học công nghệ
Hàm số đã cho xác định liên tục với mọi (x,y) thuộc R²Ta có đạo hàm của𝜕𝑧𝜕𝑥 = 2𝑥 và 𝜕𝑧𝜕𝑦 = 2𝑦 vậy tồn tại duy nhất O(0,0) là gốc tọa độ tươngứng với điểm dừng. Điểm này nằm trong miền D, ta có 𝑧(0,0) = 0.Tài liệu giúp bạn tham khảo ôn tập và đạt kết quả cao. Mời bạn đọc đón xem.
Thông tin :
Môn:
Trường:
Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội
Tác giả:
Tài liệu liên quan:
Preview text:
lOMoAR cPSD| 45438797
ĐẠI HỌC QUỐC GIA HÀ NỘI ĐÁP ÁN THI HẾT HỌC PHẦN HÈ 2023
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ HỌC PHẦN: GIẢI TÍCH 2 – MAT1042 Thời gian: 120 phút
Bài 1 (1 iểm): Tính giới hạn hàm số sau 2 lim (1 + 𝑥𝑦)𝑥2+𝑥𝑦 (𝑥,𝑦)→(0,2) 1 2 lim
(1 + 𝑥𝑦)𝑥2+𝑥𝑦 = 𝑒² (𝑥,𝑦)→(0,2)
Bài 2 (1,5 iểm): Cho hàm số:
𝑧(𝑥, 𝑦) = 𝑥2 + 𝑦2
Tìm cực trị của hàm số ã cho trong miền 𝐷 ược xác ịnh bởi Đáp án: 0.5
Hàm số ã cho xác ịnh liên tục với mọi (x,y) thuộc R²
Ta có ạo hàm của 𝜕𝑧 = 2𝑥 và 𝜕𝑧 = 2𝑦 vậy tồn tại duy nhất O(0,0) là gốc tọa ộ tương 𝜕𝑥 𝜕𝑦
ứng với iểm dừng. Điểm này nằm trong miền D, ta có 𝑧(0,0) = 0 0.5
Biên miền D ược cho dưới dạng
tham số như sau với 𝑡 ∈ [0, 2𝜋] + 3 cos 𝑡 𝑦 = √2 + 3 sin 𝑡
Vậy miền D còn ược viết lại bởi 𝑧 = 𝑥 (cos 𝑡 + sin 𝑡) 0.5 Trên biên D, ta có
- Max(z) = 25 khi 𝑡 = 𝜋/4
- Min(z) = 1 khi 𝑡 = 5𝜋/4 Kết luận
- Max(z) = 25 khi 𝑥 = 𝑦 =
- Min(z) = 0 khi 𝑥 = 𝑦 = 0
Bài 3 (1 iểm): Vẽ miền xác ịnh và tính tích phân sau
𝐼 = ∬(𝑥 − 𝑦)d𝑥d𝑦 𝐷
Với 𝐷 là miền bị giới hạn bởi các ường sau: 𝑦 = 2 − 𝑥2 và 𝑦 = 2𝑥 − 1 0.5 Vẽ hình 0.5 (𝑥 − 𝑦) lOMoAR cPSD| 45438797
Bài 4 (2 iểm): Tính tích phân sau
𝐼 = ∭(𝑥𝑦 + 𝑦𝑧 + 𝑧𝑥)d𝑥d𝑦d𝑧 𝑉
Với 𝑉 là hình cầu tâm 𝑂(𝑎, 𝑏, 𝑐) bán kính 𝑅. Giá trị tích phân là bao nhiêu khi 𝑎 = 𝑏 = 𝑐 = 0 0.5 Đổi biến 𝑥 = 𝑢 + 𝑎 {𝑦 = 𝑣 + 𝑏 𝑧 = 𝑤 + 𝑐 Do ó, 𝐽 = 1 và
𝐼 = ∭(𝑢𝑣 + 𝑣𝑤 + 𝑤𝑢)d𝑢d𝑣d𝑤 + ∭[𝑢(𝑏 + 𝑐) + 𝑣(𝑐 + 𝑎) + 𝑤(𝑎 + 𝑏)]d𝑢d𝑣d𝑤 𝑉 𝑉
+ ∭(𝑎𝑏 + 𝑏𝑐 + 𝑐𝑎)d𝑢d𝑣d𝑤 = 𝐼1 + 𝐼2 + 𝐼3 𝑉 0.5 Đổi biến 𝑢 = 𝑟 sin 𝜃 cos 𝜑
{𝑣 = 𝑟 sin 𝜃 sin 𝜑 𝑤 = 𝑟 cos 𝜃
Với 𝑟 ∈ [0, 𝑅], 𝜃 ∈ [0, 𝜋] và 𝜑 ∈ [0, 2𝜋] và , 𝐽 = 𝑟2 sin 𝜃 0.5 - 𝐼1 = 0 - 𝐼2 = 0
- 𝐼3 = 43𝜋 𝑅3(𝑎𝑏 + 𝑏𝑐 + 𝑐𝑎) 0.5
𝐼 =0 khi 𝑎 = 𝑏 = 𝑐 = 0
Bài 5 (1 iểm): Tính ộ cong của ường tại các iểm 𝑂(0,0), A(𝑎, 0) và 𝐵(0, 𝑏) với 𝑎, 𝑏 ≠ 0
𝑏2𝑥2 + 𝑎2𝑦2 = 𝑎²𝑏² 0.5
Phương trình ã cho là phương trình ellipse ược viết lại dưới dạng tham số 𝑥 = 𝑎 cos 𝑡 { 𝑦 = 𝑏 sin 𝑡 Do ó, 𝑥′ = −𝑎 sin 𝑡 { 𝑦′ = 𝑏 cos 𝑡 Và 𝑥′′ = −𝑎 cos 𝑡 { ′′ = −𝑏 sin 𝑡 𝑦 lOMoAR cPSD| 45438797 0.5 𝑎𝑏 𝐶 =
2 sin2 𝑡 + 𝑏2 cos2 𝑡)3/2 (𝑎
- Điểm O(0,0) không thuộc ường nên không tính ược
- Điểm A(a,0) ứng với 𝑡 = 0 nên 𝐶 = 𝑎/𝑏²
- Điểm B(0,b) ứng với 𝑡 = 𝜋/2 nên 𝐶 = 𝑏/𝑎²
Bài 6 (2 iểm): Tính trực tiếp tích phân sau và kiểm tra lại bằng công thức Green d𝑥 + (𝑥 + 𝑦2)d𝑦
Với ℒ là ường kín gồm 2 cung 𝑦 = 𝑥² và 𝑥 = 𝑦2 theo chiều dương 1
Hai ường giao nhau tại 2 iểm O(0,0) và I(1,1),
- Dọc theo cung dưới OBI ta có 𝑦 = 𝑥² hay d𝑦 = 2𝑥d𝑥, ta có 1
∮(2𝑥𝑦 − 𝑥2)d𝑥 + (𝑥 + 𝑦2) 𝑂𝐵𝐼
- Dọc theo cung dưới ICO ta có x= 𝑦² hay dx = 2𝑦dy, ta có d𝑥 + (𝑥 + 𝑦2) - Vậy 𝐼 = 1 Theo công thức Green 𝐼 = ∬ [
𝜕 (𝑥 + 𝑦2) − 𝜕 (2𝑥𝑦 − 𝑥2)] d𝑥d𝑦 = ∬(1 − 2𝑥)d𝑥d𝑦 = 1 𝜕𝑥 𝜕𝑦 30 𝐷 𝐷
Bài 7 (1.5 iểm): Giải phương trình vi phân sau với iều kiện 𝑦(0) = 0
(1 + 𝑥2)𝑦′ + 𝑥𝑦 = 1 0.5
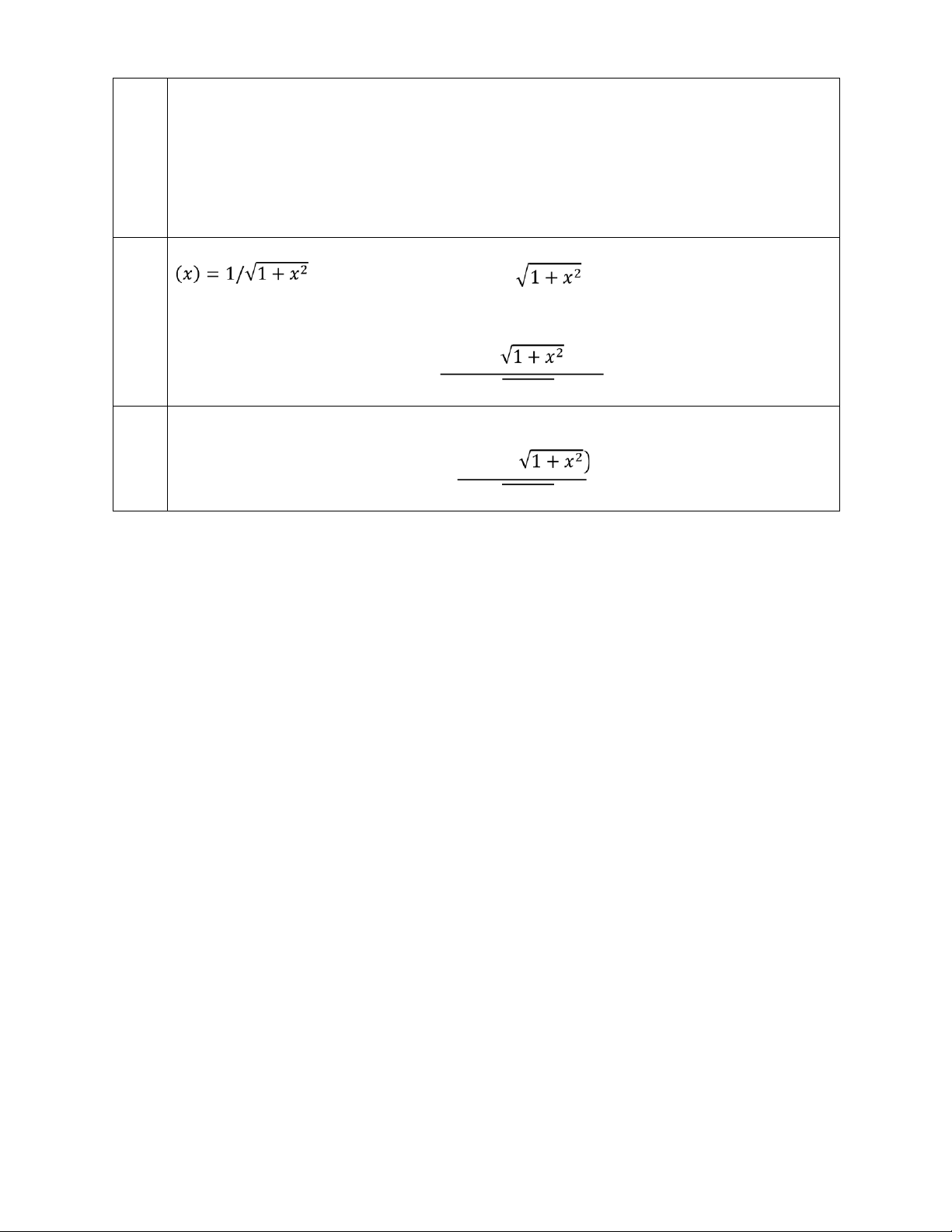
Phương trình thuần nhất tương ứng là d𝑦 −𝑥d𝑥 = 𝑦 1 + 𝑥2 Kết quả: 𝐾 𝑦 = lOMoAR cPSD| 45438797 Với 𝐾 ∈ 𝑅 0.5
chọn 𝐾 = 𝐾(𝑥), vậy 𝐾′
Giải phương trình không thuần nhất, ta 𝐾(𝑥) = ln (𝑥 + ) + 𝐶
Với 𝐶 ∈ 𝑅, vậy nghiệm tổng quát ln(𝑥 + ) + 𝐶 𝑦 = √ 1+ 𝑥 2 0.5 𝐶 = 0 Vậy ln(𝑥 + 𝑦 = √ 1+ 𝑥 2