Đề chọn đội tuyển thi HSG QG môn Toán THPT năm 2024 – 2025 sở GD&ĐT Hà Tĩnh

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN ĐỘI TUYỂN DỰ THI HỌC SINH GIỎI HÀ TĨNH
QUỐC GIA THPT NĂM HỌC 2024 − 2025 Môn thi: TOÁN
ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 180 phút
(Đề thi có 1 trang, gồm 4 bài) Ngày thi: 18/09/2024
Bài 1. (5 điểm) Cho dãy số (u xác định bởi: n ) + 2024n 1
u = a ≥ 2025, u = + ∀ ∈ + u n n ( n ) * 1 , 1 1  2025n +1
a) Chứng minh rằng dãy (u có giới hạn hữu hạn và tìm giới hạn đó. n )
b) Tính lim n(u − n 2024). n→+∞
Bài 2. (5 điểm) Xét hàm số f :  →  khác hàm hằng thoả mãn
f (xf ( y) + y) + f (x + y) = 2 f ( y) + f (xy) +1, x ∀ , y ∈
a) Chứng minh rằng với mọi x∈, f (x) = 1
− khi và chỉ khi x = 0.
b) Tìm tất cả các hàm số f thoả mãn điều kiện trên.
Bài 3. (5 điểm) Cho tam giác ABC nhọn, không cân nội tiếp đường tròn (O) có các đường
cao AD, BE, CF. Gọi A là điểm đối xứng của B qua F, A là điểm đối xứng của C qua b c
E. Gọi X là giao điểm của DE và AB, Y là giao điểm của DF và AC.
a) Chứng minh rằng bốn điểm X ,Y, A A cùng thuộc một đường tròn. b , c
b) Gọi B là điểm đối xứng của C qua D, B là điểm đối xứng của A qua F, C là c a a
điểm đối xứng của A qua E, C là điểm đối xứng của B qua .
D Chứng minh rằng bán b
kính đường tròn ngoại tiếp của các tam giác AA A BB B CC C bằng nhau. c a , b c , a b
Bài 4. (5 điểm) Với x và y nguyên, x y
∣ là ký hiệu y chia hết cho x .
a) Có tồn tại hay không các số nguyên a, ,
b c lớn hơn 1 và thoả mãn đồng thời ba tính chất: 2b a∣ −1, 2c b∣ −1 và 2a c∣ −1.
b) Tìm tất cả cặp số nguyên dương (a,b) sao cho b a a b ∣ −1.
---------------------HẾT--------------------
- Thí sinh không được sử dụng tài liệu.
- Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:…………………………………Số báo danh:………………………………….. 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN ĐỘI TUYỂN HSGQG HÀ TĨNH
NĂM HỌC 2024 – 2025
HƯỚNG DẪN CHẤM MÔN TOÁN
Chú ý : - Mọi cách giải đúng, ngắn gọn đều cho điểm tương ứng.
- Điểm toàn bài không qui tròn. CÂU NỘI DUNG ĐIỂM Dễ thấy * u > n ∀ ∈ 1 u ≥ + n ∀ ∈ n 2024 , n 0,  . Ta c/m *  bằng quy nạp. 0,5 n
Khi n =1, khẳng định đúng do giả thiết.
Giả sử khẳng định đúng với n . Thế thì 2024n +1 2024n +1 1  2024n +1 1 u = + ≥ + ≥ > + + u n n 1  2025  2024 . 1 ( ) 2025n +1 2025n +1 n  n n +1 0,5
Vì vậy khẳng định đúng với n +1. Theo nguyên lí quy nạp ta suy ra Câu 1 * u ≥ + n ∀ ∈ n 2024 ,  . 1a n 2,0đ Vì vậy, xét 2024n +1 n u − = − ≤ * ⇒ u ≤ ∀ ∈ + u n n n , + u u n n n 0 1 1 
2025n +1 2025n +1
⇒ (u là dãy không tăng. 0,5 n )
Mà (u bị chặn dưới bởi 0 nên có giới hạn hữu hạn. Đặt limu = L > n 0. n ) n→∞
Từ công thức truy hồi cho n 2024 → +∞ ta có L =
(L + )1 ⇒ L = 2024. 2025 0,5 Vậy limu = n 2024. n→∞
Bổ đề. Cho số thực q∈(0;1) và hai dãy số thực không âm (c ≥ a
n )n , ( n ) 1 n 1 ≥ 0,5 thỏa mãn: a ≤ +
∀ ≥ Khi đó nếu lim c = thì lim a = n 0. n 0 + qa c n n n n , 1. 1 n→+∞ n→+∞
Chứng minh. Vì lim c = nên với mỗi ε > 0 tồn tại n ∈ n 0,  sao cho n→+∞ 0 c < ε n ∀ ≥ n n , .0
Khi đó, với mọi n ≥ n +1 ta có 0 Câu 0,5 2
a ≤ qa + ε ≤ + + = + + ≤ − q qa ε ε − q a − q ε n n ( n ) n ( 1)  1b 1 2 2 n−n n−n 1 − − 3,0đ 0 0 n 0 ≤ q a + q ++ q + ε ε < q a + (1) n ( 1) n 0 0 n 1− q Vì q∈(0, ) 1 nên n− 0 lim n
q a = Do đó tồn tại n ≥ n sao cho n 0. 0 n→+∞ 1 0 n− 0 n q a < ε n ∀ ≥ n (2) n , 0 1 Từ (1) và (2) suy ra 2 − q a < ε n ∀ ≥ n 0,5 n , .1 1− q Do (a
là dãy số thực không âm nên lim a = n 0. n )n 1 ≥ n→+∞ 2
Trở lại bài toán. Đặt v = n u − n ∀ ∈ n ( n ) * 2024 ,  .
Áp dụng kết quả ở câu a, ta có 1 * u ≥ + n ∀ ∈ v ≥ n ∀ ∈ n 2024 ,  nên * n 1,  . n
Lại có từ công thức truy hồi suy ra v + + n  v n 2024 1 1 n  * + 2024 = +  2025, n ∀ ∈ n +1 2025n +1 n  v + 0,5 + n v n 2024 1 n 1 1 * ⇒ = ⋅ + , n ∀ ∈
n +1 2025n +1 n 2025n +1
(n + )1(2024n + )1 n +1 * ⇒ v = + ∀ ∈ + v n n n , 1  n(2025n + ) 1 2025n +1
(n + )1(2024n + )1 1 ⇒ v − = − + ∀ ∈ + v n n 1 
n(2025n + ) ( n ) * 1 , . 1 1 n (n + ) 1 (2024n + ) 1 Mặt khác 2024 2025 lim = < nên tồn tại * n ∈ sao cho n→+∞ n(2025n + ) 1 2025 2026 0 (n + ) 1 (2024n + ) 1 2025 0,5 ( < n ∀ ≥ n n 2025n + ) , 0 1 2026 2025 1 ⇒ v − < − + ∀ ≥ + v n n n 1 n 1 , . 1 ( ) 0 2026 n Do 1
lim = 0, áp dụng bổ đề cho dãy các số thực không âm (v − ta n )1 n→+∞ n n≥ 0 n 0,5
suy ra: lim n(u − = v = n 2024) lim n 1. n→+∞ n→+∞
Đặt g (x) = f (x) +1, x
∀ ∈ . Khi đó từ phương trình hàm ban đầu ta có
g (xg( y) − x + y) + g(x + y) = 2g( y) + g(xy), x
∀ , y ∈ (1)
Kí hiệu P(u,v) là phép thế x = u, y = v vào (1). 0,5
P(0,0) ⇒ 2g (0) = 3g (0) ⇒ g (0) = 0.
P(x,0) ⇒ g (−x) + g (x) = 0, x
∀ ∈ ⇒ g là hàm lẻ.
Câu Giả sử tồn tại x ∈,x ≠ 0 sao cho g(x = 0. P(x,x cho ta 0 ) 0 ) 0 0 2a
g (x − x + g x + x = g xx , x ∀ ∈ 0 ) ( 0 ) ( 0) 
2,0đ Ở đây thay x bởi −x ta có 1,0
g (x + x + g x − x = g −xx , x ∀ ∈ 0 ) ( 0 ) ( 0) 
Dẫn đến g (xx = g −xx , x ∀ ∈ . 0 ) ( 0) 
Mà g là hàm lẻ nên g (xx = 0, x
∀ ∈ ⇒ g x = 0, x ∀ ∈ 0 ) ( )  ⇒ f (x) = 1, − x
∀ ∈, vô lí vì f không là hàm hằng. 0,5
Vậy g (x) = 0 ⇔ x = 0 , nên f (x) = 1 − ⇔ x = 0. 3
P(x x) ⇒ g (xg (x)) + g ( x) = g (x) + g ( 2 , 2 2 x ), x ∀ ∈ . 
Thay x bởi −x và chú ý g là hàm lẻ ta có 1,0
g(xg(x)) = g( 2x)
g (xg (x)) − g ( x) = − g (x) + g ( 2 2 2 x ) ⇒  , x ∀ ∈ .  g
 (2x) = 2g ( x) Lại có P( 2 − ,2) ⇒ g ( 2
− g (2) + 4) = 2g (2) + g ( 4 − ). Mà g ( 4 − ) = −g (4) = 2
− g (2) nên g ( 2 − g (2) + 4) = 0 0,5 Câu ⇒ 2
− g (2) + 4 = 0 (Áp dụng câu a) ⇒ g (2) = 2 ⇒ g ( ) 1 =1. 2b Do đó P(x )
,1 cho ta: g (x + )
1 = g (x) +1, x ∀ ∈ (2) 3,0đ 0,5 Mặt khác g (− ) 1 = −g ( ) 1 = 1 − nên P( 1, − y) cho ta
g ( y − g( y) − ) 1 + g ( y − )
1 = 2g ( y) + g (−y), y ∀ ∈ .  0,5
Áp dụng (2) ta suy ra g ( y − g( y)) = 0, y ∀ ∈
⇒ y − g ( y) = 0, y
∀ ∈ ⇒ g ( y) = y, y ∀ ∈ . 
⇒ f ( y) = y −1, y ∀ ∈ .
 Thử lại ta thấy thoả mãn. 0,5
Vậy: f (x) = x −1, x ∀ ∈ .  Câu 3a 2,0đ 4
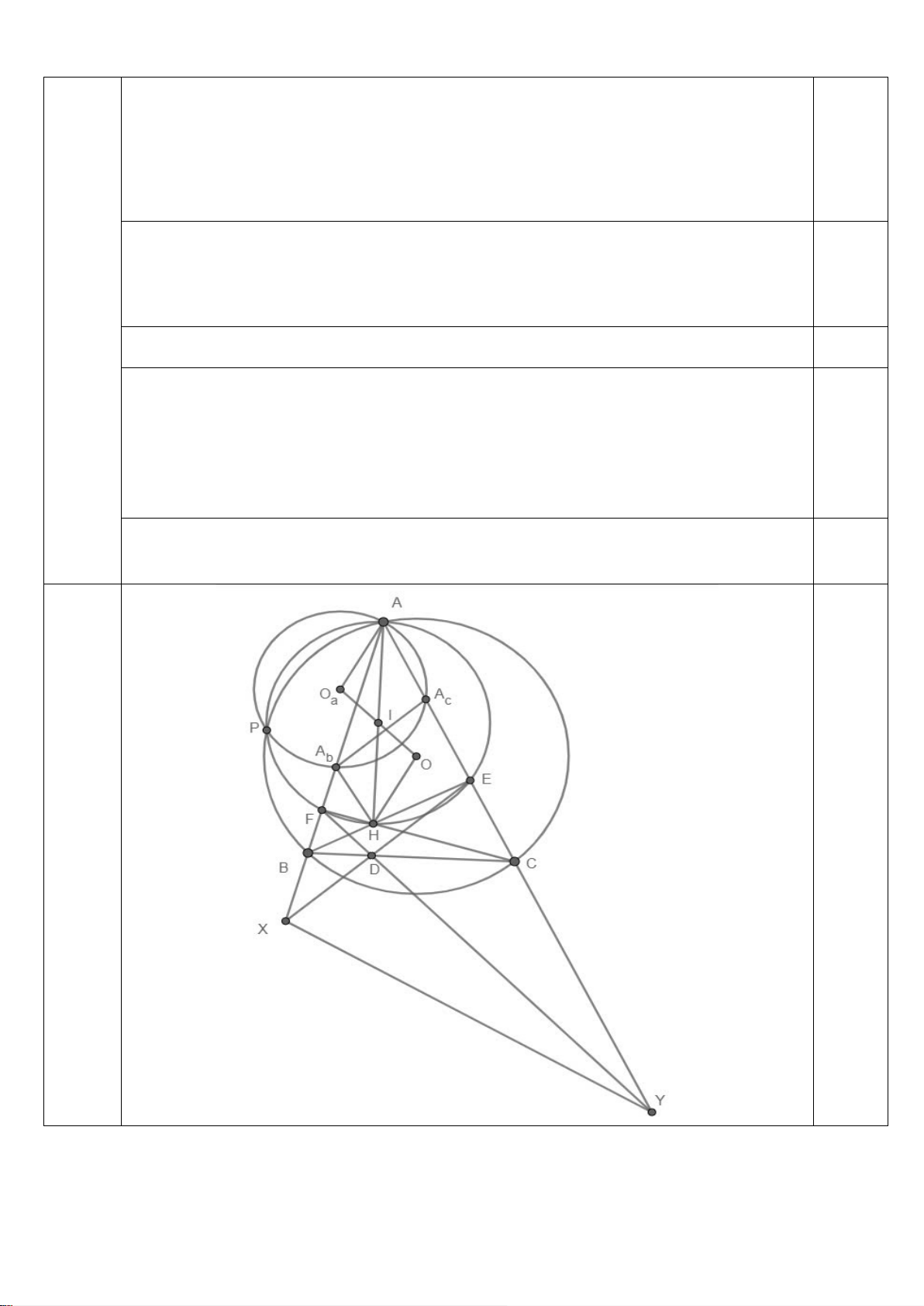
Xét thế hình như hình vẽ. Các trường hợp khác tương tự.
Gọi H là trực tâm của tam giác ABC . Ta có  =  =  HB B HBA HDE a 1,0
⇒ Tứ giác B HDX nội tiếp ⇒ AA AX = AH AD b. . . a
Tương tự, ta có AA AY = AH AD c. . 1,0
⇒ AA AX = AA AY ⇒ X Y A A đồng viên. b. c. , , b, c
Gọi N là tâm đường tròn Euler của tam giác ABC.
Ta có tứ giác ABDE nội tiếp ⇒ X . A XB = X . D XE 0,5 ⇒℘ =℘ . Tương tự ℘ =℘ X /(O) X /(N ) Y /(O) Y /(N )
⇒ XY là trục đẳng phương của (N ) và (O) ⇒ XY ⊥ ON. 0,5
Mà O, N,H thẳng hàng nên XY ⊥ OH. (1)
Từ câu a ta có XY và A A đối song trong  BAC. Câu b c
Do đó gọi O là tâm đường tròn AA A thì XY ⊥ AO Kết hợp với (1) suy 0,5 a. 3b a b c ra AO OH a | .
3,0đ Gọi I là trung điểm của AH thì I là tâm đường tròn đi qua ,AH,E,F.
Gọi P là giao điểm của ( AEF ) và (O). Khi đó P ∆ FB  P
∆ EC (g.g) mà 0,5
A A lần lượt đối xứng với B,C qua F, E nên suy ra b , c P ∆ A B  P ∆ A C c g c b c ( . . ).
Từ đó ta có  =  ⇒  =  PA B PA C
PA A PA A suy ra tứ giác APA A nội tiếp b c b c b c
hay ba đường tròn (O
I O đồng trục AP suy ra O,I,O thẳng hàng. a ),( ),( ) a 0,5
Chứng tỏ OO chia đôi AH. Mà AO  OH nên AO HO là hình bình hành a a a ⇒ AO = OH a .
Vì vậy, bán kính đường tròn ngoại tiếp tam giác AA A bằng OH. b c
Chứng minh tương tự với hai tam giác BB B CC C ta suy ra đpcm. 0,5 c a , a b
Giả sử tồn tại các số nguyên a, ,
b c >1 thoả mãn yêu cầu bài toán. 0,5 Thế thì do 2b
a∣ −1 nên a lẻ. Tương tự, b,c là các số lẻ.
Xét p là ước nguyên tố nhỏ nhất trong tất cả các ước nguyên tố của a, , b .c
Không mất tính tổng quát coi p . a ∣ 0,5
Câu Thế thì p lẻ. Đặt h = ord Áp dụng định lý Fermat nhỏ ta suy ra h p ∣ −1. p 2.
4a Ngoài ra từ giả thiết ta có 2b a∣ −1⇒ h b ∣ ⇒ h ( ∣b, p − ) 2,0đ 1 . 0,5 Chú ý nếu ,
b p −1 cùng chia hết cho số nguyên tố q nào đó thì q là một ước
nguyên tố của b nhỏ hơn p, mâu thuẫn. Vì vậy (b, p − ) 1 =1 0,5 ⇒ h 1
∣⇒ h =1 ⇒ p 2 ∣ −1 =1, vô lí.
Vậy không tồn tại các số nguyên a, ,
b c >1 thoả mãn yêu cầu bài toán. 5
Nếu a =1 hoặc b =1 thì hiển nhiên ta có b a a b ∣ −1.
Xét a,b >1. Gọi p là ước nguyên tố nhỏ nhất của . a Thế thì a p b ∣ −1 (  , b p) =1 ⇒ 
. Hơn nữa theo định lý Fermat nhỏ ta có ord b p ∣ − p 1 0,5 ord b a  ∣ p
⇒ ord b∣a p − = ⇒ p b ∣ − p ( , ) 1 1 1. Xét hai trường hợp:
TH1. p ≥ 3. Áp dụng bổ đề LTE ta có v ( a
b − = v b − + v a p )1 p( )1 p( )
⇒ bv (a) = v ( b
a ≤ v b − + v a ⇒ v a b − ≤ v b − p ( )( ) 1 p ( ) 1 . p p ) p( )1 p( ) 0,5
Mà v a ≥ nên b v b p − − ≤ − ⇒ ≤ b − p ( ) b 1 1 1 1. p ( ) 1
Tuy nhiên, bằng quy nạp ta chứng minh được Câu x b 1 − b 1 2 x, x  p 2 − > ∀ ∈ ⇒ >
> b −1, mâu thuẫn.
4b TH2. p = 2. Áp dụng bổ đề LTE ta có 3,0đ ( a v b − ) 1 = v ( 2
b −1 −1+ v a 2 2 ) 2 ( ) 0,5 ⇒ ( ) = ( b bv a v a ) ≤ v ( 2
b −1 −1+ v a ⇒ (b − )
1 v (a) ≤ v ( 2 b −1 −1. 2 2 ) 2 2 2 ) 2 ( )
Mà v a ≥1 nên b −1≤ v ( 2 b −1 −1. 2 ) 2 ( )
Nếu b ≡1 (mod4) thì b 1 v (b ) b 1 1 2 − − ≤ − ⇒
≤ b −1. Tương tự TH1 ta có 2 0,5 điều vô lí.
Nếu b ≡ 3 (mod4) thì b 1 v (b ) b 1 1 2 − − ≤ + ⇒
≤ b +1. Dễ dàng kiểm tra b ≥ 4 2
không thoả nên b ≤ 3 ⇒ b = 3. Ngoài ra, đẳng thức xảy ra nên v a =1. Đặt 2 ( ) 0,5
a = 2a trong đó a lẻ ⇒ (2 3 a ∣ −1⇒ 9a a a ∣ −1. 0 )3 2 0 3 0 0 0 0
Tương tự như trên, nếu a >1, ta có ước nguyên tố nhỏ nhất của a là ước 0 0 của 9 −1 ⇒ 2 a
∣ , vô lí. Vì vậy a =1⇒ a = 2. 0 0
Tóm lại các cặp số nguyên dương ( 0,5
a,b) thoả mãn là (1,k ),(k, ) 1 ,(2,3), trong đó * k ∈ bất kì. HẾT 6
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN ĐỘI TUYỂN DỰ THI HỌC SINH GIỎI HÀ TĨNH
QUỐC GIA THPT NĂM HỌC 2024 - 2025 Môn thi: TOÁN
ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 180 phút
(Đề thi có 1 trang, gồm 3 bài)
Ngày thi thứ hai: 19/9/2024
Bài 5. (6 điểm) Đặt S là tập hợp các đa thức 2n 2n 1
P(x) = a x + a x − + + + hệ số − a x a n n ... 2 2 1 1 0
thực thỏa mãn đồng thời cả hai điều kiện sau: i) Với i = 0,1, ,
… 2n, thì 2024 ≤ a ≤ i 2025.
ii) Tồn tại một số thực α sao cho P(α) = 0.
a) Chứng minh rằng tồn tại một đa thức có bậc 4048 trong tập hợp S.
b) Tìm số nguyên dương n nhỏ nhất sao cho tồn tại đa thức f ∈ S thỏa mãn deg f = 2 . n
Bài 6. (7 điểm) Cho tam giác ABC nhọn, không cân nội tiếp đường tròn (O). Đường trung
trực của các đoạn thẳng AB, AC lần lượt cắt AC, AB tại E, F. Đường thẳng EF cắt
đường thẳng BC tại .
D Đường thẳng AD cắt đường tròn (O) tại điểm thứ hai là S.
a) Gọi M , N lần lượt là các điểm đối xứng với O qua AC, A .
B Chứng minh rằng sáu điểm ,
A S,E,F,M , N cùng thuộc một đường tròn. b) Qua ,
A B,C lần lượt kẻ các đường thẳng song song với BC,C ,
A AB, chúng cắt nhau
tạo thành tam giác XYZ. Gọi H là trực tâm của tam giác ABC, I là điểm đối xứng với H qua .
O Chứng minh rằng đường tròn Euler của các tam giác XYZ,HIX ,HIY,HIZ đồng quy tại S.
Bài 7. (7 điểm) Với mỗi số nguyên dương n , đếm số cách điền các số 0,1, , … 5 vào các ô của
bảng ô vuông n × n thoả mãn:
a) Tổng các số trong mỗi hàng đều chia hết cho 2, còn tổng các số trong mỗi cột đều chia hết cho 3.
b) Tương tự câu a, nhưng thêm điều kiện tổng các số trong mỗi đường chéo chính chia hết
cho 6, (mỗi bảng ô vuông n × n có hai đường chéo chính).
---------------------HẾT--------------------
- Thí sinh không được sử dụng tài liệu.
- Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:…………………………………Số báo danh:……………………… 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN ĐỘI TUYỂN DỰ THI HỌC SINH GIỎI HÀ TĨNH
QUỐC GIA THPT NĂM HỌC 2024 – 2025
HƯỚNG DẪN CHẤM MÔN TOÁN Chú ý:
- Mọi cách giải đúng, ngắn gọn đều cho điểm tương ứng.
- Điểm toàn bài không qui tròn. CÂU NỘI DUNG ĐIỂM
Câu 5a Rõ ràng, với n = 2024, ta có thể chọn a =
∀ ≤ k ≤ n và k 2024, 0 2 2,0 2,0đ a = ∀ ≤ < thì P( 1) − = 0. + k n k 2025, 0 2 1
Ta sẽ chứng minh n = 2024 là số nguyên dương nhỏ nhất thỏa mãn.
Giả sử tồn tại đa thức P(x) có bậc 2n < 2.2024 và đa thức này có một nghiệm thực. 0,5
Ta có thể thấy P(x) ≥ 2024 > 0 với x ≥ 0, do đó nghiệm của đa thức trên là số âm.
Nên đặt Q(x) = P(−x) thì Q(x) phải có một nghiệm thực dương.
Bây giờ, ta chỉ cần chứng minh rằng Q(x) > 0 với x > 0. 0,5
Ta có Q(1) = 2024(n +1) − 2025n = 2024 − n > 0.
Giả sử x ≠1. Khi đó, Q(x) > 0 2n 2n−2 2n 1 2024(x x ... 1) 2025(x − ⇔ + + + ≥ + ... + x) Câu 5b 0,5 2n+2 2n  −   −  2n+2 4,0đ x 1 x 1 x −1 1 ⇔ 2024. ≥   2025 . x ⇔ ≥1+ . 2  2  x 1   x 1  − −  2 x( n x −1) 2024 2n+2 Vì n − +
< 2024 nên chỉ cần chứng minh x 1 1 n 1 ≥1+ = , hay chứng 2 x( n x −1) n n 0,5 minh 2n 2n−2 2 2n 1 − 2n−3 nx + nx
+ . . + nx + n ≥ (n +1)x + (n +1)x
+ ... + (n +1)x, với mọi x > 0.
Nhưng với mọi k ∈ + n n  ta có 2k 1 2k 2k+2 nx ≤ x + x theo BĐT AM-GM. 0,5 2 2 Ngoài ra, ta có k 2n−k 2n x + x
≤ x +1 (điều này tương đương với i 2 ( 1)( n i x x − −
−1) ≥ 0 và rõ ràng là đúng). Cộng các bất đẳng thức loại thứ 0,5
nhất cho tất cả các k từ 0 đến n −1 và loại thứ hai cho tất cả các k lẻ từ 1
đến 2n −1 ta có đpcm.
Do đó, với n < 2024 một đa thức như vậy không thể tồn tại. Vậy đáp số là n = 2024. 0,5 2 Câu 6a 3,0đ
Ta có các tam giác ABE, ACF lần lượt cân tại E,F nên  1,0 =  = 
ABE ACF BAC ⇒ B,C,E,F đồng viên ⇒ .
DB DC = DE.DF. Mặt khác ,
A S,B,C nằm trên đường tròn (O) ⇒ . DA DS = . DB DC 1,0 ⇒ DE.DF = . DA DS ⇒ ,
A S,E,F đồng viên. (1)
Lại có O,M đối xứng với nhau qua AC nên  =  =  MEA OEA OFA
⇒ M ∈( AEF ). Tương tự N ∈( AEF ). 1,0
Kết hợp với (1) ta có điều phải chứng minh.
Xét thế hình như hình vẽ, các trường hợp khác làm tương tự. Đường cao qua ,
A B,C của tam giác ABC cắt lại (O) lần lượt tại H H H BC a , b ,
c. Gọi P là điểm đối xứng của O qua .
Nhận thấy MF  HH . Mặt khác từ câu a, ,
A S,M ,E,F đồng viên. Do đó 1,0 b
(MS,MF) ≡ ( AS, AF) ≡ (H S H B π b , b )(mod )
⇒ S,M ,H thẳng hàng. Tương tự, S, N,H thẳng hàng. b c
Như vậy S nằm trên đường thẳng đối xứng của OH qua AC, AB , nên S là
điểm Anti - Steiner của đường thẳng OH trong tam giác ABC. Dẫn đến S
cũng nằm trên đường thẳng đối xứng với OH qua BC.
Câu 6b ⇒ S,P,H thẳng hàng. a
4,0đ Bây giờ, gọi G là trọng tâm của tam giác ABC. Ta có phép vị tự tâm G tỉ số 1
− biến tam giác ABC thành tam giác XYZ. Do đó suy ra H,I lần lượt 1,0 2
là tâm đường tròn ngoại tiếp và trực tâm tam giác XYZ.
Ngoài ra, đường tròn (HBC) và (O) đối xứng với nhau qua BC nên P là tâm của (HBC).
⇒ P là trung điểm của HX. Chú ý ta có O là trung điểm của HI. 3
Gọi R là trung điểm của XI . Thế thì
(SP,SO) ≡ (SH SO ≡ H O SH π a ,
) ( a , a )(mod ).
Xét phép đối xứng qua đường thẳng BC ta có
(H O SH ≡ HO HX π 1,0 a , a ) ( , )(mod )
⇒ (SP,SO) ≡ (HO,HX ) ≡ (RP,RO)(modπ ).
Dẫn đến S ∈(OPR) là đường tròn Euler của tam giác HIX.
Tương tự S cũng nằm trên đường tròn Euler của các tam giác HIY,HIZ.
Hơn nữa, đường tròn Euler của tam giác XYZ là (ABC) đi qua S. 1,0
Vậy ta có điều phải chứng minh.
Xét bảng con (n − ) 1 ×(n − ) 1 ở góc trên bên trái. 0,5
Ta có số cách điền các số 0,1, ,
… 5 vào các ô của bảng này là (n− )2 1 6 .
Với mỗi cách điền như vậy, ô bên phải cùng của mỗi hàng trong n −1 hàng
đầu tiên có 3 cách điền, ô bên dưới cùng của mỗi cột trong n −1 cột đầu 1,0
Câu 7a tiên có 2 cách điền. 3,0đ
Khi đó chỉ còn ô ở góc dưới bên phải chưa được điền số, gọi x là tổng n −1
số đã được điền ở hàng n , y là tổng của n −1 số đã được điền ở cột n , ta 1,0
có duy nhất c∈{0,1, , … } 5 sao cho 2 c ∣ + x và 3 c ∣ + . y
Vì vậy có duy nhất cách điền ô ở góc dưới bên phải.
Ta suy ra số cách điền bảng thoả mãn là (n− )2 1 n 1 − n 1 − n(n− ) 1 6 .3 .2 = 6 . 0,5
Xét bảng con (n − 2)×(n − 2) ở giữa bảng (không tính hai hàng thứ 1 và
thứ n , không tính hai cột thứ 1 và thứ n ) như hình dưới đây: x1 b1 ... bn-2 x2 a1 ... c1 ... ... ... ... ... 1,0 an-2 ... cn-2 x4 d1 ... dn-2 x3 Câu 7b Ta có ( )2 2
6 n− cách điền các số 0,1 ,
… 5 vào các ô của bảng này.
4,0đ Đồng thời, các ô x , x có 2
6 cách điền. Khi đó các ô x , x có duy nhất một 1 2 3 4 1,0
cách điền (do tổng các số trong mỗi đường chéo chính chia hết cho 6).
Ngoài ra điền theo thứ tự: a ,a , , … a có 3
6n− cách điền, a có 2 cách điền, 1 2 n−3 n−2 b ,b , , … b có 3
6n− cách điền, b có 3 cách điền, 1 2 n−3 n−2 1,5 c ,c , , … c có 3
3n− cách điền, c có 1 cách điền, 1 2 n−3 n−2 d ,d , , … d có 3
2n− cách điền, d có 1 cách điền. 1 2 n−3 n−2
Suy ra bảng đã cho có (n− )2 2 2 n−3 n−3 n−3 n−3 (n+ ) 1 (n−2) 6 .6 .6 .2.6 .3.3 .2 = 6 cách điền. 0,5 HẾT 4
Document Outline