Đề chọn học sinh giỏi Toán 7 năm 2024 – 2025 phòng GD&ĐT Tiền Hải – Thái Bình

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI CẤP HUYỆN TIỀN HẢI Năm học 2024 -2025 Môn: TOÁN 7
(Thời gian làm bài 120 phút) Bài 1 (4,5 điểm). 0 1) Thực hiện phép tính: 2 1 25  2024 11 72 1 :  − − − 2 4  2025    12 7 6 3 2) Rút gọn biểu thức: 3 .5 + 9 .25 A = 27 .25 + (3 .5)6 5 3 2 3) Cho 2 2 2 2 C = + + + ...+ . So sánh C với 1. 1.3 3.5 5.7 2023.2025 Bài 2 (4,0 điểm). 1) Cho x +12 y −13 z + 5 = = và 3 3x − 5 =19 7 9 6
Tính giá trị biểu thức M = 2x + y − z +1997
2) Tìm các số nguyên x, y sao cho xy − x + y = 4 .
3) Tìm số nguyên tố ab (a > b > 0) sao cho ab − ba là số chính phương. Bài 3 (3,5 điểm).
1) Nhà trường dự định chia một số quyển vở cho ba lớp 7A; 7B; 7C theo tỉ lệ 7; 6; 5.
Nhưng sau đó vì có học sinh chuyển giữa 3 lớp nên phải chia lại theo tỉ lệ 6; 5; 4. Như vậy
đã có lớp nhận được ít hơn dự định là 8 quyển vở. Tính số quyển vở mỗi lớp nhận được. 2) Tìm x biết: 2 2 x + 2x −1 = x + 3 Bài 4 (6,0 điểm).
Cho tam giác ABC vuông tại A có (AB < AC). Trên cạnh BC lấy điểm N sao cho
BN = BA. Kẻ BH vuông góc với AN tại H. 1) Chứng minh A ∆ BH = N
∆ BH và BH là tia phân giác của  ABN .
2) Lấy điểm M thuộc tia CB sao cho CM = CA, tia phân giác của  ACB cắt AN tại E.
Chứng minh tam giác AME cân và ME song song với BH.
3) Gọi I là giao điểm của CE và AM. Chứng minh 1 IH = MN. 2 Bài 5 (2,0 điểm).
Cho 4 số tự nhiên a; b; c; d thỏa mãn a > b > c > d.
Chứng minh: P = (a − b)(a − c)(a − d)(b − c)(b − d)(c − d) chia hết cho 12.
…………Hết…………
Họ và tên thí sinh:……………………………. Phòng thi:…………
Thí sinh không được sử dụng máy tính cầm tay. Cán bộ coi thi không giải thích gì thêm
Chữ kí cán bộ coi thi số 1:……………… Chữ kí cán bộ coi thi số 2:………………
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM TIỀN HẢI
KỲ KHẢO SÁT HỌC SINH GIỎI CẤP HUYỆN Năm học 2024 -2025 Môn: TOÁN 7 (Gồm 05 trang) I. Hướng dẫn chung
1. Hướng dẫn chấm chỉ trình bày các bước cơ bản của 1 cách giải. Nếu thí sinh làm
theo cách khác mà đúng thì vẫn cho điểm tối đa.
2. Bài làm của thí sinh đúng đến đâu cho điểm đến đó theo đúng biểu điểm.
3. Bài hình học, thí sinh vẽ hình đúng ý nào thì chấm điểm ý đó, thí sinh vẽ sai hình
hoặc không vẽ hình thì cho 0 điểm bài hình đó.
4. Bài có nhiều ý liên quan tới nhau, nếu thí sinh mà công nhận ý trên (hoặc làm ý trên không
đúng) để làm ý dưới mà thí sinh làm đúng thì cho 0 điểm điểm ý đó.
5. Điểm của bài thi là tổng điểm các Bài làm đúng và tuyệt đối không làm tròn.
II. Đáp án và thang điểm Ý NỘI DUNG BIỂU ĐIỂM Bài 1 (4,5 điểm). 0 1) Thực hiện phép tính: 2 1 25  2024 11 72 1 :  − − − 2 4  2025    12 7 6 3 2) Rút gọn biểu thức: 3 .5 + 9 .25 A = 27 .25 + (3 .5)6 5 3 2 3) Cho 2 2 2 2 C = + + + ...+ . So sánh C với 1. 1.3 3.5 5.7 2023.2025 0 0,75 2 1 25  2024 11 72 1 :  − − − 2 4  2025    1) 3 5 1,5đ = 121− 72 − : −1 2 2 3 2 3 27 0,75 = 49 − . −1= 7 − −1= 2 5 5 5 12 7 6 3 12 7 2 6 2 3 3 .5 + 9 .25 3 .5 + (3 ) .(5 ) 0,5 A = = 27 .25 (3 .5)6 3 5 2 3 2 6 6 5 3 2 (3 ) .(5 ) + + (3 ) .5 2) 12 7 12 6 12 6 3 .5 + 3 .5 3 .5 (5 +1) 0,5 1,5đ A = = 15 6 12 6 12 6 3 3 .5 + 3 .5 3 .5 (3 +1) 6 3 0,5 A = = 28 14 3) 1,0 Ta có 2 2 2 2 C = + + + ...+ 1,5đ 1.3 3.5 5.7 2023.2025 1 1 1 1 1 1 1 1 =1− + − + − + ... + − =1− 3 3 5 5 7 2023 2025 2025 1 0,5 Vì 1− <1 suy ra C < 1. 2025 Bài 2 (4,0 điểm). 1) Cho x +12 y −13 z + 5 = = và 3 3x − 5 =19 7 9 6
Tính giá trị biểu thức M = 2x + y − z +1997
2) Tìm các số nguyên x, y sao cho xy − x + y = 4 .
3) Tìm số nguyên tố ab (a > b > 0) sao cho ab − ba là số chính phương. Vì 3 3x − 5 =19 suy ra x = 2 0,25 + − + 0,25 1) 2 12 y 13 z 5 Suy ra = = = 2 1,5đ 7 9 6
Chỉ ra được y = 31; z = 7 0,5
Thay x = 2; y = 31; z = 7 tính đúng được M = 2025 0,5 Ta có xy − x + y = 4 0,5 Suy ra (x +1)(y −1) = 3
Do x; y là số nguyên x + 1 và y – 1 là các số nguyên nên x + 1 và
y – 1 là các ước của 3. 2) x + 1 1 3 -1 -3 0,75 1,5đ y - 1 3 1 -3 -1 x 0 2 -2 -4 y 4 2 -2 0 tm tm tm tm
Vậy các cặp số (x;y) thỏa mãn là (0;4); (2;2); (-2;-2); (-4;0). 0,25 3)
Ta có ab − ba =10a + b − (10b + a) = 9a − 9b = 9(a − b) 0,5 1,0đ
Do ab − ba là số chính phương và 9 là số chính phương nên
a – b là số chính phương.
Vì a > b > 0 suy ra 1≤ a − b ≤ 8 nên a – b = 1 hoặc a – b = 4.
Với a − b =1 suy ra ab∈{21;32;43;54;65;76;87; } 98 0,5
Với a − b = 4 suy ra ab∈{51;62;73;84; } 95
Vậy các số nguyên tố ab thỏa mãn yêu cầu đề bài là 43 và 73. Bài 3 (3,5 điểm).
1) Nhà trường dự định chia một số quyển vở cho ba lớp 7A; 7B; 7C theo tỉ lệ 7; 6; 5.
Nhưng sau đó vì có học sinh chuyển giữa 3 lớp nên phải chia lại theo tỉ lệ 6; 5; 4. Như vậy đã
có lớp nhận được ít hơn dự định là 8 quyển vở. Tính số quyển vở mỗi lớp nhận được. 2) Tìm x biết: 2 2 x + 2x −1 = x + 3
Gọi tổng số quyển vở 3 lớp nhận được là m * (m∈ )
Gọi số quyển vở dự định chia cho lớp 7A; 7B; 7C lần lượt là a; b; c * (a;b;c∈ ) 0,25 a b c Theo bài ra ta có = = + + = 7 6 5 và a b c m a b c a + b + c m Suy ra = = = = 7 6 5 7 + 6 + 5 18 7m 6m 5m 0,25 Suy ra a = ;b = ;c = (1) 18 18 18
Gọi số quyển vở thực tế chia lại cho lớp 7A; 7B; 7C lần lượt là x; y; z * (x;y;z∈ ) 1) x y z
Theo bài ra ta có = = và x + y + z = m 2,0đ 6 5 4 0,5 x y z x + y + z m Suy ra = = = = 6 5 4 6 + 5 + 4 15 6m 5m 4m Suy ra x = ;y = ;z = (2) 15 15 15
So sánh (1) và (2) ta có a < x; b = y; c > z
Nên lớp 7C đã nhận ít hơn dự định là 8 quyển vở Suy ra c − z = 8 5m 4m 0,5 − = 8 25m 24m m do đó − = = 8 18 15 90 90 90 Suy ra m = 720 (tm)
Tính đúng được số quyển vở nhận được của lớp 7A là 288, lớp 7B 0,5 là 240 và lớp 7C là 192. Ta có 2 x ≥ 0; 2x −1 ≥ 0 0,5 Nên 2 x + 2x −1 ≥ 0 suy ra 2 2 x + 2x −1 = x + 2x −1 + − = + 0,5 2) Ta có: 2 2 x 2x 1 x 3 1,5đ 2 2 x + 2x −1 = x + 3 2x −1 = 3
Suy ra 2x −1 = 3 Hoặc 2x −1 = 3 − 0,5
Tính đúng và kết luận x = 2 hoặc x = -1 Bài 4 (6,0 điểm).
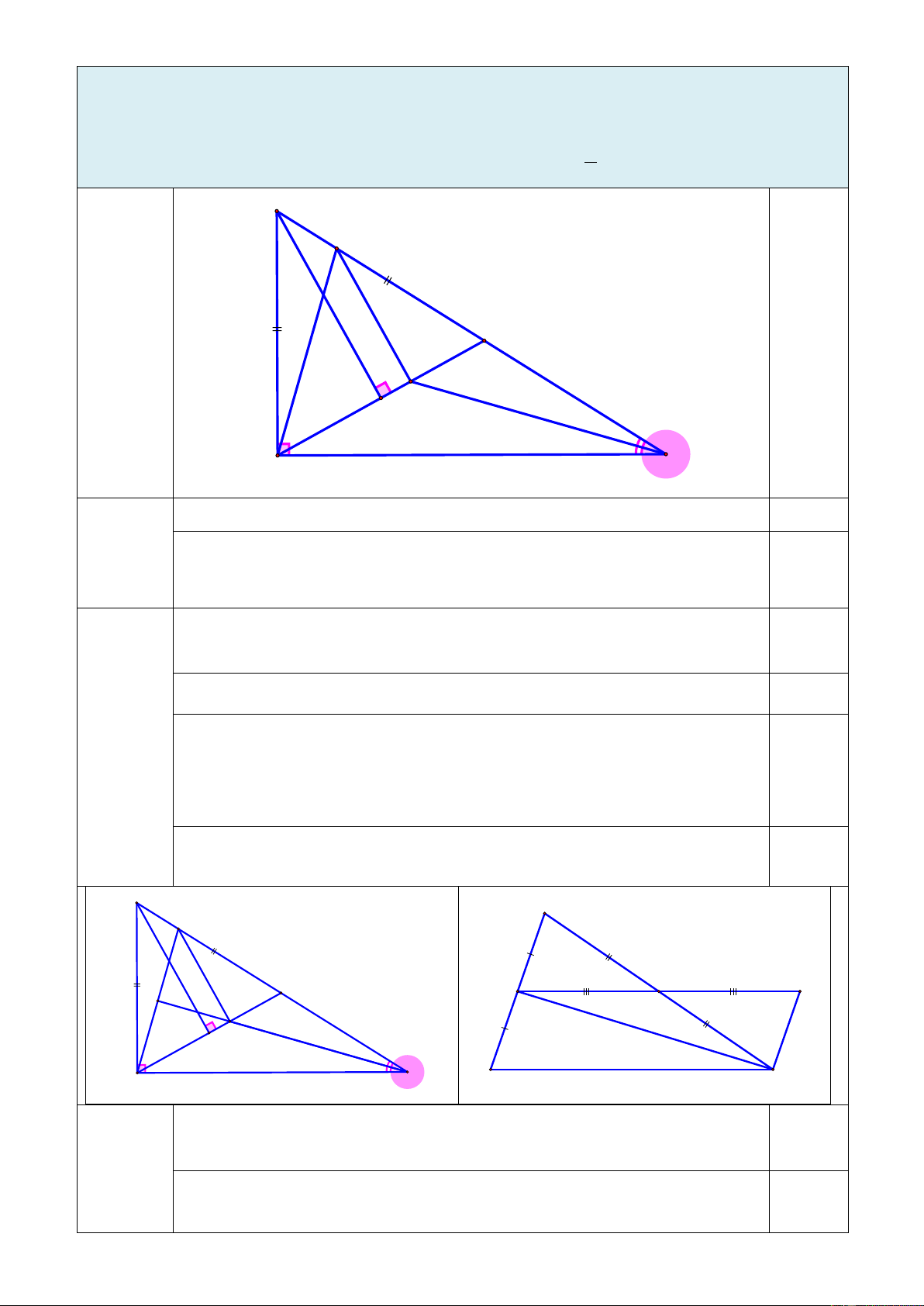
Cho tam giác ABC vuông tại A có (AB < AC). Trên cạnh BC lấy điểm N sao cho
BN = BA. Kẻ BH vuông góc với AN tại H. 1) Chứng minh A ∆ BH = N
∆ BH và BH là tia phân giác của  ABN .
2) Lấy điểm M thuộc tia CB sao cho CM = CA, tia phân giác của  ACB cắt AN tại E.
Chứng minh tam giác AME cân và ME song song với BH.
3) Gọi I là giao điểm của CE và AM. Chứng minh 1 IH = MN. 2 B M N E H A C a) Chỉ ra được A ∆ BH= N
∆ BH (cạnh huyền-cạnh góc vuông) 1,5 2,5đ Từ A ∆ BH= N ∆ BH suy ra  =  ABH NBH 1,0
Vậy BH là tia phân giác của  ABN Chỉ ra được A ∆ EC= M ∆ EC (c.g.c) 1,25
Từ đó suy ra AE = ME suy ra tam giác AEM cân tại E. Từ A ∆ EC= M ∆ EC suy ra  =  CME CAE (1) 0,25 b) Ta có  +  0 CAE BAN = 90 0,5 2,5đ
Vì tam giác BHN vuông tại H suy ra  +  0 NBH HNB = 90 Vì A ∆ BH= N ∆ BH suy ra  =  HNB BAN nên  =  NBH CAE (2)
Từ (1) và (2) suy ra  =  NBH CME 0,5
mà 2 góc này ở vị trí đồng vị nên BH song song với ME. B A M N H I I K E H A C M N Chỉ ra A ∆ IC= M
∆ IC(c.g.c) suy ra được I là trung điểm của AM 0,25 c) Vì A ∆ BH= N
∆ BH(cmt) suy ra được H là trung điểm của AN 1,0đ
Trên tia đối của HI lấy điểm K sao cho HI = HK. Chỉ được tam giác A ∆ HI= NHK ∆ (cgc)
suy ra được AI = NK = MI và AI song song NK.
Chứng minh được tam giác M ∆ I N = KNI ∆ (cgc) 0,5 1 1
Suy ra MN = IK mà IH = IK nên IH = MN. 2 2 Bài 5 (2,0 điểm).
Cho 4 số tự nhiên a; b; c; d thỏa mãn a > b > c > d.
Chứng minh: P = (a − b)(a − c)(a − d)(b − c)(b − d)(c − d) chia hết cho 12.
* Với 4 số tự nhiên a; b; c; d thỏa mãn a > b > c > d tồn tại hai số chia
cho 3 có cùng số dư. Suy ra hiệu của hai số đó chia hết cho 3. Do đó 0,75 P3 (1)
* Với 4 số tự nhiên a; b; c; d thỏa mãn a > b > c > d
+ Nếu có hai trong 4 số a; b; c; d có cùng số dư thì hiệu hai số chia hết cho 4. 2,0 Do đó P4 0,75
+ Nếu 4 số a; b; c; d khi chia cho 4 có số dư là 0; 1; 2; 3 suy ra trong 4
số a; b; c; d có hai số chẵn và hai số lẻ. Giả sử a; b chẵn thì (a − b)2
và c; d lẻ thì (c − d)2 . Do đó P4 (2)
Vì (3; 4) = 1 nên từ (1) và ( 2) suy ra P 12  0,5
Document Outline

• de-chon-hoc-sinh-gioi-toan-7-nam-2024-2025-phong-gddt-tien-hai-thai-binh
• HSG TOÁN 7 2025