PHÒNG GIÁO DỤC VÀ ĐÀO TẠO TÂN SƠN
ĐỀ THI CHỌN HỌC SINH NĂNG KHIẾU LỚP 6, 7, 8 CẤP HUYỆN NĂM HỌC 2023-2024 ĐỀ CHÍNH THỨC MÔN: TOÁN 7
Thời gian làm bài 120 phút (không tính thời gian giao đề). Đề có 04 trang.
Lưu ý: Thí sinh làm bài trên tờ giấy thi, không làm bài trên đề thi; Phần trắc nghiệm
khách quan chỉ có một lựa chọn đúng.
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN: (16 câu; 8,0 điểm)  1 1  2023  1  2023
Câu 1. Kết quả phép tính A   .  1 .     là  3 6  2024  2  2024 1 2023 2  023 A. B. 0 C. D. 2 2024 2024 5 1  7 12 Câu 2. Tìm x, biết:  x   3 9 5 1  83 2  7 183 9  A. . B. . C. . D. . 85 53 85 29
Câu 3. Cho dãy tỉ số bằng nhau a  b  c  d b  c  d  a c  d  a  b d  a  b  c   
và a  b  c  d   0 . d a b c  b  c  c  d  d  a  a  b 
Giá trị của biểu thức A  1 1 1 1 80      bằng  a  b  c  d 
A. 1. B. -1. C. 1 hoặc -1. D. 81.
Câu 4. Đại lượng y tỉ lệ nghịch với đại lượng x theo hệ số là 2 , thì đại lượng x
tỉ lệ nghịch với đại lượng y theo hệ số là 1 1 A. . B. 2  . C.  . D. 2 . 2 2
Câu 5. Cho biết 20 công nhân xây xong một ngôi nhà hết 60 ngày . Hỏi 15 công
nhân xây ngôi nhà đó hết bao nhiêu ngày? (giả sử năng suất làm việc của mỗi công nhân là như nhau)
A. 120. B. 170. C. 80. D. 270. x 6 8x  3y
Câu 6. Biết  . Khi đó giá trị của biểu thức A  là y 5 3x  8y 3 9 3 9  A. . B. . C. . D. . 2 5 2 5 2
Câu 7. Cho x, y thoả mãn 6  2x2024 2023  3y  x
 0 . Giá trị của biểu thức P  26x  3y bằng A. 142. B.123. C.108. D. 75. Câu 8. Cho biết 4 3 x  2x  3  0 . Giá trị của biểu thức 5 4 P(x)  4
 x  8x 12x  2024 là A. P(x)  2024. B. P(x)  2005. C. P(x)  2008. D. P(x)  2023. 2 Câu 9. Cho đa thức 2 2023 2 2024 f (x)  (4x  6x  3) .(2x  4x  3) . Tổng các hệ số của 5 đa thức f (x) bằng 1 2  1 7 A. . B. . C. . D. . 5 5 5 5 Câu 10. Cho  0
xOy  60 , điểm A nằm trên Oy. Qua A vẽ tia Am nằm phía trong góc 
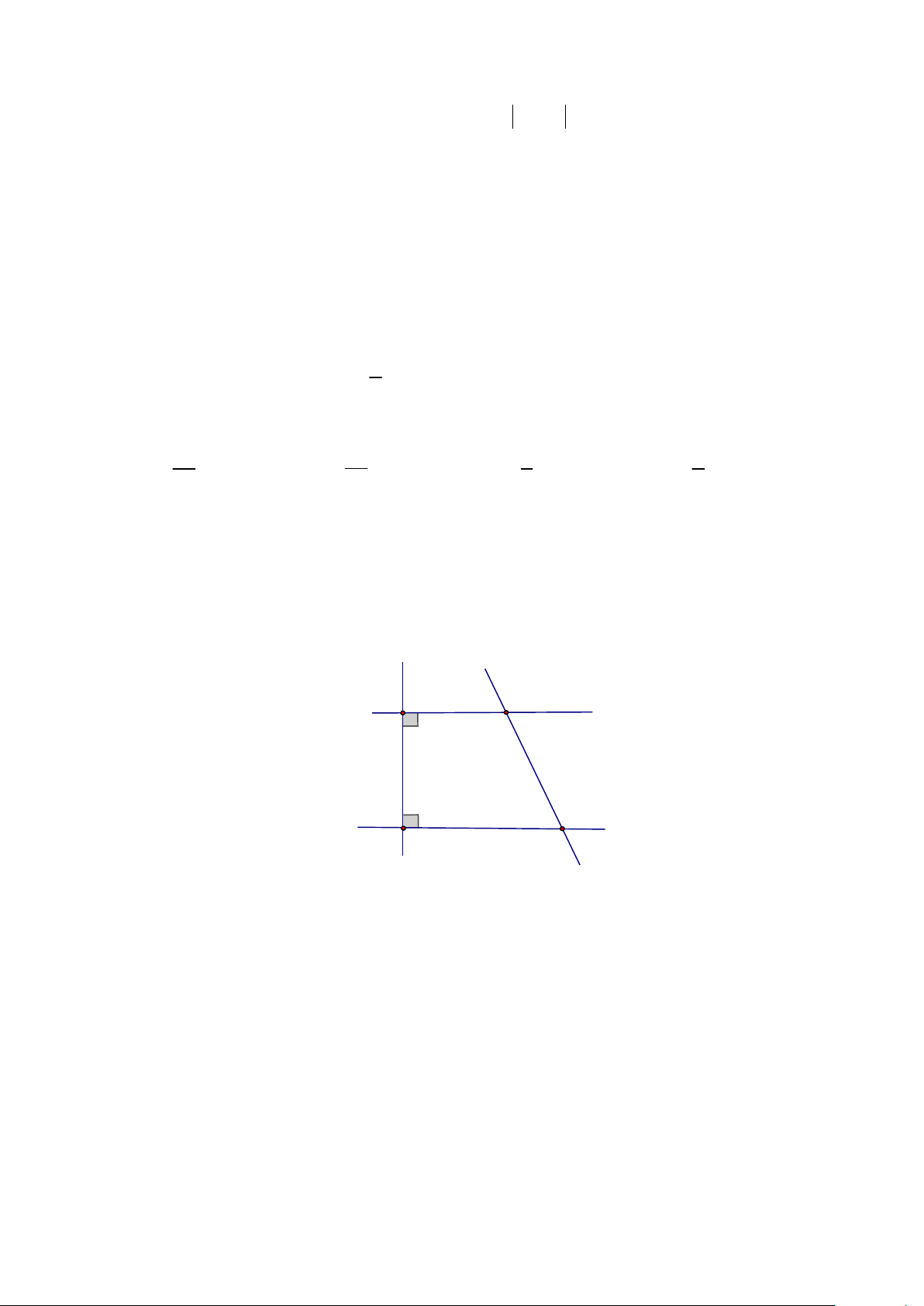
xOy . Để Am song song với Ox thì số đo của góc OAm bằng A. 0 120 . B. 0 80 . C. 0 60 . D. 0 150 . Câu 11 Cho hình vẽ: d c M a 1 1 b N
Hai đường thẳng a, b cùng vuông góc với đường thẳng d . Một đường thẳng
c cắt a, b tại M , N . Biết  M   0 N  56 Số đo của  N là 1 1 1 A. 0 109 . B. 0 62 . C. 0 71 . D. 0 142 .
Câu 12. Cho ABC  MN . P Biết AB  7c ,
m MP  5cm và chu vi của tam giác
ABC bằng 19cm . Độ dài cạnh NP và BC là A. NP  BC  7c . m B. NP  5c ; m BC  8c . m C. NP  BC  11c . m D. NP  BC  10c . m 3
Câu 13. Cho ABC và PQR có AB  PQ . Điều kiện để A  BC  P  QR là A. AC  Q ; R  A  . P B. AC  P ; R  A  . P C. B  ; R A  . P D. BC  Q ; R  B  . P
Câu 14. Cho tam giác ABC có AB  AC  18c ; m AC  AB  8c . m Khi đó ta có A. B   C. B. B   C. C. B   C. D. 2B   C. Câu 15. Cho MNP có 
N  70, P  50 . Kẻ tia phân giác ND D  MP. Khẳng
định nào sau đây đúng? A. MD  MN. B. MN  N . D C. ND  N . P D. ND  MN. a
Câu 16. Gieo ngẫu nhiên xúc xắc (6 mặt) một lần. Gọi
là xác xuất của biến cố b
“Mặt xuất hiện của xúc xắc có số chấm là số chia hết cho 3”. Giá trị biểu thức 2023a  b là A. 2022. B. 2026. C. 2024. D. 2025.
II. PHẦN TỰ LUẬN (04 câu; 12,0 điểm) Câu 17 (3,0 điểm).
a) Cho p là số nguyên tố lớn hơn 3, biết p  2 cũng là số nguyên tố. Chứng
minh rằng: p+7 là bội của 6.
b) Tìm các số nguyên x, y thoả mãn: 2 x  xy  2  x  y . Câu 18 (4,0 điểm). 1 1 1 1 1 1 1 1
a) Cho A  1    ...   và B    ... 2 3 4 2023 2024 1013 1014 2024 Tính   2024 A B x  2y 2024
b). Cho x, y là các số nguyên dương thỏa mãn  . Tìm giá trị nhỏ x  y 2023 nhất của x ? x y z
c) Cho xyz  1. Tính giá trị của biểu thức A    .
xy  x 1 yz  y 1 xz  z 1
Câu 19 (4,0 điểm). Cho tam giác ABC cân tại A ( AB  BC ). Gọi N là trung
điểm của AC , qua N kẻ đường thẳng vuông góc với AC cắt đường thẳng BC tại
M . Trên tia đối của tia AM lấy điểm F sao cho AF  BM . a) Chứng minh:  MAC   ABC . b) Chứng minh: AM  CF .
c) Lấy điểm D trên cạnh AC , điểm E trên cạnh AB sao cho AD  AE . 4 BC  DE
Trên tia BM lấy I sao cho BI  DE . Chứng minh: 𝐸𝐼 // 𝐷𝐵 và BD  . 2 1 1 1 1
Câu 20 (1,0 điểm). Tìm x biết: x   x   x  ... x   50x 1.3 3.5 5.7 97.99
Họ và tên thí sinh:………………………………………….Số báo danh:…………………..
Cán bộ coi thi không giải thích gì thêm!