Đề cuối học kỳ 2 Toán 12 năm 2023 – 2024 trường Lạc Hồng – TP HCM

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra cuối học kỳ 2 môn Toán 12 năm học 2023 – 2024 trường THCS & THPT Lạc Hồng, thành phố Hồ Chí Minh; đề thi có đáp án trắc nghiệm mã đề 101 – 102. Mời bạn đọc đón xem!

86 43 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

17 trang 6 tháng trước

Tác giả:

Profile M. Hậu
Mã đề 101 Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO KIỂM TRA CUỐI HỌC KỲ II
THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC: 2023 - 2024
TRƯỜNG THCS &THPT LẠC HỒNG MÔN: TOÁN KHỐI LỚP: 12
TỔ TOÁN-TIN Thời gian: 90 phút (không kể thời gian phát đề)
ĐỀ CHÍNH THỨC
(Đề thi có 5 trang) Mã đề: 101
Họ và tên học sinh :.............................................................................. Số báo danh : .................
Câu 1: Cho hàm số
2
32fx x
. Trong các khẳng định sau, khẳng định nào đúng?
A.
3
2f x dx x x C
. B.
() 6f x dx x C
.
C.
3
1
2
3
f x dx x x C 
. D.
3
32
f x dx x x C 
.
Câu 2: Trong không gian
Oxyz
, hình chiếu vuông góc của điểm
(3; 2;5)A
trên mặt phẳng
()Oxy
có tọa
độ là.
A.
. B.
0; 2; 0
. C.
0; 0; 5
. D.
0; 2; 5
.
Câu 3: Trong hình vẽ bên, điểm M biểu diễn số phức
z
. Số phức
z
là.
A.
12i
. B.
12i
. C.
2 i
. D.
2 i
.
Câu 4: Cho hai số phức
1
43zi
và
2
1zi
. Phần ảo của số phức
12
zz
bằng.
A. 4. B. 1. C. −2. D. 5.
Câu 5: Tìm các số thực
,ab
thỏa mãn
2 ( 3 4 ) 10 6a b ii i 
, với
i
là đơn vị ảo. Tính
2Pa b
.
A. 7. B. 5. C. 3. D. 2.
Câu 6: Trong không gian
Oxyz
, mặt phẳng
P
đi qua điểm
3; 1; 4M
và vuông góc với đường thẳng
312
:
1 12
xyz
d


có phương trình là.
A.
2 12 0xy z
. B.
2 12 0xy z
.
C.
3 4 12 0xy z
. D.
3 4 12 0xy z
.
Câu 7: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
1; 2; 1A 
. Phương trình chính tắc của
đường thẳng qua
A
và vuông góc
: 3 2 70
Px y z 
.
A.
121
1 32
xyz

. B.
121
1 32
xyz

.
C.
132
1 21
xy z

. D.
121
1 21
xyz

.
Mã đề 101 Trang 2
Câu 8: Cho số phức
z
thỏa mãn
17
zi i
. Tính môđun của
z
.
A.
42z
. B.
5
z
. C.
4
z
. D.
3z
.
Câu 9: Trong không gian
Oxyz
, cho
(3;1;5)A
và
(1;3; 1)B
. Trung điểm của đoạn thẳng
AB
có tọa độ
là.
A.
. B.
(4;4;4)
. C.
(1;1;1)
. D.
( 1;1; 3)
.
Câu 10: Biết rằng
.
x
xe
là một nguyên hàm của hàm số
()fx
. Gọi
()Fx
là một nguyên hàm của
'( ).
x
f xe
thỏa mãn
(0) 1F
. Tính giá trị của
(1)F
.
A.
1
( 1)
2
e
F
. B.
1
( 1)
2
e
F
. C.
1
( 1)
2
F 
. D.
1
( 1)
2
F
.
Câu 11: Diện tích
S
của hình phẳng giới hạn bởi các đường
2
yx
,
2y 
,
0x
và
1x
được tính
bởi công thức nào sau đây.
A.
1
2
0
2d
Sx x
. B.
1
2
0
2dS xx
.
C.
1
2
2
0
2dSx x
. D.
1
2
0
2dSx x
.
Câu 12: Trong không gian
Oxyz
, cho hai điểm
2; 4;1 1;1; 3
,AB
và mặt phẳng
: 3 2z 5 0Px y 
. Lập phương trình mặt phẳng
Q đi qua hai điểm
A
,
B
và vuông góc
với mặt phẳng
P .
A.
3 2 50xyz 
. B.
3 20xy 
.
C.
3 2 11 0yz
. D.
2 3 11 0yz
.
Câu 13: Diện tích hình phẳng giới hạn bởi hai đường
2
5yx x 
và
35yx
bằng
A.
4
3
. B.
304
15
. C.
304
15
. D.
4
3
.
Câu 14: Trong không gian
Oxyz
, điểm nào dưới đây thuộc đường thẳng
d
:
3
1
23
xt
yt
zt



?
A.
1; 3; 5P
. B.
1; 1; 3M
. C.
1; 1; 3
Q
. D.
3; 1; 2
N
.
Câu 15: Cho
Fx
là một nguyên hàm của hàm
1
2
fx
x
; biết
02F
. Tính
2
F
.
A.
22 ln 2F 
. B.
2 ln 2 22F 
. C.
2
2 ln 2F 
. D.
2 ln 2 22F 
.
Câu 16: Biết hàm số
()fx
có đạo hàm
'( )fx
liên tục trên
và
(0)f
,
0
'( )f x dx
. Tính
()f
.
A.
()f 
. B.
()f 
. C.
() 0f
. D.
() 2f 
.
Câu 17: Cho số
z
thỏa mãn
2 4 1 3 4 23iz z i i 
. Môđun của
z
bằng.
A.
5
. B.
13
. C. 5. D. 13.
Câu 18: Trong không gian
Oxyz
, cho mặt phẳng
:3 2 4 1 0
xyz 
. Vectơ nào dưới đây là một
vectơ pháp tuyến của
?
A.
2
3;2;4n

. B.
1
3; 4;1n 

. C.
3
2; 4;1n 

. D.
4
3;2; 4n 

.
Mã đề 101 Trang 3
Câu 19: Cho
3
1
( ) 12
f x dx
. Tính
3
1
3()
I f x dx
.
A.
36
I
. B.
9I
. C.
4I
. D.
6I
.
Câu 20: Trong không gian
Oxyz
, cho mặt cầu
222
(): 62420.Sx y z x y z 
Bán kính của mặt
cầu đã cho bằng.
A.
23
. B.
22
. C. 4. D. 3.
Câu 21: Tính thể tích của vật thể tạo nên khi quay quanh trục
Ox
hình phẳng
D
giới hạn bởi đồ thị
2
:2Py xx

và trục
Ox
bằng:
A.
16
15
V
. B.
13
15
V
. C.
19
15
V
. D.
17
15
V
.
Câu 22: Biết tích phân
2
0
5f x dx
và
2
0
4g x dx 
. Khi đó
2
0
f x g x dx



bằng.
A. −9. B. 9. C. 2. D. 1.
Câu 23: Môđun của số phức
2 i
bằng.
A.
3
. B. 5. C.
5
. D. 3.
Câu 24: Gọi
1
z
;
2
z
là hai nghiệm của phương trình
2
2 90
zz 
. Tính giá trị biểu thức
22
12
Az z
.
A.
62
. B.
92
. C. 6. D. 18.
Câu 25: Biết
3
Fx x
là một nguyên hàm của hàm số
fx
trên
. Giá trị của
3
1
2dfx x



bằng.
A. 28. B. 24. C. 30. D.
161
10
.
Câu 26: Trong không gian
Oxyz
, cho mặt cầu
2 22
: 2 4 14Sx y z 
. Tâm của
S
có tọa
độ là.
A.
2; 4; 1
. B.
2; 4; 1
. C.
2; 4; 1
. D.
2;4;1
.
Câu 27: Tìm nguyên hàm của hàm số
cos 1fx x
.
A.
( ) sinf x dx x C
B.
( ) sin
f x dx x x C
C.
( ) sin
f x dx x C
. D.
( ) sin
f x dx x x C 
Câu 28: Trong không gian
Oxyz
, cho mặt phẳng
: 2 5 0.Px yz 
Điểm nào dưới đây thuộc
P
?
A.
5; 0; 0N
. B.
(2;1;5)M
. C.
0; 0; 5P
. D.
2; 1; 5
Q
.
Câu 29: Cho số phức
z a bi
với
,ab
thỏa mãn
32 5zi
và
34zi
là số thuần ảo. Tính
giá trị của biểu thức
2S ab
.
A. 2. B. 6. C. −7. D. −5.
Câu 30: Cho số phức
54
zi
. Điểm biểu diễn của số phức
z
là.
A.
(5;4)M
. B.
(5; 4)M
. C.
(5;4)Mi
. D.
(5; 4 )Mi
.
Câu 31: Cho hàm số
()fx
xác định và có đạo hàm trên
0; 
thỏa
22
() 2.() 3 5x f x xf x x

và
(1) 5f
. Tính
5
1
()f x dx
.
A.
100 5 ln 5
. B.
12
5 ln 5
5
. C.
56
5 ln 5
5
. D.
56
ln 5
5
.
Mã đề 101 Trang 4
Câu 32: Cho số phức
,
z a bi a b
thỏa mãn
2 10z iz i 
và
3z
. Tính giá trị của
biểu thức
2P ab
.
A.
5P
. B.
2P
. C.
2P 
. D.
10P
.
Câu 33: Trong không gian
Oxyz
, cho đường thẳng và mặt phẳng
( ): 1 0Px yz
. Đường thẳng
qua
3; 2; 2
A
cắt trục
Oy
và song song
P
có phương trình.
A.
33
23
22
xt
yt
zt



. B.
3
2
2
xt
yt
zt



. C.
33
2
22
xt
yt
zt



. D.
32
2
2
xt
yt
zt



.
Câu 34: Cho hai số phức
1
13
zi
và
2
3zi

. Số phức
12
2zz
bằng.
A.
72i
. B.
7 i
. C.
55i
. D.
42i
.
Câu 35: Cho số phức
z
thỏa mãn
2zi

. Tìm phần ảo của số phức
3
w (1 )z

.
A. −26. B. 26. C. −18. D. 18.
Câu 36: Cho hàm số
()fx
liên tục trên
và
58
05
() 5, () 7f x dx f x dx

. Tính
8
0
()
I f x dx
.
A.
6I
. B.
2
I
. C.
12
I
. D.
4I
.
Câu 37: Tìm số phức liên hợp của số phức
(3 2 )
zi i
.
A.
32zi
. B.
23zi

. C.
23zi
. D.
32zi

.
Câu 38: Trong không gian
Oxyz
, đường thẳng đi qua
1; 2; 1A
và
2; 1; 3
B
có phương trình tham số
là:
A.
1
2
12
xt
yt
zt



. B.
12
2
13
xt
yt
zt



. C.
2
12
3
xt
yt
zt



. D.
1
2
12
xt
yt
zt



.
Câu 39: Trong không gian
Oxyz
cho hai điểm
(2; 1;1)I
và
( 1;1;3)A
. Phương trình mặt cầu tâm I và
đi qua A là.
A.
2 22
( 2) ( 1) ( 1) 17
xyz 
. B.
22 2
( 1) ( 1) ( 3) 17xyz  
.
C.
2 22
( 2) ( 1) ( 1) 1xyz 
. D.
22 2
( 1) ( 1) ( 3) 1xyz  
.
Câu 40: Tập hợp điểm biểu diễn của số phức
z
thỏa mãn
23 4zi

.
A. Đường tròn tâm
( 2;3)I
, bán kính
4R
. B. Đường tròn tâm
(2; 3)I
, bán kính
4R
.
C. Đường tròn tâm
( 2;3)I
, bán kính
2R
. D. Đường tròn tâm
(2; 3)I
, bán kính
2R
.
Câu 41: Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
222
( ) : ( 1) ( 1) ( 2) 9Sx y z 
và điểm
(2;3; 1)A
. Xét điểm
M
thuộc
()S
sao cho đường thẳng
AM
tiếp xúc với mặt cầu
()S
. Điểm
M
luôn thuộc mặt phẳng có phương trình nào sau đây.
A.
4 40x yz 
. B.
4 40x yz 
.
C.
4 40x yz 
. D.
4 40x yz 
.
Câu 42: Giả sử tích phân
5
1
ln 3 ln 5
31
dx
I ab
xx

với a, b là các số thực. Tính giá trị của biểu thức
22
3S a ab b
.
A.
5S
. B.
0S
. C.
4S
. D.
1S
.
Mã đề 101 Trang 5
Câu 43: Hàm số
()fx
liên tục trên đoạn
[0;1]
thỏa
23
2
() ( )
31
f x xfx
x

. Tính
1
0
()
I f x dx
.
A.
3
I
. B.
2I

. C.
2I
. D.
3I 
.
Câu 44: Cho hai hàm số
432
bx cx xf x ax 
và
32
2xg mx nxx 
với
,,, ,abcmn
. Biết
hàm số
y fx gx
có ba điểm cực trị là −1,1,3. Diện tích hình phẳng giới hạn bởi hai đường
'y fx
và
y gx
bằng.
A.
10
3
. B.
8
3
. C.
31
6
. D.
32
3
.
Câu 45: Trên tập hợp các số phức, xét phương trình
22
2 1 0,z az b 
(
,ab
là các tham số thực). Có
bao nhiêu cặp số thực
;
ab
sao cho phương trình đó có hai nghiệm
12
,
zz
thỏa mãn
12
32z iz i 
.
A. 4. B. 3. C. 1. D. 2.
Câu 46: Tính giá trị của biểu thức
2023 2023
13 13
Pi i 
.
A.
2023
2P
. B.
2022
2P
. C.
2024
2P
. D.
1012
2P
.
Câu 47: Cho số phức z thỏa
1 5 82iz i 
. Tập hợp biểu diễn số phức z là đường tròn có tâm và
bán kính là
A.
3; 2 , 8IR
. B.
3; 2 , 4 2
IR
.
C.
5; 1 , 4 2
IR

. D.
5; 1 , 2 2IR

.
Câu 48: Cho hàm số
2
25 1
34 1
xx
fx
xx


. Tính giá trị của biểu thức tích phân sau đây
1
2
00
2 sin 3 . cos .T f x dx f x x dx


A.
53
2
. B. 20. C. 16. D.
37
2
.
Câu 49: Xét số phức
z a bi

,ab
thỏa mãn
43 5
zi

. Tính
2P ba

khi
13 1z iz i 
đạt giá trị lớn nhất.
A.
10P
. B.
8P
. C.
2P
. D.
6P
.
Câu 50: Trong không gian
Oxyz
, cho đường thẳng
121
:
111
xyz
d


và mặt cầu
222
: 2 4 6 13 0Sx y z x y z
. Lấy điểm
;;Mabc
với
0a
thuộc đường thẳng
d
sao cho từ
M
kẻ được ba tiếp tuyến
MA
,
MB
,
MC
đến mặt cầu
S
thỏa mãn góc
60
AMB 
,
90BMC 
,
120CMA

. Tổng
2
P abc 
bằng.
A. −2. B. 3. C. −3. D. 2.
-----------------------------------Hết -----------------------------
Mã đề 102 Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO KIỂM TRA CUỐI HỌC KỲ II
THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC: 2023 - 2024
TRƯỜNG THCS &THPT LẠC HỒNG MÔN: TOÁN KHỐI LỚP: 12
TỔ TOÁN-TIN Thời gian: 90 phút (không kể thời gian phát đề)
ĐỀ CHÍNH THỨC
(Đề thi có 5 trang) Mã đề: 102
Họ và tên học sinh :.............................................................................. Số báo danh : .................
Câu 1: Trong không gian
Oxyz
, cho mặt cầu
222
: 3 1 26Sx y z 
. Tâm của
S
có tọa
độ là.
A.
1; 2; 3
. B.
3; 1; 2
. C.
. D.
3; 1; 2
.
Câu 2: Cho số phức
z
thỏa mãn
17
zi i

. Tính môđun của
z
.
A.
3z
. B.
5z
. C.
42z
. D.
4z
.
Câu 3: Cho số phức
54
zi
. Điểm biểu diễn của số phức
z
là.
A.
(5; 4 )
Mi
. B.
(5;4)M
. C.
(5; 4)M
. D.
(5;4)
Mi
.
Câu 4: Cho hàm số
2
35fx x
. Trong các khẳng định sau, khẳng định nào đúng?
A.
() 6f x dx x C
. B.
3
35f x dx x x C 
.
C.
3
5f x dx x x C

. D.
3
1
5
3
f x dx x x C 
.
Câu 5: Trong không gian
Oxyz
, điểm nào dưới đây thuộc đường thẳng
d
:
1
5
23
xt
yt
zt



?
A.
1; 2; 5P
. B.
1; 1; 3Q
. C.
1; 5; 2N
. D.
1; 1; 3M
.
Câu 6: Tìm các số thực
,
ab
thỏa mãn
2 ( 3 4 ) 10 6a b ii i 
, với
i
là đơn vị ảo. Tính
2P ab
.
A. 8. B. 3. C. 5. D. 7.
Câu 7: Tìm nguyên hàm của hàm số
cos 2
fx x
.
A.
( ) sin 2f x dx x x C
B.
( ) sinf x dx x C
C.
( ) sin 2f x dx x x C 
D.
( ) sinf x dx x C
.
Câu 8: Cho hai số phức
1
13
zi
và
2
3zi
. Số phức
12
2zz
bằng.
A.
7 i
. B.
42i
. C.
55i
. D.
72i
.
Câu 9: Diện tích hình phẳng giới hạn bởi hai đường
2
27yx x
và
47yx
bằng
A.
304
15
. B.
4
3
. C.
304
15
. D.
4
3
.
Câu 10: Biết
3
Fx x
là một nguyên hàm của hàm số
fx
trên
. Giá trị của
3
1
2dfx x



bằng.
A.
161
10
. B. 30. C. 24. D. 28.
Mã đề 102 Trang 2
Câu 11: Trong không gian
Oxyz
cho hai điểm
(2; 1;1)I
và
(1;1;3)A
. Phương trình mặt cầu tâm I và đi
qua A là.
A.
22 2
( 1) ( 1) ( 3) 7x yz

B.
2 22
( 2) ( 1) ( 1) 9
xyz

C.
22 2
( 1) ( 1) ( 3) 9x yz
D.
2 22
( 2) ( 1) ( 1) 3
xyz

Câu 12: Môđun của số phức
12i
bằng.
A. 3. B. 5. C.
5
. D.
3
.
Câu 13: Trong không gian
Oxyz
, đường thẳng đi qua
1; 2; 1A
và
2; 1; 1B
có phương trình tham số là:
A.
1
32
2
xt
yt
zt



. B.
1
23
12
xt
yt
zt



. C.
1
12
xt
yt
zt



. D.
1
23
12
xt
yt
zt



.
Câu 14: Tập hợp điểm biểu diễn của số phức
z
thỏa mãn
34 4zi
.
A. Đường tròn tâm
( 3;4)
I
, bán kính
2
R
. B. Đường tròn tâm
( 3;4)I
, bán kính
4R
.
C. Đường tròn tâm
(3; 4)
I
, bán kính
4R
. D. Đường tròn tâm
(3; 4)I
, bán kính
2R
.
Câu 15: Diện tích
S
của hình phẳng giới hạn bởi các đường
2
yx
,
2y 
,
1x 
và
1x
được tính
bởi công thức nào sau đây.
A.
1
2
1
2d
Sx x

. B.
1
2
1
2dSx x

.
C.
1
2
1
2dS xx

. D.
1
2
2
1
2d
Sx x

.
Câu 16: Biết hàm số
()fx
có đạo hàm
'( )fx
liên tục trên
và
(0)f
,
0
'( ) 3f x dx
. Tính
()f
.
A.
() 3f 
. B.
() 4f

. C.
() 2f

. D.
() 2f

.
Câu 17: Trong không gian
Oxyz
, hình chiếu vuông góc của điểm
(3;2;5)A
trên mặt phẳng
()Oxz
có tọa
độ là.
A.
0; 2; 0
. B.
(3;0;5)
. C.
0; 0; 5
. D.
3; 2; 5
.
Câu 18: Biết tích phân
2
0
7f x dx
và
2
0
5
g x dx 
. Khi đó
2
0
f x g x dx



bằng.
A. 2. B. 1. C. −12. D. 12.
Câu 19: Trong không gian
Oxyz
, cho mặt phẳng
: 2 3 0.Px yz 
Điểm nào dưới đây thuộc
P
?
A.
(2;1;5)M
. B.
0; 0; 3P
. C.
2; 1; 3Q
. D.
3; 0; 0N
.
Câu 20: Trong hình vẽ bên, điểm M biểu diễn số phức
z
. Số phức
z
là.
A.
2 i
. B.
12i
. C.
12i
. D.
2 i
.
Mã đề 102 Trang 3
Câu 21: Trong không gian
Oxyz
, cho
(1;1;5)
A
và
(3;1; 5)B
. Trung điểm của đoạn thẳng
AB
có tọa độ
là.
A.
(2;1;0)
. B.
( 1;1; 3)
. C.
. D.
(2;0;5)
.
Câu 22: Cho hai số phức
1
43
zi
và
2
1
zi
. Phần thực của số phức
12
zz
bằng.
A. 5. B. 4. C. 1. D. −2.
Câu 23: Cho số phức
z
thỏa mãn
2zi
. Tìm phần ảo của số phức
3
w ( 4)z
.
A. −11. B. 11. C. 2. D. −2.
Câu 24: Cho
3
1
( ) 12f x dx
. Tính
3
1
3()I f x dx
.
A.
4I
. B.
9
I
. C.
6
I
. D.
36I
.
Câu 25: Trong không gian
Oxyz
, cho mặt cầu
222
( ) : 4 2 6 2 0.Sx y z x y z 
Bán kính của mặt
cầu đã cho bằng.
A. 3. B.
23
. C. 4. D.
22
.
Câu 26: Trong không gian
Oxyz
, mặt phẳng
P
đi qua điểm
3; 1; 4M
và vuông góc với đường thẳng
322
:
11 2
xyz
d


có phương trình là.
A.
2 12 0xy z
. B.
2 60xy z
.
C.
3 4 12 0xy z
. D.
3 4 60xy z
.
Câu 27: Cho hàm số
()
fx
liên tục trên
và
49
14
() 9, () 3f x dx f x dx

. Tính
9
1
()
I f x dx
.
A.
12
I
. B.
2I
. C.
4I
. D.
6I
.
Câu 28: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
1; 2; 1A
. Phương trình chính tắc của đường
thẳng qua
A
và vuông góc
: 3 2 70Px y z 
.
A.
121
1 32
xyz

. B.
121
1 21
xyz

.
C.
132
1 21
xy z


. D.
121
1 32
xyz


.
Câu 29: Trong không gian
Oxyz
, cho mặt phẳng
: 2 3 40xyz

. Vectơ nào dưới đây là một
vectơ pháp tuyến của
?
A.
4
3;2; 4n 

. B.
2
2;3; 4n 

. C.
3
2; 4;1n 

. D.
1
1; 2;3n 

.
Câu 30: Tìm số phức liên hợp của số phức
(2 3 )zi i
.
A.
23zi
. B.
32zi
. C.
23zi
. D.
32zi
.
Câu 31: Gọi
1
z
;
2
z
là hai nghiệm của phương trình
2
2 80
zz 
. Tính giá trị biểu thức
22
12
Az z
.
A. 8. B.
82
. C.
27
. D. 16.
Câu 32: Cho số
z
thỏa mãn
3 4 3 9 19iz z i i 
. Môđun của
z
bằng.
A.
5
. B. 13. C. 5. D.
13
.
Câu 33: Cho số phức
z a bi
với
,ab
thỏa mãn
25 4
zi
và
23zi
là số thực. Tính giá
trị của biểu thức
3Sa b
.
A. −5. B. −7. C. 6. D. 10.
Mã đề 102 Trang 4
Câu 34: Cho hàm số
2
34 1
25 1
xx
fx
xx


. Tính giá trị của biểu thức tích phân sau đây
1
2
00
2 sin 2 . cos .T f x dx f x x dx


A.
99
4
. B.
223
12
. C.
229
12
. D.
101
4
.
Câu 35: Cho hai hàm số
432
bx cx xf x ax 
và
32
3xg mx
nxx 
với
,,, ,abcmn
. Biết
hàm số
y fx gx
có ba điểm cực trị là −1,2,3. Diện tích hình phẳng giới hạn bởi hai đường
'y fx
và
y gx
bằng.
A.
51
6
. B.
61
12
. C.
71
9
. D.
10
3
.
Câu 36: Trong không gian
Oxyz
, cho hai điểm
2;1; 3 1; 2; 3,AB
và mặt phẳng
: 2z 3 0Px y
. Lập phương trình mặt phẳng
Q
đi qua hai điểm
A
,
B
và vuông góc với mặt phẳng
P
.
A.
3 2 11 0xyz
. B.
2 3 11 0xy
.
C.
3 80x yz 
. D.
2 3 11 0yz
.
Câu 37: Trên tập hợp các số phức, xét phương trình
22
2 3 0,z az b 
(
,ab
là các tham số thực). Có
bao nhiêu cặp số thực
;ab
sao cho phương trình đó có hai nghiệm
12
,zz
thỏa mãn
12
53z iz i 
.
A. 3. B. 1. C. 4. D. 2.
Câu 38: Biết rằng
.
x
xe
là một nguyên hàm của hàm số
()fx
. Gọi
()Fx
là một nguyên hàm của
'( ).
x
f xe
thỏa mãn
(0) 1F
. Tính giá trị của
(1)
F
.
A.
1
( 1)
2
F 
. B.
1
( 1)
2
e
F
. C.
1
( 1)
2
F
. D.
1
( 1)
2
e
F
.
Câu 39: Tính thể tích của vật thể tạo nên khi quay quanh trục
Ox
hình phẳng
D
giới hạn bởi đồ thị
2
:2Py xx
và trục
Ox
bằng:
A.
19
15
V
. B.
13
15
V
. C.
17
15
V
. D.
16
15
V
.
Câu 40: Trong không gian
Oxyz
, cho đường thẳng và mặt phẳng
( ): 3 0Pxyz
. Đường thẳng
qua
3; 2; 2
A
cắt trục
Oz
và song song
P
có phương trình.
A.
33
22
25
xt
yt
zt



. B.
33
22
25
xt
yt
zt



. C.
3
2
2
xt
yt
zt



. D.
3
25
2
x
yt
zt


.
Câu 41: Cho số phức
,z a bi a b
thỏa mãn
26 12 0z iz i
và
4z
. Tính giá trị của
biểu thức
2P ab
.
A.
2P 
. B.
10P
. C.
2P
. D.
5P
.
Câu 42: Giả sử tích phân
5
1
ln 5 ln 3
31
dx
I ab
xx

với a, b là các số thực. Tính giá trị của biểu thức
22
23S a ab b
.
A.
4S
. B.
9S
. C.
5S
. D.
6S
.
Mã đề 102 Trang 5
Câu 43: Hàm số
()fx
liên tục trên đoạn
[0;1]
thỏa
23
4
() ( )
81
f x xfx
x

. Tính
1
0
()
I f x dx
.
A.
2
I
. B.
2I 
. C.
3I
. D.
3I 
.
Câu 44: Cho số phức z thỏa
1 5 62iz i

. Tập hợp biểu diễn số phức z là đường tròn có tâm và
bán kính là
A.
3; 2 , 6IR

. B.
5; 1 , 6IR
.
C.
3; 2 , 3 2
IR
. D.
5; 1 , 3 2
IR

.
Câu 45: Cho hàm số
()
fx
xác định và có đạo hàm trên
0; 
thỏa
22
() 2.() 3 4x f x xf x x

và
(1) 3f
. Tính
3
1
()f x dx
.
A.
12 4 ln 3
. B.
8
3 ln 5
3
. C.
8
4 ln 3
3
. D.
16
4 ln 3
3
.
Câu 46: Cho
Fx là một nguyên hàm của hàm
1
2
fx
x
; biết
02F
. Tính
2F .
A.
ln 2 2
2F
. B.
ln 2 22F
.
C.
2 ln 2 22F
. D.
2 ln 2 22F
.
Câu 47: Tính giá trị của biểu thức
2023 2023
33
Pi i 
.
A.
2024
2P
. B.
2022
2P
. C.
1012
2P
. D.
2023
2P
.
Câu 48: Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
2 22
( ) : ( 2) ( 2) ( 1) 8Sx y z 
và điểm
(1;3; 1)
A
. Xét điểm
M
thuộc
()S
sao cho đường thẳng
AM
tiếp xúc với mặt cầu
()
S
. Điểm
M
luôn thuộc mặt phẳng có phương trình nào sau đây.
A.
5 2 60xyz 
. B.
5 2 60xyz 
.
C.
5 2 60xyz 
. D.
5 40x yz 
.
Câu 49: Trong không gian
Oxyz
, cho đường thẳng
121
:
111
xyz
d


và mặt cầu
222
: 2 4 6 13 0Sx y z x y z
. Lấy điểm
;;Mabc
với
0a
thuộc đường thẳng
d
sao cho từ
M
kẻ được ba tiếp tuyến
MA
,
MB
,
MC
đến mặt cầu
S
thỏa mãn góc
60AMB 
,
90BMC 
,
120CMA

. Tổng
2P a bc
bằng.
A. −4. B. 3. C. −3. D. 4.
Câu 50: Xét số phức
z a bi
,ab
thỏa mãn
43 5zi
. Tính
3P ba
khi
13 1z iz i 
đạt giá trị lớn nhất.
A.
2P
. B.
6P
. C.
10P
. D.
8P
.
-----------------------------------Hết -----------------------------
ĐỀ 101 ĐỀ 102 ĐỀ 103 ĐỀ 104
ĐỀ 105 ĐỀ 106 ĐỀ 107 ĐỀ 108
1
A D B A B D B A
2
A B B C C D C B
3
D C A B A B B D
4
C C C A C A C C
5
A C C C B D C D
6
A A B D A D A C
7
B C A D A B A D
8
B A B B C C B B
9
A D B C D B D C
10
C B B B B A B C
11
A B D B A A D A
12
D C B D B B C A
13
A D D B D D B A
14
D C C A B B A A
15
A B C B D C D B
16
D B C C B D C B
17
A B C A D D B B
18
D A A A A C D D
19
A C A C C A A C
20
C A A A D B A B
21
A A B C B C D C
22
D A D C D B B B
23
C B D C A B A B
24
D D B D A C B D
25
C C C B C D C A
ĐÁP ÁN TOÁN LỚP 12- HK2
26
A B A D A D B C
27
D A B B C D A D
28
B A C A B A D C
29
A D C A B C C B
30
A D D C A D D D
31
C D B B D A B B
32
B A C B B B D C
33
C A A C D A D A
34
C B B A A C B A
35
B C A C C A A B
36
C C B C C A A B
37
B D B D C A B A
38
D A A A D B A D
39
A D A B C B C B
40
B A D B B B D B
41
B C D C C C C B
42
A B B D C C C C
43
B D A C B B B A
44
B A A A D D D C
45
D C D C D D B B
46
C B D D D C B C
47
A A B A D B D D
48
D B C B C C B C
49
C A B C A B D C
50
C B C B C D A C
https://toanmath.com/de-thi-hk2-toan-12
Xem thêm: ĐỀ THI HK2 TOÁN 12
I. MỤC TIÊU ĐỀ KIỂM TRA
1. Mục đích
- Nhằm kiểm tra khả năng tiếp thu kiến thức chương trình TOÁN 12. Từ kết quả kiểm tra các em tự đánh giá mình trong việc học tập
nội dung trên, từ đó điều chỉnh hoạt động học .
- Thực hiện yêu cầu trong phân phối chương trình của Bộ Giáo dục và Đào tạo theo chương trình giảm tải.
- Đánh giá quá trình giảng dạy của giáo viên, từ đó có thể điều chỉnh phương pháp, hình thức dạy học nếu thấy cần thiết.
2. Về kiến thức : Yêu cầu HS cần nắm rõ và hiểu được nội dung các bài học của
• NGUYÊN HÀM
• TÍCH PHÂN
• SỐ PHỨC.
• HỆ TỌA ĐỘ OXYZ
3. Về kĩ năng
- Học sinh biết được các kiến thức về vấn đề cốt lõi
- Nắm được cách sử dụng các định lí , tính chất , phương pháp làm bài
- Vận dụng được kiến thức làm những bài kiểm tra đánh giá.
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THCS VÀ THPT LẠC HỒNG
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ II
NĂM HỌC 2023 - 2024
MÔN: TOÁN. KHỐI LỚP: 12
Thời gian: 90 phút
MT CHÍNH THỨC
MÃ ĐỀ: ĐỀ GỐC
II. HÌNH THỨC ĐỀ KIỂM TRA
- Hình thức : 100% Trắc nghiệm (50 câu)
III. THIẾT LẬP MA TRẬN
1. Ma trận đề kiểm tra
BẢNG MA TRẬN TOÁN 12
Nội dung Đơn vị kiến thức Câu hỏi theo mức độ
Tổng
số câu
Tổng
điểm
Tổng
thời
gian
Nhận biết Thông hiểu Vận dụng
Số câu
Thời
gian
Số câu
Thời
gian
Số câu
Thời
gian
NGUYÊN HÀM
NGUYÊN HÀM
2
2
2
0.4
2
PHƯƠNG PHÁP
NGUYÊN HÀM
ĐỔI BIẾN, TỪNG PHÂN 1 1 1 2 2 0.4 3
TÍCH PHÂN
TÍCH PHÂN
2
4
2
0.4
4
PHƯƠNG PHÁP
TÍCH PHÂN
ĐỔI BIẾN, TỪNG PHẦN 2 3 3 7 1 3 6 1.2 13
ỨNG DỤNG
DIỆN TÍCH, THỂ TÍCH
TRÒN XOAY
2 3 3 7 1 3 6 1.2 13
SỐ PHỨC
ĐỊNH NGHĨA, PHÉP
TOÁN
6 8 9 15 2 7 17 3.4 30
HỆ TỌA ĐỘ
OXYZ
HỆ TỌA ĐỘ OXYZ 1 1 2 3 3 0.6 4
PHƯƠNG TRÌNH
MẶT CẦU
PHƯƠNG TRÌNH MẶT
CẦU
1 1 1 2 1 3 3 0.6 6
PHƯƠNG TRÌNH
MẶT PHẲNG
PHƯƠNG TRÌNH MẶT
PHẲNG
2 2 2 3 1 3 5 1.0 8
PHƯƠNG TRÌNH
ĐƯỜNG THẲNG
PHƯƠNG TRÌNH
ĐƯỜNG THẲNG
2 2 1 2 1 3 4 0.8 7
ĐẶC TẢ MA TRẬN
Nội dung kiến thức Đơn vị kiến thức Chuẩn kiến thức kĩ năng cần kiểm tra
Số câu hỏi theo mức độ
nhận thức
Nhận
biết
Thông
hiểu
Vận
dụng
Vận
dụng cao
Nguyên hàm Công thức nguyên hàm
Nhận biết : Tìm được nguyên hàm bằng công
thức
Thông hiểu : Biến đổi áp dụng công thức
2
Phương pháp nguyên hàm Đổi biến- từng phần
Vận dụng: áp dụng được đổi biến, từng phân
tìm nguyên hàm
2
Tích phân Định nghĩa – tính chất
Nhận biết: Áp dụng được định nghĩa, tính chất
Thông hiểu: Áp dụng được định nghĩa, tính
chất có biến đổi
Vận dụng: dùng tính chất chèn cận giải bài
toán hàm từng khoảng
2
Phương pháp tích phân Đổi biến –từng phần Vận dụng: giải bài toán hàm ẩn, có tham số a,b
2
3 1
ứng dụng tích phân
Diện tích hình phẳng,
thể tích tròn xoay
Nhận biết: áp dụng được công thức
Thông hiểu: Tìm được hai đường thẳng x=a;
x=b
2 3 1
Số phức
Các khái niệm và phép
toán
Nhận biết: áp dụng được định nghĩa
Thông hiểu: Thực hiện được phép toán
Vận dụng: Giải được bài toán tìm số phức thỏa
điều kiện cho trước
6 9 2
Hệ tọa độ Oxyz Hệ tọa độ Oxyz
Nhận biết: Nhớ được định nghĩa
Thông hiểu: biến đổi được công thức
1 2
Phương trình mặt cầu Phương trình mặt cầu
Nhận biết: Tìm được tọa độ tâm và bán kính
Thông hiểu: Viết được phương trình mặt cầu
khi tìm được tâm và bán kính
1 1 1
Vận dụng: Thực hiện được các biến đổi liên
quan phương trình mặt cầu
Phương trình mặt phẳng Phương trình mặt phẳng
Nhận biết: Nhớ được định nghĩa
Thông hiểu: Viết được phương trình mặt phẳng
khi có vtpt
Vận dụng: Tìm 2 vtcp và viết phương trình mặt
phẳng
2 2 1
Phương trình đường thẳng
Phương trình đường
thẳng
Nhận biết: Nhớ được định nghĩa
Thông hiểu: viết phương trình đường thẳng khi
có điểm đi qua và vtcp
Vận dụng: Giải được bài toán có yếu tố giao
điểm, hình chiếu, tìm 2 vtpt
2 1 1
| 1/17
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA CUỐI HỌC KỲ II THÀNH PHỐ HỒ CHÍ MINH
NĂM HỌC: 2023 - 2024
TRƯỜNG THCS &THPT LẠC HỒNG MÔN: TOÁN KHỐI LỚP: 12 TỔ TOÁN-TIN
Thời gian: 90 phút (không kể thời gian phát đề) ĐỀ CHÍNH THỨC (Đề thi có 5 trang) Mã đề: 101
Họ và tên học sinh :..............................................................................
Số báo danh : .................
Câu 1: Cho hàm số f x 2
 3x  2 . Trong các khẳng định sau, khẳng định nào đúng? A. f  x 3
dx x  2x C .
B. f(x)dx  6x C  . C. f  x 1 3
dx x  2x C . D. f  x 3
dx  3x  2x C . 3
Câu 2: Trong không gian Oxyz , hình chiếu vuông góc của điểm (
A 3;2; 5 ) trên mặt phẳng (Oxy) có tọa độ là. A. (3;2;0). B. 0;2;0. C. 0;0;5. D. 0;2;5.
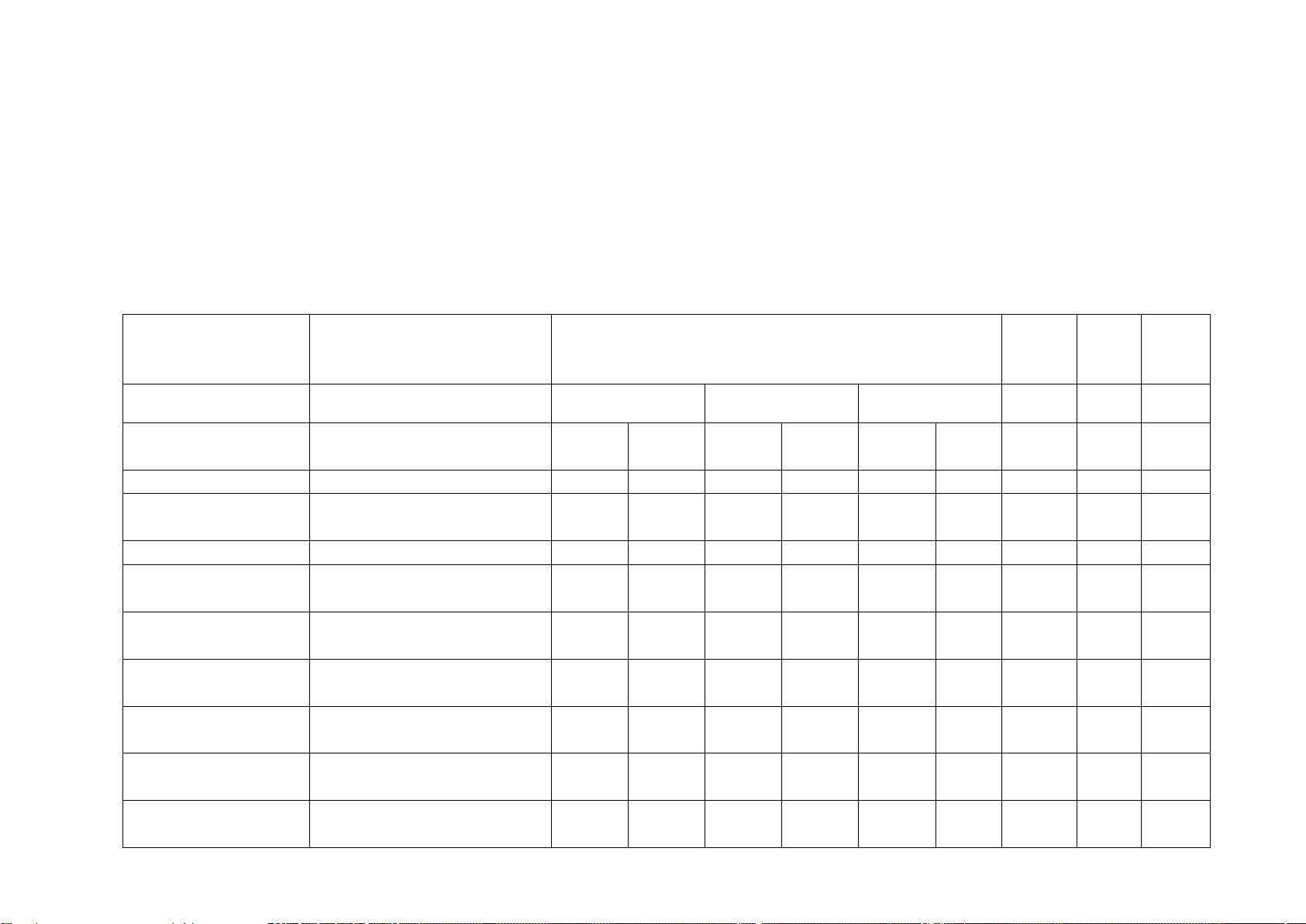
Câu 3: Trong hình vẽ bên, điểm M biểu diễn số phức z . Số phức z là. A. 1 2i . B. 1  2i . C. 2  i . D. 2 i .
Câu 4: Cho hai số phức z  4  3i và z  1  i . Phần ảo của số phức z z bằng. 1 2 1 2 A. 4. B. 1. C. −2. D. 5.
Câu 5: Tìm các số thực a,b thỏa mãn 2a  (3b  4i )i  10  6i , với i là đơn vị ảo. Tính P a  2b . A. 7. B. 5. C. 3. D. 2.
Câu 6: Trong không gian Oxyz , mặt phẳng P đi qua điểm M 3;1;4 và vuông góc với đường thẳng x  3 y  1 z  2 d :   có phương trình là. 1 1 2
A. x y  2z 12  0 .
B. x y  2z  12  0.
C. 3x y  4z 12  0 .
D. 3x y  4z  12  0.
Câu 7: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1; 2;  1 . Phương trình chính tắc của
đường thẳng qua A và vuông góc P : x  3y  2z  7  0.
A. x 1 y  2 z 1 x y z    . B. 1 2 1   . 1 3 2 1 3 2
C. x 1 y  3 z  2 x y z    . D. 1 2 1   . 1 2 1 1 2 1 Mã đề 101 Trang 1
Câu 8: Cho số phức z thỏa mãn z 1  i  7  i . Tính môđun của z . A. z  4 2 . B. z  5 . C. z  4 . D. z  3 .
Câu 9: Trong không gian Oxyz , cho (
A 3;1; 5 ) và B(1; 3;1) . Trung điểm của đoạn thẳng AB có tọa độ là. A. (2;2;2) . B. (4;4;4). C. (1;1;1). D. (1;1; 3).
Câu 10: Biết rằng . x
x e là một nguyên hàm của hàm số f (x) . Gọi F(x) là một nguyên hàm của '( ). x f x e
thỏa mãn F(0)  1. Tính giá trị của F(1). A. 1 ee F(1)  . B. 1 F(1)  . C. 1 F(1)   . D. 1 F(1)  . 2 2 2 2
Câu 11: Diện tích S của hình phẳng giới hạn bởi các đường 2
y x , y  2 , x  0 và x  1 được tính
bởi công thức nào sau đây. 1 1 A. S   2 x   2dx . B. S    2
2  x dx . 0 0 1 1
C. S x   2 2 2 dx . D. S   2 x   2dx . 0 0
Câu 12: Trong không gian Oxyz , cho hai điểm A2; 4; 1,B 1;1;  3 và mặt phẳng
P:x  3y  2z 5  0. Lập phương trình mặt phẳng Q đi qua hai điểm A,B và vuông góc
với mặt phẳng P.
A. x  3y  2z  5  0 .
B. 3x y  2  0 .
C. 3y  2z 11  0 .
D. 2y  3z 11  0 .
Câu 13: Diện tích hình phẳng giới hạn bởi hai đường 2
y x x  5 và y  3x  5 bằng A. 4 . B. 304 . C. 304 . D. 4 . 3 15 15 3 x   3 t 
Câu 14: Trong không gian Oxyz , điểm nào dưới đây thuộc đường thẳng d : y   1t ?
z  2  3t 
A. P 1;3;5.
B. M 1;1;3.
C. Q 1;1;3.
D. N 3;1;2.
Câu 15: Cho F x là một nguyên hàm của hàm f x 1 
; biết F 0  2. Tính F 2. x  2
A. F 2  ln2  2 .
B. F 2  2ln2 2 . C. F 2  ln2 2 .
D. F 2  2ln2  2.
Câu 16: Biết hàm số f(x) có đạo hàm f '(x) liên tục trên  và f(0)  , f '(x)dx  . Tính f(). 0
A. f()  .
B. f()  .
C. f()  0.
D. f()  2.
Câu 17: Cho số z thỏa mãn 2 iz  4z 1 3i  4  23i . Môđun của z bằng. A. 5 . B. 13 . C. 5. D. 13.
Câu 18: Trong không gian Oxyz , cho mặt phẳng  : 3x  2y  4z 1  0 . Vectơ nào dưới đây là một
vectơ pháp tuyến của ?    
A. n  3;2;4 .
B. n  3; 4;1 .
C. n  2; 4;1 .
D. n  3;2; 4 . 4   3   1   2   Mã đề 101 Trang 2 3 3
Câu 19: Cho f(x)dx  12 
. Tính I  3f(x)dx  . 1 1 A. I  36 . B. I  9 . C. I  4 . D. I  6 .
Câu 20: Trong không gian Oxyz , cho mặt cầu 2 2 2
(S) : x y z  6x  2y  4z  2  0. Bán kính của mặt cầu đã cho bằng. A. 2 3 . B. 2 2 . C. 4. D. 3.
Câu 21: Tính thể tích của vật thể tạo nên khi quay quanh trục Ox hình phẳng D giới hạn bởi đồ thị P 2
: y  2x x và trục Ox bằng: A. 16 V  . B. 13 V  . C. 19 V  . D. 17 V  . 15 15 15 15 2 2 2
Câu 22: Biết tích phân f
 xdx  5 và g
 xdx  4. Khi đó f
  xg x  dx bằng.   0 0 0 A. −9. B. 9. C. 2. D. 1.
Câu 23: Môđun của số phức 2 i bằng. A. 3 . B. 5. C. 5 . D. 3.
Câu 24: Gọi z ;z là hai nghiệm của phương trình 2
z  2z  9  0 . Tính giá trị biểu thức 2 2 A zz . 1 2 1 2 A. 6 2 . B. 9 2 . C. 6. D. 18. 3 Câu 25: Biết   3
F x x là một nguyên hàm của hàm số f x trên  . Giá trị của 2  f   x  dx bằng.   1 A. 28. B. 24. C. 30. D. 161 . 10
Câu 26: Trong không gian 2 2 2
Oxyz , cho mặt cầu S : x  2  y  4  z  
1  4 . Tâm của S có tọa độ là. A. 2;4;  1 . B. 2;4;  1 . C. 2;4;  1 .
D. 2;4;  1 .
Câu 27: Tìm nguyên hàm của hàm số f x  cosx 1.
A. f(x)dx  sin x C
B. f(x)dx  sin x x C
C. f(x)dx  sin x C  .
D. f(x)dx  sin x x C
Câu 28: Trong không gian Oxyz , cho mặt phẳng P : x 2y z  5  0. Điểm nào dưới đây thuộc P?
A. N 5;0;0. B. M(2;1;5).
C. P 0;0;5.
D. Q 2;1;5.
Câu 29: Cho số phức z a bi với a,b   thỏa mãn z  3  2i  5 và z 3 i 4 là số thuần ảo. Tính
giá trị của biểu thức S  2a b . A. 2. B. 6. C. −7. D. −5.
Câu 30: Cho số phức z  5  4i . Điểm biểu diễn của số phức z là. A. M(5;4) . B. M(5; 4).
C. M( 5; 4i ) .
D. M(5;4i ).
Câu 31: Cho hàm số f(x) xác định và có đạo hàm trên 0; thỏa 2 2 x f (
x)  2x.f (x)  3x  5 và 5 f (1)  5 . Tính f (x)dx  . 1 A. 100  5 ln 5 . B. 12  5 ln 5 . C. 56  5 ln 5 . D. 56  ln 5 . 5 5 5 Mã đề 101 Trang 3
Câu 32: Cho số phức z a bi a,b   thỏa mãn z  2  i z 1  i  0 và z  3. Tính giá trị của
biểu thức P  2a b . A. P  5 . B. P  2 .
C. P  2 . D. P  10 .
Câu 33: Trong không gian Oxyz , cho đường thẳng và mặt phẳng (P) : x y z  1  0 . Đường thẳng 
qua A3;2;2 cắt trục Oy và song song P có phương trình. x   3  3tx   3 t x   3  3t x   3  2t     A. y
  2  3t . B. y   2 t . C. y   2 t . D. y   2 t .     z   2  2t     z   2  t  z   2  2t  z   2  t 
Câu 34: Cho hai số phức z  1 3i và z  3  i . Số phức 2z z bằng. 1 2 1 2 A. 7  2i . B. 7 i . C. 5  5i . D. 4  2i .
Câu 35: Cho số phức z thỏa mãn z  2  i . Tìm phần ảo của số phức 3 w  (1  z) . A. −26. B. 26. C. −18. D. 18. 5 8 8
Câu 36: Cho hàm số f(x) liên tục trên  và f(x)dx  5, f(x)dx  7  
. Tính I f(x)dx  . 0 5 0 A. I  6 . B. I  2 . C. I  12 . D. I  4 .
Câu 37: Tìm số phức liên hợp của số phức z i(3 2i ).
A. z  3  2i .
B. z  2  3i .
C. z  2  3i .
D. z  3  2i .
Câu 38: Trong không gian Oxyz , đường thẳng đi qua A1;2; 
1 và B 2;1;3 có phương trình tham số là: x   1 tx   1  2t x   2 t x   1 t     A. y   2 t . B. y   2 t . C. y   12t . D. y   2 t .     z   1  2t     z   1  3t  z   3  t  z   1  2t 
Câu 39: Trong không gian Oxyz cho hai điểm I(2;1;1) và (
A  1;1; 3 ) . Phương trình mặt cầu tâm I và đi qua A là. A. 2 2 2
(x  2)  (y  1)  (z  1)  17 . B. 2 2 2
(x  1)  (y  1)  (z  3)  17 . C. 2 2 2
(x  2)  (y  1)  (z  1)  1 . D. 2 2 2
(x  1)  (y  1)  (z  3)  1 .
Câu 40: Tập hợp điểm biểu diễn của số phức z thỏa mãn z 2  3i  4 .
A. Đường tròn tâm I(2;3), bán kính R  4 .
B. Đường tròn tâm I(2; 3), bán kính R  4 .
C. Đường tròn tâm I(2;3), bán kính R  2.
D. Đường tròn tâm I(2; 3), bán kính R  2.
Câu 41: Trong không gian với hệ tọa độ Oxyz , cho mặt cầu 2 2 2
(S) : (x  1)  (y  1)  (z  2)  9 và điểm (
A 2; 3;1) . Xét điểm M thuộc (S) sao cho đường thẳng AM tiếp xúc với mặt cầu (S) . Điểm
M luôn thuộc mặt phẳng có phương trình nào sau đây.
A. x  4y z  4  0 .
B. x  4y z  4  0.
C. x  4y z  4  0.
D. x  4y z  4  0 . 5
Câu 42: Giả sử tích phân dx I
a ln 3  b ln 5 
với a, b là các số thực. Tính giá trị của biểu thức 1 x 3x  1 2 2
S a ab  3b . A. S  5 . B. S  0 . C. S  4 . D. S  1 . Mã đề 101 Trang 4 1
Câu 43: Hàm số f(x) liên tục trên đoạn [ 0;1] thỏa 2 3 2
f (x)  x f (x ) 
. Tính I f(x)dx  . 3x  1 0 A. I  3. B. I  2. C. I  2 .
D. I  3 .
Câu 44: Cho hai hàm số f x 4 3 2
ax bx cx x và g x 3 2
mx nx  2x với a, , b , c , m n   . Biết
hàm số y f xg x có ba điểm cực trị là −1,1,3. Diện tích hình phẳng giới hạn bởi hai đường
y f 'x và y gx bằng. A. 10 . B. 8 . C. 31 . D. 32 . 3 3 6 3
Câu 45: Trên tập hợp các số phức, xét phương trình 2 2
z  2az b  1  0, (a, b là các tham số thực). Có
bao nhiêu cặp số thực a;b  sao cho phương trình đó có hai nghiệm z ,z thỏa mãn 1 2
z iz  3  2i . 1 2 A. 4. B. 3. C. 1. D. 2. 2023 2023
Câu 46: Tính giá trị của biểu thức P  1 3i  1  3i . A. 2023 P  2 . B. 2022 P  2 . C. 2024 P  2 . D. 1012 P  2 .
Câu 47: Cho số phức z thỏa 1  iz  5  i  8 2 . Tập hợp biểu diễn số phức z là đường tròn có tâm và bán kính là
A. I 3;2,R  8 .
B. I 3;2,R  4 2 .
C. I 5; 
1 , R  4 2 .
D. I 5;  1 , R  2 2 .  Câu 48:  
Cho hàm số f x 2x 5  x 1  
. Tính giá trị của biểu thức tích phân sau đây 2 3
x  4 x   1  1 2 T f
 2xdx f
 sinx  3.cosx.dx 0 0 A. 53 . B. 20. C. 16. D. 37 . 2 2
Câu 49: Xét số phức z a bi a,b   thỏa mãn z  4  3i  5 . Tính P  2b a khi
z  1  3i z  1  i đạt giá trị lớn nhất. A. P  10 . B. P  8 . C. P  2 . D. P  6 .
Câu 50: Trong không gian x y z
Oxyz , cho đường thẳng 1 2 1 d :   và mặt cầu 1 1 1 S 2 2 2
: x y z  2x  4y  6z  13  0 . Lấy điểm M a;b; c với a  0 thuộc đường thẳng d
sao cho từ M kẻ được ba tiếp tuyến MA , MB , MC đến mặt cầu S thỏa mãn góc  AMB  60 ,  BMC  90 , 
CMA  120 . Tổng P  2a b c bằng. A. −2. B. 3. C. −3. D. 2.
-----------------------------------Hết ----------------------------- Mã đề 101 Trang 5
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA CUỐI HỌC KỲ II THÀNH PHỐ HỒ CHÍ MINH
NĂM HỌC: 2023 - 2024
TRƯỜNG THCS &THPT LẠC HỒNG MÔN: TOÁN KHỐI LỚP: 12 TỔ TOÁN-TIN
Thời gian: 90 phút (không kể thời gian phát đề) ĐỀ CHÍNH THỨC (Đề thi có 5 trang) Mã đề: 102
Họ và tên học sinh :..............................................................................
Số báo danh : .................
Câu 1: Trong không gian 2 2 2
Oxyz , cho mặt cầu S : x  3  y  
1  z  2  6 . Tâm của S có tọa độ là. A. 1;2;3. B. 3;1;2. C. 3;1  ;1 . D. 3;1;2.
Câu 2: Cho số phức z thỏa mãn z 1i  7  i . Tính môđun của z . A. z  3 . B. z  5 . C. z  4 2 . D. z  4 .
Câu 3: Cho số phức z  5  4i . Điểm biểu diễn của số phức z là.
A. M(5;4i ). B. M(5;4). C. M(5; 4).
D. M( 5; 4i ) .
Câu 4: Cho hàm số f x 2
 3x  5 . Trong các khẳng định sau, khẳng định nào đúng?
A. f(x)dx  6x C  . B. f  x 3
dx  3x  5x C . C. 1 f  x 3
dx x  5x C . D. f  x 3
dx x  5x C . 3 x   1t 
Câu 5: Trong không gian Oxyz , điểm nào dưới đây thuộc đường thẳng d : y   5 t ?
z  2  3t 
A. P 1;2;5.
B. Q 1;1;3.
C. N 1;5;2.
D. M 1;1;3.
Câu 6: Tìm các số thực a,b thỏa mãn 2a  (3b  4i )i  10  6i , với i là đơn vị ảo. Tính P  2a b . A. 8. B. 3. C. 5. D. 7.
Câu 7: Tìm nguyên hàm của hàm số f x  cosx  2.
A. f(x)dx  sin x  2x C
B. f(x)dx  sin x C
C. f(x)dx  sin x  2x C
D. f(x)dx  sin x C  .
Câu 8: Cho hai số phức z  1 3i và z  3  i . Số phức z  2z bằng. 1 2 1 2 A. 7 i . B. 4  2i . C. 5  5i . D. 7  2i .
Câu 9: Diện tích hình phẳng giới hạn bởi hai đường 2
y x  2x  7 và y  4x  7 bằng A. 304 . B. 4. C. 304 . D. 4 . 15 3 15 3 3 Câu 10: Biết   3
F x x là một nguyên hàm của hàm số f x trên  . Giá trị của 2  f   x  dx bằng.   1 A. 161 . B. 30. C. 24. D. 28. 10 Mã đề 102 Trang 1
Câu 11: Trong không gian Oxyz cho hai điểm I(2;1;1) và (
A 1;1; 3 ) . Phương trình mặt cầu tâm I và đi qua A là. A. 2 2 2
(x  1)  (y  1)  (z  3)  7 B. 2 2 2
(x  2)  (y  1)  (z  1)  9 C. 2 2 2
(x  1)  (y  1)  (z  3)  9 D. 2 2 2
(x  2)  (y  1)  (z  1)  3
Câu 12: Môđun của số phức 1 2i bằng. A. 3. B. 5. C. 5 . D. 3 .
Câu 13: Trong không gian Oxyz , đường thẳng đi qua A1;2;  1 và B 2;1; 
1 có phương trình tham số là: x   1 tx   1 t x   1 t x   1 t     A. y
  3  2t . B. y   2  3t . C. y   1 2t . D. y   2  3t .     z   2 t     z   1  2t  z   t   z   1  2t 
Câu 14: Tập hợp điểm biểu diễn của số phức z thỏa mãn z 3  4i  4 .
A. Đường tròn tâm I(3;4), bán kính R  2.
B. Đường tròn tâm I(3;4) , bán kính R  4 .
C. Đường tròn tâm I(3; 4) , bán kính R  4 .
D. Đường tròn tâm I(3; 4) , bán kính R  2.
Câu 15: Diện tích S của hình phẳng giới hạn bởi các đường 2
y x , y  2 , x  1 và x  1 được tính
bởi công thức nào sau đây. 1 1 A. S   2 x   2dx . B. S   2 x   2dx . 1 1 1 1 C. 2 S    2 2  x dx .
D. S  2 x   2 dx . 1 1
Câu 16: Biết hàm số f(x) có đạo hàm f '(x) liên tục trên  và f(0)  , f '(x)dx  3  . Tính f(). 0
A. f()  3.
B. f()  4.
C. f()  2 .
D. f()  2.
Câu 17: Trong không gian Oxyz , hình chiếu vuông góc của điểm (
A 3;2; 5 ) trên mặt phẳng (Oxz) có tọa độ là. A. 0;2;0. B. (3;0;5). C. 0;0;5. D. 3;2;5. 2 2 2
Câu 18: Biết tích phân f
 xdx  7 và g
 xdx  5. Khi đó f
  xg x  dx bằng.   0 0 0 A. 2. B. 1. C. −12. D. 12.
Câu 19: Trong không gian Oxyz , cho mặt phẳng P : x 2y z  3  0. Điểm nào dưới đây thuộc P? A. M(2;1;5).
B. P 0;0;3.
C. Q 2;1;3.
D. N 3;0;0.
Câu 20: Trong hình vẽ bên, điểm M biểu diễn số phức z . Số phức z là. A. 2 i . B. 1  2i . C. 1 2i . D. 2  i . Mã đề 102 Trang 2
Câu 21: Trong không gian Oxyz , cho (
A 1;1; 5 ) và B( 3;1; 5 ) . Trung điểm của đoạn thẳngAB có tọa độ là. A. (2;1;0). B. (1;1; 3). C. (2;2;2) . D. (2;0;5).
Câu 22: Cho hai số phức z  4  3i và z  1  i . Phần thực của số phức z z bằng. 1 2 1 2 A. 5. B. 4. C. 1. D. −2.
Câu 23: Cho số phức z thỏa mãn z  2  i . Tìm phần ảo của số phức 3 w  (z  4) . A. −11. B. 11. C. 2. D. −2. 3 3
Câu 24: Cho f(x)dx  12 
. Tính I  3f(x)dx  . 1 1 A. I  4 . B. I  9 . C. I  6 . D. I  36 .
Câu 25: Trong không gian Oxyz , cho mặt cầu 2 2 2
(S) : x y z  4x  2y  6z  2  0. Bán kính của mặt cầu đã cho bằng. A. 3. B. 2 3 . C. 4. D. 2 2 .
Câu 26: Trong không gian Oxyz , mặt phẳng P đi qua điểm M 3;1;4 và vuông góc với đường thẳng x  3 y  2 z  2 d :   có phương trình là. 1 1 2
A. x y  2z 12  0 .
B. x y  2z  6  0.
C. 3x y  4z 12  0 .
D. 3x y  4z  6  0. 4 9 9
Câu 27: Cho hàm số f(x) liên tục trên  và f(x)dx  9, f(x)dx  3  
. Tính I f(x)dx  . 1 4 1 A. I  12 . B. I  2 . C. I  4 . D. I  6 .
Câu 28: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1; 2; 1. Phương trình chính tắc của đường
thẳng qua A và vuông góc P : x  3y  2z  7  0.
A. x 1 y  2 z 1 x y z    . B. 1 2 1   . 1 3 2 1 2 1
C. x 1 y  3 z  2 x y z    . D. 1 2 1   . 1 2 1 1 3 2
Câu 29: Trong không gian Oxyz , cho mặt phẳng  : x 2y  3z  4  0 . Vectơ nào dưới đây là một
vectơ pháp tuyến của ?    
A. n  3;2; 4 .
B. n  2;3; 4 .
C. n  2; 4;1 .
D. n  1; 2;3 . 1   3   2   4  
Câu 30: Tìm số phức liên hợp của số phức z i(2 3i ).
A. z  2  3i .
B. z  3  2i .
C. z  2  3i .
D. z  3  2i .
Câu 31: Gọi z ;z là hai nghiệm của phương trình 2
z  2z  8  0 . Tính giá trị biểu thức 2 2 A zz . 1 2 1 2 A. 8. B. 8 2 . C. 2 7 . D. 16.
Câu 32: Cho số z thỏa mãn 3 iz  4z  3  i  9 19i . Môđun của z bằng. A. 5 . B. 13. C. 5. D. 13 .
Câu 33: Cho số phức z a bi với a,b   thỏa mãn z  2  5i  4 và z 2 i 3 là số thực. Tính giá
trị của biểu thức S a  3b . A. −5. B. −7. C. 6. D. 10. Mã đề 102 Trang 3  Câu 34:  
Cho hàm số f x 3x 4  x 1  
. Tính giá trị của biểu thức tích phân sau đây 2 2
x  5 x   1  1 2 T f
 2xdx f
 sinx  2.cosx.dx 0 0 A. 99 . B. 223 . C. 229 . D. 101 . 4 12 12 4
Câu 35: Cho hai hàm số f x 4 3 2
ax bx cx x và g x 3 2
mx nx  3x với a, , b , c , m n   . Biết
hàm số y f xg x có ba điểm cực trị là −1,2,3. Diện tích hình phẳng giới hạn bởi hai đường
y f 'x và y gx bằng. A. 51 . B. 61 . C. 71 . D. 10 . 6 12 9 3
Câu 36: Trong không gian Oxyz , cho hai điểm A2;1;  3 ,B 1; 2; 
3 và mặt phẳng P :x y  2z  3  0
. Lập phương trình mặt phẳng Q đi qua hai điểm A,B và vuông góc với mặt phẳng P.
A. x  3y  2z 11  0.
B. 2x  3y 11  0 .
C. x  3y z  8  0 .
D. 2y  3z 11  0 .
Câu 37: Trên tập hợp các số phức, xét phương trình 2 2
z  2az b  3  0, (a, b là các tham số thực). Có
bao nhiêu cặp số thực a;b  sao cho phương trình đó có hai nghiệm z ,z thỏa mãn 1 2
z iz  5  3i . 1 2 A. 3. B. 1. C. 4. D. 2.
Câu 38: Biết rằng . x
x e là một nguyên hàm của hàm số f (x) . Gọi F(x) là một nguyên hàm của '( ). x f x e
thỏa mãn F(0)  1. Tính giá trị của F(1). A. 1 ee F(1)   . B. 1 F(1)  . C. 1 F(1)  . D. 1 F(1)  . 2 2 2 2
Câu 39: Tính thể tích của vật thể tạo nên khi quay quanh trục Ox hình phẳng D giới hạn bởi đồ thị P 2
: y  2x x và trục Ox bằng: A. 19 V  . B. 13 V  . C. 17 V  . D. 16 V  . 15 15 15 15
Câu 40: Trong không gian Oxyz , cho đường thẳng và mặt phẳng (P) : x y z  3  0 . Đường thẳng 
qua A3;2;2 cắt trục Oz và song song P có phương trình. x   3  3tx   3  3t x   3 t x   3     A. y
  2 2t . B. y
  2  2t . C. y   2 t . D. y
  2 5t .     z   2  5t     z   2  5t  z   2  t  z   2  t 
Câu 41: Cho số phức z a bi a,b   thỏa mãn z  2  6i z 1  2i  0 và z  4. Tính giá trị của
biểu thức P  2a b .
A. P  2 . B. P  10 . C. P  2 . D. P  5 . 5
Câu 42: Giả sử tích phân dx I
a ln 5  b ln 3 
với a, b là các số thực. Tính giá trị của biểu thức 1 x 3x  1 2 2
S a  2ab  3b . A. S  4 . B. S  9 . C. S  5 . D. S  6 . Mã đề 102 Trang 4 1
Câu 43: Hàm số f(x) liên tục trên đoạn [ 0;1] thỏa 2 3 4
f (x)  x f (x ) 
. Tính I f(x)dx  . 8x  1 0 A. I  2 . B. I  2. C. I  3. D. I  3.
Câu 44: Cho số phức z thỏa 1iz  5 i  6 2 . Tập hợp biểu diễn số phức z là đường tròn có tâm và bán kính là
A. I 3;2,R  6 .
B. I 5;  1 , R  6 .
C. I 3;2,R  3 2 .
D. I 5;  1 , R  3 2 .
Câu 45: Cho hàm số f(x) xác định và có đạo hàm trên 0; thỏa 2 2 x f (
x)  2x.f (x)  3x  4 và 3 f (1)  3 . Tính f (x)dx  . 1 A. 12  4 ln 3 . B. 8  3 ln 5 . C. 8  4 ln 3. D. 16  4 ln 3 . 3 3 3
Câu 46: Cho F x là một nguyên hàm của hàm f x 1 
; biết F 0  2. Tính F 2. x  2
A. F 2  ln2 2.
B. F 2  ln2  2 .
C. F 2  2ln2  2 .
D. F 2  2ln2 2. 2023 2023
Câu 47: Tính giá trị của biểu thức P  3 i  3  i . A. 2024 P  2 . B. 2022 P  2 . C. 1012 P  2 . D. 2023 P  2 .
Câu 48: Trong không gian với hệ tọa độ Oxyz , cho mặt cầu 2 2 2
(S) : (x  2)  (y  2)  (z  1)  8 và điểm (
A 1; 3;1) . Xét điểm M thuộc (S) sao cho đường thẳng AM tiếp xúc với mặt cầu (S) . Điểm
M luôn thuộc mặt phẳng có phương trình nào sau đây.
A. x  5y  2z  6  0.
B. x  5y  2z  6  0 .
C. x  5y  2z  6  0.
D. x  5y z  4  0 .
Câu 49: Trong không gian x y z
Oxyz , cho đường thẳng 1 2 1 d :   và mặt cầu 1 1 1 S 2 2 2
: x y z  2x  4y  6z  13  0 . Lấy điểm M a;b; c với a  0 thuộc đường thẳng d
sao cho từ M kẻ được ba tiếp tuyến MA , MB , MC đến mặt cầu S thỏa mãn góc  AMB  60 ,  BMC  90 , 
CMA  120 . Tổng P a  2b c bằng. A. −4. B. 3. C. −3. D. 4.
Câu 50: Xét số phức z a bi a,b   thỏa mãn z  4  3i  5 . Tính P  3b a khi
z  1  3i z  1  i đạt giá trị lớn nhất. A. P  2 . B. P  6 . C. P  10 . D. P  8 .
-----------------------------------Hết ----------------------------- Mã đề 102 Trang 5
ĐÁP ÁN TOÁN LỚP 12- HK2
ĐỀ 101 ĐỀ 102 ĐỀ 103 ĐỀ 104 ĐỀ 105 ĐỀ 106 ĐỀ 107 ĐỀ 108 1 A D B A B D B A 2 A B B C C D C B 3 D C A B A B B D 4 C C C A C A C C 5 A C C C B D C D 6 A A B D A D A C 7 B C A D A B A D 8 B A B B C C B B 9 A D B C D B D C 10 C B B B B A B C 11 A B D B A A D A 12 D C B D B B C A 13 A D D B D D B A 14 D C C A B B A A 15 A B C B D C D B 16 D B C C B D C B 17 A B C A D D B B 18 D A A A A C D D 19 A C A C C A A C 20 C A A A D B A B 21 A A B C B C D C 22 D A D C D B B B 23 C B D C A B A B 24 D D B D A C B D 25 C C C B C D C A 26 A B A D A D B C 27 D A B B C D A D 28 B A C A B A D C 29 A D C A B C C B 30 A D D C A D D D 31 C D B B D A B B 32 B A C B B B D C 33 C A A C D A D A 34 C B B A A C B A 35 B C A C C A A B 36 C C B C C A A B 37 B D B D C A B A 38 D A A A D B A D 39 A D A B C B C B 40 B A D B B B D B 41 B C D C C C C B 42 A B B D C C C C 43 B D A C B B B A 44 B A A A D D D C 45 D C D C D D B B 46 C B D D D C B C 47 A A B A D B D D 48 D B C B C C B C 49 C A B C A B D C 50 C B C B C D A C
Xem thêm: ĐỀ THI HK2 TOÁN 12
https://toanmath.com/de-thi-hk2-toan-12
SỞ GIÁO DỤC VÀ ĐÀO TẠO
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ II THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THCS VÀ THPT LẠC HỒNG NĂM HỌC 2023 - 2024
MÔN: TOÁN. KHỐI LỚP: 12 Thời gian: 90 phút MT CHÍNH THỨC
MÃ ĐỀ: ĐỀ GỐC
I. MỤC TIÊU ĐỀ KIỂM TRA 1. Mục đích
- Nhằm kiểm tra khả năng tiếp thu kiến thức chương trình TOÁN 12. Từ kết quả kiểm tra các em tự đánh giá mình trong việc học tập
nội dung trên, từ đó điều chỉnh hoạt động học .
- Thực hiện yêu cầu trong phân phối chương trình của Bộ Giáo dục và Đào tạo theo chương trình giảm tải.
- Đánh giá quá trình giảng dạy của giáo viên, từ đó có thể điều chỉnh phương pháp, hình thức dạy học nếu thấy cần thiết.
2. Về kiến thức : Yêu cầu HS cần nắm rõ và hiểu được nội dung các bài học của • NGUYÊN HÀM • TÍCH PHÂN • SỐ PHỨC.
• HỆ TỌA ĐỘ OXYZ 3. Về kĩ năng
- Học sinh biết được các kiến thức về vấn đề cốt lõi
- Nắm được cách sử dụng các định lí , tính chất , phương pháp làm bài
- Vận dụng được kiến thức làm những bài kiểm tra đánh giá.
II. HÌNH THỨC ĐỀ KIỂM TRA
- Hình thức : 100% Trắc nghiệm (50 câu)
III. THIẾT LẬP MA TRẬN
1. Ma trận đề kiểm tra
BẢNG MA TRẬN TOÁN 12 Tổng Nội dung
Đơn vị kiến thức
Câu hỏi theo mức độ Tổng Tổng
số câu điểm thời gian Nhận biết Thông hiểu Vận dụng Số câu Thời gian Số câu Thời gian Số câu Thời gian NGUYÊN HÀM NGUYÊN HÀM 2 2 2 0.4 2 PHƯƠNG PHÁP
NGUYÊN HÀM ĐỔI BIẾN, TỪNG PHÂN 1 1 1 2 2 0.4 3 TÍCH PHÂN TÍCH PHÂN 2 4 2 0.4 4 PHƯƠNG PHÁP TÍCH PHÂN
ĐỔI BIẾN, TỪNG PHẦN 2 3 3 7 1 3 6 1.2 13 ỨNG DỤNG
DIỆN TÍCH, THỂ TÍCH TRÒN XOAY 2 3 3 7 1 3 6 1.2 13 SỐ PHỨC ĐỊNH NGHĨA, PHÉP TOÁN 6 8 9 15 2 7 17 3.4 30 HỆ TỌA ĐỘ OXYZ HỆ TỌA ĐỘ OXYZ 1 1 2 3 3 0.6 4
PHƯƠNG TRÌNH PHƯƠNG TRÌNH MẶT MẶT CẦU CẦU 1 1 1 2 1 3 3 0.6 6
PHƯƠNG TRÌNH PHƯƠNG TRÌNH MẶT MẶT PHẲNG PHẲNG 2 2 2 3 1 3 5 1.0 8 PHƯƠNG TRÌNH PHƯƠNG TRÌNH ĐƯỜNG THẲNG ĐƯỜNG THẲNG 2 2 1 2 1 3 4 0.8 7 ĐẶC TẢ MA TRẬN
Số câu hỏi theo mức độ nhận thức
Nội dung kiến thức
Đơn vị kiến thức
Chuẩn kiến thức kĩ năng cần kiểm tra Vận Nhận Thông dụng biết hiểu Vận dụng cao
Nhận biết : Tìm được nguyên hàm bằng công Nguyên hàm
Công thức nguyên hàm thức 2
Thông hiểu : Biến đổi áp dụng công thức Phương pháp nguyên hàm Đổi biến- từng phần
Vận dụng: áp dụng được đổi biến, từng phân tìm nguyên hàm 2
Nhận biết: Áp dụng được định nghĩa, tính chất
Thông hiểu: Áp dụng được định nghĩa, tính Tích phân
Định nghĩa – tính chất chất có biến đổi 2
Vận dụng: dùng tính chất chèn cận giải bài toán hàm từng khoảng Phương pháp tích phân
Đổi biến –từng phần V 2
ận dụng: giải bài toán hàm ẩn, có tham số a,b 3 1
Nhận biết: áp dụng được công thức ứng dụng tích phân
Diện tích hình phẳng, Thông hiểu: Tìm được hai đường thẳng x=a; thể tích tròn xoay x=b 2 3 1
Nhận biết: áp dụng được định nghĩa Số phức
Các khái niệm và phép Thông hiểu: Thực hiện được phép toán toán
Vận dụng: Giải được bài toán tìm số phức thỏa 6 9 2 điều kiện cho trước Hệ tọa độ Oxyz Hệ tọa độ Oxyz
Nhận biết: Nhớ được định nghĩa
Thông hiểu: biến đổi được công thức 1 2
Nhận biết: Tìm được tọa độ tâm và bán kính Phương trình mặt cầu
Phương trình mặt cầu Thông hiểu: Viết được phương trình mặt cầu 1 1 1
khi tìm được tâm và bán kính
Vận dụng: Thực hiện được các biến đổi liên
quan phương trình mặt cầu
Nhận biết: Nhớ được định nghĩa
Thông hiểu: Viết được phương trình mặt phẳng
Phương trình mặt phẳng Phương trình mặt phẳng khi có vtpt 2 2 1
Vận dụng: Tìm 2 vtcp và viết phương trình mặt phẳng
Nhận biết: Nhớ được định nghĩa
Thông hiểu: viết phương trình đường thẳng khi
Phương trình đường thẳng Phương trình đường thẳng có điểm đi qua và vtcp 2 1 1
Vận dụng: Giải được bài toán có yếu tố giao
điểm, hình chiếu, tìm 2 vtpt
Document Outline

  • Đề 101
  • Đề 102
  • ĐÁP ÁN TOÁN 12- HK2
    • Sheet1
  • MA TRAN ĐỀ TOÁN 12 -HKII