Đề cuối học kỳ 2 Toán 12 năm 2024 – 2025 sở GD&ĐT Kiên Giang

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC 2024 – 2025 KIÊN GIANG
MÔN: TOÁN - LỚP 12
Thời gian làm bài: 90 phút, không kể thời gian phát đề
ĐỀ CHÍN H THỨC Ngày kiểm tra: 14/5/2025 (Đề có 4 trang)
Họ tên : .............................................................. Số báo danh : ................... Mã đề 0123
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Trong không gian Oxyz , phương trình nào trong các phương trình sau là phương trình
tổng quát của một mặt phẳng? A. 1 2 3 + + = 1. B. x y −1 = = z . x y z 2 4 C. 2 2 2
x + y + z −1 = 0 .
D. 2x − 3z +1 = 0. 3
Câu 2: Tích phân x e dx ∫ có giá trị bằng 0 A. 3 1− e . B. 3 e −1. C. 3 e +1. D. 477 . 25
Câu 3: Họ các nguyên hàm của hàm số f (x) = cos x − sin x là
A. cos x − sin x + C . B. sin x + cos x + C .
C. sin x − cos x + C .
D. sin 2x + C .
Câu 4: Nguyên hàm F(x) của hàm số f (x) 2
= 3x + 4x thỏa mãn F(1) = 5 là A. 3 2
F(x) = 9x + 8x −12 . B. 3 2
F(x) = x + 2x + 5.
C. F(x) = 6x + 4. D. 3 2
F(x) = x + 2x + 2 .
Câu 5: Trong không gian Oxyz , cho mặt cầu (S ) 2 2 2
: (x −1) + (y − 2) + (z − 3) =16 . Bán kính của mặt cầu bằng A. 16. B. 2. C. 4. D. 8.
Câu 6: Cho A, B là 2 biến cố bất kì và P(B) > 0 . Kí hiệu A∩ B = AB , công thức tính xác suất
có điều kiện nào sau đây đúng? P AB P( A B)
A. P( A B) ( ) = .
B. P( AB) = . P( A) P(B) P AB
C. P( A B) = P( AB).P(B) .
D. P( A B) ( ) = . P(B)
Câu 7: Trong không gian Oxyz, tọa độ một vectơ chỉ phương của đường thẳng có phương trình x 2 y 1 : z d − + = = là 3 − 1 2 A. (2; 1; − 0) . B. ( 3 − ;1;2). C. ( 2 − ;1;0) . D. (3;1; 2 − ) . Trang 1/4 – Mã đề 0123
Câu 8: Thể tích của khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau xung quanh trục Ox: 2
y = 5x − 6x , y = 0 , x = 0 , x =1. A. 1 . B. 8 . C. π . D. 8π . 2 15 2 15
Câu 9: Công ty X tổ chức buổi trình diễn ánh sáng với 1000 drone, điều khiển từ trạm trung tâm
để tạo hình khối 3D đẹp mắt, sử dụng hệ thống định vị RTK (Real Time Kinematic) đảm bảo độ
chính xác. Trong quá trình bay, drone có thể gặp sự cố mất tín hiệu kết nối do nhiễu sóng, và khi
đó, nó tự động phát tín hiệu cảnh báo qua kênh dự phòng. Tuy nhiên, hệ thống cảnh báo không
hoàn hảo, có thể báo nhầm ngay cả khi drone hoạt động bình thường. Dựa trên thống kê từ những
buổi trình diễn trước đó: Xác suất một drone gặp sự cố mất kết nối là 0,005; xác suất drone bình
thường bị báo nhầm phát tín hiệu cảnh báo là 0,001; xác suất drone gặp sự cố tín hiệu phát tín
hiệu cảnh báo là 0,99. Trong buổi trình diễn, một drone được ghi nhận phát tín hiệu cảnh báo.
Xác suất để drone này thực sự gặp sự cố mất tín hiệu kết nối là bao nhiêu? (làm tròn kết quả đến phần trăm). A. 0,06. B. 0,83. C. 0,79. D. 0,33.
Câu 10: Cho hai biến cố ,
A B thỏa mãn P( A) = 0,3;P(B | A) = 0,4;P(B A) = 0,5. Khi đó, P(B) bằng A. 0,47 . B. 0,06. C. 0,27 . D. 0,43.
Câu 11: Trong không gian Oxyz , mặt cầu tâm M (1;2;4) tiếp xúc mặt phẳng 2x + y − 2z +1 = 0 có bán kính bằng A. 4 . B. 1. C. 3 . D. 2 . 3 4
Câu 12: Trong không gian Oxyz , đường thẳng nào sau đây vuông góc với đường thẳng x = 2 + t : 
∆ y =1+ t ? z =  2t A.
x − 2 y − 4 z + 4 d : − − + = = . B.
x 1 y 2 z 1 d : = = . 1 2 3 − 1 2 3 C.
x −1 y − 2 z +1 d : − − + = = . D.
x 1 y 2 z 1 d : = = . 1 1 1 − 2 3 1 Trang 2/4 – Mã đề 0123
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí
sinh chọn đúng hoặc sai.
Câu 1: Trong không gian Oxyz , cho 3 điểm D(4; − 0; ) 1 , E (
2;2;3), F(5;3;7) . Gọi T là trung
điểm của đoạn DE .
a) Tọa độ của điểm T là (3;1 ) ;1 .
b) Phương trình mặt cầu (S ) có đường kính DE là 2 2 2
(x − 3) + (y −1) + (z −1) = 24.
c) Một trạm phát sóng điện thoại được đặt tại điểm T, có bán kính phủ sóng R = 6 (km).
Nếu một người dùng ở vị trí F thì nhận được tín hiệu sóng của trạm.
d) Nếu 2 người dùng đều nhận được tín hiệu của trạm phát sóng thì khoảng cách giữa 2 người dùng lớn hơn 5km.
Câu 2: Cho hàm số ( ) x f x = e −1.
a) Họ nguyên hàm của hàm số là x
e − x + C (với C là hằng số).
b) Gọi F(x) là một nguyên hàm của f (x) trên , với F(0) = 3 thì ( ) x
F x = e − x + 2. 1 1 c) Cho g
∫ (x)dx = 7, ta có  f
∫ (x) + g(x)dx = 7e  . 0 0
d) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f (x), trục Ox và đường thẳng x = 2 bằng 2 e − 3.
Câu 3: Trong không gian Oxyz , cho hai điểm B(1;2;− )
1 , C (0;2;3) và mặt phẳng
(P) : x + 3y − 2z +1 = 0.
a) Mặt phẳng (P) có véctơ pháp tuyến n = (1;3; 2 − ).
b) Mặt phẳng (P) đi qua điểm B.
c) Mặt phẳng (Q) qua C và song song với (P) có phương trình là x + 3y − 2z −12 = 0.
d) Góc giữa mặt phẳng (P) và đường thẳng
x −1 y − 2 z +1 d : = =
(làm tròn kết quả đến 2 3 2
hàng đơn vị, theo đơn vị độ) bằng 0 27 .
Câu 4: Lớp 12A có 70% học sinh thích chơi thể thao. Biết rằng, nếu 01 học sinh thích chơi thể
thao thì xác xuất học sinh đó biết chơi cầu lông là 0,8; học sinh không thích chơi thể thao thì xác
xuất học sinh đó biết chơi cầu lông là 0,1. Chọn ngẫu nhiên 01 học sinh .
a) Xác suất học sinh này không thích chơi thể thao là 0,3.
b) Xác suất học sinh này không biết chơi cầu lông với điều kiện không thích chơi thể thao là 0,41.
c) Xác suất học sinh này biết chơi cầu lông là 0,59.
d) Xác suất học sinh này thích chơi thể thao với điều kiện biết chơi cầu lông là 0,95 (làm tròn
kết quả đến hàng phần trăm). Trang 3/4 – Mã đề 0123
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Cho hàm số f (x) = x x có một nguyên hàm là F (x) thỏa F ( ) 1 = 3. Tính F (4) .
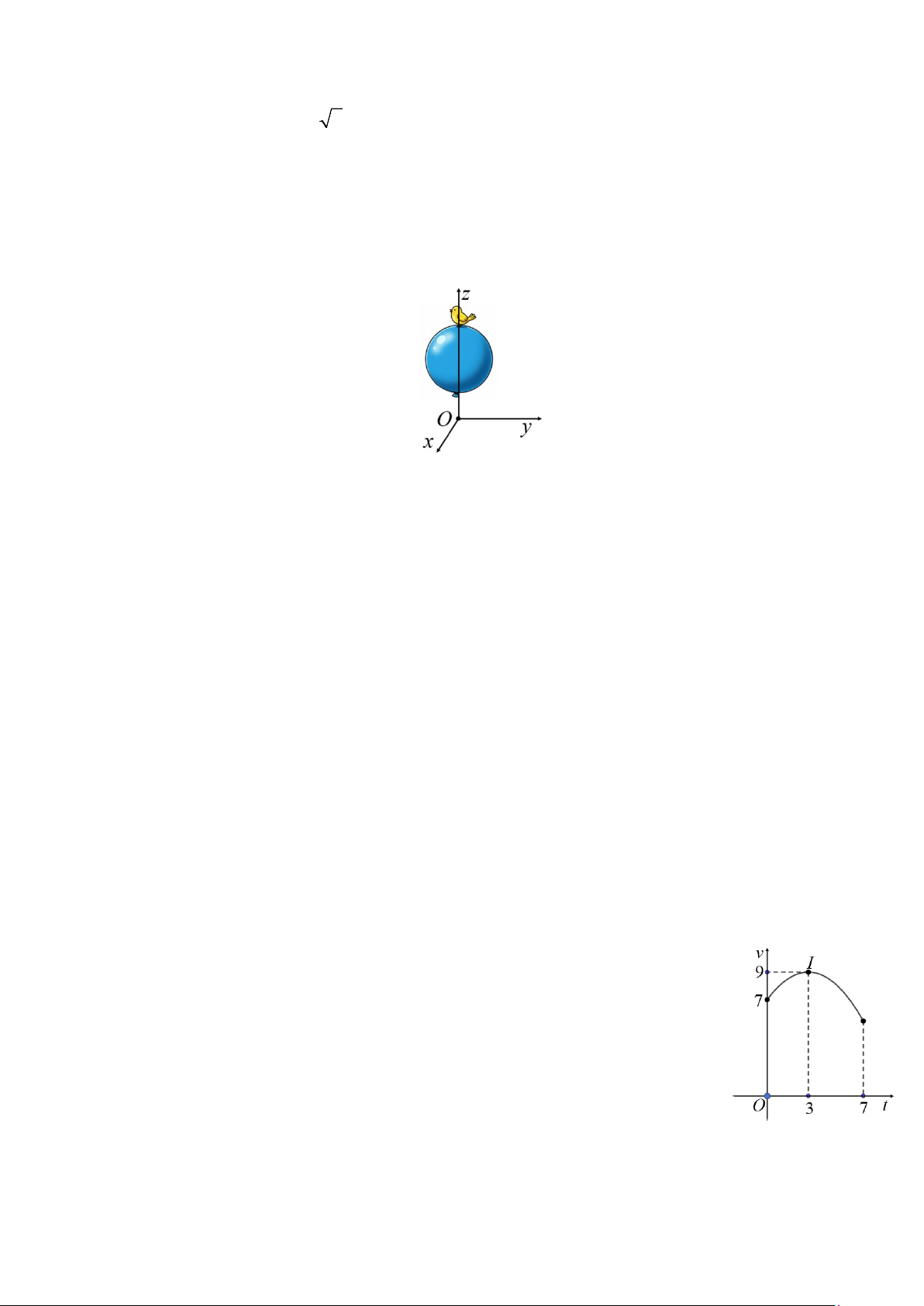
Câu 2: Một quả bóng bay hình cầu có phương trình 2 2
x + y + (z − 2)2 =1 trong hệ trục tọa độ
Oxyz (với mặt phẳng (Oxy) là mặt đất, đơn vị trên trục là mét). Giả sử một chú chim bay lên cao
và đậu lên đỉnh của quả bóng bay (xem hình vẽ minh họa). Hỏi chú chim cách mặt đất bao nhiêu mét? 3 3
Câu 3: Cho f (x)dx = 7 ∫
. Tính ∫[ f (x)+ 4x]dx. 1 − 1 −
Câu 4: Trong một trò chơi bắn súng 3D, một nhân vật đứng tại điểm A(2;1;3) và bắn một viên
đạn theo hướng có vectơ chỉ phương u = (1;2;2) . Viên đạn di chuyển theo một đường thẳng
trong không gian Oxyz. Một bức tường chắn được mô tả bởi mặt phẳng có phương
2x − y + 2z −10 = 0 . Biết rằng hệ tọa độ được đo bằng mét và viên đạn di chuyển với tốc độ
không đổi. Để tạo hiệu ứng vật lý chân thực trong game, nhà phát triển cần tính khoảng cách từ
điểm bắn A đến điểm mà viên đạn chạm vào bức tường (gọi là điểm P). Khoảng cách AP này
giúp xác định thời gian viên đạn bay đến tường và hiển thị hiệu ứng va chạm sống động trên đồ
họa 3D . Tính khoảng cách AP đó.
Câu 5: Hiện nay, học tập trực tuyến sử dụng trí tuệ nhân tạo (AI) làm gia sư đang rất phổ biến.
Một học sinh sử dụng ứng dụng học tập AI để ôn thi. Có hai loại câu hỏi mà ứng dụng đưa ra:
câu hỏi dễ và câu hỏi khó. Xác suất để ứng dụng chọn loại câu hỏi dễ là 79%. Khi gặp câu hỏi
dễ, xác suất học sinh trả lời sai là 10%. Khi gặp câu hỏi khó, xác suất trả lời đúng chỉ là 65%.
Tính xác suất để học sinh trả lời đúng một câu hỏi ngẫu nhiên từ ứng dụng (tính kết quả theo
đơn vị %, làm tròn kết quả đến một chữ số thập phân).
Câu 6: Một vật chuyển động trong 7 giờ với vận tốc v (km / h) phụ thuộc vào
thời gian t (h) có đồ thị là một phần của đường parabol có đỉnh I (3;9) và trục
đối xứng song song với trục tung như hình bên phải. Tính quãng đường mà vật
di chuyển được trong 7 giờ (làm tròn kết quả đến phần mười). -------- HẾT--------
Thí sinh không được sử dụng tài liệu, giám thị không giải thích gì thêm. Trang 4/4 – Mã đề 0123
HƯỚNG DẪN CHẤM KIỂM TRA (gồm có 01 trang) 0123 Phần I Câu 1 D Câu 2 B Câu 3 B Câu 4 D Câu 5 C Câu 6 D Câu 7 B Câu 8 D Câu 9 B Câu 10 A Câu 11 B Câu 12 C Phần II Câu 1 ĐSSS Câu 2 ĐĐSĐ Câu 3 ĐSSĐ Câu 4 ĐSĐĐ Phần III Câu 1 15.4 Câu 2 3 Câu 3 23 Câu 4 0.75 Câu 5 84.8 Câu 6 56.3 -------- HẾT-------- Trang 5/4 – Mã đề 0123
Xem thêm: ĐỀ THI HK2 TOÁN 12
https://toanmath.com/de-thi-hk2-toan-12
Document Outline

• Toan12HK2_SoGD_KienGiang
• Đề Thi HK2 Toán 12