Đề cuối kì 2 Toán 12 năm 2022 – 2023 trường THPT Phú Lộc – TT Huế

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra cuối học kỳ 2 môn Toán 12 năm học 2022 – 2023 .Mời bạn đọc đón xem.

39 20 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

7 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Đề kiểm tra cuối học kì 2, năm học 2022-2023, môn Toán 12. Trang 1/4 - Mã đề 132
TRƯỜNG THPT PHÚ LỘC
TỔ TOÁN - TIN
ĐỀ KIỂM TRA CUỐI KÌ II, NĂM HỌC 2022-2023
MÔN: TOÁN 12
(Đề thi gồm có 04 trang)
Thời gian làm bài 90 phút, không kể thời gian phát đề
Họ và tên học sinh: ………………………………………., Lớp: …..
Mã đề 132
I.
PHẦN TRẮC NGHIỆM (7,0 điểm)
Câu 1. Cho hình phẳng
(
)
H
giới hạn bởi các đường có phương trình:
1
yx= +
,
0
y =
,
1x =
,
2x =
. Gọi
V
là thể tích của khối tròn xoay được tạo thành khi quay
( )
H
xung quanh trục
. Mệnh
đề nào dưới đây đúng?
A.
( )
2
2
1
1V x dx
π
= +
∫
. B.
( )
2
2
1
1V x dx= +
∫
.
C.
( )
2
1
1V x dx= +
∫
. D.
( )
2
1
1V x dx
π
= +
∫
.
Câu 2. Cho hai số phức
12zi= +
. Số phức
1
z
bằng
A.
12i−
. B.
12i−−
. C.
12
55
i−
. D.
12
55
i−−
.
Câu 3. Diện tích hình phẳng được tô đậm trong hình bên dưới bằng
A.
14
11
( ).d ( ).dS fx x fx x
−
= +
∫∫
. B.
14
11
( ).d ( ).dS fx x fx x
−
=−−
∫∫
.
C.
14
11
( ).d ( ).dS fx x fx x
−
= −
∫∫
. D.
14
11
( ).d ( ).dS fx x fx x
−
=−+
∫∫
.
Câu 4. Trên mặt phẳng tọa độ điểm biểu diễn số phức
12zi=−+
là điểm nào trong các điểm sau?
(hình vẽ dưới đây)
A.
P
. B.
C.
N
. D.
Q
.
Câu 5. Họ nguyên hàm của hàm số
( )
2022
fx x=
là
A.
2023
1
2022
xC+
. B.
2022
2022xC+
.
C.
2023
1
2023
xC+
. D.
2021
2022xC+
.
Câu 6. Cho hai số phức
1
23zi= −
,
2
4zi= +
. Số phức
12
zz−
bằng
A.
62i−
. B.
24i−
. C.
22i−−
. D.
24i−−
.
Đề kiểm tra cuối học kì 2, năm học 2022-2023, môn Toán 12. Trang 2/4 - Mã đề 132
Câu 7. Cho
( ) ( )
,f x gx
là các hàm số xác định và liên tục trên
. Mệnh đề nào sau đây sai?
A.
( )
( )
22f x dx f x dx=
∫∫
. B.
( ) ( ) ( ) ( )
f x g x dx f x dx g x dx−= −


∫ ∫∫
.
C.
( )
(
) ( ) ( )
..f x g x dx f x dx g x dx=
∫ ∫∫
. D.
( ) ( ) ( ) ( )
f x g x dx f x dx g x dx
+= +


∫ ∫∫
.
Câu 8. Biết một nguyên hàm của hàm số
( )
1
21
fx
x
=
−
là hàm số
(
)
Fx
thỏa mãn
(
)
13
F
= −
. Khi
đó
( )
Fx
là hàm số nào sau đây?
A.
( )
1
ln 2 1 3
2
Fx x
= −+
. B.
(
)
2ln 2 1 3Fx x
= −+
.
C.
( )
( )
1
ln 2 1 3
2
Fx x
= −−
. D.
( )
1
ln 2 1 3
2
Fx x
= −−
.
Câu 9. Nếu
1
0
( )d 3fx x=
∫
và
1
0
( )d 4gx x= −
∫
thì
1
0
[() 2()]df x gx x−
∫
bằng
A.
1
−
. B.
7
. C.
5−
. D.
11
.
Câu 10. Trong không gian
Oxyz
, cho mặt phẳng
( )
:2 2 1 0P x yz− + +−=
. Vectơ nào dưới đây là
một vectơ pháp tuyến của
( )
P
?
A.
( )
2;1; 1a = −
. B.
( )
2;2;1a = −
. C.
( )
2;2;0a = −
. D.
( )
2;2; 1a =−−
.
Câu 11. Trong không gian với hệ tọa độ
Oxyz
, tìm tổng tất cả các giá trị nguyên dương của tham
số
m
để phương trình
2 22
224 0x y z x y zm+ +− + − +=
là phương trình của một mặt cầu
A.
6
. B.
21
. C.
5
. D.
15
.
Câu 12. Trong không gian
Oxyz
, cho mặt phẳng
( )
:3 2 2 10 0xyz
α
−+−=
. Điểm nào dưới đây
thuộc
( )
α
?
A.
( )
1;2; 2P −
. B.
( )
3; 1;4
Q
−
. C.
( )
2;2;10N −
. D.
( )
2; 2;3M −
.
Câu 13. Trong không gian
Oxyz
, cho các điểm
( )
3; 2; 0
A
,
( )
1; 4; 3B
. Tọa độ vectơ
AB

là
A.
( )
2; 2; 3−−
. B.
( )
2; 2;3−
. C.
( )
2; 2; 3−− −
. D.
( )
2; 2;3−
.
Câu 14. Gọi
( )
H
là hình phẳng giới hạn bởi các đường
,
x
ye=
trục
, 0, 1Ox x x= =
. Tính thể tích
khối tròn xoay được tạo thành khi quay hình phẳng
( )
H
quanh trục
.
A.
( )
2
1
2
e
π
−
. B.
( )
2
1
2
e
π
+
. C.
( )
1
2
e
π
−
. D.
( )
2
1e
π
−
.
Câu 15. Trong không gian với hệ trục tọa độ
Oxyz
, đường thẳng
d
đi qua
( )
1; 2; 1
A −
có một
vectơ chỉ phương
(
)
2 ;1; 0u
có phương trình tham số là
A.
1
2
xt
yt
zt
= +
= −
=
. B.
12
2
1
xt
yt
z
= +
= +
= −
. C.
12
2
xt
yt
zt
= +
= +
= −
. D.
2
22
xt
yt
zt
= +
= +
= −
.
Câu 16. Trong tập số phức, một căn bậc hai của
9−
là
A.
3
. B.
9
. C.
3i
. D.
9i
.
Câu 17. Phương trình mặt phẳng
( )
P
đi qua điểm
( )
1; 3; 2M −
và song song với mặt phẳng
( )
:2 5 1 0Q x yz+ ++=
là
A.
3 2 15 0xyz+−+=
. B.
2 5 15 0x yz+ +− =
.
C.
2 5 19 0x yz+ ++ =
. D.
3 2 19 0xyz+−−=
.
Câu 18. Cho số phức
13zi= −
. Môđun của số phức
( )
1 iz−
bằng
A.
25
. B.
52
. C.
10
. D.
20
.
Đề kiểm tra cuối học kì 2, năm học 2022-2023, môn Toán 12. Trang 3/4 - Mã đề 132
Câu 19. Cho
( )
Fx
là một nguyên hàm của hàm số
( )
fx
trên đoạn
[ ]
0; 4
và thỏa mãn
( )
01F =
,
( )
45F = −
. Khi đó
( )
4
0
f x dx
∫
bằng
A.
6−
. B.
4
. C.
6
. D.
4−
.
Câu 20. Trong không gian
Oxyz
, cho ba điểm
( )
3; 2; 2A
−
,
( )
1; 0;1B
và
( )
2; 1; 3C −
. Viết phương
trình mặt phẳng đi qua
A
và vuông góc với
BC
.
A.
2 50xy z−+ −=
. B.
2 30xy z++ +=
. C.
2 30xy z−+ +=
. D.
2 10xy z+ + −=
.
Câu 21. Trong không gian
,Oxyz
điểm nào dưới đây thuộc đường thẳng
( )
12
:3
45
xt
dy t
zt
= +
=−+
= +
?
A.
( )
4;1;3Q
. B.
( )
3; 2; 1P −−
. C.
( )
2;1;5N
. D.
( )
1; 3;4M −
.
Câu 22. Cho hàm số
( )
fx
liên tục trên
và
( )
( )
2
0
3
3 d 17fx x x+=
∫
. Tính
( )
3
0
dfx x
∫
.
A.
9−
. B.
10−
. C.
7−
. D.
5−
Câu 23. Cho
( )
3
2023
2
1
2dI xx x
−
= −
∫
. Đặt
2
2tx= −
, mệnh đề nào sau đây đúng?
A.
3
2023
1
1
d
2
I tt
−
=
∫
. B.
7
2023
1
1
d
2
I tt
−
=
∫
. C.
3
2023
1
dItt
−
=
∫
. D.
7
2023
1
dItt
−
=
∫
.
Câu 24. Cho hai số phức
1
12zi= −
và
2
2zi= +
. Số phức
12
zz+
bằng
A.
3 i−+
. B.
33i−−
. C.
3 i−
. D.
3 i+
.
Câu 25. Cho số phức
2022 2023zi=−+
. Số phức liên hợp của số phức
z
là
A.
2022 2023zi= +
. B.
2022 2023zi=−−
. C.
2022 2023zi=−+
. D.
2022 2023zi= −
.
Câu 26. Ký hiệu
0
z
là nghiệm phức có phần ảo dương của phương trình
2
2 6 50zz+ +=
. Trên mặt phẳng tọa độ điểm nào dưới đây là điểm biểu diễn số phức
0
w iz=
.
A.
2
13
;
22
M

−−


. B.
3
31
;
22
M

−−


. C.
1
13
;
22
M

−


. D.
4
31
;
22
M

−


.
Câu 27. Số phức thỏa mãn là
A.
14
17 17
i−−
. B.
14
17 17
i−+
. C.
14i−+
. D.
14i−−
.
Câu 28. Cho hàm số
(), ()y f x y gx= =
liên tục trên
[ ]
1;3
. Gọi
S
là diện tích miền phẳng giới hạn
bởi đồ thị hàm số
(), ()y f x y gx= =
và hai đường thẳng
1, 3xx= =
. Mệnh đề nào dưới đây
đúng?
A.
( ) ( )
3
1
dS f x gx x
π
= −


∫
. B.
( ) ( )
3
1
dS f x gx x= −
∫
.
C.
( ) ( )
3
1
dS f x gx x= −


∫
. D.
( ) ( )
3
1
dS f x gx x
π
= −
∫
.
Câu 29. Nếu hàm số
( )
fx
thỏa mãn
( )
2
0
d4fx x= −
∫
thì
( )
2
0
2dfx x
∫
bằng
A.
8
. B.
2−
. C.
6−
. D.
8−
.
Câu 30. Cho các số thực
,xy
thỏa mãn
13 23.x i yi++ = −
Giá trị
2xy+
bằng
A.
1
. B.
2
. C.
1−
. D.
0
.
Câu 31. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
2023
x
y =
,
0y =
,
0x =
,
2x =
.
Mệnh đề nào dưới đây đúng?
Đề kiểm tra cuối học kì 2, năm học 2022-2023, môn Toán 12. Trang 4/4 - Mã đề 132
A.
2
2
0
2023 d
x
Sx=
∫
. B.
2
0
2023 d
x
Sx=
∫
.
C.
2
2
0
2023 d
x
Sx
π
=
∫
. D.
2
0
2023 d
x
Sx
π
=
∫
.
Câu 32. Cho hai số phức
1
12
zi
= +
và
2
1zi= −
. Phần thực của số phức
1
2
z
z
bằng
A.
3
2
. B.
1
2
−
. C.
3
2
−
. D.
1
2
.
Câu 33. Trong không gian
Oxyz
, cho hai điểm
( )
2;3;4A
và
( )
0;1;2B
. Đường thẳng
d
đi qua
trung điểm của
AB
và song song với đường thẳng
13
:
2 15
x yz
−+
∆==
−
có phương trình là
A.
234
2 15
xyz
− −−
= =
−
. B.
123
2 15
xy z−−−
= =
−
.
C.
123
2 15
xy z+++
= =
−
. D.
234
123
xyz− −−
= =
.
Câu 34. Kí hiệu
, ab
lần lượt là phần thực và phần ảo của số phức
3 2.i−
Tìm
,ab
.
A.
2, 3ab=−=
. B.
3, 2ab= = −
.
C.
2, 3a ib=−=
. D.
3, 2ab i= = −
.
Câu 35. Trong không gian
Oxyz
, cho đường thẳng
214
:
22 3
x yz
d
− −−
= =
−
. Đường thẳng
d
có
một vec tơ chỉ phương là
A.
( )
2;1;4u =
. B.
(
)
2;2;3u
=
. C.
( )
2; 1; 4u =−−−
. D.
(
)
2;2;3u = −
.
II. PHẦN TỰ LUẬN
(3,0 điểm)
Câu 1. (1,0 điểm) Tính tích phân
2
9
0
cos .sin .I x xdx
π
=
∫
Câu 2. (1,0 điểm) Trong không gian
,Oxyz
viết phương trình tham số đường thẳng Δ đi qua điểm
(2; 4; 6)M −
, vuông góc với đường thẳng
357
:
4 12
xyz
d
−−−
= =
−
và song song với mặt phẳng
( ) : 2 3 10 0
P xy z+− + =
Câu 3. (0,5 điểm) Tìm tất cả các số phức
z
thỏa mãn
5 1 (2 6 ) 3 ( 1)
z i z iz−= − + +
.
Câu 4. (0,5 điểm) Ông Minh sở hữu một mảnh vườn
hình chữ nhật. Ông Minh dự định chia mảnh vườn đó
thành 2 khu vực, phần màu xám là trồng hoa lan, phần
còn lại là trồng hoa hồng (hai đường cong là parabol có
đỉnh đối xứng qua tâm của mảnh vườn và có chung trục
đối xứng). Biết tiền trả cho nhân công phần trồng hoa
lan là 40.000 đồng/m
2
, trồng hoa hồng là 50.000
đồng/m
2
và số tiền ông Minh trả cho nhân công trồng
hoa ở hai khu vực của mảnh vườn là bằng nhau. Tính
độ dài chiều còn lại của mảnh vườn đó.
===== Hết =====
60m
10m
10m
1
TRƯỜNG THPT PHÚ LỘC
TỔ TOÁN – TIN
Hướng dẫn chấm gồm có 03 trang
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA CUỐI KÌ II
NĂM HỌC 2022-2023
MÔN: TOÁN 12
I. PHẦN TRẮC NGHIỆM (7,0 điểm)
ĐÁP ÁN CÁC MÃ ĐỀ
Câu
Mã đề 132
Mã đề 209
Mã đề 357
Mã đề 485
1
A
A
A
A
2
C
C
C
D
3
C
B
D
C
4
A
C
B
B
5
C
C
B
B
6
D
B
B
C
7
C
B
A
A
8
D
B
B
C
9
D
A
B
B
10
B
A
D
C
11
D
B
C
D
12
C
D
D
B
13
D
B
D
D
14
A
B
B
B
15
B
B
C
B
16
C
C
C
D
17
B
A
B
D
18
A
D
A
C
19
A
A
C
C
20
C
C
A
A
21
D
C
C
B
22
B
D
A
B
23
B
B
B
B
24
C
D
D
C
25
B
A
D
B
26
A
D
B
B
27
D
B
B
B
28
B
B
D
A
29
D
D
C
D
30
A
D
A
B
31
B
D
C
C
32
B
C
B
A
33
B
C
D
C
34
B
D
A
B
35
D
B
B
C
II. PHẦN TỰ LUẬN (3 điểm)
Chú ý : Ở mỗi phần, mỗi câu, nếu học sinh có cách giải khác đáp án nhưng đúng và chặt
chẽ thì vẫn cho điểm tối đa của phần hoặc câu đó.
2
Câu
Nội dung
Điểm
Câu 1
Tính tích phân
2
9
0
cos .sin .
I x xdx
π
=
∫
Đặt
sintx=
Vi phân:
cosdt xdx
=
0,25
Đổi cận:
1; 0 0
2
x tx t
π
= ⇒= = ⇒=
0,25
Khi đó:
1
2
99
00
cos .sin
I x xdx t dt
π
= =
∫∫
0,25
( )
1
10
0
11 1
10
10 10 10
It= = −=
0,25
Câu 2
Trong không gian
,Oxyz
viết phương trình tham số đường thẳng Δ đi qua điểm
(2; 4; 6)M −
, vuông góc với đường thẳng
357
:
4 12
xyz
d
−−−
= =
−
và song song
với mặt phẳng
( ) : 2 3 10 0P xy z+− + =
Đường thẳng d có vectơ chỉ phương
( )
1
4; 1; 2u = −

.
Mặt phẳng (P) có vectơ pháp tuyến
(
)
2;1; 3
n = −
.
0,25
Do đường thẳng Δ vuông góc với đường thẳng d và song song với mặt phẳng
(P) nên Δ nhận vectơ
1
,
u un

=


làm vectơ chỉ phương.
0,25
Tính được:
( )
1;16; 6u =
0,25
Đường thẳng Δ đi qua điểm
(2; 4; 6)M −
và có vectơ chỉ phương
( )
1;16; 6u =
có
phương trình tham số là:
2
4 16
66
xt
yt
zt
= +
= +
=−+
0,25
Câu 3
Tìm tất cả các số phức
z
thỏa mãn
5 1 (2 6 ) 3 ( 1)
z i z iz−= − + +
.
Ta có:
51(26) 3(1) 512 6 3 3z iziz z zizizi−= − + + ⇔ −= − + +
5 3 2 6 13z iz z i z i⇔ − = − ++
( )
( )
( )
( )
53 2 1 6 3 1iz z z i⇔ − = + +− +
( )
( )
( )
53 2 1 6 3iz z z i⇒ − = + +− +
( )
( )
(
)
22
53. 2 1 6 3iz z z
⇔ − = + +− +
(
)
( ) (
)
22
2
3
5 3. 2 1 6 3zz z
⇔ +− = + +− +
( ) ( )
22
2 22
34. 2 1 6 3 34. 40 32 10zz z z zz
⇔=++−+⇔=−+
2
6 32 10 0 5zz z⇔− + − = ⇔ =
hoặc
1
3
z =
0,25
Khi
5z =
, thay
5z =
vào (1) ta được
( )
11 27
5 3 11 27
53
i
iz i z
i
−
⇔ − = − ⇔=
−
0,25
3
( )
( )
( )
2
2
11 27 5 3
43
53
ii
z zi
−+
= ⇔=−
+−
Khi
1
3
z =
, thay
1
3
z =
vào (1) ta được
(
)
5
5
3
53
3 53
i
iz i z
i
+
⇔ − = +⇔ =
−
( )
(
)
2
2
5
53
85
3
51 17
53
ii
z zi

++


= ⇔= +
+−
Vậy có hai số phức
1
4 3,zi= −
2
85
51 17
zi= +
Câu 4
Ông Minh sở hữu một mảnh vườn
hình chữ nhật. Ông Minh dự định
chia mảnh vườn đó thành 2 khu vực,
phần màu xám là trồng hoa lan,
phần còn lại là trồng hoa hồng (hai
đường cong là parabol có đỉnh đối
xứng qua tâm của mảnh vườn và có
chung trục đối xứng). Biết tiền trả
cho nhân công phần trồng hoa lan là
40.000 đồng/m
2
, trồng hoa hồng là
50.000 đồng/m
2
và số tiền ông Minh trả cho nhân công trồng hoa ở hai khu vực
của mảnh vườn là bằng nhau. Tính độ dài chiều còn lại của mảnh vườn đó.
Gán hệ trục Oxy như hình vẽ, Gốc tọa độ
O là tâm của mảnh vườn.
Gọi I, J lần lượt là đỉnh của hai parabol.
Đặt IO = c (c > 0). Suy ra AD = 20 + 2c.
Parabol (P) có đỉnh I(0;c), đi qua hai
điểm A(30;10 + c), B(-30;10 + c) là hàm
số có dạng
2
y ax c= +
.
Do (P) đi qua điểm A(30;10 + c) nên
2
1
10 .30
90
ca c a+= +⇔=
Diện tích phần màu xám là:
30
2
1
30
1
2. 10
90
S c x c dx
−


= +− +




∫
30
30
2 32
1
30
30
11
2. 10 10 800
90 270
S x dx x x m
−
−

=−=− =


∫
0,25
Diện tích mảnh vườn:
( )
2
. 60. 20 2
ABCD
S AB CD c m= = +
Suy ra diện tích khu vực còn lại
2
21
1200 120 800 120 400
ABCD
SS S c c m= −= + − = +
Do số tiền trả nhân công của hai khu vực bằng nhau nên ta có:
( )
800.40000 120 400 .50000 32000000 600000 2000000 2c cc= + ⇔ = + ⇔=
Vậy độ dài chiều còn lại của mảnh vườn là 24m
0,25
N
M
J
D
C
B
A
I
O
y
x
60m
10m
10m
| 1/7
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT PHÚ LỘC
ĐỀ KIỂM TRA CUỐI KÌ II, NĂM HỌC 2022-2023 TỔ TOÁN - TIN MÔN: TOÁN 12
(Đề thi gồm có 04 trang)
Thời gian làm bài 90 phút, không kể thời gian phát đề
Họ và tên học sinh: ………………………………………., Lớp: ….. Mã đề 132
I. PHẦN TRẮC NGHIỆM (7,0 điểm)
Câu 1. Cho hình phẳng (H ) giới hạn bởi các đường có phương trình: y = x +1, y = 0, x =1, x = 2
. Gọi V là thể tích của khối tròn xoay được tạo thành khi quay (H ) xung quanh trục Ox . Mệnh
đề nào dưới đây đúng? 2 2
A. V = π (x + ∫ )2 1 dx .
B. V = (x + ∫ )2 1 dx . 1 1 2 2
C. V = (x + ∫ )1dx .
D. V = π (x + ∫ )1dx . 1 1
Câu 2. Cho hai số phức z =1+ 2i . Số phức 1 bằng z A. 1− 2i . B. 1 − − 2i . C. 1 2 − i . D. 1 2 − − i . 5 5 5 5
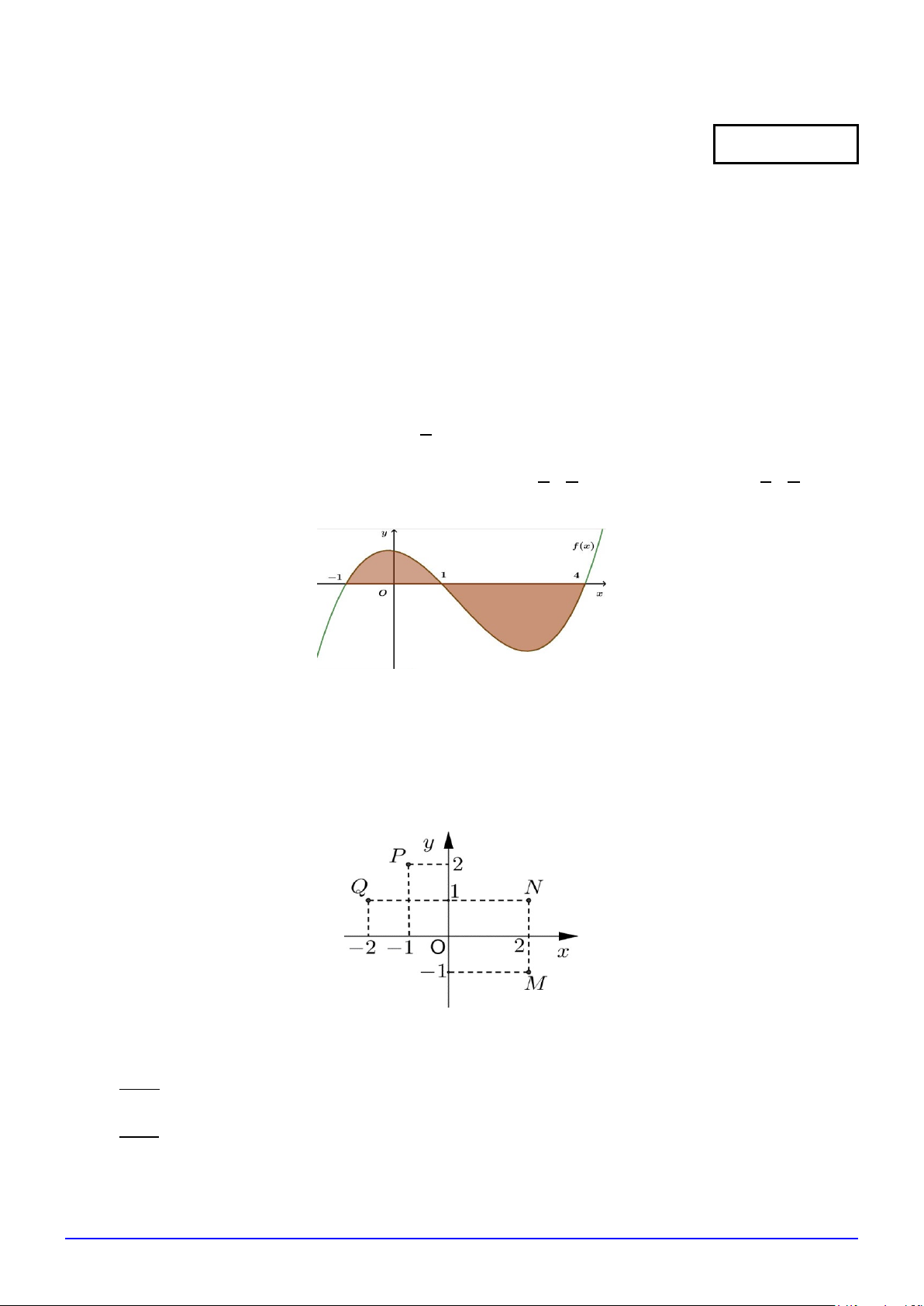
Câu 3. Diện tích hình phẳng được tô đậm trong hình bên dưới bằng 1 4 1 4
A. S = f (x).dx + f (x).dx ∫ ∫ .
B. S = − f (x).dx − f (x).dx ∫ ∫ . 1 − 1 1 − 1 1 4 1 4
C. S = f (x).dx − f (x).dx ∫ ∫ .
D. S = − f (x).dx + f (x).dx ∫ ∫ . 1 − 1 1 − 1
Câu 4. Trên mặt phẳng tọa độ điểm biểu diễn số phức z = 1
− + 2i là điểm nào trong các điểm sau? (hình vẽ dưới đây) A. P . B. M. C. N . D. Q .
Câu 5. Họ nguyên hàm của hàm số ( ) 2022 f x = x là A. 1 2023 x + C . B. 2022 2022 + . 2022 x C C. 1 2023 x + C . D. 2021 2022 + . 2023 x C
Câu 6. Cho hai số phức z = 2 −3i , z = 4 + i . Số phức z − z bằng 1 2 1 2 A. 6 − 2i . B. 2 − 4i . C. 2 − − 2i . D. 2 − − 4i .
Đề kiểm tra cuối học kì 2, năm học 2022-2023, môn Toán 12. Trang 1/4 - Mã đề 132
Câu 7. Cho f (x), g (x) là các hàm số xác định và liên tục trên  . Mệnh đề nào sau đây sai? A. 2 f
∫ (x)dx = 2 f ∫ (x)dx. B.f
∫ (x)− g(x)dx = f
∫ (x)dx− g ∫ (x)dx. C. f
∫ (x).g(x)dx = f ∫ (x) . dx g ∫ (x)dx. D.f
∫ (x)+ g(x)dx = f
∫ (x)dx+ g ∫ (x)dx .
Câu 8. Biết một nguyên hàm của hàm số f (x) 1 =
là hàm số F (x) thỏa mãn F ( ) 1 = 3 − . Khi 2x −1
đó F (x) là hàm số nào sau đây?
A. F (x) 1 = ln 2x −1 + 3.
B. F (x) = 2ln 2x −1 + 3 . 2
C. F (x) 1 = ln (2x − ) 1 − 3 .
D. F (x) 1
= ln 2x −1 − 3. 2 2 1 1 1
Câu 9. Nếu f (x)dx = 3 ∫
và g(x)dx = 4 − ∫
thì [f (x) − 2g(x)]dx ∫ bằng 0 0 0 A. 1 − . B. 7 . C. 5 − . D. 11 .
Câu 10. Trong không gian Oxyz , cho mặt phẳng (P): 2
− x + 2y + z −1 = 0 . Vectơ nào dưới đây là
một vectơ pháp tuyến của (P) ?    
A. a = (2;1;− ) 1 . B. a = ( 2; − 2; ) 1 . C. a = ( 2; − 2;0) . D. a = ( 2; − 2;− ) 1 .
Câu 11. Trong không gian với hệ tọa độ Oxyz , tìm tổng tất cả các giá trị nguyên dương của tham
số m để phương trình 2 2 2
x + y + z − 2x + 2y − 4z + m = 0 là phương trình của một mặt cầu A. 6 . B. 21. C. 5. D. 15.
Câu 12. Trong không gian Oxyz , cho mặt phẳng (α ):3x − 2y + 2z −10 = 0 . Điểm nào dưới đây thuộc (α ) ? A. P(1;2; 2
− ) . B. Q(3; 1;
− 4) . C. N ( 2; − 2;10) . D. M ( 2; − 2;3).
Câu 13. Trong không gian Oxyz , cho các điểm A(3;2;0), B(1;4;3) . Tọa độ vectơ  AB là A. (2; 2; − 3 − ). B. (2; 2; − 3). C. ( 2; − − 2;− 3) . D. ( 2; − 2;3).
Câu 14. Gọi (H ) là hình phẳng giới hạn bởi các đường x
y = e , trục Ox, x = 0, x =1. Tính thể tích
khối tròn xoay được tạo thành khi quay hình phẳng (H ) quanh trục Ox . A. π ( 2 π π e − ) 1 . B. ( 2e + )1 . C. (e − ) 1 .
D. π ( 2e − )1 . 2 2 2
Câu 15. Trong không gian với hệ trục tọa độ Oxyz , đường thẳng d đi qua A(1;2;− ) 1 có một 
vectơ chỉ phương u(2;1;0) có phương trình tham số là  x = 1+ tx =1+ 2tx =1+ 2tx = 2 + t A.    
y = 2 − t .
B.y = 2 + t .
C.y = 2 +t .
D.y = 2 + 2t .  z =     t z = 1 −  z = t −  z = t − 
Câu 16. Trong tập số phức, một căn bậc hai của 9 − là A. 3. B. 9. C. 3i . D. 9i .
Câu 17. Phương trình mặt phẳng (P) đi qua điểm M (1;3; 2
− ) và song song với mặt phẳng
(Q):2x +5y + z +1= 0 là
A. x + 3y − 2z +15 = 0.
B. 2x + 5y + z −15 = 0 .
C. 2x + 5y + z +19 = 0 .
D. x + 3y − 2z −19 = 0.
Câu 18. Cho số phức z =1−3i . Môđun của số phức (1−i) z bằng A. 2 5 . B. 5 2 . C. 10. D. 20 .
Đề kiểm tra cuối học kì 2, năm học 2022-2023, môn Toán 12. Trang 2/4 - Mã đề 132
Câu 19. Cho F (x) là một nguyên hàm của hàm số f (x) trên đoạn [0;4] và thỏa mãn F (0) =1, 4 F (4) = 5
− . Khi đó f (x)dx ∫ bằng 0 A. 6 − . B. 4 . C. 6 . D. 4 − .
Câu 20. Trong không gian Oxyz , cho ba điểm A(3;2; 2 − ) , B(1;0; ) 1 và C (2; 1; − 3). Viết phương
trình mặt phẳng đi qua A và vuông góc với BC .
A. x − y + 2z −5 = 0 . B. x + y + 2z + 3 = 0 . C. x − y + 2z + 3 = 0 . D. x + y + 2z −1= 0. x =1+ 2t
Câu 21. Trong không gian Oxyz, điểm nào dưới đây thuộc đường thẳng (d ) : y = 3 − + t ? z = 4+  5t
A. Q(4 ;1; 3) . B. P(3; − 2 ; − )
1 . C. N (2 ;1; 5). D. M (1; −3 ; 4) . 3 3
Câu 22. Cho hàm số f (x) liên tục trên  và ∫( f (x) 2
+ 3x )dx =17. Tính f (x)dx ∫ . 0 0 A. 9 − . B. 10 − . C. 7 − . D. 5 − 3
Câu 23. Cho I = x ∫ (x −2)2023 2 dx . Đặt 2
t = x − 2 , mệnh đề nào sau đây đúng? 1 − 3 7 3 7 A. 1 2023 I = t dt 1 2023 I = t dt 2023 I = t dt 2023 I = t dt 2 ∫ . B. 2 ∫ . C. ∫ . D. ∫ . 1 − 1 − 1 − 1 −
Câu 24. Cho hai số phức z =1− 2i và z = 2 + i . Số phức z + z bằng 1 2 1 2 A. 3 − + i . B. 3 − − 3i . C. 3−i . D. 3+ i .
Câu 25. Cho số phức z = 2022 −
+ 2023i . Số phức liên hợp của số phức z là
A. z = 2022 + 2023i . B. z = 2022 −
− 2023i . C. z = 2022 −
+ 2023i . D. z = 2022 − 2023i .
Câu 26. Ký hiệu z là nghiệm phức có phần ảo dương của phương trình 0 2
2z + 6z + 5 = 0 . Trên mặt phẳng tọa độ điểm nào dưới đây là điểm biểu diễn số phức w = iz . 0 A. 1 3 M  3 1  1 3  3 1   ;  − − . B. M −  ;−
. C. M  ;− . D. M −  ; . 2 2 2       3  2 2  1  2 2  4  2 2 
Câu 27. Số phức thỏa mãn là A. 1 4 − − i . B. 1 4 − + i . C. 1 − + 4i . D. 1 − − 4i . 17 17 17 17
Câu 28. Cho hàm số y = f (x), y = g(x) liên tục trên [1; ]
3 . Gọi S là diện tích miền phẳng giới hạn
bởi đồ thị hàm số y = f (x), y = g(x) và hai đường thẳng x =1, x = 3. Mệnh đề nào dưới đây đúng? 3 3
A. S = π  f
∫ (x)− g(x)dx  . B. S = f
∫ (x)− g(x) dx. 1 1 3 3
C. S =  f
∫ (x)− g(x)dx  .
D. S = π f
∫ (x)− g(x) dx . 1 1 2 2
Câu 29. Nếu hàm số f (x) thỏa mãn f (x)dx = 4 − ∫
thì 2 f (x)dx ∫ bằng 0 0 A. 8. B. 2 − . C. 6 − . D. 8 − .
Câu 30. Cho các số thực x, y thỏa mãn x +1+ 3i = 2 −3y .i Giá trị 2x + y bằng A. 1. B. 2 . C. 1 − . D. 0 .
Câu 31. Gọi S là diện tích hình phẳng giới hạn bởi các đường 2023x y =
, y = 0, x = 0 , x = 2 .
Mệnh đề nào dưới đây đúng?
Đề kiểm tra cuối học kì 2, năm học 2022-2023, môn Toán 12. Trang 3/4 - Mã đề 132 2 2 A. 2 = 2023 x S dx ∫ . B. = 2023x S dx ∫ . 0 0 2 2 C. 2 = π 2023 x S dx ∫ . D. = π 2023x S dx ∫ . 0 0
Câu 32. Cho hai số phức z
z =1+ 2i và z =1− i . Phần thực của số phức 1 bằng 1 2 z2 A. 3 . B. 1 − . C. 3 − . D. 1 . 2 2 2 2
Câu 33. Trong không gian Oxyz , cho hai điểm A(2;3;4) và B(0;1;2). Đường thẳng d đi qua trung điểm của x − y z +
AB và song song với đường thẳng 1 3 ∆ : = = có phương trình là 2 1 − 5
A. x − 2 y −3 z − 4 − − − = = .
B. x 1 y 2 z 3 = = . 2 1 − 5 2 1 − 5
C. x +1 y + 2 z + 3 − − − = = .
D. x 2 y 3 z 4 = = . 2 1 − 5 1 2 3
Câu 34. Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức 3− 2 .i Tìm a, b. A. a = 2, − b = 3.
B. a = 3, b = 2 − . C. a = 2 − i, b = 3 .
D. a = 3, b = 2 − i .
Câu 35. Trong không gian Oxyz , cho đường thẳng x − 2 y −1 z − 4 d : = =
. Đường thẳng d có 2 − 2 3
một vec tơ chỉ phương là    
A. u = (2;1;4). B. u = (2;2;3) . C. u = ( 2
− ;−1;− 4) . D. u = ( 2; − 2;3) .
II. PHẦN TỰ LUẬN (3,0 điểm) π 2
Câu 1. (1,0 điểm) Tính tích phân 9
I = cos .xsin xd .x ∫ 0
Câu 2. (1,0 điểm) Trong không gian Oxyz, viết phương trình tham số đường thẳng Δ đi qua điểm M (2;4; 6
− ) , vuông góc với đường thẳng
x − 3 y − 5 z − 7 d : = =
và song song với mặt phẳng 4 1 − 2
(P) : 2x + y − 3z +10 = 0
Câu 3. (0,5 điểm) Tìm tất cả các số phức z thỏa mãn 5z −1= (2 − 6i) z + 3i(z +1) .
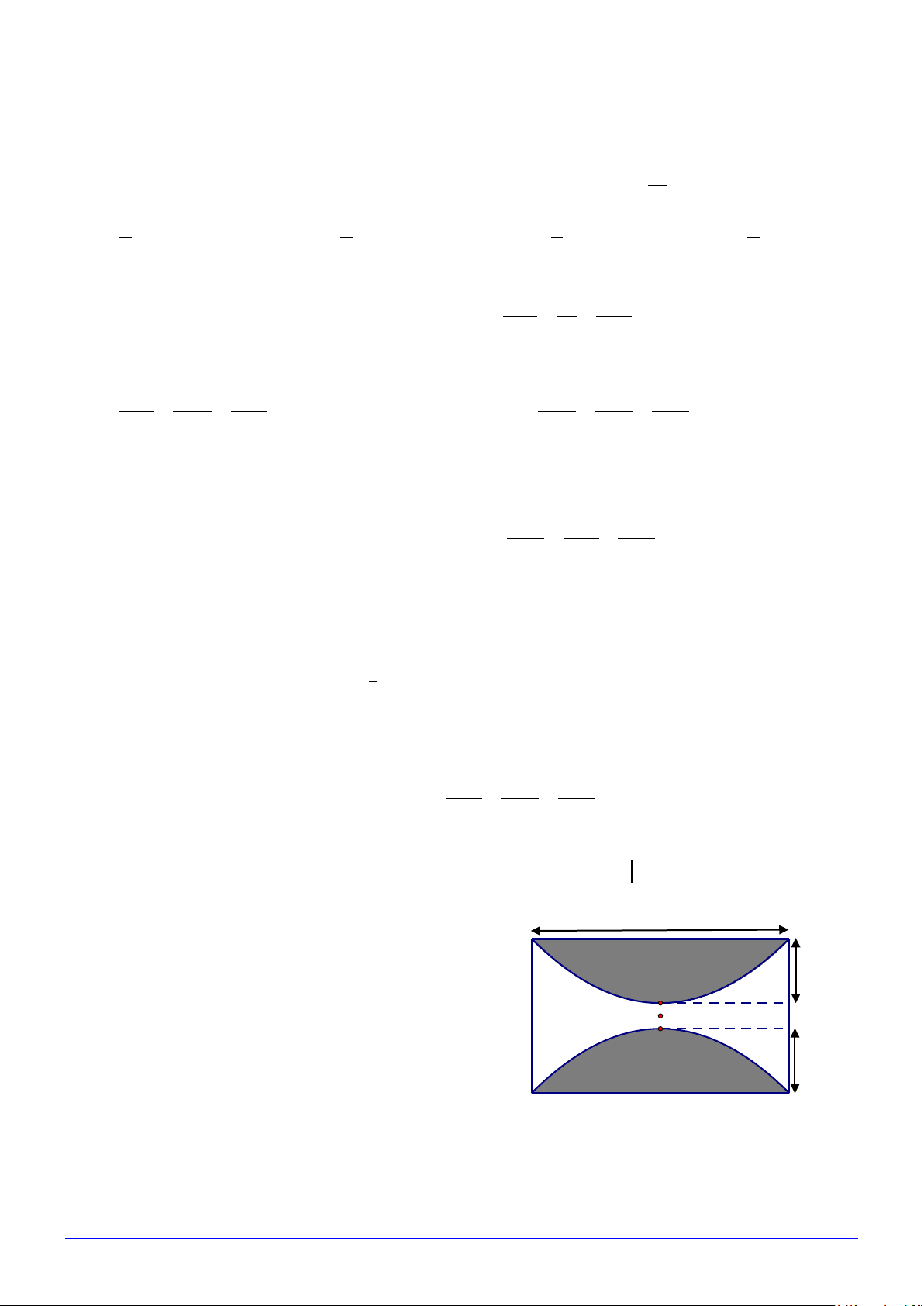
Câu 4. (0,5 điểm) Ông Minh sở hữu một mảnh vườn
hình chữ nhật. Ông Minh dự định chia mảnh vườn đó 60m
thành 2 khu vực, phần màu xám là trồng hoa lan, phần
còn lại là trồng hoa hồng (hai đường cong là parabol có 10m
đỉnh đối xứng qua tâm của mảnh vườn và có chung trục
đối xứng). Biết tiền trả cho nhân công phần trồng hoa
lan là 40.000 đồng/m2, trồng hoa hồng là 50.000
đồng/m2 và số tiền ông Minh trả cho nhân công trồng 10m
hoa ở hai khu vực của mảnh vườn là bằng nhau. Tính
độ dài chiều còn lại của mảnh vườn đó. ===== Hết =====
Đề kiểm tra cuối học kì 2, năm học 2022-2023, môn Toán 12. Trang 4/4 - Mã đề 132 TRƯỜNG THPT PHÚ LỘC
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA CUỐI KÌ II TỔ TOÁN – TIN NĂM HỌC 2022-2023
Hướng dẫn chấm gồm có 03 trang MÔN: TOÁN 12
I. PHẦN TRẮC NGHIỆM (7,0 điểm)
ĐÁP ÁN CÁC MÃ ĐỀ Câu Mã đề 132 Mã đề 209 Mã đề 357 Mã đề 485 1 A A A A 2 C C C D 3 C B D C 4 A C B B 5 C C B B 6 D B B C 7 C B A A 8 D B B C 9 D A B B 10 B A D C 11 D B C D 12 C D D B 13 D B D D 14 A B B B 15 B B C B 16 C C C D 17 B A B D 18 A D A C 19 A A C C 20 C C A A 21 D C C B 22 B D A B 23 B B B B 24 C D D C 25 B A D B 26 A D B B 27 D B B B 28 B B D A 29 D D C D 30 A D A B 31 B D C C 32 B C B A 33 B C D C 34 B D A B 35 D B B C
II. PHẦN TỰ LUẬN (3 điểm)
Chú ý : Ở mỗi phần, mỗi câu, nếu học sinh có cách giải khác đáp án nhưng đúng và chặt
chẽ thì vẫn cho điểm tối đa của phần hoặc câu đó. 1 Câu Nội dung Điểm π 2 Tính tích phân 9
I = cos .xsin xd .x ∫ 0
Đặt t = sin x
Vi phân: dt = cos xdx 0,25 π
Câu 1 Đổi cận: x = ⇒ t =1; x = 0 ⇒ t = 0 0,25 2 π 2 1 Khi đó: 9 9
I = cos .xsin xdx = t dt ∫ ∫ 0,25 0 0 1 1 10 1 I = t = ( − ) 1 1 0 = 0,25 10 10 10 0
Trong không gian Oxyz, viết phương trình tham số đường thẳng Δ đi qua điểm M (2;4; 6
− ) , vuông góc với đường thẳng
x − 3 y − 5 z − 7 d : = = và song song 4 1 − 2
với mặt phẳng (P) : 2x + y −3z +10 = 0 
Đường thẳng d có vectơ chỉ phương u = 4; 1; − 2 . 1 ( )  0,25
Mặt phẳng (P) có vectơ pháp tuyến n = (2;1; 3 − ) .
Câu 2 Do đường thẳng Δ vuông góc với đường thẳng d và song song với mặt phẳng   
(P) nên Δ nhận vectơ u = u ,n làm vectơ chỉ phương. 0,25 1   
Tính được: u = (1;16;6) 0,25 
Đường thẳng Δ đi qua điểm M (2;4; 6
− ) và có vectơ chỉ phương u = (1;16;6) có x = 2 + t 0,25
phương trình tham số là: y = 4 +16t z = 6 − +  6t
Tìm tất cả các số phức z thỏa mãn 5z −1= (2 − 6i) z + 3i(z +1) .
Ta có: 5z −1= (2 − 6i) z + 3i(z +1) ⇔ 5z −1= 2 z − 6i z + 3iz + 3i
⇔ 5z − 3iz = 2 z − 6i z +1+ 3i
⇔ (5 − 3i) z = (2 z + ) 1 + ( 6 − z + 3)i ( ) 1
⇒ (5 − 3i) z = (2 z + ) 1 + ( 6 − z + 3)i
Câu 3 ⇔ ( − i) z = ( z + )2 +(− z + )2 5 3 . 2 1 6 3 0,25 3 ⇔ 5 + ( 3
− )2 . z = (2 z + )2 1 + ( 6 − z + 3)2 2 ⇔
z = ( z + )2 + (− z + )2 2 2 34. 2 1 6
3 ⇔ 34. z = 40 z − 32 z +10 2 ⇔ 6
− z + 32 z −10 = 0 ⇔ z = 5 hoặc 1 z = 3 Khi z −
= 5 , thay z = 5 vào (1) ta được ⇔ ( − ) 11 27 5 3 =11− 27 i i z i ⇔ z = 0,25 5 − 3i 2
(11− 27i)(5+3i) z =
⇔ z = 4 − 3i 2 5 + ( 3 − )2 5 +i Khi 1 z = , thay 1
z = vào (1) ta được ⇔ ( − i) 5 3
5 3 z = + i ⇔ z = 3 3 3 5 − 3i  5 i + (5 +   3i)  3  8 5 z = ⇔ z = + i 2 5 + ( 3 − )2 51 17
Vậy có hai số phức z = 4 −3i, 8 5 z = + i 1 2 51 17
Ông Minh sở hữu một mảnh vườn
hình chữ nhật. Ông Minh dự định 60m
chia mảnh vườn đó thành 2 khu vực,
phần màu xám là trồng hoa lan, 10m
phần còn lại là trồng hoa hồng (hai
đường cong là parabol có đỉnh đối
xứng qua tâm của mảnh vườn và có
chung trục đối xứng). Biết tiền trả 10m
cho nhân công phần trồng hoa lan là
40.000 đồng/m2, trồng hoa hồng là
50.000 đồng/m2 và số tiền ông Minh trả cho nhân công trồng hoa ở hai khu vực
của mảnh vườn là bằng nhau. Tính độ dài chiều còn lại của mảnh vườn đó.
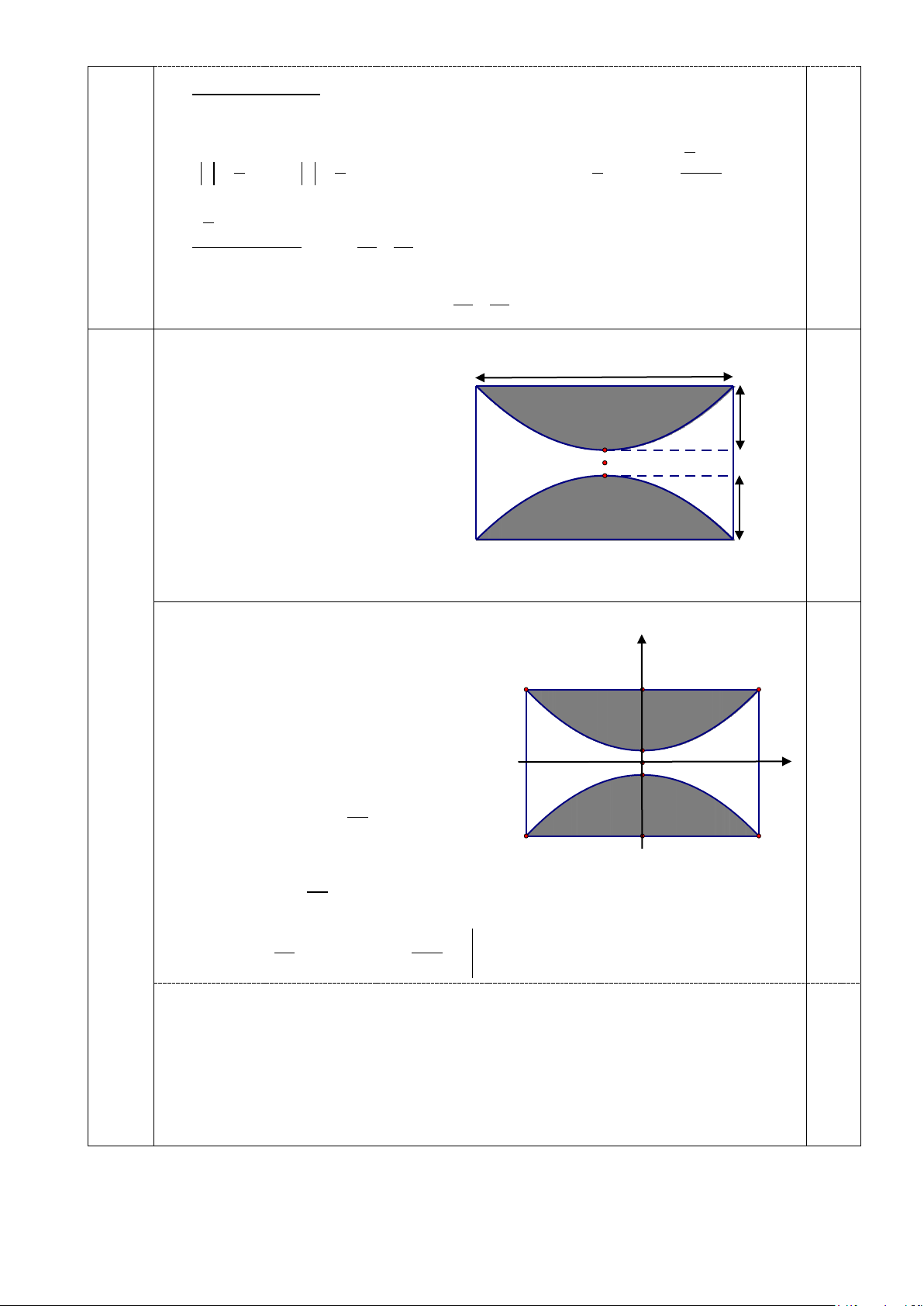
Gán hệ trục Oxy như hình vẽ, Gốc tọa độ
O là tâm của mảnh vườn. y
Gọi I, J lần lượt là đỉnh của hai parabol.
Đặt IO = c (c > 0). Suy ra AD = 20 + 2c. B M A
Parabol (P) có đỉnh I(0;c), đi qua hai
Câu 4 điểm A(30;10 + c), B(-30;10 + c) là hàm I x số có dạng 2 y = ax + c . O
Do (P) đi qua điểm A(30;10 + c) nên J 0,25 2 1 10 + c = .30 a + c ⇔ a = 90
Diện tích phần màu xám là: C N D 30   1 2 S 2. 10 ∫  c x c = + − +   dx  1  −   90 30  30 30  1 2   1 3  2 S = 2. 10 − x dx = 10x − x = ∫     800m 1 −  90   270 30  30 −
Diện tích mảnh vườn: S = AB CD = + c m ABCD ( ) 2 . 60. 20 2
Suy ra diện tích khu vực còn lại 2 S = S − S = + c − = c + m ABCD 1200 120 800 120 400 2 1 0,25
Do số tiền trả nhân công của hai khu vực bằng nhau nên ta có:
800.40000 = (120c + 400).50000 ⇔ 32000000 = 600000c + 2000000 ⇔ c = 2
Vậy độ dài chiều còn lại của mảnh vườn là 24m 3
Document Outline

  • DE_CUOI_KY_2_LOP_12_MĐ 132
  • DAP_AN_CUOI_KY_2_LOP_12