22 trang 28 lượt tải

Đề cuối kỳ 2 Toán 12 năm 2024 – 2025 trường THPT Ngô Gia Tự – Phú Yên

55

Một lớp học có 40 học sinh gồm 28 nữ và 12 nam. Trong năm học 2023-2024, có 7 học sinh nữ đạt danh hiệu học sinh giỏi và 6 học sinh nam đạt danh hiệu học sinh giỏi. Chọn ngẫu nhiên một học sinh của lớp đó. Tài liệu giúp bạn tham khảo ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

Chủ đề: Đề thi THPTQG môn Toán năm 2025 129 tài liệu

Môn: Toán 2 K tài liệu

Tác giả:

Profile

Thu Hoài

2 ngày trước
Danh sách Quiz
/22
SỞ GIÁO DỤC VÀ ĐÀO TẠO PHÚ YÊN
TRƯỜNG THPT NGÔ GIA TỰ
Mã đề thi: 1211
ĐỀ KIỂM TRA CUỐI KỲ 2 NĂM HỌC 2024 - 2025
Môn: Toán, Lớp 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . .
PHẦN I. (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Câu 1: Trong không gian
,Oxyz
mặt cầu
2 2 2
: 6 2 15 0S x y z x y
có bán kính
R
bằng
A.
5
. B.
5
. C. 15. D. 25.
Câu 2: Tìm
.
A.
1
ln2
x
e dx C
x

. B.
xx
e dx e C
. C.
ln2
xx
e dx e C
. D.
l
x
x
e dx C
e

.
Câu 3: Trong không gian
,Oxyz
mặt cầu
S
tâm
2;1; 1 ,I
bán kính bằng
3
có phương trình là
A.
2 2 2
2 1 1 3x y z
. B.
2 2 2
2 1 1 36x y z
.
C.
2 2 2
2 1 1 9x y z
. D.
2 2 2
2 1 1 9x y z
.
Câu 4: Cho hàm số
f
liên tục trên và
a
là số thực dương. Khẳng định nào sau đây luôn đúng?
A.
( ) 1
a
a
f x dx
. B.
( ) 1
a
a
f x dx 
. C.
( ) ( )
a
a
f x dx f a
. D.
( ) 0
a
a
f x dx
.
Câu 5: Trong không gian
,Oxyz
góc giữa hai đường thẳng
1
1
:
1 1 2
x y z
d

và
2
1
:2
3
xt
d y t
zt


bằng
A.
30
o
. B.
90
o
. C.
45
o
. D.
60
o
.
Câu 6: Cho hai biến cố
,AB
có
0,6; 0,7; 0,4P A P B P AB
. Xác suất
|P A B
bằng
A.
6
7
. B.
4
7
. C.
0,28
. D.
2
3
.
Câu 7: Biết
2
0
( ) 2f x dx
và
2
0
( ) 4.g x dx
Giá trị của
2
0
2 ( ) ( )f x g x dx
bằng
A.
10.
B.
6.
C.
8.
D.
12.
Câu 8: Diện tích của hình phẳng phần gạch chéo trong hình bên được tính theo công thức nào sau
đây?
A.
24
02
( )d ( )dS f x x f x x

.
B.
24
02
( )d ( )dS f x x f x x

.
C.
24
02
( )d ( )dS f x x f x x

.
D.
4
0
( )dS f x x
.
Câu 9: Trong không gian
Oxyz
, cho mặt phẳng
: 2 3 0P x y
. Vectơ nào dưới đây là một vectơ
pháp tuyến của của mặt phẳng
P
?
A.
3
1; 2;3n 
. B.
1
1; 2;0n 
. C.
2
1;0; 2n 
. D.
4
1;0;2n
.
Câu 10: Cho
A
và
B
hai biến cố độc lập. Khẳng định nào dưới đây là sai?
A.
|.P B A P A
B.
|.P A B P A
C.
|.P A B P A
D.
|.P A B P A
Câu 11: Cho hai biến cố
A
và
B
với
0PA
. Xác suất của biến cố
B
với điều kiện biến cố
A
đã
xảy ra là
A.
|
PA
P B A
PB
. B.
|.P B A P A P B
.
C.
|
P AB
P B A
PA
. D.
|
P AB
P B A
PB
Câu 12: Trong không gian
,Oxyz
cho đường thẳng
15
:
1 2 3
x y z
d


. Vectơ nào dưới đây là một
vectơ chỉ phương của d?
A.
3
1;2; 3u 
. B.
1
1; 2;3u 
. C.
4
1; 2; 3 .u
D.
2
1;2;3u
.
PHẦN II. (4 điểm) Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh
chọn đúng hoặc sai.
Câu 1. Cho hàm số
2
( ) .f x x
Gọi
()Fx
là nguyên hàm của
()fx
trên
.
a)
'( ) ( ), .F x f x x
b)
3
()
3
x
F x C
(
C
là hằng số).
c) Biết
(1) 0.F
Giá trị của
(0)F
bằng
0.
d) Với
1,a
không có giá trị nào của
a
thoả mãn
1
3 ( ) 1 0.
a
f x dx
Câu 2. Trong không gian
,Oxyz
cho hai điểm
0;2; 1A
và
3;2; 4B
và mặt phẳng
:2 2 6 0.P x y z
a) Một vectơ chỉ phương của đường thẳng
AB
là
1;0; 1a 
.
b) Mặt phẳng
P
có một vecto pháp tuyến là
2;2;1n
.
c) Đường thẳng
đi qua
A
và vuông góc với mặt phẳng
P
có phương trình chính tắc là:
21
2 2 1
x y z

.
d) Mặt cầu đường kính
AB
có phương trình là:
22
2
35
2 18.
22
x x x
Câu 3. Một lớp học có
40
học sinh gồm 28 nữ và 12 nam. Trong năm học 2023-2024, có 7 học sinh
nữ đạt danh hiệu học sinh giỏi và 6 học sinh nam đạt danh hiệu học sinh giỏi. Chọn ngẫu nhiên một
học sinh của lớp đó. Gọi
A
là biến cố “Học sinh được chọn là nữ” và
B
là biến cố “Học sinh được
chọn đạt danh hiệu học sinh giỏi”.
a) Xác suất của biến cố
A
là
0,7
.
b) Xác suất của biến cố
B
là
0,3
.
c)
A
và
B
là hai biến cố độc lập.
d) Xác suất của biến cố
A
với điều kiện biến cố B đã xảy ra là
0,25.
Câu 4. Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ
thuộc thời gian t(h) có đồ thị của vận tốc đã cho (hình bên). Trong
khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị là một
phần của parabol có đỉnh
(2;9),I
khoảng thời gian còn lại đồ thị là
một đoạn thẳng.
a) Vận tốc lớn nhất của chuyển động là 9 km/h.
b)
2
9
( ) 9
4
v t t t
với
0 3.t
c)
( ) 3v t t
với
3 4.t
d) Quãng đường vật di chuyển được trong 4 giờ là
81
4
km.
PHẦN III. (3 điểm) Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Biết tích phân
1
1
1.
e
dx a e
x



Giá trị của
a
bằng bao nhiêu?
Câu 2. Trên cửa sổ có dạng hình chữ nhật của
ngôi nhà một doanh nghiệp kinh doanh hải
sản, họa sĩ cần thiết kế logo hình con cá. Logo
là hình phẳng giới hạn bởi hai parabol với các
kích thước được cho trong hình bên (đơn vị
trên mỗi trục tọa độ là dm). Hoạ sĩ cần tính
diện tích của logo để báo giá cho doanh
nghiệp đó trước khi kí hợp đồng. Diện tích
của logo bằng
x
2
.dm
Tìm
x
(làm tròn kết
quả đến hàng đơn vị).
Câu 3. Một chiếc ô tô đang chạy với vận tốc
15 /ms
thì nhìn thấy chướng ngại vật trên đường cách
đó
40 ,m
người lái xe hãm phanh khẩn cấp. Sau khi hãm phanh, ô tô chuyển động chậm dần đều với
vận tốc
3 15 /v t t m s
, trong đó
t
(giây) là thời gian. Tính quãng đường xe ô tô đi được trong
thời gian
t
(giây) kể từ lúc đạp phanh.
Câu 4. Khi đặt hệ toạ độ
Oxyz
vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy
rằng một không gian phủ sóng điện thoại có dạng một hình cầu
()S
(tập hợp những điểm nằm trong
và nằm trên mặt cầu tương ứng). Biết mặt cầu
()S
có phương trình
2 2 2
2 4 6 5 0.x y z x y z
Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng là bao nhiêu kilômét?
Câu 5. Một mô hình cầu treo được thiết kế trong không gian tọa độ
Oxyz
như hình vẽ. Làn đường
d
đi qua hai điểm
(4;3;1)M
và
(5;7;3).N
Từ một điểm
(5;2;1)A
trên cáp treo, người ta cần tìm
tọa độ điểm
'( ; ; )A a b c
là hình chiếu vuông góc của
A
trên
d
để lắp đặt đai chịu lực nâng cho cầu.
Tính giá trị của
.a b c
Câu 6. Có hai hộp chứa bi. Hộp thứ nhất chứa 4 bi đỏ và 5 bi vàng. Hộp thứ hai chứa 6 bi đỏ và 4 bi
vàng. Chọn ngẫu nhiên một hộp và sau đó lấy ngẫu nhiên 1 bi từ hộp đó. Tính xác suất để lấy được
viên bi đỏ (làm tròn đến hàng phần trăm).
--------------HẾT-------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO PHÚ YÊN
TRƯỜNG THPT NGÔ GIA TỰ
Mã đề thi: 1213
ĐỀ KIỂM TRA CUỐI KỲ 2 NĂM HỌC 2024 - 2025
Môn: Toán, Lớp 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . .
PHẦN I. (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Câu 1: Trong không gian
,Oxyz
mặt cầu
2 2 2
: 6 2 5 0S x y z x y
có bán kính
R
bằng
A. 15. B.
5
. C. 10. D. 25.
Câu 2: Tìm
A.
2
1
dx x C
x

. B.
1
x
dx e C
x

. C.
1
lndx x C
x

. D.
1
ln .dx x C
x

Câu 3: Trong không gian
,Oxyz
mặt cầu
S
tâm
2;1; 1I
, bán kính bằng
6
có phương trình là
A.
2 2 2
2 1 1 36x y z
. B.
2 2 2
2 1 1 36x y z
.
C.
2 2 2
2 1 1 9x y z
. D.
2 2 2
2 1 1 9x y z
.
Câu 4: Cho hàm số
f
liên tục trên và
a
là số thực dương. Khẳng định nào sau đây luôn đúng?
A.
( ) 1
a
a
f x dx
. B.
( ) 1
a
a
f x dx 
. C.
( ) 0
a
a
f x dx
. D.
( ) ( )
a
a
f x dx f a
.
Câu 5: Trong không gian
,Oxyz
góc giữa hai đường thẳng
1
1
:
1 1 2
x y z
d

và
2
1
:2
3
xt
d y t
zt


bằng
A.
30
o
. B.
90
o
. C.
60
o
. D.
45
o
.
Câu 6: Cho hai biến cố
,AB
có
0,6; 0,7; 0,4P A P B P AB
. Xác suất
|P B A
bằng
A.
3
4
. B.
4
7
. C.
0,28
. D.
2
3
.
Câu 7: Biết
2
0
( ) 2f x dx
và
2
0
( ) 4.g x dx
Giá trị của
2
0
( ) 2 ( )f x g x dx
bằng
A.
12.
B.
6.
C.
8.
D.
10.
Câu 8: Diện tích của hình phẳng phần gạch chéo trong hình bên được tính theo công thức nào sau
đây?
A.
24
02
( )d ( )dS f x x f x x

.
B.
24
02
( )d ( )dS f x x f x x

.
C.
24
02
( )d ( )dS f x x f x x

.
D.
4
0
( )dS f x x
.
Câu 9: Trong không gian
Oxyz
, cho mặt phẳng
: 2 3 0P x z
. Vectơ nào dưới đây là một vectơ
pháp tuyến của của mặt phẳng
P
?
A.
3
1; 2;3n 
. B.
2
1;0; 2n 
. C.
1
1; 2;0n 
. D.
4
1;0;2n
.
Câu 10: Cho
A
và
B
hai biến cố độc lập. Khẳng định nào dưới đây là sai?
A.
|.P B A P B
B.
|.P A B P A
C.
|.P A B P B
D.
|.P A B P A
Câu 11: Cho hai biến cố
A
và
B
với
0PB
. Xác suất của biến cố
A
với điều kiện biến cố
B
đã
xảy ra là
A.
|
PA
P A B
PB
. B.
|.P A B P A P B
.
C.
|
P AB
P A B
PB
. D.
|
P AB
P A B
PA
Câu 12: Trong không gian
,Oxyz
cho đường thẳng
15
:
1 2 3
x y z
d



. Vectơ nào dưới đây là một
vectơ chỉ phương của đường thẳng d?
A.
3
1;2;3u 
. B.
1
1; 2;3u 
. C.
4
1; 2; 3 .u
D.
2
1;2;3u
.
PHẦN II. (4 điểm) Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh
chọn đúng hoặc sai.
Câu 1. Cho hàm số
2
( ) .f x x
Gọi
()Fx
là nguyên hàm của
()fx
trên
.
a)
'( ) ( ), .F x f x x
b)
3
()
3
x
F x C
(
C
là hằng số).
c) Biết
( 1) 0.F 
Giá trị của
(0)F
bằng
1
.
3
d) Với
1,a
có 3 giá trị của
a
thoả mãn
1
3 ( ) 1 0.
a
f x dx
Câu 2. Trong không gian
,Oxyz
cho hai điểm
0;2; 1A
và
3;2; 4B
và mặt phẳng
:2 2 6 0.P x y z
a) Một vectơ chỉ phương của đường thẳng
AB
là
1;0; 1a 
.
b) Mặt phẳng
P
có một vecto pháp tuyến là
2;2;1n
.
c) Đường thẳng
đi qua
A
và vuông góc với mặt phẳng
P
có phương trình chính tắc là:
21
2 2 1
x y z

.
d) Mặt cầu đường kính
AB
có phương trình là:
22
2
35
2 18.
22
x x x
Câu 3. Một lớp học có
40
học sinh gồm 28 nữ và 12 nam. Trong năm học 2023-2024, có 7 học sinh
nữ đạt danh hiệu học sinh giỏi và 6 học sinh nam đạt danh hiệu học sinh giỏi. Chọn ngẫu nhiên một
học sinh của lớp đó. Gọi
A
là biến cố “Học sinh được chọn là nữ” và
B
là biến cố “Học sinh được
chọn đạt danh hiệu học sinh giỏi”.
a) Xác suất của biến cố
A
là
0,7
.
b) Xác suất của biến cố
B
là
0,3
.
c)
A
và
B
là hai biến cố độc lập.
d) Xác suất của biến cố
A
với điều kiện biến cố B đã xảy ra là
0,35.
Câu 4. Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ
thuộc thời gian t(h) có đồ thị của vận tốc đã cho (hình bên). Trong
khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị là một
phần của parabol có đỉnh
(2;9),I
khoảng thời gian còn lại đồ thị là
một đoạn thẳng.
a) Vận tốc lớn nhất của chuyển động là 9 km/h.
b)
2
9
( ) 9
4
v t t t
với
0 3.t
c)
( ) 3v t t
với
3 4.t
d) Quãng đường vật di chuyển được trong 4 giờ là
27
km.
PHẦN III. (3 điểm) Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Biết tích phân
1
1
1.
e
dx e a
x



Giá trị của
a
bằng bao nhiêu?
Câu 2. Bạn An nhận thiết kế logo hình con mắt cho một
cơ sở y tế. Logo là hình phẳng giới hạn bởi 2 parabol
y f x
và
y g x
như hình vẽ (đơn vị trên mỗi
trục toạ độ là dm). Bạn An cần tính diện tích của logo
để báo giá cho cơ sở y tế đó trước khi kí hợp đồng. Diện
tích của logo bằng
x
2
.dm
Tìm
x
(làm tròn kết quả
đến hàng phần mười).
Câu 3. Một chiếc ô tô đang chạy với vận tốc
18 /ms
thì nhìn thấy chướng ngại vật trên đường cách
đó
60 ,m
người lái xe hãm phanh khẩn cấp. Sau khi hãm phanh, ô tô chuyển động chậm dần đều với
vận tốc
3 18 /v t t m s
, trong đó
t
(giây) là thời gian. Tính quãng đường xe ô tô đi được
trong thời gian
t
(giây) kể từ lúc đạp phanh.
Câu 4. Khi đặt hệ toạ độ
Oxyz
vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy
rằng một không gian phủ sóng điện thoại có dạng một hình cầu
()S
(tập hợp những điểm nằm trong
và nằm trên mặt cầu tương ứng). Biết mặt cầu
()S
có phương trình
2 2 2
2 4 6 2 0.x y z x y z
Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng là bao nhiêu kilômét?
Câu 5. Một mô hình cầu treo được thiết kế trong không gian tọa độ
Oxyz
như hình vẽ. Làn đường
d
đi qua hai điểm
(4;3;1)M
và
(5;7;3).N
Từ một điểm
(5;2;1)A
trên cáp treo, người ta cần
tìm tọa độ điểm
'( ; ; )A a b c
là hình chiếu vuông góc của
A
trên
d
để lắp đặt đai chịu lực nâng cho
cầu. Tính giá trị của
.a b c
Câu 6. Có hai hộp chứa bi. Hộp thứ nhất chứa 4 bi đỏ và 5 bi vàng. Hộp thứ hai chứa 6 bi đỏ và 4 bi
vàng. Bạn Cường chọn ngẫu nhiên một hộp và sau đó lấy ngẫu nhiên 1 bi từ hộp đó. Tính xác suất để
Cường lấy được viên bi đỏ (làm tròn đến hàng phần trăm).
--------------HẾT-------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO PHÚ YÊN
TRƯỜNG THPT NGÔ GIA TỰ
Mã đề thi: 1215
ĐỀ KIỂM TRA CUỐI KỲ 2 NĂM HỌC 2024 - 2025
Môn: Toán, Lớp 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . .
PHẦN I. (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Câu 1: Tìm
.
A.
1
ln2
x
e dx C
x

. B.
xx
e dx e C
. C.
ln2
xx
e dx e C
. D.
l
.
x
x
e dx C
e

Câu 2: Diện tích của hình phẳng phần gạch chéo trong hình bên dưới được tính theo công thức nào
sau đây?
A.
4
0
( )dS f x x
. B.
24
02
( )d ( )dS f x x f x x

.
C.
24
02
( )d ( )dS f x x f x x

. D.
24
02
( )d ( )dS f x x f x x

.
Câu 3: Cho hai biến cố
,AB
có
0,6; 0,7; 0,4P A P B P AB
. Xác suất
|P A B
bằng
A.
6
7
. B.
4
7
. C.
0,28
. D.
2
3
.
Câu 4: Trong không gian
,Oxyz
góc giữa hai đường thẳng
1
1
:
1 1 2
x y z
d

và
2
1
:2
3
xt
d y t
zt


bằng
A.
30
o
. B.
90
o
. C.
45
o
. D.
60
o
.
Câu 5: Cho hai biến cố
A
và
B
với
0PA
. Xác suất của biến cố
B
với điều kiện biến cố
A
đã
xảy ra là
A.
|
PA
P B A
PB
. B.
|.P B A P A P B
.
C.
|
P AB
P B A
PB
. D.
|
P AB
P B A
PA
Câu 6: Trong không gian
,Oxyz
mặt cầu
2 2 2
: 6 2 15 0S x y z x y
có bán kính
R
bằng
A.
5
. B. 15. C.
5
. D. 25.
Câu 7: Cho hàm số
f
liên tục trên và
a
là số thực dương. Khẳng định nào sau đây luôn đúng?
A.
( ) 0
a
a
f x dx
. B.
( ) ( )
a
a
f x dx f a
. C.
( ) 1
a
a
f x dx 
. D.
( ) 1
a
a
f x dx
.
Câu 8: Trong không gian
,Oxyz
cho mặt phẳng
: 2 3 0P x y
. Vectơ nào dưới đây là một
vectơ pháp tuyến của của mặt phẳng
P
?
A.
3
1; 2;3n 
. B.
1
1; 2;0n 
. C.
2
1;0; 2n 
. D.
4
1;0;2n
.
Câu 9: Biết
2
0
( ) 2f x dx
và
2
0
( ) 4.g x dx
Giá trị của
2
0
2 ( ) ( )f x g x dx
bằng
A.
8.
B.
6.
C.
10.
D.
12.
Câu 10: Trong không gian
,Oxyz
mặt cầu
S
tâm
2;1; 1 ,I
bán kính bằng
3
có phương trình là
A.
2 2 2
2 1 1 36x y z
. B.
2 2 2
2 1 1 36x y z
.
C.
2 2 2
2 1 1 9x y z
. D.
2 2 2
2 1 1 9x y z
.
Câu 11: Trong không gian
,Oxyz
cho đường thẳng
15
:
1 2 3
x y z
d


. Vectơ nào dưới đây là một
vectơ chỉ phương của d?
A.
3
1;2; 3u 
. B.
1
1; 2;3u 
. C.
4
1; 2; 3 .u
D.
2
1;2;3u
.
Câu 12: Cho
A
và
B
hai biến cố độc lập. Khẳng định nào dưới đây là sai?
A.
|.P B A P B
B.
|.P A B P B
C.
|.P A B P A
D.
|.P A B P A
PHẦN II. (4 điểm) Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh
chọn đúng hoặc sai.
Câu 1. Cho hàm số
2
( ) .f x x
Gọi
()Fx
là nguyên hàm của
()fx
trên
.
a)
'( ) ( ), .F x f x x
b)
3
()
3
x
F x C
(
C
là hằng số).
c) Biết
(1) 0.F
Giá trị của
(0)F
bằng
0.
d) Với
1,a
không có giá trị nào của
a
thoả mãn
1
3 ( ) 1 0.
a
f x dx
Câu 2. Trong không gian
,Oxyz
cho hai điểm
0;2; 1A
và
3;2; 4B
và mặt phẳng
:2 2 6 0.P x y z
a) Một vectơ chỉ phương của đường thẳng
AB
là
1;0; 1a 
.
b) Mặt phẳng
P
có một vecto pháp tuyến là
2;2;1n
.
c) Đường thẳng
đi qua
A
và vuông góc với mặt phẳng
P
có phương trình chính tắc là:
21
2 2 1
x y z

.
d) Mặt cầu đường kính
AB
có phương trình là:
22
2
35
2 18.
22
x x x
Câu 3. Một lớp học có
40
học sinh gồm 28 nữ và 12 nam. Trong năm học 2023-2024, có 7 học sinh
nữ đạt danh hiệu học sinh giỏi và 6 học sinh nam đạt danh hiệu học sinh giỏi. Chọn ngẫu nhiên một
học sinh của lớp đó. Gọi
A
là biến cố “Học sinh được chọn là nữ” và
B
là biến cố “Học sinh được
chọn đạt danh hiệu học sinh giỏi”.
a) Xác suất của biến cố
A
là
0,7
.
b) Xác suất của biến cố
B
là
0,3
.
c)
A
và
B
là hai biến cố độc lập.
d) Xác suất của biến cố
A
với điều kiện biến cố B đã xảy ra là
0,25.
Câu 4. Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ
thuộc thời gian t(h) có đồ thị của vận tốc đã cho (hình bên). Trong
khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị là một
phần của parabol có đỉnh
(2;9),I
khoảng thời gian còn lại đồ thị là
một đoạn thẳng.
a) Vận tốc lớn nhất của chuyển động là 9 km/h.
b)
2
9
( ) 9
4
v t t t
với
0 3.t
c)
( ) 3v t t
với
3 4.t
d) Quãng đường vật di chuyển được trong 4 giờ là
81
4
km.
PHẦN III. (3 điểm) Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Biết tích phân
1
1
1.
e
dx a e
x



Giá trị của
a
bằng bao nhiêu?
Câu 2. Trên cửa sổ có dạng hình chữ nhật của
ngôi nhà một doanh nghiệp kinh doanh hải
sản, họa sĩ cần thiết kế logo hình con cá. Logo
là hình phẳng giới hạn bởi hai parabol với các
kích thước được cho trong hình bên (đơn vị
trên mỗi trục tọa độ là dm). Hoạ sĩ cần tính
diện tích của logo để báo giá cho doanh
nghiệp đó trước khi kí hợp đồng. Diện tích
của logo bằng
x
2
.dm
Tìm
x
(làm tròn kết
quả đến hàng đơn vị).
Câu 3. Một chiếc ô tô đang chạy với vận tốc
15 /ms
thì nhìn thấy chướng ngại vật trên đường cách
đó
40 ,m
người lái xe hãm phanh khẩn cấp. Sau khi hãm phanh, ô tô chuyển động chậm dần đều với
vận tốc
3 15 /v t t m s
. Tính quãng đường xe ô tô đi được trong thời gian
t
(giây) kể từ lúc
đạp phanh.
Câu 4. Khi đặt hệ toạ độ
Oxyz
vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy
rằng một không gian phủ sóng điện thoại có dạng một hình cầu
()S
(tập hợp những điểm nằm trong
và nằm trên mặt cầu tương ứng). Biết mặt cầu
()S
có phương trình
2 2 2
2 4 6 5 0.x y z x y z
Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng là bao nhiêu kilômét?
Câu 5. Một mô hình cầu treo được thiết kế trong không gian tọa độ
Oxyz
như hình vẽ. Làn đường
d
đi qua hai điểm
(4;3;1)M
và
(5;7;3).N
Từ một điểm
(5;2;1)A
trên cáp treo, người ta cần
tìm tọa độ điểm
'( ; ; )A a b c
là hình chiếu vuông góc của
A
trên
d
để lắp đặt đai chịu lực nâng cho
cầu. Tính giá trị của
.a b c
Câu 6. Có hai hộp chứa bi. Hộp thứ nhất chứa 4 bi đỏ và 5 bi vàng. Hộp thứ hai chứa 6 bi đỏ và 4 bi
vàng. Chọn ngẫu nhiên một hộp và sau đó lấy ngẫu nhiên 1 bi từ hộp đó. Tính xác suất để lấy được
viên bi đỏ (làm tròn đến hàng phần trăm).
--------------HẾT------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO PHÚ YÊN
TRƯỜNG THPT NGÔ GIA TỰ
Mã đề thi: 1217
ĐỀ KIỂM TRA CUỐI KỲ 2 NĂM HỌC 2024 - 2025
Môn: Toán, Lớp 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . .
PHẦN I. (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Câu 1: Tìm
1
dx
x
.
A.
1
dx x C
x

B.
1
x
dx e C
x

C.
1
lndx x C
x

. D.
1
lndx x C
x

.
Câu 2: Diện tích của hình phẳng phần gạch chéo trong hình bên được tính theo công thức nào sau
đây?
A.
24
02
( )d ( )dS f x x f x x

.
B.
24
02
( )d ( )dS f x x f x x

.
C.
4
0
( )dS f x x
.
D.
24
02
( )d ( )dS f x x f x x

.
Câu 3: Cho hai biến cố
,AB
có
0,6; 0,7; 0,4P A P B P AB
. Xác suất
|P B A
bằng
A.
3
4
. B.
4
7
. C.
0,28
. D.
2
3
.
Câu 4: Trong không gian
,Oxyz
góc giữa hai đường thẳng
1
1
:
1 1 2
x y z
d

và
2
1
:2
3
xt
d y t
zt


bằng
A.
30
o
. B.
90
o
. C.
60
o
. D.
45
o
.
Câu 5: Cho hai biến cố
A
và
B
với
0PB
. Xác suất của biến cố
A
với điều kiện biến cố
B
đã
xảy ra là
A.
|
P AB
P A B
PB
. B.
|
P AB
P A B
PA
C.
|.P A B P A P B
. D.
|
PA
P A B
PB
.
Câu 6: Trong không gian
,Oxyz
mặt cầu
2 2 2
: 6 2 5 0S x y z x y
có bán kính
R
bằng
A.
5
. B. 15. C.
5
. D. 25.
Câu 7: Cho hàm số
f
liên tục trên và
a
là số thực dương. Khẳng định nào sau đây luôn đúng?
A.
( ) ( )
a
a
f x dx f a
. B.
( ) 1
a
a
f x dx 
. C.
( ) 0
a
a
f x dx
. D.
( ) 1
a
a
f x dx
.
Câu 8: Trong không gian
Oxyz
, cho mặt phẳng
: 2 3 0P x z
. Vectơ nào dưới đây là một vectơ
pháp tuyến của của mặt phẳng
P
?
A.
3
1; 2;3n 
. B.
2
1;0; 2n 
. C.
1
1; 2;0n 
. D.
4
1;0;2n
.
Câu 9: Biết
2
0
( ) 2f x dx
và
2
0
( ) 4.g x dx
Giá trị của
2
0
( ) 2 ( )f x g x dx
bằng
A.
8.
B.
6.
C.
12.
D.
10.
Câu 10: Trong không gian
,Oxyz
mặt cầu
S
tâm
2;1; 1I
, bán kính bằng
6
có phương trình là
A.
2 2 2
2 1 1 36x y z
. B.
2 2 2
2 1 1 36x y z
.
C.
2 2 2
2 1 1 9x y z
. D.
2 2 2
2 1 1 9x y z
.
Câu 11: Trong không gian
,Oxyz
cho đường thẳng
15
:
1 2 3
x y z
d



. Vectơ nào dưới đây là một
vectơ chỉ phương của đường thẳng d?
A.
3
1;2;3u 
. B.
1
1; 2;3u 
. C.
4
1; 2; 3 .u
D.
2
1;2;3u
.
Câu 12: Cho
A
và
B
hai biến cố độc lập. Khẳng định nào dưới đây là sai?
A.
|.P B A P A
B.
|.P A B P A
C.
|.P A B P A
D.
|.P A B P A
PHẦN II. (4 điểm) Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh
chọn đúng hoặc sai.
Câu 1. Cho hàm số
2
( ) .f x x
Gọi
()Fx
là nguyên hàm của
()fx
trên
.
a)
'( ) ( ), .F x f x x
b)
3
()
3
x
F x C
(
C
là hằng số).
c) Biết
( 1) 0.F 
Giá trị của
(0)F
bằng
1
.
3
d) Với
1,a
có 3 giá trị của
a
thoả mãn
1
3 ( ) 1 0.
a
f x dx
Câu 2. Trong không gian
,Oxyz
cho hai điểm
0;2; 1A
và
3;2; 4B
và mặt phẳng
:2 2 6 0.P x y z
a) Một vectơ chỉ phương của đường thẳng
AB
là
1;0; 1a 
.
b) Mặt phẳng
P
có một vecto pháp tuyến là
2;2;1n
.
c) Đường thẳng
đi qua
A
và vuông góc với mặt phẳng
P
có phương trình chính tắc là:
21
2 2 1
x y z

.
d) Mặt cầu đường kính
AB
có phương trình là:
22
2
35
2 18.
22
x x x
Câu 3. Một lớp học có
40
học sinh gồm 28 nữ và 12 nam. Trong năm học 2023-2024, có 7 học sinh
nữ đạt danh hiệu học sinh giỏi và 6 học sinh nam đạt danh hiệu học sinh giỏi. Chọn ngẫu nhiên một
học sinh của lớp đó. Gọi
A
là biến cố “Học sinh được chọn là nữ” và
B
là biến cố “Học sinh được
chọn đạt danh hiệu học sinh giỏi”.
a) Xác suất của biến cố
A
là
0,7
.
b) Xác suất của biến cố
B
là
0,3
.
c)
A
và
B
là hai biến cố độc lập.
d) Xác suất của biến cố
A
với điều kiện biến cố B đã xảy ra là
0,35.
Câu 4. Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ
thuộc thời gian t(h) có đồ thị của vận tốc đã cho (hình bên). Trong
khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị là một
phần của parabol có đỉnh
(2;9),I
khoảng thời gian còn lại đồ thị là
một đoạn thẳng.
a) Vận tốc lớn nhất của chuyển động là 9 km/h.
b)
2
9
( ) 9
4
v t t t
với
0 3.t
c)
( ) 3v t t
với
3 4.t
d) Quãng đường vật di chuyển được trong 4 giờ là
27
km.
PHẦN III. (3 điểm) Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Biết tích phân
1
1
1.
e
dx e a
x



Giá trị của
a
bằng bao nhiêu?
Câu 2. Bạn An nhận thiết kế logo hình con mắt cho một
cơ sở y tế. Logo là hình phẳng giới hạn bởi 2 parabol
y f x
và
y g x
như hình vẽ (đơn vị trên mỗi
trục toạ độ là dm). Bạn An cần tính diện tích của logo
để báo giá cho cơ sở y tế đó trước khi kí hợp đồng. Diện
tích của logo bằng
x
2
.dm
Tìm
x
(làm tròn kết quả đến
hàng phần mười).
Câu 3. Một chiếc ô tô đang chạy với vận tốc
18 /ms
thì nhìn thấy chướng ngại vật trên đường cách
đó
60 ,m
người lái xe hãm phanh khẩn cấp. Sau khi hãm phanh, ô tô chuyển động chậm dần đều với
vận tốc
3 18 /v t t m s
. Tính quãng đường xe ô tô đi được trong thời gian
t
(giây) kể từ lúc
đạp phanh.
Câu 4. Khi đặt hệ toạ độ
Oxyz
vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy
rằng một không gian phủ sóng điện thoại có dạng một hình cầu
()S
(tập hợp những điểm nằm trong
và nằm trên mặt cầu tương ứng). Biết mặt cầu
()S
có phương trình
2 2 2
2 4 6 2 0.x y z x y z
Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng là bao nhiêu kilômét?
Câu 5. Một mô hình cầu treo được thiết kế trong không gian tọa độ
Oxyz
như hình vẽ. Làn đường
d
đi qua hai điểm
(4;3;1)M
và
(5;7;3).N
Từ một điểm
(5;2;1)A
trên cáp treo, người ta cần tìm
tọa độ điểm
'( ; ; )A a b c
là hình chiếu vuông góc của
A
trên
d
để lắp đặt đai chịu lực nâng cho cầu.
Tính giá trị của
.a b c
Câu 6. Có hai hộp chứa bi. Hộp thứ nhất chứa 4 bi đỏ và 5 bi vàng. Hộp thứ hai chứa 6 bi đỏ và 4 bi
vàng. Bạn Cường chọn ngẫu nhiên một hộp và sau đó lấy ngẫu nhiên 1 bi từ hộp đó. Tính xác suất để
Cường lấy được viên bi đỏ (làm tròn đến hàng phần trăm).
--------------HẾT-------------
ĐÁP ÁN TOÁN 12-CUỐI KỲ 2 NĂM HỌC 2024-2025
PHẦN 1: MÃ ĐỀ 1211
1
2
3
4
5
6
7
8
9
10
11
12
A
B
C
D
PHẦN 1: MÃ ĐỀ 1215
1
2
3
4
5
6
7
8
9
10
11
12
A
B
C
D
PHẦN II. MÃ ĐỀ 1211-1215
Câu
1
2
3
4
Đáp án
a) Đúng
b) Đúng
c) Sai
d) Đúng
a) Đúng
b) Đúng
c) Đúng
d) Sai
a) Đúng
b) Sai
c) Sai
d) Sai
a) Đúng
b) Đúng
c) Sai
d) Sai
PHẦN III. MÃ ĐỀ 1211-1215
Câu
1
2
3
4
5
6
Đáp án
2
28
37,5
6
7
0,52
PHẦN 1: MÃ ĐỀ 1213
1
2
3
4
5
6
7
8
9
10
11
12
A
B
C
D
PHẦN 1: MÃ ĐỀ 1217
1
2
3
4
5
6
7
8
9
10
11
12
A
B
C
D
PHẦN II: MÃ ĐỀ 1213-1217
Câu
1
2
3
4
Đáp án
a) Đúng
b) Đúng
c) Đúng
d) Sai
a) Đúng
b) Đúng
c) Đúng
d) Sai
a) Đúng
b) Sai
c) Sai
d) Sai
a) Đúng
b) Đúng
c) Sai
d) Đúng
PHẦN III: MÃ ĐỀ 1213-1217
Câu
1
2
3
4
5
6
Đáp án
-2
9,8
54
8
7
0,52
HƯỚNG DẪN GIẢI PHẦN TRẢ LỜI NGẮN MÃ ĐỀ 1211-1215
Câu 1. Biết tích phân
1
1
1.
e
dx a e
x



Giá trị của
a
bằng bao nhiêu?
Giải
Ta có
1
1
1 2 2.
e
dx e a
x



Câu 2. Trên cửa sổ có dạng hình chữ nhật của
ngôi nhà một doanh nghiệp kinh doanh hải sản,
họa sĩ cần thiết kế logo hình con cá. Logo là
hình phẳng giới hạn bởi hai parabol với các
kích thước được cho trong hình bên (đơn vị trên
mỗi trục tọa độ là dm). Hoạ sĩ cần tính diện tích
của logo để báo giá cho doanh nghiệp đó trước
khi kí hợp đồng. Diện tích của logo bằng
x
2
.dm
Tìm
x
(làm tròn kết quả đến hàng đơn
vị).
Giải
Parabol
y f x
có dạng
2
f x ax bx c
.
Parabol nhận
Oy
làm trục đối xứng nên
0.b
Vì đồ thị đi qua điểm
4;0
và
0;2
1
8
a
và
2.c
2
1
2
8
f x x
Tương tự
2
3
3
16
g x x
.
Diện tích của logo là
44
22
55
5
5 28( ).
16
S f x g x dx x dx dm



Câu 3. Một chiếc ô tô đang chạy với vận tốc
15 /ms
thì nhìn thấy chướng ngại vật trên đường cách
đó
40 ,m
người lái xe hãm phanh khẩn cấp. Sau khi hãm phanh, ô tô chuyển động chậm dần đều với
vận tốc
3 15 /v t t m s
, trong đó
t
(giây) là thời gian. Tính quãng đường xe ô tô đi được trong
thời gian
t
(giây) kể từ lúc đạp phanh.
Giải
Khi xe dừng hẳn thì
0 3 15 0 5v t t t
.
Quãng đường xe ô tô đi được trong thời gian
t
(giây) là
5
0
3 15 37,5 .s t dx m
Câu 4. Khi đặt hệ toạ độ
Oxyz
vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy
rằng một không gian phủ sóng điện thoại có dạng một hình cầu
()S
(tập hợp những điểm nằm trong
và nằm trên mặt cầu tương ứng). Biết mặt cầu
()S
có phương trình
2 2 2
2 4 6 5 0.x y z x y z
Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng là bao nhiêu kilômét?
Giải
Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng bằng đường kính mặt cầu:
Mặt cầu có bán kính
3R 
đường kính mặt cầu
2 6.R
Câu 5. Một mô hình cầu treo được thiết kế trong không gian tọa độ
Oxyz
như hình vẽ. Làn đường
d
đi qua hai điểm
(4;3;1)M
và
(5;7;3).N
Từ một điểm
(5;2;1)A
trên cáp treo, người ta cần tìm
tọa độ điểm
'( ; ; )A a b c
là hình chiếu vuông góc của
A
trên
d
để lắp đặt đai chịu lực nâng cho cầu.
Tính giá trị của
.a b c
Giải.
Gọi
()P
là mặt phẳng đi qua điểm
A
và vuông góc với
,MN
'A
là giao điểm của
()P
và
.d
Đường thẳng
d
đi qua điểm
(4;3;1)M
và nhận
(1;4;2)MN
làm vectơ chỉ phương nên có
phương trình tham số là:
4
3 4
12
xt
yt
zt
Mặt phẳng
()P
đi qua
(5;2;1)A
và nhận
(1;4;2)MN
làm vectơ pháp tuyến nên có phương
trình:
1( 5) 4( 2) 2( 1) 0 4 2 15 0x y z x y z
Tọa độ điểm
'A
là nghiệm của hệ phương trình
27 / 7
27 17 5
17 / 7 ' ; ; 7.
7 7 7
5 / 7
x
y A a b c
z
Câu 6. Có hai hộp chứa bi. Hộp thứ nhất chứa 4 bi đỏ và 5 bi vàng. Hộp thứ hai chứa 6 bi đỏ và 4 bi
vàng. Chọn ngẫu nhiên một hộp và sau đó lấy ngẫu nhiên một bi từ hộp đó. Tính xác suất để lấy được
viên bi đỏ (làm tròn đến hai chữ số thập phân).
Giải.
Gọi A là biến cố “chọn hộp thứ nhất” và B là biến cố “chọn hộp thứ hai”.
Gọi C là biến cố “lấy được viên bi đỏ”
Ta có
1
,
2
P A P B
4
C\ ,
9
PA
3
C\B .
5
P
Xác suất cần tìm là
P C P AC BC
.
Vì AC, BC là hai biến cố xung khắc nên ta có
. C\ . C\BP AC BC P AC P BC P A P A P B P
.
Vậy
1 4 1 3 47
. . 0,52
2 9 2 5 90
PC
HƯỚNG DẪN GIẢI PHẦN TRẢ LỜI NGẮN MÃ ĐỀ 1213-1217
Câu 1. Biết tích phân
1
1
1.
e
dx e a
x



Giá trị của
a
bằng bao nhiêu?
Giải
Ta có
1
1
1 2.
e
dx e a a
x



Câu 2. Bạn An nhận thiết kế logo hình con mắt cho một
cơ sở y tế. Logo là hình phẳng giới hạn bởi 2 parabol
y f x
và
y g x
như hình vẽ (đơn vị trên mỗi
trục toạ độ là dm). Bạn An cần tính diện tích của logo
để báo giá cho cơ sở y tế đó trước khi kí hợp đồng. Diện
tích của logo bằng
x
2
.dm
Tìm
x
(làm tròn kết quả đến
hàng phần mười).
Giải
Parabol
y f x
có dạng
2
f x ax bx c
.
Parabol
y f x
nhận
Oy
làm trục đối xứng nên
0.b
Vì đồ thị đi qua điểm
0; 1
và
2;0
1
4
a
và
1.c 
2
1
1
4
f x x
.
Tương tư ta có
2
1
2
4
g x x
.
Khi đó, diện tích S của phần logo là:
6
2
6
9,8S g x f x dx dm
.
Câu 3. Một chiếc ô tô đang chạy với vận tốc
18 /ms
thì nhìn thấy chướng ngại vật trên đường cách
đó
60 ,m
người lái xe hãm phanh khẩn cấp. Sau khi hãm phanh, ô tô chuyển động chậm dần đều với
vận tốc
3 18 /v t t m s
, trong đó
t
(giây) là thời gian. Tính quãng đường xe ô tô đi được trong
thời gian
t
(giây) kể từ lúc đạp phanh.
Giải

Tài liệu khác của Toán

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO PHÚ YÊN
ĐỀ KIỂM TRA CUỐI KỲ 2 NĂM HỌC 2024 - 2025
TRƯỜNG THPT NGÔ GIA TỰ Môn: Toán, Lớp 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề) Mã đề thi: 1211
Họ và tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . .
PHẦN I. (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Câu 1: Trong không gian Oxyz, mặt cầu S  2 2 2
: x y z  6x  2y 15  0 có bán kính R bằng A. 5 . B. 5 . C. 15. D. 25. Câu 2: Tìm x e dx  . x l x 1 A. e dx   C. B. x x
e dx e C. C. x x
e dx e ln 2  C. D. e dx   C. x ln 2 x e
Câu 3: Trong không gian Oxyz, mặt cầu  S  tâm I 2;1;  
1 , bán kính bằng 3 có phương trình là A.  2 2 2
x  2   y  2   z  2 2 1 1  3.
B. x  2   y   1  z   1  36 . C.  2 2 2
x  2   y  2   z  2 2 1 1  9 .
D. x  2   y   1  z   1  9 .
Câu 4: Cho hàm số f liên tục trên
và a là số thực dương. Khẳng định nào sau đây luôn đúng? a a a a A.
f (x)dx  1  . B.
f (x)dx  1   . C.
f (x)dx f (a)  . D.
f (x)dx  0  . a a a ax  1 t x y 1 z
Câu 5: Trong không gian Oxyz, góc giữa hai đường thẳng d :  
và d :  y  2t 1 1 1 2  2
z  3 t  bằng A. 30o . B. 90o . C. 45o . D. 60o .
Câu 6: Cho hai biến cố ,
A B có P 
A  0,6; PB  0,7; PAB  0,4 . Xác suất P A | B bằng 6 4 2 A. . B. . C. 0, 28 . D. . 7 7 3 2 2 2 Câu 7: Biết
f (x)dx  2 
và g(x)dx  4. 
Giá trị của 2 f (x)  g(x)dx bằng 0 0 0 A. 10. B. 6. C. 8. D. 12.
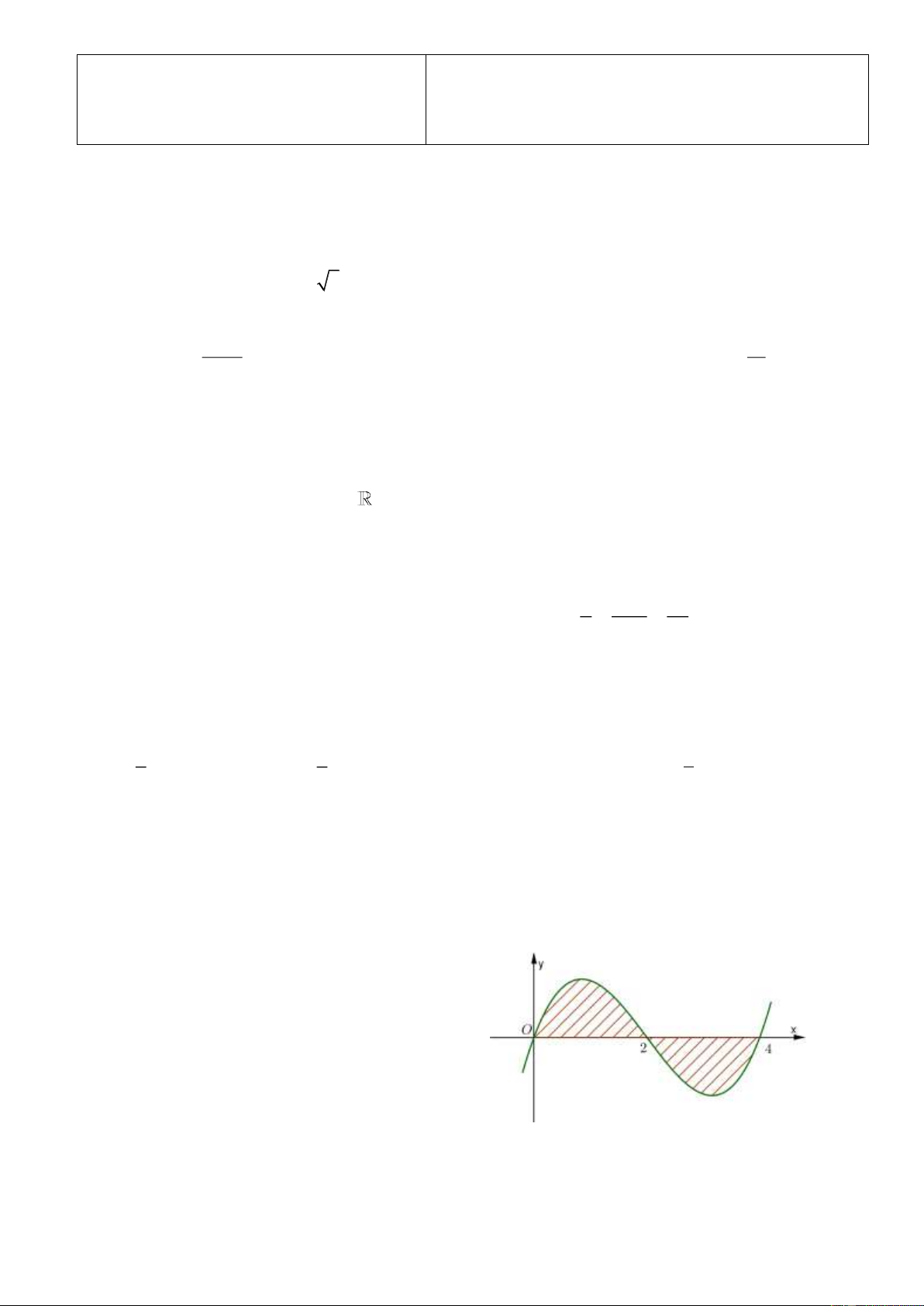
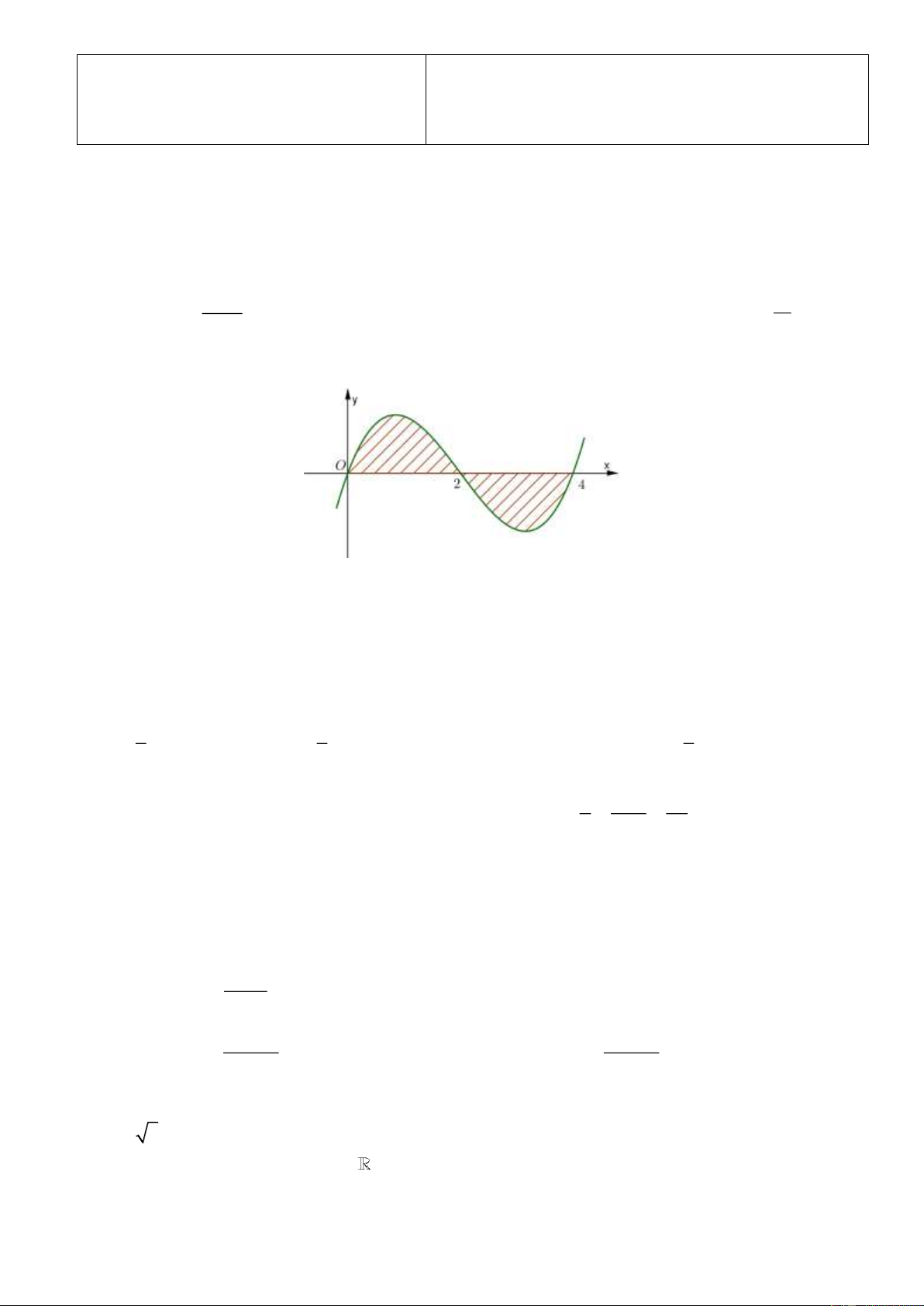
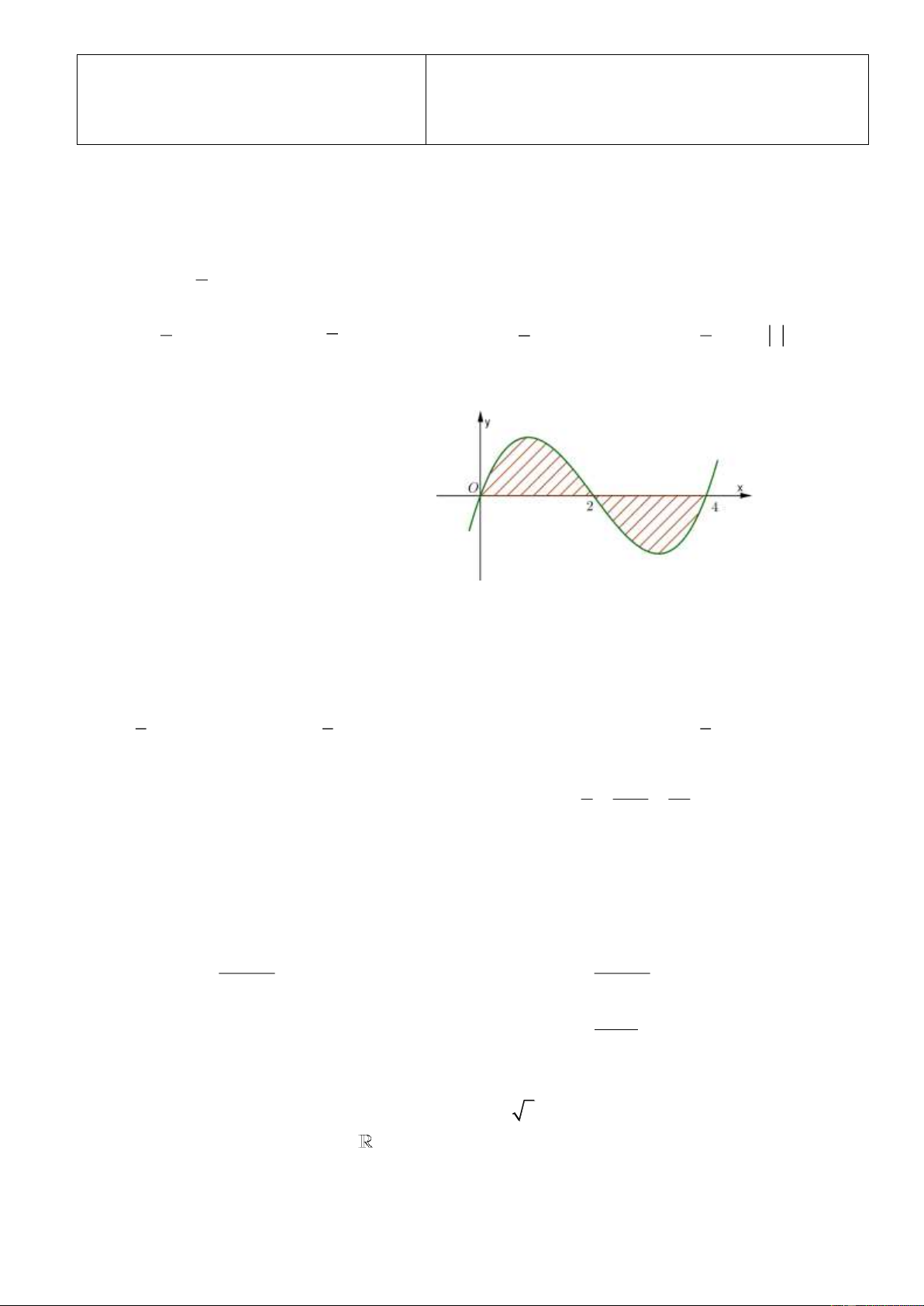
Câu 8: Diện tích của hình phẳng phần gạch chéo trong hình bên được tính theo công thức nào sau đây? 2 4 A. S
f (x)dx f (x)dx   . 0 2 2 4
B. S   f (x)dx f (x)dx   . 0 2 2 4 C. S
f (x)dx f (x)dx   . 0 2 4 D. S f (x)dx. 0
Câu 9: Trong không gian Oxyz , cho mặt phẳng  P : x  2 y  3  0 . Vectơ nào dưới đây là một vectơ
pháp tuyến của của mặt phẳng  P ? A. n  1; 2
 ;3 . B. n  1; 2
 ;0 . C. n  1;0; 2  .
D. n  1;0; 2 . 4   2   1   3  
Câu 10: Cho A và B hai biến cố độc lập. Khẳng định nào dưới đây là sai?
A. P B | A  PA.
B. P A | B  PA.
C. P A | B  P A.
D. P A | B   P A.
Câu 11: Cho hai biến cố A và B với P A  0 . Xác suất của biến cố B với điều kiện biến cố A đã xảy ra là P A
A. P B | A    .
B. PB | A  PA.PB. P BP AB P AB
C. P B | A    .
D. P B | A    P AP Bx y z
Câu 12: Trong không gian Oxyz, cho đường thẳng 1 5 d :  
. Vectơ nào dưới đây là một 1 2 3
vectơ chỉ phương của d? A. u  1; 2; 3
. B. u  1; 2
 ;3 . C. u  1; 2  ; 3
 . D. u  1;2;3 . 2   4   1   3  
PHẦN II. (4 điểm) Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. Câu 1. Cho hàm số 2
f (x)  x . Gọi F(x) là nguyên hàm của f (x) trên .
a) F '(x)  f (x), x   . 3 x b) F (x) 
C (C là hằng số). 3
c) Biết F(1)  0. Giá trị của F(0) bằng 0. a
d) Với a  1, không có giá trị nào của a thoả mãn 3 f (x)   1 dx  0. 1
Câu 2. Trong không gian Oxyz, cho hai điểm A0;2;  1 và B3;2; 4   và mặt phẳng
P:2x  2y z 6  0.
a) Một vectơ chỉ phương của đường thẳng AB là a  1;0;   1 .
b) Mặt phẳng P có một vecto pháp tuyến là n  2;2;  1 .
c) Đường thẳng  đi qua A và vuông góc với mặt phẳng P có phương trình chính tắc là: x y  2 z  1   . 2 2 1 2 2  3  2  5 
d) Mặt cầu đường kính AB có phương trình là: x    
x  2  x   18.    2   2 
Câu 3. Một lớp học có 40 học sinh gồm 28 nữ và 12 nam. Trong năm học 2023-2024, có 7 học sinh
nữ đạt danh hiệu học sinh giỏi và 6 học sinh nam đạt danh hiệu học sinh giỏi. Chọn ngẫu nhiên một
học sinh của lớp đó. Gọi A là biến cố “Học sinh được chọn là nữ” và B là biến cố “Học sinh được
chọn đạt danh hiệu học sinh giỏi”.
a) Xác suất của biến cố A là 0, 7 .
b) Xác suất của biến cố B là 0, 3 .
c) A và B là hai biến cố độc lập.
d) Xác suất của biến cố A với điều kiện biến cố B đã xảy ra là 0, 25.
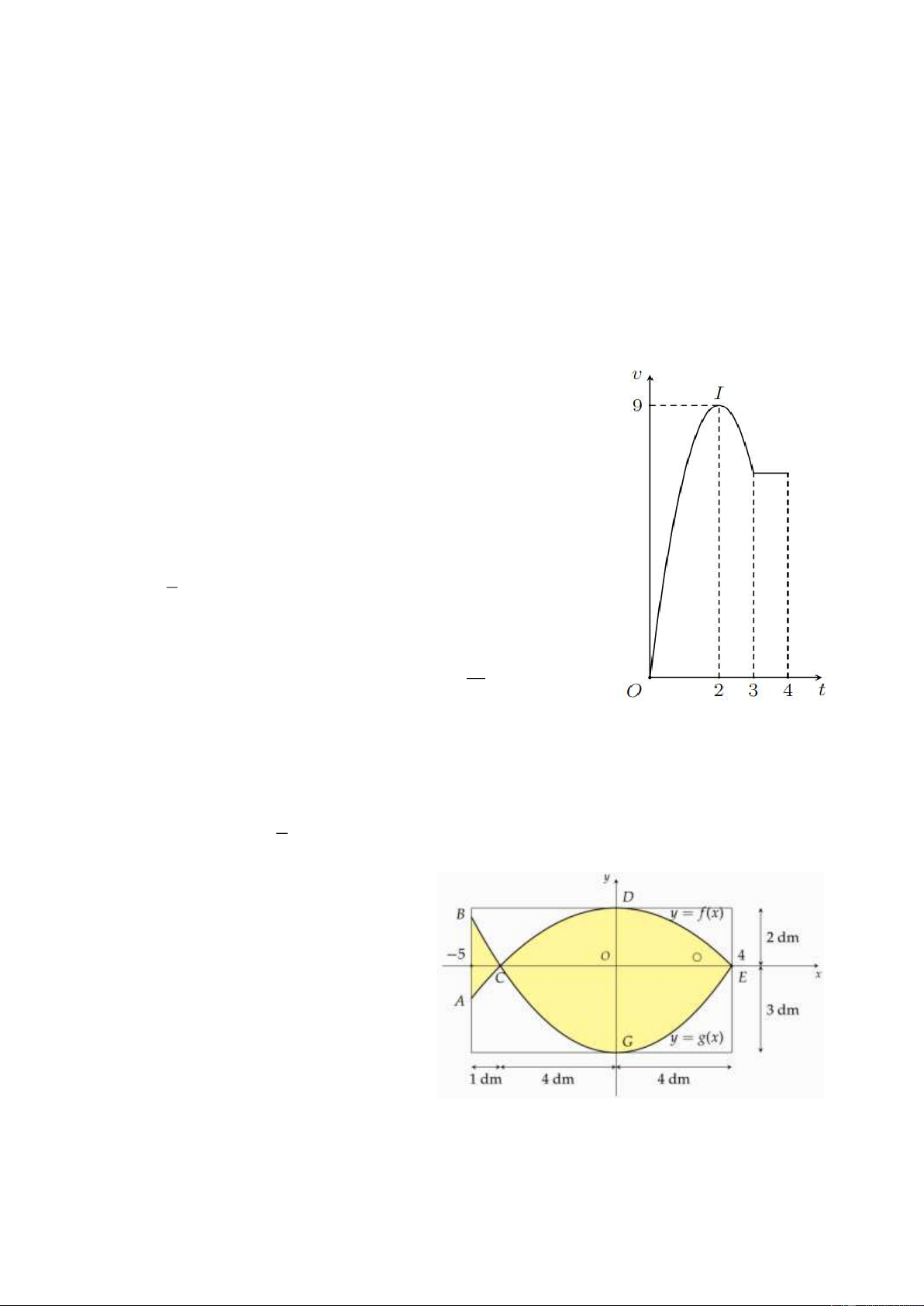
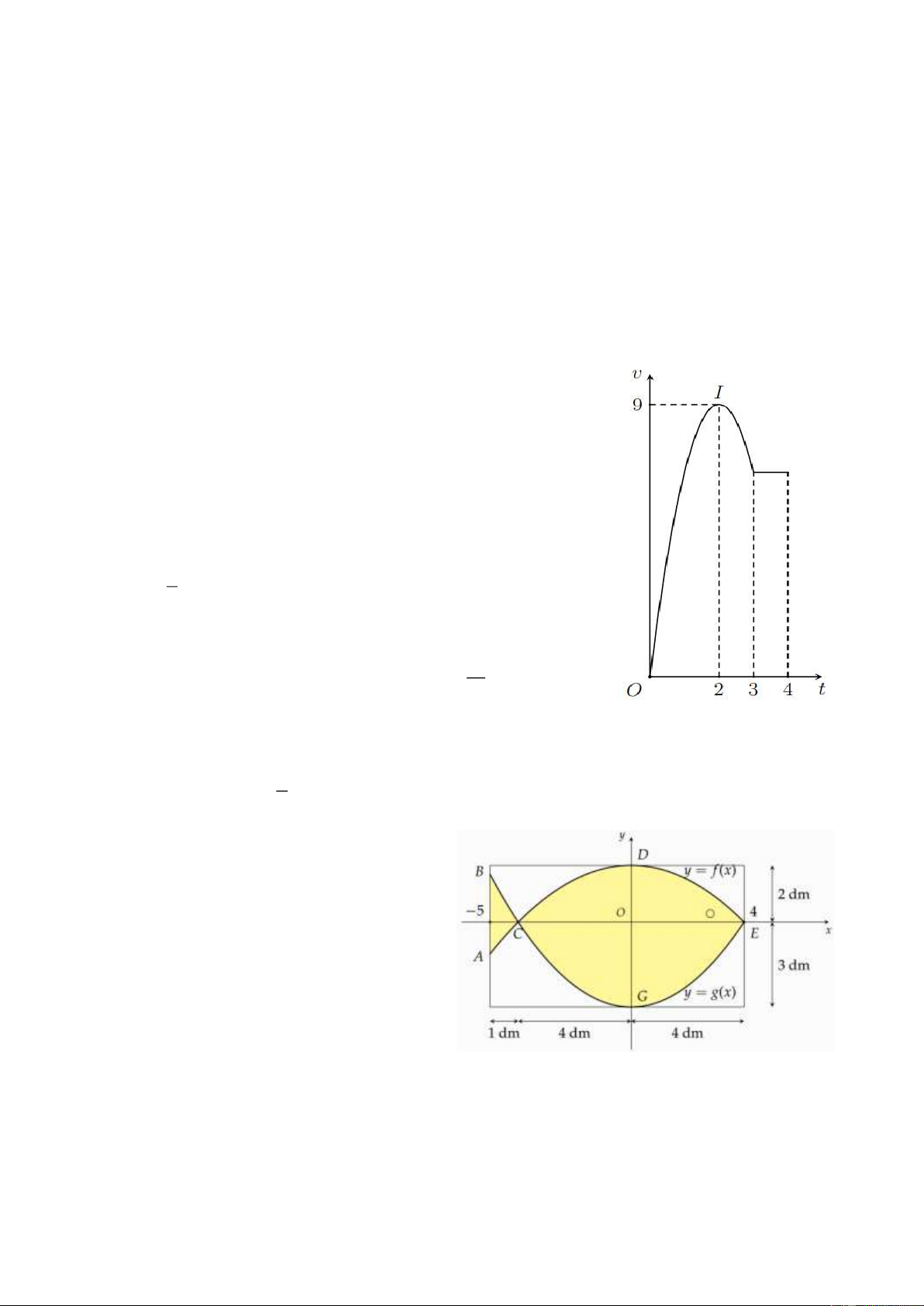
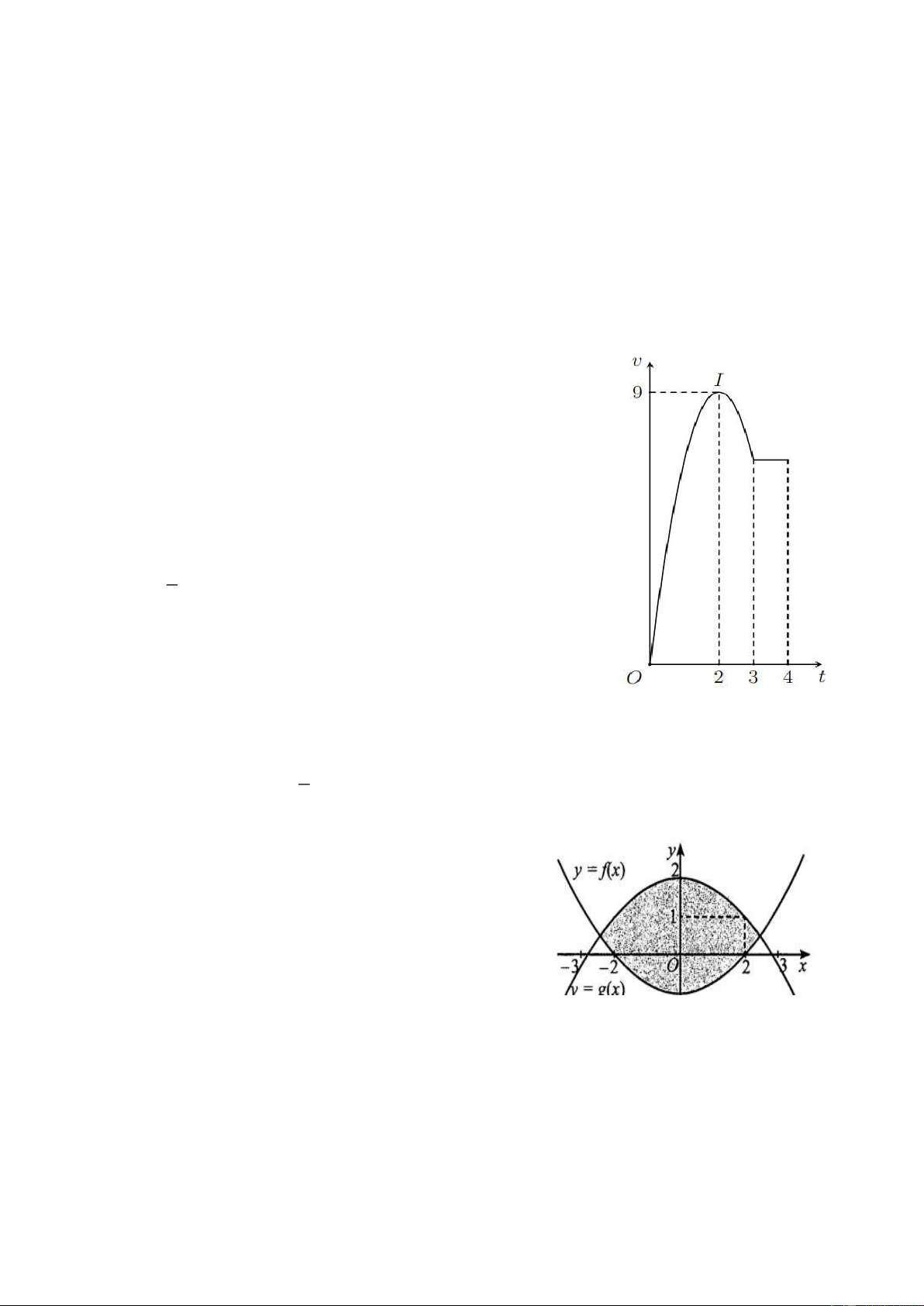
Câu 4. Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ
thuộc thời gian t(h) có đồ thị của vận tốc đã cho (hình bên). Trong
khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị là một
phần của parabol có đỉnh I (2;9), khoảng thời gian còn lại đồ thị là một đoạn thẳng.
a) Vận tốc lớn nhất của chuyển động là 9 km/h. 9 b) 2 v(t)  
t  9t với 0  t  3. 4
c) v(t)  3t với 3  t  4.
d) Quãng đường vật di chuyển được trong 4 giờ là 81 km. 4
PHẦN III. (3 điểm) Thí sinh trả lời từ câu 1 đến câu 6. e  1 
Câu 1. Biết tích phân
1 dx a  . e  
Giá trị của a bằng bao nhiêu?  x  1
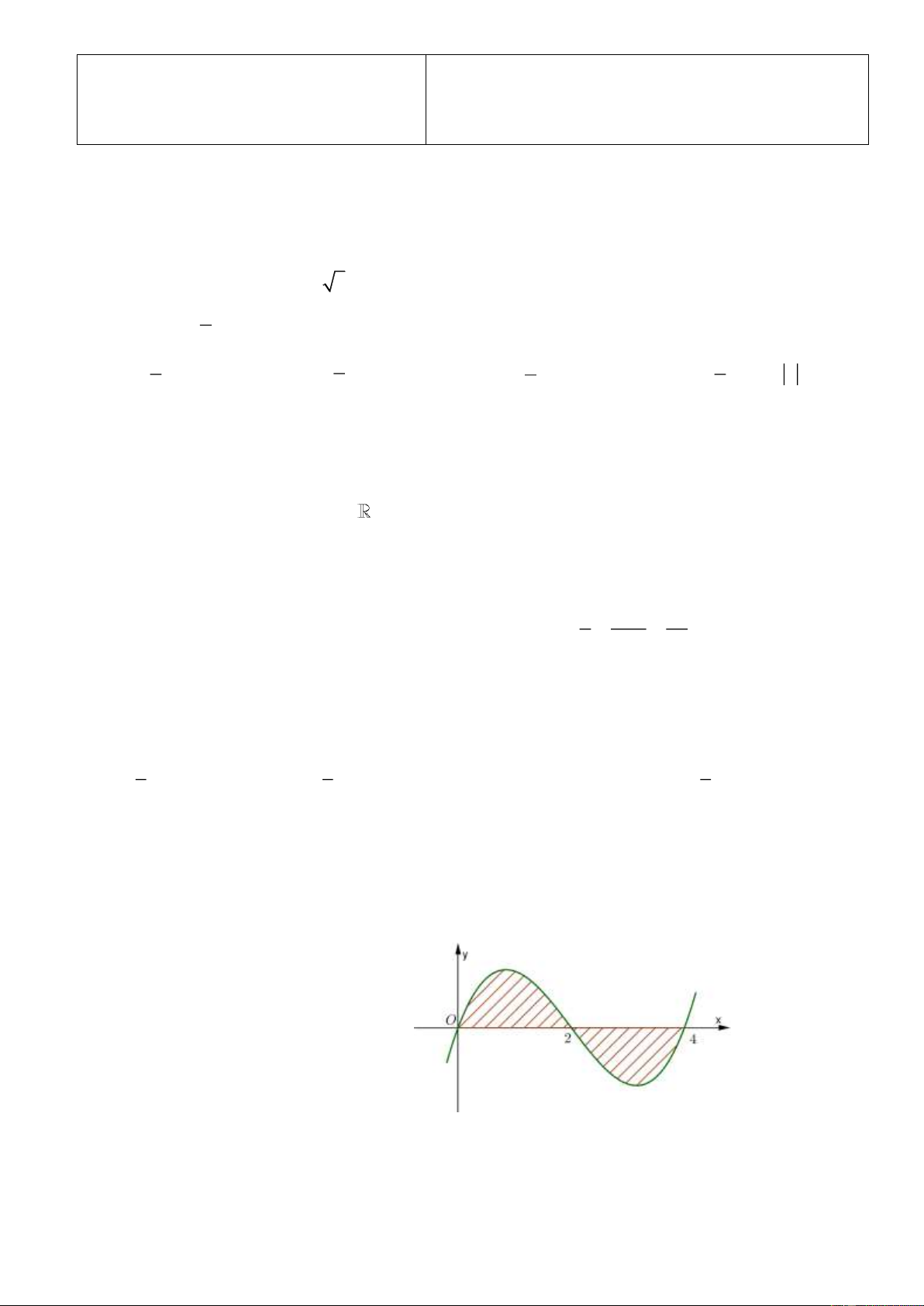
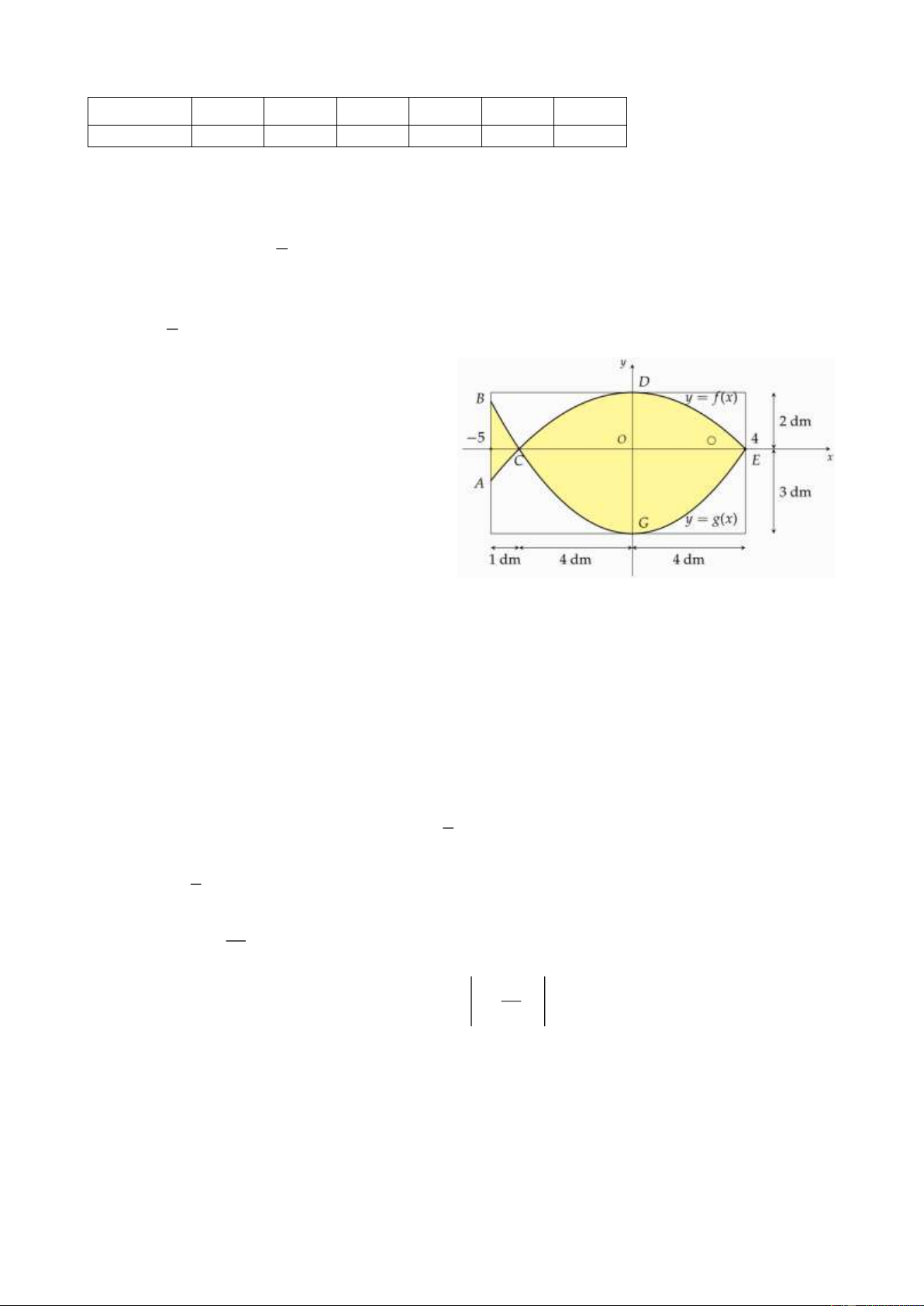
Câu 2. Trên cửa sổ có dạng hình chữ nhật của
ngôi nhà một doanh nghiệp kinh doanh hải
sản, họa sĩ cần thiết kế logo hình con cá. Logo
là hình phẳng giới hạn bởi hai parabol với các
kích thước được cho trong hình bên (đơn vị
trên mỗi trục tọa độ là dm). Hoạ sĩ cần tính
diện tích của logo để báo giá cho doanh
nghiệp đó trước khi kí hợp đồng. Diện tích của logo bằng x 2
dm . Tìm x (làm tròn kết
quả đến hàng đơn vị).
Câu 3. Một chiếc ô tô đang chạy với vận tốc 15m / s thì nhìn thấy chướng ngại vật trên đường cách đó 40 ,
m người lái xe hãm phanh khẩn cấp. Sau khi hãm phanh, ô tô chuyển động chậm dần đều với
vận tốc v t   3
t 15m / s , trong đó t (giây) là thời gian. Tính quãng đường xe ô tô đi được trong
thời gian t (giây) kể từ lúc đạp phanh.
Câu 4. Khi đặt hệ toạ độ Oxyz vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy
rằng một không gian phủ sóng điện thoại có dạng một hình cầu (S ) (tập hợp những điểm nằm trong
và nằm trên mặt cầu tương ứng). Biết mặt cầu (S ) có phương trình 2 2 2
x y z  2x  4y  6z  5  0.
Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng là bao nhiêu kilômét?
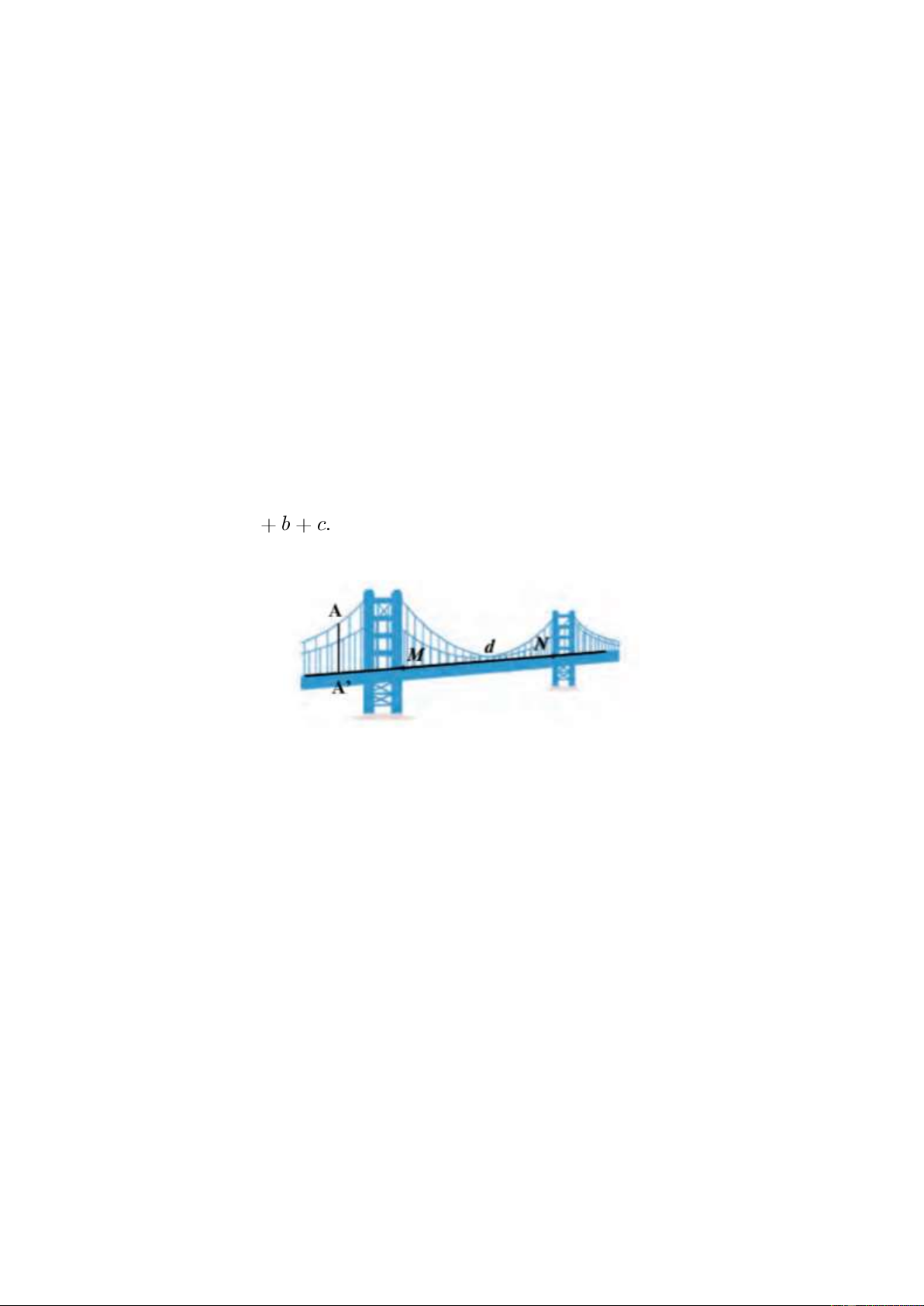
Câu 5. Một mô hình cầu treo được thiết kế trong không gian tọa độ Oxyz như hình vẽ. Làn đường
d đi qua hai điểm M(4;3;1) và N(5;7;3). Từ một điểm (
A 5;2;1) trên cáp treo, người ta cần tìm
tọa độ điểm A'(a; ;
b c) là hình chiếu vuông góc của A trên d để lắp đặt đai chịu lực nâng cho cầu.
Tính giá trị của a b . c
Câu 6. Có hai hộp chứa bi. Hộp thứ nhất chứa 4 bi đỏ và 5 bi vàng. Hộp thứ hai chứa 6 bi đỏ và 4 bi
vàng. Chọn ngẫu nhiên một hộp và sau đó lấy ngẫu nhiên 1 bi từ hộp đó. Tính xác suất để lấy được
viên bi đỏ (làm tròn đến hàng phần trăm).
--------------HẾT-------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO PHÚ YÊN
ĐỀ KIỂM TRA CUỐI KỲ 2 NĂM HỌC 2024 - 2025
TRƯỜNG THPT NGÔ GIA TỰ Môn: Toán, Lớp 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề) Mã đề thi: 1213
Họ và tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . .
PHẦN I. (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Câu 1: Trong không gian Oxyz, mặt cầu S  2 2 2
: x y z  6x  2y  5  0 có bán kính R bằng A. 15. B. 5 . C. 10. D. 25. 1 Câu 2: Tìm dxx 1 1 1 1 A. 2
dx x C. B. x
dx e C. C.
dx  ln x C. D.
dx  ln x C.  x x x x
Câu 3: Trong không gian Oxyz, mặt cầu  S  tâm I 2;1;  
1 , bán kính bằng 6 có phương trình là A.  2 2 2
x  2   y  2   z  2 2 1 1  36 .
B. x  2   y   1  z   1  36 . C.  2 2 2
x  2   y  2   z  2 2 1 1  9 .
D. x  2   y   1  z   1  9 .
Câu 4: Cho hàm số f liên tục trên
và a là số thực dương. Khẳng định nào sau đây luôn đúng? a a a a A.
f (x)dx  1  . B.
f (x)dx  1   . C.
f (x)dx  0  . D.
f (x)dx f (a)  . a a a ax  1 t x y 1 z
Câu 5: Trong không gian Oxyz, góc giữa hai đường thẳng d :  
và d :  y  2t 1 1 1 2  2
z  3 t  bằng A. 30o . B. 90o . C. 60o . D. 45o .
Câu 6: Cho hai biến cố ,
A B có P 
A  0,6; PB  0,7; PAB  0,4 . Xác suất P B | A bằng 3 4 2 A. . B. . C. 0, 28 . D. . 4 7 3 2 2 2 Câu 7: Biết
f (x)dx  2 
và g(x)dx  4. 
Giá trị của  f (x)  2g(x)dx bằng 0 0 0 A. 12. B. 6. C. 8. D. 10.
Câu 8: Diện tích của hình phẳng phần gạch chéo trong hình bên được tính theo công thức nào sau đây? 2 4 A. S
f (x)dx f (x)dx   . 0 2 2 4
B. S   f (x)dx f (x)dx   . 0 2 2 4 C. S
f (x)dx f (x)dx   . 0 2 4 D. S f (x)dx. 0
Câu 9: Trong không gian Oxyz , cho mặt phẳng  P : x  2z  3  0 . Vectơ nào dưới đây là một vectơ
pháp tuyến của của mặt phẳng  P ? A. n  1; 2
 ;3 . B. n  1;0; 2
. C. n  1; 2
 ;0 . D. n  1;0;2 . 4   1   2   3  
Câu 10: Cho A và B hai biến cố độc lập. Khẳng định nào dưới đây là sai?
A. P B | A  PB.
B. P A | B  P A.
C. P A | B  PB.
D. P A | B   P A.
Câu 11: Cho hai biến cố A và B với P B  0 . Xác suất của biến cố A với điều kiện biến cố B đã xảy ra là P A
A. P A | B    .
B. P A | B  PA.P B. P BP AB P AB
C. P A | B    .
D. P A | B    P BP Ax y z
Câu 12: Trong không gian Oxyz, cho đường thẳng 1 5 d :  
. Vectơ nào dưới đây là một 1 2 3
vectơ chỉ phương của đường thẳng d? A. u  1
 ;2;3 . B. u  1; 2
 ;3 . C. u  1; 2  ; 3
 . D. u  1;2;3 . 2   4   1   3  
PHẦN II. (4 điểm) Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. Câu 1. Cho hàm số 2
f (x)  x . Gọi F(x) là nguyên hàm của f (x) trên .
a) F '(x)  f (x), x   . 3 x b) F (x) 
C (C là hằng số). 3 1 c) Biết F( 1
 )  0. Giá trị của F(0) bằng . 3 a
d) Với a  1, có 3 giá trị của a thoả mãn 3 f (x)   1 dx  0. 1
Câu 2. Trong không gian Oxyz, cho hai điểm A0;2;  1 và B3;2; 4   và mặt phẳng
P:2x  2y z 6  0.
a) Một vectơ chỉ phương của đường thẳng AB là a  1;0;   1 .
b) Mặt phẳng P có một vecto pháp tuyến là n  2;2;  1 .
c) Đường thẳng  đi qua A và vuông góc với mặt phẳng P có phương trình chính tắc là: x y  2 z  1   . 2 2 1 2 2  3  2  5 
d) Mặt cầu đường kính AB có phương trình là: x    
x  2  x   18.    2   2 
Câu 3. Một lớp học có 40 học sinh gồm 28 nữ và 12 nam. Trong năm học 2023-2024, có 7 học sinh
nữ đạt danh hiệu học sinh giỏi và 6 học sinh nam đạt danh hiệu học sinh giỏi. Chọn ngẫu nhiên một
học sinh của lớp đó. Gọi A là biến cố “Học sinh được chọn là nữ” và B là biến cố “Học sinh được
chọn đạt danh hiệu học sinh giỏi”.
a) Xác suất của biến cố A là 0, 7 .
b) Xác suất của biến cố B là 0, 3 .
c) A và B là hai biến cố độc lập.
d) Xác suất của biến cố A với điều kiện biến cố B đã xảy ra là 0,35.
Câu 4. Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ
thuộc thời gian t(h) có đồ thị của vận tốc đã cho (hình bên). Trong
khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị là một
phần của parabol có đỉnh I (2;9), khoảng thời gian còn lại đồ thị là một đoạn thẳng.
a) Vận tốc lớn nhất của chuyển động là 9 km/h. 9 b) 2 v(t)  
t  9t với 0  t  3. 4
c) v(t)  3t với 3  t  4.
d) Quãng đường vật di chuyển được trong 4 giờ là 27 km.
PHẦN III. (3 điểm) Thí sinh trả lời từ câu 1 đến câu 6. e  1 
Câu 1. Biết tích phân 1 dx e  . a  
Giá trị của a bằng bao nhiêu?  x  1
Câu 2. Bạn An nhận thiết kế logo hình con mắt cho một
cơ sở y tế. Logo là hình phẳng giới hạn bởi 2 parabol
y f x và y g x như hình vẽ (đơn vị trên mỗi
trục toạ độ là dm). Bạn An cần tính diện tích của logo
để báo giá cho cơ sở y tế đó trước khi kí hợp đồng. Diện
tích của logo bằng x 2
dm . Tìm x (làm tròn kết quả đến hàng phần mười).
Câu 3. Một chiếc ô tô đang chạy với vận tốc 18m / s thì nhìn thấy chướng ngại vật trên đường cách
đó 60m, người lái xe hãm phanh khẩn cấp. Sau khi hãm phanh, ô tô chuyển động chậm dần đều với
vận tốc v t   3
t 18m / s , trong đó t (giây) là thời gian. Tính quãng đường xe ô tô đi được
trong thời gian t (giây) kể từ lúc đạp phanh.
Câu 4. Khi đặt hệ toạ độ Oxyz vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy
rằng một không gian phủ sóng điện thoại có dạng một hình cầu (S ) (tập hợp những điểm nằm trong
và nằm trên mặt cầu tương ứng). Biết mặt cầu (S ) có phương trình 2 2 2
x y z  2x  4y  6z  2  0.
Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng là bao nhiêu kilômét?
Câu 5. Một mô hình cầu treo được thiết kế trong không gian tọa độ Oxyz như hình vẽ. Làn đường
d đi qua hai điểm M(4; 3;1) và N(5;7; 3). Từ một điểm (
A 5;2;1) trên cáp treo, người ta cần
tìm tọa độ điểm A'(a; ;
b c) là hình chiếu vuông góc của A trên d để lắp đặt đai chịu lực nâng cho
cầu. Tính giá trị của a b . c
Câu 6. Có hai hộp chứa bi. Hộp thứ nhất chứa 4 bi đỏ và 5 bi vàng. Hộp thứ hai chứa 6 bi đỏ và 4 bi
vàng. Bạn Cường chọn ngẫu nhiên một hộp và sau đó lấy ngẫu nhiên 1 bi từ hộp đó. Tính xác suất để
Cường lấy được viên bi đỏ (làm tròn đến hàng phần trăm).
--------------HẾT-------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO PHÚ YÊN
ĐỀ KIỂM TRA CUỐI KỲ 2 NĂM HỌC 2024 - 2025
TRƯỜNG THPT NGÔ GIA TỰ Môn: Toán, Lớp 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề) Mã đề thi: 1215
Họ và tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . .
PHẦN I. (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án. Câu 1: Tìm x e dx  . x l x 1 A. e dx   C. B. x x
e dx e C. C. x x
e dx e ln 2  C
. D. e dx   C.  x ln 2 x e
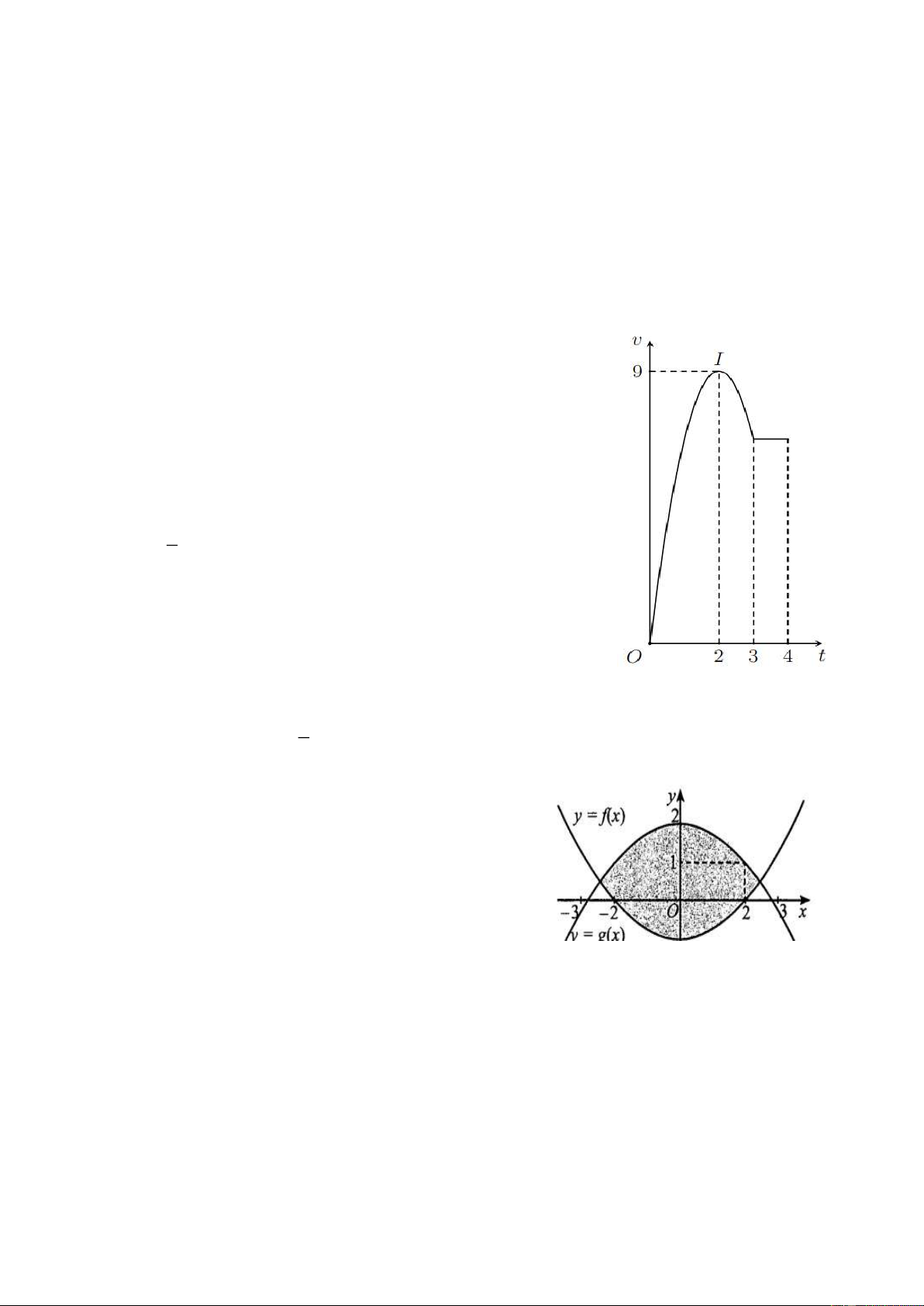
Câu 2: Diện tích của hình phẳng phần gạch chéo trong hình bên dưới được tính theo công thức nào sau đây? 4 2 4 A. S f (x)dx.
B. S   f (x)dx f (x)dx   . 0 0 2 2 4 2 4 C. S
f (x)dx f (x)dx   . D. S
f (x)dx f (x)dx   . 0 2 0 2
Câu 3: Cho hai biến cố ,
A B có P 
A  0,6; PB  0,7; PAB  0,4 . Xác suất P A | B bằng 6 4 2 A. . B. . C. 0, 28 . D. . 7 7 3 x  1 t x y 1 z
Câu 4: Trong không gian Oxyz, góc giữa hai đường thẳng d :  
và d :  y  2t 1 1 1 2  2
z  3 t  bằng A. 30o . B. 90o . C. 45o . D. 60o .
Câu 5: Cho hai biến cố A và B với P A  0 . Xác suất của biến cố B với điều kiện biến cố A đã xảy ra là P A
A. P B | A    .
B. PB | A  PA.PB. P BP AB P AB
C. P B | A    .
D. P B | A    P BP A
Câu 6: Trong không gian Oxyz, mặt cầu S  2 2 2
: x y z  6x  2y 15  0 có bán kính R bằng A. 5 . B. 15. C. 5 . D. 25.
Câu 7: Cho hàm số f liên tục trên
và a là số thực dương. Khẳng định nào sau đây luôn đúng? a a a a A.
f (x)dx  0  . B.
f (x)dx f (a)  . C.
f (x)dx  1   . D.
f (x)dx  1  . a a a a
Câu 8: Trong không gian Oxyz, cho mặt phẳng  P : x  2 y  3  0 . Vectơ nào dưới đây là một
vectơ pháp tuyến của của mặt phẳng  P ? A. n  1; 2
 ;3 . B. n  1; 2
 ;0 . C. n  1;0; 2  .
D. n  1;0; 2 . 4   2   1   3   2 2 2 Câu 9: Biết
f (x)dx  2 
và g(x)dx  4. 
Giá trị của 2 f (x)  g(x)dx bằng 0 0 0 A. 8. B. 6. C. 10. D. 12.
Câu 10: Trong không gian Oxyz, mặt cầu  S  tâm I 2;1;  
1 , bán kính bằng 3 có phương trình là A.  2 2 2
x  2   y  2   z  2 2 1 1  36 .
B. x  2   y   1  z   1  36 . C.  2 2 2
x  2   y  2   z  2 2 1 1  9 .
D. x  2   y   1  z   1  9 . x y z
Câu 11: Trong không gian Oxyz, cho đường thẳng 1 5 d :  
. Vectơ nào dưới đây là một 1 2 3
vectơ chỉ phương của d? A. u  1; 2; 3
. B. u  1; 2
 ;3 . C. u  1; 2  ; 3  .
D. u  1; 2;3 . 2   4   1   3  
Câu 12: Cho A và B hai biến cố độc lập. Khẳng định nào dưới đây là sai?
A. P B | A  PB.
B. P A | B  PB.
C. P A | B  P A.
D. P A | B   P A.
PHẦN II. (4 điểm) Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. Câu 1. Cho hàm số 2
f (x)  x . Gọi F(x) là nguyên hàm của f (x) trên .
a) F '(x)  f (x), x   . 3 x b) F (x) 
C (C là hằng số). 3
c) Biết F(1)  0. Giá trị của F(0) bằng 0. a
d) Với a  1, không có giá trị nào của a thoả mãn 3 f (x)   1 dx  0. 1
Câu 2. Trong không gian Oxyz, cho hai điểm A0;2;  1 và B3;2; 4   và mặt phẳng
P:2x  2y z 6  0.
a) Một vectơ chỉ phương của đường thẳng AB là a  1;0;   1 .
b) Mặt phẳng P có một vecto pháp tuyến là n  2;2;  1 .
c) Đường thẳng  đi qua A và vuông góc với mặt phẳng P có phương trình chính tắc là: x y  2 z  1   . 2 2 1 2 2  3  2  5 
d) Mặt cầu đường kính AB có phương trình là: x    
x  2  x   18.    2   2 
Câu 3. Một lớp học có 40 học sinh gồm 28 nữ và 12 nam. Trong năm học 2023-2024, có 7 học sinh
nữ đạt danh hiệu học sinh giỏi và 6 học sinh nam đạt danh hiệu học sinh giỏi. Chọn ngẫu nhiên một
học sinh của lớp đó. Gọi A là biến cố “Học sinh được chọn là nữ” và B là biến cố “Học sinh được
chọn đạt danh hiệu học sinh giỏi”.
a) Xác suất của biến cố A là 0, 7 .
b) Xác suất của biến cố B là 0, 3 .
c) A và B là hai biến cố độc lập.
d) Xác suất của biến cố A với điều kiện biến cố B đã xảy ra là 0, 25.
Câu 4. Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ
thuộc thời gian t(h) có đồ thị của vận tốc đã cho (hình bên). Trong
khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị là một
phần của parabol có đỉnh I (2;9), khoảng thời gian còn lại đồ thị là một đoạn thẳng.
a) Vận tốc lớn nhất của chuyển động là 9 km/h. 9 b) 2 v(t)  
t  9t với 0  t  3. 4
c) v(t)  3t với 3  t  4.
d) Quãng đường vật di chuyển được trong 4 giờ là 81 km. 4
PHẦN III. (3 điểm) Thí sinh trả lời từ câu 1 đến câu 6. e  1 
Câu 1. Biết tích phân
1 dx a  . e  
Giá trị của a bằng bao nhiêu?  x  1
Câu 2. Trên cửa sổ có dạng hình chữ nhật của
ngôi nhà một doanh nghiệp kinh doanh hải
sản, họa sĩ cần thiết kế logo hình con cá. Logo
là hình phẳng giới hạn bởi hai parabol với các
kích thước được cho trong hình bên (đơn vị
trên mỗi trục tọa độ là dm). Hoạ sĩ cần tính
diện tích của logo để báo giá cho doanh
nghiệp đó trước khi kí hợp đồng. Diện tích của logo bằng x 2
dm . Tìm x (làm tròn kết
quả đến hàng đơn vị).
Câu 3. Một chiếc ô tô đang chạy với vận tốc 15m / s thì nhìn thấy chướng ngại vật trên đường cách đó 40 ,
m người lái xe hãm phanh khẩn cấp. Sau khi hãm phanh, ô tô chuyển động chậm dần đều với
vận tốc v t   3
t 15m / s . Tính quãng đường xe ô tô đi được trong thời gian t (giây) kể từ lúc đạp phanh.
Câu 4. Khi đặt hệ toạ độ Oxyz vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy
rằng một không gian phủ sóng điện thoại có dạng một hình cầu (S ) (tập hợp những điểm nằm trong
và nằm trên mặt cầu tương ứng). Biết mặt cầu (S ) có phương trình 2 2 2
x y z  2x  4y  6z  5  0.
Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng là bao nhiêu kilômét?
Câu 5. Một mô hình cầu treo được thiết kế trong không gian tọa độ Oxyz như hình vẽ. Làn đường
d đi qua hai điểm M(4; 3;1) và N(5;7; 3). Từ một điểm (
A 5;2;1) trên cáp treo, người ta cần
tìm tọa độ điểm A'(a; ;
b c) là hình chiếu vuông góc của A trên d để lắp đặt đai chịu lực nâng cho
cầu. Tính giá trị của a b . c
Câu 6. Có hai hộp chứa bi. Hộp thứ nhất chứa 4 bi đỏ và 5 bi vàng. Hộp thứ hai chứa 6 bi đỏ và 4 bi
vàng. Chọn ngẫu nhiên một hộp và sau đó lấy ngẫu nhiên 1 bi từ hộp đó. Tính xác suất để lấy được
viên bi đỏ (làm tròn đến hàng phần trăm).
--------------HẾT------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO PHÚ YÊN
ĐỀ KIỂM TRA CUỐI KỲ 2 NĂM HỌC 2024 - 2025
TRƯỜNG THPT NGÔ GIA TỰ Môn: Toán, Lớp 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề) Mã đề thi: 1217
Họ và tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . .
PHẦN I. (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án. 1 Câu 1: Tìm dx  . x 1 1 1 1 A. x
dx x C B.
dx e C C.
dx  ln x C. D.
dx  ln x C. x x x x
Câu 2: Diện tích của hình phẳng phần gạch chéo trong hình bên được tính theo công thức nào sau đây? 2 4 A. S
f (x)dx f (x)dx   . 0 2 2 4
B. S   f (x)dx f (x)dx   . 0 2 4 C. S f (x)dx. 0 2 4 D. S
f (x)dx f (x)dx   . 0 2
Câu 3: Cho hai biến cố ,
A B có P 
A  0,6; PB  0,7; PAB  0,4 . Xác suất P B | A bằng 3 4 2 A. . B. . C. 0, 28 . D. . 4 7 3 x  1 t x y 1 z
Câu 4: Trong không gian Oxyz, góc giữa hai đường thẳng d :  
và d :  y  2t 1 1 1 2  2
z  3 t  bằng A. 30o . B. 90o . C. 60o . D. 45o .
Câu 5: Cho hai biến cố A và B với P B  0 . Xác suất của biến cố A với điều kiện biến cố B đã xảy ra là P AB P AB
A. P A | B    .
B. P A | B    P BP AP A
C. P A | B  PA.P B.
D. P A | B    . P B
Câu 6: Trong không gian Oxyz, mặt cầu S  2 2 2
: x y z  6x  2y  5  0 có bán kính R bằng A. 5 . B. 15. C. 5 . D. 25.
Câu 7: Cho hàm số f liên tục trên
và a là số thực dương. Khẳng định nào sau đây luôn đúng? a a a a A.
f (x)dx f (a)  . B.
f (x)dx  1   . C.
f (x)dx  0  . D.
f (x)dx  1  . a a a a
Câu 8: Trong không gian Oxyz , cho mặt phẳng  P : x  2z  3  0 . Vectơ nào dưới đây là một vectơ
pháp tuyến của của mặt phẳng  P ? A. n  1; 2
 ;3 . B. n  1;0; 2
. C. n  1; 2  ;0 .
D. n  1;0; 2 . 4   1   2   3   2 2 2 Câu 9: Biết
f (x)dx  2 
và g(x)dx  4. 
Giá trị của  f (x)  2g(x)dx bằng 0 0 0 A. 8. B. 6. C. 12. D. 10.
Câu 10: Trong không gian Oxyz, mặt cầu  S  tâm I 2;1;  
1 , bán kính bằng 6 có phương trình là A.  2 2 2
x  2   y  2   z  2 2 1 1  36 .
B. x  2   y   1   z   1  36 . C.  2 2 2
x  2   y  2   z  2 2 1 1  9 .
D. x  2   y   1   z   1  9 . x y z
Câu 11: Trong không gian Oxyz, cho đường thẳng 1 5 d :  
. Vectơ nào dưới đây là một 1 2 3
vectơ chỉ phương của đường thẳng d? A. u  1
 ;2;3 . B. u  1; 2
 ;3 . C. u  1; 2  ; 3
 . D. u  1;2;3 . 2   4   1   3  
Câu 12: Cho A và B hai biến cố độc lập. Khẳng định nào dưới đây là sai?
A. P B | A  PA.
B. P A | B  PA.
C. P A | B  P A.
D. P A | B   P A.
PHẦN II. (4 điểm) Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. Câu 1. Cho hàm số 2
f (x)  x . Gọi F(x) là nguyên hàm của f (x) trên .
a) F '(x)  f (x), x   . 3 x b) F (x) 
C (C là hằng số). 3 1 c) Biết F( 1
 )  0. Giá trị của F(0) bằng . 3 a
d) Với a  1, có 3 giá trị của a thoả mãn 3 f (x)   1 dx  0. 1
Câu 2. Trong không gian Oxyz, cho hai điểm A0;2;  1 và B3;2; 4   và mặt phẳng
P:2x  2y z 6  0.
a) Một vectơ chỉ phương của đường thẳng AB là a  1;0;   1 .
b) Mặt phẳng P có một vecto pháp tuyến là n  2;2;  1 .
c) Đường thẳng  đi qua A và vuông góc với mặt phẳng P có phương trình chính tắc là: x y  2 z  1   . 2 2 1 2 2  3  2  5 
d) Mặt cầu đường kính AB có phương trình là: x    
x  2  x   18.    2   2 
Câu 3. Một lớp học có 40 học sinh gồm 28 nữ và 12 nam. Trong năm học 2023-2024, có 7 học sinh
nữ đạt danh hiệu học sinh giỏi và 6 học sinh nam đạt danh hiệu học sinh giỏi. Chọn ngẫu nhiên một
học sinh của lớp đó. Gọi A là biến cố “Học sinh được chọn là nữ” và B là biến cố “Học sinh được
chọn đạt danh hiệu học sinh giỏi”.
a) Xác suất của biến cố A là 0, 7 .
b) Xác suất của biến cố B là 0, 3 .
c) A và B là hai biến cố độc lập.
d) Xác suất của biến cố A với điều kiện biến cố B đã xảy ra là 0,35.
Câu 4. Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ
thuộc thời gian t(h) có đồ thị của vận tốc đã cho (hình bên). Trong
khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị là một
phần của parabol có đỉnh I (2;9), khoảng thời gian còn lại đồ thị là một đoạn thẳng.
a) Vận tốc lớn nhất của chuyển động là 9 km/h. 9 b) 2 v(t)  
t  9t với 0  t  3. 4
c) v(t)  3t với 3  t  4.
d) Quãng đường vật di chuyển được trong 4 giờ là 27 km.
PHẦN III. (3 điểm) Thí sinh trả lời từ câu 1 đến câu 6. e  1 
Câu 1. Biết tích phân 1 dx e  . a  
Giá trị của a bằng bao nhiêu?  x  1
Câu 2. Bạn An nhận thiết kế logo hình con mắt cho một
cơ sở y tế. Logo là hình phẳng giới hạn bởi 2 parabol
y f x và y g x như hình vẽ (đơn vị trên mỗi
trục toạ độ là dm). Bạn An cần tính diện tích của logo
để báo giá cho cơ sở y tế đó trước khi kí hợp đồng. Diện
tích của logo bằng x 2
dm .Tìm x (làm tròn kết quả đến hàng phần mười).
Câu 3. Một chiếc ô tô đang chạy với vận tốc 18m / s thì nhìn thấy chướng ngại vật trên đường cách
đó 60m, người lái xe hãm phanh khẩn cấp. Sau khi hãm phanh, ô tô chuyển động chậm dần đều với
vận tốc v t   3
t 18m / s . Tính quãng đường xe ô tô đi được trong thời gian t (giây) kể từ lúc đạp phanh.
Câu 4. Khi đặt hệ toạ độ Oxyz vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy
rằng một không gian phủ sóng điện thoại có dạng một hình cầu (S ) (tập hợp những điểm nằm trong
và nằm trên mặt cầu tương ứng). Biết mặt cầu (S ) có phương trình 2 2 2
x y z  2x  4y  6z  2  0.
Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng là bao nhiêu kilômét?
Câu 5. Một mô hình cầu treo được thiết kế trong không gian tọa độ Oxyz như hình vẽ. Làn đường
d đi qua hai điểm M(4; 3;1) và N(5;7; 3). Từ một điểm (
A 5;2;1) trên cáp treo, người ta cần tìm
tọa độ điểm A'(a; ;
b c) là hình chiếu vuông góc của A trên d để lắp đặt đai chịu lực nâng cho cầu.
Tính giá trị của a b . c
Câu 6. Có hai hộp chứa bi. Hộp thứ nhất chứa 4 bi đỏ và 5 bi vàng. Hộp thứ hai chứa 6 bi đỏ và 4 bi
vàng. Bạn Cường chọn ngẫu nhiên một hộp và sau đó lấy ngẫu nhiên 1 bi từ hộp đó. Tính xác suất để
Cường lấy được viên bi đỏ (làm tròn đến hàng phần trăm).
--------------HẾT-------------
ĐÁP ÁN TOÁN 12-CUỐI KỲ 2 NĂM HỌC 2024-2025 PHẦN 1: MÃ ĐỀ 1211 1 2 3 4 5 6 7 8 9 10 11 12 A B C D PHẦN 1: MÃ ĐỀ 1215 1 2 3 4 5 6 7 8 9 10 11 12 A B C D
PHẦN II. MÃ ĐỀ 1211-1215 Câu 1 2 3 4 Đáp án a) Đúng a) Đúng a) Đúng a) Đúng b) Đúng b) Đúng b) Sai b) Đúng c) Sai c) Đúng c) Sai c) Sai d) Đúng d) Sai d) Sai d) Sai
PHẦN III. MÃ ĐỀ 1211-1215 Câu 1 2 3 4 5 6 Đáp án 2 28 37,5 6 7 0,52 PHẦN 1: MÃ ĐỀ 1213 1 2 3 4 5 6 7 8 9 10 11 12 A B C D PHẦN 1: MÃ ĐỀ 1217 1 2 3 4 5 6 7 8 9 10 11 12 A B C D
PHẦN II: MÃ ĐỀ 1213-1217 Câu 1 2 3 4 Đáp án a) Đúng a) Đúng a) Đúng a) Đúng b) Đúng b) Đúng b) Sai b) Đúng c) Đúng c) Đúng c) Sai c) Sai d) Sai d) Sai d) Sai d) Đúng
PHẦN III: MÃ ĐỀ 1213-1217 Câu 1 2 3 4 5 6 Đáp án -2 9,8 54 8 7 0,52
HƯỚNG DẪN GIẢI PHẦN TRẢ LỜI NGẮN MÃ ĐỀ 1211-1215 e  1 
Câu 1. Biết tích phân
1 dx a  . e  
Giá trị của a bằng bao nhiêu?  x  1 Giải e  1  Ta có
1 dx  2  e a  2.    x  1
Câu 2. Trên cửa sổ có dạng hình chữ nhật của
ngôi nhà một doanh nghiệp kinh doanh hải sản,
họa sĩ cần thiết kế logo hình con cá. Logo là
hình phẳng giới hạn bởi hai parabol với các
kích thước được cho trong hình bên (đơn vị trên
mỗi trục tọa độ là dm). Hoạ sĩ cần tính diện tích
của logo để báo giá cho doanh nghiệp đó trước
khi kí hợp đồng. Diện tích của logo bằng x 2
dm . Tìm x (làm tròn kết quả đến hàng đơn vị). Giải
Parabol y f x có dạng   2
f x ax bx c .
Parabol nhận Oy làm trục đối xứng nên b  0. 1
Vì đồ thị đi qua điểm 4;0 và 0;2  a   và c  2. 8  f x 1 2   x  2 8 3
Tương tự g x 2  x  3 . 16 4 4 5
Diện tích của logo là S   f
  x gx 2 2 dx  5 
x dx  28(dm ).   16 5  5 
Câu 3. Một chiếc ô tô đang chạy với vận tốc 15m / s thì nhìn thấy chướng ngại vật trên đường cách đó 40 ,
m người lái xe hãm phanh khẩn cấp. Sau khi hãm phanh, ô tô chuyển động chậm dần đều với
vận tốc v t   3
t 15m / s , trong đó t (giây) là thời gian. Tính quãng đường xe ô tô đi được trong
thời gian t (giây) kể từ lúc đạp phanh. Giải
Khi xe dừng hẳn thì v t  0  3
t 15  0  t  5 .
Quãng đường xe ô tô đi được trong thời gian t (giây) là 5 s   3
t 15dx  37,5m. 0
Câu 4. Khi đặt hệ toạ độ Oxyz vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy
rằng một không gian phủ sóng điện thoại có dạng một hình cầu (S ) (tập hợp những điểm nằm trong
và nằm trên mặt cầu tương ứng). Biết mặt cầu (S ) có phương trình 2 2 2
x y z  2x  4y  6z  5  0.
Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng là bao nhiêu kilômét? Giải
Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng bằng đường kính mặt cầu:
Mặt cầu có bán kính R  3 đường kính mặt cầu 2R  6.
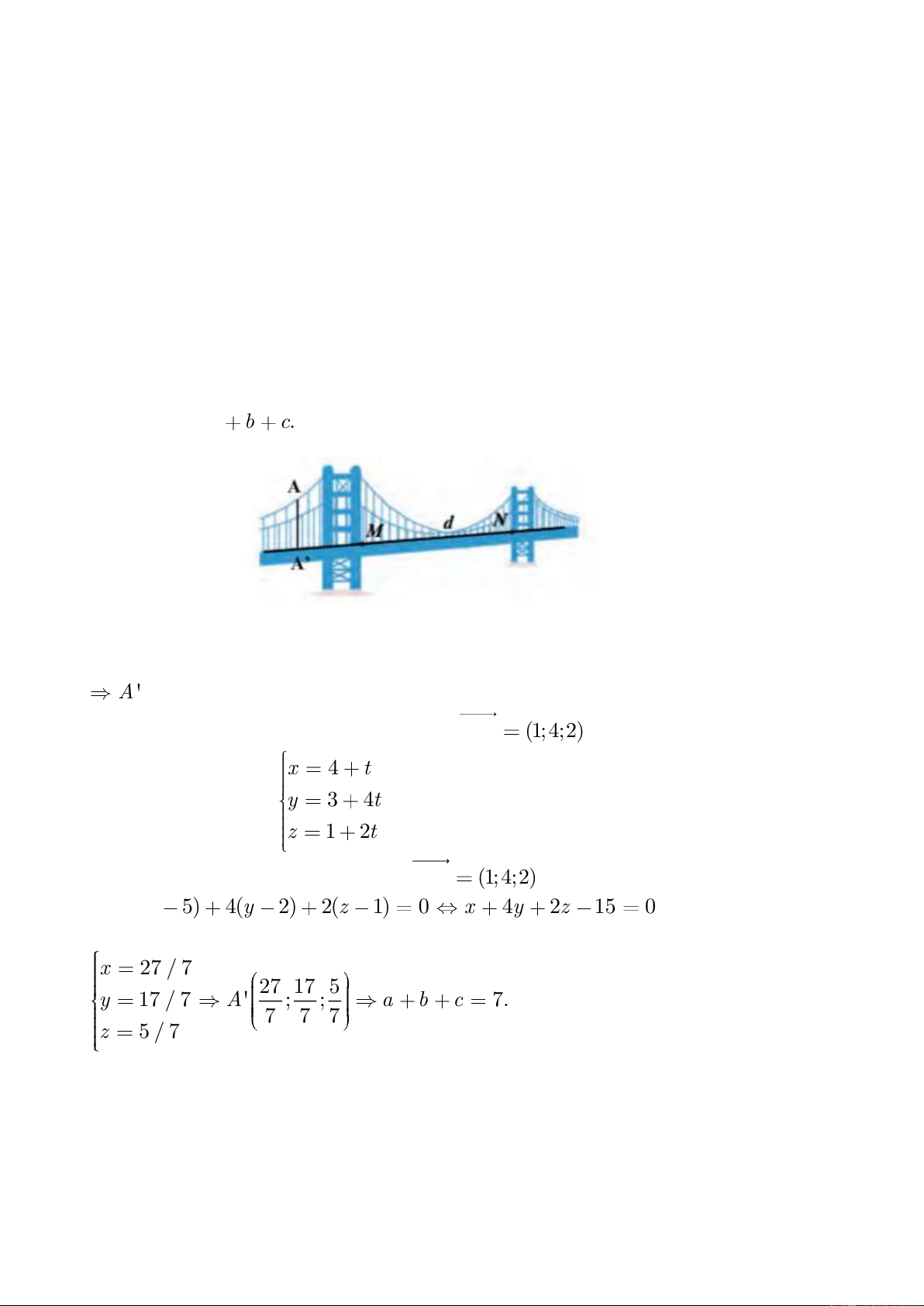
Câu 5. Một mô hình cầu treo được thiết kế trong không gian tọa độ Oxyz như hình vẽ. Làn đường
d đi qua hai điểm M(4;3;1) và N(5;7;3). Từ một điểm (
A 5;2;1) trên cáp treo, người ta cần tìm
tọa độ điểm A'(a; ;
b c) là hình chiếu vuông góc của A trên d để lắp đặt đai chịu lực nâng cho cầu.
Tính giá trị của a b . c Giải.
Gọi (P ) là mặt phẳng đi qua điểm A và vuông góc với MN,
A ' là giao điểm của (P) và d.
Đường thẳng d đi qua điểm M(4; 3;1) và nhận MN
(1; 4;2) làm vectơ chỉ phương nên có x 4 t
phương trình tham số là: y 3 4t z 1 2t
Mặt phẳng (P ) đi qua (
A 5;2;1) và nhận MN
(1; 4;2) làm vectơ pháp tuyến nên có phương trình:1(x 5) 4(y 2) 2(z 1) 0 x 4y 2z 15 0
Tọa độ điểm A ' là nghiệm của hệ phương trình x 27 / 7 27 17 5 y 17 / 7 A' ; ; a b c 7. 7 7 7 z 5 / 7
Câu 6. Có hai hộp chứa bi. Hộp thứ nhất chứa 4 bi đỏ và 5 bi vàng. Hộp thứ hai chứa 6 bi đỏ và 4 bi
vàng. Chọn ngẫu nhiên một hộp và sau đó lấy ngẫu nhiên một bi từ hộp đó. Tính xác suất để lấy được
viên bi đỏ (làm tròn đến hai chữ số thập phân). Giải.
Gọi A là biến cố “chọn hộp thứ nhất” và B là biến cố “chọn hộp thứ hai”.
Gọi C là biến cố “lấy được viên bi đỏ” 1 4 3 Ta có P A P B , P C\A , P C\B . 2 9 5
Xác suất cần tìm là P C P AC BC .
Vì AC, BC là hai biến cố xung khắc nên ta có P AC BC P AC P BC
P A .P C\A P B .P C\B . 1 4 1 3 47 Vậy P C . . 0, 52 2 9 2 5 90
HƯỚNG DẪN GIẢI PHẦN TRẢ LỜI NGẮN MÃ ĐỀ 1213-1217 e  1 
Câu 1. Biết tích phân 1 dx e  . a  
Giá trị của a bằng bao nhiêu?  x  1 Giải e  1  Ta có 1
dx e a a  2  .   x  1
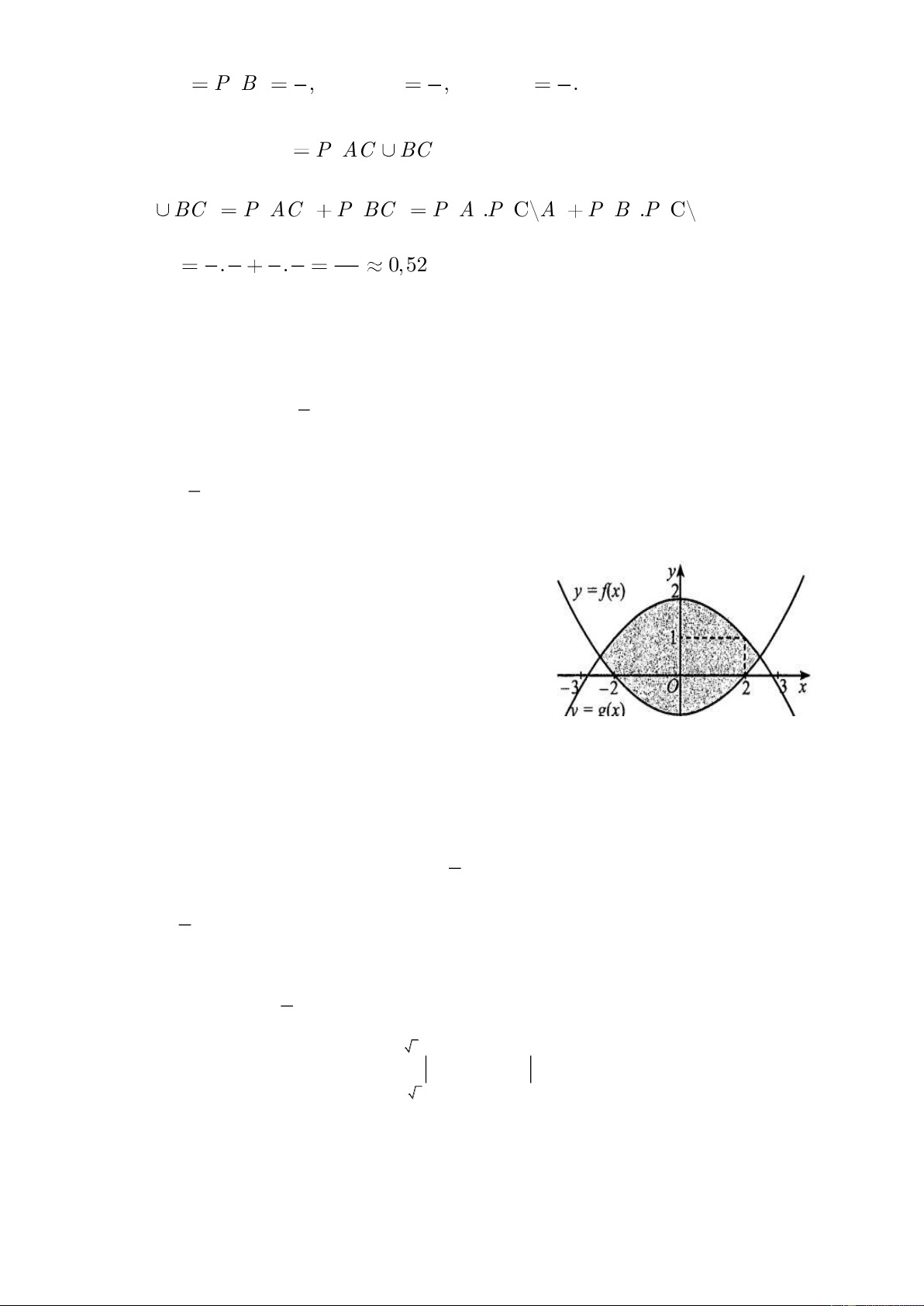
Câu 2. Bạn An nhận thiết kế logo hình con mắt cho một
cơ sở y tế. Logo là hình phẳng giới hạn bởi 2 parabol
y f x và y g x như hình vẽ (đơn vị trên mỗi
trục toạ độ là dm). Bạn An cần tính diện tích của logo
để báo giá cho cơ sở y tế đó trước khi kí hợp đồng. Diện
tích của logo bằng x 2
dm .Tìm x (làm tròn kết quả đến hàng phần mười). Giải
Parabol y f x có dạng   2
f x ax bx c .
Parabol y f x nhận Oy làm trục đối xứng nên b  0. 1
Vì đồ thị đi qua điểm 0;  1
 và 2;0  a  và c  1.  4
f x 1 2  x 1. 4 1
Tương tư ta có g x 2   x  2. 4 6
Khi đó, diện tích S của phần logo là: S g
 x f x 2 dx  9,8dm .  6
Câu 3. Một chiếc ô tô đang chạy với vận tốc 18m / s thì nhìn thấy chướng ngại vật trên đường cách
đó 60m, người lái xe hãm phanh khẩn cấp. Sau khi hãm phanh, ô tô chuyển động chậm dần đều với
vận tốc v t   3
t 18m / s , trong đó t (giây) là thời gian. Tính quãng đường xe ô tô đi được trong
thời gian t (giây) kể từ lúc đạp phanh. Giải

Tài liệu liên quan: