






Preview text:
TRƯỜNG THPT PHAN CHÂU TRINH
HƯỚNG DẪN ÔN TẬP CUỐI KÌ I, NĂM HỌC: 2025 – 2026 TỔ TOÁN
TOÁN 11 (Thời gian làm bài 90 phút)
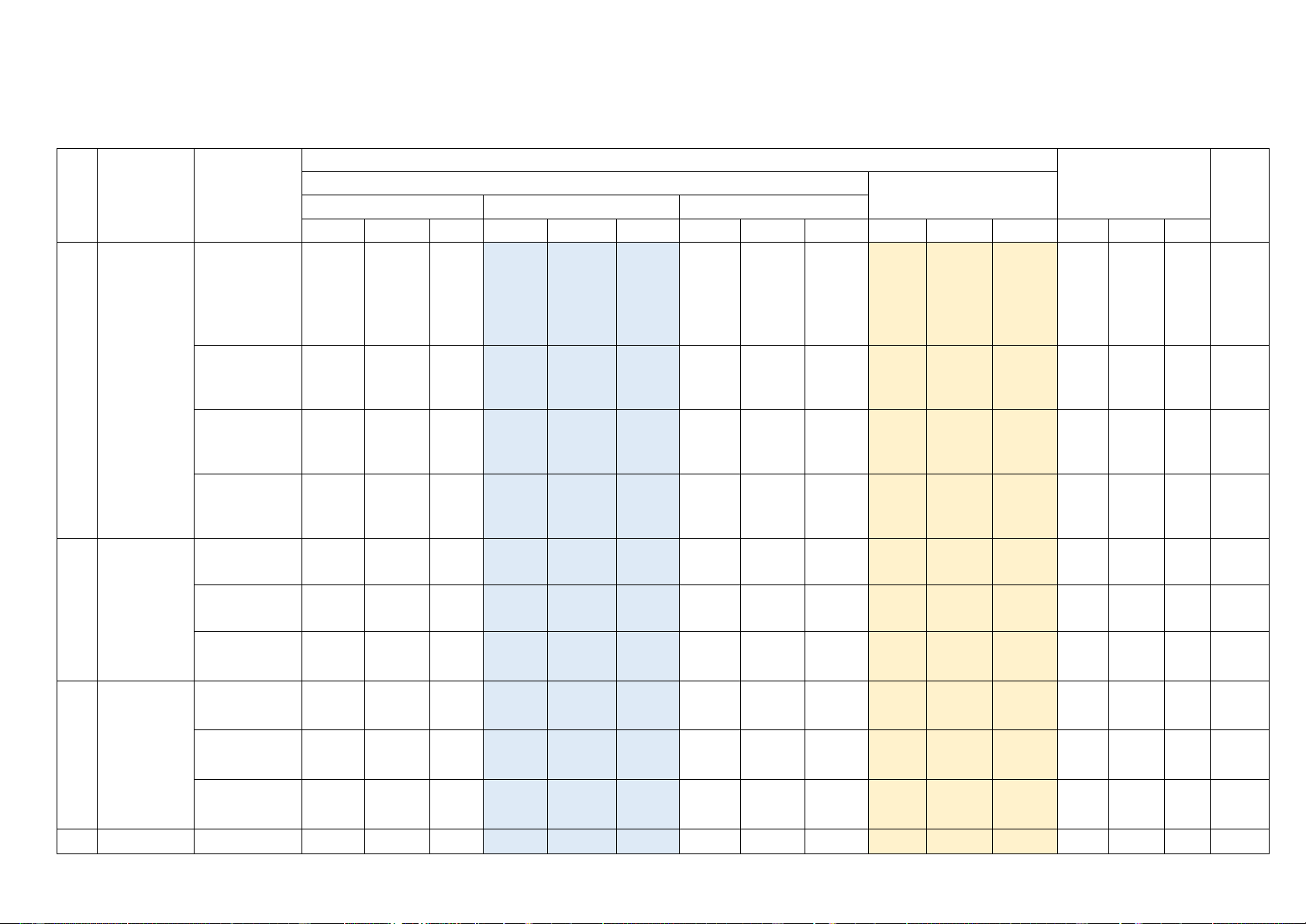
A. MA TRẬN ĐỀ KIỂM TRA Nội
Mức độ đánh giá dung/đơn TNKQ Tổng TT Chương Tự vị luận kiến Nhiều lựa chọn Đúng - Sai Trả lời ngắn Điểm thức Biết Hiểu VD Biết Hiểu VD Biết Hiểu VD Biết Hiểu VD Biết Hiểu VD Góc lượng giác. Giá trị 1 lượng giác 1 0,25 của góc Hàm số lượng giác lượng giác Các phép 1 và phương biến đổi 1 1 1 1 0,75
trình lượng lượng giác giác Hàm số 1 -2 đ lượng giác 1 0,25 và đồ thị Phương trình lượng giác 1 1 1 0,75 cơ bản 1 Dãy số 1 1 0,25 Dãy số. Cấp số 2
cộng và cấp Cấp số cộng 1 1 0,5 số nhân- 1,5đ Cấp số nhân 1 1 1 0,75 1 Giới hạn của 1 1 0,25 Giới hạn. dãy số
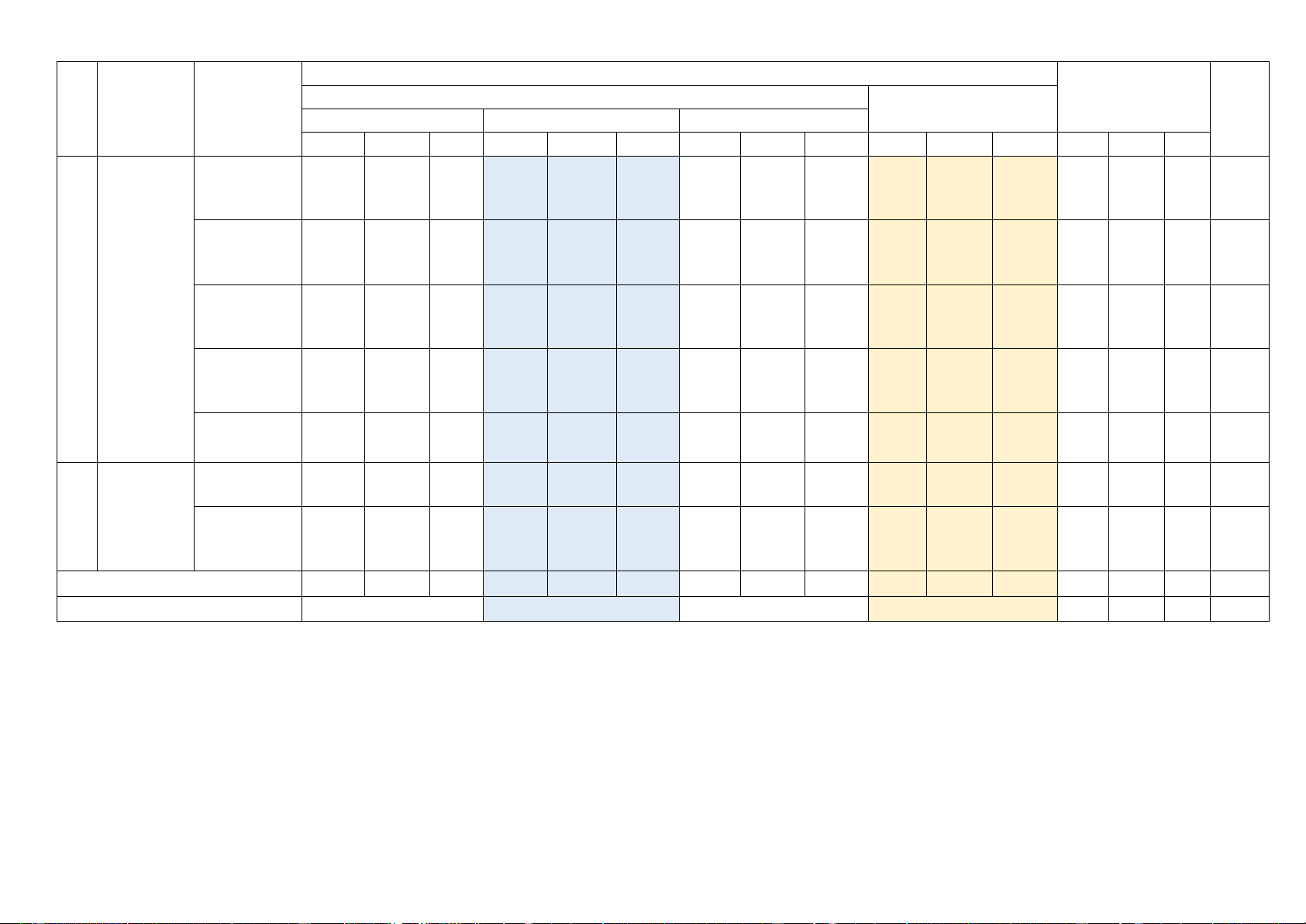
Hàm số liên Giới hạn của 1 2 3 tục hàm số 1 2 0,75 2đ Hàm số liên tục 1 1 1 2 1 1 4 Đường Đường thẳng 1 1 1 1 0,5 Trang 1/14 Nội
Mức độ đánh giá dung/đơn TNKQ Tổng TT Chương Tự vị luận kiến Nhiều lựa chọn Đúng - Sai Trả lời ngắn Điểm thức Biết Hiểu VD Biết Hiểu VD Biết Hiểu VD Biết Hiểu VD Biết Hiểu VD thẳng và và mặt phẳng mặt phẳng trong không trong gian không gian. Hai đường Quan hệ 1 thẳng song 1 0,25 song song song 3,5đ Đường thẳng 1 và mặt phẳng 1 1 1 1 1 0,75 song song Hai mặt 1 1 phẳng song 1 1 1 1 1,5 song Phép chiếu 1 1 1 1 0,5 song song Mẫu SL ghép 1 1 0,25 Thống nhóm kê 5 1 đ Các số đặc trưng đo xu 1 2 1 2 0,75 thế trung tâm Tổng số câu 9 3 5 6 1 1 2 3 2 15 10 3 Tổng số điểm 3 3 1,5 2,5 10 Trang 2/14 B. ĐỀ THAM KHẢO ĐỀ 1
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn (12 câu - 3,0 điểm).Học sinh trả lời từ câu 1 đến
câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án. Câu 1. Biết , A ,
B C là các góc của tam giác .
ABC Khẳng định nào đúng? A. sin C s
inA B.
B. cosC cos A B. C A B A B C C. tan tan . D. cot tan . 2 2 2 2
Câu 2. Trong các phương trình sau, phương trình nào vô nghiệm? 2025 A. tan x .
B. sin x . C. cos x . D. cot x 2 025. 2 2026 1 1 1 1
Câu 3. Cho dãy số u xác định bởi: u n n 1.3 3.5 5.7
(2n 1) (2n
. Số hạng thứ 2021 bằng: 1) 2021 2020 2021 A. 2021. B. . C. . D. . 4043 4043 4041 u
u u 10
Câu 4. Cho cấp số cộng (u ) thỏa 2 3 5 . Khẳng định nào sai? n u u 26 4 6 d
A. d.u 3.
B. d u 1. C. 3.
D. d u 4. 1 1 u 1 1
Câu 5. Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau: Thời gian (phút) [9,5;12,5) [12,5;15,5) [15,5;18,5) [18,5; 21,5) [21,5; 24,5) Số học sinh 3 12 15 24 2
Tìm tứ phân vị thứ ba Q ? 3
A. Q 20 .
B. Q 19 . C. Q 21,5 . D. Q 20,5 . 3 3 3 3
Câu 6. Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:
Thời gian (phút) [9,5;12,5) [12,5;15,5) [15,5;18,5) [18,5; 21,5) [21,5; 24,5) Số học sinh 3 12 15 24 2
Trung vị của mẫu số liệu ghép nhóm này bằng A. 18, 5 . B. 17, 5 . C. 18,1. D. 17 .
Câu 7. Dãy số nào sau đây có giới hạn bằng 0? n n n 6 3 9 A. . B. . C. . D. 2 n 4n . 5 8 3 x 4
Câu 8. Giới hạn lim x 2 x 2 3 bằng x A. 2 . B. . C. 3. D. .
Câu 9. Cho hình chóp S.ABCD có đáy là hình thang ABCD AD / /BC. Gọi I là giao điểm của AB và
DC , M là trung điểm SC . DM cắt SAB tại J . Khẳng định nào sau đây sai?
A. S, I , J thẳng hàng.
B. DM SCI .
C. JM SAB .
D. SI SAB SCD .
Câu 10. Cho hình chóp S.ABCD có đáy là hình bình hành. Qua S kẻ Sx; Sy lần lượt song song với
AB , AD . Gọi O là giao điểm của AC và BD . Khi đó, khẳng định nào dưới đây đúng?
A. Giao tuyến của SAC và SBD là đường thẳng Sx .
B. Giao tuyến của SBD và SAC là đường thẳng Sy .
C. Giao tuyến của SAB và SCD là đường thẳng Sx .
D. Giao tuyến của SAD và SBC là đường thẳng Sx . Trang 3/14
Câu 11. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Nếu hai mặt phẳng ( ) và ( ) song song với nhau thì mọi đường thẳng nằm trong mặt phẳng ( ) đều
song song với mặt phẳng ( ) .
B. Nếu hai mặt phẳng ( ) và ( ) song song với nhau thì mọi đường thẳng nằm trong mặt phẳng ( ) đều
song song với mọi đường thẳng nằm trong mặt phẳng ( ) .
C. Nếu hai đường thẳng song song với nhau lần lượt nằm trong hai mặt phẳng phân biệt mặt phẳng ( ) và
( ) thì ( ) và ( ) song song với nhau.
D. Qua một điểm nằm ngoài mặt phẳng cho trước ta vẽ được một và chỉ một đường thẳng song song với mặt phẳng cho trước đó.
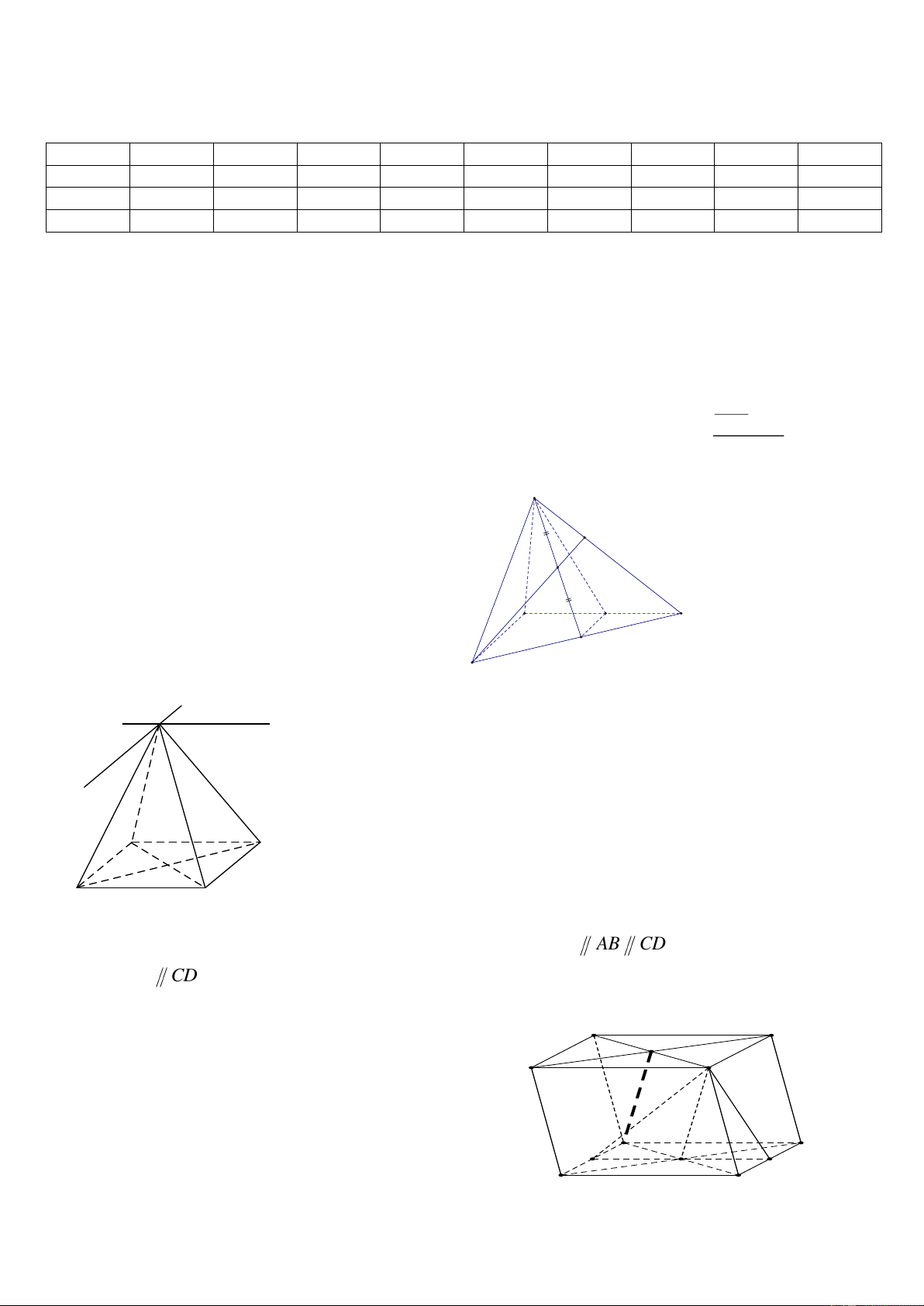
Câu 12. Cho hình hộp ABC . D A B C D
. Gọi O AC BD và O A C B D
. Điểm M , N lần lượt là
trung điểm của AB và .
CD Qua phép chiếu song song theo phương AO lên mặt phẳng ABCD thì hình
chiếu của tam giác C M N là
A. Đoạn thẳng MN .
B. Điểm O .
C. Tam giác CMN . D. Đoạn thẳng BD .
PHẦN II. Câu trắc nghiệm đúng sai. (03 câu – 3,0 điểm)
Học sinh trả lời từ câu 1 đến câu 3. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. 2 Câu 1. Cho hàm số x x f (x) sin cos 1 . 2 2
a) Đồ thị hàm số y f (x) nhận trục Oy làm trục đối xứng.
b) Hàm số y f (x) có chu kỳ tuần hoàn là T 2 .
c) Hàm số y f (x) đồng biến trên 0; . 2
d) Tổng các nghiệm thuộc khoảng 0; 2 của phương trình f (x) cos x là một số lớn hơn .
Câu 2. Trong cuộc tổng điều tra dân số năm 2019 , tỷ lệ tăng dân số mỗi năm của tỉnh A giai đoạn năm
2009 2019 là 0,5% . Do thực hiện các chính sách về dân số nên tỉnh A dự kiến tỷ lệ tăng dân số mỗi năm
trong giai đoạn năm 2020 2030 chỉ còn lại là 0,35% . Theo thống kê, số dân tỉnh A năm 2024 nhiều hơn
năm 2016 là 68270 người. Gọi a (người) là dân số của tỉnh A vào năm 2009 , * a N .
a) Khi đó số dân mỗi năm của tỉnh A từ năm 2009 đến năm 2019 là một cấp số nhân với u ,
a q 1 0,5% 1,005. 1
b) Dân số của tỉnh A năm 2020 là 11 a 11 .1,005 . 1 0,35% . a 1,005 .1,0035 .
c) a 1932500;1932515.
d) Số dân tỉnh A năm 2030 xấp xỉ 2,2 triệu người (làm tròn đến hàng đơn vị của triệu người)
Câu 3. Cho hình hộp ABC . D A B C D
. Trên các cạnh AA , BB , CC lần lượt lấy ba điểm M, N, P sao A M 1 B N 2 C P 1 cho ; ;
MNP cắt cạnh DD tại Q . AA 3 BB 3 CC . Mặt phẳng 2 a) N ,
P DD là hai đường thẳng cắt nhau.
b) MN // CDD'C ' . c) NP // M . Q D Q 1 d) DD . 3
PHẦN III. Câu trắc nghiệm trả lời ngắn. (03 câu – 1,5 điểm).
Học sinh trả lời từ Câu 1 đến Câu 3.
Câu 1. Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày
xuất hiện bệnh nhân đầu tiên biến đổi theo một hàm số thời gian (tính theo ngày) là 2 3
g(t) 45t t (người).
g(t) g(10) Tính lim t 10 t ? 10
Câu 2. Tìm hiểu thời gian sử dụng internet trong tuần trước của một số học sinh thu được kết quả sau: Trang 4/14
Tính thời gian sử dụng internet trung bình trong tuần trước của các bạn học sinh này (làm tròn đến hàng phần chục)?
Câu 3. Cho tứ diện ABCD biết AC 12c , m BD 8c ,
m M trên cạnh BC sao cho BM 3MC . Gọi P
là mặt phẳng qua M , song song với các cạnh AC, BD và cắt A , B A ,
D CD lần lượt tại N , P và Q . Tính
chu vi tứ giác MNPQ (đơn vị cm ).
PHẦN IV. Tự luận (04 câu-2,5 điểm) 3 1 a a
Câu 1. (0,5 điểm) Cho
a 2,sin a . Tính 2 2 P sin 2cos . 2 3 2 2 2
3 x 4x x
Câu 2 (0,5 điểm) Tính lim . x x 1 x 3 2 (x>1)
Câu 3.(0,5 điểm) Cho hàm số x 1 f (x)
. Tìm tất cả các giá trị của m để hàm số f x 1 2 m m (x 1) 4
liên tục tại x 1.
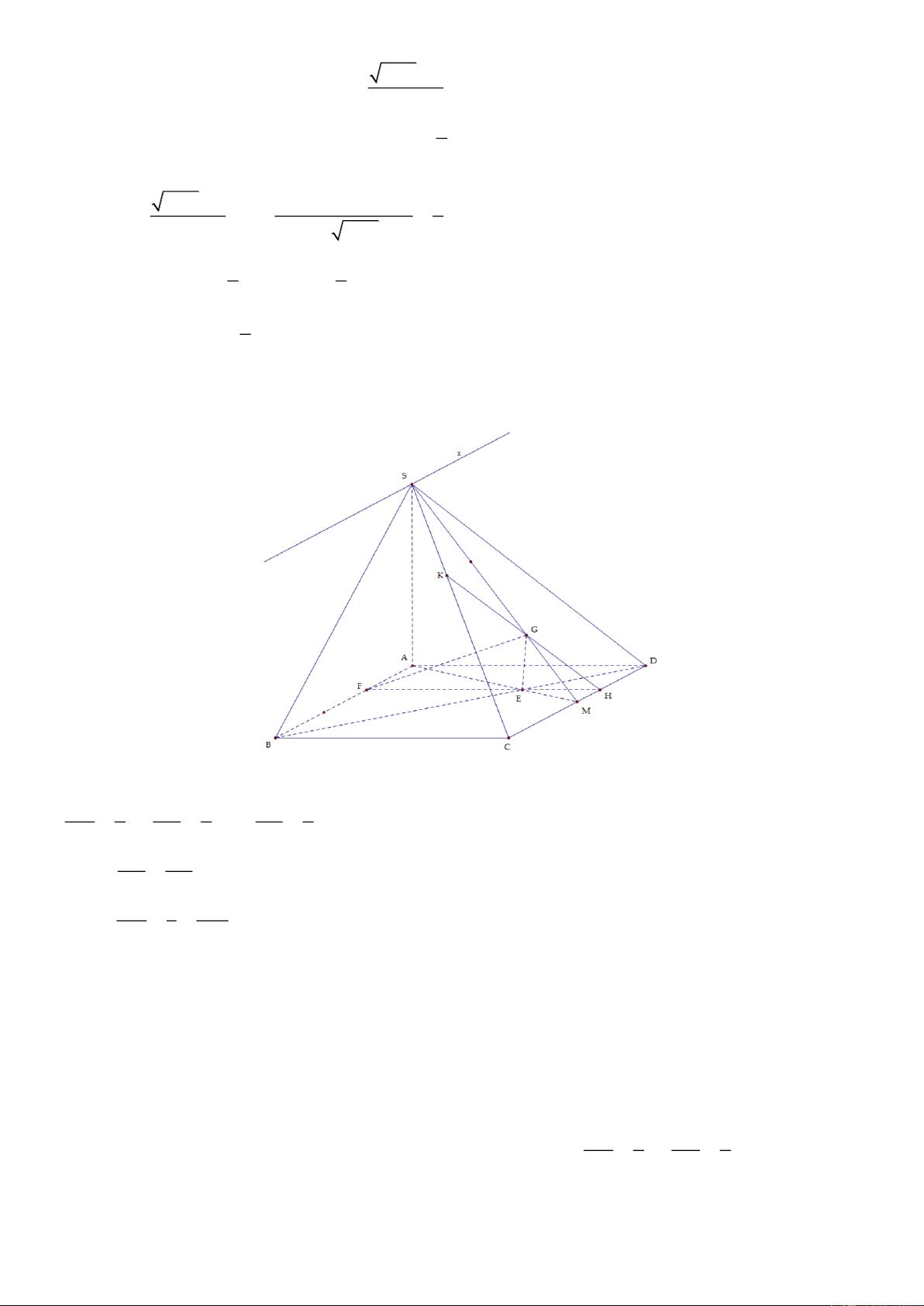
Câu 4 (1,0 điểm) Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành. M là trung điểm CD
. G là trọng tâm tam giác SCD , E là giao điểm của AM và BD , F là điểm trên cạnh AB sao cho AB 3AF .
a) Chứng minh mặt phẳng GEF song song với mặt phẳng SAD. S K
d) Gọi K là giao điểm của SC và mặt phẳng EFG , tính tỉ số . KC
---------HẾT--------- ĐỀ 2
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. (Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án).
Câu 1: Trong tam giác ABC , đẳng thức nào dưới đây luôn đúng?
A. sin A B cosC .
B. cos A sin B . A B C
C. tan A cot B . D. cos sin . 2 2 2
Câu 2: Bánh xe của người đi xe đạp quay được 2 vòng trong 5 giây. Hỏi trong 1 giây, bánh xe quay
được một góc bao nhiêu độ? A. 144 . B. 288. C. 36 . D. 72 .
Câu 3: Tìm giá trị lớn nhất M của hàm số 2
y 4sin x 2 sin(2x ) 4
A. M 2. B. M 2 1. C. M 2 1. D. M 2 2.
Câu 4: Một cấp số nhân có năm số hạng mà hai số hạng đầu tiên là các số dương, tích của số hạng đầu và
số hạng thứ ba bằng 1, tích của số hạng thứ ba và số hạng cuối bằng 1 . Tìm số hạng đầu u và công bội q 16 1
của cấp số nhân đã cho. 1 u 2 u 2 1 u 1 1 u A. 1 2 . B. . 1 C. . 1 D. 1 2 . q q q 2 2 2 q 2 Trang 5/14 1 u
Câu 5: Cho dãy số (u ) được xác định 1 2
. Số hạng tổng quát u của dãy số là số hạng nào dưới n n u u 2 n 1 n đây? 1 1 1 1 A. u 2 n 1 . B. u 2 n 1 . C. u 2 . n D. u 2 . n n 2 n 2 n 2 n 2
Câu 6: Điều tra về số tiền mua đồ dùng học tập trong một tháng của 40 học sinh, ta có mẫu số liệu như
sau (đơn vị: nghìn đồng): Giá trị (x) [10; 15) [15; 20) [20; 25) [25; 30) [30; 35) [35; 40) Tần số 2 5 15 8 9 1
Số trung bình của mẫu số liệu là A. 22, 5. B. 25 . C. 25, 5 . D. 27 .
Câu 7: Giá trị đại diện của nhóm [20; 40) là A. 10. B. 20. C. 30. D. 40.
Câu 8: Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Ba điểm phân biệt.
B. Một điểm và một đường thẳng.
C. Hai đường thẳng song song.
D. Bốn điểm phân biệt.
Câu 9: Tìm mệnh đề đúng trong các mệnh đề sau:
A. Qua một điểm nằm ngoài mặt phẳng cho trước, ta vẽ được một và chỉ một đường thẳng song song với mặt phẳng cho trước đó.
B. Nếu hai mặt phẳng và song song với nhau thì mọi đường thẳng nằm trong mặt phẳng đều
song song với mọi đường thẳng nằm trong mặt phẳng .
C. Nếu hai đường thẳng song song với nhau lần lượt nằm trong hai mặt phẳng phân biệt và thì
và song song với nhau.
D. Nếu hai mặt phẳng và song song với nhau thì mọi đường thẳng nằm trong mặt phẳng đều
song song với mặt phẳng .
Câu 10: Cho hình hộp ABC . D A B C D
có AC cắt BD tại O và A'C ' cắt B'D' B D
tại O ' . Khi đó mặt phẳng AB D
song song với mặt phẳng nào dưới đây? A. A O C.
B. BDA .
C. BDC . D. BCD . u
Câu 11: Cho các dãy số u , v và limu ,
a limv thì lim n bằng n n n n vn A. 1. B. 0. C. . D. . x 2 khi x 2
Câu 12: Cho hàm số f x x 2 2 . Chọn mệnh đề đúng? 4 khi x 2
A. Hàm số liên tục tại x 2.
B. Hàm số gián đoạn tại x 2. C. f (4) 2.
D. lim f x 2 . x2
PHẦN II. Câu trắc nghiệm đúng sai. (Thí sinh trả lời từ câu 1 đến câu 3. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai).
Câu 1: Từ một vị trí ban đầu trong không gian, vệ tinh X chuyển động theo quỹ đạo là một đường tròn
quanh Trái Đất và luôn cách tâm Trái Đất một khoảng bằng 9200 km . Sau 2 giờ thì vệ tinh X hoàn thành
hết một vòng di chuyển.
a) Quãng đường vệ tinh X chuyển động được sau 1 giờ là: 28902,65 ( ) km .
b) Quãng đường vệ tinh X chuyển động được sau 1,5 giờ là: 43353,98 ( ) km .
c) Sau khoảng 5,3 giờ thì X di chuyển được quãng đường 240000 ( ) km . 9
d) Giả sử vệ tinh di chuyển theo chiều dương của đường tròn, sau 4,5 giờ thì vệ tinh vẽ nên một góc rad. 2 Trang 6/14
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M , N lần lượt là trung điểm
của các cạnh AB và CD , P là trung điểm cạnh SA . Khi đó: a) MN / /(SBC). b) MN / /(SA ) D .
c) SB cắt mặt phẳng (MNP)
d) SC cắt mặt phẳng (MNP) x 2 khi x 1
Câu 3: Cho hàm số f (x) . Khi đó: 2
x 1 khi x 1
a) Giới hạn lim f ( ) x 5 x 2
b) Giới hạn lim f (x) 3 . x 1
c) Giới hạn lim f ( ) x 2 x 1
d) Hàm số tồn tại giới hạn khi x 1
PHẦN III. Câu trắc nghiệm trả lời ngắn (1,5 điểm). (Thí sinh trả lời từ câu 1 đến câu 3).
Câu 1: Tần số của ba phím liên tiếp Sol, La, Si trên một cây đàn organ tạo thành một cấp số nhân.
Biết tần số của hai phím Sol và Si lần lượt là 415 Hz và 466 Hz . Tính tần số của phím La (làm tròn đến hàng đơn vị). 2 x 4 khi x 2
Câu 2: Cho hàm số f x x 2
. Tìm số nguyên dương m để hàm số liên tục tại x 2 0 2
m 3m khi x 2
Câu 3: Trong mặt phẳng cho tứ giác ABCD , điểm E . Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong năm điểm , A , B C, , D E ?
PHẦN IV. Tự luận (2,5 điểm) (Thí sinh trả lời từ câu 1 đến câu 4).
Câu 1: Cho dãy số tăng , a ,
b c (c Z ) theo thứ tự lập thành cấp số nhân; đồng thời ,
a b 8, c theo thứ tự lập thành cấp số cộng và ,
a b 8, c 64 theo thứ tự lập thành cấp số nhân. Tính giá trị biểu thức P a b 2 . c
Câu 2: Số cuộc gọi điện thoại một người thực hiện mỗi ngày trong 30 ngày được lựa chọn ngẫu nhiên được thống kê trong bảng sau: Số cuộc gọi [3;5] [6;8] [9;11] [12;14] [15;17] Số ngày 5 13 7 3 2
a) Tìm mốt của mẫu số liệu ghép nhóm trên.
b) Hãy dự đoán xem khả năng người đó thực hiện bao nhiêu cuộc gọi mỗi ngày là cao nhất.
Câu 3: Cho tứ diện ABCD, gọi M là trọng tâm của tam giác ABC và N là hình chiếu song song của điểm EN
M theo phương CD lên mặt phẳng ABD . Tính tỉ số ? ED
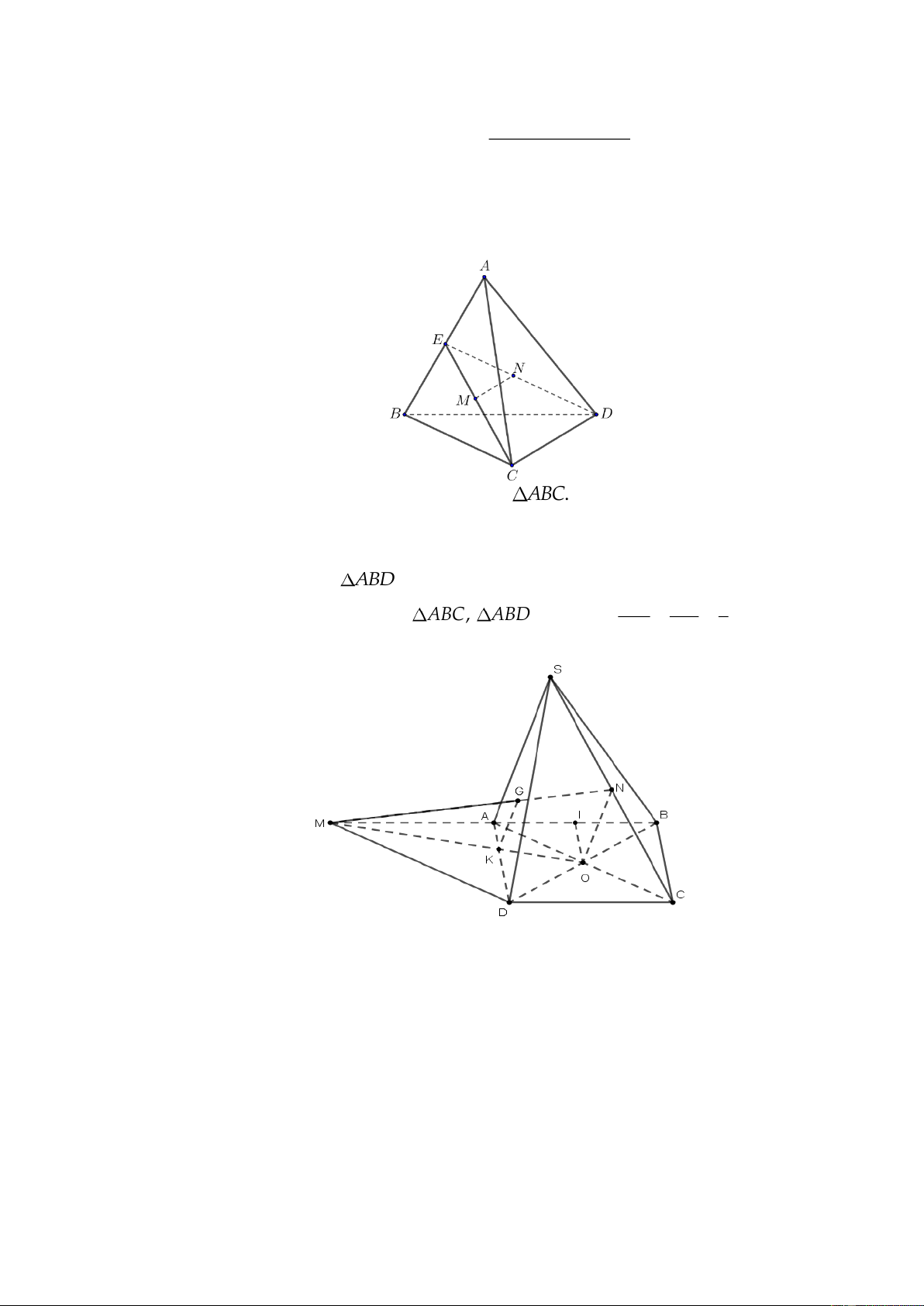
Câu 4: Cho hình chóp S. ABCD có đáy là hình bình hành tâm O. Gọi N là trung điểm của cạnh SC . Lấy
điểm M đối xứng với B qua A , OM cắt AD tại K. Gọi G là giao điểm của đường thẳng MN với mặt phẳng (SAD).
a) Xác định giao tuyến của các mặt phẳng (SAC) và (SBD), (SAB) và (SCD).
b) Chứng minh GK / /ON. c) Tỉ số GM ? GN
-------------HẾT------------- Trang 7/14 ĐÁP ÁN ĐỀ 1
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn (12 câu - 3,0 điểm). Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Câu 9 Câu 10 D B B B A C B D C C Câu 11 Câu 12 A A Câu 4. (
u d) (u 2d) (u 4d) 10 u 3d 10 u 1 1 1 1 1 1
(u 3d) (u 5d) 26 u 4d 13 d 3 1 1 1
Vậy d 3,u 1 . 1 Câu 5. Do x , x đều thuộc nhóm [18,5; 21,5) nên nhóm này chứa Q . Do đó, 42 43 3 3.56 30
p 4;a 18,5;m 24;m m m 31215 30;a a 3 và ta có 4 Q 18,5 3 20. 4 4 1 2 3 5 4 3 24 Câu 9. S
Ta có DM SAB DM SAI J. J . M A B I C D Câu 10. S y x A D O B C
S SABSCD
Ta có: AB SAB; CD SCD Sx SAB SCD với Sx AB CD . AB CD Câu 12. Ta có: O C
AO và O C
AO nên tứ giác O C O A A' D'
là hình bình hành O A C O . O'
Do đó hình chiếu của điểm C qua phép chiếu song song B' C' theo phương O A
lên mặt phẳng ABCD là điểm O.
Mặt khác điểm M và N thuộc mặt phẳng ABCD nên A D
hình chiếu của M và N qua phép chiếu song song theo M N O phương O A
lên mặt phẳng ABCD lần lượt là điểm B C M và N. Trang 8/14
Vậy qua phép chiếu song song theo phương AO lên mặt phẳng ABCD thì hình chiếu của tam giác C M N
là đoạn thẳng MN .
PHẦN II. Câu trắc nghiệm đúng sai. (03 câu – 3,0 điểm) Câu 1: SĐĐĐ Câu 2: ĐSSĐ Câu 3: SĐĐS 2 Câu 1. Cho hàm số x x f (x) sin cos 1 . Ta có các KQ sau: 2 2 2 x x f (x) sin cos 1 sin x
; hàm số là hàm số lẻ, chu kỳ 2, đồng biến trên 0; . 2 2 2
sin x cos x sin
x x k,k Z . Với x 5 0;2
x , x . 2 4 4 4
Câu 2. a) Gọi a (người) là dân số của tỉnh A vào năm 2009 , * a N .
Khi đó số dân mỗi năm của tỉnh A từ năm 2009 đến năm 2019 là một cấp số nhân với u ,
a q 1 0,5% 1,005 . 1 b) Số dân năm 2019 là 7 u . a 1,005 và 10 u . a 1,005 . 8 11
Dân số của tỉnh A năm 2020 là 10 a 10 .1,005 . 1 0,35% . a 1,005 .1,0035. c) Số dân năm 2016 10 u . a 1,005 . 11
Khi đó số dân mỗi năm của tỉnh A từ năm 2020 đến năm 2030 là một cấp số nhân với * 10 * u .
a 1,005 .1,0035, q 1 0,35% 1 ,0035 . 1 Sô dân năm 2024 là * u 10 . a 1,005 .1,0035 4 10 5 .1,0035 . a 1,005 .1,0035 . 5 Theo đề ta có, 10 5 7 . a 1,005 .1,0035 .
a 1,005 68270 a 2000006 (người).
d) Vậy số dân tỉnh A năm 2030 là 10 11
2000000.1,005 .1,0035 2184656 (người) xấp xỉ 2,2 triệu người.
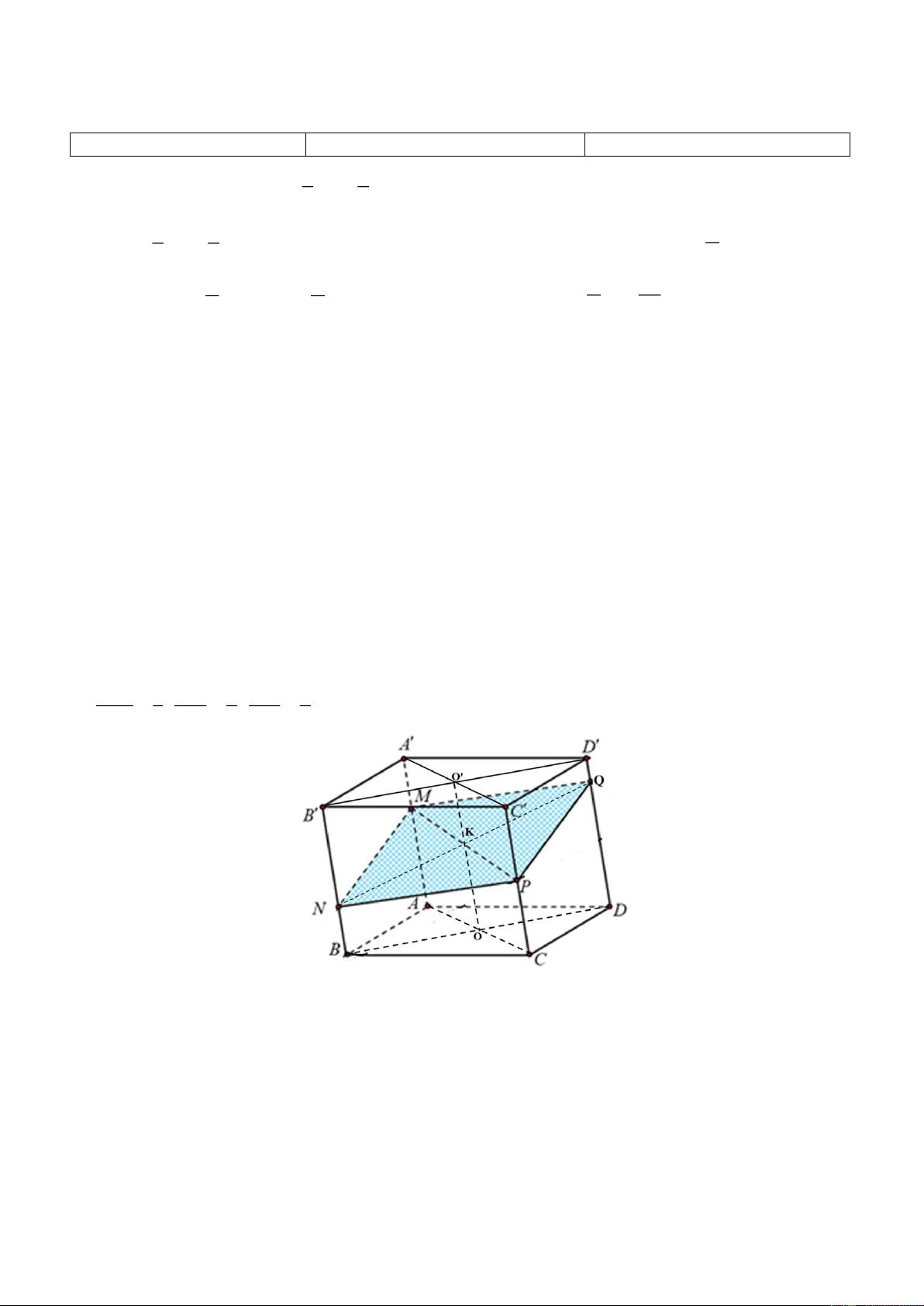
Câu 3. Cho hình hộp ABC . D A B C D
. Trên các cạnh AA , BB , CC lần lượt lấy ba điểm M, N, P sao A M 1 B N 2 C P 1 cho ; ;
MNP cắt cạnh DD tại Q . AA 3 BB 3 CC . Mặt phẳng 2 a) N , P DD chéo nhau.
b) ABB' A' / / CDD'C ', MN ABB' A' MN // CDD'C '. BB C C // AA D D c) Ta có
MNP BB C C
NP NP // MQ. MNP AA D D MQ
d) AABB//CCDD
MNP AA B B
MN MN // PQ . Suy ra MNPQ là hình bình hành. MNP CC D D PQ Trang 9/14
đặt DQ x 0
BNQD là hình thang có O là trung điểm BD, OO'/ /BB '/ /DD' nên KO là đường trung bình có NB DQ OK 2
CPMA là hình thang có O là trung điểm BD, OO'/ /BB'/ /DD' nên KO là đường trung bình có CP AM OK 2 NB DQ CP AM 1 1 2 5 D'Q 1 nên
DD' xDD' DD' DD' x . 2 2 3 2 3 6 DD' 6
PHẦN III. Câu trắc nghiệm trả lời ngắn. (03 câu – 1,5 điểm). Câu 1: 600 Câu 2: 8,4 Câu 3: 22 2 3 2 3
g(t) g(10)
45t t 45 1 0 10 Câu 1. lim lim 600 t 1 0 t 1 0 t 10 t . 10
Câu 2. Trong mỗi khoảng, giá trị đại diện là trung bình cộng của giá trị hai đầu mút .
Thời gian sử dụng internet trung bình trong tuần trước của các bạn học sinh này là:
8 2,5 16 7,5 4 12,5 2 17,5 2 22,5 x 8,4375 8 16 4 2 . 2 Câu 3.
Tứ giác MNPQ là hình bình hành. A 3 1 N P
Chu vi: 2(MN N ) P 2 .12 .8 22
cm. 4 4 12 B 8 D
PHẦN IV. Tự luận (04 câu-2,5 điểm) M 3 1 Q
Câu 1. (0,5 điểm) Cho
a 2,sin a . Tính C 2 3 a a 2 2 P sin 2cos . 2 2 Ta có 3 a a
a 2 cosa 0,sin 0,cos 0. 2 2 2 1 2 2 a 1 cos a 3 2 2 a 1 cos a 3 2 2 2 2
sin a cos a sin ;cos 3 3 2 2 6 2 2 6 a a 1 2 2 2 2 P sin 2cos . 2 2 6 2
3 x 4x x
Câu 2 (0,5 điểm) lim 5 x x . 1 1 2
3 x x 4
3 x 4x x x Ta có lim lim 5 x x 1 x 1 x 1 x Trang 10/14 x 3 2 (x>1)
Câu 3.(0,5 điểm) Cho hàm số x 1 f (x)
. Tìm tất cả các giá trị của m để hàm số f x 1 2 m m (x 1) 4
liên tục tại x 1. x 3 2 x 1 1 lim lim x 1 x 1 x 1
x 1 x32 4 1 1 Ta có 2 2
lim m m m m x 1 4 4 1 2
f (1) m m 4
Để hàm số liên tục tại x 1thì lim f (x) lim f (x) f (1) m 0,m 1 . x 1 x 1
Câu 4 (0,5 điểm) a) Gọi O = BD ∩AC
Có AM và DO là 2 đường trung tuyến của tam giác ACD nên E là trọng tâm tam giác ADC, suy ra DE 2 BE 2 BF 2 , mà DO 3 BD 3 BA 3 BE BF Suy ra
EF / /ADnên EF / /SAD BD BA ME 1 MG Ta có:
EG / /SA nên EG / /SAD MA 3 S M
FEG: EF EG E
Do đó EF / / SAD
FEG / /SAD EG / / SAD
ABCD: EF CD H b)
Nên K SC FEG
SCD : HG SC K
FEG / /SAD HD 1 KS 1 Do
SAD SCD SD HK / / D S Mà HD A F . HC 2 KC 2 FEG
SCD HK Trang 11/14 ĐỀ 2
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Câu 1 2 3 4 5 6 7 8 9 10 11 12 Chọn D A D B B B C C D C B A
PHẦN II. Câu trắc nghiệm đúng sai. (Thí sinh trả lời từ câu 1 đến câu 3. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai). Câu 1 2 3 Đáp án a) Đúng a) Đúng a) Sai b) Đúng b) Đúng b) Đúng c) Sai c) Sai c) Đúng d) Đúng d) Sai d) Sai
PHẦN III. Câu trắc nghiệm trả lời ngắn (1,5 điểm) (Thí sinh trả lời từ câu 1 đến câu 3).
Câu 1: Tần số của ba phím liên tiếp Sol, La, Si trên một cây đàn organ tạo thành một cấp số nhân.
Biết tần số của hai phím Sol và Si lần lượt là 415 Hz và 466 Hz . Tính tần số của phím La (làm tròn đến hàng đơn vị). TL: 440. 2 x 4 khi x 2
Câu 2: Cho hàm số f x x 2
. Tìm số nguyên dương m để hàm số liên tục tại x 2 0 2
m 3m khi x 2 . TL: 1.
Câu 3: Trong mặt phẳng cho tứ giác ABCD , điểm E . Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong năm điểm , A , B C, , D E ? TL: 7
PHẦN IV. Tự luận (2,5 điểm) (Thí sinh trả lời từ câu 1 đến câu 4). Câu 1: 2 ac b 2 ac b (1)
Ta có a c 2(b 8)
a 2b 16c (2) 2
a(c 64) (b 8) 2
ac 64a b 16b 64 (3)
Thay (1) vào (3) ta được: 2 2
b 64a b 16b 64 4a b 4 (4) c 8 a
a 2b 16 c
Kết hợp (2) với (4) ta được: 7 (5) 4a b 4 4c 60 b 7
Thay (5) vào (1) ta được: c 36 2 2
7(c 8)c (4c 60) 9c 424c 3600 0
100 c 36 (c Z) c 9
Với c 36 a 4,b 12 P 4 12 72 64.
Câu 2Do số cuộc gọi là số nguyên nên ta hiệu chỉnh lại như sau: Số cuộc gọi [2,5;5,5) [5,5;8,5) [8,5;11,5) [11,5;14,5) [14,5;17,5) Số ngày 5 13 7 3 2 Trang 12/14
a) Nhóm chứa mốt của mẫu số liệu trên là nhóm [5,5;8,5) .
Do đó u 5,5;n
5;n 13;n 7;u u 8,55,5 3. m m 1 m m 1 m 1 m 13 5
Mốt của mẫu số liệu ghép nhóm là: M 5,5 . O
.3 7,2 13 5 13 7
b) Dựa vào kết quả trên ta có thể dự đoán rằng khả năng người đó thực hiện 7 cuộc gọi mỗi ngày là cao nhất. Câu 3:
Gọi E là trung điểm của AB, M là trọng tâm của AB . C
N là hình chiếu song song của điểm M theo phương CD lên mặt phẳng ABD suy ra MN//CD
Do đó N là trọng tâm của ABD . Vì EM EN 1
M, N lần lượt là trọng tâm của ABC, ABD nên suy ra . EC ED 3 Câu 4:
a) Xác định giao tuyến của các mặt phẳng (SAC) và (SBD), (SAB) và (SCD).
Ta có S, O là hai điểm chung của hai mặt phẳng (SAC) và (SBD)
Nên (SAC) (SB ) D S . O
Ta có ABCD là hình bình hành nên AB / /CD
mà AB (SAB),CD (SC ) D
Nên (SAB) (SCD) d
Với d là đường thẳng đi qua S và song song với AB hoặc . CD
b) Chứng minh GK / /ON. Trang 13/14 O N // SA ON OMN Ta có:
GK//ON//SA SA SAD OMN
SAD GK c) Tỉ số GM 3 GN
Áp dụng định lí Talet cho GK // ON GM KM , ta có: (1) GN KO
Gọi I là trung điểm của AB , vì O là trung điểm của BD nên theo tính chất đường trung bình, OI // AD ,
Vậy theo định lí Talet: KM AM AB 2. (2) KO AI AI
Từ (1) và (2), ta có GM 2 . GN -------------HẾT----------- Trang 14/14




