Đề cương giữa học kỳ 2 Toán 6 năm 2023 – 2024 trường THCS Vĩnh Hưng – Hà Nội

UBND QUẬN HOÀNG MAI
TRỌNG TÂM ÔN TẬP GIỮA HỌC KÌ II – LỚP 6
TRƯỜNG THCS VĨNH HƯNG
Năm học: 2023 - 2024 MÔN TOÁN A. LÝ THUYẾT
I. SỐ HỌC VÀ XÁC SUẤT THỐNG KÊ
1) Thu thập, tổ chức, biểu diễn, phân tích và xử lí dữ liệu. 2) Biểu đồ cột kép.
3) Mô hình xác suất trong một số trò chơi và thí nghiệm đơn giản.
4) Xác suất thực nghiệm trong một số trò chơi và thí nghiệm đơn giản.
5) Phân số với tử và mẫu là số nguyên.
6) So sánh các phân số. Hỗn số dương.
7) Phép cộng, phép trừ phân số. II. HÌNH HỌC
1) Điểm. Đường thẳng.
2) Hai đường thẳng cắt nhau. Hai đường thẳng song song. 3) Đoạn thẳng. 4) Tia. B. BÀI TẬP
Dạng 1. Một số yếu tố thống kê và xác suất
Bài 1. Bạn Cúc muốn điều tra về các môn thể thao được yêu thích của các bạn trong lớp.
Mỗi bạn chỉ nêu một môn thể thao yêu thích nhất và không có ai không tham gia trả lời
phiếu điều tra của bạn Cúc. Em hãy giúp Cúc hoàn thành công việc bằng cách điền vào cột
số 3 trong bảng rồi trả lời các câu hỏi sau: Môn thể thao Kiểm đếm Số bạn chọn Bóng đá Cầu lông Bóng chuyền Đá cầu Bóng bàn Bóng rổ : 5 người : 1 người
a) Nêu đối tượng thống kê và tiêu chí thống kê mà bạn Cúc quan tâm?
b) Môn thể thao nào được các bạn trong lớp của Cúc yêu thích nhất.
c) Có bao nhiêu học sinh trong lớp của bạn Cúc?
d) Có bao nhiêu bạn thích bóng đá hơn bóng chuyền?
Bài 2. Thời gian làm một bài tập Toán (tính bằng phút) của 20 học sinh lớp 6A được ghi lại trong bảng sau: 10 5 8 8 9 7 8 9 14 8 5 7 8 10 9 8 10 7 14 8
a) Hãy gọi tên bảng dữ liệu trên.
b) Hãy lập bảng thống kê tương ứng.
c) Hãy cho biết đối tượng thống kê và tiêu chí thống kê.
Bài 3. Biểu đồ tranh dưới đây cho ta thông tin về loại quả yêu thích của các bạn học sinh khối lớp 6.
Loại quả Số học sinh yêu thích Táo Chuối Dưa hấu Cam Bưởi : 10 học sinh. : 5 học sinh
Hãy đọc biểu đồ trên và trả lời các câu hỏi sau:
a) Loại quả nào được học sinh khối lớp 6 yếu thích nhiều nhất?
b) Loại quả nào được học sinh khối lớp 6 yêu thích ít nhất?
c) Em hãy đọc số lượng học sinh yêu thích đối với từng loại quả.
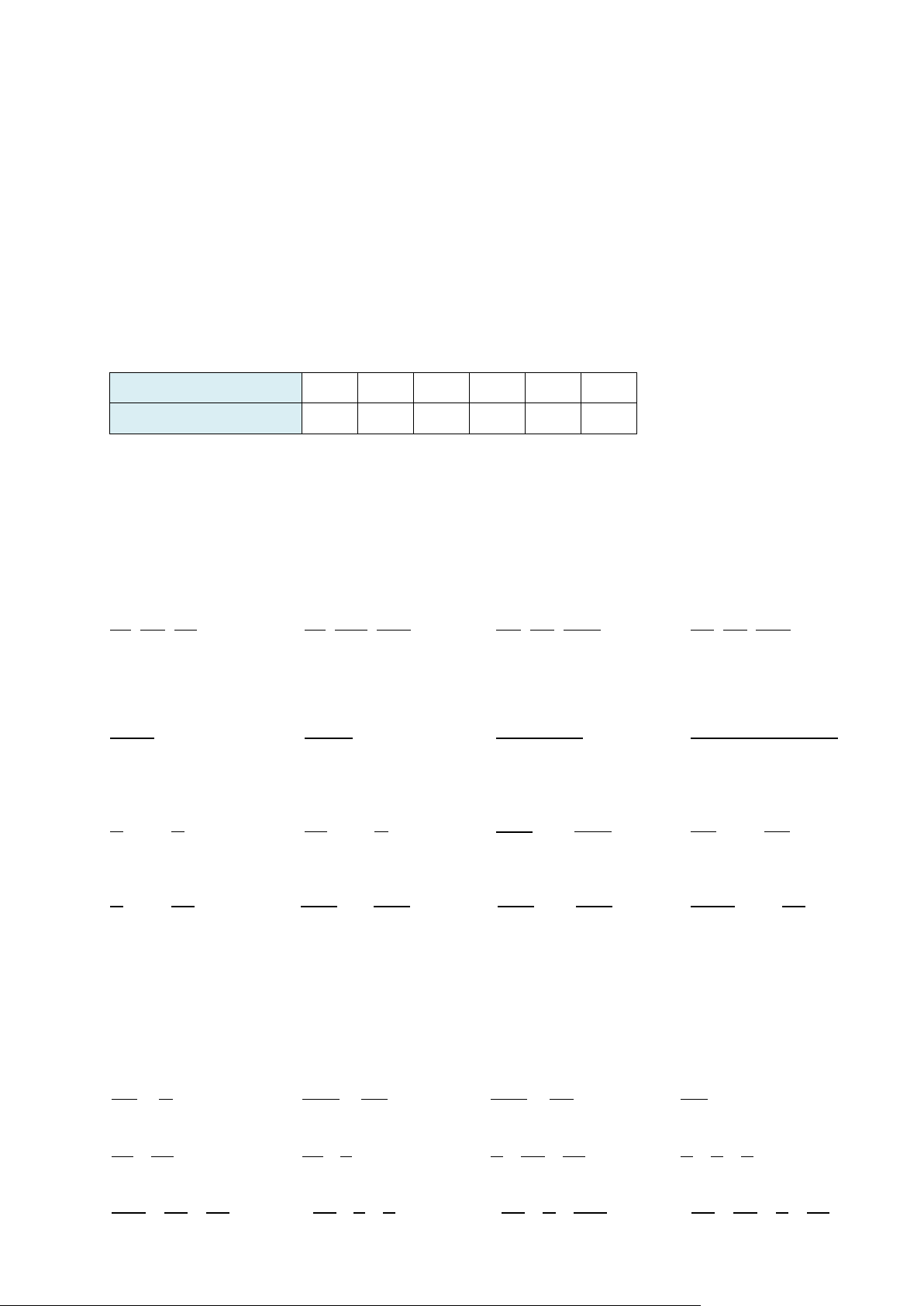
Bài 4. Biểu đồ cột kép sau đây biểu diễn số xe ô tô bán được của mẫu xe X và Y trong các
năm từ 2012 đến 2015 của một Showroom ô tô. 140 120 120 Số xe bán được 100 80 70 70 ếc) 60 60 50 55 50 50 c ( Chi 40 X đượ 20 Y n 0 xe bá 2012 2013 2014 2015 Số
a) Năm nào mẫu xe X bán được nhiều nhất?
b) Những năm nào mẫu xe X bán được nhiều hơn mẫu xe Y? Trong các năm đó mẫu xe X
bán được nhiều hơn mẫu xe Y là bao nhiêu?
c) Tính tổng lượng xe của mẫu xe X bán được trong 4 năm?
d) Tính tổng lượng xe của mẫu xe Y bán được trong 4 năm? Bài 5.
a) Nếu tung một đồng xu 20 lần liên tiếp, có 14 lần xuất hiện mặt N thì xác suất thực nghiệm
xuất hiện mặt N bằng bao nhiêu?
b) Nếu tung một đồng xu 25 lần liên tiếp, có 13 lần xuất hiện mặt S thì xác suất thực nghiệm
xuất hiên mặt S bằng bao nhiêu?
c) Nếu tung một đồng xu 50 lần liên tiếp, có 24 lần xuất hiện mặt N thì xác suất thực nghiệm
xuất hiện mặt S bằng bao nhiêu? Bài 6.
a) Nếu gieo một xúc xắc 15 lần liên tiếp, có 4 lần xuất hiện mặt 1 chấm thì xác suất thực
nghiệm xuất hiện mặt 1 chấm bằng bao nhiêu?
b) Nếu gieo một xúc xắc 9 lần liên tiếp, có 2 lần xuất hiện mặt 6 chấm thì xác suất thực
nghiệm xuất hiện mặt 6 chấm bằng bao nhiêu?
Bài 7. Minh gieo một con xúc xắc 100 lần và ghi lại số chấm xuất hiện ở mỗi lần gieo được kết quả như sau: Số chấm xuất hiện 1 2 3 4 5 6 Số lần 15 20 18 22 10 15
Tính xác suất thực nghiệm của các sự kiện sau:
a) Số chấm xuất hiện là số chẵn.
b) Số chấm xuất hiện lớn hơn 4.
Dạng 2. Quy đồng; rút gọn; so sánh phân số
Bài 1. Quy đồng mẫu các phân số sau: a) 8 7 − 13 − − − − ; ; b) 5 11 49 ; ; c) 7 13 9 ; ; d) 17 5 64 ; ; 15 18 90 12 15 60 − 30 60 40 − 60 18 90
Bài 2. Rút gọn các phân số sau: a) 315 − b) 25.13 c) 6.9 − 2.17 d) 1989.1990 + 3978 540 26.35 63.3 −119 1992.1991 − 3984
Bài 3. So sánh các phân số sau: a) 6 và 3 b) 7 và 7 c) − − 14 − và 60 d) 3 và 1 7 5 10 8 21 72 4 − 4 − e) 7 và 19 f) 18 − và 15 − g) − − 72 và 98 h) 1256 và 18 9 17 31 37 73 99 1257 17
Dạng 3. Thực hiện phép tính
Bài 1. Tính (rút gọn nếu có thể): 1) −3 + 5 2) −12 20 5 + 9 3) − + 4) 36 + 6 8 7 7 −2 3 10 −7 5) 7 8 25 3 1 3 1 3 7 2 + 6) + 7) − − − − 8) − − 12 16 10 6 6 6 6 5 5 5 9) 7 8 2 7 6 2 3 2 12 5 7 4 17 − − 10) − − − 11) − − − − 12) − − − − − −25 25 25 5 5 5 7 7 7 3 3 3 3
Bài 2. Thực hiện phép tính (tính hợp lí nếu có thể): 1) 3 4 − − + 2) 1 2 2 + + 5 15 3 5 15 3) 17 11 − − − 2 4) 8 7 13 + − 18 6 15 18 90 5) 21 18 3 − − + 6) 2 1 3 5 5 + + + + 28 60 5 7 9 7 9 6 − − 7) 3 − 6 − 1 28 − 1 − 1 −     + + + + + 8) 1 5 2 8 3  +  +  + +  31 17 25 31 17 5  4 13  11 13 4 
Dạng 4. Tìm x Bài 1. Tìm x: 1) x 2 x x − = 2) 1 1 − = 3) 3 2 = + 5 3 3 2 5 15 5 3 4) 11 13 85 x + x − + = 5) 3 1 = 6) 12 1 = 8 6 x 15 3 4 2 7) 1 1 1 − − − x 2 = + 8) 1 x − =1 − 9) 5 7 1 − x = + 2 4 3 3 4 6 12 3
Bài 2.Tìm x nguyên biết: 1) 3 x 3 < ≤ 2) 5 x 5 < ≤ 3) 4 x 4 < ≤ 23 21 18 56 52 50 37 34 31
Dạng 5. Bài toán có lời văn
Bài 1. Trong phong trào kế hoạch nhỏ “Thu gom giấy vụn” do Liên đội phát động: Khối 6
thu gom được 1 số giấy vụn, khối 7 thu gom được 11 số giấy vụn, Khối 8 thu gom được 6 30
1 số giấy vụn, Khối 9 góp số giấy vụn còn lại. Khối 9 đã góp bao nhiêu phần số giấy vụn 5của trường?
Bài 2. Ba người cùng làm một công việc. Nếu làm riêng, người thứ nhất mất 6 giờ, người
thứ hai mất 5 giờ và người thứ ba mất 7 giờ mới làm xong công việc đó. Hỏi nếu ba người
cùng làm thì sau 1 giờ làm được bao nhiêu phần công việc?
Bài 3. Người ta mở hai vòi nước cung chảy vào một bể. Vòi thứ nhất mỗi giờ chảy được 1 7
bể. vòi thứ hai mỗi giờ chảy được 1 bể. Nếu mở đồng thời cả hai vòi, mỗi giờ được mấy 5 phần bể?
Bài 4. Ba bạn tham gia một cuộc thi chạy tiếp sức. Bạn thứ nhất cần phải chạy 3 quãng 8
đường, bạn thứ 2 cần phải chạy 1 quãng đường. Hỏi bạn thứ ba cần chạy bao nhiêu phần 4
quãng đường để về đến đích?
Dạng 6. Một số bài toán hình học
Bài 1. Vẽ hình theo cách diễn đạt sau:
a) Cho đường thẳng a, lấy điểm A thuộc đường thẳng a.
b) Vẽ tiếp đường thẳng b đi qua điểm A.
c) Lấy điểm B thuộc đường thẳng b mà không thuộc đường thẳng a.
d) Lấy điểm C vừa thuộc đường thẳng a vừa thuộc đường thẳng b? Khi đó điểm A và điểm
C là hai điểm có vị trí như thế nào?
Bài 2. Vẽ hai tia Ax và Ay đối nhau, lấy điểm C thuộc tia Ax, lấy điểm B thuộc tia Ay.
a) Trong ba điểm A, B, C điểm nào nằm giữa hai điểm còn lại?
b) Trên hình vẽ có bao nhiêu đoạn thẳng? Hãy kể tên các đoạn thẳng đó.
c) Kể tên các tia trùng với tia Ay.
Bài 3. Cho đoạn thẳng AB = 6cm. M thuộc đoạn AB, biết AM = 2cm. Tính MB.
Bài 4. Gọi I là một điểm thuộc đoạn MN. Biết MN = 8cm. So sánh hai đoạn MI và NI, khi
đó điểm I có phải là trung điểm của đoạn thẳng MN không? Vì sao? Biết: a) MI = 4cm b) MI = 5cm.
Dạng 7. Một số bài tập nâng cao
Bài 1. Tính tổng sau: 7 7 7 7 7 a) A = + + + ..... + + . 2.4 4.6 6.8 94.96 96.98 2 2 2 2 2 2 5 5 5 5 5 5 b) B = + + + + + .
1.6 6.11 11.16 16.21 21.26 26.31
Bài 2. Chứng minh rằng các phân số sau là tối giản ( * n ∈ N ): n +1 a) 2n + 3 b) 3n +1 c) 2n + 3 4n + 8 4n +1
Bài 3. Tìm tất cả các số nguyên n sao cho các phân số sau có giá trị là số nguyên: 12 a) 2n + 3 b) 2n + 5 c) 3n −1 7 n − 3
-------------------- HẾT --------------------