







Preview text:
SỞ GD & ĐT THÁI NGUYÊN
ĐỀ CƯƠNG ÔN TẬP GIỮA KÌ 1
TRƯỜNG THPT LƯƠNG NGỌC QUYẾN
NĂM HỌC 2021 – 2022. MÔN: TOÁN 10 I. NỘI DUNG ÔN TẬP 1. Đại số
- Chƣơng 1: Mệnh đề, Tập hợp.
- Chƣơng 2: Hàm số, Hàm số bậc nhất, Hàm số bậc 2. 2. Hình học
- Chƣơng 1: Véc tơ (Véc tơ, Tổng hiệu véc tơ, Tích một số và một véc tơ) II. CÂU HỎI ÔN TẬP A- TRẮC NGHIỆM
CHỦ ĐỀ 1: MỆNH ĐỀ - TẬP HỢP Câu 1. Mệnh đề 2 " x : x 100" khẳng định rằng:
A. Bình phƣơng của một số tự nhiên bằng 100 .
B. Bình phƣơng của một số x bằng 100 .
C. Chỉ có một số tự nhiên mà bình phƣơng của nó bằng 100 .
D. Có ít nhất một số tự nhiên mà bình phƣơng của nó bằng 100 . Câu 2.
Cho hai tập hợp A 1; 4 và B 2;8 . Tìm A \ B . A. 2; 4 . B. 1; 2 . C. 1;8 . D. 4;8 . Câu 3.
Tập hợp A x
| 3 1 2x
1 đƣợc viết lại dƣới dạng đoạn, khoảng, nửa khoảng là A. 0; 2 . B. 1; 2. C. 0; 2 . D. 1;0 . Câu 4.
Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A. Các số nguyên đều chia hết cho 10 .
B. là số vô tỉ. C. Em thấp hơn anh.
D. Hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau. A 1; 2;3;5; 7 B 2; 4;5;6; 8 Câu 5. Cho và
. Tập hợp A \ B là
A. 1; 2;3; 4;5;6;7; 8 . B. 1;3; 7 . C. 4;6; 8 . D. 2; 5 . A 2 ;5 B 0; Câu 6. Cho tập hợp và . Tìm A B . A. 0;5 . B. 2;0 .
C. 2; . D. 5; . Câu 7.
Cho mệnh đề chứa biến P x 2
: 3x 5 x , với x là số thực. Mệnh đề nào dƣới đây đúng? A. P 3 . B. P 4 . C. P 1 . D. P 5 . Câu 8.
Cho hai tập hợp M 3
;3, N 1;8. Xác định M N.
A. M N 3 ;8.
B. M N 1
;3. C. M N 3 ;
1 . D. M N 3 ;8. Câu 9.
Cho hai tập hợp A 1; 5 , B 2; 6 . Xác định A . B
A. A B .
B. A B 5; 6 .
C. A B 1 ; 6 .
D. A B 2; 5 .
Câu 10. Cho hai tập hợp A và B . Hình nào sau đây minh họa A B B . B B A A A. . B. . Trang 1 B A B A C. . D. .
Câu 11. Viết A: “Tập hợp các số thực lớn hơn 1 và nhỏ hơn 4” dƣới dạng chỉ ra tính chất đặc trƣng?
A. A x :1 x 4 .
B. A 2; 3 .
C. A x :1 x 4 .
D. A x :1 x 4 .
Câu 12. Cho hai tập hợp P 2 x | x
4 , Q x |2x
1 . Xác định P \ Q .
A. P \ Q 2 ;1;1; 2 .
B. P \ Q 1; 2 .
C. P \ Q 0 .
D. P \ Q 0;1; 2 .
Câu 13. Chọn mệnh đề sai: A. " x
, x 3 x 3" .
B. “Có một số nguyên chia hết cho 7”.
C. “Nếu a 0 thì a 1 a 2 ”.
D. “Nếu tứ giác ABCD là hình vuông thì hai đƣờng chéo của nó bằng nhau”.
Câu 14. Lớp 10A có 38 học sinh. Có 27 học sinh thích nhảy, 24 học sinh thích hát, 3 học sinh không
thích cả hát và nhảy. Hỏi lớp 10A có bao nhiêu học sinh vừa thích hát vừa thích nhảy? A. 51 học sinh. B. 3 học sinh. C. 16 học sinh. D. 8 học sinh.
Câu 15. Cho mệnh đề chứa biến P x 2
: " x x " . Chọn khẳng định đúng?
A. P 2 . B. P 0 . C. P 2 .
D. P .
Câu 16. Cho tập hợp A 2 ; \ 0 . Xác định C A . A. C A ; 2 0 . B. C A ; 2 0 . C. C A ; 2 \ 0 . D. C A ; 2 \ 0 .
Câu 17. Mệnh đề nào sau đây là mệnh đề đúng? A. x
x x 2 " , 2 2 " . B. 2 " x
, x 2 x 4" . C. 2 " x , x 0". D. 2 " x
, x 2 0".
Câu 18. Biểu diễn tập hợp x |1 x 1 4 trên trục số. A. . B. C. . D. .
Câu 19. Cho tập hợp A x : x
3 . Viết tập hợp bằng cách liệt kê các phần tử.
A. A 0;1; 2 . B. A 2 ; 1 ;0;1;
2 . C. A 2; 1;1; 2 .
D. A 1; 2 .
Câu 20. Phủ định của mệnh đề: “ 2 x
: x 0 ” là: A. 2 x : x 0 . B. 2 x : x 0 . C. 2 x : x 0 . D. 2 x : x 0 .
Câu 21. Mệnh đề nào sau đây là sai? A. 2
n là số lẻ n là số lẻ. B. Phƣơng trình 2
x mx n 0 có hai nghiệm trái dấu khi và chỉ khi n 0 .
C. Hình chữ nhật có hai đƣờng chéo vuông góc là một hình vuông và ngƣợc lại. D. Phƣơng trình 2
x ax b 0 có nghiệm khi và chỉ khi 2
a 4b 0 .
Câu 22. Số phần tử của tập hợp A 1; 2; 2019; 2020; 20 21 là A. 2021. B. 4 . C. 1. D. 5.
Câu 23. Cho mệnh đề “ 3 là số nguyên tố”. Tìm mệnh đề phủ định?
A. “ 3 không phải là số nguyên ”.
B. “ 3 không phải là số nguyên tố”. Trang 2
C. “ 3 là số nguyên ”.
D. “ 3 là số chia hết cho 1 và chính nó”.
A 1; 2; 3; 4; 5 B 0; 2; 4; 6; 8; 10 Câu 24. Cho và
, tập A B là A. 0; 2; 4 . B. 1; 3; 5 . C. 4; 2 .
D. 0;1;2;3;4;5;6;8; 10 .
Câu 25. Kí hiệu A là tập hợp các chữ cái trong câu “TRƢỜNG CHU VĂN AN”, và B là tập hợp các
chữ cái trong câu “CÓ KÍNH VÀ THƠ MỘNG”. Hãy xác định A \ B . A. ; R Ö; AÊ . B. ;
R Ö; U; AÊ .
C. T; Ô; N; ;
G C; H; A . D. ;
R Ö; U; ; AÊ N.
Câu 26. Cho các phát biểu sau đây:
(I): Các em hãy cố gắng học thật tốt!
(II): Số 20 chia hết cho 6 .
(III): Số 5 là số nguyên tố.
(IV): Số x là số chẵn.
Có bao nhiêu phát biểu ở trên là một mệnh đề? A. 1. B. 2. C. 3. D. 4.
Câu 27. Câu nào dƣới đây là mệnh đề A. Mấy giờ rồi?
B. Hôm nay, trời đẹp! C. x 2 10 . D. 11 3.
Câu 28. Trong các tập hợp sau đây, tập nào có đúng một tập hợp con ? A. 1 . B. ;1 . C. . D. .
Câu 29. Cho các phát biểu sau: (I) 5 3 15 . (II) x 2 9 .
(III) a b 5 . (IV) 8 10 5 .
Có bao nhiêu phát biểu là mệnh đề chứa biến ? A. 1. B. 3. C. 2. D. 4.
Câu 30. Cho tập hợp .
A Chọn khẳng định đúng.
A. A A.
B. A A. C. A. D. A . CHỦ ĐỀ 2:
TẬP XÁC ĐỊNH CỦA HÀM SỐ - HÀM SỐ CHẴN – HÀM SỐ LẺ Câu 1.
Cho hai hàm số f x 3
x 3x và 3 2
g x x x . Khi đó
A. f x lẻ, g x không chẵn không lẻ.
B. f x và g x cùng lẻ.
C. f x chẵn, g x lẻ.
D. f x lẻ, g x chẵn. Câu 2. Để hàm số 2
f x ax bx c là hàm số chẵn thì A. b 1. B. b 2 . C. b 1 . D. b 0 . Câu 3.
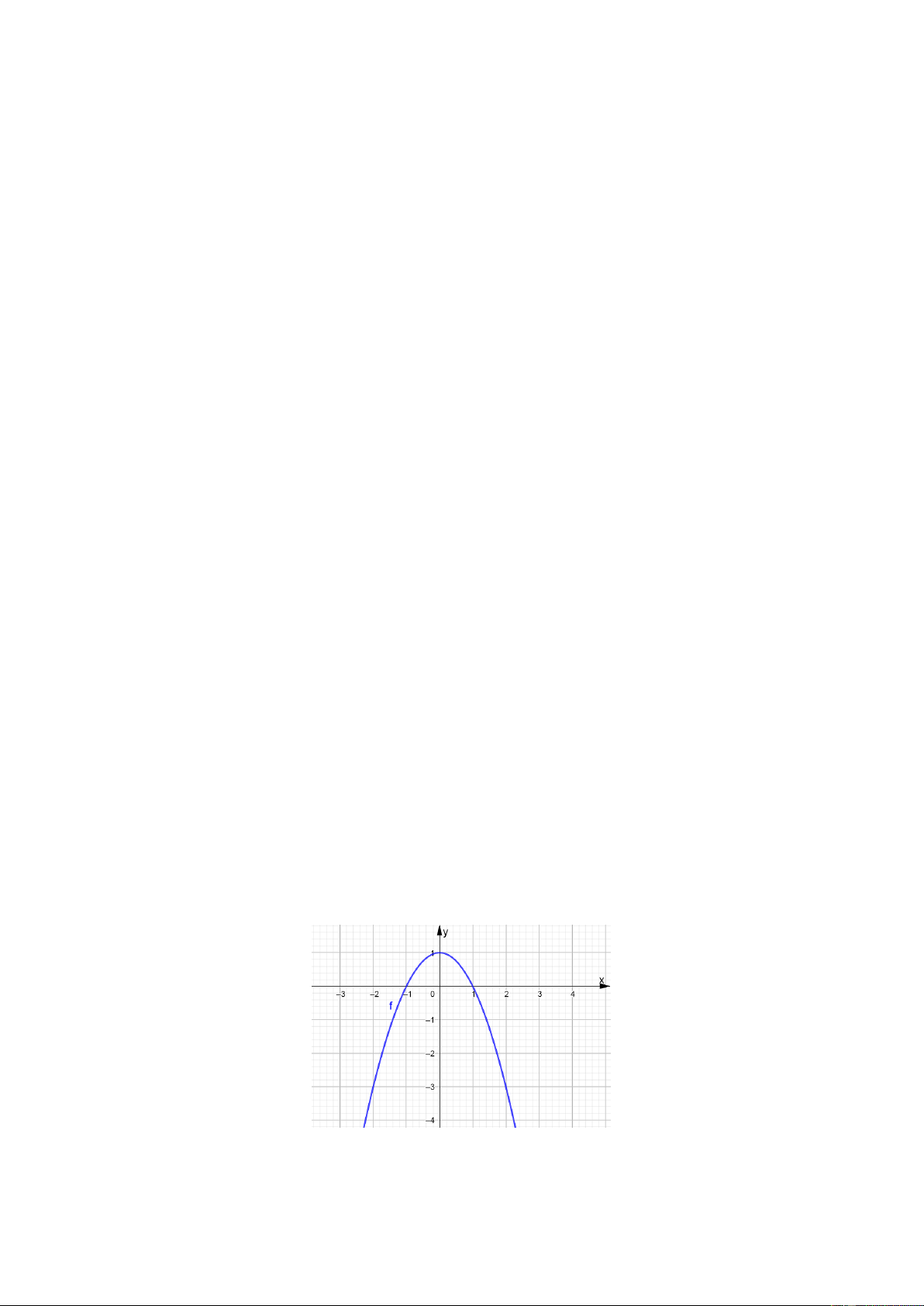
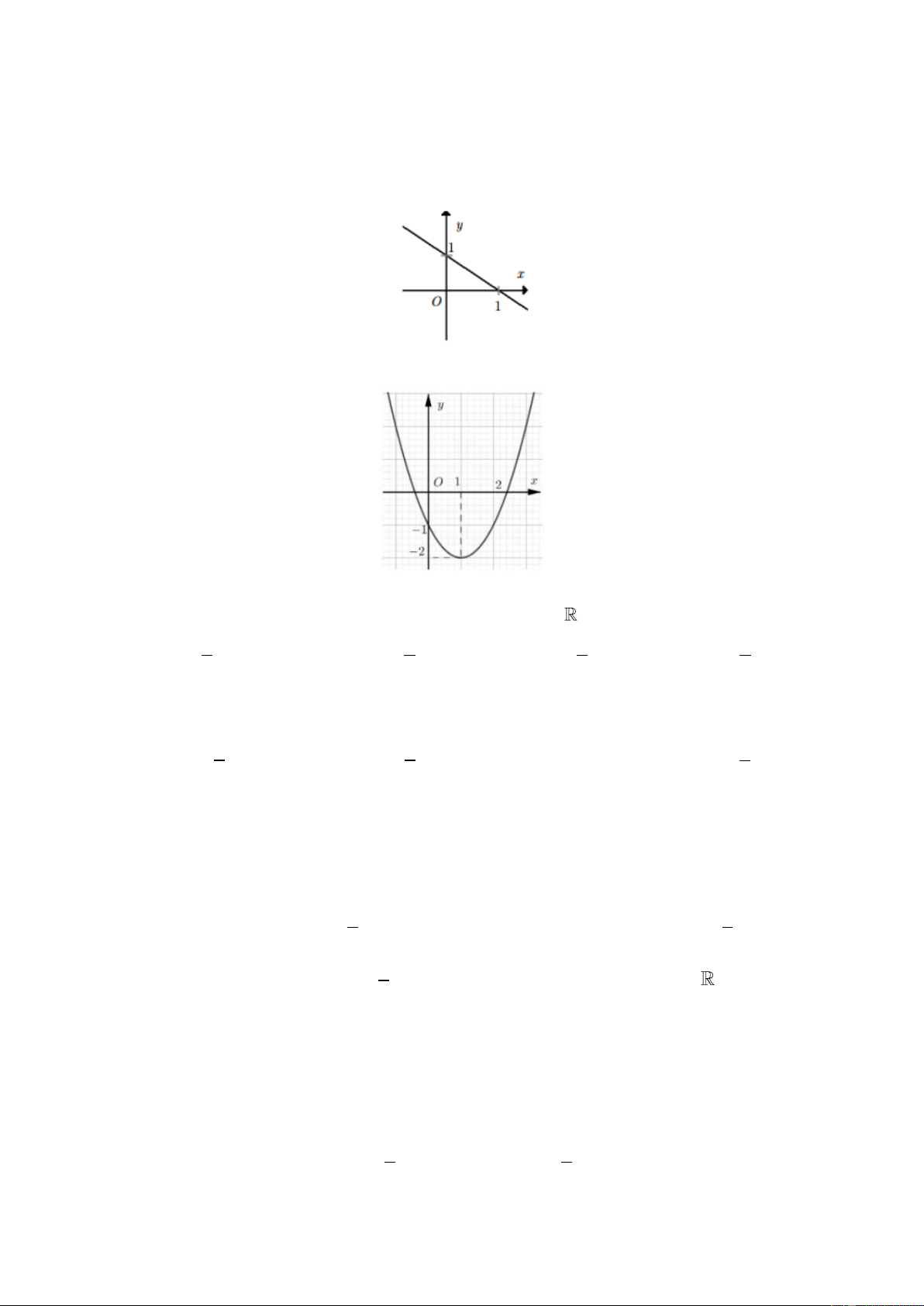
Cho hàm số y f x có đồ thị nhƣ hình vẽ . Khẳng định nào sau đây đúng?
A. Hàm số y f x là hàm số lẻ.
B. Hàm số y f x là hàm số chẵn.
C. Hàm số y f x vừa chẵn, vừa lẻ. Trang 3
D. Hàm số y f x là hàm số không chẵn, không lẻ. Câu 4.
Tập xác định của hàm số f x 1 x 3 là 1 x A. D . B. D ; 1 3; . C. D ; 1 3; .
D. D 1; 3 . 3x 4 Câu 5.
Tập xác định của hàm số y là
x 2 x 4 A. D 4 ; \ 2 . B. D \ 2 . C. D 4 ; \ 2 . D. D . Câu 6. Cho các hàm số 3 4
y 2x 3; y x ; y
x 1; y 3x . Trong đó, có bao nhiêu hàm số là hàm số chẵn? A. 2 . B. 4 . C. 0 . D. 1. Câu 7.
Hàm số nào sau đây là hàm số lẻ?
A. y x 1. B. 2 y x .
C. y x . D. 2 y x 1. Câu 8.
Tập xác định của hàm số f x x 1 là
A. D 1; . B. D .
C. D 1; . D. D \ 1 . Câu 9.
Hàm số nào sau đây có tập xác định D ? 1 1 A. y .
B. y 2x 3 . C. y x . D. y . x x 1
Câu 10. Tập xác định của hàm số y
2 x 7 x là A. D 7 ;2 . B. D 7 ;2 . C. D 7 ;2 . D. D 7 ;2 .
Câu 11. Tập xác định của hàm số y 2x 3 là 3 3 3 A. D ; . B. D ; . C. ; . D. D . 2 2 2
Câu 12. Hàm số nào sau đây là hàm số không chẵn không lẻ? 1
A. y 2x 3 . B. 2 y x . C. 4 y x . D. y . x
Câu 13. Hàm số nào sau đây không phải hàm số chẵn ? A. 4 2
y x x . B. 2 y x . C. 2 y x 1.
D. y 2x 3 .
2x 1 khi x 0
Câu 14. Cho hàm số f x
. Tập xác định của hàm số f x là 2
x 1 khi x 0 A. D .
B. D ;0 . C. D \ 0 .
D. D 0; .
Câu 15. Hàm số nào sau đây có tập xác định D ? 1 1 3x 5 A. y . B. y . C. y x 1 . D. y . 2x 3 2 x 1 4 x 1 khi x 0
Câu 16. Cho hàm số: y x 1
. Tập xác định của hàm số là
x 2 khi x 0 A. D \ 1 . B. D .
C. D 2; . D. D 2 ; \ 1 . Câu 17. Cho hàm số 2
f x x x . Khẳng định nào sau đây đúng.
A. Đồ thị của hàm số f x nhận gốc tọa độ làm tâm đối xứng.
B. f x là hàm số lẻ. Trang 4
C. f x là hàm số chẵn.
D. Đồ thị của hàm số f x nhận trục hoành làm trục đối xứng. 3x 1
Câu 18. Tập xác định D của hàm số y là x 1
A. D 1; . B. D \ 1 .
C. D 1; . D. D .
Câu 19. Cho các hàm số 3
y x, y 2x 1, y
x, y x . Trong đó, có bao nhiêu hàm số là hàm số lẻ? A. 4 . B. 2 . C. 3 . D. 1.
Câu 20. Trong các hàm số sau, hàm số nào không phải là hàm số chẵn? 3
A. y x x. B. y 4 x .
C. y x . D. y 1.
CHỦ ĐỀ 3: HÀM SỐ BẬC NHẤT – HÀM SỐ BẬC HAI Câu 1.
Tìm tất cả các giá trị thực của tham số m để đƣờng thẳng y 2
m 3 x 2m 3 song song
với đƣờng thẳng y x 1. A. m 2 . B. m 1. C. m 2 . D. m 2 . 1 Câu 2. Cho parabol 2
y ax bx 4 có trục đối xứng là đƣờng thẳng x
và đi qua điểm A1;3 . 3
Tổng giá trị a 2b là 1 1 A. . B. 1. C. . D. 1 . 2 2 Câu 3.
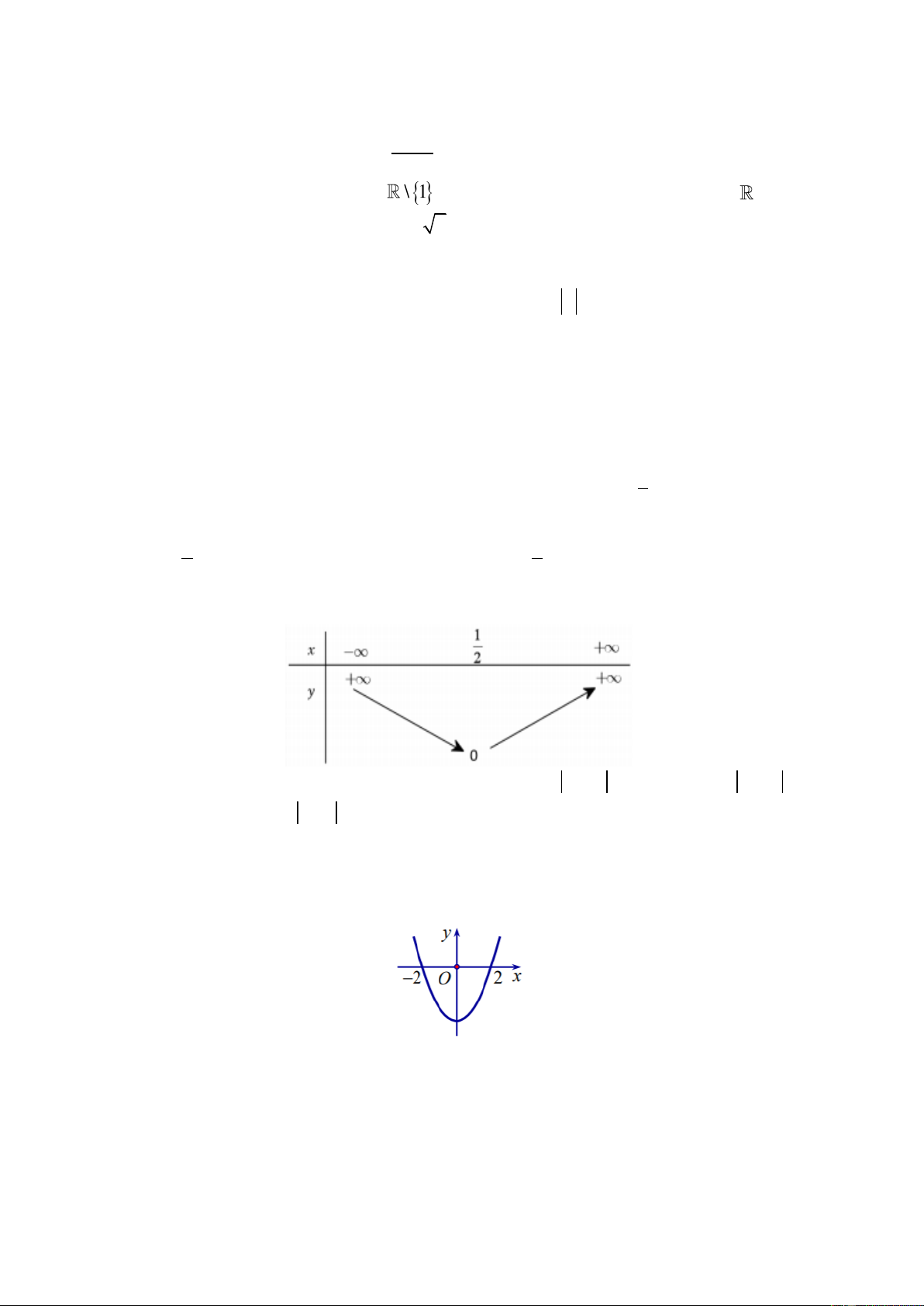
Bảng biến thiên ở dƣới là bảng biến thiên của hàm số nào trong các hàm số đƣợc cho ở bốn
phƣơng án A, B, C, D sau đây?
A. y 2x 1.
B. y 1 2x .
C. y 2x 1 .
D. y 1 2x . Câu 4.
Cho hàm số f x x 2 . Khẳng định nào sau đây là đúng?
A. f x là hàm số vừa chẵn, vừa lẻ.
B. f x là hàm số không chẵn, không lẻ.
C. f x là hàm số chẵn.
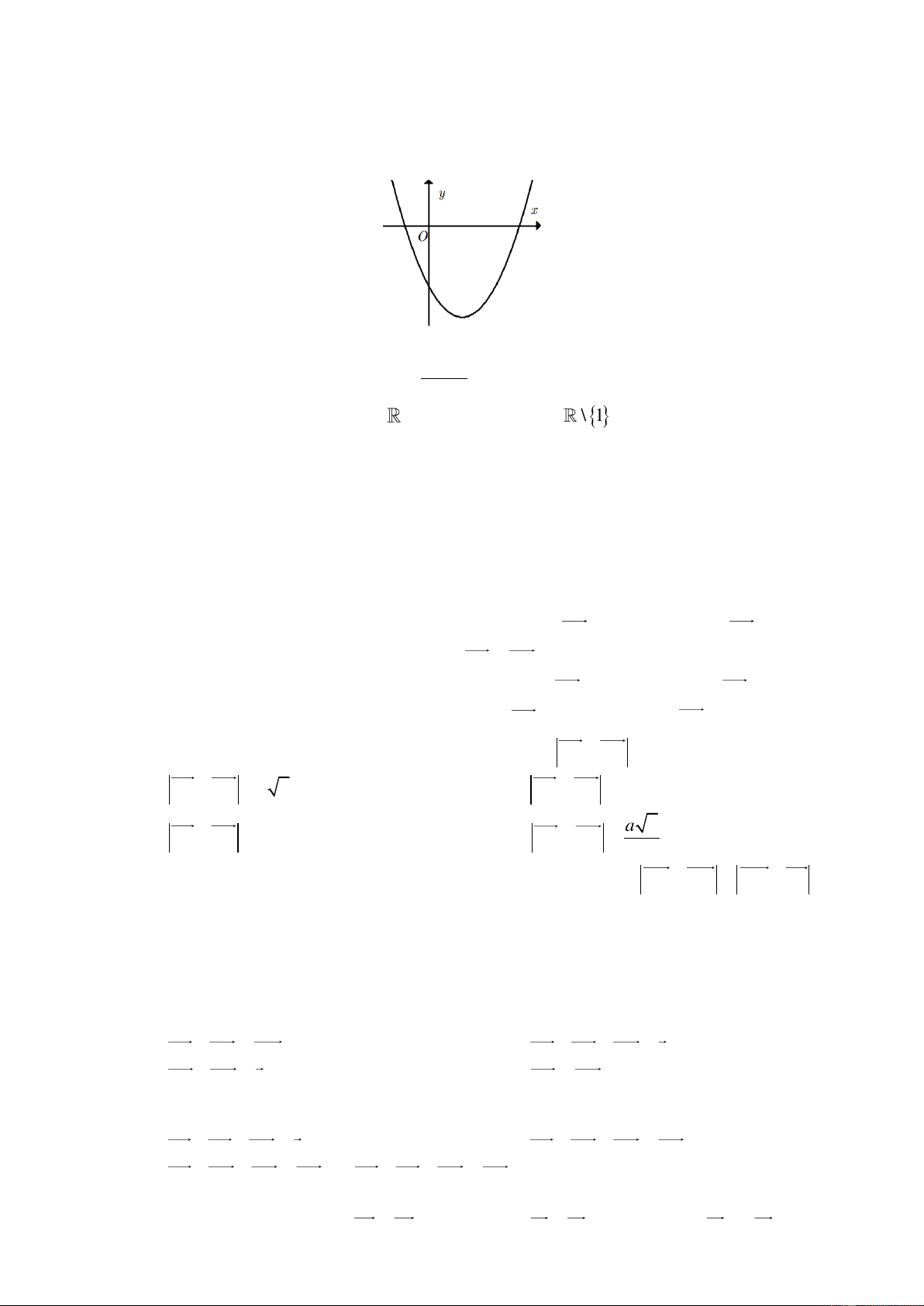
D. f x là hàm số lẻ. Câu 5. Cho parabol 2
y ax bx c a 0 , P có đồ thị nhƣ hình vẽ:
Biết đồ thị P cắt trục Ox tại các điểm lần lƣợt có hoành độ là 2
, 2 . Tập nghiệm của bất
phƣơng trình y 0 là A. 2; 2 . B. 2; 2 . C. ; 2 2; . D. ; 2 2; . Câu 6.
Tìm giá trị của tham số m để hàm số 2
y x 2x 2m 3 có giá trị nhỏ nhất trên đoạn 2;5 bằng 3 . Trang 5 21 5 A. m 3 . B. m . C. m . D. m 1. 2 2 2 Câu 7. Hàm số y x 6x 5 có
A. Giá trị nhỏ nhất khi x 3 .
B. Giá trị nhỏ nhất khi x 3 .
C. Giá trị lớn nhất khi x 3 .
D. Giá trị lớn nhất khi x 3 . Câu 8.
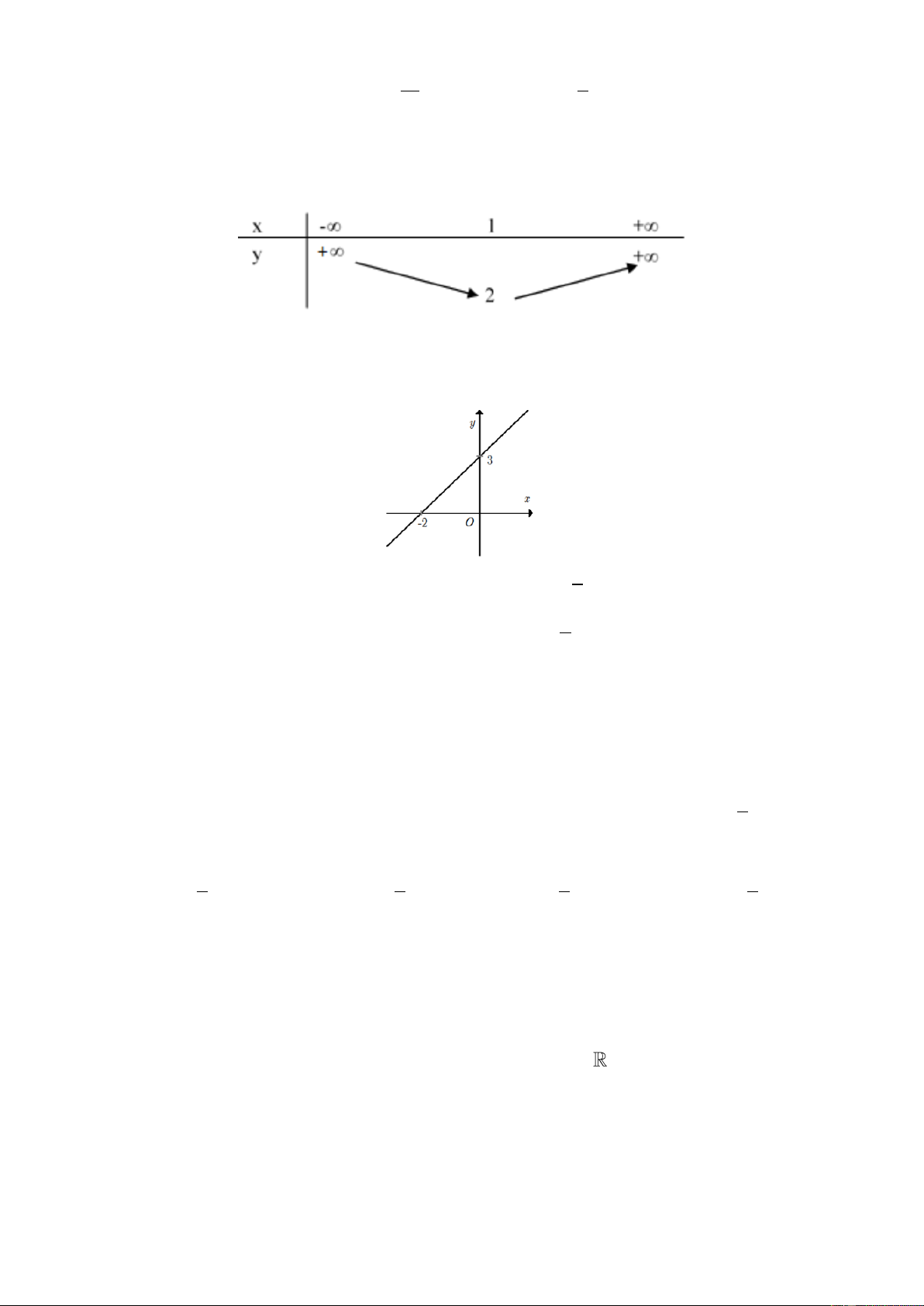
Bảng biến thiên sau là của hàm số nào? A. 2
y 2x 4x 4. B. 2 y 3
x 6x 1. C. 2
y x 2x 1. D. 2
y x 2x 2. Câu 9.
Cho hàm số y ax b có đồ thị là hình bên. Tìm a và b 3 A. a 2 và b 3. B. a và b 2 . 2 3 C. a 3 và b 3. D. a và b 3. 2
Câu 10. Tìm giá trị thực của tham số m để ba đƣờng thẳng y 2 ,
x y x 3, y mx 5 phân biệt và đồng qui. A. m 5 . B. m 5 . C. m 7 . D. m 7 .
Câu 11. Tìm giá trị của tham số m để parapol P 2
: y mx 2x 3 có trục đối xứng đi qua điểm A2;3 . 1 A. m 1. B. m 1 . C. m 2 . D. m . 2
Câu 12. Trục đối xứng của parapol P 2
: y x 5x 7 là đƣờng thẳng có phƣơng trình 5 5 5 5 A. x . B. x . C. x . D. x . 2 2 4 4
Câu 13. Tìm giá trị thực của m để hai đƣờng thẳng d : y
mx 3 và : y x m cắt nhau tại một
điểm nằm trên trục tung. A. m 3 . B. m 0 . C. m 3 . D. m 3 .
Câu 14. Tọa độ giao điểm của đƣờng thẳng 2 d : y
x 4 và parabol y x 7x 12 là
A. 2; 2 và 4;8
B. 2; 6 và 4;8 . C. 2; 2 và 4; 0 .
D. 2; 2 và 4; 0 . Câu 15. Tìm y 2 m m để hàm số
1 x m 4 nghịch biến trên . A. m 1 .
B. Với mọi m . C. m 1. D. m 1 .
Câu 16. Chọn mệnh đề sai trong các mệnh đề sau: A. Hàm số 2
y 2x 4x nghịch biến trên khoảng ;
2 và đồng biến trên khoảng 2; . B. Hàm số 2
y 2x 4x có bề lõm quay lên trên. C. Hàm số 2
y 2x 4x nghịch biến trên khoảng ;1
và đồng biến trên khoảng 1; . Trang 6
D. Trục đối xứng của parabol 2
y 2x 4x là đƣờ ng thẳng x 1.
Câu 17. Cho hàm số y 2x m 1. Tìm giá trị thực của m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 3 . A. m 7 . B. m 7 . C. m 7 . D. m 3 .
Câu 18. Đồ thị hình vẽ là đồ thị của một hàm số trong bốn hàm số đƣợc liệt kê ở bốn phƣơng án A, B,
C, D dƣới đây. Hỏi đó là hàm số nào?
A. y x 2 .
B. y x 1.
C. y x 1.
D. y 2x 1.
Câu 19. Đồ thị bên là của hàm số nào sau đây? A. 2
y 2x 4x 1. B. 2
y x 2x 1. C. 2
y x 2x 3 . D. 2
y x 2x 2 .
Câu 20. Tìm m để hàm số y 2m
1 x m 3 đồng biến trên . 1 1 1 1 A. m . B. m . C. m . D. m . 2 2 2 2
Câu 21. Tìm tất cả các giá trị thực của tham số m để đƣờng thẳng d : y 3m 2 x 7m 1 vuông góc
với đƣờng : y 2x 1. 5 1 5 A. m . B. m . C. m 0 . D. m . 6 2 6
Câu 22. Cho parabol P 2
: y x 3x m và đƣờng thẳng d : y x 2m 1. Tìm giá trị của tham số
m đề d cắt P tại hai điểm phân biệt. A. m 3 . B. m 0 . C. m 3 . D. m 0 .
Câu 23. Cho hàm số f x 4 3x . Khẳng định nào sau đây đúng? 3 4
A. Hàm số đồng biến trên ; .
B. Hàm số nghịch biến trên ; . 4 3 4
C. Hàm số đồng biến trên ; .
D. Hàm số đồng biến trên . 3
Câu 24. Để đồ thị hàm số 2 2
y mx 2mx m 1 m 0 có đỉnh nằm trên đƣờng thẳng y x 2, thì
tham số m nhận giá trị thuộc khoảng nào dƣới đây? A. 2;6 .
B. ; 2 . C. 0; 2 . D. 2; 2 .
Câu 25. Cho hàm số y x 1 có đồ thị là đƣờng thẳng . Đƣờng thẳng tạo với hai trục tọa độ một
tam giác có diện tích S bằng bao nhiêu? 1 3 A. S 2 . B. S . C. S . D. S 1. 2 2
Câu 26. Cho parabol P 2
: y ax bx c có trục đối xứng là đƣờng thẳng x 1. Khi đó 4a 2b bằng Trang 7 A. 1. B. 0 . C. 2 . D. 1 .
Câu 27. Tìm tất cả các giá trị thực của m để đƣờng thẳng 2
y m x 2 cắt đƣờng thẳng y 4x 3 . A. m 2 . B. m 2 . C. m 2 . D. m 2 . Câu 28. Cho hàm số 2
y ax bx c có đồ thị nhƣ hình bên dƣới. Khẳng định nào sau đây đúng?
A. a 0,b 0,c 0 .
B. a 0,b 0,c 0 . C. a 0,b 0,c 0 . D. a 0,b 0, c 0 . 3x 1
Câu 29. Tìm tập xác định D của hàm số y . 2x 2
A. D 1; . B. D . C. D \ 1 .
D. D 1; . Câu 30. Cho hàm số 2
y x 2x 4 có đồ thị P . Tìm mệnh đề sai.
A. P có đỉnh I 1;3 .
C. P có trục đối xứng là đƣờng thẳng x 1.
B. min y 4, x 0; 3 .
D. max y 7, x 0; 3 .
CHỦ ĐỀ 4: VECTƠ – TỔNG VÀ HIỆU CỦA HAI VECTƠ Câu 1. Cho ba điểm , A ,
B C phân biệt. Khi đó :
A. Điều kiện cần để , A ,
B C thẳng hàng là với mọi M , MA cùng phƣơng với AB .
B. Điều kiện cần để , A ,
B C thẳng hàng là AB AC .
C. Điều kiện đủ để , A ,
B C thẳng hàng là với mọi M , MA cùng phƣơng với AB .
D. Điều kiện cần và đủ để , A ,
B C thẳng hàng là AB cùng phƣơng với AC . Câu 2.
Cho tam giác ABC vuông cân tại A có AB a . Tính AB AC .
A. AB AC a 2 .
B. AB AC a . a 2
C. AB AC 2a .
D. AB AC . 2
Câu 3.Cho tam giác ABC . Tập hợp tất cả các điểm M thỏa mãn đẳng thức MB MC BM BA là
A. Trung trực đoạn BC . B. Đƣờng thẳng AB .
C. Đƣờng thẳng qua A và song song với BC . D. Đƣờng tròn tâm A ,bán kính BC . Câu 4.
Cho tam giác ABC . Có bao nhiêu vectơ khác vectơ-không có điểm đầu và điểm cuối là các đỉnh , A , B C ? A. 4 . B. 6 . C. 3 . D. 9 . Câu 5.
Cho tam giác ABC có AB AC và đƣờng cao AH . Đẳng thức nào sau đây đúng?
A. AB AC AH .
B. HA HB HC 0 .
C. HB HC 0 .
D. AB AC . Câu 6.
Cho hình bình hành ABCD . Gọi G là trọng tâm của tam giác ABC . Mệnh đề nào sau đây đúng?
A. GA GB GD 0 .
B. GA GC GD CD .
C. GA GC GD BD . D. GA GB GC CD . Câu 7.
Cho hai điểm A và B phân biệt. Điều kiện để I là trung điểm AB là
A. IA IB .
B. AI BI .
C. IA IB .
D. IA IB . Trang 8 Câu 8.
Cho AB 0 và một điểm C . Có bao nhiêu điểm D thỏa mãn AB CD ? A. Vô số. B. 1. C. 2 . D. 0 . Câu 9.
Cho lục giác đều ABCDEF có tâm O . Đẳng thức nào sau đây sai?
A. OB OE .
B. AB AF .
C. OD BC .
D. AB ED .
Câu 10. Cho hình vuông ABCD . Khẳng định nào sau đây đúng?
A. AB BC .
B. AB CD .
C. AC BD .
D. Hai vecto AB, AC cùng hƣớng.
Câu 11. Cho hình bình hành ABCD . Đẳng thức nào sau đây đúng?
A. AB BC CA.
B. AB BC AC .
C. AB BC BD .
D. AB BC DB .
Câu 12. Cho lục giác đều ABCDEF tâm O . Số các vectơ bằng OC có điểm đầu và điểm cuối là các đỉnh của lục giác là A. 2. B. 3. C. 4. D. 6.
Câu 13. Cho tứ giác ABCD . Gọi M , N , P , Q lần lƣợt là trung điểm của AB , BC , CD , DA . Khẳng định nào sau đây sai ?
A. MQ NP .
B. MN QP .
C. MN AC .
D. QP MN .
Câu 14. Cho a và b là các vectơ khác 0 với a là vectơ đối của b . Khẳng định nào sau đây sai ?
A. Hai vectơ a , b cùng độ dài.
B. Hai vectơ a , b cùng phƣơng.
C. Hai vectơ a , b chung điểm đầu.
D. Hai vectơ a , b ngƣợc hƣớng.
Câu 15. Cho bốn điểm phân biệt A, B,C , D thỏa mãn AB CD . Khẳng định nào sau đây sai?
A. AB CD .
B. ABCD là hình bình hành.
C. AB cùng phƣơng CD .
D. AB cùng hƣớng CD .
Câu 16. Cho ba điểm , A ,
B C phân biệt. Khẳng định nào sau đây đúng?
A. AB AC BC .
B. MP NM NP .
C. CA BA CB .
D. AA BB AB .
Câu 17. Gọi O là giao điểm của hai đƣờng chéo hình bình hành ABCD . Đẳng thức nào sau đây sai?
A. CB DA.
B. AB DC .
C. OA OC .
D. OB DO .
Câu 18. Cho hình thoi ABCD cạnh a và BAD 60 . Đẳng thức nào sau đây đúng?
A. BD a .
B. BC DA .
C. AB AD .
D. BD AC .
Câu 19. Gọi O là tâm của hình bình hành ABCD . Đẳng thức nào sau đây là sai?
A. OA OB CD .
B. OB OC OD OA.
C. AB AD DB .
D. BC BA DC DA .
Câu 20. Mệnh đề nào sau đây là đúng?
A. Có ít nhất hai vectơ cùng phƣơng với mọi vectơ.
B. Có vô số vectơ cùng phƣơng với mọi vectơ.
C. Có duy nhất một vectơ cùng phƣơng với mọi vectơ.
D. Không có vectơ nào cùng phƣơng với mọi vectơ.
Câu 21. Gọi M , N lần lƣợt là trung điểm của cạnh A ,
B AC của tam giác đều ABC . Hỏi cặp vectơ nào sau đây cùng hƣớng?
A. MA và MB .
B. AN và CA .
C. MN và CB .
D. AB và MB .
Câu 22. Cho tam giác ABC với M là trung điểm BC . Mệnh đề nào sau đây đúng?
A. AB AC AM .
B. MA MB AB .
C. MA MB MC .
D. AM MB BA 0 .
Câu 23. Mệnh đề nào sau đây sai? Trang 9
A. 0 cùng phƣơng với mọi vectơ. B. AB 0 .
C. 0 cùng hƣớng với mọi vectơ. D. AA 0 .
Câu 24. Cho tam giác ABC vuông cân đỉnh A , đƣờng cao AH . Khẳng định nào sau đây sai?
A. AH AB AH AC .
B. AH HB AH HC .
C. BC BA HC HA .
D. AH AB AH .
Câu 25. Cho tam giác ABC đều cạnh a . Gọi M là trung điểm BC . Khẳng định nào sau đây đúng? a 3 a 3
A. AM a . B. AM .
C. MB MC . D. AM . 2 2
Câu 26. Tính tổng MN PQ RN NP QR . A. MR . B. MN . C. MP . D. PR .
Câu 27. Với DE (khác vectơ – không) thì độ dài đoạn ED đƣợc gọi là
A. Phƣơng của ED .
B. Hƣớng của ED .
C. Giá của ED .
D. Độ dài của ED .
Câu 28. Cho hình vuông ABCD cạnh a . Tính AB DA .
A. AB DA a 2 .
B. AB DA a .
C. AB DA 0 .
D. AB DA 2a .
Câu 29. Vectơ có điểm đầu là D , điểm cuối là E đƣợc kí hiệu là A. DE . B. ED . C. DE . D. DE .
Câu 30.Cho hình bình hành ABCD có O là giao điểm của hai đƣờng chéo. Hỏi vectơ AO DO bằng
vectơ nào trong các vectơ sau?
A. BC . B. BA . C. DC . D. AC .
CHỦ ĐỀ 6: TÍCH CỦA VECTƠ VỚI MỘT SỐ Câu 1.
Cho điểm B nằm giữa hai điểm A và C , với AB 2a , AC 6a . Mệnh đề nào sau đây đúng? A. BC 2 AB . B. BC 2 BA . C. BC 2 AB .
D. BC 4AB . Câu 2.
Cho G và G ' lần lƣợt là trọng tâm của tam giác ABC và A' B 'C ' . Khi đó tổng
AA' BB ' CC ' bằng A. 3GG ' . B. 4GG ' . C. 2GG ' . D. GG ' . Câu 3.
Khẳng định nào sau đây sai?
A. Nếu AB AC thì AB AC .
B. Nếu 3AB 7AC 0 thì , A , B C thẳng hàng
C. AB CD DC BA .
D. Nếu AB CD thì , A ,
B C, D thẳng hàng. Câu 4.
Khẳng định nào sai?
A. 1.a a .
B. Hai vectơ ka và a cùng hƣớng khi k 0 .
C. Hai vectơ ka và a cùng hƣớng khi k 0 . D. Hai vec tơ a và k.a cùng phƣơng. Câu 5.
Cho tam giác ABC với I là trung điểm của AB . Tìm điểm M thỏa mãn hệ thức
MA MB 2MC 0 .
A. M là trung điểm của IC .
B. M là trung điểm của BC .
C. M là trung điểm của IA .
D. M là điểm trên cạnh IC sao cho IM 2M . C Câu 6.
Cho tam giác ABC và một điểm M tùy ý. Hãy xác định vị trí của điểm D sao cho
CD MA MB 2MC . Trang 10
A. D là đỉnh của hình bình hành ACBD .
B. D là đỉnh của hình bình hành ACBD .
C. D là trọng tâm của tam giác ABC .
D. D là trực tâm của tam giác ABC . Câu 7.
Cho tam giác ABC vuông cân đỉnh A , đƣờng cao AH . Khẳng định nào sau đây sai?
A. BC BA HA HC . B. AH AB AH .
C. AH HB AH HC .
D. AH AB AC AH . 1 Câu 8.
Cho đoạn thẳng AB và M là một điểm trên đoạn AB sao cho MA AB . Trong các khẳng 5
định sau, khẳng định nào sai? 1 1 4 A. MA MB . B. AM AB . C. MB AB . D. MB 4 MA . 4 5 5 Câu 9.
Biết rằng hai vectơ a và b không cùng phƣơng nhƣng hai vectơ 3a 2b và x
1 a 4b cùng
phƣơng. Khi đó giá trị của x bằng A. 7 . B. 7 . C. 5 . D. 6 .
Câu 10. Cho tam giác vuông cân ABC tại A có AB 1. Tính AB AC . 2
A. AB AC 1.
B. AB AC .
C. AB AC 2 .
D. AB AC 2 . 2
Câu 11. Cho tam giác ABC và điểm M thỏa mãn điều kiện MA MB MC 0 . Mệnh đề nào sau đây sai?
A. BA BC BM .
B. MA BC .
C. AM AB AC .
D. Tứ giác MABC là hình bình hành.
Câu 12. Cho I là trung điểm của đoạn thẳng AB . Với điểm M bất kỳ, ta luôn có: 1
A. MA MB MI .
B. MA MB 2MI . C. MA MB 3MI .
D. MA MB MI . 2
Câu 13. Cho tam giác ABC đều cạnh a . Khi đó AB AC bằng a 3
A. AB AC 2a .
B. AB AC a .
C. AB AC a 3 . D. AB AC . 2
Câu 14. Cho hình bình hành ABCD tâm O và điểm M bất kì. Khẳng định nào sau đây đúng?
A. MA MB MC MD 2MO .
B. MA MB MC MD 4MO .
C. MA MB MC MD 3MO .
D. MA MB MC MD MO .
Câu 15. Cho tam giác ABC . Mệnh đề nào sau đây đúng?
A. AB AC BC .
B. AB AC BC .
C. AB AC BC .
D. AB AC 2BC .
Câu 16. Cho G là trọng tâm của tam giác ABC . Trong các mệnh đề sau mệnh đề nào đúng? 2
A. CA CB CG .
B. AB AC
AG . C. BA BC 3BG .
D. AB AC BC 0 . 3
Câu 17. Cho tam giác OAB . Gọi M là điểm trên cạnh AB thỏa mãn MA 2MB . Mệnh đề nào sau đây sai?
A. 3OM OA 2OB .
B. AM 2BM 0. 1 2 C. OM OA OB . D. AM 2 BM . 3 3
Câu 18. Cho ba điểm phân biệt A , B , C . Nếu AB 3
AC thì đẳng thức nào sau đây đúng? A. BC 2 AC .
B. BC 2AC . C. BC 4 AC .
D. BC 4AC .
Câu 19. Cho tam giác ABC vuông tại A có AB 3, AC 4 . Tính CA AB
A. CA AB 2 .
B. CA AB 5 .
C. CA AB 2 13 .
D. CA AB 13 . Trang 11
Câu 20. Cho tam giác ABC có trọng tâm G và I là trung điểm của BC . Mệnh đề nào sau đây đúng ?
A. GA 2GI .
B. GB GC GA . 1
C. GB GC 2GI . D. IG IA . 2
Câu 21. Cho hai vectơ a và b không cùng phƣơng. Hai vectơ nào sau đây cùng phƣơng ? 1 1 A. a b và a b .
B. a b và 2a 2b . 2 2 C. 3
a b và a 3b .
D. a b và a b .
Câu 22. Tìm giá trị của m sao cho a mb , biết rằng a và b ngƣợc hƣớng, a 5 , b 15 . 1 1 A. m . B. m 3 . C. m . D. m 3 . 3 3
Câu 23. Cho hình bình hành ABCD . Tổng các vectơ AB AC AD bằng A. 5AC . B. 2AC . C. AC . D. 3AC .
Câu 24. Cho hình thoi ABCD tâm O , cạnh 2a , góc BAD 60 . Tính độ dài vectơ AB AD .
A. AB AD 2a 3 .
B. AB AD a 3 .
C. AB AD 3a .
D. AB AD 3a 3 .
Câu 25. Cho tam giác ABC và điểm M thỏa mãn MB MC AB . Tìm vị trí điểm M.
A. M là trung điểm BC .
B. M là điểm thứ tƣ của hình bình hành ABCM .
C. M là trung điểm AC .
D. M là trung điểm AB .
Câu 26. Cho tam giác ABC với M , N, P lần lƣợt là trung điểm của BC,C ,
A AB . Khẳng định nào sau đây sai?
A. AP BM CN 0 .
B. PB MC PM .
C. AB BC AC 0 .
D. MN NP PM 0 .
Câu 27. Cho hai vectơ a và b không cùng phƣơng. Hai vectơ nào sau đây là cùng phƣơng? 1 1
A. u 2a b và v 4a b .
B. u 2a 3b và v a b . 2 2 2 3 1 1 C. u
a 3b và v 2a 6b .
D. u 2a b và v a b . 3 2 3 4
Câu 28. Cho hình bình hành ABCD có O là giao điểm của AC và .
BD Khẳng định nào sau đây sai?
A. OA OB OC OD .
B. AB AD AC . 1 C. OA BACB.
D. OB OA DA . 2
Câu 29. Cho tam giác OAB . Gọi M và N lần lƣợt là trung điểm của OA và OB . Mệnh đề nào sau đây sai?
A. OA 2OM .
B. ON BN . 1
C. AB 2.NM . D. NB OB . 2
Câu 30. Cho tam giác ABC có điểm O thỏa mãn OA OB 2OC OA OB . Khẳng định nào sau đây là đúng?
A. Tam giác ABC vuông tại C .
B. Tam giác ABC đều.
C. Tam giác ABC cân tại C .
D. Tam giác ABC cân tại B . B. TỰ LUẬN
Bài 1. Cho tam giác ABC vuông cân tại A có AB = 4. Xác định độ dài của các vectơ: Trang 12
a) AB AC b) BC BA c) BC AC
Bài 2. Cho 3 điểm A, B, C. Tìm vị trí điểm M thoả:
a) AB AC MC 0 b) MA MB MC 0
Bài 3. Cho hình bình hành ABCD. Với M bất kỳ, chứng minh rằng:
a) AC BA AD b) MA MC MB MD
Bài 4. Cho hình thang vuông ABCD có 2 đáy AB=a, CD=2a, đƣờng cao AD=a. Hãy xác định các vectơ
sau và tính độ dài: CD BA , AC BD , DA AB CD , AB EA , AC DA .
Bài 5. Cho tam giác ABC có trọng tâm G. Gọi M, N lần lƣợt là trung điểm của BC và AB.
a. So sánh các cặp vectơ sau:
CG , CN ; GC , GN ; CM , BC ; AB , AN b. Chứng minh:
AB AC 2MB ; MA MB CA ; CB AB 2CN 2 AM
Bài 6. Cho 3 điểm A, B, C. Xác định các điểm M,N thoả mãn: 1 a. BN
AC b. 3MC 2AB 0 2
Bài 7. Cho tam giác ABC. Xác định các điểm M, N, P thoả mãn:
a. 2MA MB MC 0 b. NB NA NC 0 c. PA 2PB 0
Bài 8. Cho HCN ABCD. Gọi I, J lần lƣợt là trung điểm AB,CD. N là trung điểm BC. Chứng minh:
a. DN 2IB NB b. 2JN JA JB 2IN
Bài 9. Cho 2 điểm phân biệt P, Q. Hãy xác định các điểm M, N sao cho: 1
a. 3.MP 2.MQ 0 b.
PN 2. QN 0 3
Bài 10. Cho 4 điểm A, B, C, D. Gọi I, J lần lƣơt là trung điểm BC và CD. Chứng minh:
2.( AB AI JA DA) 3. DB
Bài 11. Cho tam giác ABC có AM là trung tuyến, I là trung điểm AM.
a. Chứng minh: 2.IA IB IC 0
b. Với điểm O bất kỳ, chứng minh: 2.OAOB OC 4OI
Bài 12. Cho tam giác ABC có I là tâm đƣờng tròn nội tiếp và AB , c AC , b BC . a Chứng minh: . a IA . b IB . c IC 0.
Bài 13 Cho tam giác ABC có trung tuyến AM . Gọi I là trung điểm AM và K là điểm thuộc AC sao 1 cho AK
AC . Chứng minh ba điểm B , I , K thẳng hàng. 3
Bài 14 Cho tam giác ABC với H , O , G lần lƣợt là trực tâm, tâm đƣờng tròn ngoại tiếp và trọng tâm
của tam giác. Chứng minh OH 3OG .
Bài 15 :Cho tập hợp A 1;3;5; 7 B 2; 4;5; 7 C 6;5; 7 a) Tìm A ; B A ; B A \ ; B B \ A
b) AC; A C; A \ C
Bài 16. Hãy tìm tập xác định D của các hàm số sau a) b) Trang 13 c) d)
Bài 17: Hãy xác định tính chẵn, lẻ của hàm số cho dƣới đây:
Bài 18: Tính a và b sao cho đồ thị của hàm số y ax b thỏa mãn từng trƣờng hợp sau:
a) Đi qua hai điểm A(2;8) và B(-1;0).
b) Đi qua điểm C(5;3) và song song với đƣờng thẳng d : y= -2x - 8.
c) Đi qua điểm D(3;-2) và vuông góc với đƣờng thẳng d1 : y = 3x - 4.
Bài 19. Chứng minh đƣờng thẳng:
a. y = - x + 3 cắt (P): y = -x2 - 4x +1. b. y=2x-5 tiếp xúc với (P): y = x2 - 4x + 4
Bài 20. Cho hàm số: y = x2 - 2x + m - 1. Tìm giá trị của m để đồ thị hàm số:
a. Không cắt trục Ox.
b. Tiếp xúc với trục Ox. Bài 21:
a) Xác định parabol P 2
: y ax bx 2 , biết rằng P đi qua điểm M 1;5 và có trục đối xứng là đƣờ 1 ng thẳng x . 4 1 11
b) Xác định parabol P 2
: y ax 2x c , biết rằng I ;
là đỉnh của P . 2 2
c) Tìm parabol P : 2
y ax bx c , biết rằng P đi qua ba điểm A1;
1 , B 2;3 , C 1; 3 .
d) Tìm parabol P : 2
y ax bx c , biết rằng hàm số đạt giá trị lớn nhất bằng 5 tại x 2 và có đồ thị
đi qua điểm M 1; 1 . Bài 22: 2
a) Xét sự biến thiên và vẽ đồ thị hàm số: y x 2x . 2
b) Tìm tọa độ giao điểm của đƣờng thẳng d: y x 2 và đồ thị hàm số y x 2x .
c) Tìm m để phƣơng trình 2
x 2x m có 4 nghiệm phân biệt.
---------------------------HẾT------------------- Trang 14




