Đề cương giữa kỳ 2 Toán 10 năm 2022 – 2023 THPT Lương Ngọc Quyến – Thái Nguyên

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề cương hướng dẫn ôn tập kiểm tra giữa học kỳ 2 môn Toán 10 năm học 2022 – 2023 trường THPT Lương Ngọc Quyến, tỉnh Thái Nguyên.

51 26 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 10

Môn: Toán 10

Thông tin:

14 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
1
SỞ GD&ĐT THÁI NGUYÊN
TRƯỜNG THPT LƯƠNG NGỌC QUYẾN
ĐỀ CƯƠNG ÔN TẬP KIỂM TRA GIỮA HỌC KỲ II, MÔN TOÁN, LỚP 10
NĂM HỌC 2022-2023
I. NỘI DUNG ÔN TẬP
1. ĐẠI SỐ: Chương VI: Hàm số và đồ thị
Bài 15. Hàm số
1. Xác định hàm số
2. Tìm tập xác định, tập giá trị của hàm số.
3. Xét tính đồng biến và nghịch biến của hàm số dựa vào đồ thị.
4. Đồ thị hàm số.
Bài 16. Hàm số bậc 2
1. Sự biến thiên của hàm số bậc hai.
2. Tọa độ đỉnh, trục đối xứng của đồ thị hàm số bậc hai.
3. Sự tương giao của đồ thị hàm số bậc hai và đường thẳng.
4. Bảng biến thiên và đồ thị của hàm số bậc hai.
5. Ứng dụng thực tế.
Bài 17. Dấu của tam thức bậc 2
1. Dấu tam thức bậc hai.
2. Bất phương trình bậc hai.
3. Ứng dụng thực tế.
Bài 18. Phương trình quy về phương trình bậc 2
1. Giải phương trình chứa ẩn trong căn bậc hai.
2. Ứng dụng thực tế.
2. HÌNH HỌC VÀ ĐO LƯỜNG
Bài 19. Phương trình đường thẳng
1. Vectơ pháp tuyến, vectơ chỉ phương, hệ số góc của đường thẳng.
2. Viết phương trình tham số, phương trình tổng quát của đường thẳng.
3. Tìm tọa độ điểm thỏa mãn điều kiện cho trước.
Bài 20. Vị trí tương đối của hai đường thẳng. Góc và khoảng cách.
1. Xét vị trí tương đối của hai đường thẳng khi biết phương trình của chúng.
2. Tính góc giữa hai đường thẳng.
3. Tính khoảng cách từ một điểm đến một đường thẳng.
4. Viết phương trình đường thẳng có liên quan đến yếu tố góc và khoảng cách.
Bài 21. Đường tròn trong mặt phẳng tọa độ
1. Xác định tọa độ tâm và bán kính của đường tròn khi biết phương trình.
2. Viết phương trình đường tròn.
3. Viết phương trình tiếp tuyến của đường tròn tại 1 điểm.
II. CÂU HỎI TRẮC NGHIỆM VÀ TỰ LUẬN
A. TRẮC NGHIỆM
Bài 15. Hàm số
Câu 1. Xét hai đại lượng x, y phụ thuộc vào nhau theo các hệ thức dưới đây. Những trường hợp nào thì y
không là hàm số của x?
A.
2
2 1
y x
. B.
2
2 3 4
y x x
. C.
4 2
y x
. D.
2 3
y x
.
Câu 2. Cho hàm số được cho bởi bảng sau
Gi
ờ
đo
nhiệt độ
1
4
7
10
13
16
19
22
Nhi
ệ
t đ
ộ
(
0
C)
28
27
28
32
31
29
28
27
Bảng 1. Dự báo thời tiết ngày 01/05/ 2022 tại Hà Nội
Tập xác định của hàm số là
A.
27;28;29;31;32
. B.
1;4;7;10;13;16;19;22
.
C.
1;4;7;10;13;16;19;22;27;28;29;31;32
. D.
*
.
Câu 3. Tập xác định của hàm số
4 2
2018 2019y x x
là
A.
1;
. B.
;0
. C.
0;
. D.
;
.
Câu 4. Trong các hàm số sau, hàm số nào có tập xác định là
?
A.
3 2
3 1y x x . B.
2
2x
y
x
. C.
2
2 3x
y
x
. D.
2
1
x
y
x
Câu 5. Tập xác định
D
của hàm số
5 2
1
x
y
x
là
A.
D
. B.
1;D
. C.
1;D
. D.
\ 1D R
.
Câu 6. Tập xác định của hàm số
2
3
5 6
x
y
x x
là
A.
\ 1;6D
B.
\ 1; 6D
C.
1;6D
D.
1; 6D
Câu 7. Tập xác định
D
của hàm số
3 1y x
là
A.
0;D
. B.
0;D
. C.
1
;
3
D
. D.
1
;
3
D
.
Câu 8 Tập xác định của hàm số
4 2
y x x
là
A.
2;4D
B.
2;4D
C.
2;4D
D.
;2 4;D  
Câu 9. Tập xác định của hàm số
3 4
1
x
y
x
là
A.
\ 1
. B.
. C.
1;
. D.
1;
.
Câu 10. Cho hàm số
y f x
có tập xác định là
5;5
và đồ thị của nó được biểu diễn bởi hình dưới
đây.
Tập giá trị của hàm số là
A.
5;5
. B.
. C.
2;2
. D.
0;2
.
Câu 11. Hàm số
1
y
x
có
A. Tập xác định là
0
\
và tập giá trị là
. B. Tập xác định và tập giá trị cùng là
0
\
.
C. Tập xác định là
và tập giá trị là
0
\
. D. Tập xác định và tập giá trị cùng là
.
Câu 12. Cho hàm số
2
3 1; 1
2 ; 1
x x khi x
f x
x khi x
. Tính
2f
.
A.
1
. B.
4
. C.
7
. D.
0
.
Câu 13. Chọn khẳng định đúng.
A. Hàm số
( )y f x
được gọi là nghịch biến trên
K
nếu
1 2 1 2 1 2
; , ( ) ( )x x K x x f x f x
.
B. Hàm số
( )y f x
được gọi là đồng biến trên
K
nếu
1 2 1 2 1 2
; , ( ) ( )x x K x x f x f x .
C. Hàm số
( )y f x
được gọi là đồng biến trên
K
nếu
1 2 1 2 1 2
; , ( ) ( )x x K x x f x f x .
D. Hàm số
( )y f x
được gọi là đồng biến trên
K
nếu
1 2 1 2 1 2
; , ( ) ( )x x K x x f x f x .
Câu 14. Cho hàm số có đồ thị như hình vẽ.
Chọn đáp án sai.
A. Hàm số nghịch biến trên khoảng
; 1
. B. Hàm số đồng biến trên khoảng
1;
.
C. Hàm số nghịch biến trên khoảng
1;1
. D. Hàm số đồng biến trên khoảng
1;0
.
Câu 15. Cho hàm số có đồ thị như hình bên dưới.
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng
0;3
. B. Hàm số đồng biến trên khoảng
;1
.
C. Hàm số nghịch biến trên khoảng
0; 2
. D. Hàm số đồng biến trên khoảng
;3
.
Câu 16. Cho hàm số
y f x
có bảng biến thiên như sau
Đặt
5
h x x f x
. Khẳng định nào dưới đây là đúng?
A.
3 1 2h h h
B.
1 2 3h h h
C.
2 1 3h h h
D.
3 2 1h h h
Câu 17. Điểm sau đây không thuộc đồ thị hàm số
2
4 4x x
y
x
?
A.
2;0A
. B.
1
3;
3
B
. C.
1; 1C
. D.
1; 3D
.
Câu 18. Cho hàm số
2
5
x a
f x
x
có
4 13f
. Khi đó giá trị của
a
là
A.
11a
. B.
21a
. C.
3a
. D.
3a
.
Câu 19. Đường cong trong hình nào dưới đây không phải là đồ thị của một hàm số
y f x
?
A. B. C. D.
Câu 20. Cho hàm số
3 2
3 3y x x . Có bao nhiêu điểm trên đồ thị hàm số có tung độ bằng 1?
A. 0 B. 1 C. 2 D. 3
Câu 21. Cho hàm số
2
2 2 3
khi 2
1
1 khi 2
x
x
f x
x
x x
. Tính
2 2P f f
.
A.
5
3
P
. B.
8
3
P
. C.
6P
. D.
4P
.
Bài 16. Hàm số bậc 2
Câu 1. Cho hàm số bậc hai có đồ thị , đỉnh của được xác định bởi công
thức nào?
A. . B. . C. . D. .
Câu 2. Trục đối xứng của đồ thị hàm số , là đường thẳng nào dưới đây?
A. B. C. D.
2
b
y
a
.
Câu 3. Hàm số , đồng biến trong khoảng nào sau đây?
A. B. C. D.
Câu 4. Hàm số
2
4 11y x x đồng biến trên khoảng nào trong các khoảng sau đây?
A.
( 2; )
B.
( ; ) 
C.
(2; )
D.
( ; 2)
Câu 5. Parabol có phương trình trục đối xứng là
A. . B. . C. . D. .
Câu 6. Cho hàm số
2
y ax bx c
có bảng biến thiên dưới đây. Đáp án nào sau đây là đúng?
A.
2
2 2.y x x
B.
2
2 2.y x x
C.
2
+ 3 2.y x x
D.
2
2 2.y x x
Câu 7. Bảng biến thiên của hàm số
2
2 4 1y x x
là bảng nào sau đây?
A. . B. .
C.
.
D.
.
2
y ax bx c
0
a
P
P
;
2 4
b
I
a a
;
4
b
I
a a
;
4
b
I
a a
;
2 2
b
I
a a
2
y ax bx c
( 0)
a
.
2
b
x
a
.
2
c
x
a
.
4
x
a
2
y ax bx c
( 0)
a
; .
2
b
a

; .
2
b
a
; .
4a
; .
4
a

2
2 3
y x x
1
x
2
x
1
x
2
x
Câu 8. Parabol có hoành độ đỉnh là
A. . B. . C. . D. .
Câu 9. Điểm là đỉnh của Parabol nào sau đây?
A. . B. . C. . D. .
Câu 10. Cho đi qua điểm Khi đó
A. B. C. D.
Câu 11. Đồ thị hàm số , có hệ số là
A. B. C. D.
Câu 12. Cho parabol có đồ thị như hình sau
Phương trình của parabol này là
A. . B. . C. . D. .
Câu 13. Đồ thị nào sau đây là đồ thị của hàm số
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Câu 14. Cho hàm số
2
y ax bx c có đồ thị là parabol trong hình vẽ. Khẳng định nào sau đây là
đúng?
A.
0; 0; 0a b c
. B.
0; 0; 0a b c
. C.
0; 0; 0a b c
. D.
0; 0; 0a b c
.
Câu 15. Cho hàm số . Có đồ thị như hình vẽ dưới đây. Hỏi mệnh đề nào đúng?
2
: 2 6 3
P y x x
3
x
3
2
x
3
2
x
3
x
2;1
I
2
4 5
y x x
2
2 4 1
y x x
2
4 5
y x x
2
4 3
y x x
2
( ) : 1
P y x bx
1;3 .
A
1.
b
1.
b
3.
b
2.
b
2
y ax bx c
( 0)
a
a
0.
a
0.
a
1.
a
2.
a
2
y ax bx c
2
1
y x x
2
2 4 1
y x x
2
2 1
y x x
2
2 4 1
y x x
2
2 3
y x x
Hình
2
x
y
O 1
Hình
3
x
y
O
1
Hình
4
x
y
O 1
2
y ax bx c
A. . B. . C. . D. .
Câu 16. Tìm giá trị nhỏ nhất của hàm số .
A. . B. . C. . D. .
Câu 17. Giá trị nhỏ nhất của hàm số đạt được tại
A. . B. . C. . D. .
Câu 18. Cho hàm số . Khẳng định nào sau đây là đúng?.
A. Đồ thị hàm số không cắt trục tung.
B. Đồ thị hàm số cắt trục hoành tại gốc tọa độ.
C. Đồ thị hàm số không có trục đối xứng.
D. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng .
Câu 19. Tọa độ giao điểm của đường thẳng và parabol là
A. và . B. và . C. và . D. và .
Câu 20. Gọi và là tọa độ giao điểm của và . Giá trị của
bằng.
A. 7. B. . C. 15. D. .
Bài 17. Dấu của tam thức bậc 2
Câu 1. Tìm khẳng định đúng trong các khẳng định sau?
A.
2
3 2 5f x x x
là tam thức bậc hai. B.
2 4f x x
là tam thức bậc hai.
C.
3
3 2 1f x x x
là tam thức bậc hai. D.
4 2
1f x x x
là tam thức bậc hai.
Câu 2. Cho
2
f x ax bx c
,
0a
và
2
4b ac
. Cho biết điều kiện của
khi
f x
luôn cùng
dấu với hệ số
a
với mọi
x
.
A.
0
. B.
0
. C.
0
. D.
0
.
Câu 3. Cho
2
f x ax bx c
,
0a
. Điều kiện để
0,f x x
là
A.
0
0
a
. B.
0
0
a
. C.
0
0
a
. D.
0
0
a
.
Câu 4. Cho
2
f x ax bx c
,
0
a
. Điều kiện để
0,f x x
là
A.
0
0
a
. B.
0
0
a
. C.
0
0
a
. D.
0
0
a
.
Câu 5. Cho
2
f x ax bx c
,
0a
và
2
4 0b ac
. Khi đó mệnh đề nào đúng?
A.
0,f x x
. B.
0,f x x
. C.
f x
không đổi dấu. D. Tồn tại x để
0f x
Câu 6. Cho hàm số
2
f x ax bx c
có đồ thị như hình vẽ dưới đây.
0, 0, 0
a b c
0, 0, 0
a b c
0, 0, 0
a b c
0, 0, 0
a b c
2
4 1
y x x
3
1
3
13
2
2 3
y x x
2
x
1
x
0
x
1
x
2
2 3 1
y x x
1
: 4
d y x
2
7 12
y x x
2;6
4;8
2;2
4;8
2; 2
4;0
2;2
4;0
;
A a b
;
B c d
2
: 2
P y x x
: 3 6
y x
b d
7
15
Khẳng định nào sau đây đúng?
A.
0, 0;2f x x
. B.
0, 0;2f x x
.
C.
0, 1;f x x
. D.
0, 0; 2f x x
.
Câu 7. Tam thức nào dưới đây luôn dương với mọi
x
?
A.
2
1f x x x
. B.
2
2 1f x x x
. C.
2
1f x x x
. D.
2
4f x x x
.
Câu 8. Bảng xét dấu nào sau đây là bảng xét dấu của tam thức
2
6f x x x
?
A. . B. .
C. . D. .
Câu 9. Tam thức
2
2 3
y x x
nhận giá trị dương khi và chỉ khi
A.
–3x
hoặc
–1x
. B.
–1x
hoặc
3x
. C.
–2x
hoặc
6x
. D.
–1 3 x
.
Câu 10. Tam thức nào sau đây nhận giá trị âm với mọi
2x
?
A.
2
5 6x x
. B.
2
16 x
. C.
2
2 3x x
. D.
2
5 6x x
.
Câu 11. Cho tam thức
2
8x 16f x x
. Khẳng định nào sau đây là đúng?
A. Phương trình
0f x
vô nghiệm. B.
0f x
với mọi
x
.
C.
0f x
với mọi
x
. D.
0f x
khi
4x
.
Câu 12. Tìm tập xác định của hàm số
2
2 5 2y x x
.
A.
1
;
2
D
. B.
[2; )
. C.
1
; [2; )
2
 
. D.
1
;2
2
.
Câu 13. Tập nghiệm của bất phương trình
2
2 14 20 0x x
là
A.
;2 5;S  
. B.
;2 5;S  
.
C.
2;5S
. D.
2;5S
.
Câu 14. Bất phương trình
2
2 3x x
có bao nhiêu nghiệm nguyên?
A.
5
. B.
4
. C.
3
. D.
2
.
Câu 15. Để
2
1 2 7 0
f x x m x m
với mọi x thì
A.
3 9m
. B.
3 9m m
. C.
3 9m
. D.
3 9m m
.
Câu 16. Cho
2
( ) 2 ( 2) 4f x x m x m . Tìm
m
để
( )f x
âm với mọi
x
.
A.
14 2m
. B.
14 2m
. C.
2 14m
. D.
14m
hoặc
2m
.
Câu 17. Tìm tất cả giá trị của tham số
m
để bất phương trình
2
2 1 0x x m
vô nghiệm
A.
0m
. B.
0m
. C.
0m
. D.
0m
.
Câu 18. Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
1 2 1 3 8 0
m x m x m
nghiệm đúng với mọi
x
.
A.
1m
. B.
3m
. C.
3
2
m
. D.
3
3
2
m
.
Câu 19. Cho phương trình
2
2 1 2 2 4 0
m x m x m
. Tất cả các giá trị của m để phương trình đã
cho có hai nghiệm trái dấu là
8
A.
1
2
4
m
m
. B.
1
4
2
m
. C.
1
4
2
m
. D.
1
2
4
m
m
.
Câu 20. Phương trình
2
1 1 0
x m x
vô nghiệm khi và chỉ khi
A.
1.
m
B.
3 1.
m
C.
3
m
hoặc
1.
m
D.
3 1.
m
Bài 18. Phương trình quy về phương trình bậc 2
Câu 1. Phương trình
2
3 4 2 2
x x x
có tập nghiệm là
A.
2;3
. B.
1;6
. C.
3;2
. D.
6;1
.
Câu 2. Tập nghiệm của phương trình
2
2 9 9 3
x x x
là
A.
6
. B. . C.
3
. D.
3;6
.
Câu 3. Số nghiệm của phương trình
2
3 3 1
x x
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 4. Số nghiệm của phương trình 3 2
x x
là
A.
2
.
B.
1
. C.
3
.
D.
0
.
Câu 5. Phương trình
2
2 3 5 1
x x x
có nghiệm là
A.
1
x
. B.
2
x
. C.
3
x
. D.
4
x
.
Câu 6. Tổng các nghiệm của phương trình:
2 1 2
x x
bằng:
A.
6
. B.
1
. C.
5
. D.
2
.
Các câu hỏi trong bài 19, 20, 21 đều xét trong mặt phẳng tọa độ Oxy
Bài 19. Phương trình đường thẳng
Câu 1. Một vectơ pháp tuyến của đường thẳng
2 3 6 0
x y
là
A.
4
2; 3
n
. B.
2
2;3
n
. C.
3
3;2
n
. D.
1
3;2
n
.
Câu 2. Một vectơ chỉ phương của đường thẳng
2 3
3
x t
y t
là
A.
1
2;–3 .
u
B.
2
3;–1 .
u
C.
3
3; 1 .
u
D.
4
3;–3
u
.
Câu 3: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm
3;2
A
và
?
1;4
B
A.
1
1;2 .
u
B.
2
2
.
;1
u
C.
3
2;6 .
u
D.
4
1;1 .
u
Câu 4. Đường thẳng chứa trục Ox có vectơ chỉ phương là
A.
1
1;0 .
u
B.
2
.
1;1
u
C.
3
0;6 .
u
D.
4
0; 1 .
u
Câu 5. Đường thẳng chứa trục Ox có vectơ pháp tuyến là
A.
1
1;0 .
u
B.
2
.
1;1
u
C.
3
1;0 .
u
D.
4
0; 1 .
u
Câu 6. Vectơ chỉ phương của đường thẳng
1
3 2
x y
là
A.
4
2;3
u
B.
2
3; 2
u
C.
3
3;2
u
D.
1
2;3
u
Câu 7. Cho đường thẳng
:3 7 15 0
d x y
. Mệnh đề nào sau đây sai?
A.
7;3
u
là vecto chỉ phương của
d
. B.
d
có hệ số góc
3
7
k
.
C.
d
không đi qua góc tọa độ. D.
d
đi qua hai điểm
1
;2
3
M
và
5;0
N
.
Câu 8. Đường thẳng nào trong các đáp án sau có hệ số góc bằng 1.
9
A.
2
3 2
x t
y t
. B.
2 4
3 2
x t
y t
. C.
2
2 3
x t
y t
. D.
2 2
3 2
x t
y t
.
Câu 9. Cho đường thẳng
có phương trình tổng quát: . Vectơ nào sau đây là vectơ chỉ
phương của đường thẳng .
A. B. C. D.
Câu 10. Mệnh đề nào sau đây đúng? Đường thẳng
: 2 5 0
d x y
:
A. Đi qua
1; 2
A
. B. Có phương trình tham số:
2
x t
t R
y t
.
C.
d
có hệ số góc
1
2
k
. D.
d
cắt
d
có phương trình:
2 0
x y
.
Câu 11. Viết phương trình tham số của đường thẳng đi qua
3;4
A
và có vectơ chỉ phương
3; 2
u
A.
3 3
2 4
x t
y t
. B.
3 6
2 4
x t
y t
. C.
3 2
4 3
x t
y t
. D.
3 3
4 2
x t
y t
.
Câu 12. Đường thẳng đi qua
1;2
A
, nhận
2; 4
n
làm vectơ pháp tuyến có phương trình là
A.
2 4 0
x y
. B.
4 0
x y
. C.
2 5 0
x y
. D.
2 4 0
x y
.
Câu 13. Cho hai điểm
1; 3
A
,
2;5
B
. Viết phương trình tổng quát của đường thẳng đi qua hai điểm
,
A B
.
A.
8 3 1 0
x y
. B.
8 3 1 0
x y
. C.
3 8 30 0
x y
. D.
3 8 30 0
x y
.
Câu 14. Phương trình tham số của đường thẳng qua
1; 1
M
,
4;3
N
là
A.
3
4
x t
y t
. B.
1 3
1 4
x t
y t
. C.
3 3
4 3
x t
y t
. D.
1 3
1 4
x t
y t
.
Câu 15. Cho ba điểm
1; 2 , 5; 4 , 1;4
A B C
. Đường cao
AA
của tam giác ABC có phương trình
A.
3 4 8 0
x y
. B.
3 4 11 0
x y
. C.
6 8 11 0
x y
. D.
8 6 13 0
x y
.
Câu 16. Cho hai điểm
1; 2
A
,
1;2
B
. Đường trung trực của đoạn thẳng
AB
có phương trình là
A.
2 0
x y
. B.
2 0
x y
. C.
2 0
x y
. D.
2 1 0
x y
.
Câu 17. Lập phương trình tổng quát đường thẳng đi qua điểm
2;1
A
và song song với đường thẳng
2 3 2 0
x y
.
A.
3 2 8 0
x y
. B.
2 3 7 0
x y
. C.
3 2 4 0
x y
. D.
2 3 7 0
x y
.
Câu 18 Cho đường thẳng
2 3
:
1
x t
y t
t
và điểm
1; 6
M
. Phương trình đường thẳng đi qua
M
và vuông góc với
là
A.
3 9 0
x y
. B.
3 17 0
x y
. C.
3 3 0
x y
. D.
3 19 0
x y
.
Câu 19. Cho đường thẳng
: 2 1 0
d x y
và điểm
2;3
M
. Phương trình đường thẳng
đi qua điểm
M
và vuông góc với đường thẳng
d
là
A.
2 8 0
x y
. B.
2 4 0
x y
. C.
2 1 0
x y
. D.
2 7 0
x y
.
Câu 20. Cho tam giác ABC có
2;3 , 1; 2 , 5;4 .
A B C
Đường trung trực trung tuyến AM có phương
trình tham số
A.
2
3 2 .
x
t
B.
2 4
3 2 .
x t
y t
C.
2
2 3 .
x t
y t
D.
2
3 2 .
x
y t
Câu 21. Cho tam giác
ABC
với
2;4
A
; ; . Trung tuyến đi qua điểm nào dưới đây?
A. . B. . C. . D. .
–2 3 –1 0
x y
3;2
.
2;3
.
–3;2
.
2; –3
.
2;1
B
5;0
C
CM
9
14;
2
5
10;
2
7; 6
1;5
10
Bài 20. Vị trí tương đối của hai đường thẳng. Góc và khoảng cách
Câu 1. Góc giữa hai đường thẳng
1 1 1 1
: 0
a x b y c
và
2 2 2 2
: 0
a x b y c
được xác định theo công
thức:
A.
1 2 1 2
1 2
2 2 2 2
1 1 2 2
cos ,
.
a a b b
a b a b
. B.
1 2 1 2
1 2
2 2 2 2
1 1 2 2
cos ,
.
a a b b
a b a b
.
C.
1 2 1 2
1 2
2 2 2 2
1 1 1 1
cos ,
a a b b
a b a b
. D.
1 2 1 2 1 2
1 2
2 2
cos ,
a a b b c c
a b
.
Câu 2. Giao điểm
M
của
1 2
:
3 5
x t
d
y t
và
:3 2 1 0
d x y
. Toạ độ của
M
là
A.
11
2; .
2
M
B.
1
0; .
2
M
C.
1
0; .
2
M
D.
1
;0 .
2
M
Câu 3. Cho đường thẳng
1
: 2 3 15 0
d x y
và
2
: 2 3 0
d x y
. Khẳng định nào sau đây đúng?
A.
1
d
và
2
d
cắt nhau và không vuông góc với nhau. B.
1
d
và
2
d
song song với nhau.
C.
1
d
và
2
d
trùng nhau. D.
1
d
và
2
d
vuông góc với nhau.
Câu 4. Vị trí tương đối của hai đường thẳng
1
3 4
:
2 6
x t
d
y t
và
2
2 2
:
8 4
x t
d
y t
là
A. trùng nhau. B. song song.
C. vuông góc với nhau. D. cắt nhau nhưng không vuông góc nhau.
Câu 5. Cho đường thẳng d : 4x+3y-2=0 và d’ :
1 3
2 4
x t
y t
. Khi đó hai đường thẳng
A. trùng nhau. B. song song.
C. cắt nhau nhưng không vuông góc. D. vuông góc.
Câu 6. Phương trình nào sau đây biểu diển đường thẳng không song song với đường thẳng
: 2 1
d y x
?
A.
2 5 0.
x y
B.
2 5 0.
x y
C.
2 0.
x y
D.
2 5 0.
x y
Câu 7. Góc giữa hai đường thẳng
: 3 7 0
a x y
và
: 3 1 0
b x y
là
A.
30
. B.
90
. C.
60
. D.
45
.
Câu 8. Với giá trị nào của
m
thì hai đường thẳng
1
:3 4 1 0
x y
và
2
2
: 2 1 1 0
m x m y
trùng nhau.
A.
2
m
. B. mọi
m
. C. không có
m
. D.
1
m
.
Câu 9. Cho ba đường thẳng lần lượt có phương trình
1
:3 4 15 0
d x y
,
2
:5 2 1 0
d x y
và
3
: 2 1 9 13 0
d mx m y m
. Tìm tất cả các giá trị của tham số
m
để ba đường thẳng đã cho cùng đi
qua một điểm.
A.
1
.
5
m
B.
5.
m
C.
1
.
5
m
D.
5.
m
Câu 10. Tìm côsin góc giữa
2
đường thẳng
1
:
2 2 0
x y
và
2
:
0
x y
.
A.
10
.
10
B.
2.
C.
2
.
3
D.
3
3
.
Câu 11. Tìm góc giữa đường thẳng và .
A. . B. . C. . D. .
Câu 12. Đường thẳng đi qua điểm và tạo với đường thẳng
một góc . Khi đó bằng
2
1
: 6 5 15 0
x y
2
10 6
:
1 5
x t
y t
90
60
0
45
3 0, ,ax by a b
1;1
M
:3 7 0
x y
45
a b
11
A. B. C. D.
Câu 13. Cho và . Tìm để
A. . B. hoặc . C. hoặc . D. .
Câu 14. Xác định giá trị của để góc tạo bởi hai đường thẳng và đường thẳng
một góc bằng .
A. . B. . C. . D. .
Câu 15. Lập phương trình đi qua và tạo với đường thẳng một góc
A. B.
C. D.
Câu 16. Cho điểm và đường thẳng với . Khi đó khoảng cách
là
A. . B. .
C. . D. .
Câu 17. Khoảng cách từ điểm đến đường thẳng là
A. . B. . C. . D. .
Câu 18. Khoảng cách từ điểm đến đường thẳng là
A. . B. . C. . D. .
Câu 19. Cho đường thẳng . Trong các điểm , , ,
điểm nào cách xa đường thẳng nhất?
A. . B. . C. . D. .
Câu 20. Khoảng cách giữa hai đường thẳng và bằng
A.
1
10
. B.
5
2
. C.
5
. D.
1
5
.
Câu 21. Cho đường thẳng d: x – y + 3 = 0. Phương trình đường thẳng song song với d và cách d một
khoảng bằng
2
là
A.
1 0
x y
và
3 0
x y
. B.
1 0
x y
.
C.
3 0
x y
. D.
3 0
x y
và
1 0
x y
.
Bài 21. Đường tròn trong mặt phẳng tọa độ
Câu 1. Xác định tâm và bán kính của đường tròn
2 2
: 1 2 9.
C x y
A. Tâm
1;2 ,
I
bán kính
3
R
. B. Tâm
1;2 ,
I
bán kính
9
R
.
6.
4.
3.
1.
:3 0
d x y
': 1 0
d mx y
m
1
cos , '
10
d d
0
m
4
3
m
0
m
3
4
m
0
m
3
m
a
2
1 2
x at
y t
3 4 12 0
x y
45
2
; 14
7
a a
2
; 14
7
a a
1; 14
a a
2; 14
a a
2;1
A
: 2 3 4 0
d x y
45 .
5 11 0; 5 3 0.
x y x y
5 11 0; 5 3 0.
x y x y
5 11 0; 5 3 0.
x y x y
5 2 12 0; 2 5 1 0.
x y x y
0 0
;
M x y
: 0
ax by c
2 2
0
a b
;
M
d
0 0
;
2 2 2
M
ax by c
d
a b c
0 0
;
2 2 2
M
ax by c
d
a b c
0 0
;
2 2
M
ax by c
d
a b
0 0
;
2 2
M
ax by c
d
a b
5; 1
M
:3 2 13 0
x y
13
2
2
28
13
2 13
15;1
M
2 3
:
x t
y t
5
1
10
10
16
5
: 21 11 10 0
x y
20; 3
M
0;4
N
19;5
P
1;5
Q
N
M
P
Q
1
:3 4 6 0
d x y
2
:6 8 13 0
d x y
12
C. Tâm
1; 2 ,
I
bán kính
3
R
. D. Tâm
1; 2 ,
I
bán kính
9
R
.
Câu 2. Phương trình đường tròn có tâm
1;2
I
và bán kính
5
R
là
A.
2 2
2 4 20 0
x y x y
. B.
2 2
2 4 20 0
x y x y
.
C.
2 2
2 4 20 0
x y x y
. D.
2 2
2 4 20 0
x y x y
.
Câu 3. Để
2 2
2 2 0 (1)
x y ax by c
là phương trình đường tròn, điều kiện cần và đủ là
A.
2 2
0
a b c
. B.
2 2
0
a b c
. C.
2 2
4 0
a b c
. D.
2 2
4 0
a b c
.
Câu 4. Phương trình nào sau đây là phương trình của đường tròn?
(I)
2 2
4 15 12 0
x y x y
.
(II)
2 2
3 4 20 0
x y x y
.
(III)
2 2
2 2 4 6 1 0
x y x y
.
A. Chỉ (I). B. Chỉ (II). C. Chỉ (III). D. Chỉ (I) và (III).
Câu 5. Đường tròn
2 2
3 3 – 6 9 9 0
x y x y
có bán kính bằng bao nhiêu?
A.
15
2
. B.
5
2
. C.
25
. D.
5
.
Câu 6. Tâm của đường tròn
2 2
0
10 1x y x
cách trục Oy một khoảng bằng
A. 5. B. 0. C. 10. D. -5.
Câu 7. Đường tròn tâm
(3; 1)
I
và bán kính
2
R
có phương trình là
A.
2 2
( 3) ( 1) 4
x y
. B.
2 2
( 3) ( 1) 4
x y
.
C.
2 2
( 3) ( 1) 4
x y
. D.
2 2
( 3) ( 1) 4
x y
.
Câu 8. Đường tròn tâm
( 1;2)
I
và đi qua điểm
(2;1)
M
có phương trình là
A.
2 2
2 4 5 0
x y x y
. B.
2 2
2 4 3 0.
x y x y
C.
2 2
2 4 5 0
x y x y
. D.
2 2
2 4 5 0.
x y x y
Câu 9. Cho hai điểm
(5; 1)
A
,
( 3;7)
B
. Đường tròn có đường kính
AB
có phương trình là
A.
2 2
2 6 22 0
x y x y
. B.
2 2
2 6 22 0.
x y x y
C.
2 2
2 1 0
x y x y
. D.
2 2
6 5 1 0.
x y x y
Câu 10. Đường tròn
( )
C
tâm
( 4;3)
I
và tiếp xúc với trục tung có phương trình là
A.
2 2
3 0
4 9x y x y
. B.
2 2
( 4) ( 3) 16
x y
.
C.
2 2
( 4) ( 3) 16
x y
. D.
2 2
8 6 12 0.
x y x y
Câu 11. Đường tròn
( )
C
tâm
(4; 3)
I
và tiếp xúc với đườngthẳng
: 3 4 5 0
x y
có phương trình là
A.
2 2
( 4) ( 3) 1
x y
. B.
2 2
( 4) ( 3) 1
x y
.
C.
2 2
( 4) ( 3) 1
x y
. D.
2 2
( 4) ( 3) 1
x y
.
Câu 12. Cho ba điểm
3; 5
A
,
2; 3
B
,
6; 2
C
. Đường tròn ngoại tiếp tam giác
ABC
có phương trình
là
A.
2 2
25 19 68 0
x y x y
. B.
2 2
3 3 25 19 68 0
x y x y
.
C.
2 2
25 19 68 0
x y x y
. D.
2 2
3 3 25 19 68 0
x y x y
.
Câu 13. Cho đường tròn
2 2
: 3 1 10
C x y
. Phương trình tiếp tuyến của
C
tại
4;4
A
là
A.
3 5 0
x y
. B.
3 4 0
x y
. C.
3 16 0
x y
. D.
3 16 0
x y
.
Câu 14. Cho đường tròn (C): x
2
+ y
2
– 2x – 4y – 4 = 0 và điểm A(1; 5). Tiếp tuyến của đường tròn (C) tại
điểm A có phương trình là
A. y – 5 = 0. B. y + 5 = 0. C. x + y – 5 = 0. D. x – y – 5 = 0.
B. TỰ LUẬN
Bài 1. Vẽ các parabol sau trên mặt phẳng Oxy.
a.
2
( ) : 4 3P y x x . b.
2
( ) : 2P y x x c.
2
( ) : 2 4 3P y x x d.
2
1 3
( ):
2 2
P y x x
Bài 2. Xác định parabol
2
1y ax bx trong mỗi trường hợp sau
a. Đi qua điểm M(1;-2) và N(-2;19). b. Có đỉnh I (-2;37)
c. Có trục đối xứng là x = -1 và tung độ của đỉnh bằng 5.
Bài 3. Xác định parabol
2
y ax bx c trong mỗi trường hợp sau
a. Có đỉnh I (1;2) và đi qua điểm M(0;3).
b. Đi qua điểm A (1;2) và có tung độ của điểm thấp nhất bằng 2.
Bài 3. Giải các bất phương trình
a.
2
3 2 1 0x x
b.
2
36 12 1 0x x
c.
2 2 2
( ) 3( ) 2 0x x x x
d.
2
2 2
2 3 4 3
3 1.
2 2
x x x
x x
e.
2
2
2 3
2
1
x x
x
Bài 4. Giải các phương trình sau
a.
2 2
77 212 2x x x x
b.
2 2
25 26x x x x
c.
2
2 13 16 6x x x
d.
2
3 1 4x x x
e.
2 3 3x x
.
Bài 5. Cho tam thức
2
2 90f x x mx m
. Xác định tham số
m
để
a.
0 f x x
b.
0 f x x
c.
0 0;2f x x
Bài 6. Cho tam thức
2
2 110f x x mx m
. Xác định tham số
m
để
a.
0 f x x
b.
0 f x x
c.
0 3;f x x 
Bài 7. Tìm tất cả các giá trị của
m
để hàm số sau xác định với mọi
x
.
2
1
( 1) 2( 2) 2
f x
m x m x m
Bài 8. Tìm tất cả các giá trị của tham số
m
để bất phương trình sau nghiệm đúng với
x
2 2
3x 2( 1) 2 3 2 0 m x m m .
Bài 9. Tìm tất cả các giá trị của tham số
m
để bất phương trình sau vô nghiệm
2
2 2 4 2 8 0m x m x m
.
Bài 10. Một rạp chiếu phim có sức chứa 1000 người. Với giá vé là 40.000đ trung bình sẽ có khoảng 300
người đến rạp xem phim mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu phim đã khảo sát thị trường và
thấy rằng nếu giá vé cứ giảm 10.000đ thì sẽ có thêm 100 người đến rạp mỗi ngày. Tìm mức giá vé để
doanh thu từ tiến bán vé mỗi ngày của rạp là lớn nhất.
Bài 11.
Mặt cắt đứng của cột cây số trên quốc lộ có dạng nửa hình tròn ở
phía trên và phía dưới có dạng hình chữ nhật (xem hình bên). Biết
rằng đường kính của nửa hình tròn cũng là cạnh của hình chữ nhật.
Tim kích thước của hình chữ nhật, biết rằng diện tích của phần nửa
hình tròn bằng 0,3 lần diện tích của hình chữ nhật. Lấy
3,14
và
làm tròn kết quả đến chữ số thập phận thứ hai.
Bài 12. Trong mặt phẳng Oxy, cho ba điểm A (-1;0), B(1;2), C(3;3).
a. Viết phương trình tham số và phương trình tổng quát của đường thẳng AB.
b. Viết phương trình đường trung trực của đoạn thẳng AB.
c. Viết phương trình đường thẳng đi qua A và vuông góc với BC.
d. Viết phương trình đường thẳng đi qua A và song song với BC.
Bài 13. Trong mặt phẳng Oxy, cho tam giác MNP có M (2;1), N(-3;0), P(1;4)
a. Vi
ế
t
phương tr
ình t
ổ
ng quát c
ủ
a đư
ờ
ng cao k
ẻ
t
ừ
M c
ủ
a tam giác MNP.
Tính di
ệ
n tích tam giác MNP.
14
b. Viết phương trình tổng quát của đường trung tuyến kẻ từ N của tam giác MNP.
c. Viết phương trình của đường trung bình của tam giác ứng với cạnh MN của tam giác MNP.
Bài 14. Trong mặt phẳng Oxy, cho đường thẳng
: 2 5 0
x y
.
a. Viết phương trình đường thẳng đi qua điểm A (3;1) và song song với với đường thẳng .
b. Viết phương trình đường thẳng đi qua điểm B (-1;0) và vuông góc với với đường thẳng .
c. Viết phương trình đường thẳng song song với đường thẳng và cách điểm O một khoảng bằng
5
.
d. Tìm tọa độ hình chiếu vuông góc của điểm M (2;-3) trên đường thẳng .
Bài 15. Trong mặt phẳng Oxy, cho điểm M(2;1) và đường thẳng
2
:
2
x t
y t
.
a. Tìm điểm N thuộc đường thẳng sao cho
2
MN
.
b. Tim điểm A thuộc đường thẳng sao cho tam giác ABC vuông tại A với B(1;1), C(-5;0).
Bài 16. Trong mặt phẳng Oxy, viết phương trình đường tròn (C) biết
a. Có tâm I(3;1) và bán kính
2
R
.
b. Đường kính AB với A(4;1), B(-2;-5).
c. Có tâm I(3;1) và đi qua điểm M(-1;7).
d. Có tâm
1;2
I
và tiếp xúc với đường thẳng
: 2 7 0
x y
.
e. Có tâm I thuộc đường thẳng
: 1 0
x y
và đi qua hai điểm P(6;2), Q(-1;3).
Bài 17. Trong mặt phẳng Oxy, cho đường tròn (C) có phương trình
2 2
6 4 12 0
x y x y
. Viết phương
trình tiếp tuyến của đường tròn (C) tại điểm M(0;-2).
--------------------------HẾT----------------------
| 1/14
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT THÁI NGUYÊN
TRƯỜNG THPT LƯƠNG NGỌC QUYẾN
ĐỀ CƯƠNG ÔN TẬP KIỂM TRA GIỮA HỌC KỲ II, MÔN TOÁN, LỚP 10 NĂM HỌC 2022-2023 I. NỘI DUNG ÔN TẬP
1. ĐẠI SỐ: Chương VI: Hàm số và đồ thị Bài 15. Hàm số 1. Xác định hàm số
2. Tìm tập xác định, tập giá trị của hàm số.
3. Xét tính đồng biến và nghịch biến của hàm số dựa vào đồ thị. 4. Đồ thị hàm số. Bài 16. Hàm số bậc 2
1. Sự biến thiên của hàm số bậc hai.
2. Tọa độ đỉnh, trục đối xứng của đồ thị hàm số bậc hai.
3. Sự tương giao của đồ thị hàm số bậc hai và đường thẳng.
4. Bảng biến thiên và đồ thị của hàm số bậc hai. 5. Ứng dụng thực tế.
Bài 17. Dấu của tam thức bậc 2
1. Dấu tam thức bậc hai.
2. Bất phương trình bậc hai. 3. Ứng dụng thực tế.
Bài 18. Phương trình quy về phương trình bậc 2
1. Giải phương trình chứa ẩn trong căn bậc hai. 2. Ứng dụng thực tế.
2. HÌNH HỌC VÀ ĐO LƯỜNG
Bài 19. Phương trình đường thẳng
1. Vectơ pháp tuyến, vectơ chỉ phương, hệ số góc của đường thẳng.
2. Viết phương trình tham số, phương trình tổng quát của đường thẳng.
3. Tìm tọa độ điểm thỏa mãn điều kiện cho trước.
Bài 20. Vị trí tương đối của hai đường thẳng. Góc và khoảng cách.
1. Xét vị trí tương đối của hai đường thẳng khi biết phương trình của chúng.
2. Tính góc giữa hai đường thẳng.
3. Tính khoảng cách từ một điểm đến một đường thẳng.
4. Viết phương trình đường thẳng có liên quan đến yếu tố góc và khoảng cách.
Bài 21. Đường tròn trong mặt phẳng tọa độ
1. Xác định tọa độ tâm và bán kính của đường tròn khi biết phương trình.
2. Viết phương trình đường tròn.
3. Viết phương trình tiếp tuyến của đường tròn tại 1 điểm.
II. CÂU HỎI TRẮC NGHIỆM VÀ TỰ LUẬN A. TRẮC NGHIỆM Bài 15. Hàm số
Câu 1. Xét hai đại lượng x, y phụ thuộc vào nhau theo các hệ thức dưới đây. Những trường hợp nào thì y không là hàm số của x? A. 2 y  2x 1. B. 2 y  2x  3x  4 . C. 4 2 y  x . D. y  2x  3 .
Câu 2. Cho hàm số được cho bởi bảng sau Giờ đo 1 4 7 10 13 16 19 22 nhiệt độ Nhiệt độ 28 27 28 32 31 29 28 27 (0C)
Bảng 1. Dự báo thời tiết ngày 01/05/ 2022 tại Hà Nội 1
Tập xác định của hàm số là A. 27; 28;29;31;3 
2 . B. 1;4;7;10;13;16;19;2  2 .
C. 1; 4;7;10;13;16;19;22;27;28;29;31;3  2 . D. *  .
Câu 3. Tập xác định của hàm số 4 2
y  x  2018x  2019 là A. 1;  . B.  ;  0. C. 0;   . D.  ;    .
Câu 4. Trong các hàm số sau, hàm số nào có tập xác định là ? 2 x  2 2x  3 x  2 A. 3 2 y  x  3x 1. B. y  . C. y  . D. y  x 2 x x 1 5x  2
Câu 5. Tập xác định D của hàm số y  là x 1 A. D   . B. D  1; . C. D  1; . D. D  R \   1 . 3  x
Câu 6. Tập xác định của hàm số y  là 2 x  5x  6 A. D   \ 1  ;  6 B. D   \1;  6 C. D   1  ;  6 D. D  1;  6
Câu 7. Tập xác định D của hàm số y  3x 1  là 1   1  A. D  0;   . B. D 0;   . C. D  ;  . D. D  ;   . 3   3  Câu 8
Tập xác định của hàm số y  4  x  x  2 là A. D  2;4
B. D  2;4 C. D  2;  4 D. D   ;  2 4; 3x  4 Câu 9.
Tập xác định của hàm số y  là x 1 A.  \  1 . B.  . C. 1; . D. 1; .
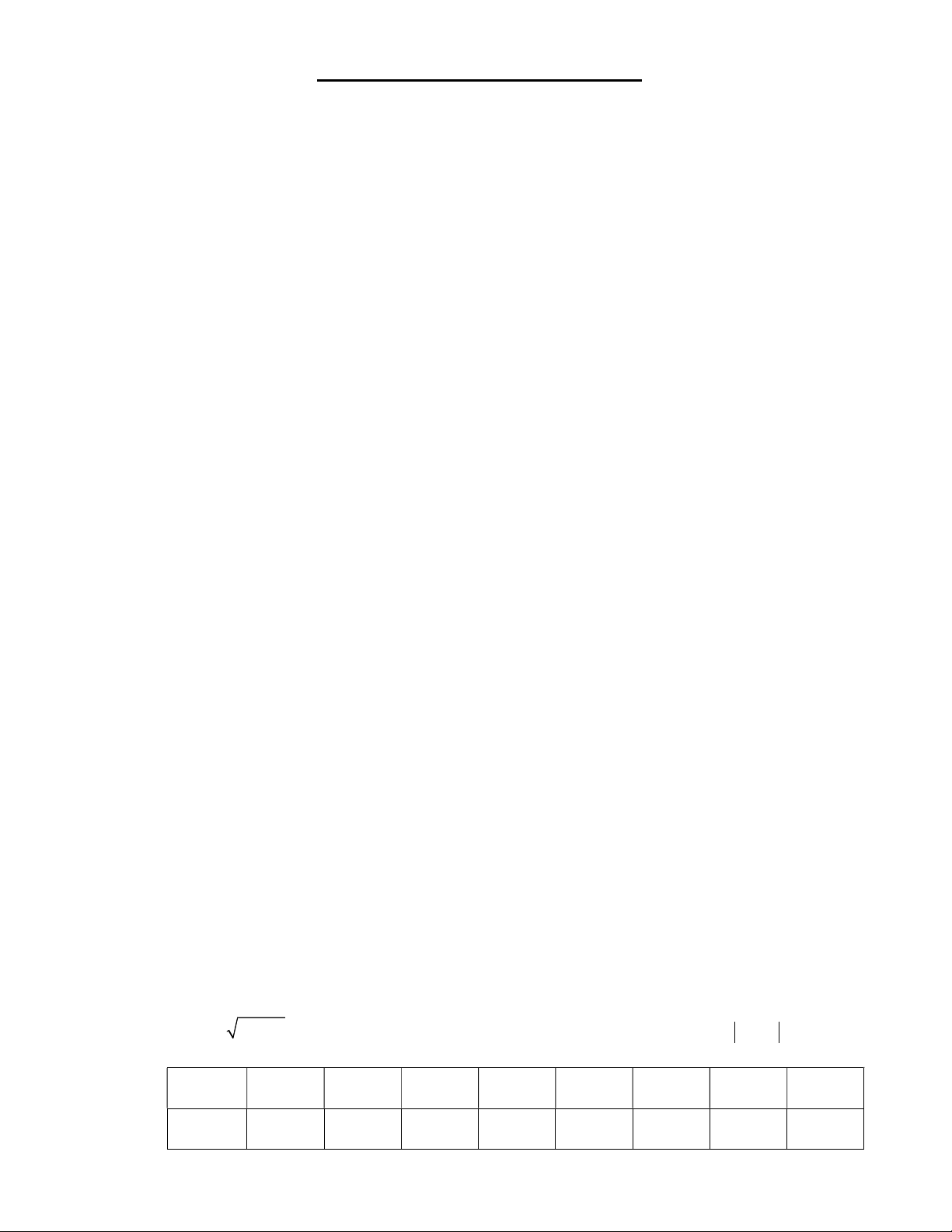
Câu 10. Cho hàm số y  f  x có tập xác định là  5  ; 
5 và đồ thị của nó được biểu diễn bởi hình dưới đây.
Tập giá trị của hàm số là A.  5  ;5 . B.  . C.  2  ;2. D. 0;2 . 1 Câu 11. Hàm số y  có x
A. Tập xác định là \ 
0 và tập giá trị là 
. B. Tập xác định và tập giá trị cùng là \  0 .
C. Tập xác định là 
và tập giá trị là \ 
0 . D. Tập xác định và tập giá trị cùng là  . 2 x  3x 1; khi x  1
Câu 12. Cho hàm số f  x   . Tính f  2  . x  2 ; khi x  1 A. 1  . B. 4. C. 7  . D. 0.
Câu 13. Chọn khẳng định đúng.
A. Hàm số y  f (x) được gọi là nghịch biến trên K nếu x
 ; x  K, x  x  f (x )  f (x ) . 1 2 1 2 1 2
B. Hàm số y  f (x) được gọi là đồng biến trên K nếu x
 ; x  K, x  x  f (x )  f (x ) . 1 2 1 2 1 2
C. Hàm số y  f (x) được gọi là đồng biến trên K nếu x
 ; x  K, x  x  f (x )  f (x ) . 1 2 1 2 1 2
D. Hàm số y  f (x) được gọi là đồng biến trên K nếu x
 ; x  K, x  x  f (x )  f (x ) . 1 2 1 2 1 2
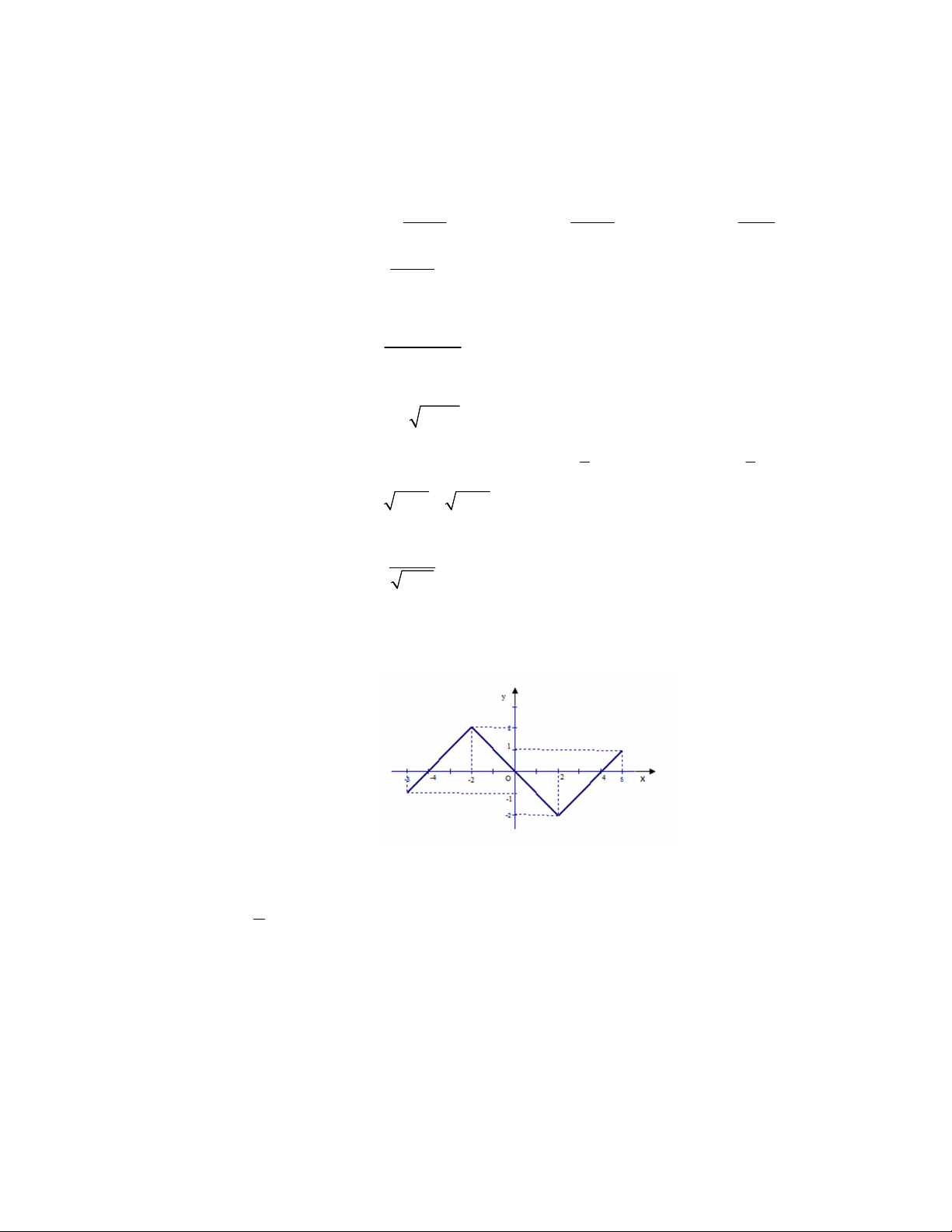
Câu 14. Cho hàm số có đồ thị như hình vẽ. Chọn đáp án sai.
A. Hàm số nghịch biến trên khoảng  ;   
1 . B. Hàm số đồng biến trên khoảng 1; .
C. Hàm số nghịch biến trên khoảng  1  ; 
1 . D. Hàm số đồng biến trên khoảng  1  ;0 .
Câu 15. Cho hàm số có đồ thị như hình bên dưới.
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng 0;  3 .
B. Hàm số đồng biến trên khoảng  ;   1 .
C. Hàm số nghịch biến trên khoảng 0; 2 .
D. Hàm số đồng biến trên khoảng  ;  3 .
Câu 16. Cho hàm số y  f  x có bảng biến thiên như sau
Đặt h x  5x  f  x . Khẳng định nào dưới đây là đúng? A. h3  h  1  h2 B. h  1  h2  h3 C. h2  h 
1  h3 D. h3  h2  h  1 2 x  4x  4
Câu 17. Điểm sau đây không thuộc đồ thị hàm số y  ? x  1  A. A2;0 . B. B 3;   . C. C 1;  1 . D. D 1  ; 3   .  3  x  a
Câu 18. Cho hàm số f  x 2  có f  4
  13. Khi đó giá trị của a là x  5 A. a  11. B. a  21. C. a  3  . D. a  3.
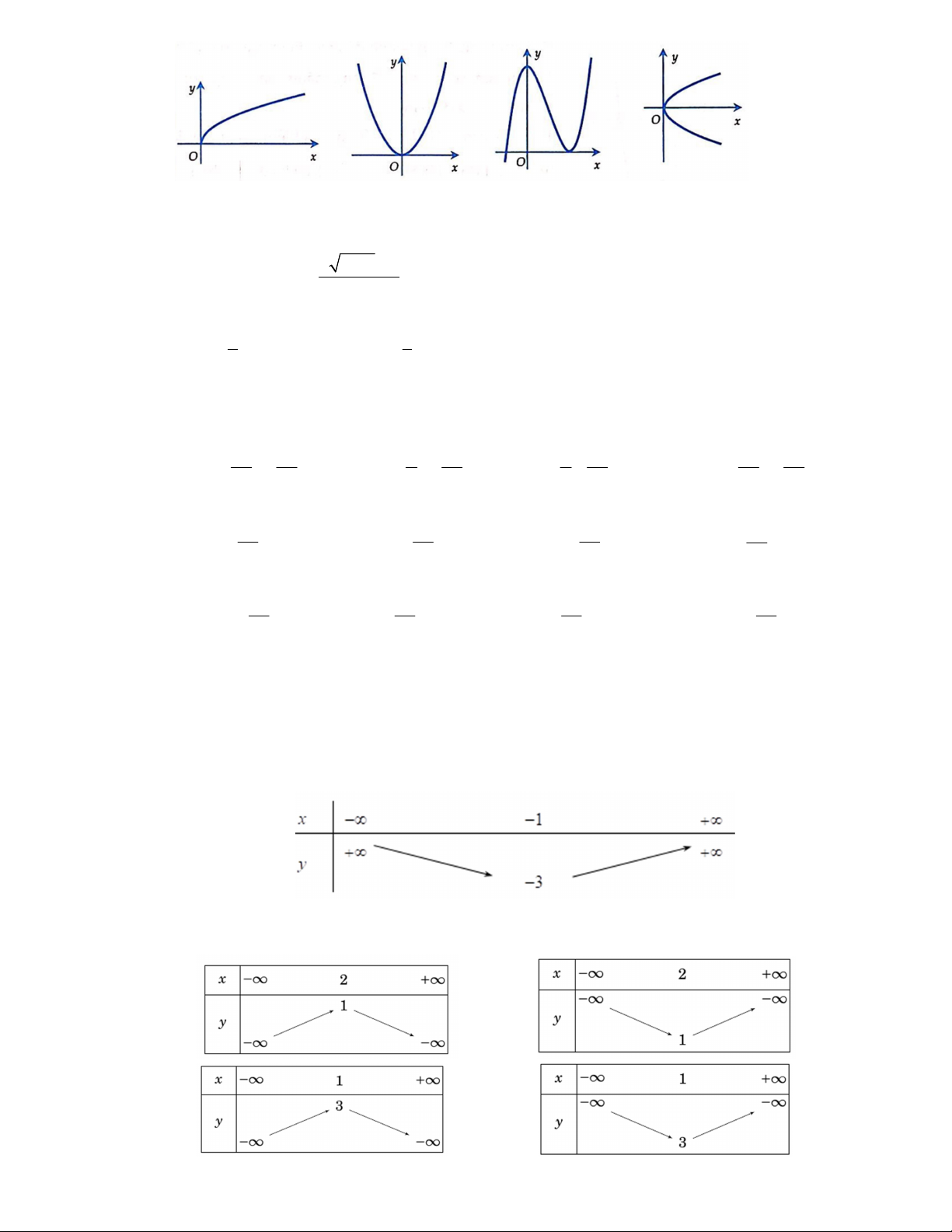
Câu 19. Đường cong trong hình nào dưới đây không phải là đồ thị của một hàm số y  f  x ? A. B. C. D. Câu 20. Cho hàm số 3 2
y  x  3x  3 . Có bao nhiêu điểm trên đồ thị hàm số có tung độ bằng 1? A. 0 B. 1 C. 2 D. 3 2 x  2  3  
Câu 21. Cho hàm số f x khi x 2   x 1
. Tính P  f 2  f  2  .  2 x 1 khi x  2 5 8 A. P  . B. P  . C. P  6 . D. P  4 . 3 3 Bài 16. Hàm số bậc 2
Câu 1. Cho hàm số bậc hai 2
y  ax  bx  c a  0 có đồ thị P , đỉnh của P được xác định bởi công thức nào?  b    b    b    b   A. I  ;  . B. I  ;  . C. I ; . D. I  ;  .          2a 4a   a 4a   a 4a   2a 2a 
Câu 2. Trục đối xứng của đồ thị hàm số 2
y  ax  bx  c , (a  0) là đường thẳng nào dưới đây? b c  b A. x   . B. x   . C. x   . D. y   . 2a 2a 4a 2a Câu 3. Hàm số 2
y  ax  bx  c , (a  0) đồng biến trong khoảng nào sau đây?  b   b        A.  ;   .   B.  ;   .   C.  ;   .   D.  ;   .    2a   2a   4a   4a  Câu 4. Hàm số 2
y  x  4x 11 đồng biến trên khoảng nào trong các khoảng sau đây? A. (2; ) B. (;) C. (2;) D. (;2) Câu 5. Parabol 2
y  x  2x  3 có phương trình trục đối xứng là A. x  1  . B. x  2 . C. x  1 . D. x  2  . Câu 6. Cho hàm số 2
y  ax bx c có bảng biến thiên dưới đây. Đáp án nào sau đây là đúng? A. 2 y  x  2x  2. B. 2 y  x  2x  2. C. 2 y  x + 3x  2. D. 2 y  x  2x  2.
Câu 7. Bảng biến thiên của hàm số 2 y  2
 x  4x 1 là bảng nào sau đây? A. . B. . C. . D. . Câu 8. Parabol  P 2
: y  2x  6x  3 có hoành độ đỉnh là A. x  3  3 . B. x  3 . C. x   . D. x  3. 2 2 Câu 9. Điểm I  2  ; 
1 là đỉnh của Parabol nào sau đây? A. 2 y  x  4x  5 . B. 2 y  2x  4x 1. C. 2 y  x  4x  5 . D. 2 y   x  4x  3 . Câu 10. Cho 2
(P) : y  x  bx 1 đi qua điểm A 1  ;3. Khi đó A. b  1  . B. b  1. C. b  3. D. b  2  .
Câu 11. Đồ thị hàm số 2
y  ax  bx  c , (a  0) có hệ số a là A. a  0. B. a  0. C. a  1. D. a  2. Câu 12. Cho parabol 2
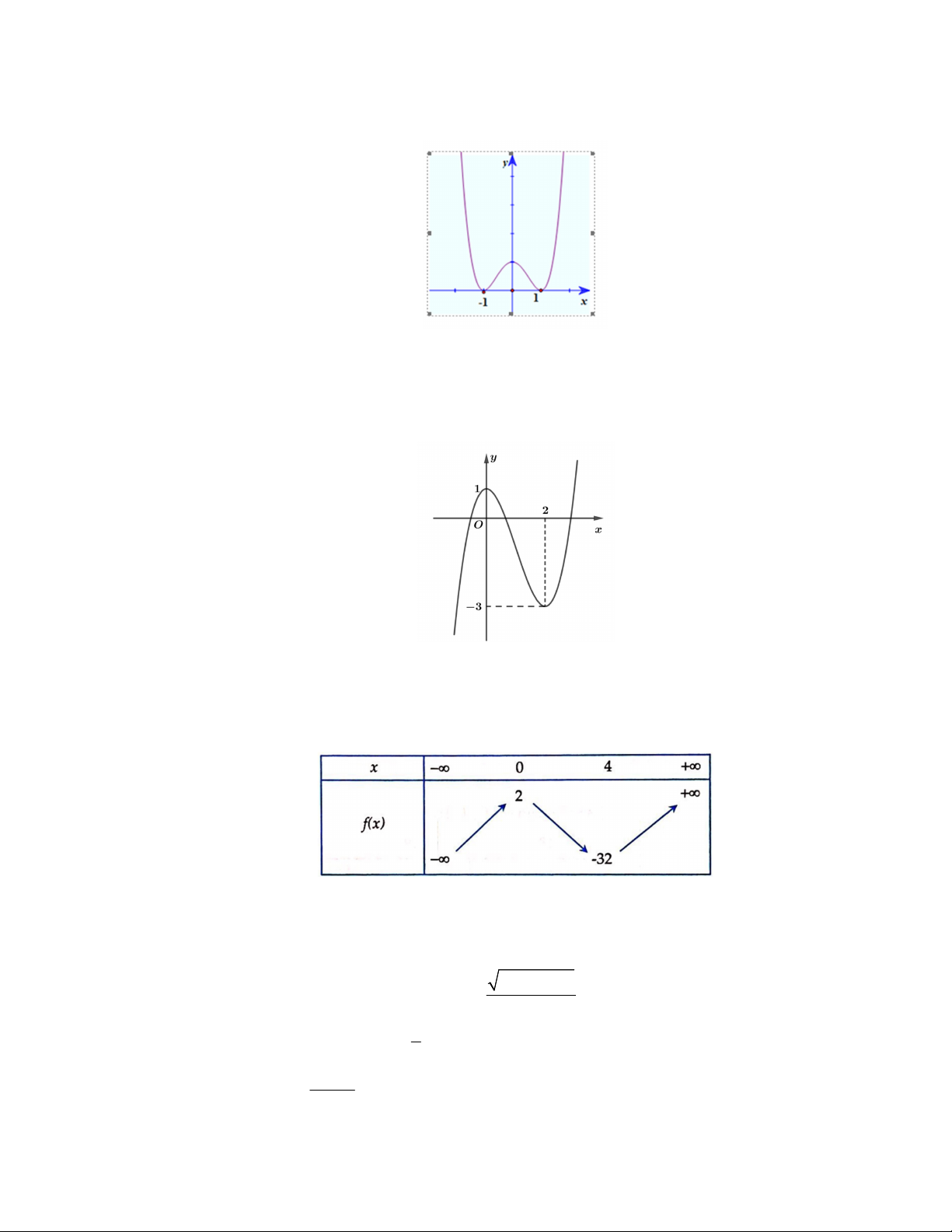
y  ax  bx  c có đồ thị như hình sau
Phương trình của parabol này là A. 2 y  x  x 1. B. 2 y  2x  4x 1. C. 2 y  x  2x 1. D. 2 y  2x  4x 1.
Câu 13. Đồ thị nào sau đây là đồ thị của hàm số 2 y  x  2x  3 y y y O 1 x x O 1 O 1 x Hình 2 Hình 3 Hình 4
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4. Câu 14. Cho hàm số 2
y  ax  bx  c có đồ thị là parabol trong hình vẽ. Khẳng định nào sau đây là đúng?
A. a  0; b  0; c  0 . B. a  0; b  0; c  0 . C. a  0; b  0; c  0 . D. a  0; b  0; c  0 . Câu 15. Cho hàm số 2
y  ax  bx  c . Có đồ thị như hình vẽ dưới đây. Hỏi mệnh đề nào đúng?
A. a  0, b  0, c  0 .
B. a  0, b  0, c  0 . C. a  0, b  0, c  0 . D. a  0, b  0, c  0 .
Câu 16. Tìm giá trị nhỏ nhất của hàm số 2 y  x  4x 1 . A. 3  . B. 1. C. 3 . D. 13 .
Câu 17. Giá trị nhỏ nhất của hàm số 2
y  x  2x  3 đạt được tại A. x  2  . B. x  1  . C. x  0 . D. x 1. Câu 18. Cho hàm số 2
y  2x  3x 1 . Khẳng định nào sau đây là đúng?.
A. Đồ thị hàm số không cắt trục tung.
B. Đồ thị hàm số cắt trục hoành tại gốc tọa độ.
C. Đồ thị hàm số không có trục đối xứng.
D. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 1.
Câu 19. Tọa độ giao điểm của đường thẳng d : y  x  4 và parabol 2 y  x  7x 12 là A.  2  ;6 và  4
 ;8 . B. 2;2 và 4;8. C. 2; 2
  và 4;0 . D. 2;2 và 4;0 . Câu 20. Gọi A ;
a b và B c;d  là tọa độ giao điểm của P 2
: y  2x  x và  : y  3x  6 . Giá trị của b  d bằng. A. 7. B. 7  . C. 15. D. 1  5 .
Bài 17. Dấu của tam thức bậc 2
Câu 1. Tìm khẳng định đúng trong các khẳng định sau? A. f  x 2
 3x  2x  5 là tam thức bậc hai.
B. f  x  2x  4 là tam thức bậc hai. C. f  x 3
 3x  2x 1 là tam thức bậc hai. D. f  x 4 2
 x  x 1 là tam thức bậc hai. Câu 2. Cho   2
f x  ax  bx  c , a  0 và 2
  b  4ac . Cho biết điều kiện của  khi f  x luôn cùng
dấu với hệ số a với mọi x   . A.   0 . B.   0 . C.   0 . D.   0 . Câu 3. Cho   2
f x  ax  bx  c , a  0 . Điều kiện để f  x  0, x    là a  0 a  0 a  0 a  0 A.  . B.  . C.  . D.  .   0   0   0   0 Câu 4. Cho   2
f x  ax  bx  c , a  0 . Điều kiện để f  x  0, x    là a  0 a  0 a  0 a  0 A.  . B.  . C.  . D.  .   0   0   0   0 Câu 5. Cho   2
f x  ax  bx  c , a  0 và 2
  b  4ac  0 . Khi đó mệnh đề nào đúng? A. f  x  0, x
  . B. f  x  0, x
   . C. f x không đổi dấu. D. Tồn tại x để f x  0 Câu 6. Cho hàm số   2
f x  ax  bx  c có đồ thị như hình vẽ dưới đây.
Khẳng định nào sau đây đúng?
A. f  x  0,x 0; 2 .
B. f  x  0,x 0; 2.
C. f  x  0,x 1; .
D. f  x  0,x 0;2 .
Câu 7. Tam thức nào dưới đây luôn dương với mọi x   ? A. f  x 2  x  x 1. B. f  x 2
 x  2x 1 . C. f  x 2
 x  x 1. D. f  x 2  x  4x .
Câu 8. Bảng xét dấu nào sau đây là bảng xét dấu của tam thức f  x 2  x  x  6 ? A. . B. . C. . D. . Câu 9. Tam thức 2
y  x  2x 3 nhận giá trị dương khi và chỉ khi
A. x  –3 hoặc x  –1. B. x  –1 hoặc x  3. C. x  –2 hoặc x  6 . D. –1 x  3.
Câu 10. Tam thức nào sau đây nhận giá trị âm với mọi x  2 ? A. 2 x  5x  6 . B. 2 16  x . C. 2 x  2x  3 . D. 2 x  5x  6 .
Câu 11. Cho tam thức f  x 2
 x  8x 16 . Khẳng định nào sau đây là đúng?
A. Phương trình f  x  0 vô nghiệm.
B. f  x  0 với mọi x  .
C. f  x  0 với mọi x  .
D. f  x  0 khi x  4 .
Câu 12. Tìm tập xác định của hàm số 2 y  2x  5x  2 .  1   1  1  A. D   ;   . B. [2; ) . C.  ;  [2;)  . D. ; 2 . 2   2    2   
Câu 13. Tập nghiệm của bất phương trình 2 2x 14x  20  0 là
A. S  ;25; .
B. S  ;2  5;  . C. S  2;5 . D. S  2;5.
Câu 14. Bất phương trình 2
x  2x  3 có bao nhiêu nghiệm nguyên? A. 5 . B. 4 . C. 3 . D. 2 . Câu 15. Để f x 2  x  m  
1 x  2m  7  0 với mọi x thì A. 3   m  9 .
B. m  3  m  9 . C. 3   m  9 . D. m  3  m  9 . Câu 16. Cho 2 f (x)  2
 x  (m  2)x  m  4 . Tìm m để f (x) âm với mọi x. A. 14  m  2 . B. 14  m  2 . C. 2   m  14 . D. m  1  4 hoặc m  2 .
Câu 17. Tìm tất cả giá trị của tham số m để bất phương trình 2
x  2x  m 1  0 vô nghiệm A. m  0 . B. m  0 . C. m  0 . D. m  0 .
Câu 18. Tìm tất cả các giá trị của tham số m để bất phương trình m   2 1 x  2m   1 x  3m  8  0
nghiệm đúng với mọi x   . 3 3 A. m  1  . B. m  3 . C. m   . D.   m  3 . 2 2
Câu 19. Cho phương trình  m   2 2
1 x  2m  2 x  m  4  0 . Tất cả các giá trị của m để phương trình đã
cho có hai nghiệm trái dấu là  1  1 m  1 1 m  A.  2       . B. m 4 . C. m 4 . D. 2 . 2 2  m  4 m  4 Câu 20. Phương trình 2 x  m  
1 x 1  0 vô nghiệm khi và chỉ khi A. m 1. B. 3  m  1.
C. m  3 hoặc m 1. D. 3  m 1.
Bài 18. Phương trình quy về phương trình bậc 2 Câu 1. Phương trình 2
x  3x  4  2x  2 có tập nghiệm là A.  2  ;  3 . B.  1  ;  6 . C.  3  ;  2 . D. 6;  1 .
Câu 2. Tập nghiệm của phương trình 2
2x  9x  9  3  x là A.   6 . B. . C.   3  . D.  3  ;  6 .
Câu 3. Số nghiệm của phương trình 2 x  3  3x 1 là A. 0 . B. 1. C. 2 . D. 3 .
Câu 4. Số nghiệm của phương trình 3x  2  x là A. 2 . B. 1. C. 3 . D. 0 . Câu 5. Phương trình 2
2x  3x  5  x 1 có nghiệm là A. x  1 . B. x  2 . C. x  3 . D. x  4 .
Câu 6. Tổng các nghiệm của phương trình: 2x 1  x  2 bằng: A. 6 . B. 1 . C. 5 . D. 2 .
Các câu hỏi trong bài 19, 20, 21 đều xét trong mặt phẳng tọa độ Oxy
Bài 19. Phương trình đường thẳng
Câu 1. Một vectơ pháp tuyến của đường thẳng 2x  3y  6  0 là     A. n  2;  3 . B. n  2;3 . C. n  3; 2 . D. n  3  ;2 . 1   3   2   4   x  2  3t
Câu 2. Một vectơ chỉ phương của đường thẳng  là  y  3   t     A. u  2; –3 . B. u  3; –1 . C. u  3; 1 . D. u  3; –3 . 4   3   2   1  
Câu 3: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm A 3  ;2 và B 1;4?     A. u  1; 2 . B. u  2;1 . C. u  2  ;6 . D. u  1;1 . 4   3   2   1  
Câu 4. Đường thẳng chứa trục Ox có vectơ chỉ phương là     A. u  1;0 . B. u  1;1 . C. u  0;6 . D. u  0; 1  . 4   3   2   1  
Câu 5. Đường thẳng chứa trục Ox có vectơ pháp tuyến là     A. u  1; 0 . B. u  1;1 . C. u  1  ;0 . D. u  0; 1  . 4   3   2   1   x y
Câu 6. Vectơ chỉ phương của đường thẳng   1 là 3 2     A. u4   2  ;3 B. u2  3; 2 C. u3  3;2 D. u1  2;3
Câu 7. Cho đường thẳng d  : 3x  7y 15  0. Mệnh đề nào sau đây sai?  3
A. u  7;3 là vecto chỉ phương của d  .
B. d  có hệ số góc k  . 7  1 
C. d  không đi qua góc tọa độ.
D. d  đi qua hai điểm M  ;2   và N 5;0 .  3 
Câu 8. Đường thẳng nào trong các đáp án sau có hệ số góc bằng 1. 8 x  2  t x  2   4t x  2  t x  2  2t A.  . B.  . C.  . D.  .  y  3  2t  y  3 2t  y  2   3t  y  3  2t
Câu 9. Cho đường thẳng  có phương trình tổng quát: –2x  3y –1  0 . Vectơ nào sau đây là vectơ chỉ
phương của đường thẳng  . A. 3;2. B. 2;3. C. –3;2. D. 2; –3.
Câu 10. Mệnh đề nào sau đây đúng? Đường thẳng d  : x  2y  5  0 : x  t A. Đi qua A1; 2   .
B. Có phương trình tham số:  t R.  y  2  t 1
C. d  có hệ số góc k  .
D. d  cắt d có phương trình: x  2y  0 . 2 
Câu 11. Viết phương trình tham số của đường thẳng đi qua A3;4 và có vectơ chỉ phương u  3; 2   x  3  3t x  3  6t x  3  2t x  3  3t A.  . B.  . C.  . D.  .  y  2  4t  y  2  4t  y  4  3t  y  4  2t 
Câu 12. Đường thẳng đi qua A 1
 ;2, nhận n  2; 4
  làm vectơ pháp tuyến có phương trình là A. x  2y  4  0 . B. x  y  4  0 . C. x  2y  5  0. D. x  2y  4  0 .
Câu 13. Cho hai điểm A1; 3   , B 2
 ;5 . Viết phương trình tổng quát của đường thẳng đi qua hai điểm , A B . A. 8x  3y 1  0 . B. 8x  3y 1  0. C. 3  x  8y  30  0 . D. 3  x  8y  30  0.
Câu 14. Phương trình tham số của đường thẳng qua M 1;  1 , N 4;3 là x  3 t x  1 3t x  3  3t x  1 3t A.  . B.  . C.  . D.  . y  4  t  y  1 4t  y  4  3t  y  1 4t
Câu 15. Cho ba điểm A1; 2  , B5; 4  ,C 1  ;4. Đường cao A 
A của tam giác ABC có phương trình A. 3x  4 y  8  0 . B. 3x  4 y 11  0 .
C. 6x  8y 11  0 . D. 8x  6 y 13  0 .
Câu 16. Cho hai điểm A1; 2   , B 1
 ;2. Đường trung trực của đoạn thẳng AB có phương trình là A. 2x  y  0 . B. x  2 y  0 . C. x  2 y  0 . D. x  2 y 1  0 .
Câu 17. Lập phương trình tổng quát đường thẳng đi qua điểm A2; 
1 và song song với đường thẳng 2x  3y  2  0 . A. 3x  2 y 8  0 . B. 2x  3y  7  0 . C. 3x  2 y  4  0 . D. 2x  3y  7  0 . x  2  3t
Câu 18 Cho đường thẳng  : 
t  và điểm M  1
 ; 6. Phương trình đường thẳng đi qua  y  1 t
M và vuông góc với  là A. 3x  y  9  0 . B. x  3y 17  0 . C. 3x  y  3  0 . D. x  3y 19  0 .
Câu 19. Cho đường thẳng d :x  2y 1  0 và điểm M 2;3 . Phương trình đường thẳng  đi qua điểm
M và vuông góc với đường thẳng d là A. x  2y 8  0 . B. x  2y  4  0 . C. 2x  y 1  0 . D. 2x  y  7  0 .
Câu 20. Cho tam giác ABC có A 2  ;3, B1; 2  ,C  5
 ;4.Đường trung trực trung tuyến AM có phương trình tham số x  2 x  2   4t x  2  t x  2  A.  B.  C.  D.  3  2t.  y  3 2t.  y  2   3t.  y  3  2t.
Câu 21. Cho tam giác ABC với A2;4 ; B2; 
1 ; C 5;0 . Trung tuyến CM đi qua điểm nào dưới đây?  9   5  A. 14;   . B. 10;    . C.  7  ; 6. D.  1  ;5 .  2   2  9
Bài 20. Vị trí tương đối của hai đường thẳng. Góc và khoảng cách
Câu 1. Góc giữa hai đường thẳng  : a x  b y  c  0 và  : a x  b y  c  0 được xác định theo công 1 1 1 1 2 2 2 2 thức: a a  b b a a  b b A. cos ,   1 2 1 2  . B. cos  ,   . 1 2  1 2 1 2 1 2 2 2 2 2 a  b . a  b 2 2 2 2 a  b . a  b 1 1 2 2 1 1 2 2 a a  b b a a  b b  c c C. cos ,   1 2 1 2  . D. cos  ,   . 1 2  1 2 1 2 1 2 1 2 2 2 2 2 a  b  a  b 2 2 a  b 1 1 1 1 x   t
Câu 2. Giao điểm M của d  1 2 : 
và d : 3x  2y 1  0 . Toạ độ của M là y  3   5t  11  1   1   1  A. M 2;  .   B. M 0; .   C. M 0;  .   D. M  ; 0 .    2   2   2   2 
Câu 3. Cho đường thẳng d : 2x  3y 15  0 và d : x  2 y  3  0 . Khẳng định nào sau đây đúng? 1 2
A. d và d cắt nhau và không vuông góc với nhau. B. d và d song song với nhau. 1 2 1 2
C. d và d trùng nhau. D. d và d vuông góc với nhau. 1 2 1 2 x  3 4t x  2  2t
Câu 4. Vị trí tương đối của hai đường thẳng d : và d : là 1    y  2  6t 2  y  8   4t A. trùng nhau. B. song song.
C. vuông góc với nhau. D. cắt nhau nhưng không vuông góc nhau. x  1   3t
Câu 5. Cho đường thẳng d : 4x+3y-2=0 và d’ : 
. Khi đó hai đường thẳng  y  2  4t
A. trùng nhau. B. song song.
C. cắt nhau nhưng không vuông góc. D. vuông góc.
Câu 6. Phương trình nào sau đây biểu diển đường thẳng không song song với đường thẳng d  : y  2x 1 ? A. 2x  y  5  0. B. 2x  y  5  0. C. 2x  y  0. D. 2x  y  5  0.
Câu 7. Góc giữa hai đường thẳng a : 3x  y  7  0 và b : x  3y 1  0 là A. 30 . B. 90 . C. 60 . D. 45 .
Câu 8. Với giá trị nào của m thì hai đường thẳng  : 3x  4y 1  0 và  : 2m 1 x  m y 1  0 2    2 1  trùng nhau. A. m  2 . B. mọi m . C. không có m . D. m  1  .
Câu 9. Cho ba đường thẳng lần lượt có phương trình d : 3x  4 y 15  0 , d : 5x  2 y 1  0 và 1 2
d : mx  2m 1 y  9m 13  0 . Tìm tất cả các giá trị của tham số m để ba đường thẳng đã cho cùng đi 3   qua một điểm. 1 1 A. m  . B. m  5  . C. m   . D. m  5. 5 5
Câu 10. Tìm côsin góc giữa 2 đường thẳng  : x  2y  2  0 và  : x  y  0 . 1 2 10 2 3 A. . B. 2. C. . D. . 10 3 3 x  10  6t
Câu 11. Tìm góc giữa 2 đường thẳng  : 6x  5y 15  0 và  :  . 1 2 y  1 5t A. 90 . B. 60 . C. 0 . D. 45 .
Câu 12. Đường thẳng ax  by  3  0, a, b   đi qua điểm M 1; 
1 và tạo với đường thẳng
 : 3x  y  7  0 một góc 45 . Khi đó a  b bằng 10 A. 6. B. 4  . C. 3. D. 1.
Câu 13. Cho d : 3x  y  0 và d ': mx  y 1  0 . Tìm m để d d  1 cos , '  10 A. m  4 0 . B. m  hoặc m  3
0 . C. m  hoặc m  0 . D. m   3 . 3 4 x  2  at
Câu 14. Xác định giá trị của a để góc tạo bởi hai đường thẳng  và đường thẳng  y  1 2t
3x  4y 12  0 một góc bằng 45. 2 A. a  ; a   2 14 . B. a  ; a  14 . C. a  1; a  14 . D. a  2  ;a  1  4 . 7 7
Câu 15. Lập phương trình  đi qua A2; 
1 và tạo với đường thẳng d : 2x  3y  4  0 một góc 45 . 
A. 5x  y 11  0; x  5y  3  0.
B. 5x  y 11  0; x  5y  3  0.
C. 5x  y 11  0; x  5 y  3  0.
D. 5x  2 y 12  0; 2x  5 y 1  0.
Câu 16. Cho điểm M  x ; y  : ax  by  c  0 2 2 a  b  0 0 0  và đường thẳng với . Khi đó khoảng cách d là M ; ax  by  c ax  by  c A. 0 0 d  . B. 0 0 d  . M ; 2 2 2 a  b  c M ; 2 2 2 a  b  c ax  by  c ax  by  c C. 0 0 d  . D. 0 0 d  . M ; 2 2 a  b M ; 2 2 a  b
Câu 17. Khoảng cách từ điểm M 5; 
1 đến đường thẳng  : 3x  2 y 13  0 là 13 28 A. . B. 2 . C. . D. 2 13 . 2 13 x  2  3t
Câu 18. Khoảng cách từ điểm M 15; 
1 đến đường thẳng  :  là  y  t A. 5 1 . B. . C. 10 16 . D. . 10 5
Câu 19. Cho đường thẳng  : 21x 11y 10  0 . Trong các điểm M 20; 3
  , N 0;4, P19;5 , Q1;5
điểm nào cách xa đường thẳng  nhất? A. N . B. M . C. P . D. Q .
Câu 20. Khoảng cách giữa hai đường thẳng d : 3x  4y  6  0 d : 6x 8y 13  0 1 và 2 bằng 1 5 1 A. . B. . C. 5. D. . 10 2 5
Câu 21. Cho đường thẳng d: x – y + 3 = 0. Phương trình đường thẳng song song với d và cách d một khoảng bằng 2 là
A. x  y 1  0 và x  y  3  0 . B. x  y 1  0 . C. x  y  3  0 .
D. x  y  3  0 và x  y 1  0 .
Bài 21. Đường tròn trong mặt phẳng tọa độ
Câu 1. Xác định tâm và bán kính của đường tròn C  x  2   y  2 : 1 2  9. A. Tâm I  1
 ;2, bán kính R  3. B. Tâm I  1
 ;2, bán kính R  9. 11 C. Tâm I 1; 2  , bán kính R  3. D. Tâm I 1; 2  , bán kính R  9.
Câu 2. Phương trình đường tròn có tâm I 1; 2 và bán kính R  5 là A. 2 2
x  y  2x  4y  20  0 . B. 2 2
x  y  2x  4y  20  0 . C. 2 2
x  y  2x  4y  20  0 . D. 2 2
x  y  2x  4y  20  0 . Câu 3. Để 2 2
x  y  2ax  2by  c  0 (1) là phương trình đường tròn, điều kiện cần và đủ là A. 2 2 a  b  c  0 . B. 2 2 a  b  c  0 . C. 2 2 a  b  4c  0 . D. 2 2 a  b  4c  0 .
Câu 4. Phương trình nào sau đây là phương trình của đường tròn? (I) 2 2
x  y  4x 15y 12  0 . (II) 2 2
x  y  3x  4y  20  0 . (III) 2 2
2x  2y  4x  6 y 1  0 . A. Chỉ (I). B. Chỉ (II). C. Chỉ (III). D. Chỉ (I) và (III). Câu 5. Đường tròn 2 2
3x  3y – 6x  9 y  9  0 có bán kính bằng bao nhiêu? 15 5 A. . B. . C. 25 . D. 5 . 2 2
Câu 6. Tâm của đường tròn 2 2
x  y 10x 1  0 cách trục Oy một khoảng bằng A. 5. B. 0. C. 10. D. -5.
Câu 7. Đường tròn tâm I (3; 1) và bán kính R  2 có phương trình là A. 2 2
(x  3)  ( y 1)  4 . B. 2 2
(x  3)  ( y 1)  4 . C. 2 2
(x  3)  ( y 1)  4 . D. 2 2
(x  3)  ( y 1)  4 .
Câu 8. Đường tròn tâm I (1; 2) và đi qua điểm M (2;1) có phương trình là A. 2 2
x  y  2x  4y  5  0 . B. 2 2
x  y  2x  4y  3  0. C. 2 2
x  y  2x  4 y  5  0 . D. 2 2
x  y  2x  4y  5  0.
Câu 9. Cho hai điểm A(5; 1) , B(3;7) . Đường tròn có đường kính AB có phương trình là A. 2 2
x  y  2x  6y  22  0 . B. 2 2
x  y  2x  6y  22  0. C. 2 2
x  y  2x  y 1  0 . D. 2 2
x  y  6x  5y 1  0.
Câu 10. Đường tròn (C) tâm I (4;3) và tiếp xúc với trục tung có phương trình là A. 2 2
x  y  4x  3y  9  0 . B. 2 2
(x  4)  ( y  3)  16 . C. 2 2
(x  4)  ( y  3)  16 . D. 2 2
x  y  8x  6 y 12  0.
Câu 11. Đường tròn (C) tâm I (4; 3) và tiếp xúc với đườngthẳng  : 3x  4 y  5  0 có phương trình là A. 2 2
(x  4)  ( y  3)  1. B. 2 2
(x  4)  ( y  3)  1. C. 2 2
(x  4)  ( y  3)  1. D. 2 2
(x  4)  ( y  3)  1.
Câu 12. Cho ba điểm A3; 5 , B 2; 3 , C 6; 2 . Đường tròn ngoại tiếp tam giác ABC có phương trình là A. 2 2
x  y  25x 19 y  68  0 . B. 2 2
3x  3y  25x 19y  68  0 . C. 2 2
x  y  25x 19 y  68  0 . D. 2 2
3x  3y  25x 19y  68  0 .
Câu 13. Cho đường tròn C   x  2   y  2 : 3
1  10 . Phương trình tiếp tuyến của C tại A4;4 là A. x  3y  5  0 . B. x  3y  4  0. C. x  3y 16  0 . D. x  3y 16  0 .
Câu 14. Cho đường tròn (C): x2 + y2 – 2x – 4y – 4 = 0 và điểm A(1; 5). Tiếp tuyến của đường tròn (C) tại
điểm A có phương trình là
A. y – 5 = 0. B. y + 5 = 0. C. x + y – 5 = 0. D. x – y – 5 = 0. B. TỰ LUẬN
Bài 1. Vẽ các parabol sau trên mặt phẳng Oxy. 12 a. 2
(P) : y  x  4x  3 . b. 2 (P) : y  x  2x c. 2
(P) : y  2x  4x  3 d. 1 3 2
(P) : y   x  x  Bài 2. Xác định parabol 2
y  ax  bx 1 trong mỗi trường hợp sau 2 2
a. Đi qua điểm M(1;-2) và N(-2;19). b. Có đỉnh I (-2;37)
c. Có trục đối xứng là x = -1 và tung độ của đỉnh bằng 5. Bài 3. Xác định parabol 2
y  ax  bx  c trong mỗi trường hợp sau
a. Có đỉnh I (1;2) và đi qua điểm M(0;3).
b. Đi qua điểm A (1;2) và có tung độ của điểm thấp nhất bằng 2.
Bài 3. Giải các bất phương trình a. 2 3x  2x 1  0 b. 2 36x 12x 1  0 c. 2 2 2
(x  x)  3(x  x)  2  0 2 2x 3 4x 3x 2 x  2x  3 d. 3 1. e.  2 2 2 x  2 x  2 2 x 1
Bài 4. Giải các phương trình sau a. 2 2
x  77x  212  x  x  2 b. 2 2 x  25x  26  x  x c. 2
2x 13x 16  6  x d. 2
x  3x 1  x  4 e. 2x  3  x  3 .
Bài 5. Cho tam thức f  x 2
 x  2mx  m  90 . Xác định tham số m để a. f  x  0 x
  b. f x  0 x
  c. f x  0 x  0;2
Bài 6. Cho tam thức f  x 2
 x  2mx  m 110 . Xác định tham số m để a. f  x  0 x
  b. f x  0 x
  c. f  x  0 x  3;
Bài 7. Tìm tất cả các giá trị của m để hàm số sau xác định với mọi x   . f  x 1  2
(m 1)x  2(m  2)x  2  m
Bài 8. Tìm tất cả các giá trị của tham số m để bất phương trình sau nghiệm đúng với x    2 2
3x  2(m 1)x  2m  3m  2  0 .
Bài 9. Tìm tất cả các giá trị của tham số m để bất phương trình sau vô nghiệm m  2
2 x  2m  4 x  2m 8  0 .
Bài 10. Một rạp chiếu phim có sức chứa 1000 người. Với giá vé là 40.000đ trung bình sẽ có khoảng 300
người đến rạp xem phim mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu phim đã khảo sát thị trường và
thấy rằng nếu giá vé cứ giảm 10.000đ thì sẽ có thêm 100 người đến rạp mỗi ngày. Tìm mức giá vé để
doanh thu từ tiến bán vé mỗi ngày của rạp là lớn nhất. Bài 11.
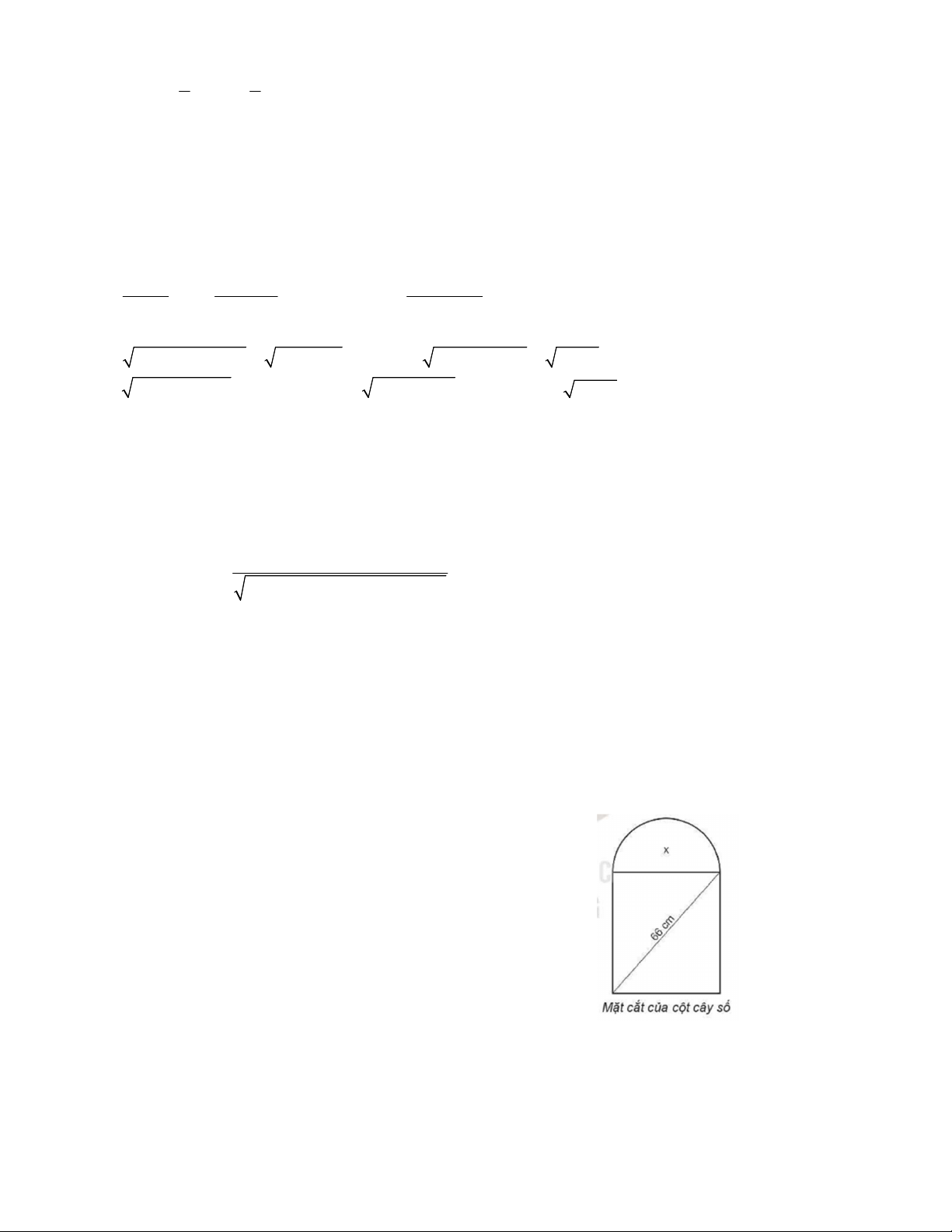
Mặt cắt đứng của cột cây số trên quốc lộ có dạng nửa hình tròn ở
phía trên và phía dưới có dạng hình chữ nhật (xem hình bên). Biết
rằng đường kính của nửa hình tròn cũng là cạnh của hình chữ nhật.
Tim kích thước của hình chữ nhật, biết rằng diện tích của phần nửa
hình tròn bằng 0,3 lần diện tích của hình chữ nhật. Lấy   3,14 và
làm tròn kết quả đến chữ số thập phận thứ hai.
Bài 12. Trong mặt phẳng Oxy, cho ba điểm A (-1;0), B(1;2), C(3;3).
a. Viết phương trình tham số và phương trình tổng quát của đường thẳng AB.
b. Viết phương trình đường trung trực của đoạn thẳng AB.
c. Viết phương trình đường thẳng đi qua A và vuông góc với BC.
d. Viết phương trình đường thẳng đi qua A và song song với BC.
Bài 13. Trong mặt phẳng Oxy, cho tam giác MNP có M (2;1), N(-3;0), P(1;4)
a. Viết phương trình tổng quát của đường cao kẻ từ M của tam giác MNP. Tính diện tích tam giác MNP.
b. Viết phương trình tổng quát của đường trung tuyến kẻ từ N của tam giác MNP.
c. Viết phương trình của đường trung bình của tam giác ứng với cạnh MN của tam giác MNP.
Bài 14. Trong mặt phẳng Oxy, cho đường thẳng  : 2x  y  5  0 .
a. Viết phương trình đường thẳng đi qua điểm A (3;1) và song song với với đường thẳng .
b. Viết phương trình đường thẳng đi qua điểm B (-1;0) và vuông góc với với đường thẳng .
c. Viết phương trình đường thẳng song song với đường thẳng  và cách điểm O một khoảng bằng 5 .
d. Tìm tọa độ hình chiếu vuông góc của điểm M (2;-3) trên đường thẳng . x  2  t
Bài 15. Trong mặt phẳng Oxy, cho điểm M(2;1) và đường thẳng  :  .  y  2t
a. Tìm điểm N thuộc đường thẳng  sao cho MN  2 .
b. Tim điểm A thuộc đường thẳng  sao cho tam giác ABC vuông tại A với B(1;1), C(-5;0).
Bài 16. Trong mặt phẳng Oxy, viết phương trình đường tròn (C) biết
a. Có tâm I(3;1) và bán kính R  2 .
b. Đường kính AB với A(4;1), B(-2;-5).
c. Có tâm I(3;1) và đi qua điểm M(-1;7). d. Có tâm I  1
 ;2 và tiếp xúc với đường thẳng  : x  2y  7  0 .
e. Có tâm I thuộc đường thẳng  : x  y 1  0 và đi qua hai điểm P(6;2), Q(-1;3).
Bài 17. Trong mặt phẳng Oxy, cho đường tròn (C) có phương trình 2 2
x  y  6x  4 y 12  0 . Viết phương
trình tiếp tuyến của đường tròn (C) tại điểm M(0;-2).
--------------------------HẾT---------------------- 14