Đề cương môn cơ học lý thuyết- Trường Đại học bách khoa - Đại học đà nẵng.

HỌC VIỆN KỸ THUẬT QUÂN SỰ BÀI TẬP LỚN
CƠ HỌC LÝ THUYẾT 1
Học viên thực hiện: Dương Văn Sơn
Lớp: Xe Quân sự 1 – c449 – d4
Giảng viên: Nguyễn Thị Cẩm Nhung
Hà Nội, tháng 11 năm 2014
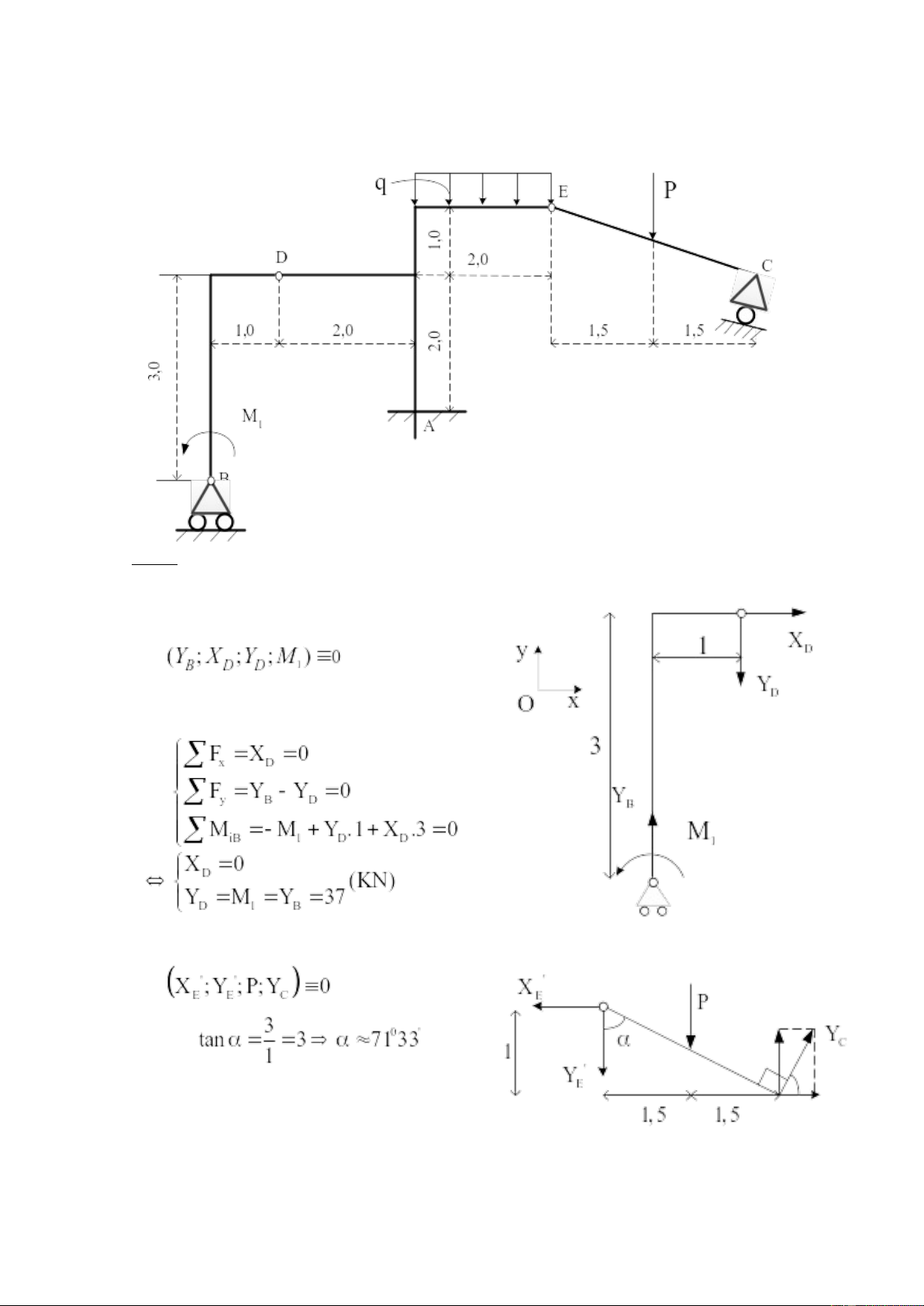
Bài 1: (Hình C-5C-26, trang 46)
Cho sơ đồ kết cấu như hình vẽ.
P = 12,0 KN; M1 = 37,0 KN.m; q = 1,1KN/cm = 110 KN/m.
Tìm phản lực liên kết của các gối tựa và áp lực trong các khớp cầu trung gian. Giải:
Chúng ta giải bài toán bằng phương pháp tách vật.
Chọn hệ trục tọa độ như hình vẽ.
1. Xét cân bằng thanh BD, ta có hệ lực cân bằng:
Các phương trình cân bằng lực:
2. Xét cân bằng thanh EC, ta có hệ lực cân bằng: Ta có:
Các phương trình cân bằng lực:
3. Xét cân bằng hệ DAE, ta có hệ cân bằng lực: Ta có:
Các phương trình cân bằng lực: Kết quả tính toán: Lực KN Mômen KN.m YB XD YD XA YA XE YE YC MA 37 0 37 -1,82 189,6 1,82 -6,6 5,68 312,66
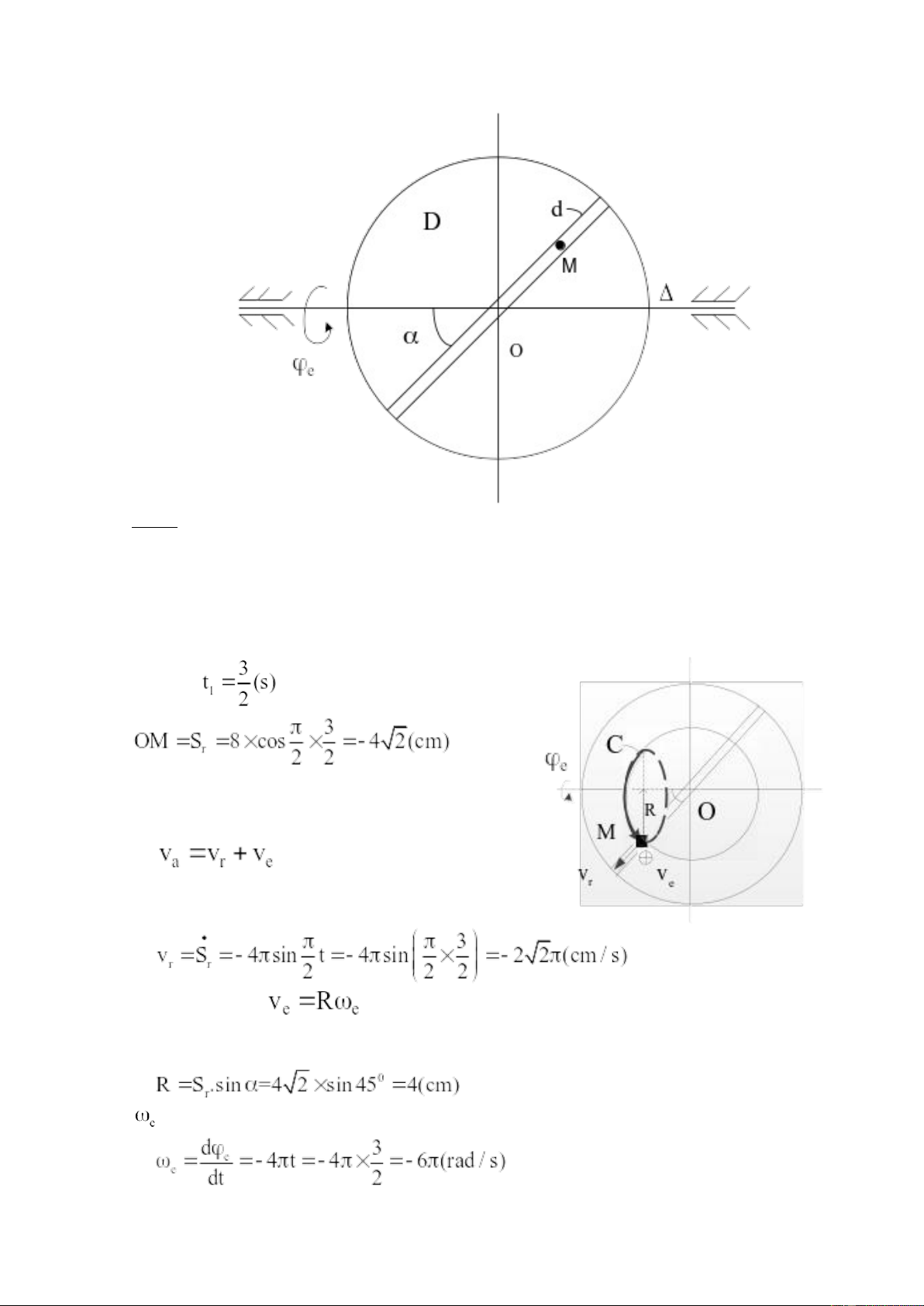
Bài 2: (Hình K-7C-26) Cho cơ hệ như hình vẽ. ; ;
Xác định vận tốc tuyệt đối, gia tốc tuyệt đối điểm M tại thời điểm t = t1. Giải:
1. Phân tích chuyển động của vật:
- Chuyển động tuyệt đối: chuyển động của M so với trục quay Δ.
- Chuyển động theo: chuyển động của đĩa tròn quanh trục Δ.
- Chuyển động tương đối: chuyển động của M trên máng d.
Vị trí của M trên đĩa tròn được xác định bằng khoảng cách OM = Sr Khi t = ta có: 2. Bài toán vận tốc.
Vận tốc tuyệt đối của M được xác định: - Vận tốc tương đối: - Vận tốc theo:
R là bán kính vòng tròn C, tâm I do trùng điểm của điểm M vạch ra tại thời điểm t1.
là vận tốc góc của đĩa tròn.
Vectơ phương tiếp tuyến với vòng tròn C theo chiều quay của vật. nên ta có: 3. Bài toán gia tốc: - Gia tốc tương đối: ngược chiều - Gia tốc theo: - Gia tốc Côriôlic: Ta xét thành phần - Gia tốc tuyệt đối:
Bài 3: ( Hình K-4c-26 )
Tìm vận tốc, gia tốc của điểm B, C trong cơ cấu. ,
OA = 25(cm), r = 20(cm), AC = 10(cm), Giải:
1. Phân tích chuyển động:
Cơ cấu trên là cơ cấu phẳng có ba khâu chuyển động.
- Đĩa I chuyển động quay quanh trục cố định qua O. - Tay quay OA quay quanh O.
- Đĩa D chuyển động song phẳng. Sự truyền động từ đĩa I và tay quay OA sang
đĩa D thực hiện nhờ sự ăn khớp trong giữa 2 đĩa I và D.
2. Bài toán vận tốc: Giải bài toán bằng phương pháp Vilit.
Chọn tay quay OA làm hệ quy chiếu động. Đứng trong hệ quy chiếu này, cặp đĩa I
và D là cặp đĩa ( bánh răng ) ăn khớp trong quay quanh các trục O và A với vận tốc góc tương đối và .
Theo định lý về tổng hợp hai chuyển quay quanh hai trục song song, ta có:
Ta có, về giá trị đại số:
Tỉ số truyền động giữa 2 đĩa: Chọn A làm điểm cực. theo chiều . - Tính theo chiều - Tính theo chiều 3. Bài toán gia tốc: Ta có không đổi nên ta có: Chọn A làm điểm cực. chiều từ A O theo chiều - Tính chiều từ C A - Tính