Đề cương môn cơ học lý thuyết- Trường Đại học bách khoa - Đại học đà nẵng.

BÀI GIẢNG CƠ HỌC LÝ THUYẾT
Giảng viên: TS. Phạm Toàn Thắng
Email: phamtoanthang@hcmut.edu.vn Phone: 0901640291
Bộ môn Cơ Kỹ thuật, P.707-H1 Khoa Khoa học Ứng dụng
Trường Đại học Bách Khoa-ĐHQG TP. HCM
môn Cơ Kỹ thuật – Khoa Khoa học Ứng d Bộ
ụng – Đại học Bách khoa Tp.HCM Downloaded Chương 7
CHUYỂN ĐỘNG PHỨC HỢP ĐIỂM NỘI DUNG
7.1. Mô hình bài toán và các định nghĩa
7.2. Định lý cộng vận tốc và gia tốc của chất điểm
7.3. Định lý cộng vận tốc và gia tốc của vật rắn
Chương 7. Chuyển động phức hợp điểm
9.1. Mô hình bài toán và các định nghĩa
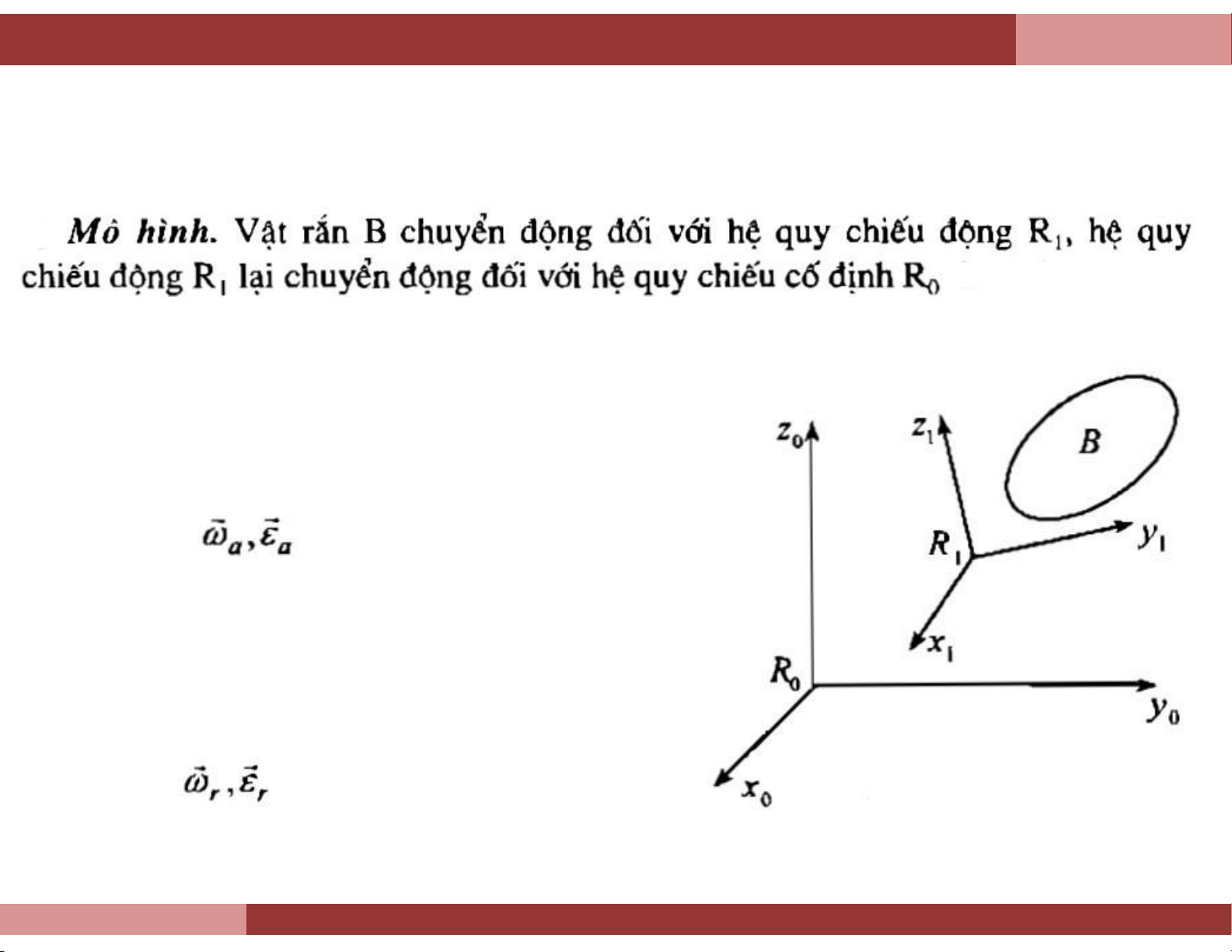
9.1.1. Chuyển động tuyệt đối, tương đối và chuyển động theo của vật rắn
Chuyển động tuyệt đối: Là chuyển động
của vật rắn B đối với hệ quy chiếu cố định.
Vận tốc và gia tốc gốc của vật rắn B xác
định trong hệ quy chiếu cố định R0 được
gọi là vận tốc góc tuyệt đối, gia tốc góc tuyệt đối:
Chuyển động tương đối: là chuyển động
của vật rắn B đối với hệ quy chiếu động
R1. Vận tốc góc, gia tốc góc của vật rắn là
là vận tốc tương đối và gia tốc tương đối, ký hiệu:
môn Cơ Kỹ thuật – Khoa Khoa học Ứng d
Chương 7. Chuyển động phức hợp điểm
9.1. Mô hình bài toán và các định nghĩa
9.1.1. Chuyển động tuyệt đối, tương đối và chuyển động theo của vật rắn
Chuyển động theo: là chuyển động của
hệ quy chiếu động R1 đối với hệ quy chiếu
cố định R0. Vận tốc góc theo và gia tốc góc theo, ký hiệu:
So sánh các định nghĩa trên với định nghĩa vận
tốc góc và gia tốc góc của vật rắn trong
chương trước, ta có các hệ thức:
Chương 7. Chuyển động phức hợp điểm
9.1. Mô hình bài toán và các định nghĩa
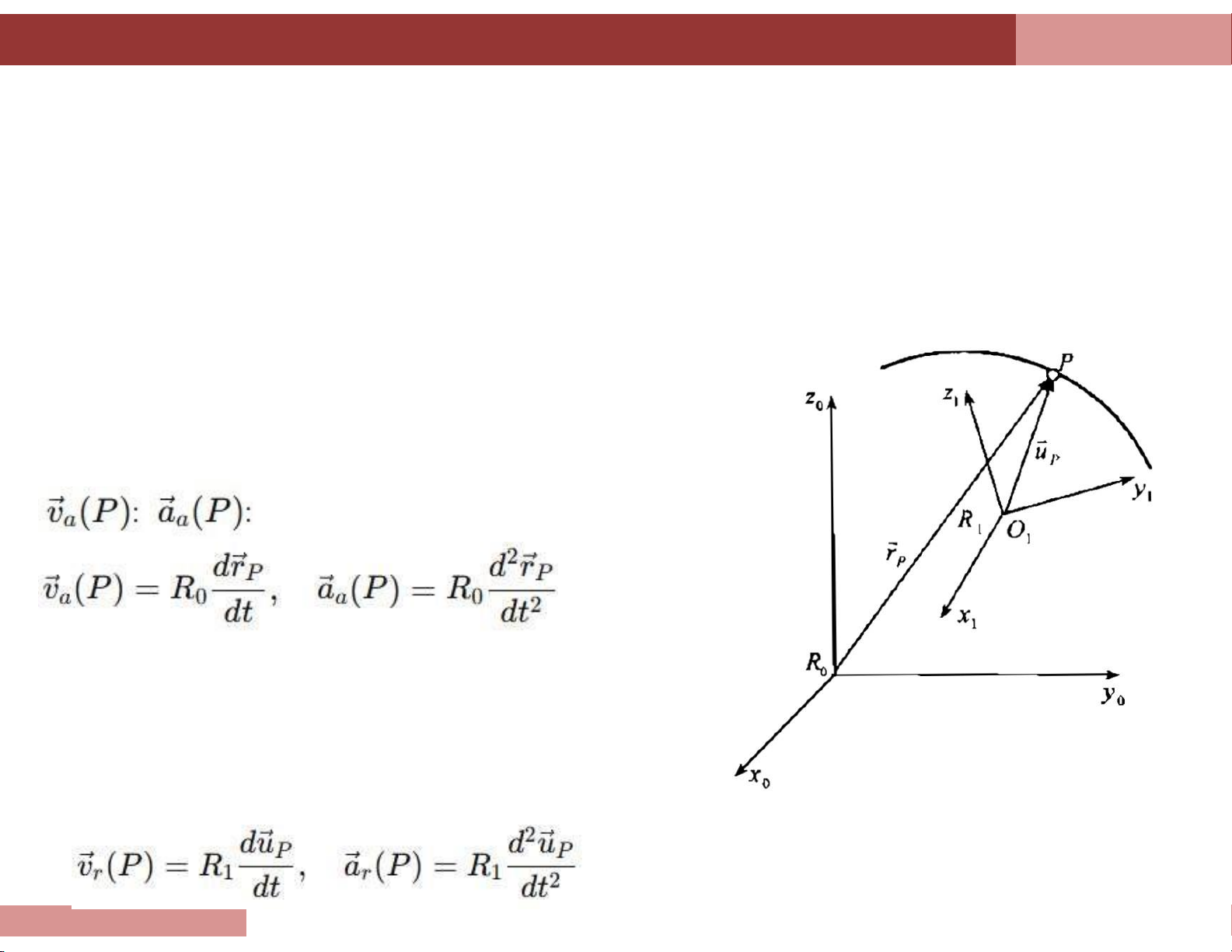
9.1.1. Chuyển động tuyệt đối, tương đối và chuyển động theo của chất điểm
Điểm P chuyển động đối với hệ quy chiếu chuyển động R1. Đồng thời, hệ
quy chiếu R1 lại chuyển động so với hệ quy chiếu cố định R0.
Chuyển động tuyệt đối: Là chuyển động của
điểm P đối với hệ quy chiếu cố định R0ếu cố
định. Vận tốc và gia tốc gốc của điểm P xác
định trong hệ quy chiếu cố định R0 được gọi là
vận tốc góc tuyệt đối, gia tốc góc tuyệt đối:
Chuyển động tương đối: là chuyển động của
điểm P đối với hệ quy chiếu động R1. Vận tốc
góc, gia tốc góc của điểm P là vận tốc tương
đối và gia tốc tương đối, ký hiệu:
Bộ môn Cơ Kỹ thuật – Khoa Khoa học Ứng d ụng – Đại học Bách khoa Tp.HCM
Chương 7. Chuyển động phức hợp điểm
9.2. Định lý cộng vận tốc và gia tốc của chất điểm
9.2.1. Định lý cộng vận tốc điểm (9.2.1)
Đạo hàm biểu thức (9.2.1) theo thời gian trong hệ quy chiếu R0, ta được: (9.2.2) Theo định nghĩa ta có
Vận tốc tương đối: (9.2.3) Vận tốc kéo theo: (9.2.4)
Chương 7. Chuyển động phức hợp điểm
9.2. Định lý cộng vận tốc và gia tốc của chất điểm
9.2.1. Định lý cộng vận tốc điểm
Vậy từ (9.2.2) thu được công thức cộng vậ t n ốc: (9.2.5) Định lý 9.1:
Tại mỗi thời điểm, vận tốc tuyệt đối của điểm P bằng tổng hình học của vận tốc
tương đối và vận tốc kéo theo của nó.
môn Cơ Kỹ thuật – Khoa Khoa học Ứng d
Chương 7. Chuyển động phức hợp điểm
9.2. Định lý cộng vận tốc và gia tốc của chất điểm
9.2.2. Định lý cộng gia tốc điểm (9.2.1)
Đạo hàm hai lần biểu thức (9.2.1) theo thời gian t ta được: (9.2.6)
Chương 7. Chuyển động phức hợp điểm
9.2. Định lý cộng vận tốc và gia tốc của chất điểm
9.2.1. Định lý cộng gia tốc điểm Chú ý rằng (9.2.7)
Thế (9.2.7) vào (9.2.6) ta được công thức cộng gia tốc: Trong đó: được gọi là
gia tốc Coriolis, mang tên nhà vật lý và kỹ sư người Pháp
Gaspard Gustave de Coriolis (1792–1843). Định lý 9.2:
Ở mỗi thời điểm, gia tốc tuyệt đối của điểm P bằng tổng hình học gia tốc tương đối, gia
tốc theo, và gia tốc Coriolis của nó. Bộ
môn Cơ Kỹ thuật – Khoa Kh oa học Ứng d
Chương 7. Chuyển động phức hợp điểm
9.3. Định lý cộng vận tốc và gia tốc gốc của vật rắn
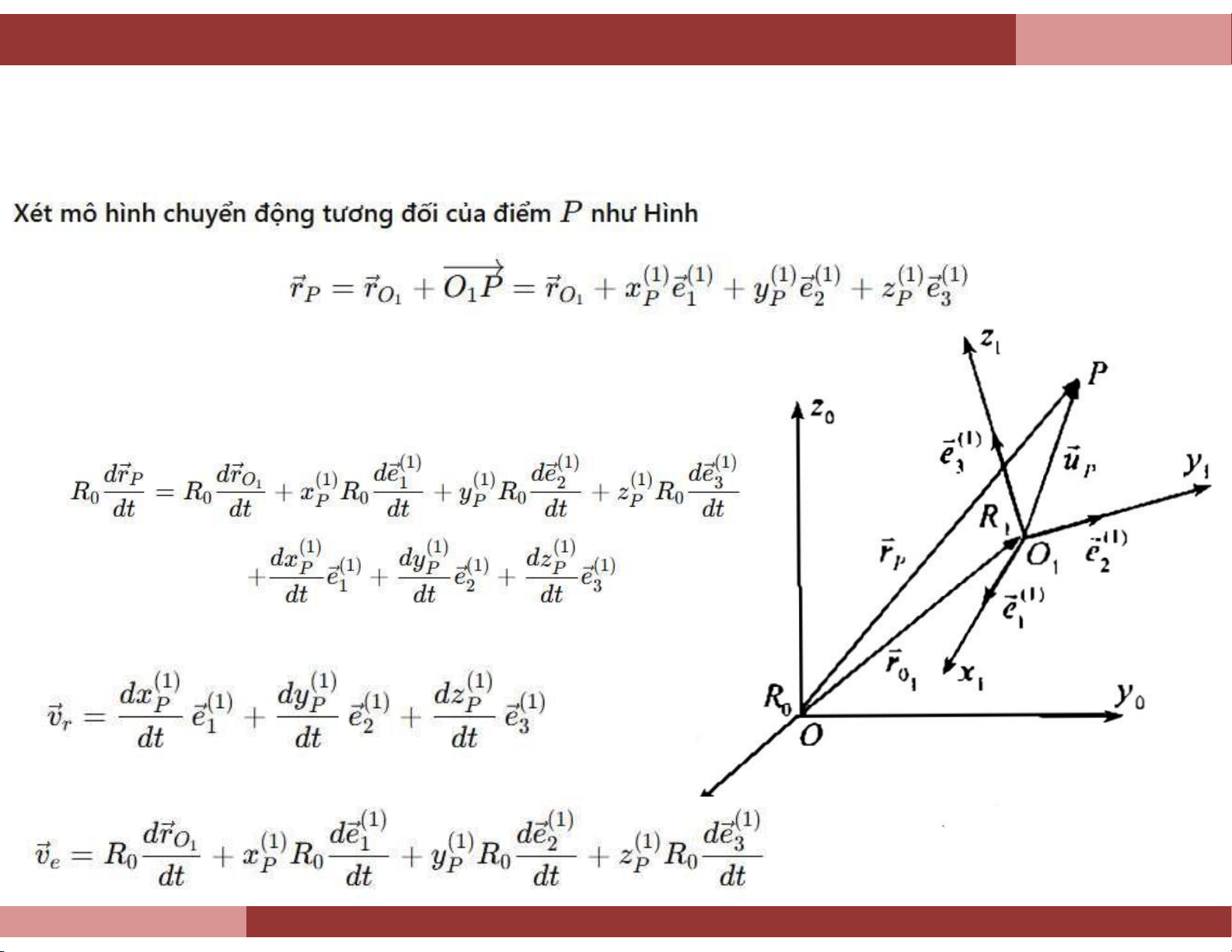
9.3.1. Đạo hàm của vector trong các hệ quy chiếu khác nhau
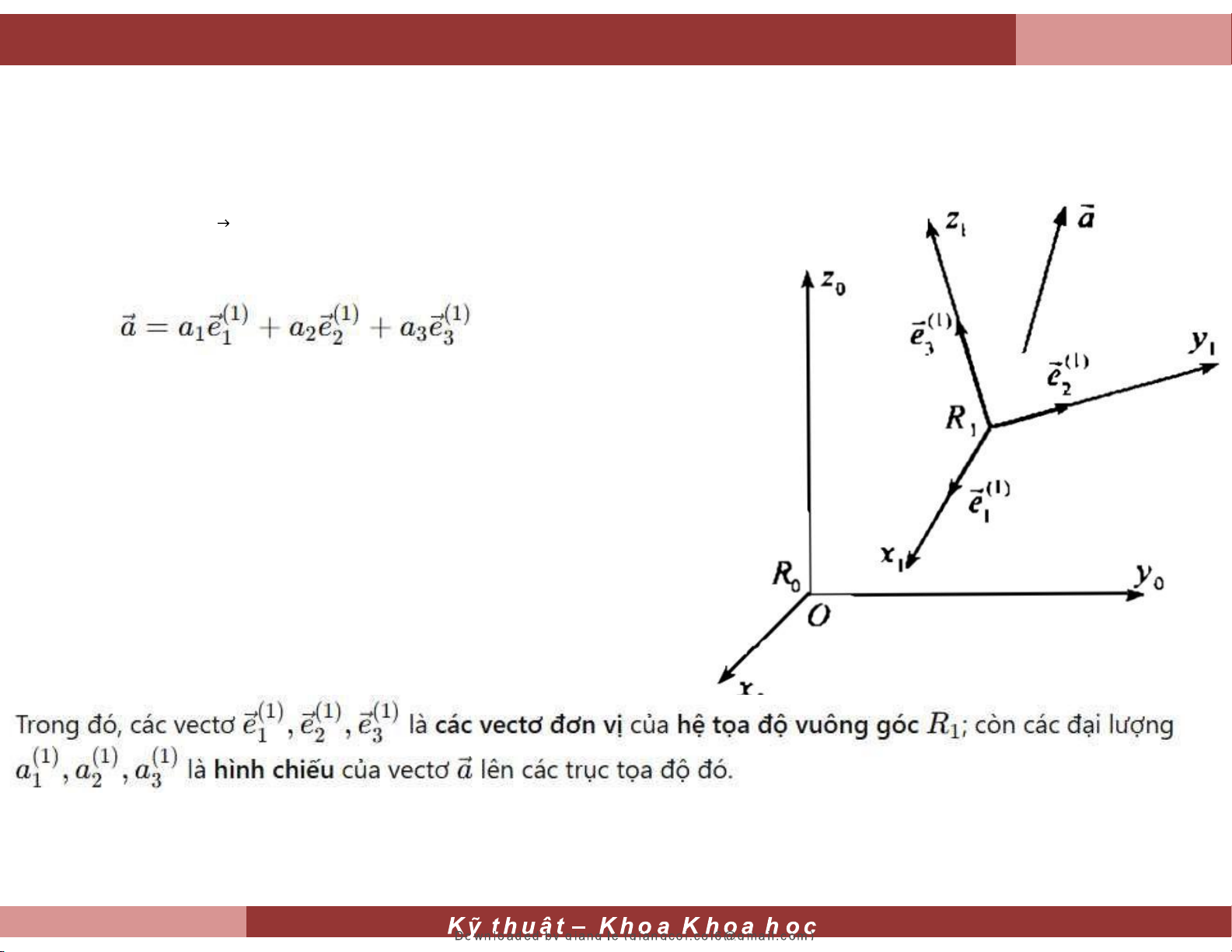
Cho vectơ a thay đổi theo thời gian trong hệ quy chiếu R1 Bộ môn Cơ
Ứng dụng – Đại học Bách khoa Tp.HCM
Chương 7. Chuyển động phức hợp điểm
9.3. Định lý cộng vận tốc và gia tốc gốc của vật rắn
9.3.1. Đạo hàm của vector trong các hệ quy chiếu khác nhau
Cho vectơ a thay đổi theo thời gian
trong hệ quy chiếu R1 (9.3.1) (9.3.2 (9.3.3)
Thế (9.3.1) vào (9.3.2) ta có
biểu diễn mối quan hệ giữa đạo
hàm của vectơ a trong hai hệ
(9.3.4) quy chiếu khác nhau — hệ cố
định R0 và hệ chuyển động R1
Chương 7. Chuyển động phức hợp điểm
9.3. Định lý cộng vận tốc và gia tốc gốc của vật rắn
9.3.2. Định lý cộng vận tốc của vật rắn (9.3.5) (9.3.6)
Mặt khác, theo (9.3.4), ta có (9.3.7)
Thế biểu thức (9.3.5) và (9.3.6) vào (9.3.7), ta có (9.3.8) hay
Chương 7. Chuyển động phức hợp điểm
9.3. Định lý cộng vận tốc và gia tốc gốc của vật rắn
9.3.2. Định lý cộng vận tốc của vật rắn
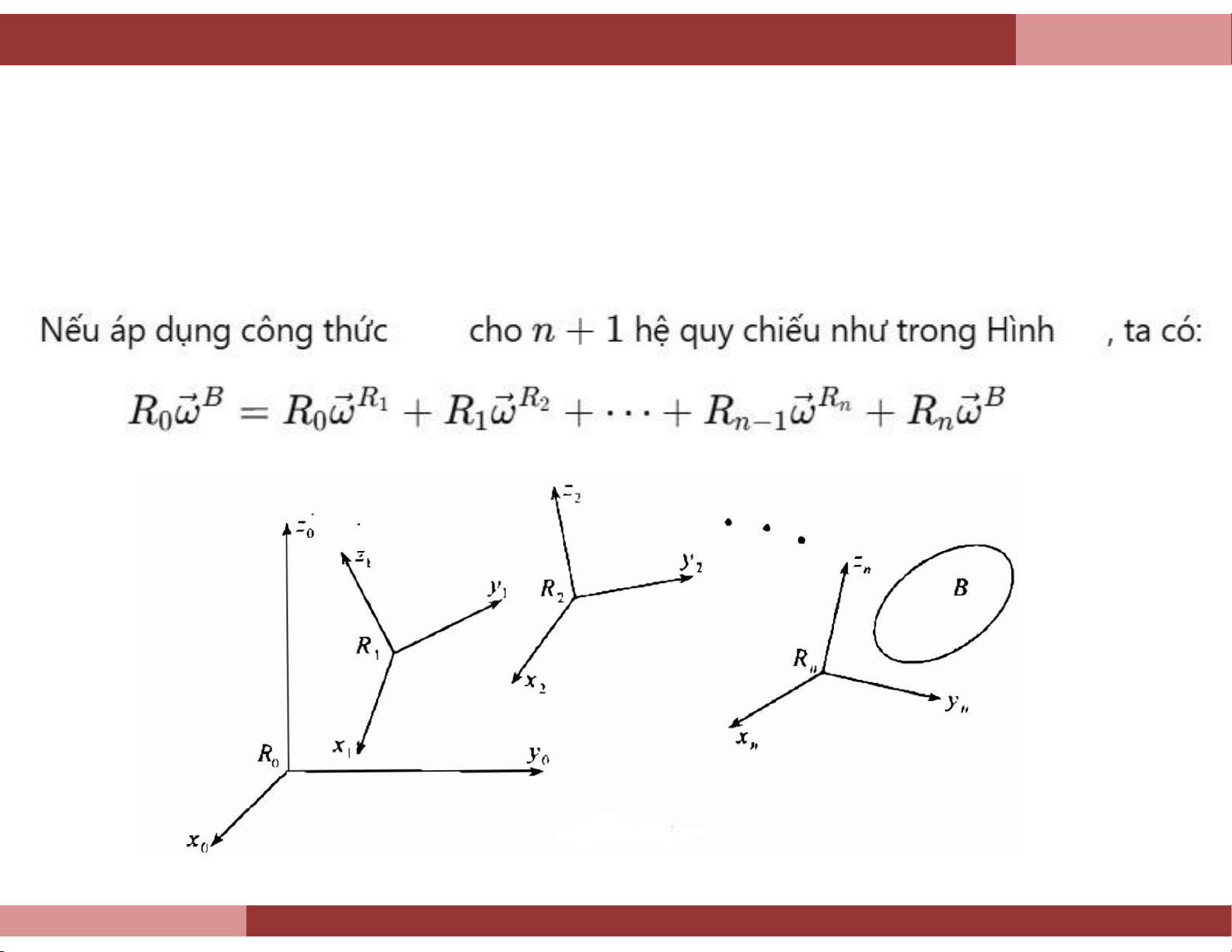
Định lý 9.3: Ở mỗi thời điểm, vận tốc góc tuyệt đối của vật rắn B bằng tổng hình
học của vận tốc góc tương đối và vận tốc góc kéo theo của nó. (9.3.9)
môn Cơ Kỹ thuật – Khoa Khoa học Ứng d
Chương 7. Chuyển động phức hợp điểm
9.3. Định lý cộng vận tốc và gia tốc gốc của vật rắn
9.3.2. Định lý cộng gia tốc của vật rắn Phương trình (9.3.8)
Gia tốc góc tuyệt đối theo công thức (9.3.4) (9.3.10) Theo định nghĩa
Thế vào công thức (9.3.10), ta có
Chương 7. Chuyển động phức hợp điểm
9.3. Định lý cộng vận tốc và gia tốc gốc của vật rắn
9.3.2. Định lý cộng gia tốc của vật rắn Định lý 9.4.
Bộ môn Cơ Kỹ thuật – Khoa Khoa học Ứng d
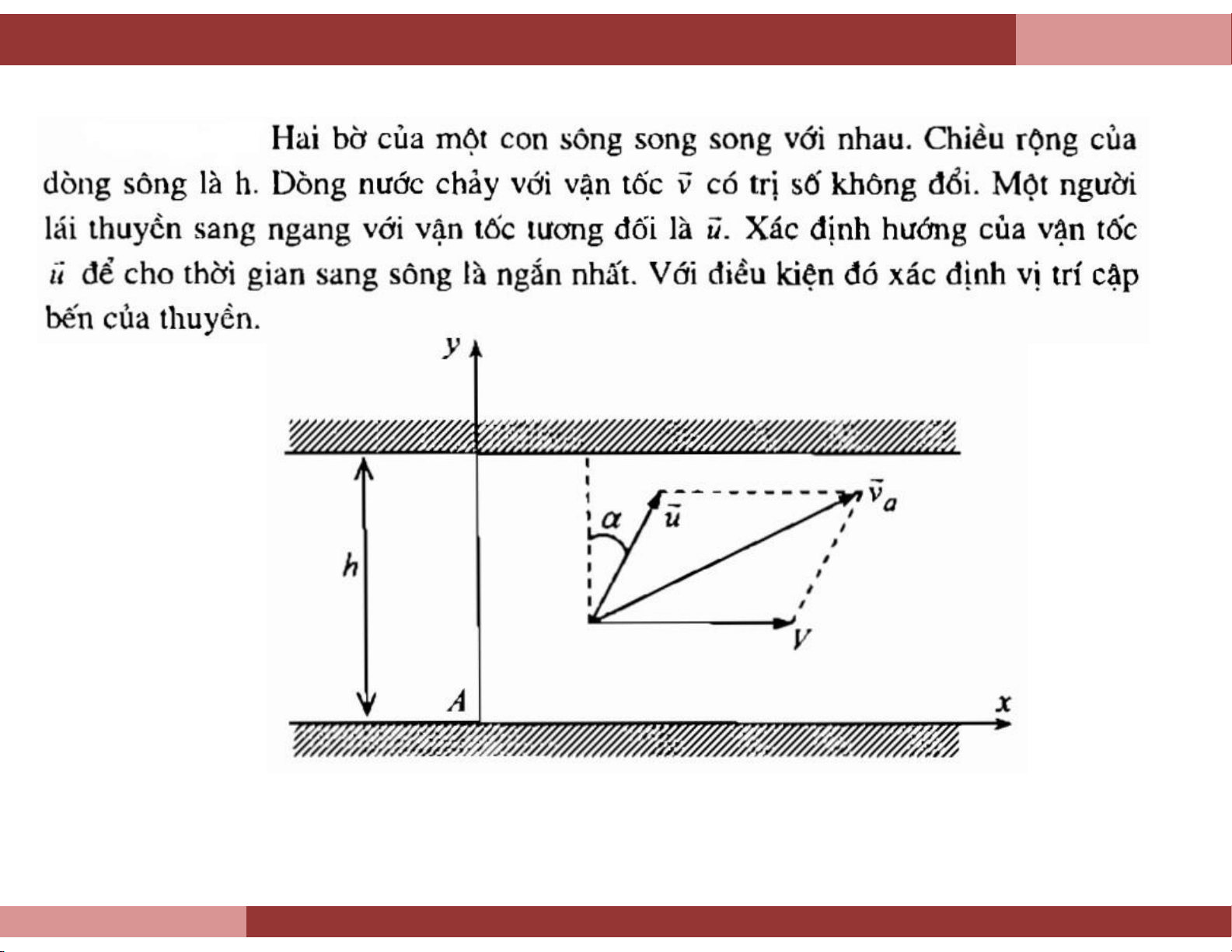
Chương 7. Chuyển động phức hợp điểm Ví dụ 1
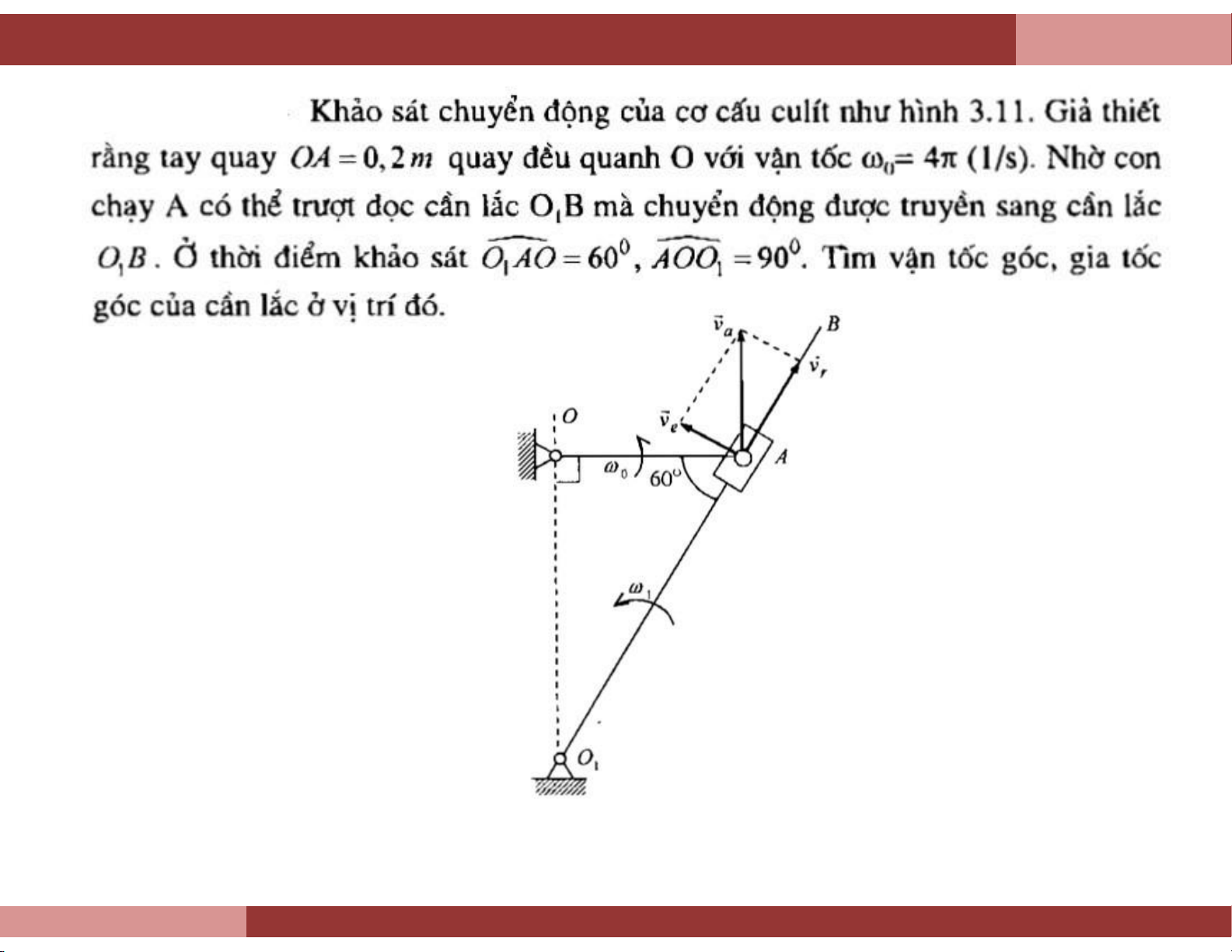
Chương 7. Chuyển động phức hợp điểm Ví dụ 2
môn Cơ Kỹ thuật – Khoa Khoa học Ứng d
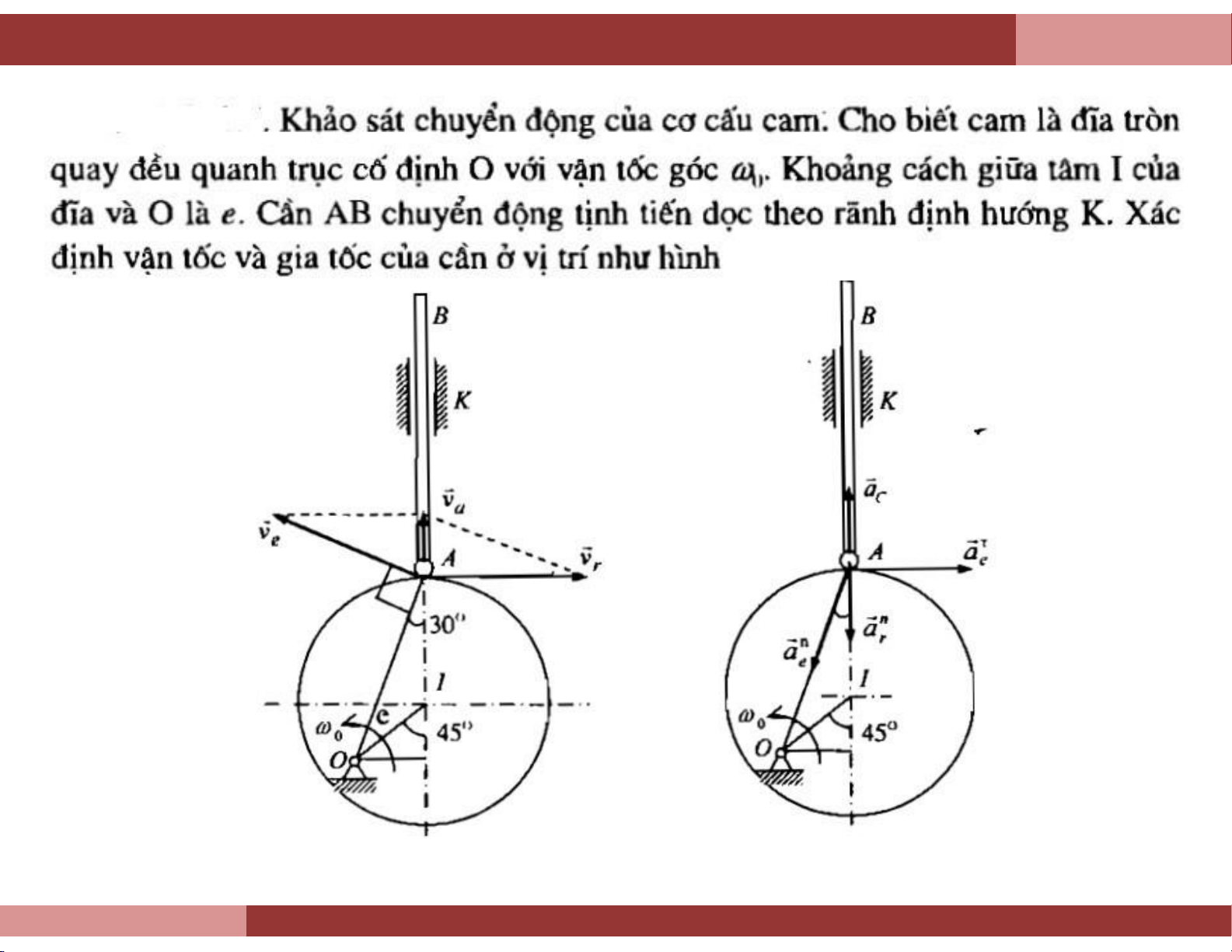
Chương 7. Chuyển động phức hợp điểm Ví dụ 3
Chương 7. Chuyển động phức hợp điểm Ví dụ 4
môn Cơ Kỹ thuật – Khoa Khoa học Ứng d