Đề cương môn vật lý- Trường Đại học bách khoa - Đại học đà nẵng.

ĐẠI HỌC ĐÀ NẴNG
TRƯỜNG ĐẠI HỌC SƯ PHẠM KHOA VẬT LÝ BÀI TẬP VẬT LÝ 2
(Điện-Từ, Quang lượng tử và Vật lí hạt nhân) DÙNG CHO SINH VIÊN
TRƯỜNG ĐẠI HỌC BÁCH KHOA LƯU HÀNH NỘI BỘ Đà Nẵng, 08/2023
CHƯƠNG 1: ĐỊNH LUẬT COULOMB VÀ TRƯỜNG TĨNH ĐIỆN
Bài 1.1. Hai viên bi nhỏ giống hệt nhau, có điện tích q1 = 2.10-6 C và q2 = - 4.10-6 C đặt cách
nhau một khoảng r trong chân không thì chúng hút nhau một lực F = 0,8 N
a) Tính khoảng cách r giữa hai viên bi.
b) Cho chúng tiếp xúc nhau rồi đưa về vị trí cũ thì chúng sẽ đẩy nhau hay hút nhau với lực F’ bằng bao nhiêu?
Bài 1.2. Hai điện tích điểm dương q1 = 3q và q2 = q
được cố định ở hai đầu đối diện của một thanh nằm
ngang có chiều dài d = 1,50 m. Điểm đặt điện tích
q1 được chọn là điểm gốc (như hình 1.1). Một điện
tích điểm thứ 3 có thể trượt không ma sát trên thanh.
a) Tại vị trí x nào thì điện tích q Hình 1.1 3 nằm cân bằng?
b) Cân bằng này có bền hay không? Tại sao?
Bài 1.3. Ba điện tích điểm đặt thẳng hàng trên một đường ngang thể hiện như hình 1.2. Biết
rằng q1 = 6 µC, q2 = 1,5 µC, q3 = -2 µC. Các khoảng cách d1 = 3cm, d2 = 2 cm. Xác định độ lớn
và hướng của lực điện: a) tác dụng lên q1 b) tác dụng lên q3
Bài 1.4. Ba điện tích điểm giống nhau, mỗi điện tích có dạ
khối lượng m = 0,1 kg, được treo bằng ba sợi dây như hình
1.3. Độ dài của các sợi dây bên trái và bên phải là L = 30,0 Hình 1.2
cm. Khi hệ ba điện tích cân bằng thì các sợi dây đồng phẳng và hợp với nhau các góc θ =
45,00. Xác định giá trị của q.
Bài 1.5. Đặt bốn điện tích điểm dương q, 2q, 3q và 4q tại bốn đỉnh
của một hình vuông cạnh a (hình 1.4). Xác định hướng và độ lớn
của điện trường tại tâm của hình vuông.
Bài 1.6. Một thanh mỏng có chiều dài l nằm dọc theo trục x và tích
điện đều với điện tích trên mỗi đơn vị chiều dài là λ (hình 1.5).
a) Chứng tỏ rằng điện trường tại P nằm trên trung trực và cách HìnhH1ìn.3h 1.4 thanh đoạn h là
b) Từ công thức trên, hãy chứng tỏ với thanh dài vô hạn thì điện trường tại P h là Hình 1.5 Hình 1.6
Bài 1.7. Thanh cách điện tích điện đều có chiều dài 14,0 cm được uốn thành nửa vòng tròn như
hình 1.6. Thanh có tổng điện tích là Q = 7,50 µC. Tìm:
a) Hướng và độ lớn của điện trường tại tâm O của nửa vòng tròn.
b) Lực điện tác dụng lên điện tích q = 1,50 µC đặt tại O.
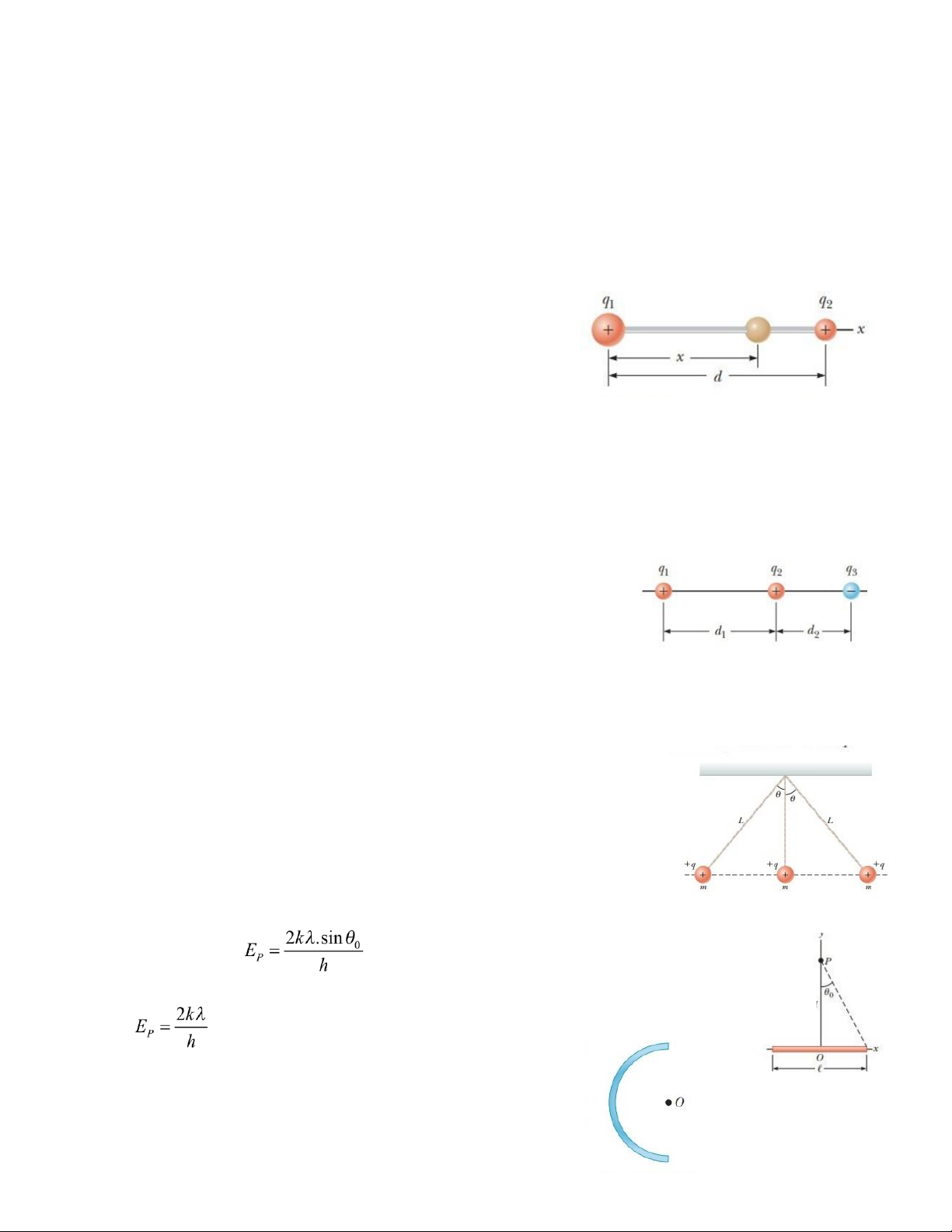
Bài 1.8. Một electron có động năng bằng 2 × 10-16J đang chuyển động sang phải dọc theo trục
của ống tia âm cực (đường nét đứt) của một máy phát dao động kí điện tử như trong hình 1.7.
Một điện trường dọc theo phương thẳng đứng, chiều hướng lên và độ lớn E = 2,0 × 104 N/C tồn
tại trong không gian giữa hai bản và có giá trị bằng 0 ở ngoài vùng không gian này. Cho me = 9,1.10-31 kg. Tính:
(a) Độ lệch theo phương đứng so với trục của ống khi electron bay ra khỏi điện trường.
(b) Góc tạo bởi phương chuyển động của electron với trục của ống sau khi ra khỏi điện trường.
(c) Vị trí electron đập vào màn huỳnh quang (tọa độ x, y) so với điểm gốc ban đầu. Bỏ qua
trọng lực tác dụng lên electron. e Hình 1.7
Chương 2: ĐỊNH LUẬT GAUSS
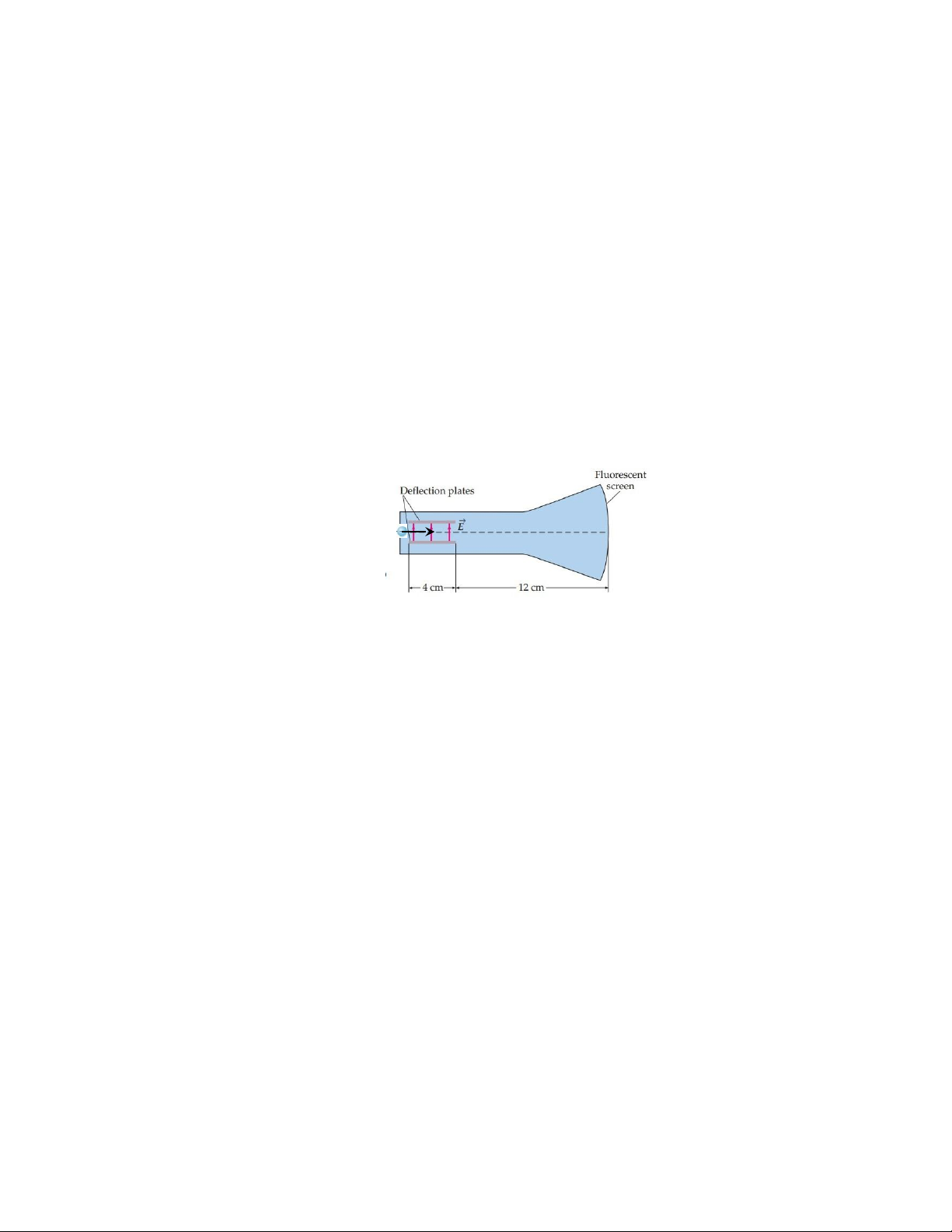
Bài 2.1: Một sợi dây dài vô hạn tích điện đều với điện tích trên mỗi đơn vị chiều dài là
λ nằm cách điểm O một khoảng d như trong Hình 2.1. Xác định điện thông gửi qua bề
mặt của một quả cầu tâm O, bán kính R do sợi dây này gây ra. Xét cả hai trường hợp: a. R < d. b. R > d. Hình 2.1
Bài 2.2: Giả sử cường độ điện trường trên mỗi mặt của khối lập phương cạnh L = 1 m
trong hình 2.3 là đồng nhất và hướng của điện trường trên mỗi mặt được chỉ rõ.
a. Tìm thông lượng điện trường qua khối lập phương.
b. Tìm tổng điện tích bên trong khối lập phương.
c. Tổng điện tích bên trong hình lập phương có thể là của một điện tích điểm duy nhất được không? Hình 2.3
Bài 2.3: Xác định độ lớn của cường độ điện trường ở bề mặt của hạt nhân chì (có số
khối là 208) chứa 82 proton và 126 neutron. Giả sử hạt nhân chì có thể tích gấp 208 lần
so với thể tích của một proton và coi proton là hình cầu bán kính 1,2×10-15m.
Bài 2.4: Một quả cầu đặc cách điện có bán kính a, mang điện tích dương là Q phân bố
đều trong thể tích của nó. Đồng tâm với quả cầu này là một quả cầu rỗng dẫn điện với
điện tích -2Q và có bán kính bên trong và bên ngoài lần lượt là b và c như trong hình
2.4. Vận dụng định luật Gauss để:
a. tìm cường độ điện trường ở các vùng 1, 2, 3 và 4 trong hình vẽ 2.4.
b. sự phân bố điện tích trên vỏ cầu khi toàn bộ hệ thống ở trạng thái cân bằng tĩnh điện. Hình 2.4
CHƯƠNG 3: ĐIỆN THẾ
3.1. Hai điện tích điểm q1 = 15 nC và q2 = -3 nC đặt cách nhau r = 30 cm. Tính
a) Điện thế tại điểm giữa các điện tích
b) Thế năng của cặp điện tích. Nêu ý nghĩa của dấu đại số ở kết quả.
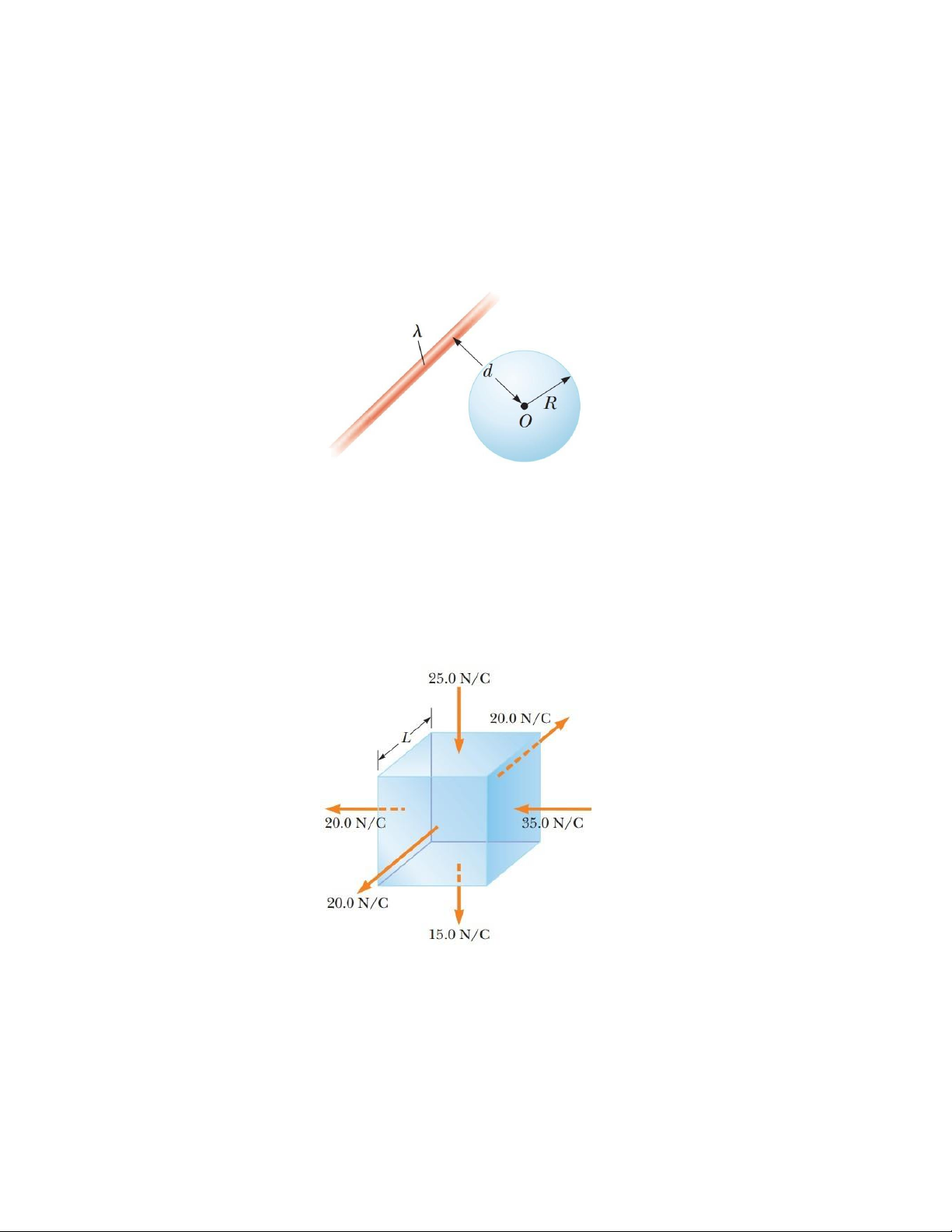
3.2. Ba hạt mang điện giống hệt nhau có độ lớn q = 11,0 μC nằm trên ba
đỉnh của một hình chữ nhật như hình bên cạnh. Kích thước của hình chữ
nhật là L = 60,0 cm và W = 15,0 cm. Tính công cần thiết để đưa một hạt
nhỏ có cùng điện tích q ở xa vô hạn vào đỉnh còn lại của hình chữ nhật.
3.3. Tính công cần thiết để thiết lập một hệ gồm bốn hạt mang điện giống
nhau, mỗi hạt có điện tích là q, tại bốn đỉnh của một hình vuông cạnh L?
3.4. Xét một vòng tròn bán kính R với tổng điện tích Q được phân bố đều
trên chu vi của nó. Tính hiệu điện thế giữa tâm của vòng và một điểm trên trục của nó cách tâm một khoảng 2R.
3.5. Có một quả cầu dẫn điện bán kính R được tích điện đều với tổng điện tích q. Xác
định điện thế bên trong và bên ngoài quả cầu.
3.6. Một thanh cách điện tích điện đều với chiều dài 14,0 cm được uốn thành nửa
đường tròn như hình vẽ. Thanh có tổng điện tích là -7,50 nC. Tìm điện thế tại tâm O
của nửa đường tròn này.
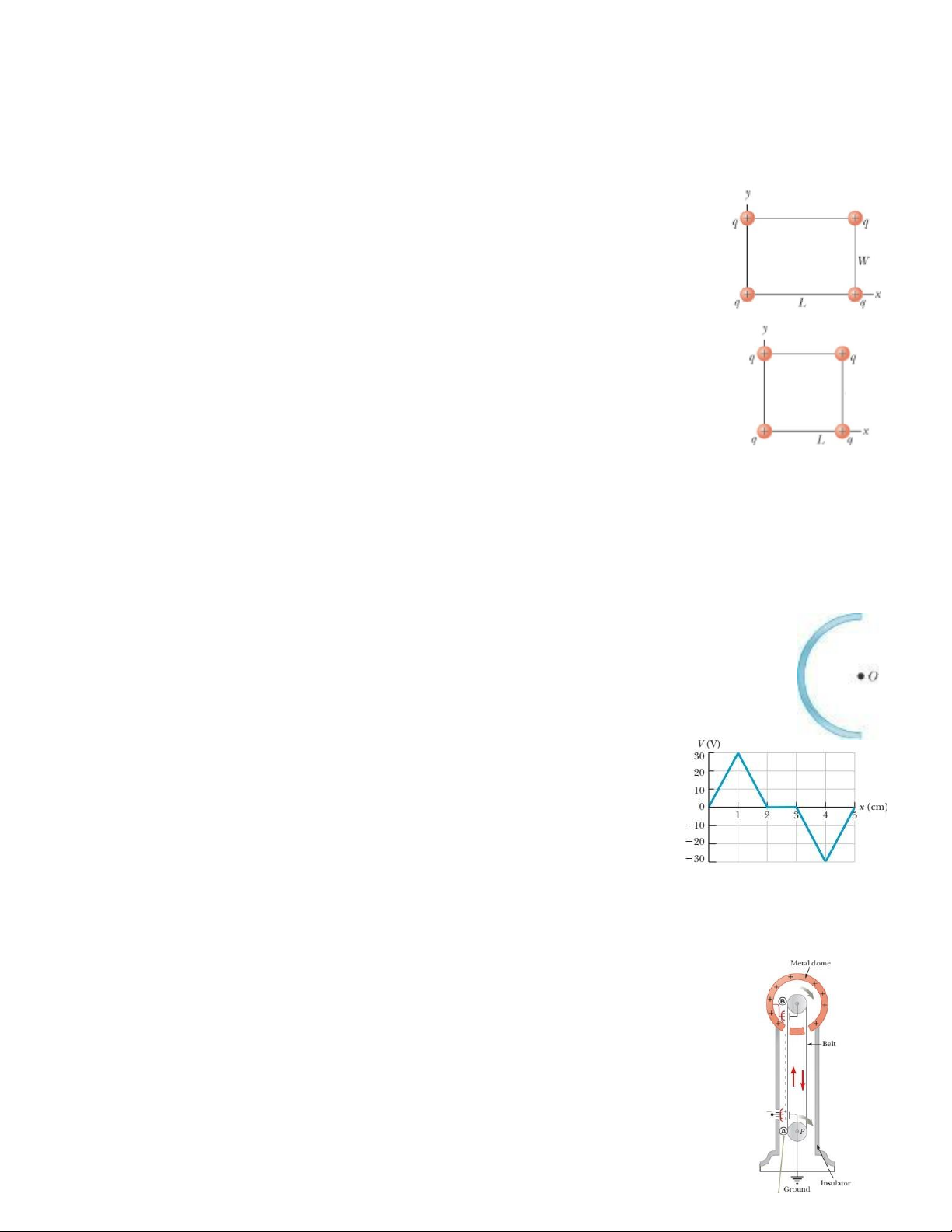
3.7. Hình bên biểu diễn đồ thị của điện thế trong một vùng không
gian theo vị trí x, tại đó điện trường song song với trục x. Vẽ đồ thị
sự phụ thuộc vào x của thành phần điện trường trên trục x (Ex).
ĐS. E =−3000 ( N C−1) ; 3000 ( N C−1) ; 0 ;−3000 ; 3000. x 3.8.
Sét có thể được nghiên cứu bằng máy phát điện Van de Graaff, bao gồm một
mái vòm hình cầu mà trên đó điện tích được tích tụ liên tục bởi một vành đai
chuyển động. Điện tích có thể được nạp cho đến khi điện trường của nó chưa
“đánh thủng” điện môi không khí. Giả sử mái vòm có đường kính 30,0 cm và được bao
quanh bởi không khí khô có giới hạn điện trường “đánh thủng” là 3x106 N/C.
a) Điện thế cực đại của mái vòm là bao nhiêu?
b) Điện tích cực đại trên mái vòm là bao nhiêu?
CHƯƠNG 5: TỪ TRƯỜNG
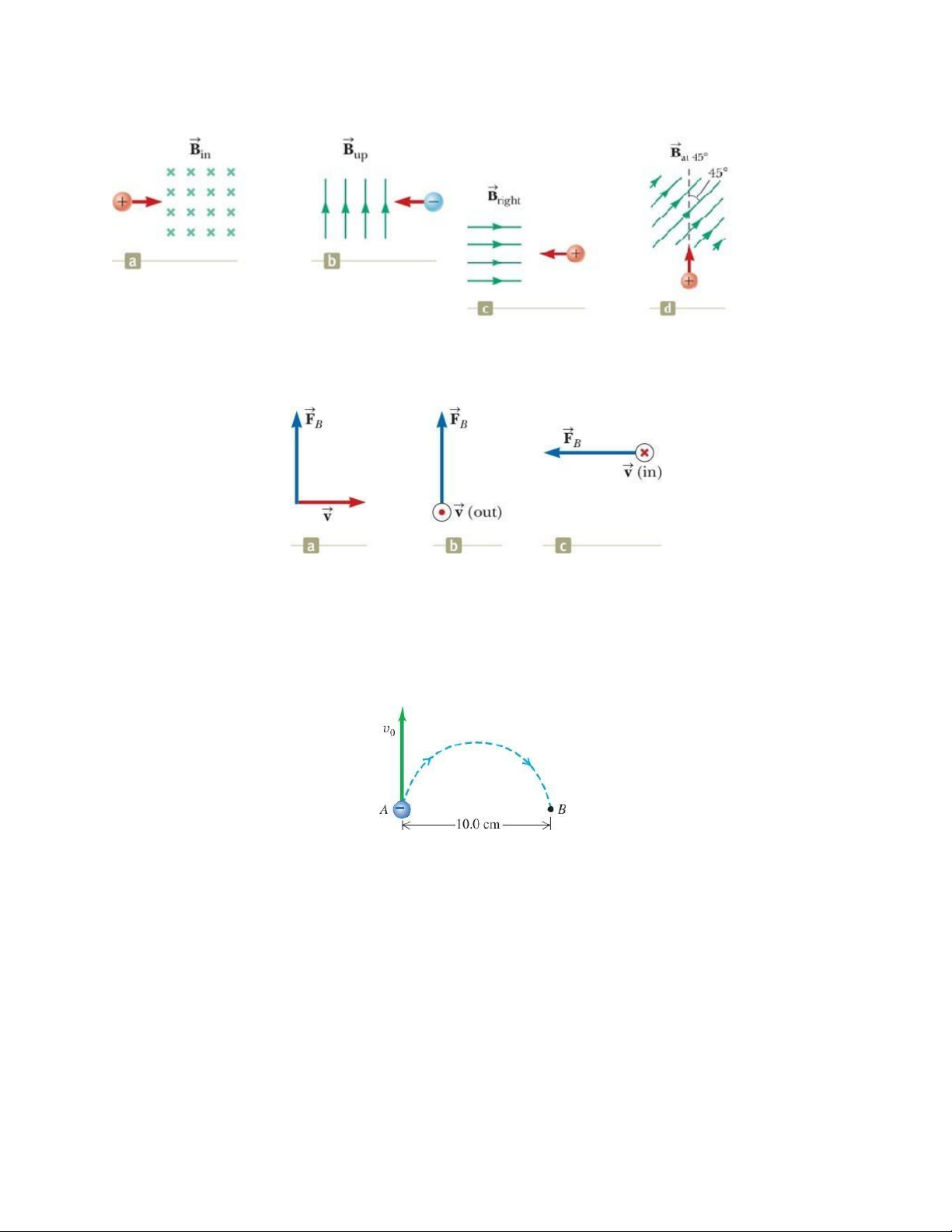
5.1. Xác định phương chiều của lực từ tác dụng lên điện tích ở các hình sau:
5.2. Xác định phương chiều của từ trường trong các hình sau. Giả sử điện tích âm chuyển
động theo phương vuông góc với từ trường.
5.3. Một electron tại điểm A trong hình vẽ có tốc độ 𝑣0 = 1,41 × 106 m/s. Tìm
a) độ lớn và hướng của từ trường làm cho electron chuyển động theo nửa đường tròn từ A đến B,
b) thời gian cần thiết để electron di chuyển từ A đến B.
5.4. Một electron va chạm đàn hồi với một electron thứ hai lúc đầu ở trạng thái nghỉ. Sau
va chạm, bán kính quỹ đạo của chúng là 1,00 cm và 2,40 cm. Quỹ đạo vuông góc với một
từ trường đều có độ lớn 0,044 T. Xác định năng lượng (tính bằng keV) của electron tới.
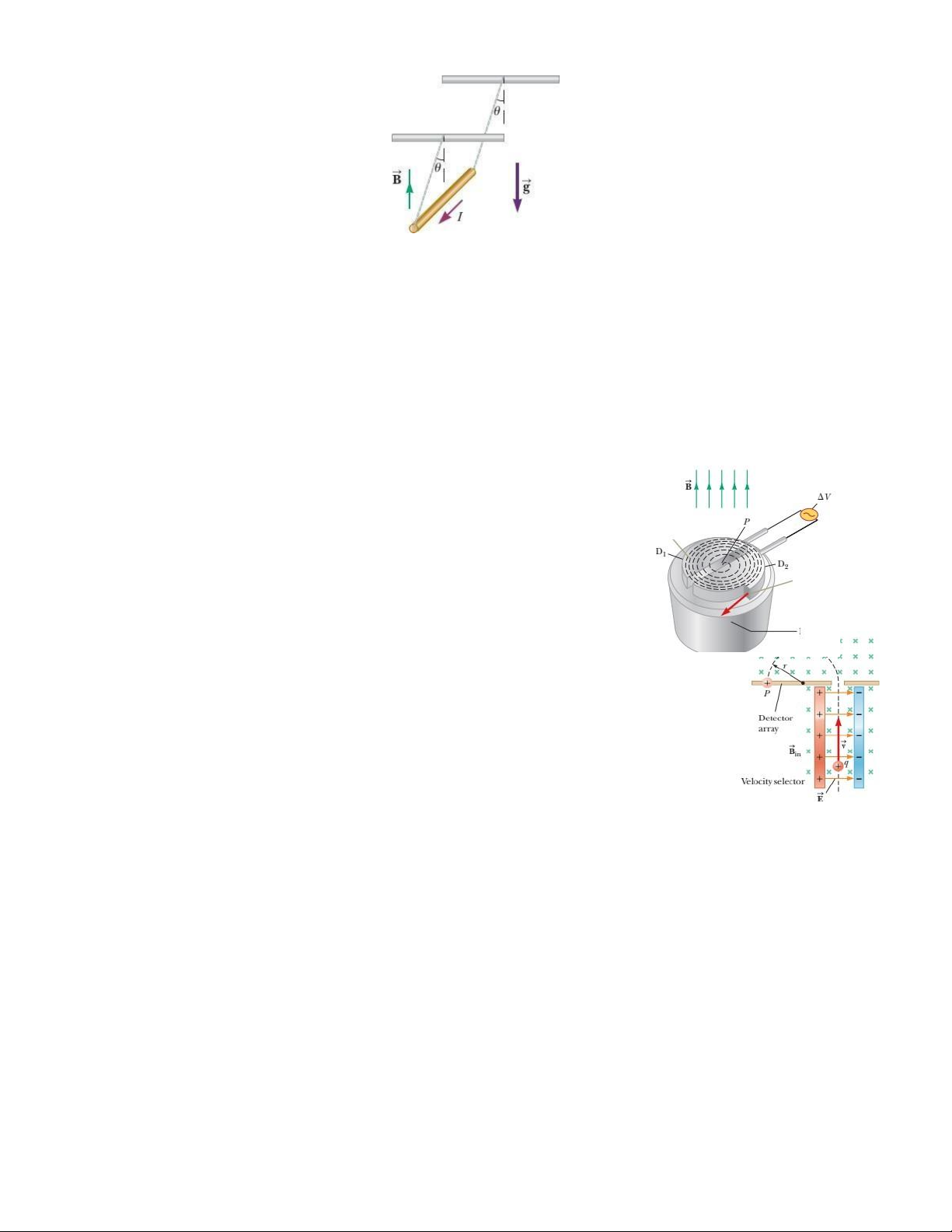
5.5. Một thanh kim loại có mật độ khối lượng trên một đơn vị chiều dài là 𝜆 và mang
dòng điện I. Thanh được treo vào hai dây trong từ trường đều thẳng đứng như hình dưới.
Các dây tạo một góc 𝜃 với phương thẳng đứng khi ở thanh cân bằng. Xác định độ lớn của từ trường.
5.6. Một electron chuyển động trong một từ trường đều B = 5.10-3 T với vận tốc hợp với
đường sức từ trường một góc α = 680. Động năng của electron là K = 1,64.10-16 J. Trong
trường hợp này quỹ đạo của electron là một hình xoắn ốc. Tìm:
a) Vận tốc của electron.
b) Bán kính của vòng xoắn ốc và chu kỳ quay của electron trên quỹ đạo.
c) Bước của đường xoắn ốc.
5.7. Cyclotron là một thiết bị có thể tăng tốc các hạt mang điện
đến tốc độ rất cao. Một số bệnh viện sử dụng phương tiện
cyclotron để sản xuất chất phóng xạ để chẩn đoán và điều trị.
Máy cyclotron có sơ đồ cấu tạo như hình vẽ. Để động năng của
electron phát ra có độ lớn 20 MeV thì từ trường đặt vào phải có
giá trị bao nhiêu, giả sử bán kính lớn nhất khi electron thoát ra là 50 cm.
5.8. Khối phổ kế là thiết bị phân tách các ion theo tỷ lệ khối
lượng trên điện tích của chúng. Sơ đồ nguyên lí và giả sử các chiều của
điện từ trường như hình vẽ. Hạt mang điện q ban đầu có tốc độ v đi qua
điện trường E = 10 kV/m và từ trường Bin = 5 mT, sau đó tiếp tục đi vào từ
trường B0,in = Bin. Bán kính r = 5 cm. Xác định tỷ số m/q trong trường hợp này.
CHƯƠNG 6 – CÁC NGUỒN TỪ TRƯỜNG Bài 6.1:
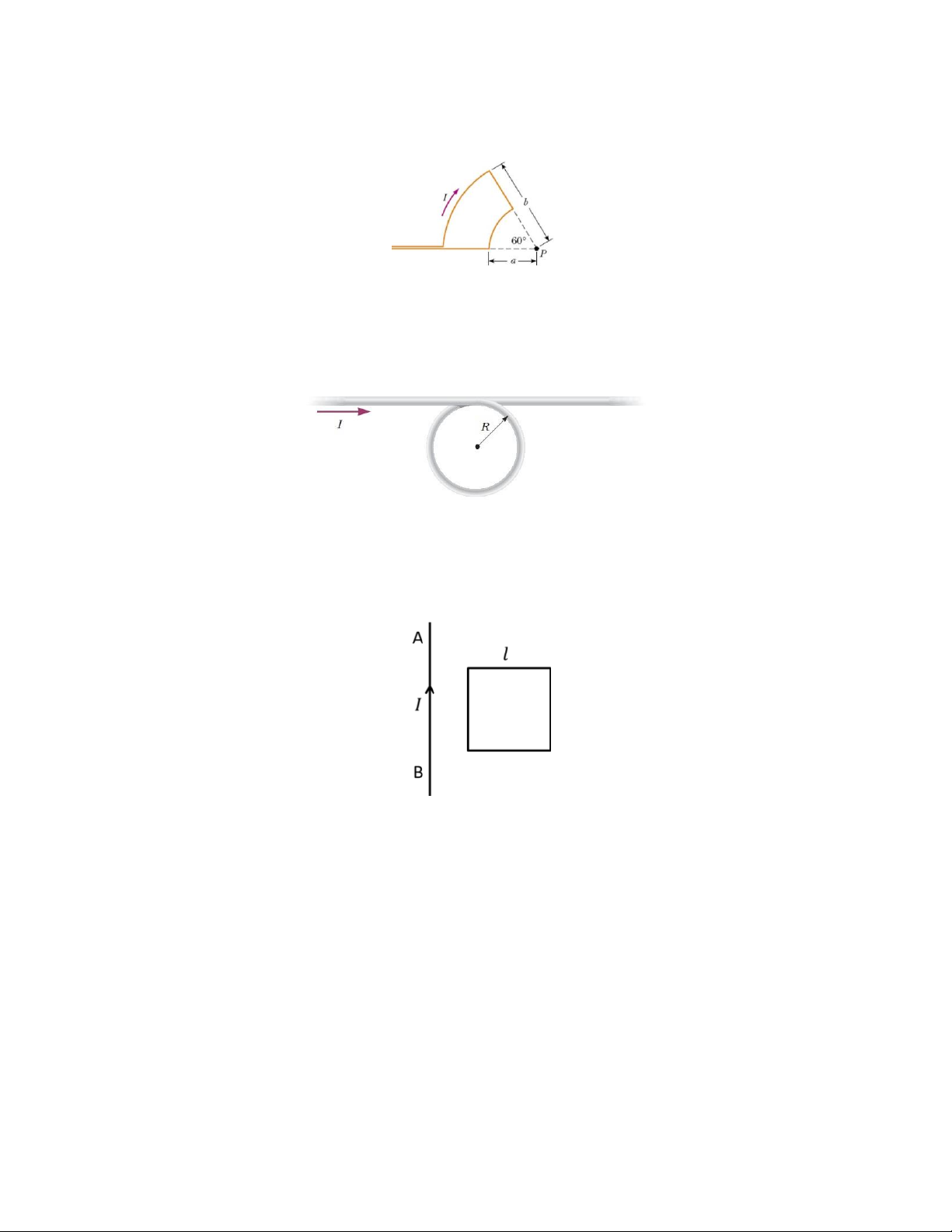
Một dây dẫn mang dòng điện I được uốn thành các cung tròn có bán kính lần lượt là a và
b đồng tâm tại điểm P như trong hình bên. Xác định phương, chiều và độ lớn của vectơ cảm ứng từ tại P. Bài 6.2:
Một dây dẫn bao gồm một vòng tròn bán kính R và hai đoạn thẳng dài như trong hình vẽ.
Dây dẫn nằm trong mặt phẳng giấy và mang dòng điện I . Xác định phương, chiều và độ
lớn của vectơ cảm ứng từ ở tâm vòng dây. Bài 6.3:
Một khung dây hình vuông, mỗi cạnh l = 2 cm được đặt gần một dòng điện thẳng dài vô
hạn AB, cường độ I = 30 A. Khung dây và dây dẫn thẳng cùng nằm trong một mặt phẳng
và dây dẫn thẳng cách cạnh gần nhất của khung dây một đoạn d = 1 cm. Tính từ thông gửi qua khung.
Bài 6.4: Xác định lực tác dụng của một dòng điện thẳng dài vô hạn lên một khung dây
dẫn hình hình chữ nhật có cạnh a = 0,15 m và cạnh l = 0,45 m. Biết rằng cường độ dòng
điện thẳng I1 = 5 A, cường độ dòng điện chạy trong khung I2 = 10 A. Dây dẫn thẳng nằm
trong mặt phẳng của khung dây, song song với 1 cạnh của khung và cách cạnh gần nhất
một đoạn c = 0,1 m. Khung dây không bị biến dạng. Chiều dòng điện cho trên hình vẽ.
Bài 6.5: Năm 1962, một Đài quan sát Địa vật lý ở Tulsa, Oklahoma đã thực hiện các
phép đo từ trường của một cơn lốc xoáy. Nếu vector cảm ứng từ tạo ra từ cơn lốc xoáy có
cường độ là 1,5×10-8 T và có hướng hướng về phía Bắc khi cơn lốc xoáy cách đài quan
sát 9 km về phía Đông thì trong phễu của cơn lốc xoáy, dòng điện đã truyền lên hay
xuống? với cường độ bằng bao nhiêu?
Bài 6.6: Trên thực tế, tại mọi nơi xung quanh Trái Đất luôn tồn tại một từ trường. Khi ta
cuốn một dây thì bên trong cuộn dây đó cũng tồn tại từ trường của Trái Đất. Giả sử ta
cuốn một cuộn dây gồm 5 vòng với đường kính cuộn dây là 10 cm. Để tạo ra một vùng
không gian không có từ trường bên trong cuộn dây thì người ta phải tạo ra một từ trường
ngược hướng và có độ lớn bằng độ lớn của từ trường Trái Đất. Hỏi phải cho một dòng
điện có cường độ bằng bao nhiêu để thỏa mãn được điều kiện trên? Cho biết từ trường
của Trái Đất có độ lớn là 5×10-5 T.
Bài 6.7: Trong các nghiên cứu về khả năng chim di cư có thể sử dụng từ trường của Trái
Đất để điều hướng bay, các loài chim di cư đã được gắn hai cuộn dây làm “mũ” và “vòng
cổ” như mô tả trong ảnh trên. Nếu hai cuộn dây trên giống nhau và đều có bán kính 1,2
cm, đặt cách nhau 2,2 cm, mỗi cuộn dây có 50 vòng thì cả hai cuộn dây “mũ” và “vòng
cổ” đều phải mang dòng điện có độ lớn bao nhiêu để tạo ra được một từ trường có độ lớn
là 4,5×10-5 T ở vị trí giữa hai cuộn dây trên?
Bài 6.8: Trong y học, để thu được hình ảnh cộng hưởng từ hạt nhân (MRI), bệnh nhân
được đưa vào một cái ống rất lớn có dạng trụ như mô tả trên ảnh. Trong ống trụ lớn bao
xung quanh bệnh nhân này có chứa cuộn dây để tạo ra từ trường đều bên trong ống dây.
a) Xét trên 10 cm chiều dài của cuộn dây, với mong muốn tạo ra được một từ trường có
độ lớn 0,1 T thì cần phải cuốn bao nhiêu vòng dây. Cho dòng điện chạy qua vòng dây có
giá trị lớn nhất là 10 A.
b) Trên thực tế, một sợi dây dẫn có thể chịu được dòng điện 10 A thì phải có đường kính
sợi dây ít nhất là 1 mm. Để cuốn được số vòng dây như ở yêu cầu của câu (a) thì phải làm như thế nào?
Chương 7: ĐỊNH LUẬT FARADAY
Bài 7.1. Để theo dõi nhịp thở của bệnh nhân, một dây đai mỏng được quấn quanh
ngực của bệnh nhân. Dây đai là một cuộn dây dẫn mảnh có 200 vòng. Khi bệnh
nhân hít vào, tiết diện cuộn dây tăng lên một lượng 39,0 cm2. Từ trường Trái đất tại
đó có độ lớn 50 μT và hợp một góc 28° với mặt phẳng cuộn dây. Giả sử mỗi lần hít
vào mất 1,8 s, tính suất điện động cảm ứng xuất hiện trong ống dây trong khoảng thời gian này.
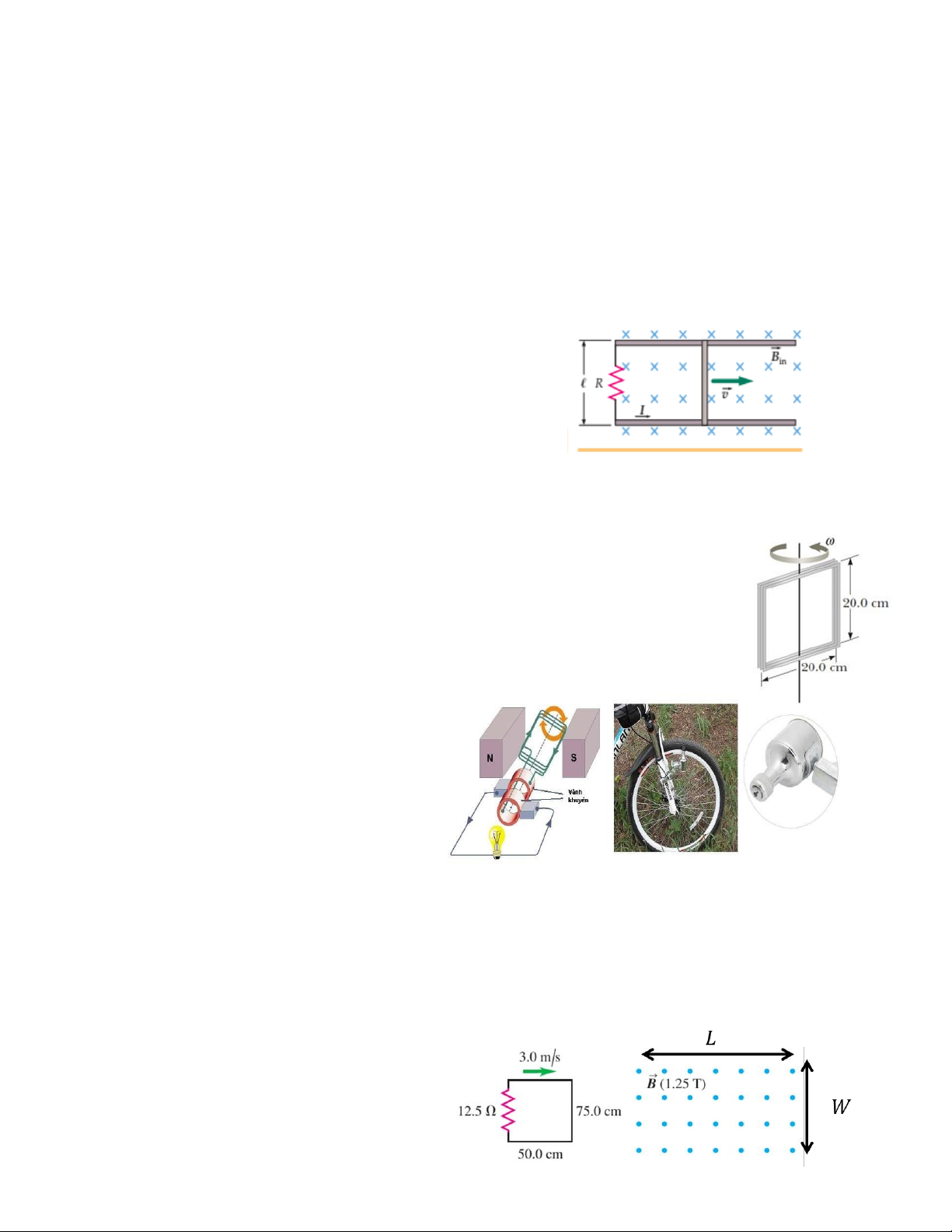
Bài 7.2. Một thanh có khối lượng mtrượt trên ray
dẫn không ma sát trong vùng có từ trường đều ⃗B
hướng vào trong như hình bên. Một tác nhân bên
ngoài đang đẩy thanh, duy trì chuyển động của nó
sang phải với tốc độ không đổi v0. Tại thời điểm t =0 0
tác nhân đột ngột ngừng đẩy và thanh tiếp tục
chuyển động về phía trước đồng thời bị chậm lại bởi lực từ. Tìm tốc độ vcủa thanh
dưới dạng một hàm của thời gian.
Bài 7.3. Để đo từ trường của trái đất, sinh viên sử dụng một cuộn dây
hình vuông mỗi cạnh 20 cm có 100 vòng quay quanh trục thẳng đứng với
tốc độ 1,5 ×103 vòng/phút như hình bên. Sức điện động cảm ứng cực đại
xuất hiện trong cuộn dây đo được là 12,6 mV. Xem từ trường của Trái đất
tại vị trí thực hiện là đều và nằm theo phương ngang. Tính từ trường của
Trái đất tại vị trí đo.
Bài 7.4. Một Dynamo của xe đạp
được cấu tạo như sơ đồ dưới, Giả sử
nam châm của Dynamo tạo ra từng
trường đều có cường độ 0,05 T, cuội
dây 200 vòng với diện tích mỗi vòng
là 3 c m2, bán kính vòng xoay của
Dynamo là 1 cm. Nếu người đạp xe
đạp với tốc độ 18 km / h thì Dynamo
tạo ra suất điện động cực đại là bao nhiêu?
Bài 7.5 . Một mạch điện hình chữ nhật di chuyển với tốc độ v = 3 m/s vào một từ
trường đều B=1,25T có chiều như hình bên. Từ trường nằm trong vùng có chiều dài
L=100 cm. Xác định chiều và độ lớn của dòng điện cảm ứng trong mạch điện trên trong các trường hợp:
a) Khi nó bắt đầu đi vào từ trường
b) Khi nó di chuyển bên trong từ trường
c) Khi nó bắt đầu đi ra khỏi từ trường
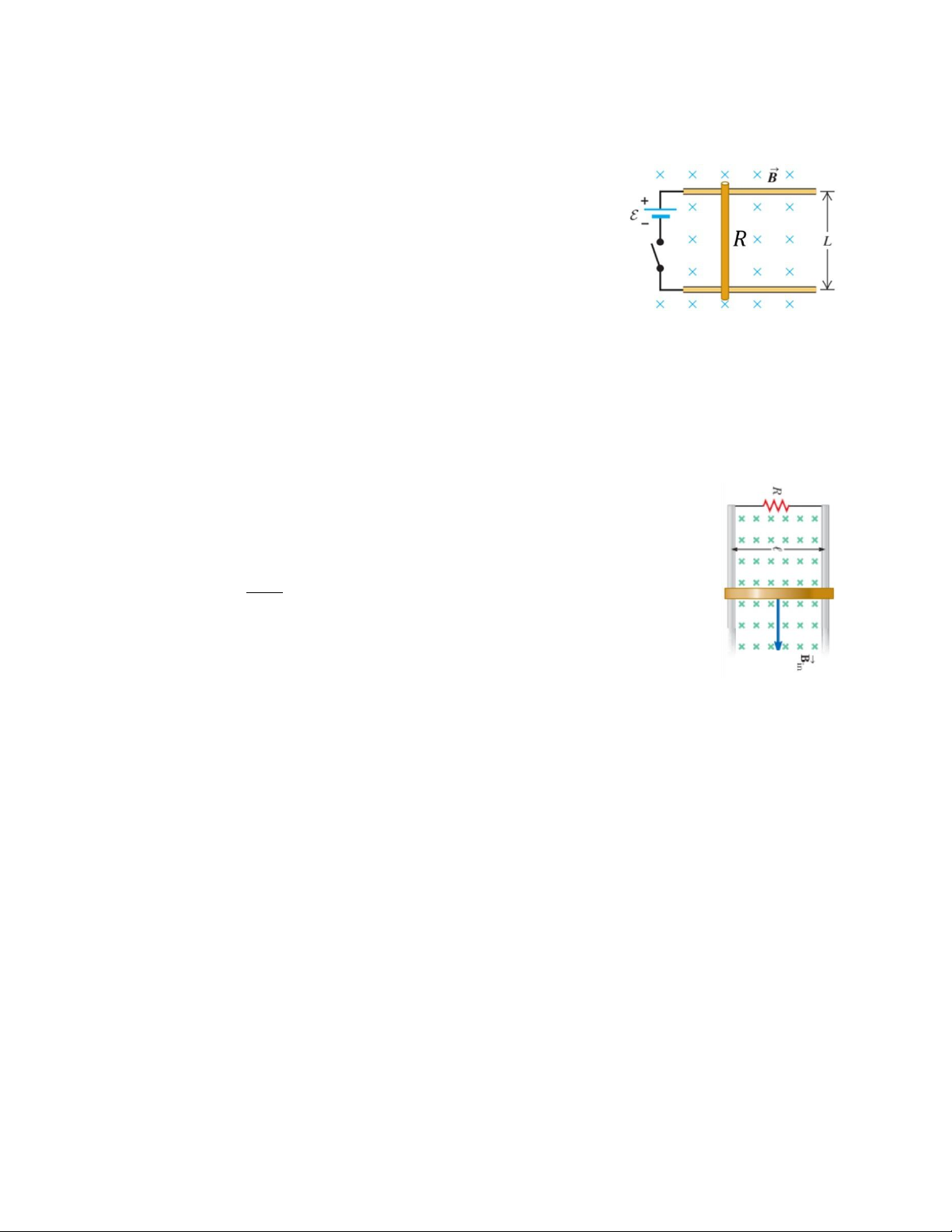
Bài 7.6. Hai thanh ray kim loại song song, nằm ngang và
cách nhau L = 20 cm, có điện trở không đáng kể như hình
bên. Hai thanh được nối với nguồn điện một chiều có
suất điện động ε = 0,5 V và có điện trở trong không đáng
kể. Một thanh dẫn có R = 0,02 Ω được đặt trên và vuông
góc với 2 thanh ray. Toàn bộ mạch điện đặt trong từ
trường đều có ⃗B vuông góc với mạch điện và độ lớn B =
1,5 T. Do lực từ tác dụng lên thanh dẫn nên thanh trượt trên hai thanh ray. Tại thời
điểm tốc độ của thanh là v = 1 m/s.
a) Vẽ chiều và tính độ lớn lực từ tác dụng lên đoạn dây dẫn.
b) Tính công suất làm dịch chuyển thanh dẫn, công suất tỏa nhiệt trên thanh dẫn
và công suất của nguồn điện.
Bài 7.7: Một thanh kim loại chiều dài , khối lượng m=0,1 kg ,nằm
ngang có thể trượt không ma sát trên hai thanh ray thẳng đứng như
trong hình bên. Dưới tác dụng của trọng lực và lực từ, thanh
chuyển động đều với vận tốc 2,0 m/s trong từ trường có chiều như
hình vẽ. lấy g= 10 m ,xác định: 2 s
a) Cường độ dòng điện chạy qua điện trở R=8 Ω
b) Công suất tỏa nhiệt trên điện trở.
c) Công suất của trọng lực. Giải thích tại sao kết quả ở hai câu b và c bằng nhau.
Bài 7.8: Một cuộn dây có độ tự cảm L=5 mH và điện trở R=15 Ω được mắc với hai
cực của một pin có suất điện động E=12,0 V có điện trở trong không đáng kể.
a) Dòng điện cuối cùng chạy trong cuộn dây là bao nhiêu?
b) Cần bao nhiêu thời gian để dòng điện đạt 99,0 phần trăm giá trị cuối cùng của nó?
Chương 9: Quang Lượng tử
Bài 9.1. Bán kính mặt trời là 6,96 × 108 m. Công suất bức xạ toàn phần của mặt trời là
3,85 × 1026 W. Xem mặt trời là vật đen tuyệt đối, tính:
a) nhiệt độ bề mặt của mặt trời,
b) bước sóng mang nhiều năng lượng nhất phát ra từ mặt trời.
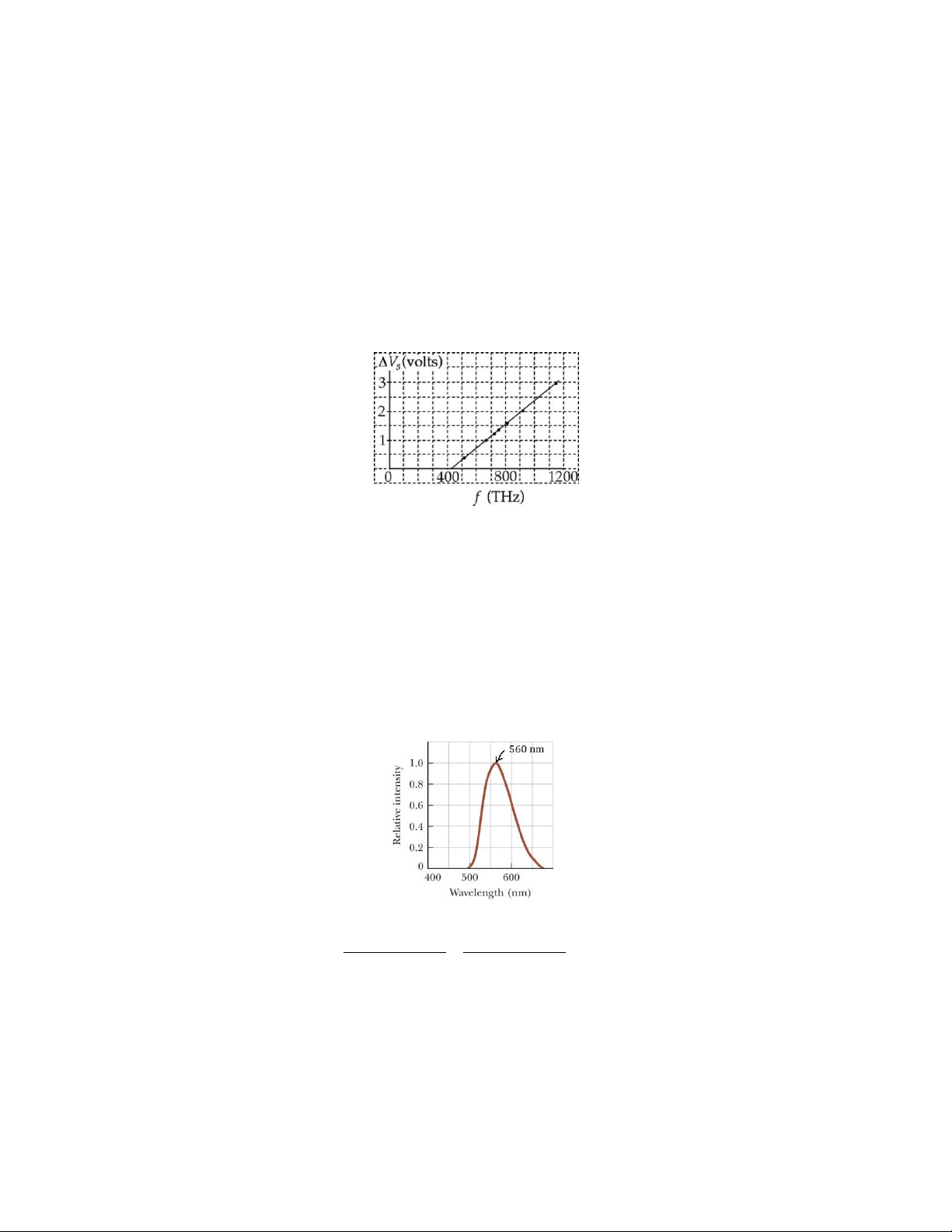
Bài 9.2. Năm 1916, R. A. Millikan đăng trên tạp chí Physical Review (Physical Review
7:362 (1916)) một kết quả nghiên cứu về hiện tượng quang điện. Theo đó, ông khảo sát
sự phụ thuộc của hiệu điện thế hãm ∆V vào tần số s
f của photon chiếu vào kim loại Na
như hình dưới. Từ đồ thị, xác định (a) công thoát của Na, (b) tỉ số h/e và (c) giới hạn quang điện của Na.
Bài 9.3. Trong hiện tượng tán xạ của tia X trên một bia kim loại, tia X tới có năng lượng
300 keV và tia X bị tán xạ tại một góc 37° so với tia tới. Xác định:
a) độ dịch chuyển bước sóng của tia X bị tán xạ,
b) năng lượng của tia X bị tán xạ,
c) động năng của electron sau tán xạ.
Bài 9.4: Hình dưới mô tả quang phổ được phát ra từ một con đom đóm. (a) Xác định
nhiệt độ của một vật đen tuyệt đối phát ra bức xạ có đỉnh trùng với đỉnh trong quang phổ
của con đom đóm. (b) Từ kết quả ở câu (a), giải thích tại sao con đom đóm không phải là vật đen tuyệt đối.
HD: (a) Từ định luật Wien, nhiệt độ của vật đen tuyệt đối:
0,2898 ×10−2 0,2898 ×10−2 T = = λ = − 5200 K 9 max 560× 10
(b) Rõ ràng nhiệt độ con đom đóm không thể là 5200 K nên con đom đóm ko phải là vật
đen tuyệt đối và bức xạ do nó chiếu ra không phải là bức xạ nhiệt.
Chương 10. Cơ học lượng tử
Câu 10.1: Một hạt chuyển động trong một hố thế sâu vô hạn có bề rộng a, hàm sóng mô
tả trạng thái của hạt có dạng a. Chuẩn hoá hàm sóng
b. Tìm xác suất của hạt nằm trong khoảng từ 0,49a đến 0,51a
Câu 10.2: Một LASER Ruby phát ra ánh sáng có bước sóng 694,3 nm. Năng lượng của
ánh sáng phát ra do sự dịch chuyển của electron trong một hộp (một chiều) từ mức năng
lượng tương ứng n = 2 xuống n = 1. Tìm chiều rộng của hộp.
Câu 10.3: Thế năng liên kết giữa các proton và notron được tính gần đúng là một hố thế
sâu vô hạn. Giả sử một proton chuyển động trong hố thế với chiều rộng 10 fm (tương
đương với kích thước hạt nhân). Nếu proton dịch chuyển từ trạng thái có năng lượng
tương ứng n = 2 về n = 1, tính năng lượng và bước sóng phát xạ của proton.
Bài 10.4 (TT). Một sinh viên có khối lượng 60 kg đi qua một cái cửa có bề rộng 75 cm.
Bề dày của bức tường chứa cửa là 15 cm. Giải thích tại sao hiện tượng nhiễu xạ không
thể xảy ra đối với bạn sinh viên. Biết rằng nhiễu xạ đáng kể xảy ra khi bề rộng khe nhỏ
hơn 10 lần bước sóng của sóng bị nhiễu xạ.
CHƯƠNG 11. VẬT LÍ NGUYÊN TỬ
Bài 11.1: Một nguyên tử hiđrô ở trạng thái với n =3, l =2 và ml = -2. Hãy xác định:
a. Năng lượng của nguyên tử.
b. Độ lớn momen quỹ đạo của electron.
c. Thành phần z của momen quỹ đạo đó.
Bài 11.2: Các nhà thiên văn học sử dụng hiệu ứng Zeeman để đo từ trường trên bề mặt
của các sao. Giả sử người ta quan sát được sự tách mức năng lượng của các nguyên tử ở
bề mặt một sao là 1,02.10-4 eV. Người ta cũng biết rằng spin toàn phần của các nguyên tử
ở các mức đó bằng không và do đó spin không đóng góp vào momen động lượng. Hãy
xác định độ lớn B của từ trường trên bề mặt của sao đó.
Bài 11.3: Nguyên tử Hiđrô có cấu hình electron là 1s1 và có một electron ở lớp ngoài
cùng. Hãy vẽ và giải thích sơ đồ mức năng lượng của nguyên tử Hiđrô và các chuyển dời
lượng tử được phép. Xét cho 2 trường hợp: a. Không kể đến spin. b. Khi kể đến spin.
Bài 11.4: Electron trong nguyên tử hydro ở trạng thái có momen động lượng quỹ đạo
L=√❑. Hãy xác định:
a. Số góc định hướng của ⃗L đối với phương z.
b. Mômen động lượng toàn phần của electron.
c. Độ biến thiên của hình chiếu của mômen động lượng quĩ đạo của electron khi nó
chuyển về trạng thái cơ bản.