Đề cương ôn tập giữa học kỳ 1 Toán 10 Cánh diều 2023-2024 (có đáp án)

ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KỲ I TOÁN 10-CÁNH DIỀU
A. PHẦN TRẮC NGHIỆM ( 4.0 điểm).
Câu 1: Phát biểu nào sau đây là một mệnh đề?
A. Thành phố Đà Nẵng đẹp quá!
B. Việt Nam nằm ở Đông Nam Á.
C. Bạn có đi học không?
D. Đề kiểm tra môn Toán hôm nay dễ quá!  x 
Câu 2: Cho hàm số y  f  x 1 khi  
Tập xác định của hàm số trên là: 0 khi x  \ A. D  \ . B. D  .
C. D   . D. D  .
Câu 3: Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình 2x  y  1 ? A. 0;0 . B.  2   ;1 .
C. 3; 7 . D. 0;  1 .
Câu 4: Giá trị lớn nhất của hàm số 2
y  x  2x  5 trên bằng A. -5. B. 6 . C. 5 . D. 2 .
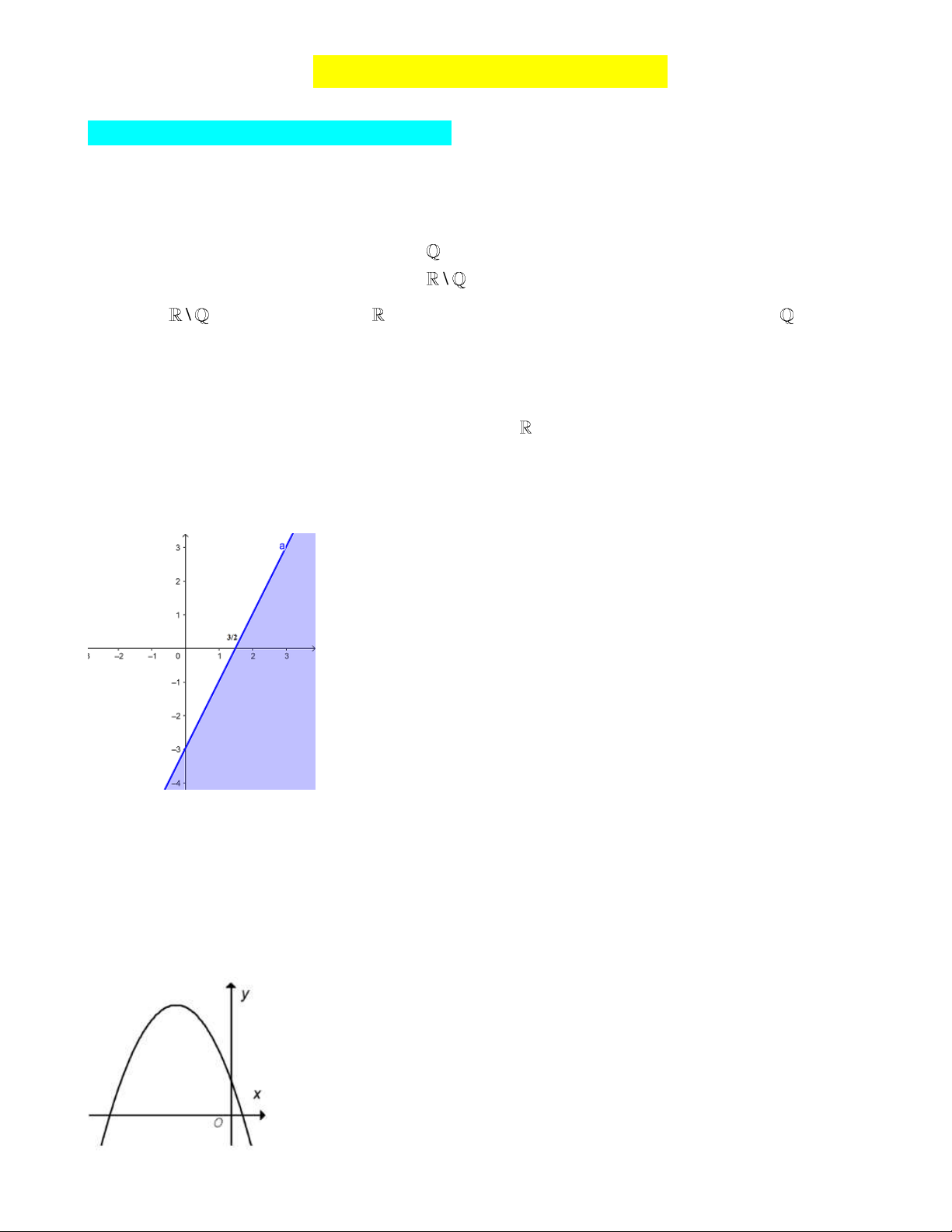
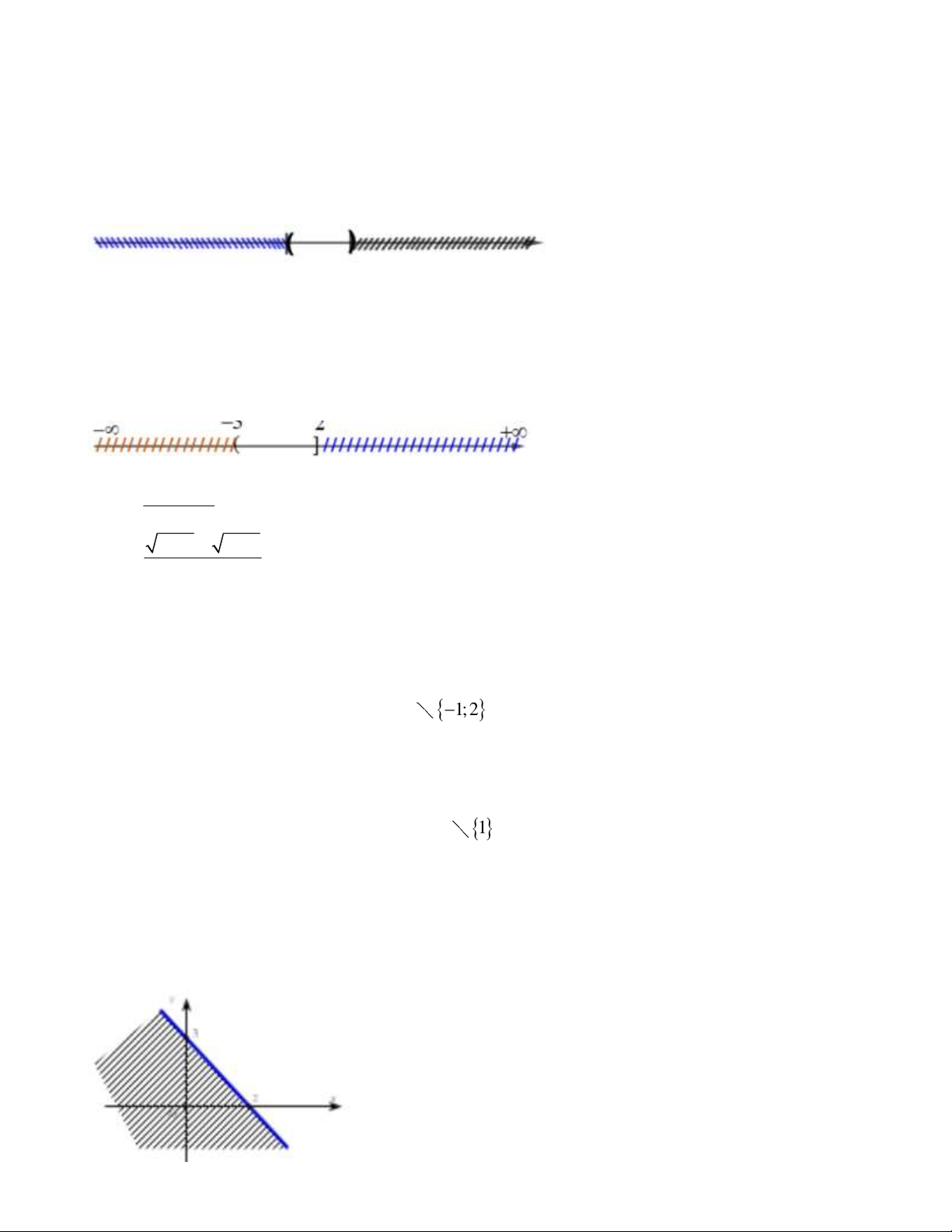
Câu 5: Phần không tô đậm (không kể các điểm nằm trên đường thẳng) trong hình vẽ sau, biểu diễn tập
nghiệm của bất phương trình nào trong các bất phương trìnhsau?
A. x  2y  3 .
B. 2x  y  3 .
C. x  2y  3 .
D. 2x  y  3 .
2x  3 khi x  2
Câu 6: Đồ thị hàm số y  f  x  
đi qua điểm có tọa độ nào sau đây? 2
x  3 khi x  2 A. 3; 6 B. 2;5 C. 2;  1 D. 0; 3 Câu 7: Cho hàm số 2
y  ax  bx  c có đồ thị như hình bên.
Khẳng định nào sau đây đúng ?
A. a  0,b  0, c  0 .
B. a  0,b  0, c  0 .
C. a  0,b  0, c  0 .
D. a  0,b  0, c  0 . Câu 8: Cho hàm số 2
y  x  4x  3 . Chọn khẳng định đúng.
A. Hàm số nghịch biến trên .
B. Hàm số đồng biến trên 2;   .
C. Hàm số đồng biến trên .
D. Hàm số nghịch biến trên 2;   . x  y  0 
Câu 9: Miền nghiệm của hệ bất phương trình x  3y  3
 không chứa điểm nào sau đây? x  y  5 
A. D 5; 4 .
B. B 6;3 .
C. C 6; 4 .
D. A3; 2 .
Câu 10: Tập hợp A  x ∣ x  x   2 7
2 x  4x   0 có bao nhiêu phần tử? A. 2 B. 3 . C. 1 . D. 5 .
Câu 11: Miền nghiệm của bất phương trình: 3 x  
1  4 y  2  5x  3 là nửa mặt phẳng chứa điểm: A.  2  ;2 .
B. 5;3 . C. 0;0 . D.  4  ,2 .
Câu 12: Cho mệnh đề 2 ( P ) x : "
: 2x  x  5  0" . Mệnh đề phủ định của ( P ) x là A. 2
"x  , 2x  x  5  0" . B. " 2
x  , 2x  x  5  0" . C. 2
"x  , 2x  x  5  0". D. 2
"x  , 2x  x  5  0".
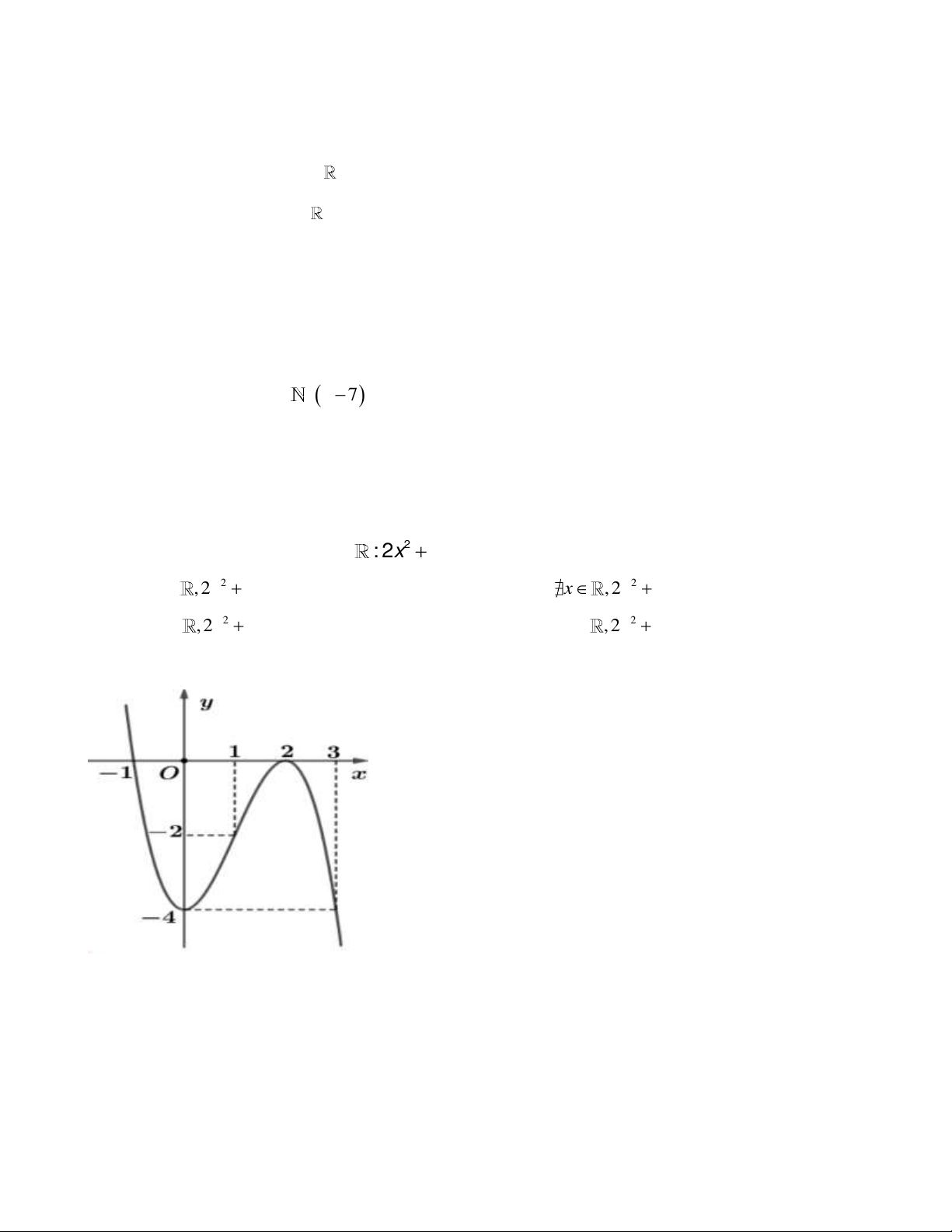
Câu 13: Cho hàm số y  f  x có đồ thị như hình bên. Đồ thị ham sồ không đi qua điểm nào A. 1; 1  .
B. 3; 4
C. 1; 0 D. 1; 2   .
Câu 14: Cho hàm số y  f  x có tập xác định là  5
 ;5 và đồ thị của nó được biểu diễn bởi hình dưới
đây.Trong câc khẳng định sau, khẳng định nào là sai?
A. Hàm số đồng biến trên khoảng  5  ; 3   .
B. Hàm số đồng biến trên khoảng  5  ; 2   và 2;5 .
C. Hàm số đồng biến trên 0; 4
D. Hàm số nghịch biến trên khoảng  2  ;2 .
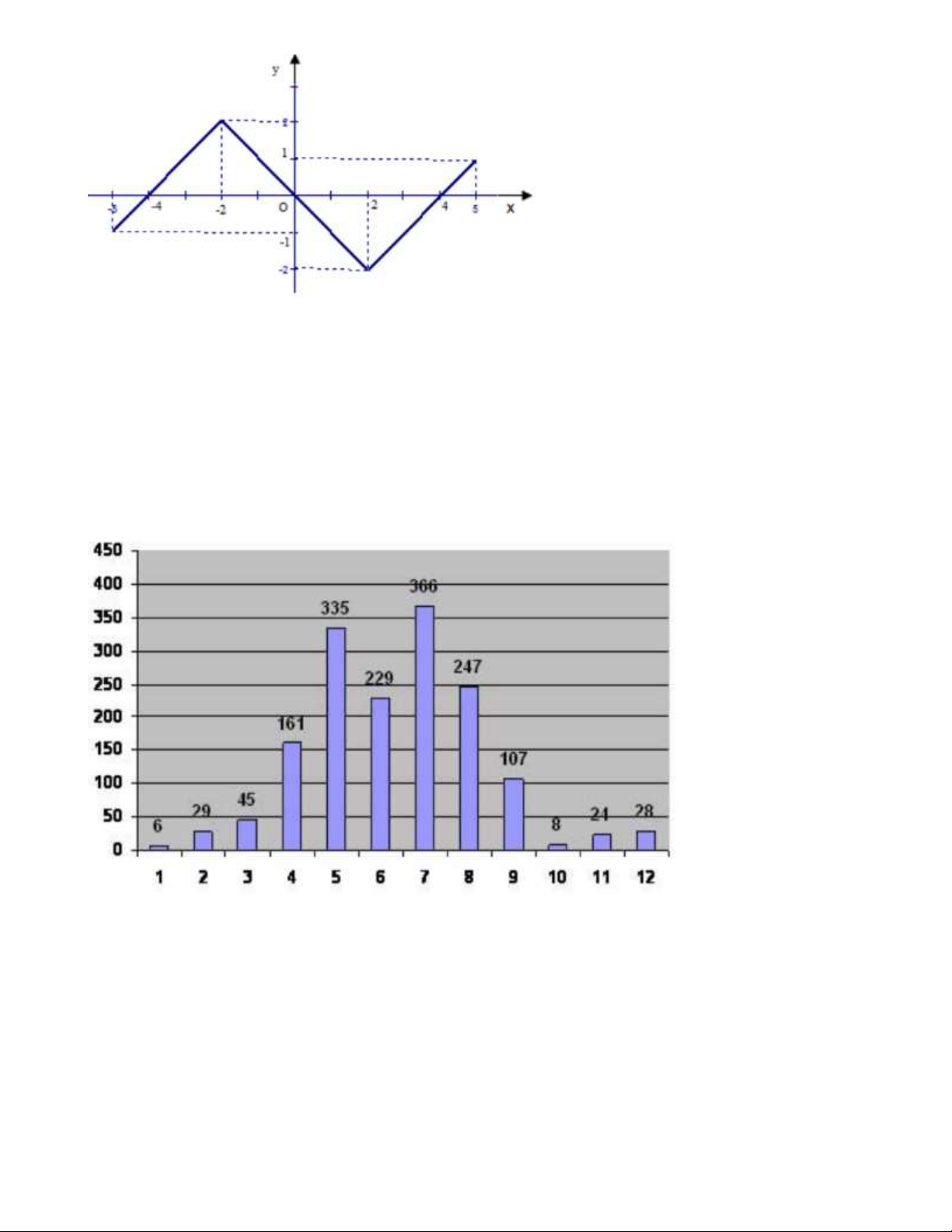
Câu 15: Biết rằng lượng mưa trung bình mm các tháng trong năm ở Hà nội được cho bởi bảng sau là
một hàm số theo tháng. Tập giá trị T của hàm số đó là:
A. T  6;8; 24; 28; 29; 45;107;161; 229; 247;335;36  6
B. T  6;366 .
C. T  1; 2;3; 4;5;6;7;8;9;10;11  ;12 .
D. T  6;8; 24; 28; 29; 45;161; 229; 247;335;36  6 .
Câu 16: Tọa độ đỉnh I của parabol 2
y  x  2x  5 là : A. 1; 4  . B. 4;  1 . C. 1; 4 D. 1;8 .
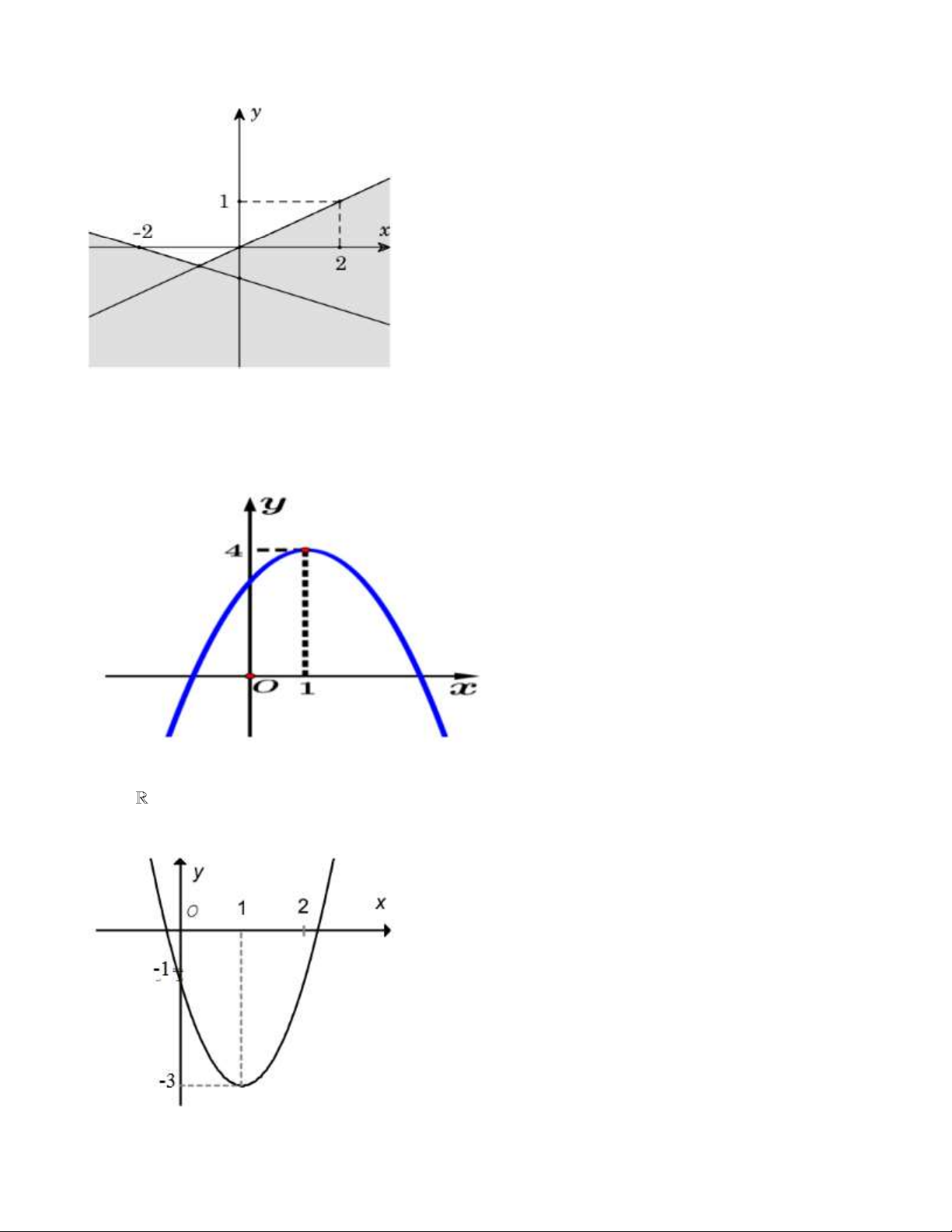
Câu 17: Phần không tô đậm trong hình vẽ dưới đây (không chứa biên), biểu diễn tập nghiệm của hệ bất
phương trình nào trong các hệ bất phương trình sau?
x  2y  0
x  2y  0
x  2y  0
x  2y  0 A.  . B.  . C.  . D.  .
x  3y  2
x  3y  2
x  3y  2
x  3y  2
Câu 18: Cho hâm số bậc hai y f  x 2 
 ax  bx  c có đồ thị như hình vẽ:
Tập giá trị của hàm số đã cho là: A. B.     ;1 C.    ;4 D.     ;1
Câu 19: Cho hàm số bậc hai có đồ thị như hình bên dưới
Hỏi đồ thị trên là đồ thị của hàm số nào? A. 2
y  2x  4x 1. B. 2
y  x  4x 1. C. 2
y  2x  4x 1. D. 2 y  2
 x  4x 1.
x  2y  5
Câu 20: Cặp số nào là một nghiệm của hệ bất phương trình  ? 3
 x  2y  6 A. 5;0 . B. 5;3 , C. 2; 2   . D. 0;3 .
PHẦN TỰ LUẬN(6,0 điểm)
Câu 1. Xác định các tập hợp sau và biểu diễn trên trục số: a)  4  ;  1  0;3 ; b) 0;2 3   ;1
Câu 2 .Tìm tập xác định của các h x  5 a) y  . 2 x  x  2
x  4  4  x b) y  . x 1
Câu 3. Biểu diễn miền nghiệm của bất phương trình 3x  2y  6 trên mặt phẳng tọa độ.
Câu 4. Vẽ đồ thị hàm số 2
y  x  2x  3 .
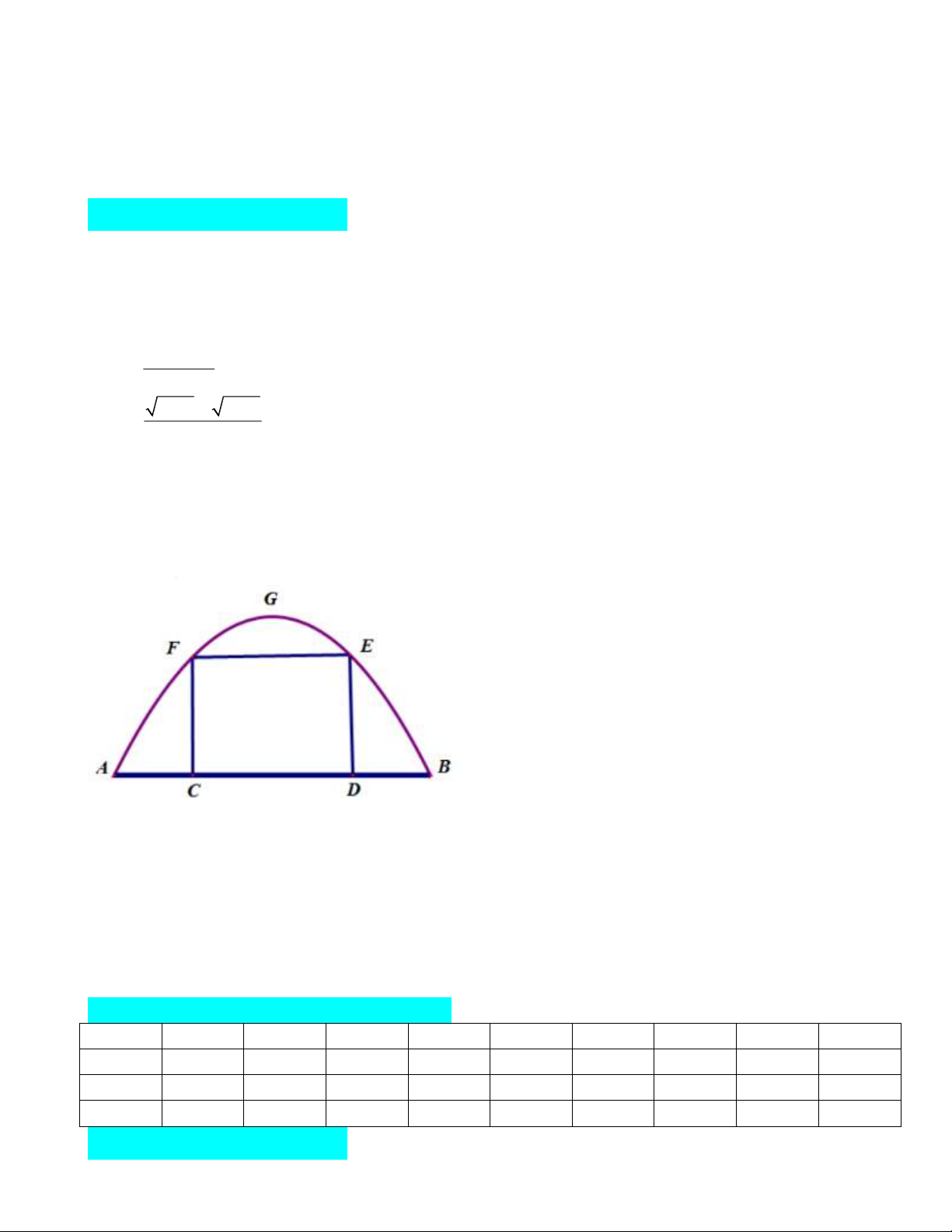
Câu 5 . Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai
cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4 m còn kích thước cửa ở
giữa là 3 m 4 m . Hãy tính khoảng cách giữa hai điểm A và B .
Câu 6. Một phân xưởng sản xuất hai loại sản phẩm A và B . Thời gian để làm ra sản phẩm
loại A nhiều gấp hai lần thời gian làm ra sản phẩm loại B . Nếu chỉ sản xuất toàn sản phẩm
loại B thì trong 1 giờ phân xưởng làm được 60 chiếc. Phân xưởng làm việc không quá 8
tiếng mỗi ngày và thị trường tiêu thụ tối đa trong một ngày là 200 sản phẩm loại A và 240
sản phẩm loại B . Tiền lãi khi bán một sản phẩm loại A là 24 nghìn đồng, một sản phẩm
loại B là 15 nghìn đồng. Tính số lượng sản phẩm loại A và sản phẩm loại B trong một
ngày mà phân xưởng cần sản xuất để tiền lãi thu được là cao nhất. ĐÁP ÁN
A. PHẦN TRẮC NGHIỆM ( 4.0 điểm). 1 2 3 4 5 6 7 8 9 10 B B D B D A B D D A 11 12 13 14 15 16 17 18 19 20 C A A C A C D C C B
PHẦN TỰ LUẬN(6,0 điểm)
Câu 1. Xác định các tập hợp sau và biểu diễn trên trục số: a)  4  ;  1  0;3 ; b) 0;2 3   ;1 Lời giải a)  4   ;1  0;3  0  ;1 b) 0;2  3   ;1   3  ;2
Câu 2 .Tìm tập xác định của các h x  5 a) y  . 2 x  x  2
x  4  4  x b) y  . x 1 Lời giải x   a) Điề 1 u kiện xác đinh: 2
x  x  2  0   x  2
Yậy tập xáe định của hàm số là D  R  1  ;  2 x  4  0 x  4     x  b) Điề 4 4
u kiện xác định: 4  2  0  x  4      x  1 x 1  0  x  1
Vậy tập xác định của hàm số là D   4  ;4   1
Câu 3. Biểu diễn miền nghiệm của bất phương trình 3x  2y  6 trên mặt phẳng tọa độ. Lời giải
Vẽ đường thẳng Δ đi qua hai điểm A2;0 và B 0;3 có phương trình là 3x  2y  6 Thay tọa độ điểm (
O 0;0) vào vế trái của bất phương trình ta được: 3.0  2.0  6 (vô lí)
vậy miềm nghiệm của BPT là miền nửa mặt phẳng bờ là đường thẳng 3x  2y  6 bao gồm
cả đường thẳng 3x  2y  6 .
Câu 4. Vẽ đồ thị hàm số 2
y  x  2x  3 . Lời giải
a  1  0 ĐTHS có bề lõm hướng lên trên Đỉnh I 1; 4  
Trục đối xứng: đường thẳng x 1.
Giao của đồ thị với trục Oy:(0; 3 
+ Giao của đồ thị với trục Ox : 3;0; 1  ;0 .
Câu 5 . Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai
cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4 m còn kích thước cửa ở
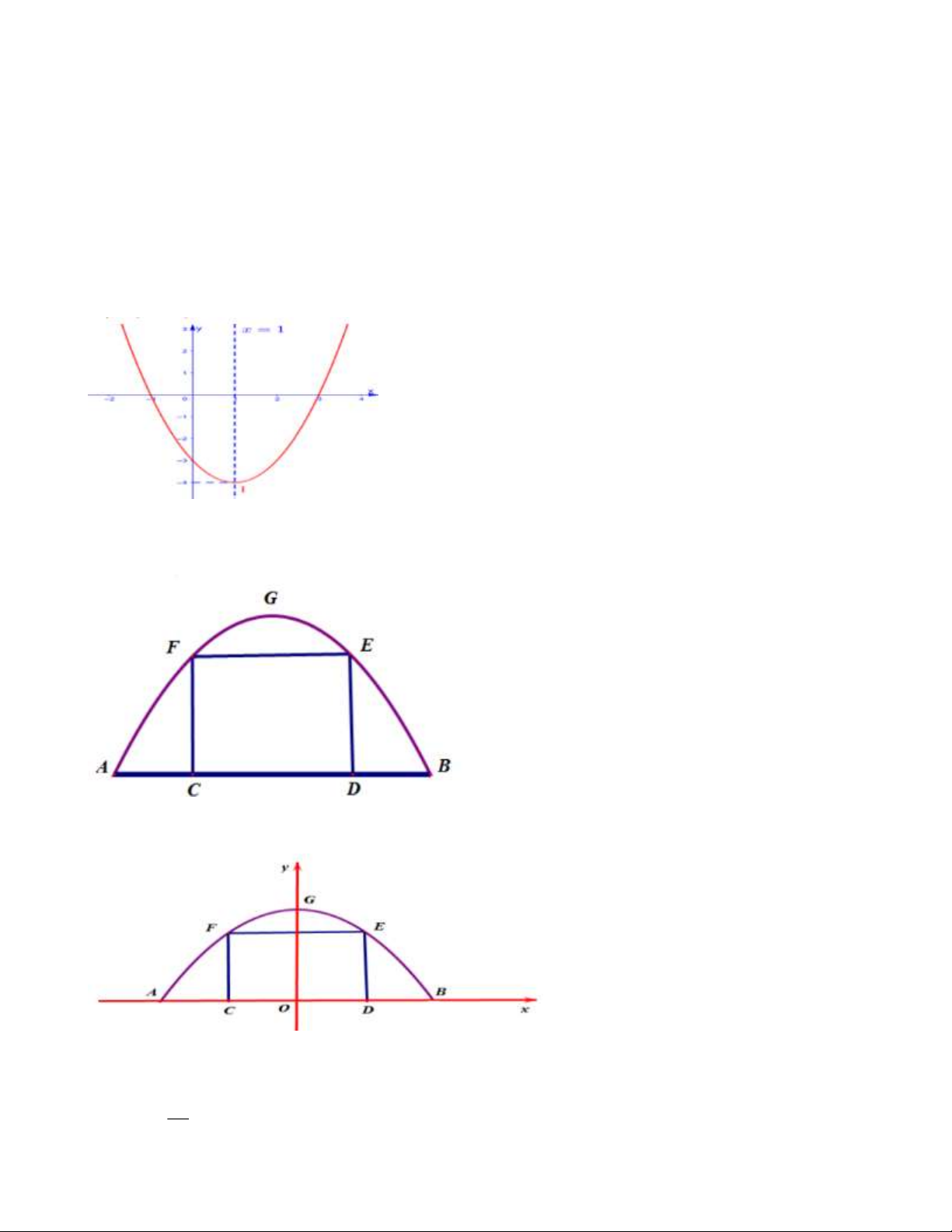
giữa là 3 m 4 m . Hãy tính khoảng cách giữa hai điểm A và B . Lời giải Chọn HTTĐ như hình vẽ
Gắn hệ trục tọa độ Oxy như hình vẽ, chiếc cổng là 1 phần của parabol P 2
: y  ax  bx  c .
Do parabol  P đối xứng qua trục tung nên có trục đối xứng  b x 0    0  b  0 . 2a
Chiều cao của cổng parabol là 4 m nên G 0;4  c  4 .  P 2
: y  ax  4 .
Lại có, kích thước cửa ở giữa là 3 m 4 m nên E   F   1 2;3 ,
2;3  3  4a  4  a   . 4 1 Vậy P 2 : y   x  4 . 4 1 x  4 Ta có 2
 x  4  0   4 x   4 Nên A 4
 ;0, B4;0 hay AB  8
Câu 6. Một phân xưởng sản xuất hai loại sản phẩm A và B . Thời gian để làm ra sản phẩm
loại A nhiều gấp hai lần thời gian làm ra sản phẩm loại B . Nếu chỉ sản xuất toàn sản phẩm
loại B thì trong 1 giờ phân xưởng làm được 60 chiếc. Phân xưởng làm việc không quá 8
tiếng mỗi ngày và thị trường tiêu thụ tối đa trong một ngày là 200 sản phẩm loại A và 240
sản phẩm loại B . Tiền lãi khi bán một sản phẩm loại A là 24 nghìn đồng, một sản phẩm
loại B là 15 nghìn đồng. Tính số lượng sản phẩm loại A và sản phẩm loại B trong một
ngày mà phân xưởng cần sản xuất để tiền lãi thu được là cao nhất. Lời giải
Gọi x, y lần lượt là số lượng sp loại A và sp loại B trong một ngày mà phân xưởng cần sản
xuất để tiền lãi thu được cao nhất.
(Điều kiện: x  N, y N )
Thiết lập được các bất trình. 0  x  200 
Chốt đưa về bài toán:Tìm x, y thoả mãn hệ BPT 0  y  240
2x  y  480 
sao cho T  24x 15y có giá trị lớn nhất.
Miền nghiệm của hệ bất phương trình (I) là miền ngũ giác ACDEO với A 0;240 ,
C 120; 240, D(200;80), E(200;0),O(0;0)
Ta có: T  24x 15y
Tại A ta có: T 0;240  3600
Tại C ta có:T 120;240  6480
Tại D ta có:T (200;80)  6000
Tại E ta có:T (200;0)  4800
Tại O ta có:T (0;0)  0
So sánh giá trị của biểu thức T tại các đỉnh, ta thấy T đạt giá trị lớn nhất bằng 6480 khi
x  120 và y  240 ứng với tọa độ đỉnh C .
Vậy để tiền lãi thu được là cao nhất, trong một ngày xưởng cần sản xuất 120sp loại A và
240sp loại B. Khi đó tiền lãi là 6480000 đồng.