Đề cương ôn tập giữa học kỳ 1 toán 10 Chân trời sáng tạo 2023-2024

ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KỲ I
TOÁN 10-CHÂN TRỜI SÁNG TẠO
A. TRẮC NGHIỆM (7,0 điểm)
Câu 1: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn? A. 2
2x  3y  0 . B. 2
x  y  2 . C. 2 2
x  4 y  6 .
D. x  4y  3  .
Câu 2: Trong các đẳng thức sau đây đẳng thức nào là đúng? 1 3 3
A. cot150  3 . B. tan150   . C. sin150   . D. cos150  . 3 2 2
Câu 3: Xét mệnh đề chứa biến: P  x : " x là số nguyên tố". Trong các mệnh đề sau, mệnh đề nào đúng?
A. P 6 .
B. P 9 .
C. P 13 D. P 15 .
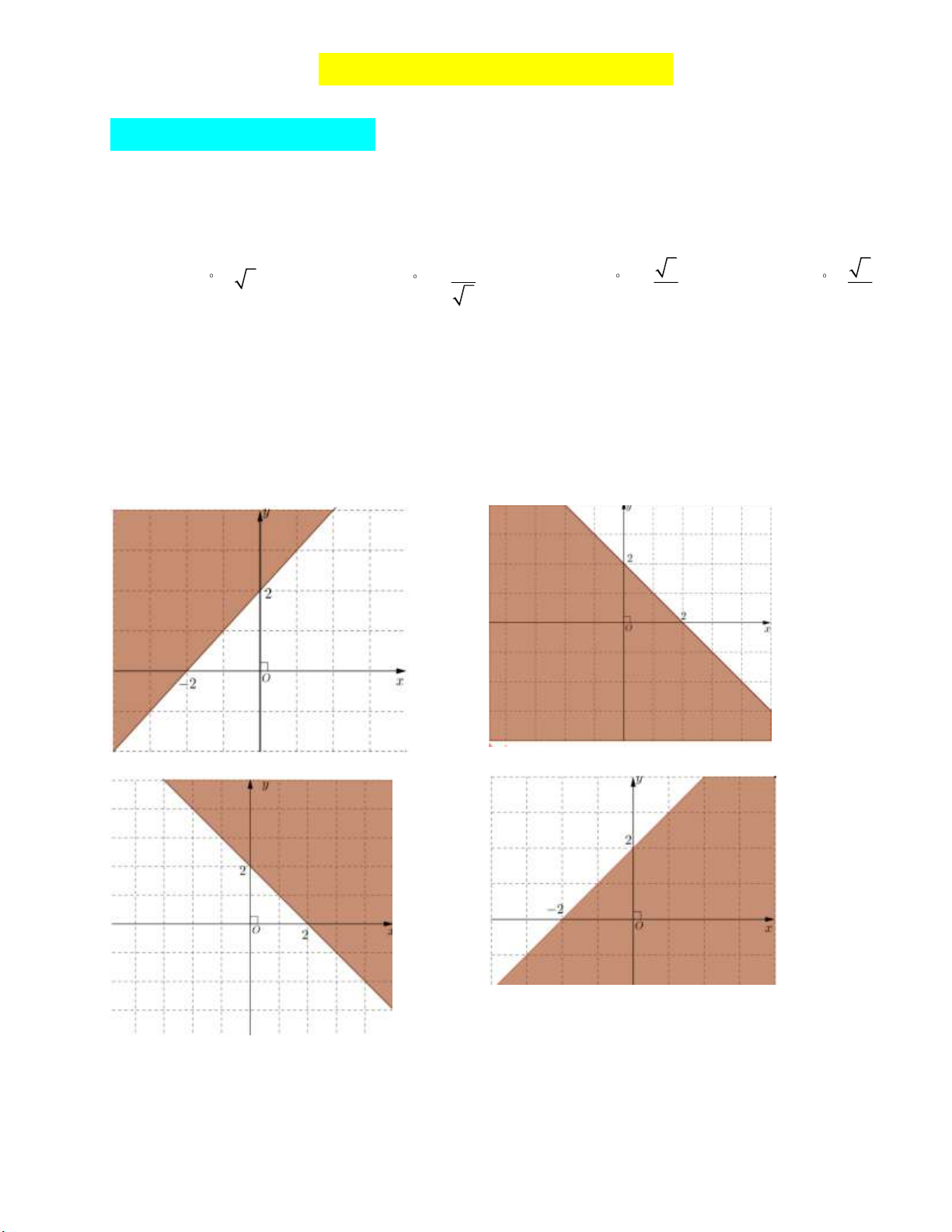
Câu 4: Miền nghiệm của bất phương trình x  y  2 là phần tô đậm trong hình vẽ của hình vẽ
nào, trong các hình vẽ sau? A. B. C. D.
Câu 5: Cho A   3
 ;2 . Tập hợp C A là A. 2;    B.    ; 3   C. 3;    . D.    ; 3   .
Câu 6: Miền không bị gạch trong hình bên đưới là hình biểu điên miền nghiệm của bất
phương trình bậc nhất nào sau đây?
A. x  2y  2  0 .
B. x  2y 1  0 .
C. x  2y  2  0 .
D. 2x  y 1  0 .
Câu 7: Trong các hệ bất phương trình sau, hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn? x  y  3 x  3  
2x  3y  4
2x  3y  4 A. y 1 . B. y  2 . C.  . D.    3 2
2 x  3 y  1 3 2
2 x  3y  1
x  y  x   xy 2 x  y   y .
Câu 8: Phát biểu nào sau đây là một mệnh đề?
A. Số 3 có phải là số tự nhiên?
B. Con đang làm gì đó.
C. New Yorklẩ thủ đô của Việt Nam.
D. Trời hôm nay đẹp quá!
Câu 9: Mệnh đề “ 2
x , x 15 " được phát biểu là
A. Bình phương của mỗi số thực bằng 15 .
B. Nếu x là một số thực thì 2 x  15 .
C. Chỉ có một số thực mà bình phương của nó bằng 15.
D. Có ít nhất một số thực mà bình phương của nó bằng 15 . 3sin  cos
Câu 10: Cho tan  2 . Giá trị của A  là sin  cos 5 7 A. 7 . B. 5 . C. . D. . 3 3
Câu 11: Cho mệnh đề: "Nếu tam giác có hai góc bằng 60 thì tam giác đó là tam giác đều".
Mệnh đề đảo của mệnh đề trên là:
A. Nếu tam giác có hai góc bằng 60 thì tam giác đó không là tam giác đều.
B. Nếu tam giác là tam giác đều thì tam giác đó có hai góc bằng 60 .
C. Tam giác là tam giác đều nếu và chỉ nếu tam giác đó có hai góc bằng 60 .
D. Nếu một tam giác là tam giác đều thì tam giác đó có hai góc bằng nhau.
Câu 12: Cách phát biểu nào sau đây không thể dùng để phát biểu mệnh đề A  B ?
A. A kéo theo B .
B. A là điều kiền đủ để có B .
C. A là điều kiền cần để có B .
D. Nếu A thì B .
Câu 13: Miền nghiệm của bất phương trình 3
 x  y  2  0 không chứa điểm nào sau đây?  1 
A. A1; 2 . B. C 1;  . C. D 3;  1 . D. B 2;  1 .  2 
Câu 14: Cho tam giác ABC có AB  4 cm, BC  7 cm,CA  9 cm . Giá trị cosA là 2 2 1 1 A. . B.  . C. . D. . 3 3 3 2
Câu 15: Trong các đẳng thức sau, đẳng thức nào đúng ?
A. sin 180  a  sina . B. sin 180  a  cosa . C. sin 180  a  cosa . D.
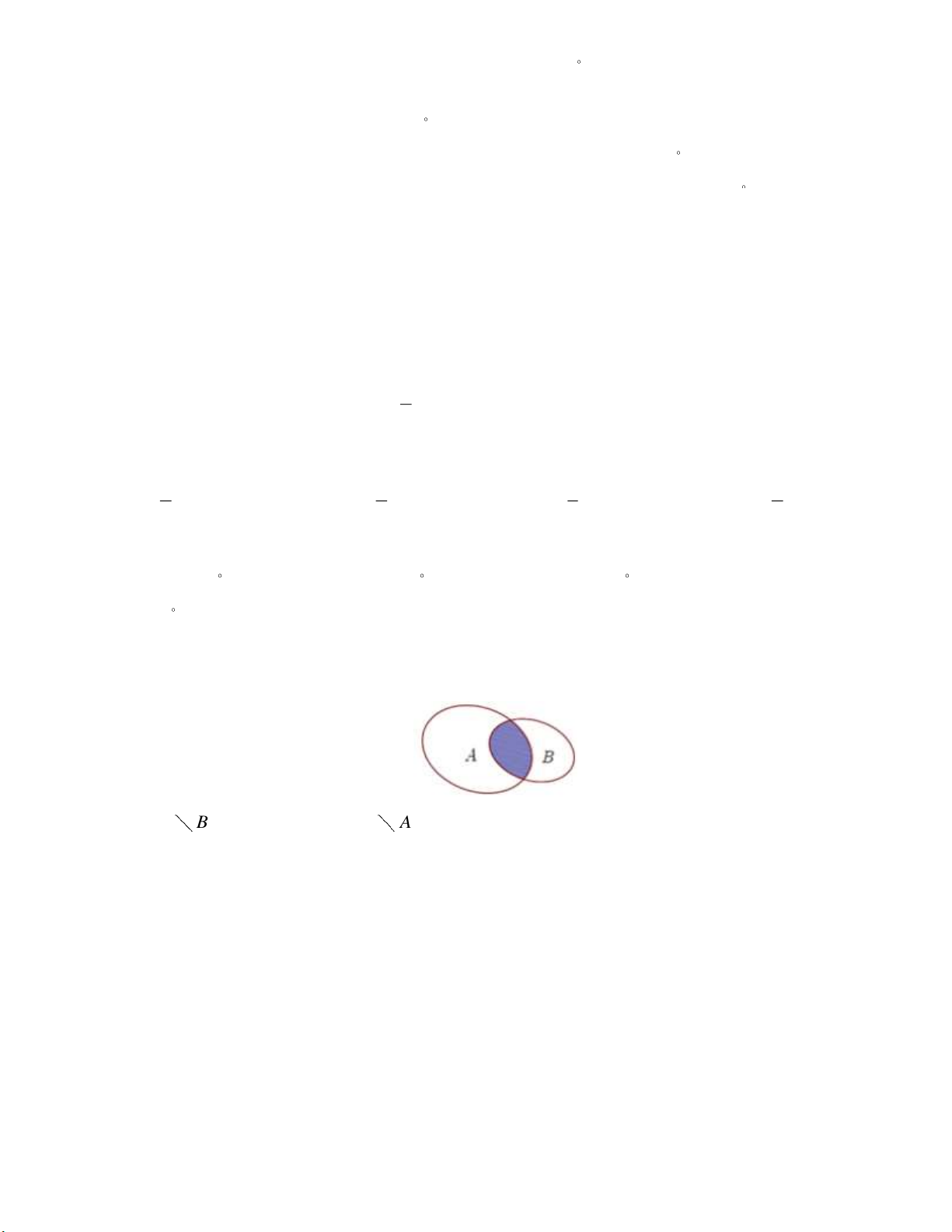
sin 180  a  si  na . Câu 16: Cho ,
A B là hai tập hợp được minh họa như hình vẽ. Phần tô đen trong hình vẽ là tập hợp nào sau đây? A. A B . B. B A .
C. A  B .
D. A  B .
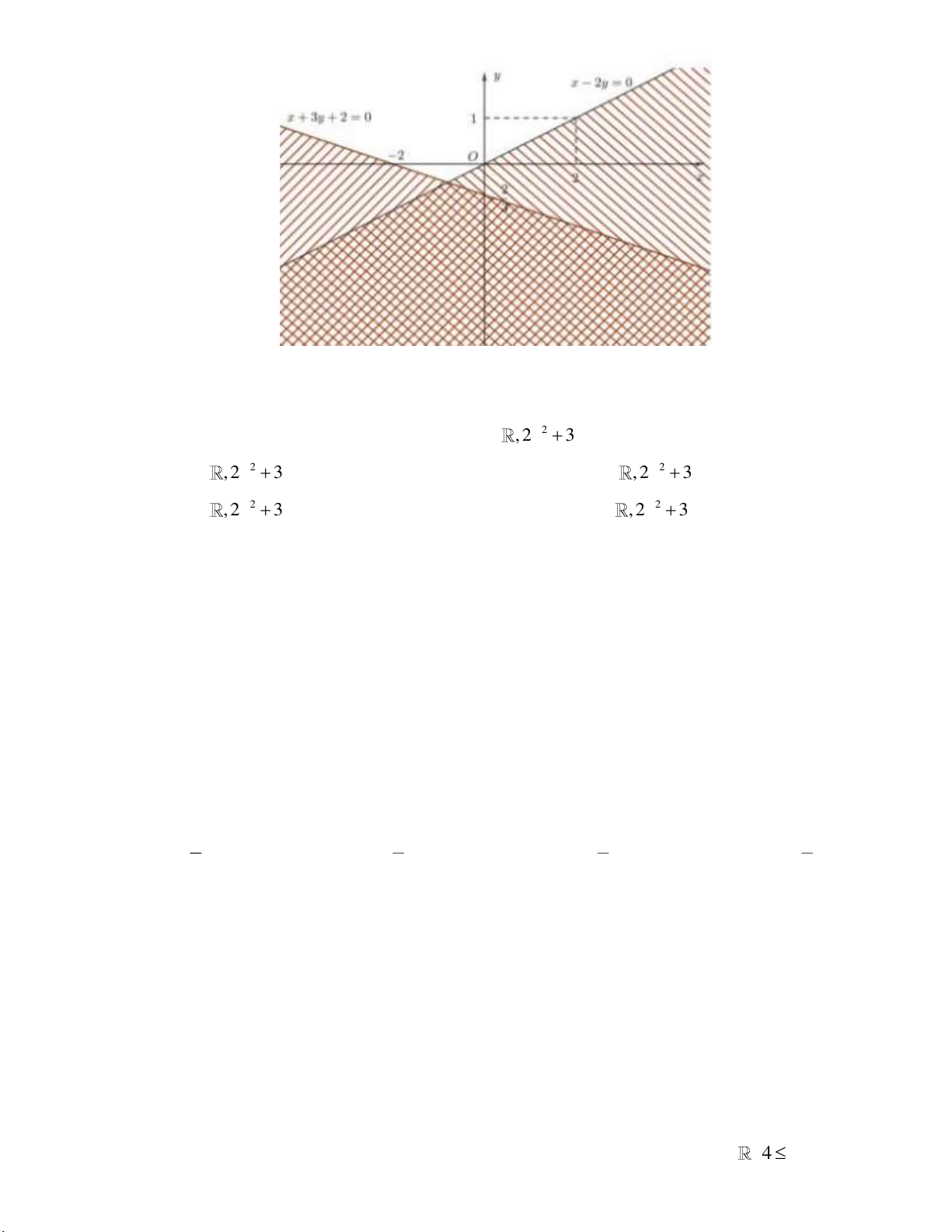
Câu 17: Trong hình vẽ dưới, phần mặt phẳng không bị gạch sọc (kể bờ) là miền nghiệm của hệ bất phương trình
x  2y  0
x  2y  0
x  2y  0
x  2y  0 A.  . B.  C.  D. 
x  3y  2 x  3y 
x  3y  2
x  3y  2
Câu 18: Mệnh đề phủ định của mệnh đề: " 2
x  ,2x  3x  5  0 " là A. " 2
x  ,2x  3x  5  0 " B. " 2
x  ,2x  3x  5  0 " C. " 2
x  ,2x  3x  5  0 " D. " 2
x  ,2x  3x  5  0 "
Câu 19: Cho tam giác ABC , mệnh đề nào sau đây đúng? A. 2 2 2
a  b  c  2b c c osA . B. 2 2 2
a  b  c  2b c c osA . C. 2 2 2
a  b  c  2b c c osB . D. 2 2 2
a  b  c  2b c c osC .
Câu 20: Điểm O 0;0 không thuộc miền nghiềm của hệ bất phương trình nào sau đây?
x  3y  0
x  3y  6  0
x  3y  6  0 A.  . B.  . C.  . D.
2x  y  4  0
2x  y  4  0
2x  y  4  0
x  3y  0  .
2x  y  4  0
Câu 21: Chọn công thức đúng trong các đáp án sau. 1 1 1 1
A. S  b s c inC . B. S  a s c inA .
C. S  b s c inB .
D. S  b s c inA . 2 2 2 2
Câu 22: Cho mệnh đề: “Có một học sinh trơng 10A không thtch học môn Toán". Mệnh đề phủ
định của mệnh đề này là
A. "Có một hoc sinh trong lớp 10A thích học môn Toán".
B. "Mọi học sinh trong lớp 10A đều không thích học môn Toán".
C. "Mọi học sinh trong lớp 10A thích học môn Văn".
D. "Mọi học sinh trong lớp 10A đều thích học môn Toán".
Câu 23: Cặp số (1;-1) là nghiệm của bất phương trình
A. x  y  0 .
B. x  y  2  0 .
C. x  3y 1  0 .
D. x  4y  1.
Câu 24: Dùng các kí hiệu khoảng, đoạn, nửa khoảng để viết tập hợp A  {x  ∣ 4  x  6}.
A. A  4;6.
B. A  4;6 .
C. A  4;6 .
D. A  4;6 . x  y  0
Câu 25: Cho hệ bất phương trình 
có tập nghiệm là S . Khẳng định nào sau đây là
2x  5y  0 khẳng định đúng?  1 2   1  A.  ;    S . B.  1  ;  1  S . C. 1;     S . D. 1  ;1  S .  2 5   2 
2x  y  4  0
Câu 26: Cho hệ bất phương trình 
. Trong các điểm sau, điểm nào thuộc miền
x  y 10  0
nghiệm của hệ bất phương trình? A. Q 4; 3  . B. M 1  ;1 . C. P  4  ;3 .
D. N 2;   1 .
Câu 27: Trong mặt phẳng tọa độ xOy , lấy điểm M trên nữa đường tròn đơn vị sao cho
xOM  150 . Tọa độ điểm M là  1 3   3 1   3 1   3 1  A. M  ;    B. M  ;    C. M   ;     D. M   ,    2 2   2 2   2 2   2 2  
Câu 28: Trong các khẳng định sau đây, khẳng định nào sai?
A. cos30  sin120
B. cos45  sin135 .
C. sin60  cos120 . D. cos45  sin45 .
Câu 29: Cho mệnh đề P đúng và mệnh đề Q sai. Mệnh đề nào sau đây là mệnh đề sai?
A. P  Q
B. P  Q
C. P  Q
D. P  Q
Câu 30: Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nứa mặt phẳng
không bị gạch trong hình vẽ sau?
A. 2x  y  3 .
B. 2x  y  3
C. x  y  3 .
D. 2x  y  3 .
Câu 31: Tập hợp  2  ;3 1; 
5 bằng tập hợp nào sau đây? A.  3  ; 2   . B.  2   ;1 C.  2   ;1 . D. 2;5 . 2
Câu 32: Cho góc nhọn  có sin  . Giá trị của tan là 3 2 2 2 2 A. tan   B. ) tan  . C. tan  . D. tan   . 7 7 7 7
Câu 33: Trong các câu dưới đây, có bao nhiêu câu là mệnh đề?
1. Hình vuông có hai đường chéo vuông góc với nhau.
2. Sông Hương chảy ngang qua thành phố Huế.
3. Năm 2022 không phải là năm nhuận.
4. Hôm nay trời đẹp quá! A. 3 . B. 4 . C. 5 . D. 2 .
Câu 34: Tam giác ABC có AB  2, AC  1 và A  60 . Tính độ dài cạnh BC .
A. BC  1.
B. BC  2 .
C. BC  2 . D. BC  3 .
Câu 35: Cho tam giác ABC , chọn công thức đúng trong các đáp án sau. 2 2 2
2c  2b  a 2 2 2 b  c a A. 2 m  . B. 2 m   . a 2 4 a 2 2 2 2 2 4 a  c b 2 a  b c C. 2 m   . D. 2 m   a 2 4 a 2 4
B. TỰ LUẬN (3,0 điểm)
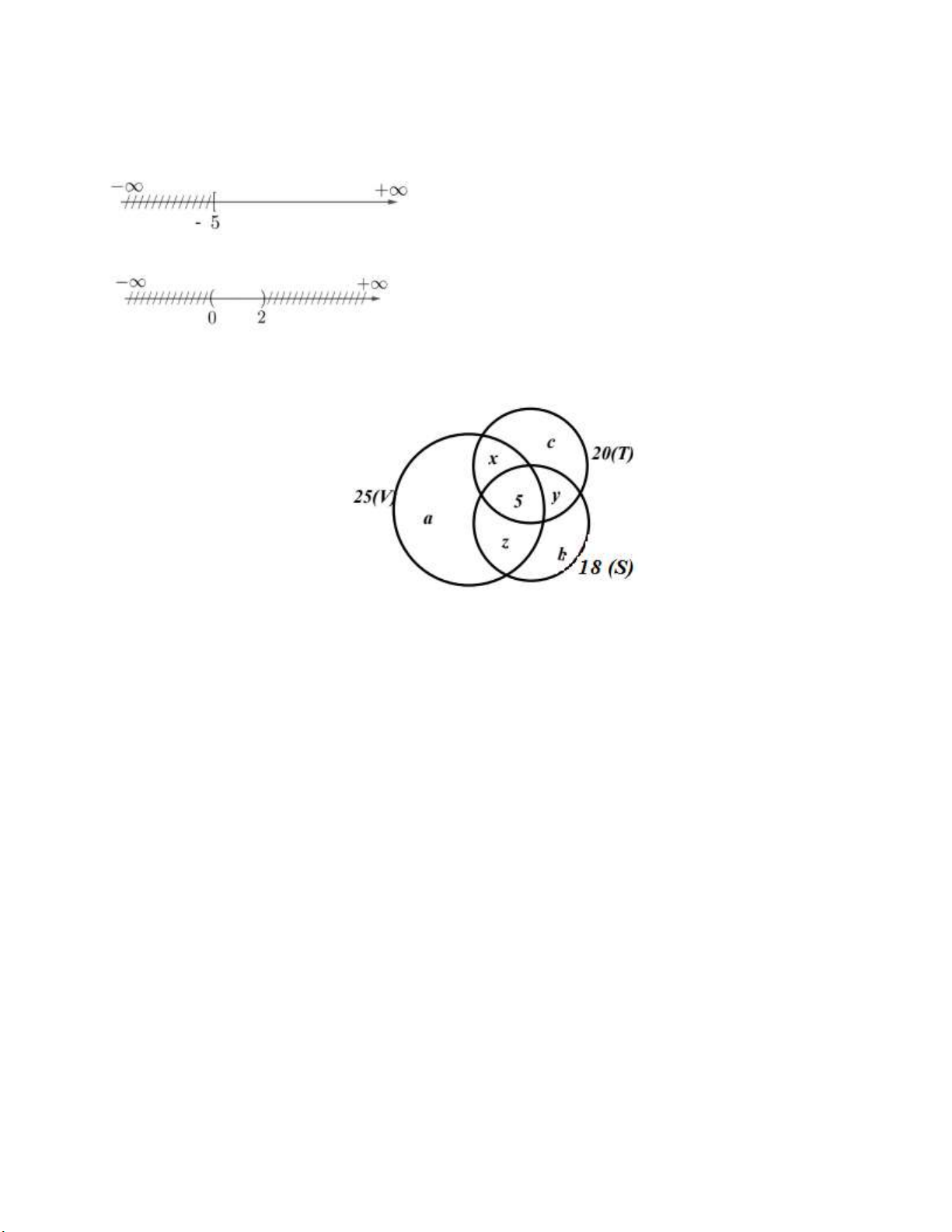
Bài 1. Cho A   5
 ;2; B  0;    . Tìm A ;
B A  B và biểu diễn kết quả trên trục số.
Bài 2. Trong lớp 10A có 45 học sinh trong đó có 25 em thích môn Văn, 20 em thích môn
Toán, 18 em thích môn Sử, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích
chỉ một môn trong ba môn trên.
Bài 3. Một công ty kinh doanh thương mại chuẩn bị cho một đợt khuyến mại nhằm thu hút
khách hàng bằng cách tiến hành quảng cáo sản phẩm của công ty trên hế thống phát thanh và
truyền hình. Chi phí cho 1 phút quảng cáo trên sóng phát thanh là 800000đồng, trên sóng
truyền hình là 4.000.000. Đài phát thanh chỉ nhận phát các chương trình quảng cáo dài ít nhất
là 5 phút. Do nhu cầu quảng cáo trên truyền hình lớn nên đài truyền hình chỉ nhận phát các
chương trình dài tối đa là 4 phút. Theo các phân tích cùng thời lượng một phút quảng cáo trên
truyền hình sẽ có hiệu quả gấp 6 lần trên sóng phát thanh. Công ty dự định chi tối đa là
16.000.000 đồng cho quảng cáo. Công ty cần đặt thời lượng quảng cáo trên sóng phát thanh và
truyền hình như thế nào để hiệu quả nhất?
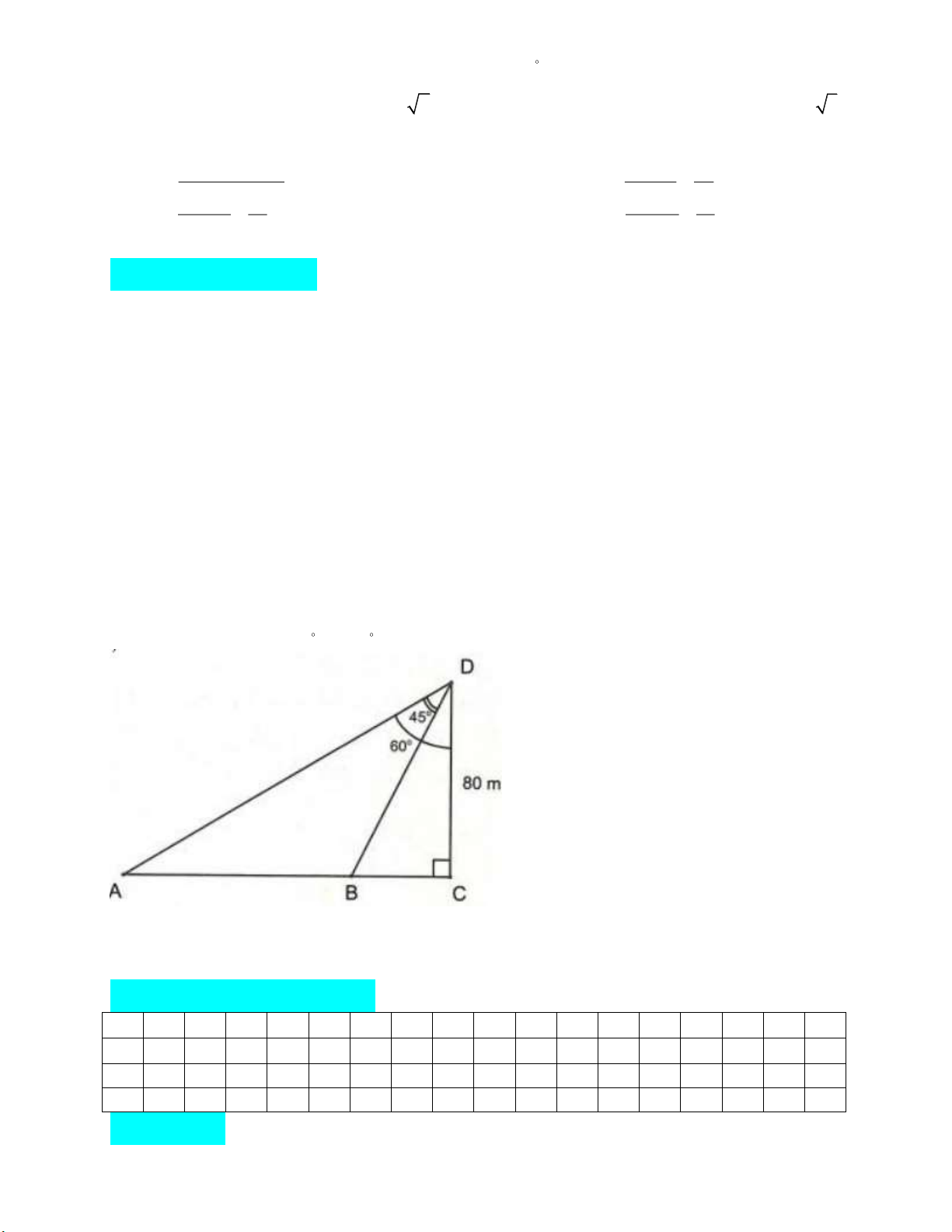
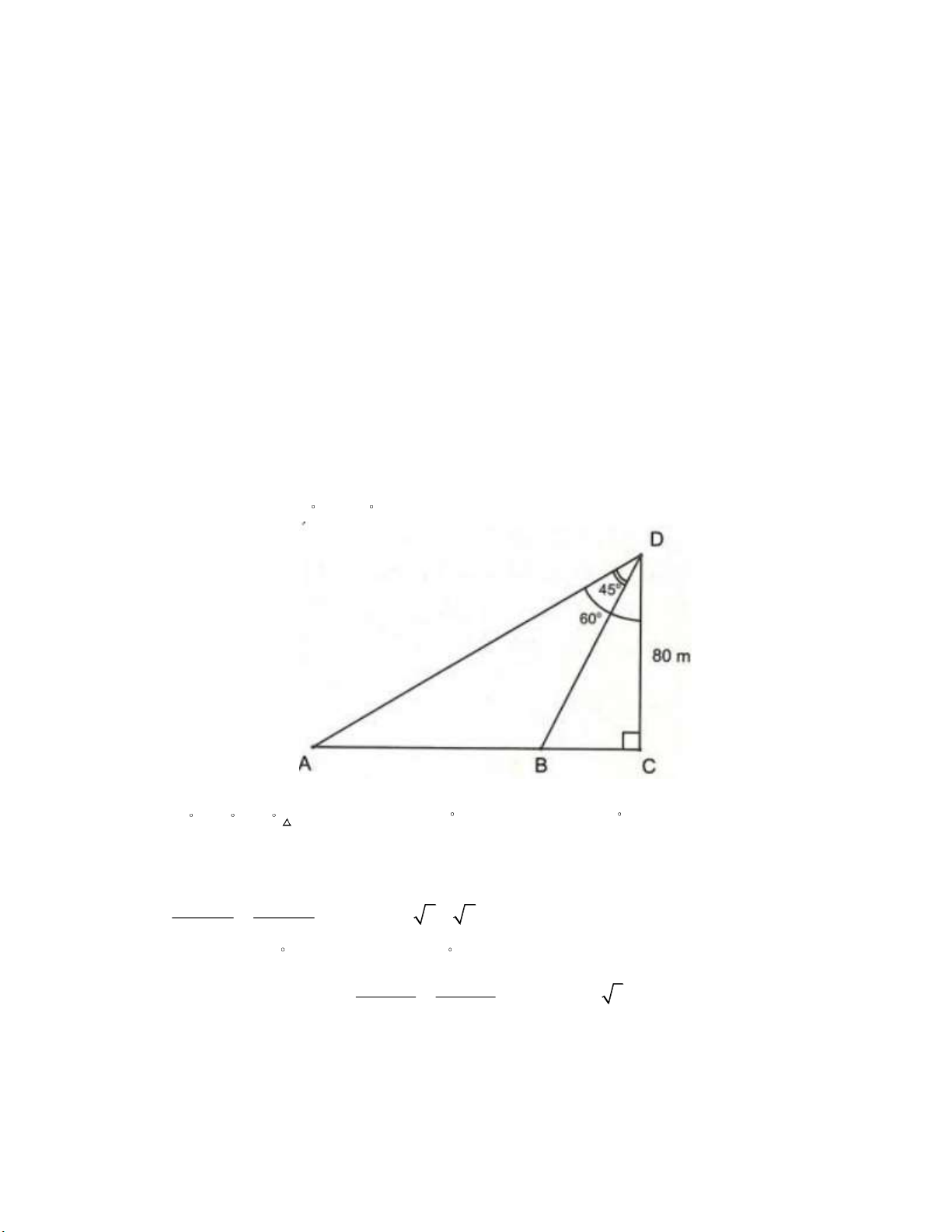
Bài 4. Từ một đỉnh tháp chiều cao CD  80 m , người ta nhìn thấy hai điểm A và B trên mặt
đất dưới các góc nhìn 60 và 45 (như hình vẽ). Biết ba điểm ,
A B, C thẳng hàng. Tính khoảng cách AB . ĐÁP ÁN
A. TRẮC NGHIỆM (7,0 điểm) 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 D B C B B C C B D A B C A A A C B
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 D B A D D D B C A D C A D B B B D A B. TỰ LUẬN
Bài 1. Cho A   5
 ;2; B  0;    . Tìm A ;
B A  B và biểu diễn kết quả trên trục số. Lời giải
A  B   5;    
A  B  0; 2
Bài 2. Trong lớp 10A có 45 học sinh trong đó có 25 em thích môn Văn, 20 em thích môn
Toán, 18 em thích môn Sử, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích
chỉ một môn trong ba môn trên. Gọi a, ,
b c theo thứ tự là số học sinh chỉ thích môn văn, sử, toán.
x là số học sinh chỉ thích hai môn văn và toán.
y là số học sinh chỉ thích hai môn sử yâ toán.
z là số học sinh chỉ thích hai môn văn và sử
Dựa vào biểu đồ ven ta có hệ phương trình:
a  x  z  5  25 
b  y  z  5 18 
c  x  y  5  20 
x  y  z  a b c 5  39
Giải hệ phương trình ta được a  b  c  20
Vậy số em thích chi một môn trong ba môn trên là 20 .
Bài 3. Một công ty kinh doanh thương mại chuẩn bị cho một đợt khuyến mại nhằm thu hút
khách hàng bằng cách tiến hành quảng cáo sản phẩm của công ty trên hệ thống phát thanh và
truyền hình. Chi phí cho 1 phút quảng cáo trên sóng phát thanh là 800.000 đồng, trên sóng
truyền hình là 4.000 .000 đồng. Đài phát thanh chỉ nhận phát các chương trình quảng cáo dài ít
nhất là 5 phút. Do nhu cầu quảng cáo trên truyền hình lớn nên đài truyền hình chỉ nhận phát
các chương trình dài tối đa là 4 phút. Theo các phân tích cùng thời lượng một phút quảng cáo
trên truyền hình sẽ có hiệu quả gấp 6 lần trên sóng phát thanh. Công ty dự định chi tối đa là
16.000 .000 đồng cho quảng cáo. Công ty cần đặt thời lượng quảng cáo trên sóng phát thanh
và truyền hình như thế nào để hiệu quả nhất? Lời giải
Gọi thời lượng công ty đặt quảng cáo trên sóng phát thanh là x (phút), trên truyền hình là y
(phút). (điều kiện x  0, y  0 )
Chi phí cho việc này là 800.000x  4.000.000 y (đồng).
Mức chi phí này không được phép vượt qua mức chi tối đa, tức là
800000x  4000000 y  16000000  x  5y  20  0 .
Theo giả thiết, ta có x  5; y  4 .
Hiệu quả chung của quảng cáo là x  6 y .
Bài toán trở thành: Tìm x, y sao cho M  ;
x y   x  6y đạt giá trị lớn nhất, với x, y thoả mãn hệ bất phương
x  5y  20  0  trình x  5 0  y  4 
Trong mặt phẳng Oxy , ta biểu diễn miền nghiệm của hệ bất phương trình * là phần tam giác
ABC với A5;3, B 5;0,C 20;0 .
Ta có M 5;3  23; M 5;0  5; M 20;0  20
Suy ra giá trị lớn nhất của M  ;
x y  bằng 23 tại 5;3 . Tức là nếu đặt thời lượng quảng cáo trên
sóng phát thanh là 5 phút và trên truyền hình là 3 phút thì sẽ đạt hiệu quả nhất.
Bài 4. Từ một đỉnh tháp chiều cao CD  80 m , người ta nhìn thấy hai điểm A và B trên mặt
đất dưới các góc nhìn 60 và 45 (như hình vẽ). Biết ba điểm ,
A B, C thẳng hàng. Tính khoảng cách AB .
BDC  60  45  15
BCD có DBC  180   DCB  BDC  75 Lời giải
Áp dụng ĐL sin trong BCD Ta c DC DB ó: 
 BD  80 6  2 sinDBC sinDCB
ACD có DAC 180  DCA ADC  30 AB DB
Áp dụng ĐL sin trong ABD : 
 AB 160 3   1 sinADB sinDAB