Đề cương ôn tập phần bài tập môn Lý thuyết mạch điện tử | Học viện Công nghệ Bưu chính Viễn thông

lOMoARcPSD| 37054152
NỘI DUNG THI LÝ THUYẾT MẠCH PHẦN BÀI TẬP Mục lục
Bài 1 ...................................................................................................................... 2
Bài 2 ...................................................................................................................... 4
Bài 3 ...................................................................................................................... 5
Bài 4 ...................................................................................................................... 6
Bài 5 ...................................................................................................................... 8
Bài 6 ...................................................................................................................... 9
Bài 7 .................................................................................................................... 10
Bài 8 .................................................................................................................... 11
Bài 9 .................................................................................................................... 13
Bài 10 .................................................................................................................. 16
Bài 11 .................................................................................................................. 18
Bài 12. ................................................................................................................. 19
Bài 13 .................................................................................................................. 21
Bài 14 .................................................................................................................. 22 Bài 15
.................................................................................................................. 23
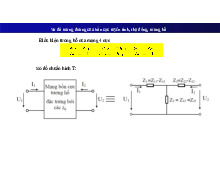
Bài 1: Cho mạch iện như hình 1 ở chế ộ xác lập với các nguồn iện áp: e t1( ) =
E1msin t e t, 6( ) = E6msin( t + )
1. Viết hệ phương trình iện thế nút (nút 4 làm gốc) với: lOMoARcPSD| 37054152 R a. 6 0 b.R = 6 0
2. Viết hệ phương trình dòng iện vòng Cách làm:
1. - Chọn nút gốc bằng 0V
- Viết phương trình cho các nút, với ẩn số là iện thế các nút:
+ Vế trái: Lấy iện áp nút ang xét nhân với tổng dẫn nạp thuộc nút ó, rồi trừ i các tích
giữa iện áp nút lân cận với dẫn nạp chung của nút lân cận và nút ang xét.
+ Vế phải: Tổng ại số các nguồn dòng ược biến ổi từ các nguồn áp ược nối vào nút ang xét.
Dấu (+) khi chiều của nguồn dòng chỉ vào nút ang xét.
Dấu (-) khi chiều của nguồn dòng i ra khỏi nút ang xét.
2. – Thành lập các vòng cho mạch
- Thành lập hệ gồm phương trình cho mạch tương ứng với các vòng kín, trong ó ẩn
số là các dòng iện vòng giả ịnh, dựa trên cơ sở áp dụng ịnh luật Krichhoff II. Bài làm:
1. Viết hệ phương trình iện thế nút (nút 4 làm gốc) với: R a. 6 0
HPT Ñieän theá nuùt: choïn nuùt 4 laøm goác: 4=0 Nuùt 1: Y 11 1
−Y12 2 −Y13 3 = Jñ1 Nuùt 2: −Y 21
1+Y22 2 −Y23 3 = Jñ2 Nuùt 3: −Y 31 1
−Y32 2 +Y33 3 = Jñ3 lOMoARcPSD| 37054152 lOMoARcPSD| 37054152
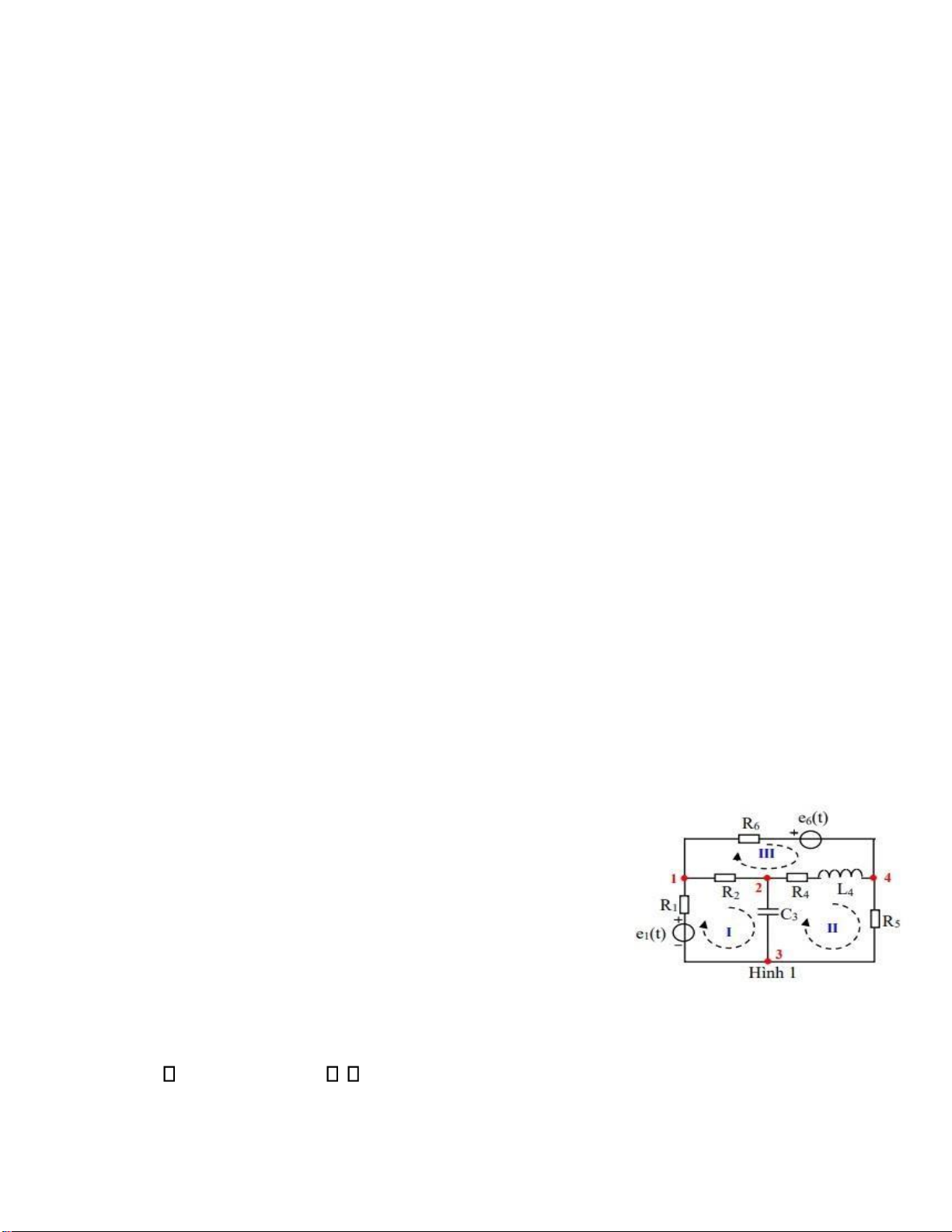
Bài 2: Cho mạch iện xác lập như hình 2, biết e t1( ) =15cos100 [ ];t V J = 4 5A (nguồn DC), R = = = = = = 1
R3 2 ;R2 R4 1 ;L1 L2 40mH M; = 20mH.
Tính dòng iện qua iện trở R1 Cách làm: - Khử hổ cảm. -
Áp dụng nguyên lý xếp chồng - Lần lượt cho:
+ Nguồn làm việc riêng lẽ. e (t) làm việc, J 1
4 hở mạch; phức hóa sơ ồ. + Nguồn J
(t) ngắn mạch; phức hóa sơ ồ. 4 làm việc, e1 -
Tính I1AC, I1DC, suy ra i1(t) Bài làm:
Khử hỗ cảm, phức hóa sơ ồ: Z = Z = Z = L1 L2 j2( ), M j2( ) 5 1 = − 45 1 3 + 3 2 lOMoARcPSD| 37054152 5 i 2 AC ( )t = cos(100 − 45 )( ) V
AÙp duïng pp ñieän theá nuùt: 2 2 1 0 12 1+ 11 ++ 21 =−52 =
12 =−=−35103 I1DC = R11 = −65 − Vaäy : ( )i = −
1 t = i1AC( )t + I1DC
65 + 52 cos(100 − 45 ),( ) V lOMoARcPSD| 37054152
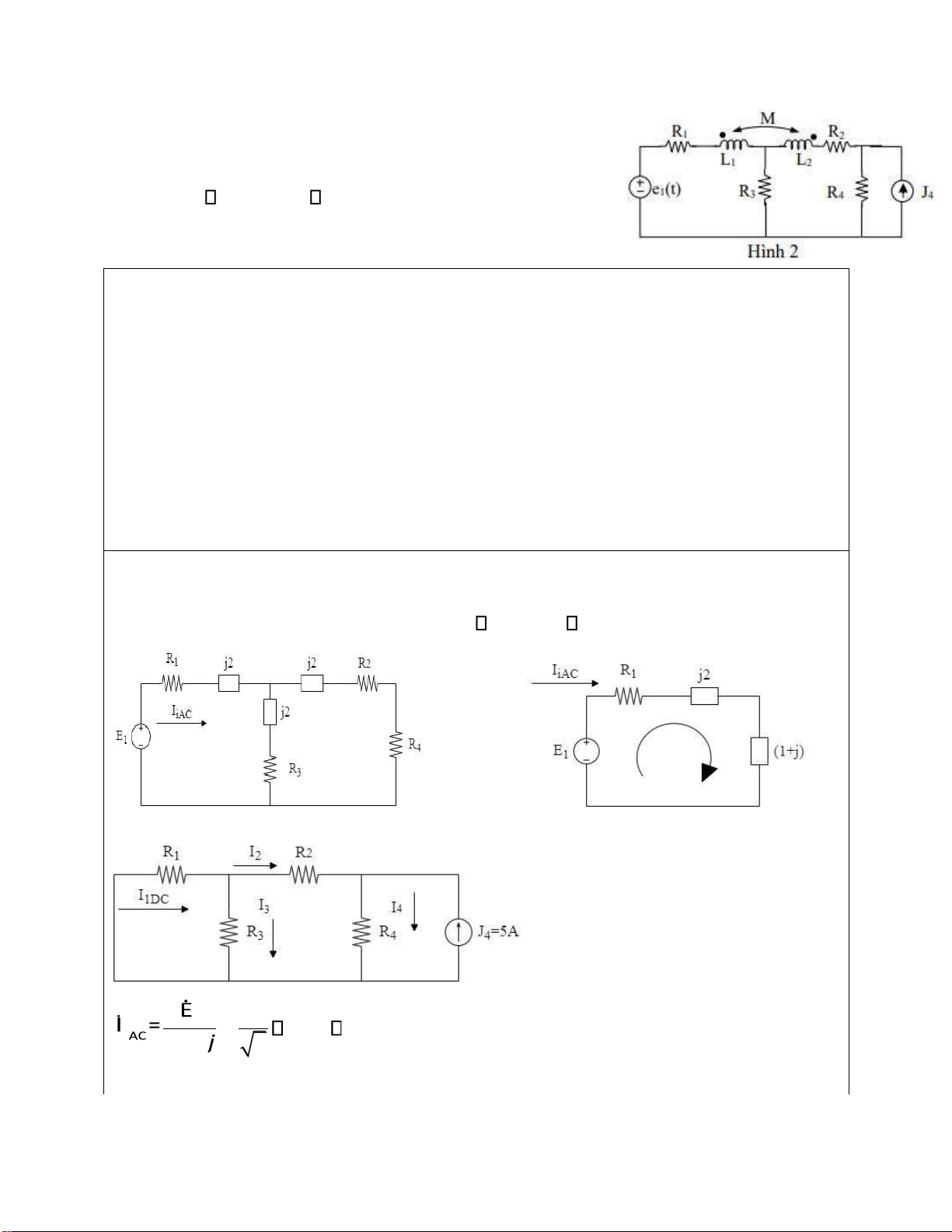
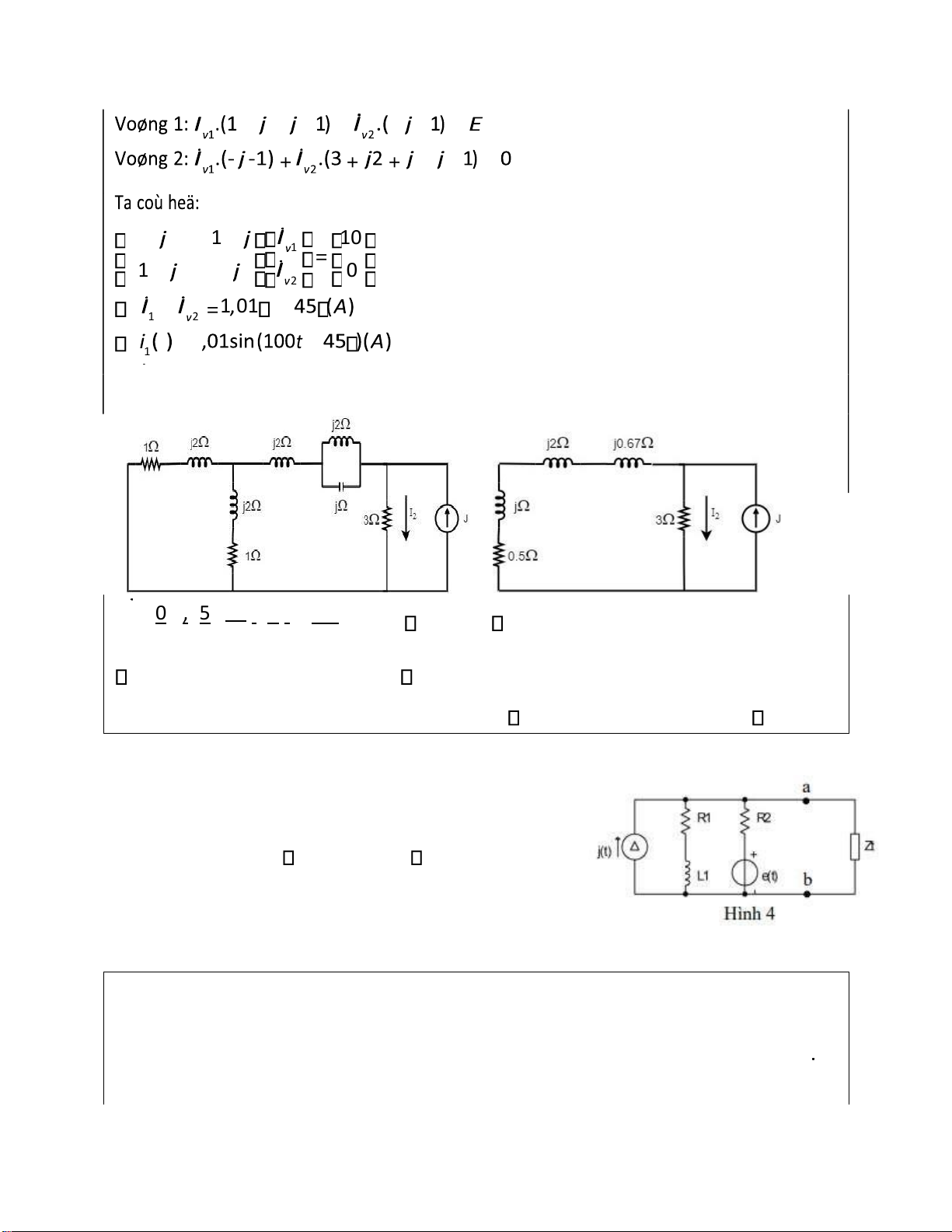
Bài 3: Cho m ạch iện như hình 3, vớ i = 2 t V .
H ãy tìm dòng iện qua iệ n tr ở 3Ω Cách làm:
- Th ự c hi ệ n phép kh ử h ỗ c ả m
- Áp d ụ ng nguyên lý x ế p ch ồ ng - L ần lượ t cho:
+ Ngu ồ n e(t) làm vi ệ c, j(t) ng ắ n m ạ ch: tính tr ở kháng trên các ph ầ n t ử L, C. Ph ứ c
hóa sơ ồ . Áp d ụng phương pháp dòng iệ n vòng, tìm .
+ Ngu ồ n j(t) làm vi ệ c, e(t) ng ắ n m ạ ch: tính tr ở kháng trên các ph ầ n t ử L, C. Ph ứ c
hóa sơ ồ . Bi ến ổi tương ương, tìm . Bài làm:
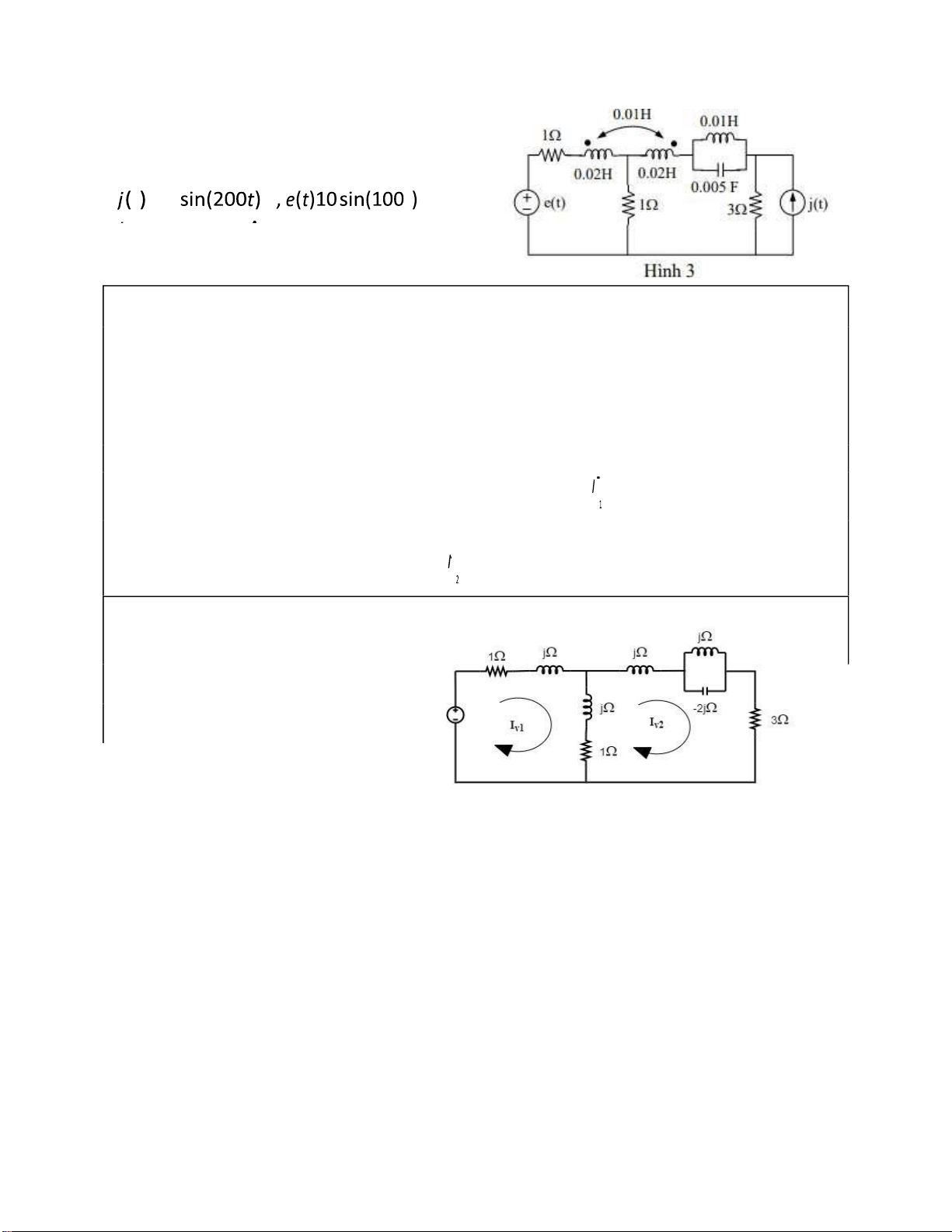
Ngu ồ n e(t) làm vi ệ c,
j(t) ng ắ n m ạ ch lOMoARcPSD| 37054152 ++++ −−= + + +++= 2 + 2 1 −− 10 1 = 1 −− 4 + 4 0 2 = 1 = 01 − 1 2 1 = 1 −
Ngu ồ n j(t) làm vi ệ c, e(t) ng ắ n m ạ ch I = 0 2
3,,55++ jj33,,6767 J =1,46 35,98 ( ) A
i2( )t =1,46sin(200t +35,98 )( ) A
Vaäy: ( )it = i1( )t + i2( )t =1,01sin(100t −45 ) +1,46sin(200t +35,98 )( ) A
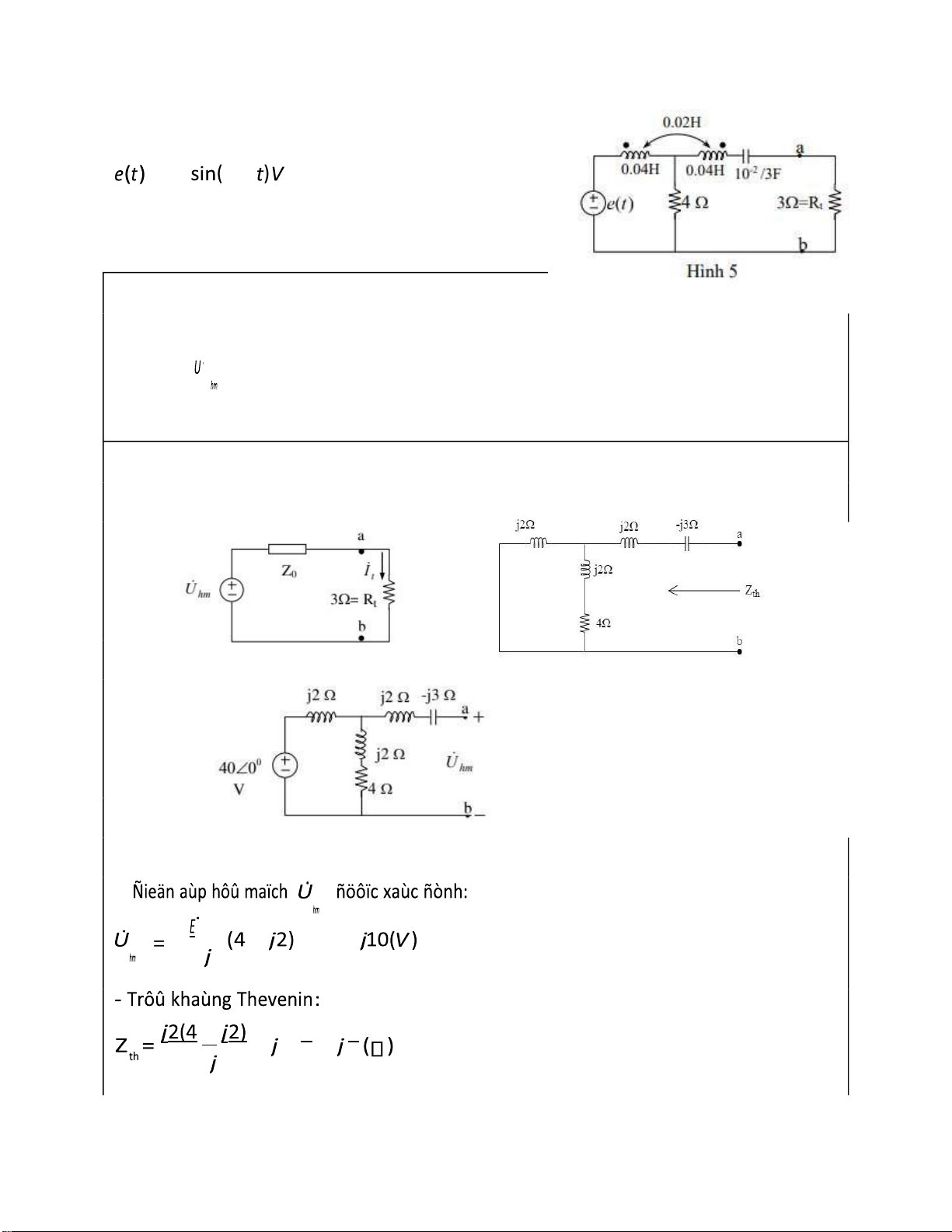
Bài 4: Cho mạch iện như hình 4 ở trạng thái xác
lập iều hòa biết: j t( ) = 2sin100 ( ),t A e t( )
=12sin(100t + 90 ) ,R = = = 1 R2 2 ,L1 0,02H a.
Tìm sơ ồ tương ương Thevenin bên trái ab.
b. Với giá trị nào của Zt thì công suất tác dụng lên Zt
lớn nhất? Hãy tính công suất ó. Cách làm:
a. - Trước hết cắt bỏ Z , phần mạch còn lại chính là phần mạch có chứa nguồn. t
- Hở mạch ab, chọn nút b làm gốc, viết phương trình iện áp cho nút a, suy ra Uhm lOMoARcPSD| 37054152 lOMoARcPSD| 37054152
Bài 5: Cho m ạch iện như hình 5, biế t: = 40 ( 100 )
a. Tìm sơ ồ Thevenin ho ặ c Norton bên trái ab
b. Hãy tìm công su ấ t tiêu th ụ trên R t Cách làm:
a. Chuy ể n các thông s ố v ề d ạ ng ph ứ c, kh ử h ỗ c ả m và h ở m ạ ch ab b. - Tính , tr
ở kháng Thevenin, tìm dòng iệ n qua R t
- Tính công su ấ t tiêu th ụ Bài làm: a. b. − = + = 30 − 4 + 4 + 1 − = + 1 4 + 4 2 2 lOMoARcPSD| 37054152 U I = t
Zth +hmRt = − =8 j 4 8,94 − 26,6 ( ) A P = 1 R = t I2m 119,9(W ) 2 lOMoARcPSD| 37054152
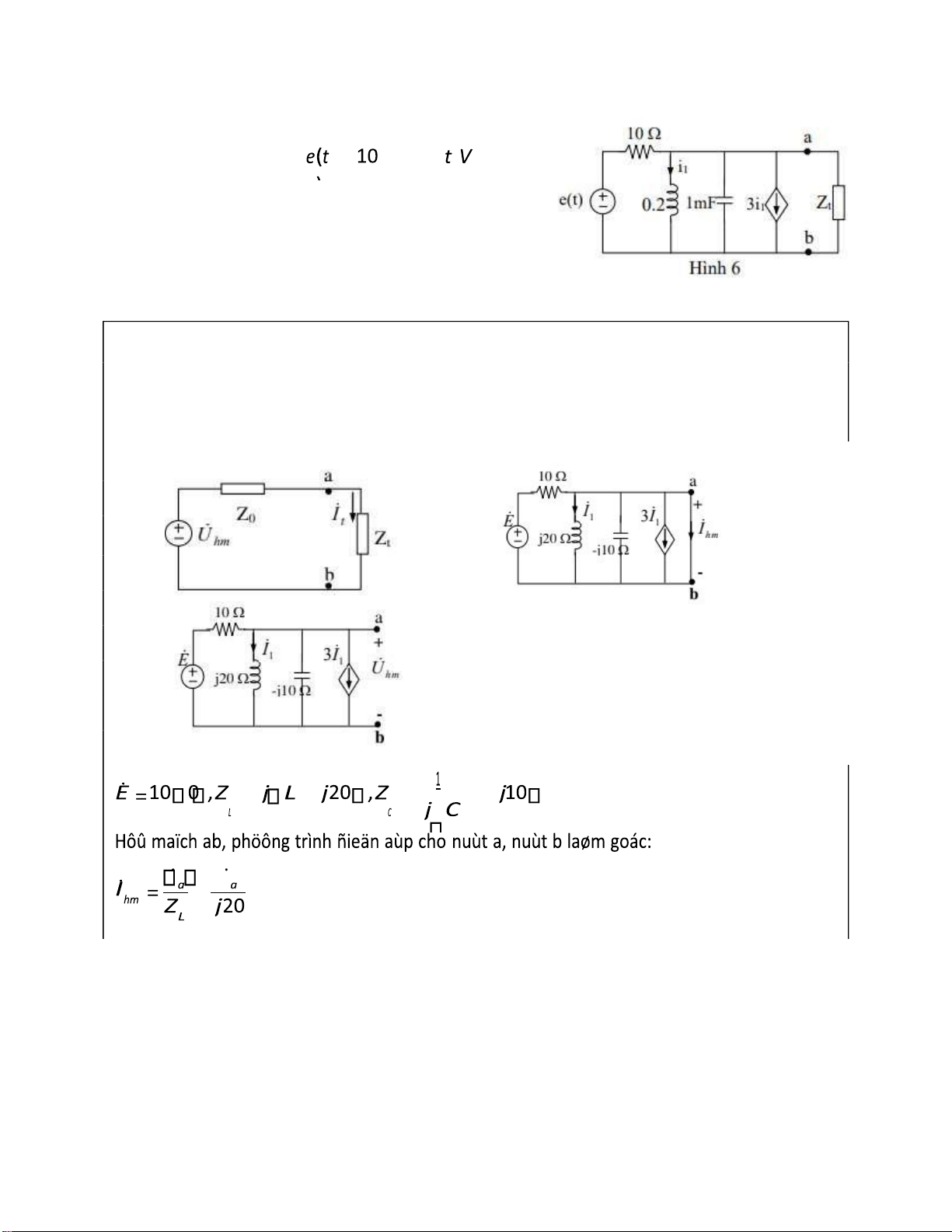
Bài 6: Cho m ạch iện như hình 6 ở tr ạ ng thái
xác l ập iề u hòa bi ế t: = cos100 a. Tìm sơ ồ
Thevenin ho ặ c Norton bên trái ab
b. Tìm công su ấ t tiêu th ị l ớ n nh ấ t có th ể ạ t ượ c trên Z t Cách làm: Tương tự câu 4 Bài làm: a. = = = = =− = = lOMoARcPSD| 37054152 = + + = − = = + 5 5 = 5 2 = 0 = 0 = 1( ) = = + 5 5( = − 5 5( thì → 2 2 = = =
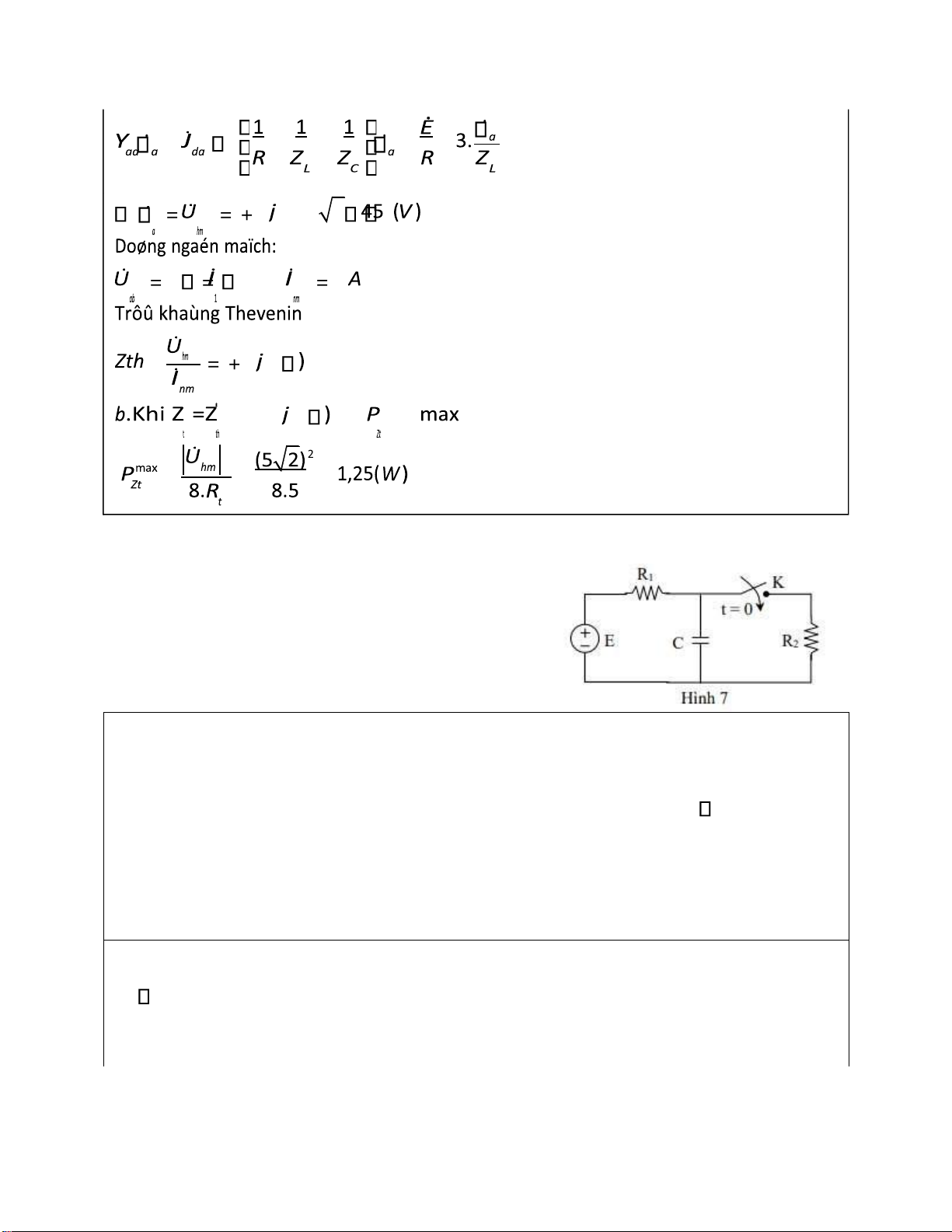
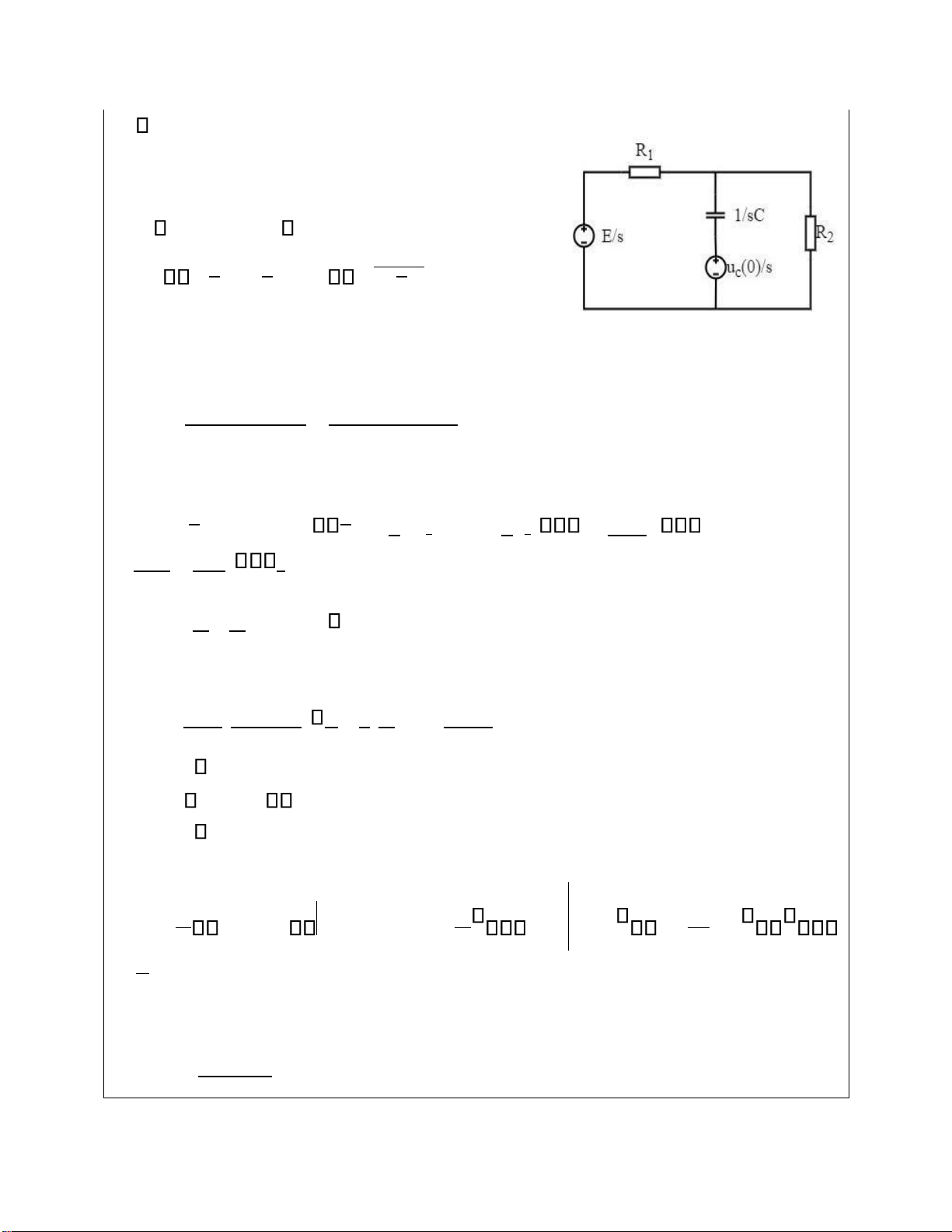
Bài 7: Cho mạch iện như hình 7, biết: R =10Ω, 1
R =90Ω, C=2μF, E=100V. Tại t=0 óng khóa K, 2
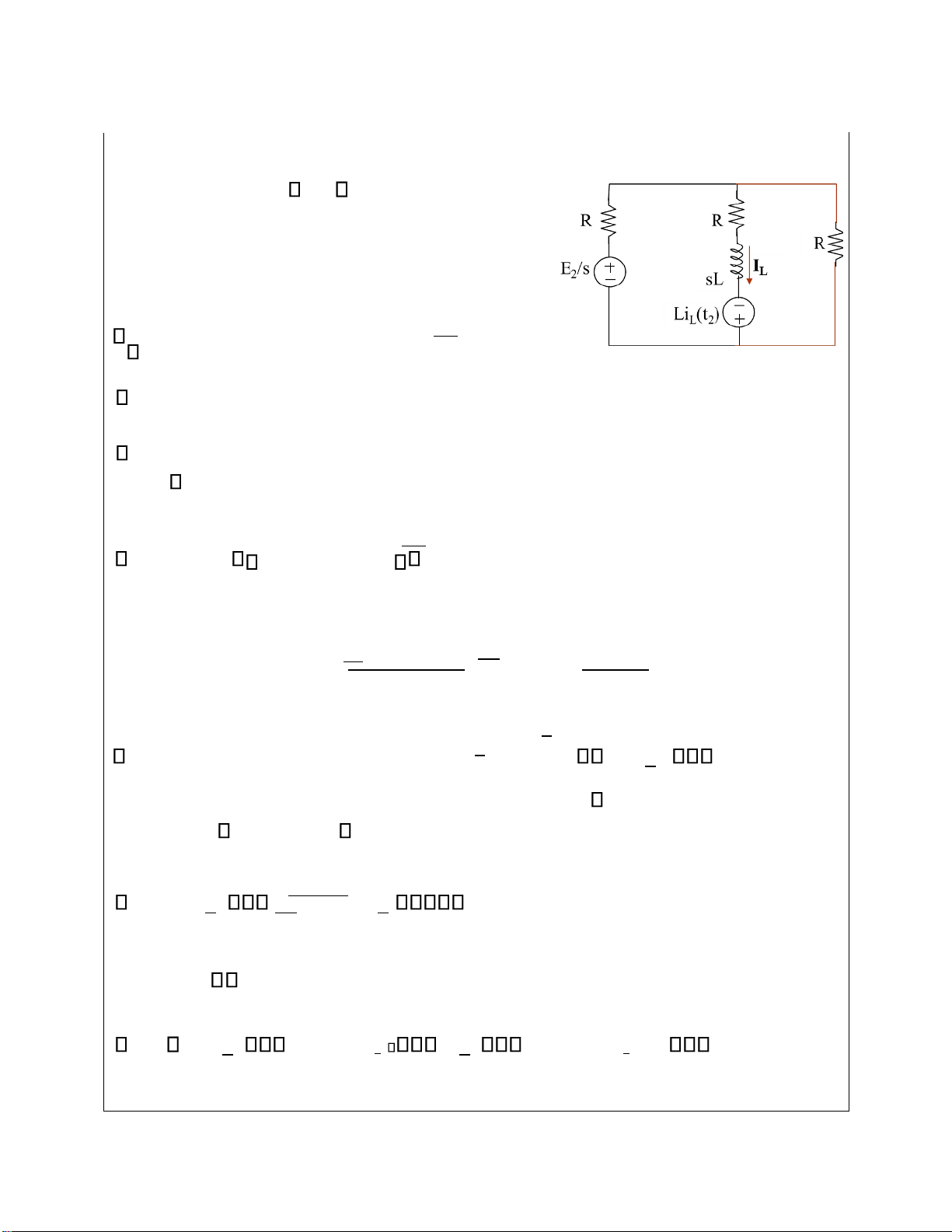
hãy xác ịnh iện áp trên tụ. Cách làm: -
Xác ịnh iều kiện ầu của bài toán (t<0) -
Lập sơ ồ tương ương toán tử cho các phần tử của mạch iện (t 0) -
Dùng ịnh luật, phương pháp phân tích mạch lập hệ phương trình cho áp ứng mạch, tìm U(s) -
Biến ổi laplace ngược tìm u(s) Bài làm
*t 0, xaùc ñònh ñieàu kieän ñaàu cuûa baøi toaùn: U (0)=U (0 ) + = - = = c c U (0 )c E 100V lOMoARcPSD| 37054152
*t 0, ñoùng khoùa K, ta coù sô ñoà töông ñöông
toaùn töû maïch AÙp duïng phöông phaùp ñieän theá nuùt: U ( )s
R11 + R12 + sC = sRE1 + Ucs(0) sC Thay soá, ta ñöôïc: + R1s = U ( )s =
RE1 RU2c(0).CR
E1C +RRU11R+c(0)2RC2s = 5.10s s ++ 6 10181006 s 1 + 1 + sC s s +
U ( )s = 5.106 +101006 s = Ks1 + s +K102 6 s s + 18 18 K = = 1 dsd U s s( ). s=0 = 90; K2 dsd U s( ). s+ 10186 s=−10 = 6 10 18 U s( ) = +90 10 6 lOMoARcPSD| 37054152 s s+ 10 18 −106 t
Bieán ñoåi Laplace ngöôïc ta coù: ( )u t = +9010.e 18
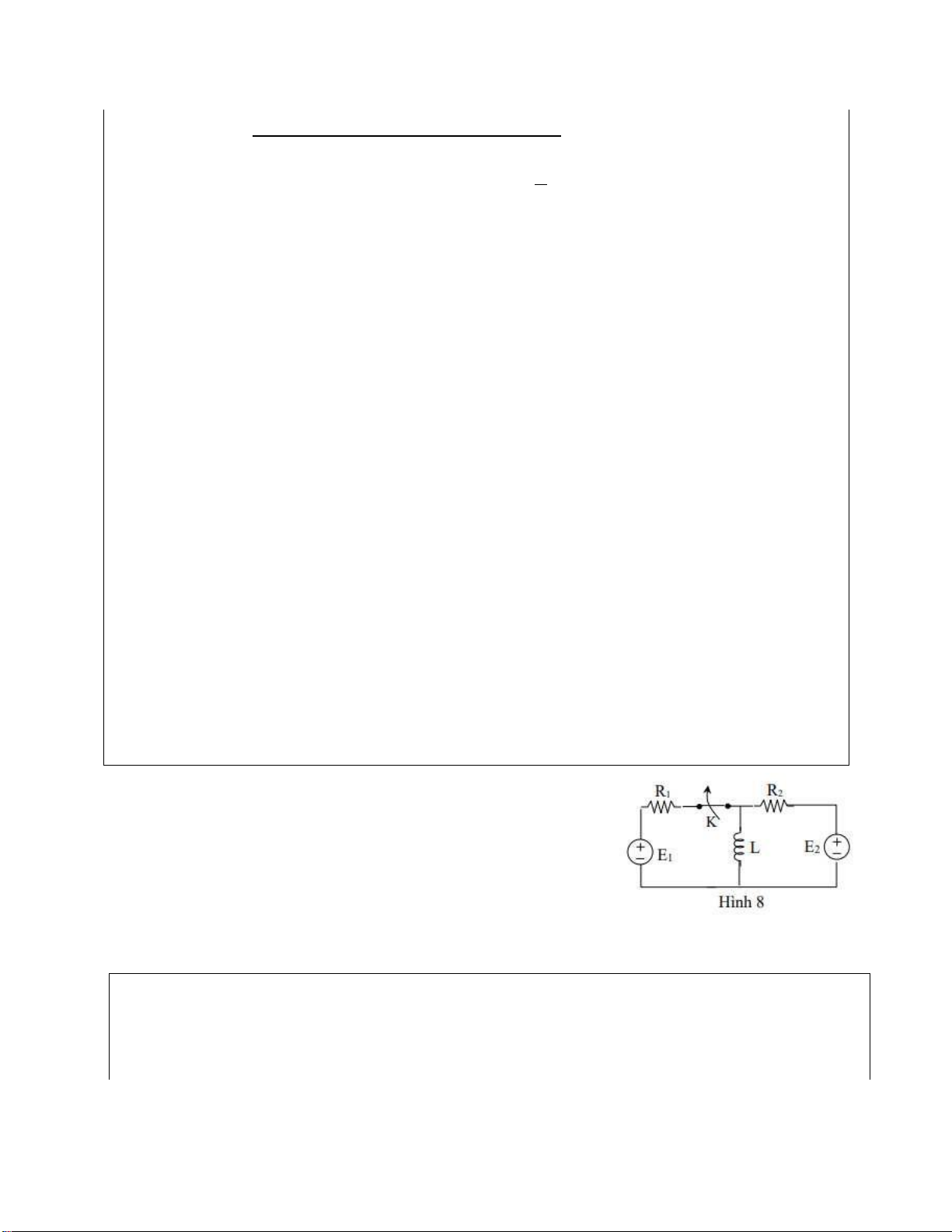
Bài 8: Cho mạch iện như hình 8, biết R =5Ω, R =10Ω, 1 2 L=1mH, E1=E2=10V.
Tại t=0 mở khóa K, hãy xác ịnh dòng iện qua L Cách làm:
- Xác ịnh iều kiện ầu của bài toán
- Khi khóa K óng: dung pp dòng iện vòng tìm iL(0) lOMoARcPSD| 37054152
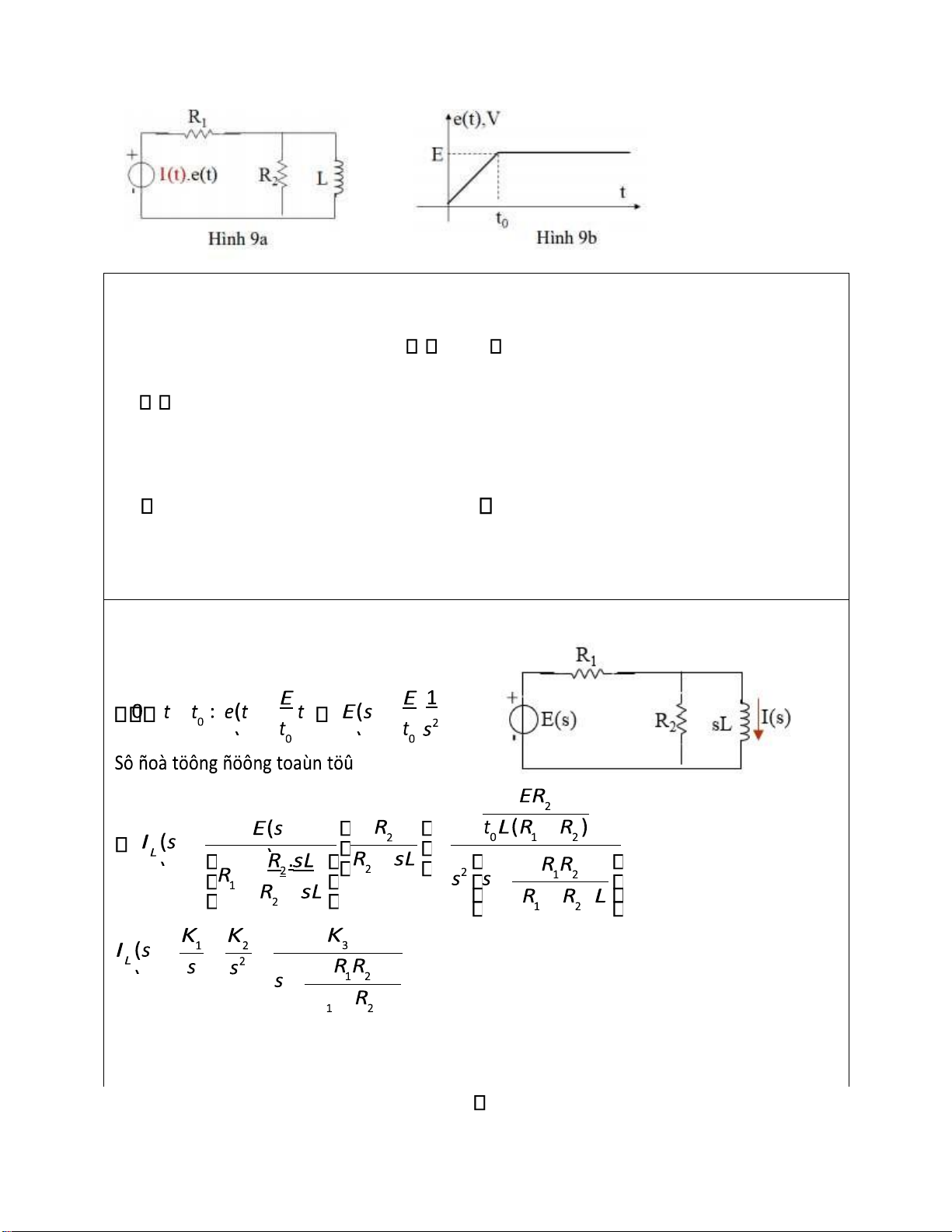
Bài 9: Cho mạch iện như hình 9a, có nguồn tác ộng như hình 9b. Tìm dòng iện & iện áp trên cuộn dây. lOMoARcPSD| 37054152 Cách làm: t t
Cách 1: Phân khoảng thời gian: 0 t 0; t0 t - 0 t
0: + Lập sơ ồ tương ương toán tử, tìm IL(s) + Suy ra, i(t) và u(t)
- t t0 : Dịch gốc thời gian về tại t=t , ặt 0 = t-t0
Dùng pp dòng iện vòng tìm IL(s), suy ra i(t) và u(t)
Cách 2: Viết biểu thức cho e(t) Bài làm: Cách 1: = = + = = + + + + ( + ) = + + + ( + ) R L lOMoARcPSD| 37054152 1d
t0 L ( ERR1 +2 R2) − 1 + = 2 2 K 1 = dsd 1 I L ( ).ss2 s=0 = ds s + 0 1 2 ( R ) 1 R2
R1 + R2 L ( 1 + 2 ) s=0 2 0 1 2 1 K − 2 = dsd I L ( ).ss2
s=0 = t0ER1 ( +2 1 2 ) K = 2 dsd I L ( ).s s + ( R1 1 ( +2 1 2 ) R+1RR2 ) 0 2 L s=− R R = E R R L
i( )t = − Et( R.R1 +2 RR22)L + t0ER1 t + E ( tR ) 01R+12 RR22 L + 0 1 + +
u( )t = L d i( )t = L . E − E e −( R1R R+ ) 1 2R2 Lt ( )V dt t0 R1 t0 R1 lOMoARcPSD| 37054152
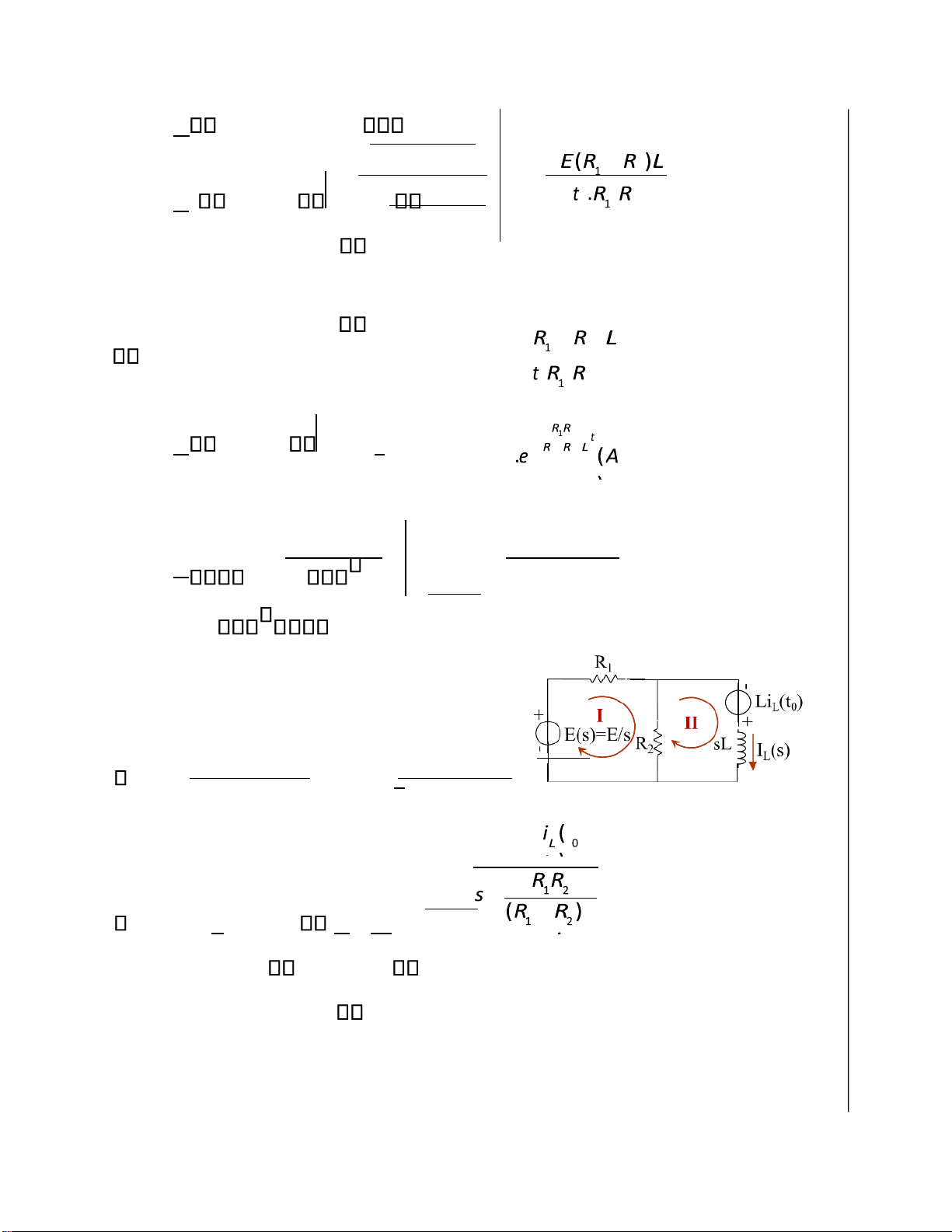
*t t0 : Dòch goác thôøi gian veà taïi t =t0, ñaët =t ti t = 1 L( )0
e, ( )e = E E s( ) = Es
Duøng pp doøng ñieän voøng ta coù heä:
R1−+R2R2sL−+R2R2 IIvv12 = E s( ) Li tL( )0 = +
IL ( )s = Iv2 = L Rs s.(.
ER1++2(RR21R R)+1+R Lsi t22)L ( )0 R sE1 − RE1 iL ( ) = RE1 + e−1 − RE1
e−(R1R R+1 2R2)L i tL( ) = RE1 + e−1 − RE1
e−(R1R R+1 2R2)L(t t− 0) lOMoARcPSD| 37054152 R R1 2
u t( ) = L dtd i tL( ) =− e−1 − RE1
(RR R1 1 2+ R2)e−(R1+R2)L(t t− 0) Cách 2:
Bieåu thöùc ( ): ( )e t
e t = E t.1( )t − E (t − t0).1(t − t0) t0 t0
E ( )s = E 2 1− e −st0 t0 s
I L ( )s = E ( )Rs2.Ls
R2 R+2 sL
R1 + R2 + Ls Thay soá, ta ñöôïc: E ER2 I ( )s = L
1tR0Rs222+.LsLs
R2 R+2 sL . 1 − e −st = 0 s2 st0+L
((RR11 R++1RRR222)) L . 1 − e −st0 R + ) − E ( R + + 1 R2)L E
E ( R1 R2 L I ( )s = lOMoARcPSD| 37054152 L
t0.Rs12 R2 + t0sR21 + s + t0 R1R21RR22 . 1 − e −st0 ) ( R + 1 R2 L − E ( R )
1 +2 RR22)L + t0ER1 t + E ( tR01R+12 RR22
L .e −(R )
1R R+1 2R2 Lt 1( )t i( )t = t0.R1 − E ( ( ) )
0R1 1+2 RR22)L + t0ER1
t − t0 + E ( tR01R+12 RR22 L .e −(R ) )
1R R+1 2R2 L(t t− 0 1( t − t ) 0 − t .R
L . E − Ee −(R ) )
1R R+1 2R2 Lt 1( )t −
L. E − ER1 e −(R1R R+1 2R2 L(t t− 0)
1(t − t0) u( )t = t0 R1 t0 R1
t0 R1 t0 lOMoARcPSD| 37054152
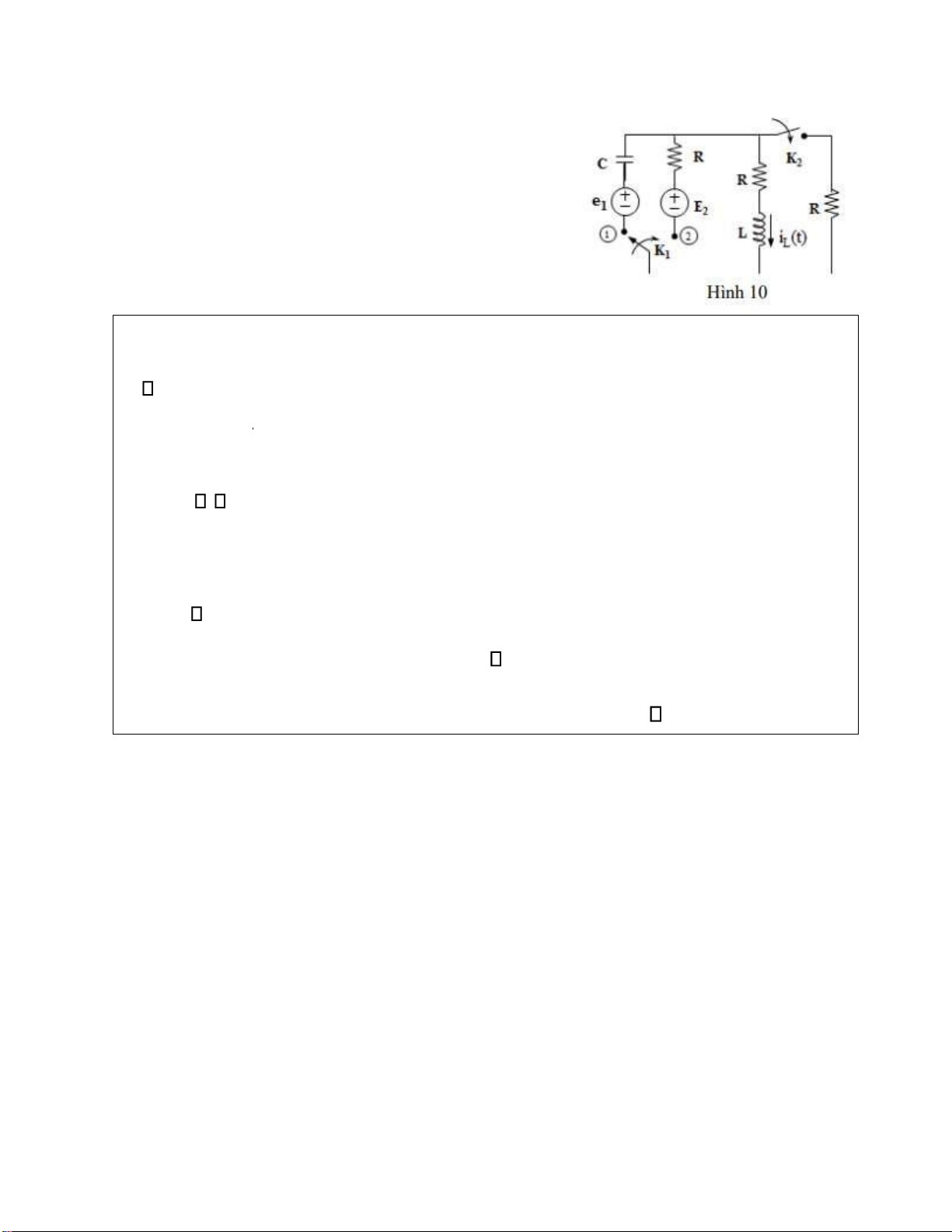
Bài 10: Cho mạch iện như hình 10. Tìm iL(t), biết
tại t1=0 khóa K1 chuyển từ 1->2 và tại t =10V; R=1Ω;
2=-ln0,2 khóa K2 óng, biết E2 L=2H; C=1F
Cách làm: Xét mạch iện tại thời iểm:
-t t1: + Khóa K1 ở vị trí 1, K2 mở, vẽ lại mạch. I i t
+ Tìm L , suy ra L ( ). t t - 1 t
2: + Khóa K1 ở vị trí 2, K2 mở, lập sơ ồ tương ương toán tử.
+ Tính I (s), biến ổi Laplace ngược suy ra i t L L ( ) - t t2:
+ Dời gốc thời gian về tại t=t
lập sơ ồ tương ương toán tử. 2 hay ặt biến =t-t2,
+ Áp dụng phương pháp dòng iện vòng, tìm I i L(s), suy ra L ( ) lOMoARcPSD| 37054152 Bài làm:
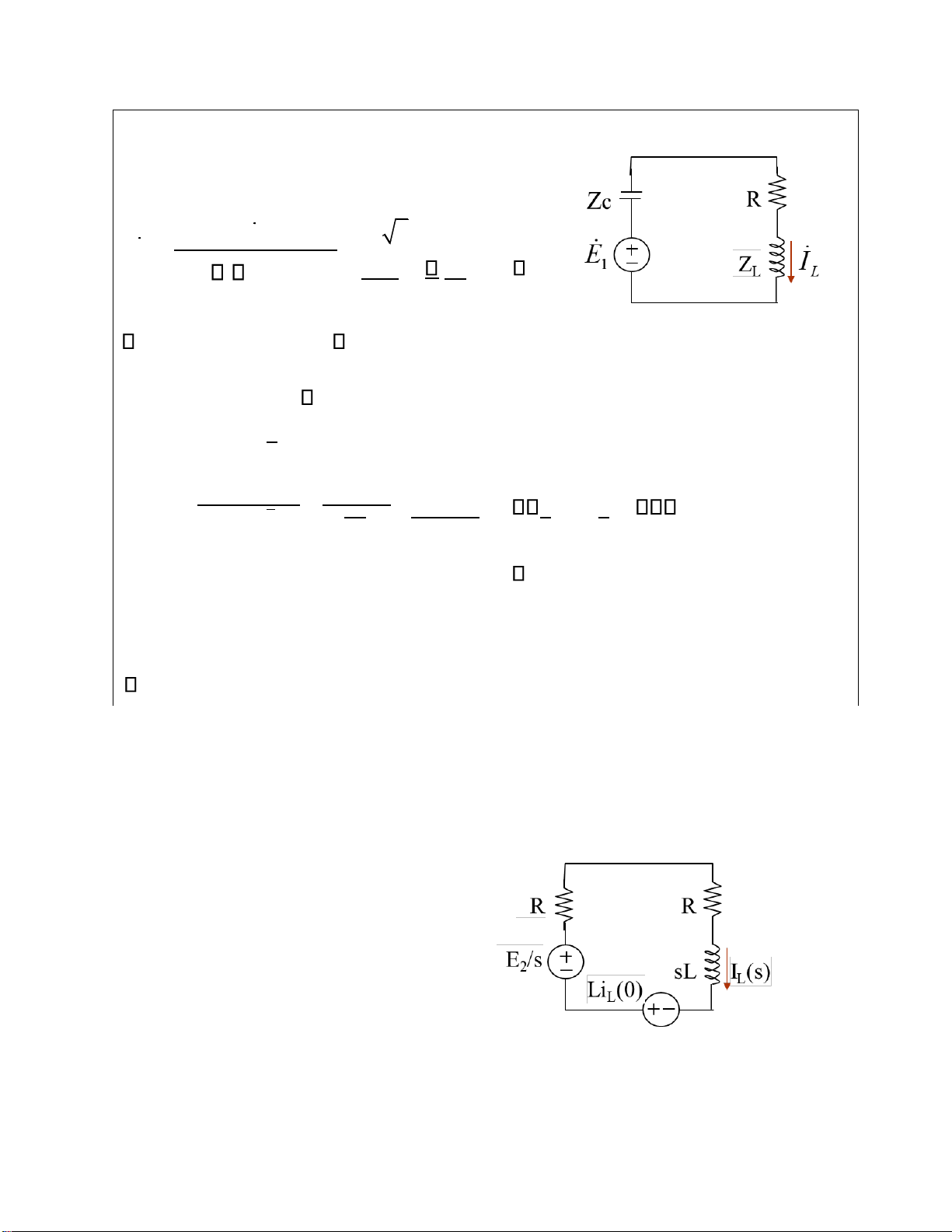
* ÔÛ thôøi ñieåm tI L = R + j( LE − 1
1/ C ) = 10 21+ j450 =10 0 ( )0 A
iL ( )t =10. os(t) (Ac ) iL(0) =10( )A * ÔÛ thôøi ñieåm t 1 tE Li (0)+ L
s2 = 20 + 10s = 5(2s +1) = 5 1s + s 1+1
I L ( )s = 2 R + sL 2s + 2 s(s +1)
iL ( )t = 5(1+ e −t )( )A i = L ( )t2
5 1( + e ln0,2 )= 6( )A lOMoARcPSD| 37054152 * ÔÛ thôøi ñieåm t t , = − 2 t
t2 AÙp duïng pp doøng ñieän voøng:
( )s +( R + sL ) I v2( )s = Es2 + LiL( )t2
(2 R + sL ) I v1
( R + sL ) I v1( )s +(2 R + sL ) I v2( )s = LiL( )t2
(3R + 2sL ) I v1( )s + I v2( )s = Es2 + 2 LiL( )t2
( )s = E2 + 2 Li = 10 L ( )t2
s + 24 = 12s + 5 ) I s
L ( )s = I v1( )s + I v2 3R + 2sL
(4s + 3 2s s + 34 I L ( )s = 13 .10s − (s +13) 4 iL ( ) == 13 10 + 8.e −34 = 13
10 + 8.e − −34(t t ) 2 ( )A lOMoARcPSD| 37054152 10. os(t) : tc =t1 0 i L ( )t =
5 1( + e −t ) : t1 t t 2 ( )A 3(t t ) 2 13 10 + 8.e − −4 : t t 2
t → : ( )iL t → (A) lOMoARcPSD| 37054152
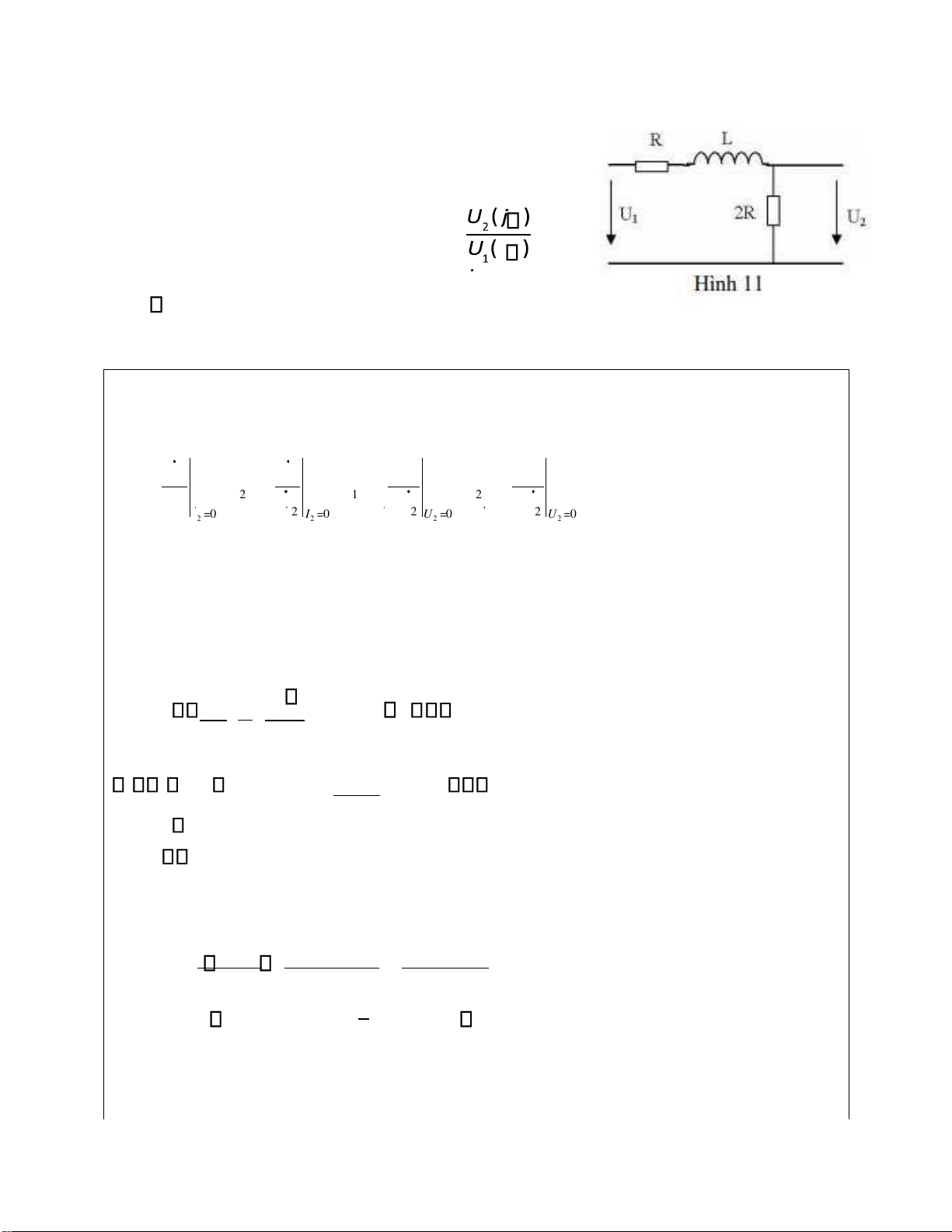
Bài 11: Cho mạng bốn cực (M4C) như
hình 11 a. Tìm ma trận truyền ạt A của M4C.
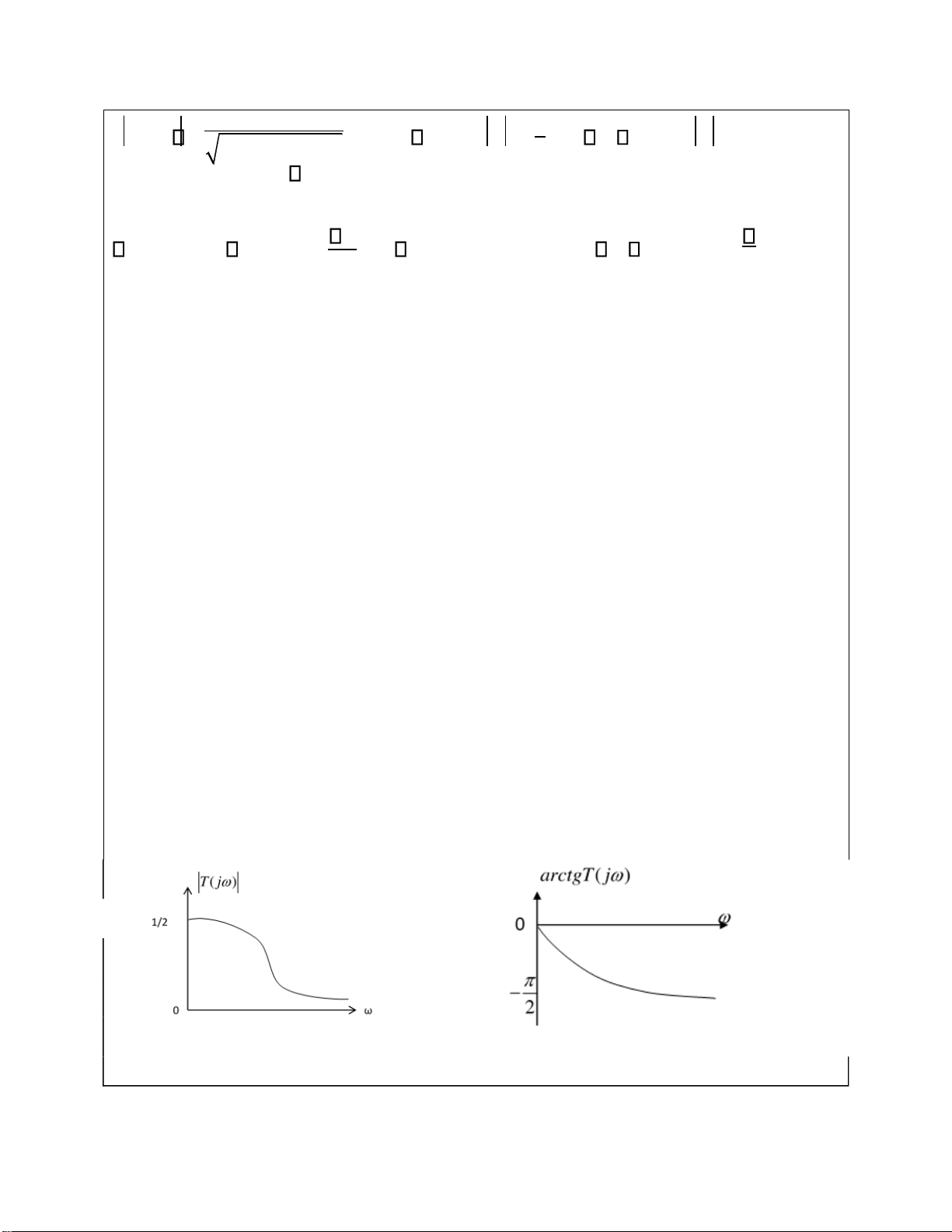
b. Vẽ ịnh tính ặc tuyến biên ộ và ặc
tuyến pha của hàm truyền ạt iện áp T
j( ) = khi ầu ra M4C có Z = t 2R.
c. Nhận xét tính chất của mạch ối với tần số. Cách làm: a.
Viết ma trận các hệ số ược tính theo các công thức: U I U I 1 1 1 1 ;a = ;a = ;a = 21 12 22 U U I − I − a = 2 = 2 I 0 = 2 I 0 = 2 U 0 U 0 = 11 2 2 2 2 b.
Tính ặc tuyến biên ộ và pha c.
Lý thuyết Bài làm: a.
3R 2+Rj L −(R + j L ) A = 1 −1 2R
b. Ñaëc tuyeán bieân ñoä U (j T j( ) = 2 ) = 1 = R U 1 j1( )
a11 −a12 Z t 2R + j L lOMoARcPSD| 37054152 T j( ) = R
:khi → 0 thì T → 1;khi → thì T → 0 (2 )R 2 +( L)22
= arctgT j( ) =−argtg L :khi → 0 thì argT → 0;khi → thì arg →− 2R 2
c. Tính ch ấ t M4C: là b ộ l ọ c thông th ấ p lOMoARcPSD| 37054152
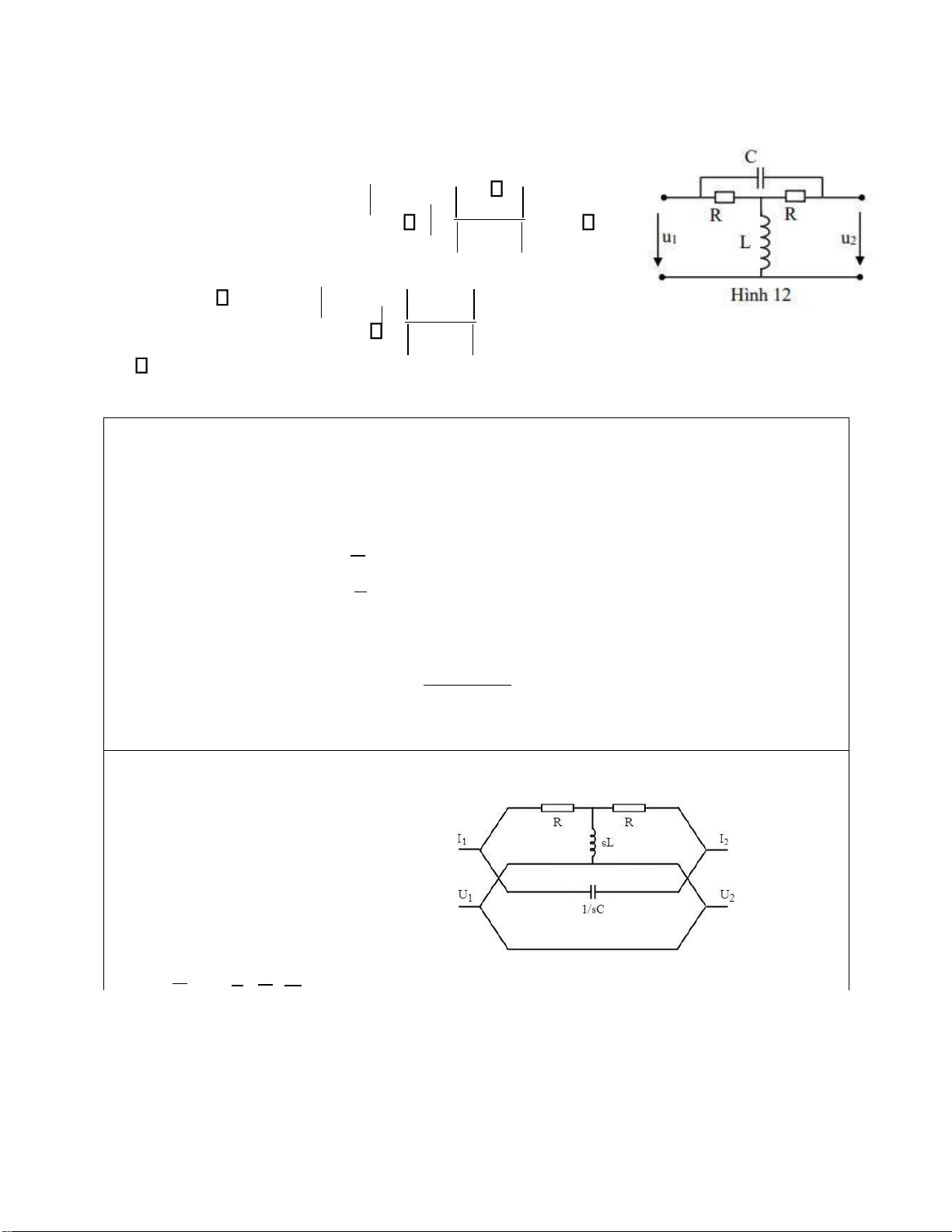
Bài 12: Cho mạng bốn cực như hình 12.
a. Tìm ma trận tham số dẫn nạp Y của mạng bốn cực U2(j )
b. Tìm và vẽ ịnh tính ồ thị K
j( ) = khi cửa 2 U j1( ) hở mạch U2(j )
c. Tìm và vẽ ồ thị của K j( ) =
khi cửa 2 ược U j1( ) nối với tải R Cách làm:
a. - Phân tích M4C thành 2 mạng thành phần mắc song song với nhau. Lần lượt xét
các mạch hình T và hình π
- Tìm thông số y , ma trận Y = Y ij t+Yπ. − = y
b. Hở mạch, áp dụng K 21 u y22 − = y
c. Khi nối tải với R, áp dụng K 21 u y + 22 1/ R Bài làm: a. Xeùt maïch hình T:
z11 = z22 = +R sL , z12 = z21 = sL
Z = RLs + R 2 + RLs = R 2 + 2 RLs z
y11 = Z11 = R 2R++2sLRLs lOMoARcPSD| 37054152 lOMoARcPSD| 37054152
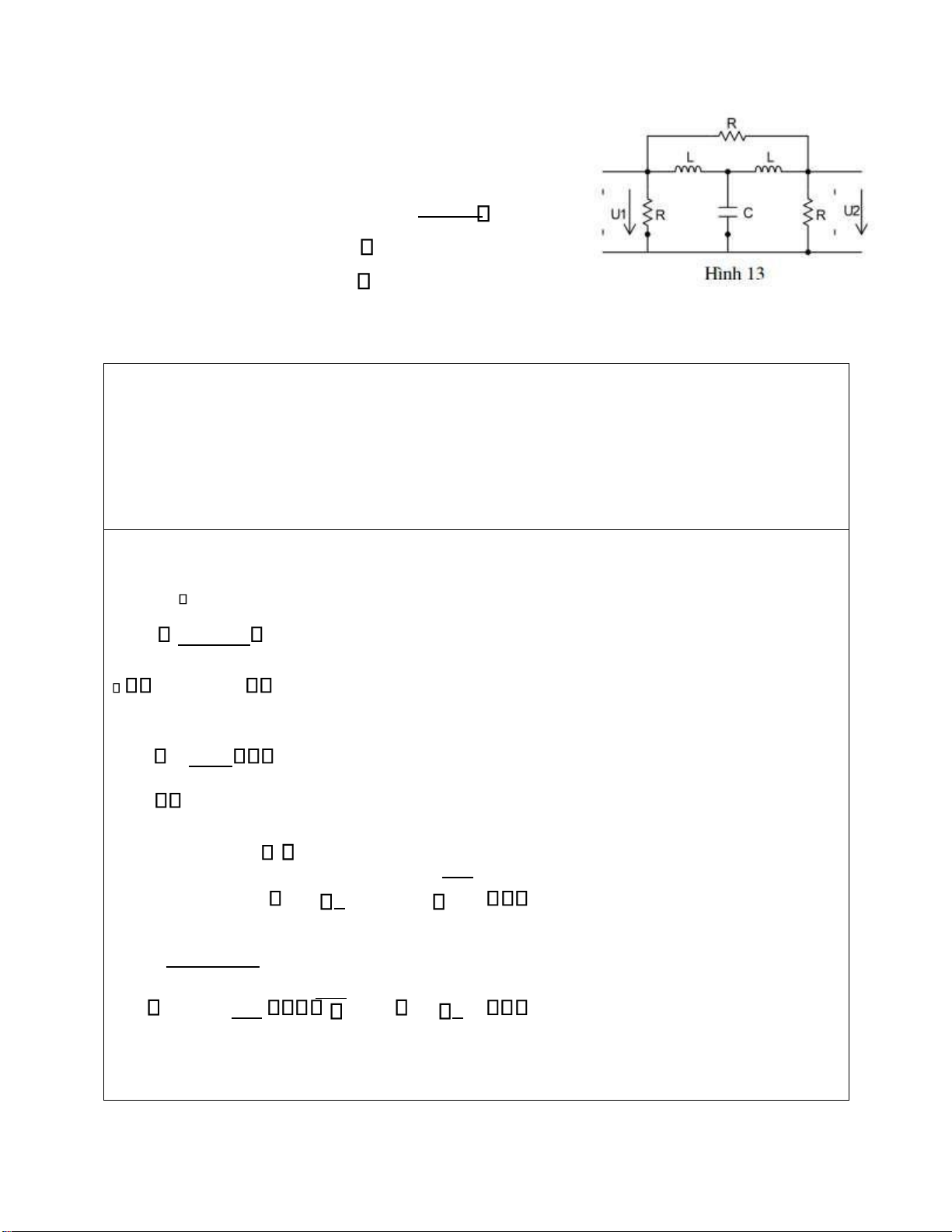
Bài 13: Cho mạng bốn cực như hình 13
a. Tìm ma trận tham số dẫn nạp Y mạng bốn cực
U2(j ) khi ầu ra
b. Tìm hàm truyền ạt áp K j( ) = U j1( )
của mạng bốn cực hở mạch Cách làm:
a. - Phân tích M4C thành 2 mạng thành phần mắc song song với nhau. Lần lượt xét
các mạch hình T và hình π (vẽ lại tương tự bài 12)
- Tìm thông số y , ma trận Y = Y ij T+Yπ. b.
Áp dụng công thức (hở mạch) Bài làm:
a,Y = Y + YT 2 1 R − R Y = − 1 2 R R −
j( L 1C ) jC
YT = 2 L2−+1 2 L .
jC j( L − 1C ) C lOMoARcPSD| 37054152
2( L )2 + 4 L − jR( L − 1 )
−( L )2 − 2 L + j R Y = −1 C C C C R 2 L2 + 2CL
−( L )2 − 2CL + j RC 2( L )2 + 4CL − jR( L − 1C ) T j( ) = y21 =
( L)2 + 2CL − j RC y22
2( L)2 + 4L − jR( L − 1 ) C C
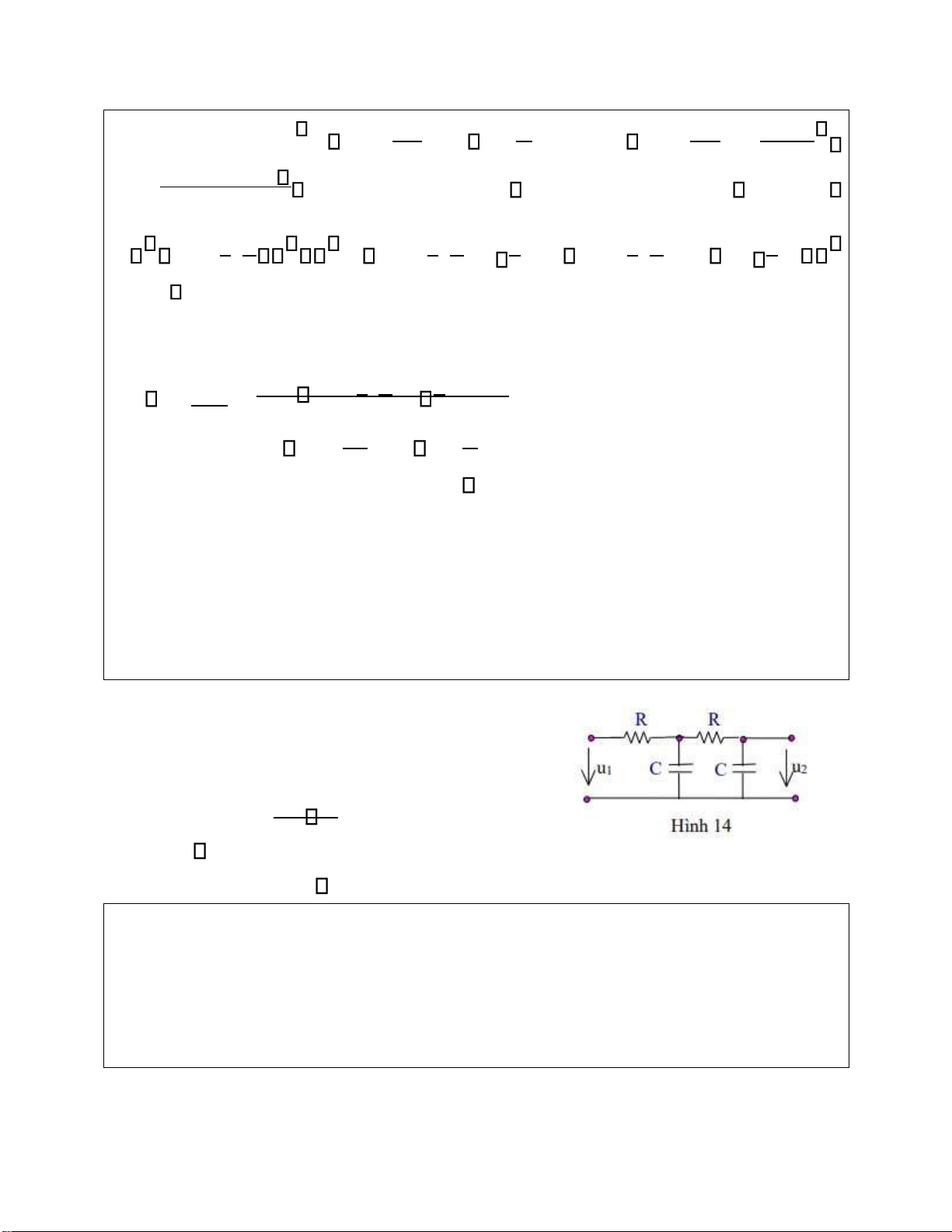
Bài 14: Cho mạng bốn cực như hình 14
a. Xác ịnh ma trận thông số truyền ạt [A]
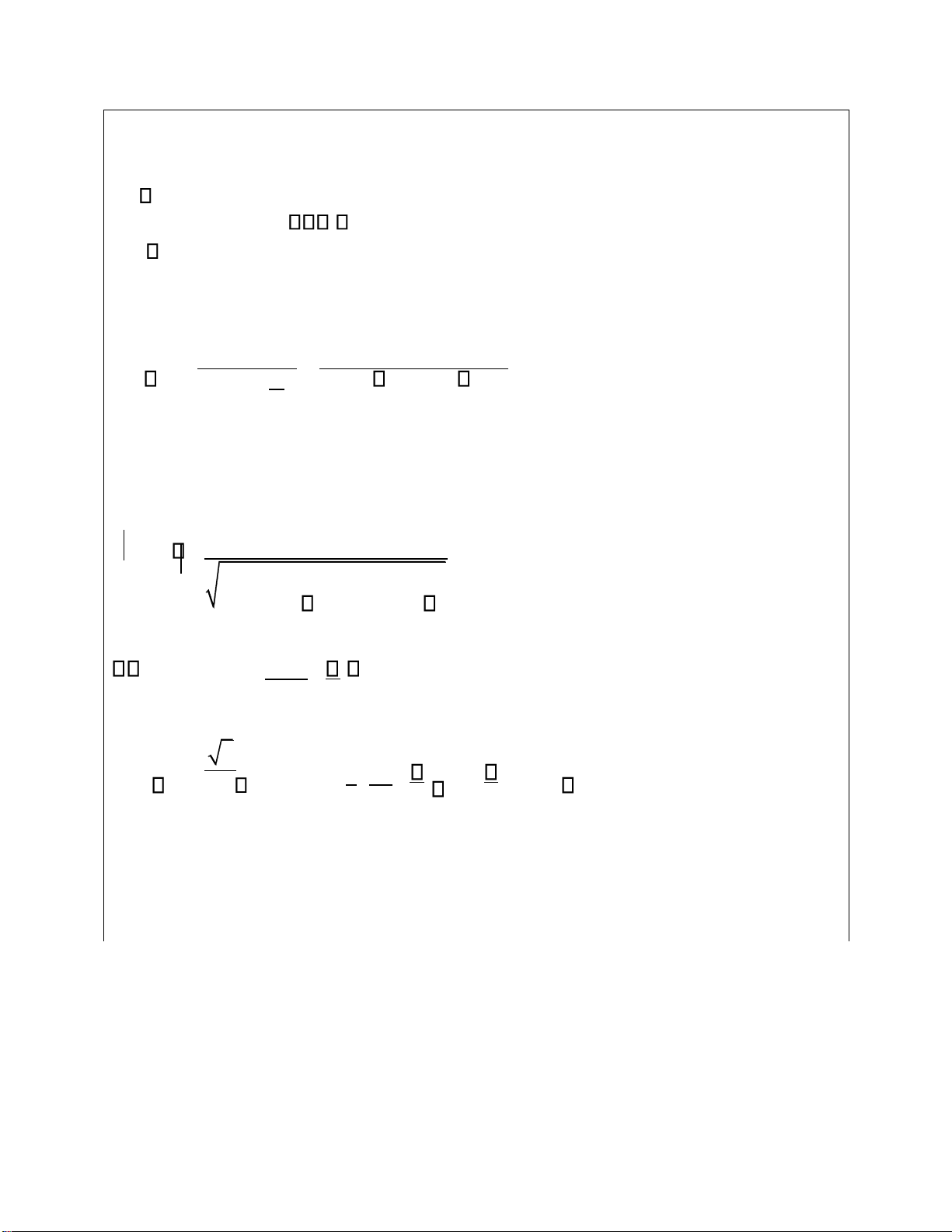
b. Vẽ ịnh tính ặc tuyến tần số của hàm truyền
U2(j ) khi Z =R. Điều kiện ạt t phức K j( ) =
U j1( ) tần số ể U1 & U2 có pha vuông góc? Cách làm:
a. Viết ma trận thông số truyền ạt [A]
Do M4C mắc liên thông. Lần lượt xét 2 M4C hình Γ: [A] = [AΓ1].[AΓ2] b.
Tính hàm truyền ạt. Xác ịnh ặc tuyến. lOMoARcPSD| 37054152 Bài làm:
a. Ma traän thoâng soá truyeàn ñaït:
A= R C s2 2 22 2 2+3+RCs2Cs+1 −−
−21R−RCSR Cs2 R C s
b. Tính haøm truyeàn ñaït T ( j ) =
1 1 = − R 2C 2 +14 jRC + 3
a11 − a12. Z t Xaùc ñònh ñaëc tuyeán T ( j ) = 1 (3− R )2 2C 2 +16 R 2C 2 2
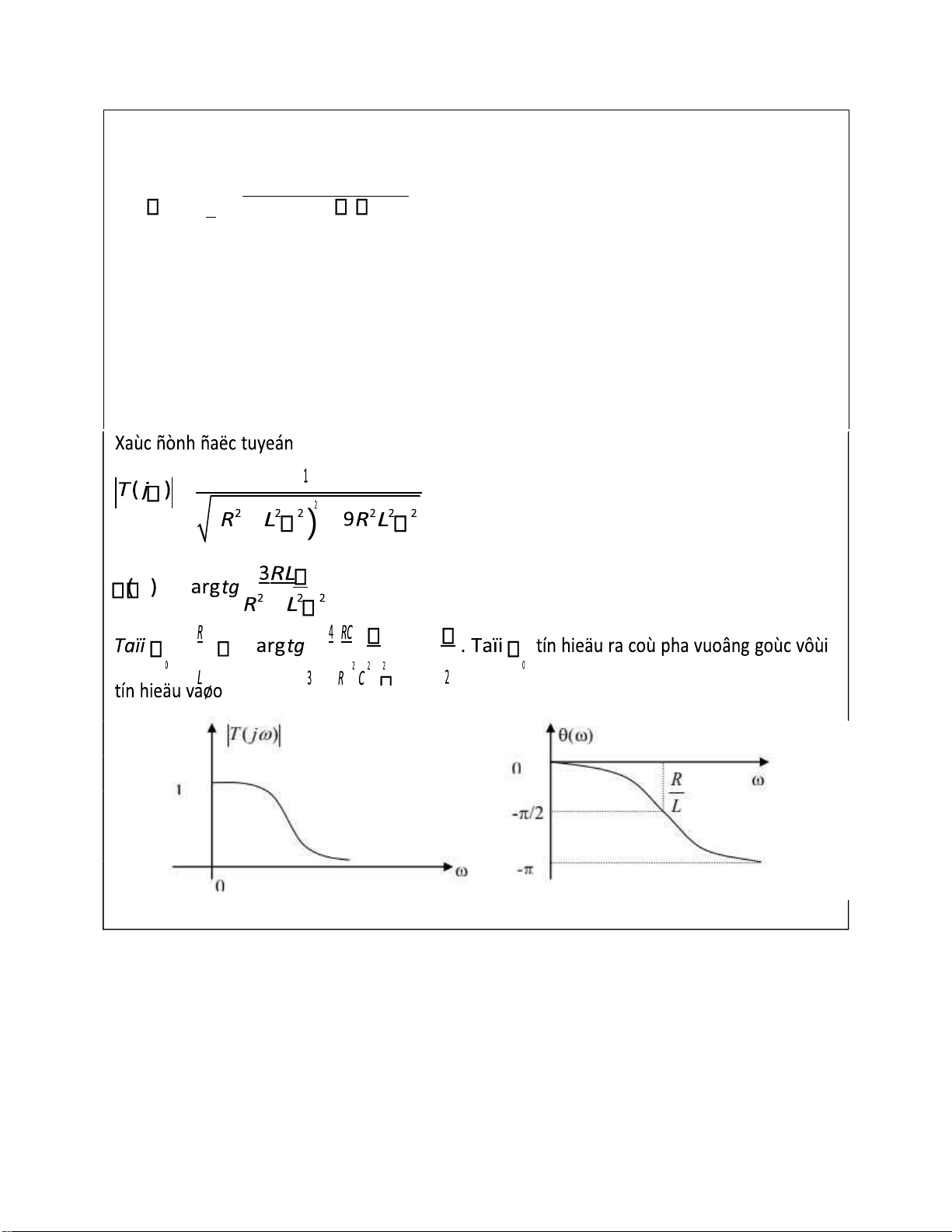
( ) =−arg tg 4 RC2C 2 2 3− R = Taïi 3 − RC 0 RC
arg tg 3−4R 2C 2 2 =− 2 . Taïi 0 tín hieäu ra coù pha vuoâng
goùc vôùi tín hieäu vaøo lOMoARcPSD| 37054152
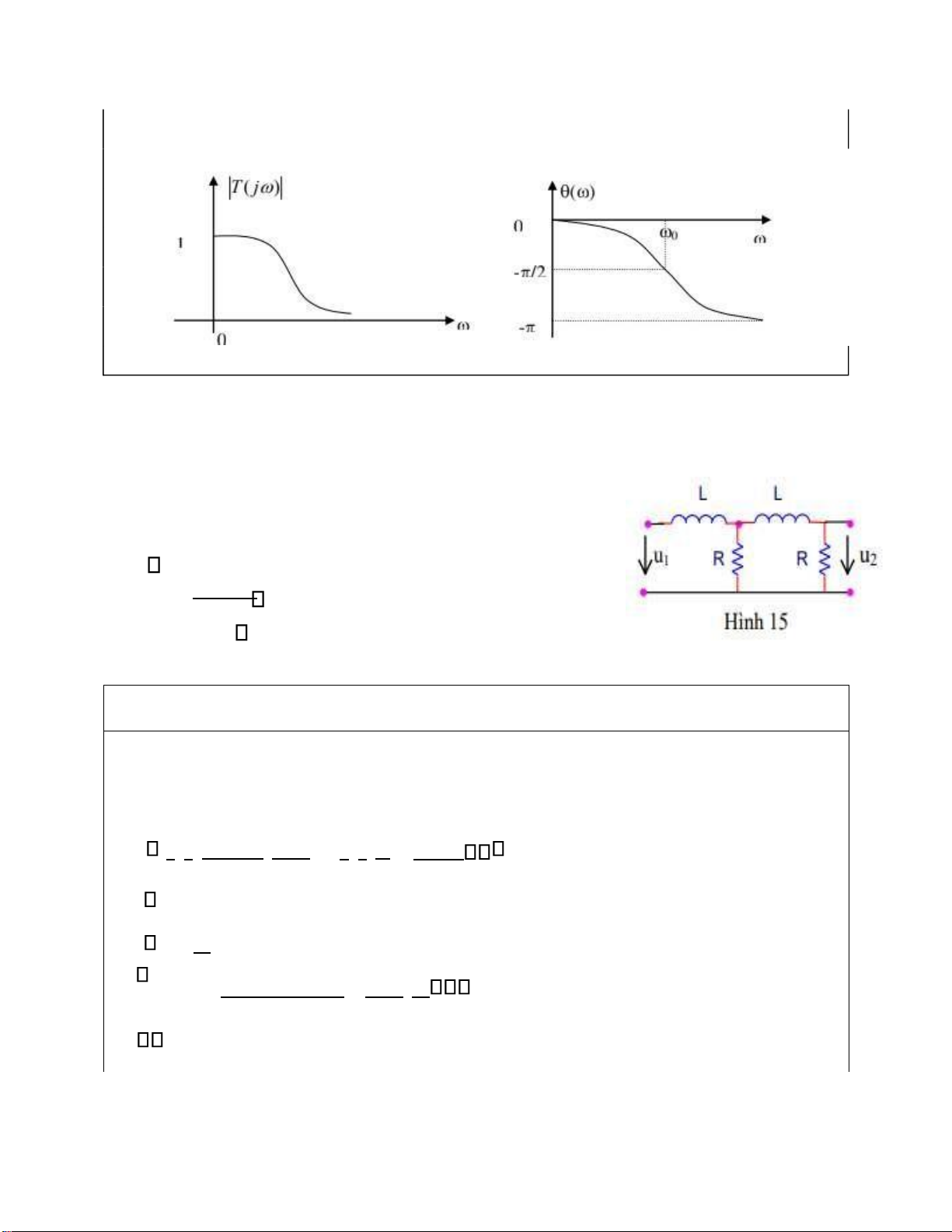
Bài 15: Mạng bốn cực (M4C) như hình 15
a. Xác ịnh ma trận thông số truyền ạt [A]
b. Vẽ ịnh tính ặc tuyến tần số của hàm truyền ạt phức K j( ) =
U2(j ) khi ầu ta M4C hở mạch. Điều kiện tần
U j1( ) số ể U1 & U2 có pha vuông góc?
Cách làm: Tương tự bài 14 Bài làm:
a. Ma traän thoâng soá truyeàn ñaït:
L2 s2 + 3RLs2 + R 2 − L2 s2 +R 22 RLs R Ls A= 2 + 2 R − Ls +2 R R 2 R lOMoARcPSD| 37054152
b. Tính haøm truyeàn ñaït T j( ) = =1 11 2 + L2 2 1+ j RL3 a R = ( − + ) =− − = − =− −