Đề cương ôn tập phần lý thuyết môn Lý thuyết mạch điện tử | Học viện Công nghệ Bưu chính Viễn thông
Đề cương ôn tập phần lý thuyết môn Lý thuyết mạch điện tử của Học viện Công nghệ Bưu chính Viễn thông với những kiến thức và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực tiễn cuộc sống. Mời bạn đọc đón xem!
Tài liệu liên quan:
Preview text:
lOMoARcPSD| 37054152
NỘI DUNG THI LÝ THUYẾT MẠCH PHẦN LÝ THUYẾT
CHƯƠNG 1: NHỮNG KHÁI NIỆM CƠ BẢN VỀ MẠCH ĐIỆN................................................................... 2
1.1. Các phần tử của mạch iện (MĐ)............................................................................................................... 2
1.2. Phân loại & trạng thái làm việc của MĐ ................................................................................................. 3
1.3. Biểu diễn phức cho ại lượng iều hòa ........................................................................................................ 4
1.4. Trở kháng và dẫn nạp ............................................................................................................................... 5
1.5. Công suất .................................................................................................................................................... 7
1.6. Biến ổi tương ương .................................................................................................................................... 9
CHƯƠNG 2: CÁC ĐỊNH LUẬT VÀ PHƯƠNG PHÁP CƠ BẢN PHÂN TÍCH MẠCH ............................ 10
2.1. Các ịnh luật kirchhoff ............................................................................................................................. 10
2.2. Phương pháp Điện thế nút (ĐTN) .......................................................................................................... 12
2.3. Phương pháp dòng iện vòng (DĐV) ....................................................................................................... 13
2.4. Nguyên lý xếp chồng ................................................................................................................................ 14
2.5. Định lý nguồn tương ương ...................................................................................................................... 15
CHƯƠNG 3: TRẠNG THÁI QUÁ ĐỘ CỦA MĐ & PHÂN TÍCH MẠCH QUÁ ĐỘ ................................. 16
3.1. Đáp ứng MĐ ở trạng thái quá ộ ............................................................................................................. 16
3.2. Biến ổi Laplace (LT) ................................................................................................................................ 17
3.3. Tính liên tục của dòng iện qua L và iện áp trên C ................................................................................ 20
3.4. Sơ ồ tương ương của các phần tử MĐ dưới dạng toán tử .................................................................... 21
3.4. Phân tích mạch quá ộ dùng biến ổi laplace ........................................................................................... 22
CHƯƠNG 4: LÝ THUYẾT MẠNG BỐN CỰC (M4C) .................................................................................. 23
4.1. Các hệ phương trình ặc tính của M4C: Z, Y, A .................................................................................... 23
4.2. Các sơ ồ tương ương của M4C ............................................................................................................... 26
4.3. Ghép nối các M4C ................................................................................................................................... 26
4.4. Hàm truyền ạt iện áp (Ku): Biểu diễn Ku theo các phần tử ma trận Z, Y, A ...................................... 27 lOMoARcPSD| 37054152
CHƯƠNG 1: NHỮNG KHÁI NIỆM CƠ BẢN VỀ MẠCH ĐIỆN
1.1. Các phần tử của mạch iện (MĐ)
1.1.1. Các phần tử thụ ộng R, L, C a. Phần tử iện trở
- Điện trở là phần tử 2 cực ặc trưng cho hiện tượng tiêu tán năng lượng iện từ.
- Quan hệ iện áp và dòng iện trên iện trở tuyến tính: u(t) = R.i(t)
- Trên R dòng iện và iện áp cùng pha i(t ) = 1 u(t ) =G.u(t ) R
G= 1 : giá trị iện dẫn, ơn vị siemen (S) hay mho (Ʊ) R b. Phần tử iện dung
- Điện dung là phần tử 2 cực ặc trưng cho hiện tượng tích phóng năng lượng iện trường.
- Điện dung là mô hình lý tưởng của tụ iện.
- C: Thông số iện dung, ơn vị Farad (F)
- Mạch ở trạng thái xác lập 1 chiều u(t)=const i(t)=0, tụ iện xem như hở mạch. c. Phần tử iện cảm
- Điện cảm là phần tử 2 cực ặc trưng cho hiện tượng tích phóng năng lượng từ trường.
- Điện cảm là mô hình lý tưởng của cuộn dây.
- L: Thông số iện cảm, ơn vị Henry (H)
- Mạch ở trạng thái xác lập 1 chiều i(t)=const u(t)=0, cuộn dây xem như ngắn mạch. lOMoARcPSD| 37054152
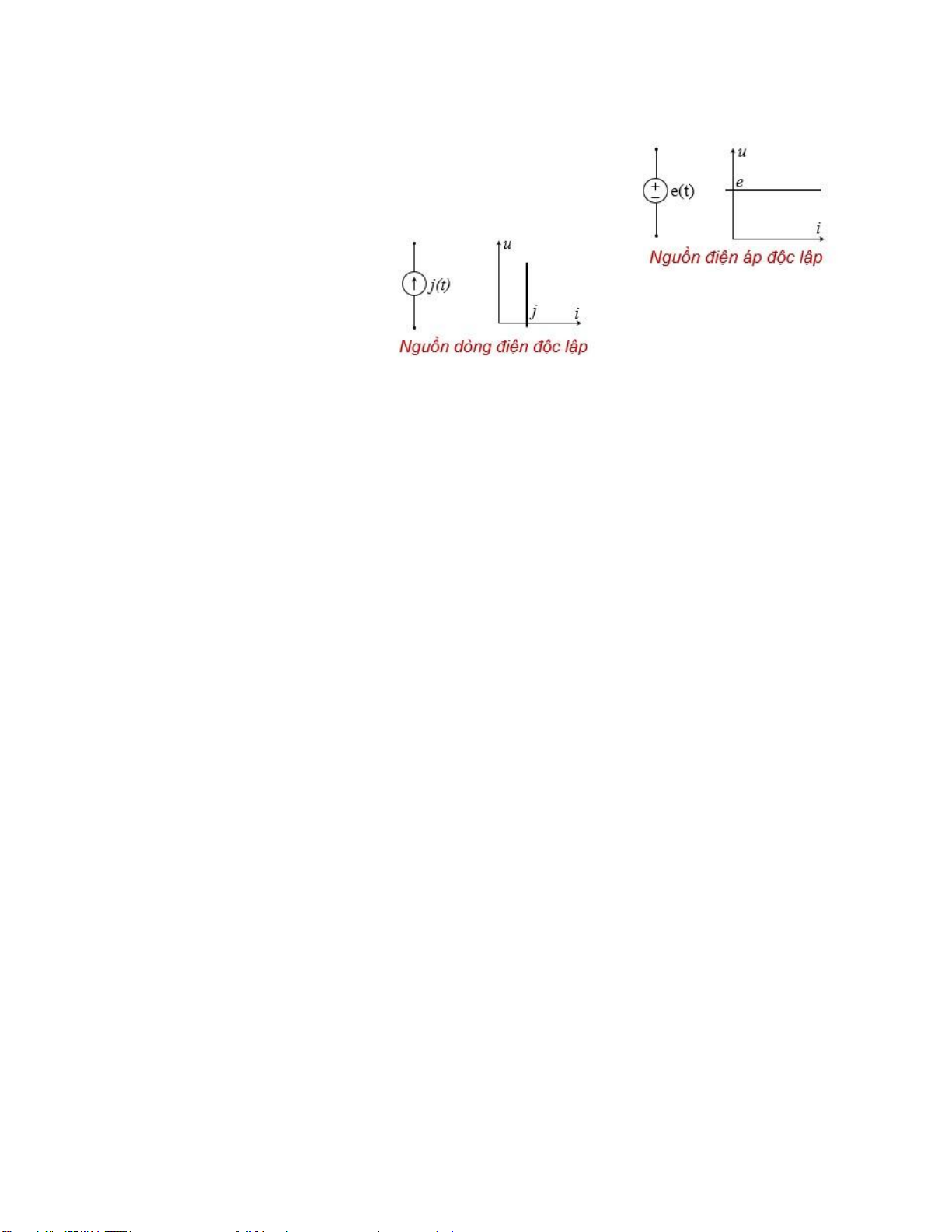
1.1.2. Các phần tử nguồn: e(t), j(t) - Nguồn iện áp ộc lập:
Nguồn iện áp ộc lập là phần tử 2 cực mà iện áp của nó
cung cấp không phụ thuộc
vào dòng iện i qua nó. -
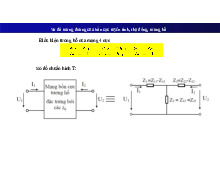
Nguồn dòng iện ộc lập:
Nguồn dòng iện ộc lập là
phần tử hai cực mà dòng
iện do nó cung cấp không phụ
thuộc vào iện áp trên hai cực của nó.
1.2. Phân loại & trạng thái làm việc của MĐ
1.2.1. Phân loại theo mạch iện: -
Mạch tuyến tính, phi tuyến
Mạch iện là tuyến tính khi các thông số trong mạch R,L,M,C là hằng số, không phụ
thuộc vào giá trị dòng iện i và iện áp u trên chúng. Thỏa mãn nguyên lý xếp chồng và nguyên lý tỉ lệ.
Mạch iện là phi tuyến khi các thông số trong mạch R,L,M,C phụ thuộc vào giá trị
dòng iện i và iện áp u trên chúng. - Mạch có thông số tập trung, phân bố
Mạch iện có thông số tập trung ở dải tần số thấp, khi kích thước của các phần tử
cũng như khoảng cách vật lý từ phần tử này tới các phần tử lân cận là rất nhỏ so với
bước sóng của tín hiệu, các mạch iện ược phân tích như tập hợp các thông số tập
trung. Lúc này khái niệm dòng dịch trong hệ phương trình Maxwell là không áng kể
so với dòng dẫn, những biến thiên của từ trường và iện trường trong không gian có
thể bỏ qua ược. Khi ó các biến chỉ phụ thuộc vào thời gian. Trong mô hình mạch tập
trung, bản chất quá trình iện từ ược mô tả thông qua các ại lượng dòng iện, iện áp,
và các hệ phương trình kirchhoff...
Mạch iện có thông số phân bố khi kích thước của các phần tử cũng như khoảng cách
vật lý từ phần tử này tới các phần tử lân cận có thể so sánh với bước sóng của tín
hiệu truyền lan, các mạch iện ược xem như có thông số phân bố. Trong mô hình này,
bản chất quá trình iện từ ược mô tả thông qua các ại lượng cường ộ iện trường, cường
ộ từ trường, mật ộ dòng, mật ộ iện tích, và các hệ phương trình Maxwell…
- Mạch tương hỗ, không tương hỗ
Mạch tương hỗ: Phần tử tương hỗ là phần tử có tính chất dẫn iện hai chiều. Mạch
iện tương hỗ là mạch iện bao gồm các phần tử tương hỗ. Các phần tử và mạch tuyến lOMoARcPSD| 37054152
tính có tính chất tương hỗ như các phần tử thụ ộng dẫn iện hai chiều R, L, C .... Các
phần tử và mạch không tương hỗ như èn iện tử, tranzito, iốt...
1.2.2. Trạng thái làm việc của MĐ
Trạng thái xác lập: u(t), i(t) trong mạch ã ổn ịnh & biến thiên theo quy luật nguồn tác ộng.
Ở chế ộ xác lập, dòng iện, iện áp trên các nhánh biến thiên theo qui luật giống với
qui luật biến thiên của các nguồn iện: ối với mạch iện một chiều (DC), dòng iện và
iện áp là không ổi; ối với mạch iện xoay chiều sin, dòng iện và iện áp biến thiên theo
qui luật sin với thời gian
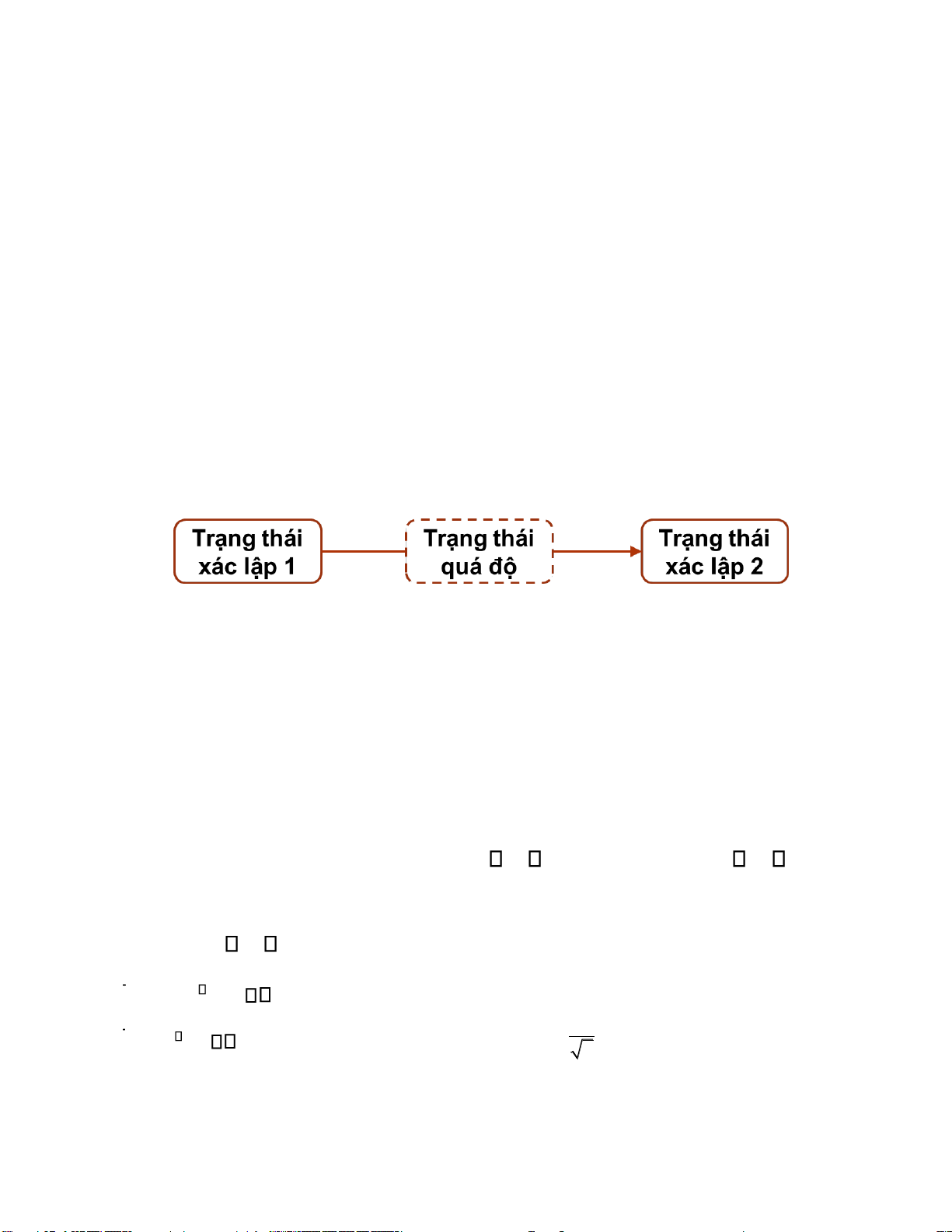
Trạng thái quá ộ: u(t), i(t) chưa ổn ịnh & biến thiên không theo quy luật nguồn tác ộng.
Khi trong mạch xảy ra ột biến, thường gặp khi óng/ngắt mạch hoặc nguồn tác ộng
có dạng xung, trong mạch sẽ xảy ra quá trình thiết lập lại sự cân bằng mới, lúc này
mạch ở Trạng thái quá ộ.
1.3. Biểu diễn phức cho ại lượng iều hòa
1.3.1. Mục ích biểu diễn phức cho ại lượng iều hòa
Việc phân tích nguồn tác ộng thành các thành phần iều hoà và biểu diễn chúng
dưới dạng phức làm cho sự tính toán các thông số trong mạch iện trở nên thuận lợi
dựa trên các phép toán về số phức. Thông qua quá trình biến ổi này mà các phương
trình vi tích phân biến thành phương trình ại số.
1.3.2. Cách biểu diễn phức của ại lượng iều hòa f(t)
Đại lượng f(t) gọi là iều hoà: f(t) = Fm cos( t+ ), hoặc f(t) = Fm sin( t+ )
f(t) có thể là dòng iện i(t), iện áp u(t), các nguồn e(t), j(t) Đại lượng iều hoà:
f(t) = Fmcos( t+ ) Biểu diễn phức:
F F e= j = m Fm
- Biên ộ phức ại lượng iều hòa
F Fe= j =F
- Hiệu dụng phức, với F = Fm 2 lOMoARcPSD| 37054152
1.3.3. Các phép tính tương ương từ Đại lượng iều hòa ↔ ảnh phức + Nhân hệ số: k.f (t ) k.F k f (t ) + + 1 1
k f (t )2 2 k .F1 1 k + Cộng trừ: .F2 2 d + Đạo hàm: f (t ) j .F dt + Tích phân: 1 f (t ) dt j .F
1.4. Trở kháng và dẫn nạp
1.4.1. Định nghĩa trở kháng Z và dẫn nạp Y -
Z chính là một toán tử có nhiệm vụ biến ổi dòng iện phức thành iện áp phức
và gọi là trở kháng của mạch, ơn vị o bằng ôm (Ω) -
Y là một toán tử có nhiệm vụ biến ổi iện áp phức thành dòng iện phức và gọi
là dẫn nạp của mạch, ơn vị o bằng Siemen (S).
Trở kháng Z và dẫn nạp Y ược xác ịnh: Z = = +U R jX ; Y = = = +1 I G jB IZ U
1.4.2. Trở kháng và dẫn nạp của các phần tử R,L,C
a. Trên phần tử iện trở R
Khi có dòng iều hòa chảy qua iện trở R: i =
R( )t = IRm cos(
t + ) → IR IRm thì
trên hai ầu iện trở sẽ xuất hiện iện áp u (t ) = = R
RIRm cos( t + )→UR RIRm
Điện áp trên hai ầu iện trở và dòng iện qua nó cùng pha với nhau. UR(t) và iR(t) cùng
ạt cực ại và cực tiểu hay bằng không tại các thời iểm giống nhau Z = UR = = 1 = =1 R
R ( ); Y R G ( −1) IR ZR R lOMoARcPSD| 37054152
b. Trên phần tử iện cảm L
Nếu qua phần tử iện cảm có dòng iện iều hòa i (t ) = L ILm cos( t + )→ I = L ILm
trên nó sẽ xuất hiện iện áp: u (t ) = = + L
LILmcos( t + + )→UL LILm 22
Điện áp u (t) nhanh pha hơn so với dòng i (t) một góc L L
hay dòng chậm pha so với 2 áp một góc 2 Z = UL = = =1 1 L L
= j L ( ); Y L ( −1) IL 2 ZL j L
c. Trên phần tử iện dung C
Khi ặt lên hai ầu của phần tử iện dung một iện áp iều hòa u (t )C = =
UCm cos( t + )→UC UCm
thì qua ó sẽ có dòng iện: i (t ) = = + C
CUCm cos( t + + )→ IC CUCm 22
Về pha, dòng iện i (t) nhanh pha hơn so với iện áp u (t) một góc C C , hay iện áp 2
chậm pha so với dòng iện một góc 2
1.4.3. Trở kháng và dẫn nạp các phần tử mắc nối tiếp, song song
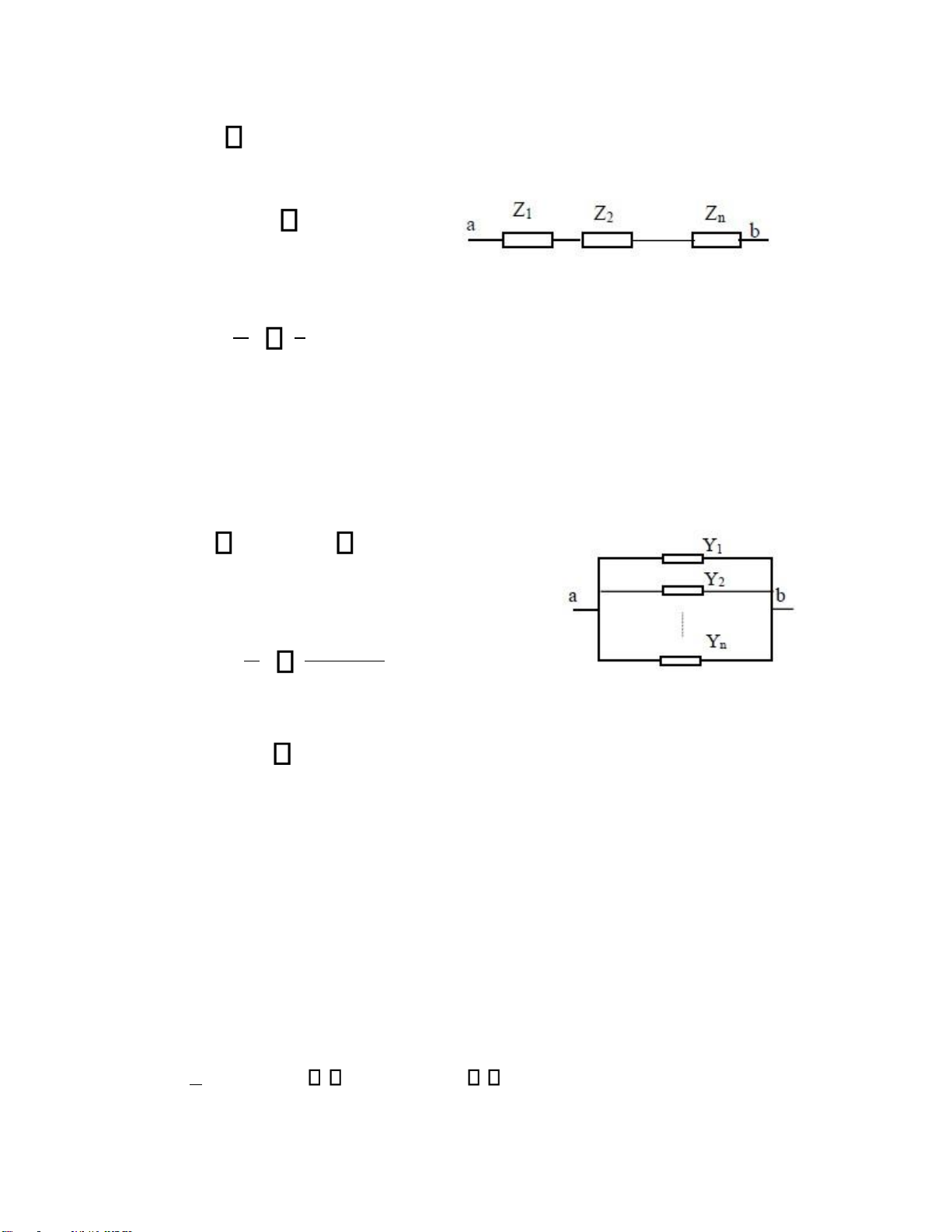
a. Trường hợp mắc nối tiếp lOMoARcPSD| 37054152
Uab =I Z. ab =I Zk k Trôû khaùng: Z = td Zk k Daãn naïp: 1 = 1 Ytd k Yk
b. Trường hợp mắc song song
Iab =UY. ab = U Yk k =U Yk k k Trôû khaùng: 1 = 1 Ztd k Zk Daãn naïp: Y = td Yk k 1.5. Công suất
1.5.1. Các khái niệm công suất: Tác dụng (P), Phản kháng (Q), Biểu kiến (S) -
Công suất tác dụng (P) còn gọi là Công suất trung bình. Công suất tác dụng có ý
nghĩa thực tiễn hơn so với công suất tức thì. Trong mạch thụ ộng, sự lệch pha của
áp và dòng luôn nằm trong giới hạn ± π/2 nên P luôn luôn dương. Thực chất P
chính là tổng công suất trên các thành phần iện trở của oạn mạch.
Đơn vị công suất tác dụng tính bằng W. 1 P = =P − − T U I cos(m m u i )=UI cos(
u i ), (W ) 2 lOMoARcPSD| 37054152
- Công suất phản kháng (Q) là phần năng lượng iện ược chuyển ngược về nguồn cung
cấp năng lượng trong mỗi chu kỳ do sự tích lũy năng lượng trong các thành phần cảm
kháng và dung kháng của mạch iện. Đây là phần công suất không có lợi của mạch iện.
Đơn vị tính là VAR (volt amperes reactive) Q = 1U I sin( − − m m u i )=UI sin( u i ), (VAr ) 2
Trong mạch thụ ộng, công suất phản kháng có thể có giá trị dương hoặc âm. Nếu
mạch có tính cảm kháng, tức iện áp nhanh pha hơn so với dòng iện, thì q sẽ có giá
trị dương. Nếu mạch có tính dung kháng, thì Qr sẽ có giá trị âm. Qr chính là công
suất luân chuyển từ nguồn tới tích lũy trong các thành phần iện kháng của mạch và
sau ó lại ược phóng trả về nguồn mà không bị tiêu tán. Nó có giá trị bằng hiệu ại số
giữa công suất trên các thành phần iện cảm và công suất trên các thành phần iện
dung. Khi Qr bằng không, có nghĩa là công suất trên các thành phần iện cảm cân
bằng với công suất trên các thành phần iện dung, hay lúc ó mạch là thuần trở. - Công
suất biểu kiến (S) còn gọi là công suất toàn phần là công suất tổng của mạch iện bao
gồm công suất hiệu dụng và công suất phản kháng. Đơn vị: VA (vôn-ampe) S = 1U I = m m UI, (VA) 2 S P Q = + 2 2 2
Công suất toàn phần mang tính chất hình thức về công suất trong mạch khi các ại
lượng dòng và áp ược o riêng rẽ mà không chú ý tới sự lệch pha giữa chúng.
1.5.2. Phối hợp Z giữa Nguồn-Tải ể P tải lên cực ại - Đặt vấn ề:
Cho biết giá trị nguồn: E = E = + m e; Zn Rn jXn Tìm trở kháng tải: Z = + t
Rt jXt sao cho P lên Zt là cực ại? lOMoARcPSD| 37054152 E E m I = = 2 2 i Z +Z + + + n t ( R R ) ( X X ) n t t n 2 1 1 E 2 m
P = RI = R t m t 2 2 2 2 ( R + R ) +( X + X ) n t n t
- Khi X t = -X n thì P -> max - Khi Xn= -Xt : R P= 1 E = n m2 1 Em2 2 R Do: R + t n R R t t 2 ( R + R ) R n 2 n t ( + R ) t R t 2 2
Nên P -> max khi R = *
t= Rn. Vậy P -> max khi Rt = Rn và Xt = -Xn hay Zt Zn Em2 P = max 8Rt
Nếu tải thuần trở Zt= Rt thì ể P tác dụng lên tải cực ạt thì: R = = + t Zn Rn2 Xn2
1.6. Biến ổi tương ương
1.6.1. Mắc nối tiếp, mắc song a. Mắc nối tiếp
Các nguồn sức iện ộng ( iện trở) mắc nối tiếp sẽ tương ương với một nguồn sức iện
ộng duy nhất có trị số bằng tổng ại số các sức iện ộng ( iện trở) ó e = − + +e1 e2 en Z = n Zk k=1 b. Mắc song song
Các nguồn dòng iện mắc song song sẽ tương ương với một nguồn dòng duy nhất có
trị số bằng tổng ại số các nguồn dòng ó lOMoARcPSD| 37054152
j = n jk Y = n Yk k=1 k=1
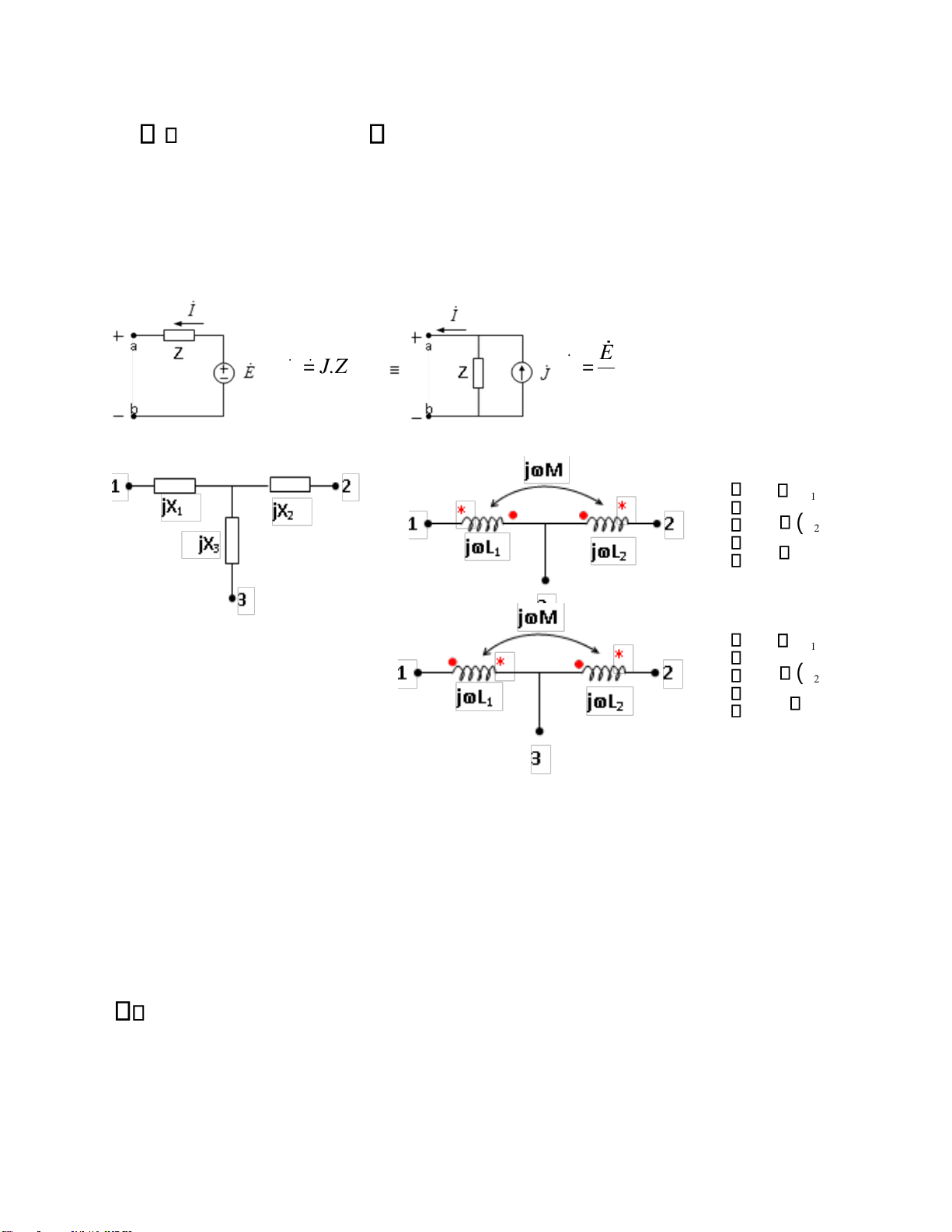
1.6.2. Nguồn áp nối tiếp Z <-> Nguồn dòng song song Z
Khi thay thế một nguồn áp mắc nối tiếp với một iện trở thành nguồn dòng mắc song
song với iện trở thế nguồn dòng có giá trị bằng nguồn áp chia cho iện trở ó.
Tương ương cho trường hợp nguợc lại (khi thay thế nguồn dòng thành nguồn áp). E E = J.Z J = Z 1.6.3.
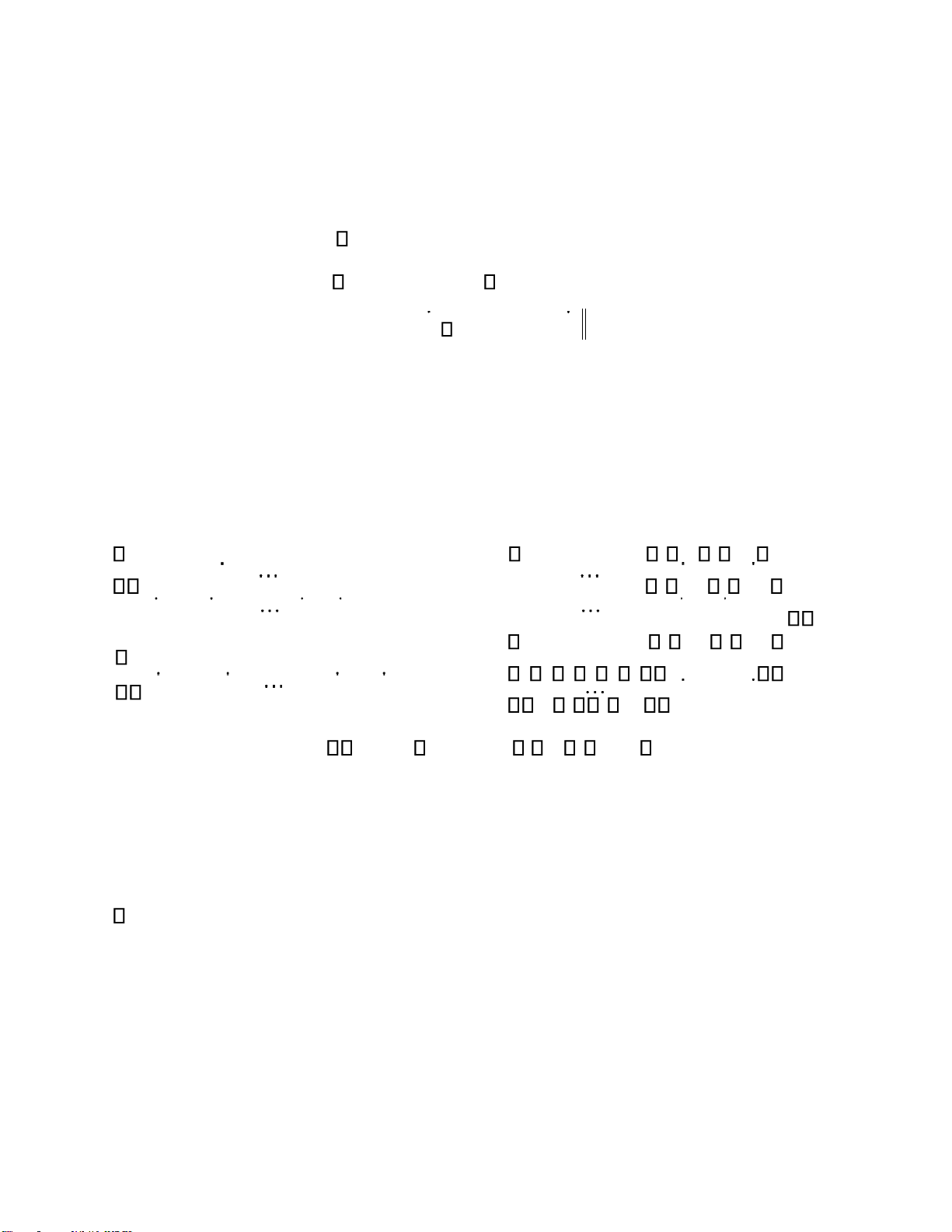
Khử hỗ cảm X = LM − 1 ( 1 ) X = LM − 2 ( 2 ) X = M 3 X = LM + 1 ( 1 ) X = LM + 2 ( 2 ) X =− M 3
CHƯƠNG 2: CÁC ĐỊNH LUẬT VÀ PHƯƠNG PHÁP CƠ BẢN PHÂN TÍCH MẠCH
2.1. Các ịnh luật kirchhoff
2.1.1. Định luật kirchhoff 1 (về dòng iện)
Định luật này phát biểu về dòng iện, nội dung của nó là: “ Tổng các dòng iện i vào
một nút bằng tổng các dòng iện i ra khỏi nút ó ”. Hoặc là: “Tổng ại số các dòng iện
tại một nút bằng không” i tk( ) = 0 Nuùt
+ Chiều dòng iện chọn bất kỳ
+ Chiều dòng i vào & dòng i ra có dấu ngược nhau lOMoARcPSD| 37054152
Tổng ại số các dòng iện i vào, ra bề mặt kín thì bằng không ( )i t = k 0 Beà maët
Định luật kirchhoff 1 dạng phức
Tổng ại số các ảnh phức của dòng iện tại một nút bất kỳ thì bằng không =Ik 0 Nuùt
Mạch iện có d nút có (d-1) phương trình dòng iện ộc lập.
2.1.2. Định luật kirchhoff 2 (về iện áp)
Định luật này phát biểu về iện áp, nội dung của nó là: “ Tổng ại số iện áp của các
nguồn trong một vòng kín thì bằng tổng ại số iện áp trên các phần tử khác trong
vòng ó ”. Hoặc là: “Tổng ại số các iện áp trên các phần tử trong vòng kín bất kỳ thì bằng không” u tk ( ) 0= Voøng kín
e tk ( )= u tk ( ) Nguoàn Phaàn töû khaùc
+ Khi phân tích mạch iện, ể việc áp dụng ịnh luật II ược thuận tiện, nếu trong mạch
chứa nguồn dòng thì cần phải chuyển nó về dạng nguồn áp.
+ Chiều của vòng chọn bất kỳ
+ Chiều i từ cực (+) (-) (dựa vào chiều của dòng iện) thì iện áp lấy dấu (+) , ngược lại lấy dấu (-)
Định luật Kirchhoff 2 dạng phức
Tổng ại số các ảnh phức của iện áp trên các phần tử trong một vòng kín bất kỳ thì bằng không. U = k 0 Voøng kín lOMoARcPSD| 37054152
Mạch iện có n nhánh và d nút thì sẽ có (n-d+1) phương trình iện áp ộc lập Số PT
ộc lập theo ĐL K1: (d-1)
Số PT ộc lập theo ĐL K2: (n-d+1)
Số PT ộc lập theo 2 ĐL K1+K2: n = số nhánh = số dòng iện trên các nhánh tìm
ược dòng trên các nhánh -
Nhờ 2 ịnh luật Kirchhoff 1, 2 có thể tìm dòng iện trên tất cả các nhánh ->
tìm các thông số khác như iện áp, công suất…của bất kỳ mạch iện nào khi biết trước các thông số của nó. -
Đối với mạch iện có nhiều nhánh, nhiều vòng thì dựa trên 2 ịnh luật Kirchhoff
1, 2 số phương trình nhiều thời gian giải p/trình ể tìm áp ứng i(t),u(t) khá lâu. -
Để giảm bớt thời gian giải theo 2 inh luật K1,2 ưa ra các phương pháp phân
tích mạch trong chương 2.
2.2. Phương pháp Điện thế nút (ĐTN)
2.2.1. Dạng MĐ thường áp dụng phương pháp ĐTN
Phương pháp Điện thế nút thường áp dụng cho mạch có nhiều nhánh mắc song song
giữa các nút, không ghép hỗ cảm
2.2.2. Hệ phương trình ĐTN cho MĐ Y − − = 11 1 − Y122
Y1d−1 d−1 Jd1 −Y − − = 21 1 + Y22 2
Y2d−1 d−1 Jd 2 −Y − + = (d−1)1 1 −Y(d−1)2 2
Y(d−1)(d−1) d−1 Jd d( −1)
Ykk: Tổng dẫn nạp nối ến nút k
Ykl: Tổng dẫn nạp giữa các nút k-l
Jdk: Tổng ại số các dòng iện i vào, ra nút k
(+) nếu nguồn dòng hướng vào nút k
(-) nếu nguồn dòng hướng ra khỏi nút k
k: Điện thế tại nút k lOMoARcPSD| 37054152
Các bước tiến hành theo p/p Điện thế nút:
1. Gán tên cho tất cả các nút, chọn một nút làm gốc và quy ước iện thế nút gốc =0.
2. Lập hệ PT iện thế ( ) cho các nút còn lại.
3. Giải hệ PT iện thế iện thế các nút dòng iện trên các nhánh. Lưu ý: Nếu
mạch iện có chứa E n t Z ( / ) J Z
2.3. Phương pháp dòng iện vòng (DĐV)
2.3.1. Dạng MĐ thường áp dụng phương pháp DĐV
Phương pháp Dòng iện vòng thường áp dụng cho mạch có ít số vòng, ghép hỗ cảm.
2.3.2. Hệ phương trình DĐV cho MĐ Hệ PT dòng iện cho L vòng: Z I + + + = 11 1v Z I12 2v Z I1L vL Ev1 Z11 Z12 Z1L Iv1 Ev1 Z I21 1v .................. ..... ..... +
.................................................... Z I + 22 2v Z
L1 ZL2 ZLL +Z Z I + + + = L1 1v Z IL2 2v Z ILL vL EvL I vL EvL I = 2L vL Ev2 = ( )
Z21 Z22 Z2L Iv2 Ev2
Z : Tổng trở kháng vòng k kk
Z : Tổng trở kháng giữa 2 vòng k kl -l
(+) nếu chiều của 2 vòng cùng chiều so nhánh chung
(-) nếu chiều của 2 vòng ngược chiều so nhánh chung
E : Tổng ại số các nguồn áp trong vòng vk k
(+) nếu chiều của vòng i từ (-) -> (+) của nguồn áp
(-) nếu chiều của vòng i từ (+) -> (-) của nguồn áp lOMoARcPSD| 37054152
Ivk : Dòng iện của vòng thứ k
Các bước tiến hành theo p/p Dòng iện vòng:
1. Vẽ chiều dòng iện các vòng.
2. Lập hệ PT dòng iện cho các vòng ( ).
3. Giải hệ PT dòng iện vòng dòng iện vòng dòng iện trên các nhánh: I = k Ivk
(+) nếu chiều I cùng chiều với vk Ik
(-) nếu chiều Ivk ngược chiều với Ik Lưu ý:
Nếu mạch iện có chứa J Z E (n/t) Z Mạch có ghép hỗ cảm
2.4. Nguyên lý xếp chồng
2.4.1. Dạng MĐ áp dụng nguyên lý xếp chồng
Nguyên lý xếp chồng thường ược áp dụng cho mạch iện có các nguồn tác ộng khác tần số.
2.4.2. Cách phân tích MĐ dùng nguyên lý xếp chồng
1. Lần lượt cho các nguồn tác ộng làm việc riêng rẽ, các nguồn không làm việc theo nguyên tắc:
- Nguồn áp -> ngắn mạch;
- Nguồn dòng -> hở mạch.
2. Tính áp ứng (u,i) tạo bởi từng nguồn tác dộng riêng rẽ.
3. Tổng cộng các áp ứng (u,i) tạo bởi các nguồn tác ộng riêng rẽ. lOMoARcPSD| 37054152
2.5. Định lý nguồn tương ương
2.5.1. Dạng MĐ áp dụng ịnh lý nguồn tương ương
Định lý thường áp dụng cho mạch iện, mà chỉ yêu cầu xác ịnh dòng iện hay iện áp
trên 01 nhánh nào ó của mạch iện.
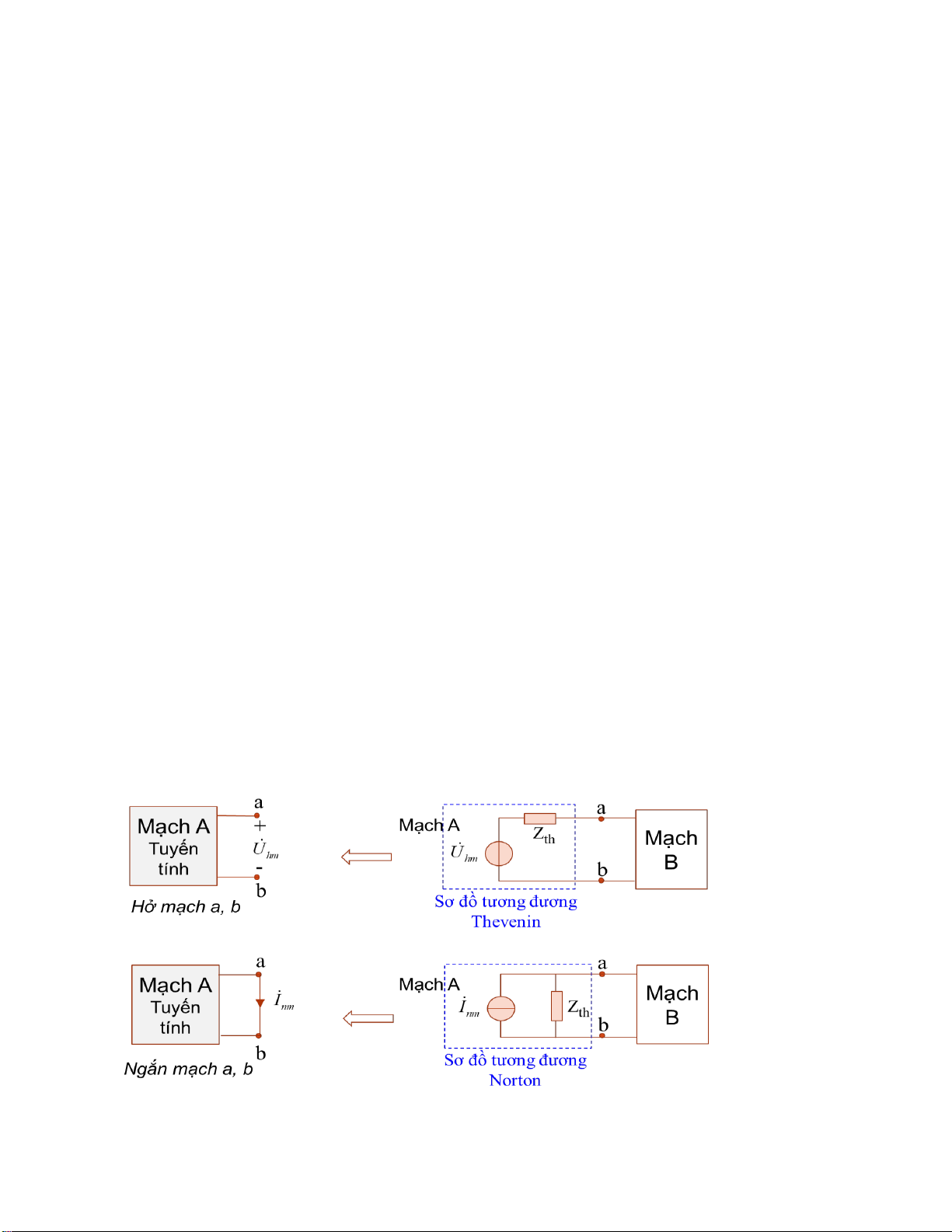
Định lý nguồn tương ương (Thevenin & Norton) dùng ể thay tương ương phần mạch
phức tạp -> 01 nguồn (áp hoặc dòng) ơn giản.
2.5.2. Định lý Thevenin
Định lý Thevenin phát biểu rằng: “Bất kỳ mạch tuyến tính nào có chứa một số iện
áp và iện trở ược thay thế bằng chỉ một iện áp duy nhất mắc nối tiếp với một iện trở
duy nhất ược nối qua tải”. Nói cách khác, có thể ơn giản hóa bất kỳ mạch iện nào,
dù phức tạp ến âu, thành một mạch hai ầu tương ương chỉ với một nguồn iện áp
không ổi duy nhất mắc nối tiếp có iện trở (trở kháng) ược nối với tải.
2.5.3. Định lý Norton
Nói cách khác Norton giảm tất cả phần tử mạch thành một iện trở duy nhất song
song với một nguồn dòng iện không ổi.
Định lý Norton phát biểu rằng: “Bất kỳ mạch tuyến tính nào chứa nhiều nguồn năng
lượng và iện trở ều có thể thay thế bằng một nguồn Dòng iện không ổi song song
với một Điện trở ơn”
2.5.4. Cách xác ịnh Điện áp hở mạch (Uhm) & Dòng iện ngắn mạch (Inm) Điện
áp hở mạch (Uhm): Nguồn dòng = 0
Dòng iện ngắn mạch (Inm): Nguồn áp = 0
2.5.5. Cách xác ịnh trở kháng Thevenin (ZTh) lOMoARcPSD| 37054152
a. Mạch A chỉ chứa các nguồn ộc lập
Triệt tiêu các nguồn ộc lập ể xác ịnh Trở kháng Thevenin. Nguyên tắc triệt tiêu:
+ Nguồn áp -> ngắn mạch +
Nguồn dòng -> hở mạch
b. Mạch A có chứa nguồn phụ thuộc Cách 1:
-- Hôû maïch a,b Ngaén maïch a,b →→ IUnmhm Zth = UInmhm Cách 2:
Triệt tiêu các nguồn ộc lập bên trong mạch A, cấp a,b nguồn E với giá trị tùy chọn, = tính dòng iện E Zth I
Triệt tiêu các nguồn ộc lập bên trong mạch A, cấp a,b nguồn Jvới giá trị tùy chọn, = tính iện áp U U Zth J
CHƯƠNG 3: TRẠNG THÁI QUÁ ĐỘ CỦA MĐ & PHÂN TÍCH MẠCH QUÁ ĐỘ
3.1. Đáp ứng MĐ ở trạng thái quá ộ
Biểu thức dòng iện & iện áp của MĐ ở trạng thái quá ộ:
Quan hệ giữa áp ứng ra và tác ộng vào có thể tồn tại dưới hình thức là một phương
trình vi phân tuyến tính hệ số hằng (bậc n) chuẩn hóa: d yn dn−1y dy d xm dm−1x dx b + + + = + + n
dtn bn−1 dtn−1 ... b1 dt +b yo am dtm am−1 dtm−1
+... a1 dt + a xo n
d y ti ( ) = m a d x ti ( ) lOMoARcPSD| 37054152 i=0 dti i=0 i dti bi
Nghiệm của hệ có dạng: y t( ) = y th( ) + yp( )t , trong ó:
+ yp( )t là thành phần nghiệm riêng, tương ứng với áp ứng cưỡng bức của hệ; có dạng
giống hàm tác ộng cùng với các thành phần vi tích phân của nó.
+ y t ( )là thành phần nghiệm của phương trình vi phân thuần nhất tương ứng bằng h
cách triệt tiêu nguồn tác ộng cưỡng bức, tương ứng với áp ứng tự do của hệ, phụ
thuộc vào các thông số nội tại của mạch và iều kiện ầu, bị suy biến và triệt tiêu dần theo thời gian.
Trong trường hợp nguồn tác ộng có tính chu kỳ hoặc một chiều, thì khi thành phần
tự do bị triệt tiêu, hệ sẽ chỉ còn lại áp ứng cưỡng bức; khi ó mạch chuyển sang trạng thái xác lập.
3.2. Biến ổi Laplace (LT)
3.2.1. Biến ổi LT một phía
Biến ổi Laplace thuận của hàm gốc f(t) trong miền thời gian sẽ tương ứng là một ảnh
F(p) trong miền tần số phức p, ược tính theo công thức:
f(t )⎯⎯→LT LT f(t )
= F(s)= f(t )e dt-st 0
trong ó s (còn ký hiệu là p) là một biến số phức ược ịnh nghĩa: s
= + j và nó ược biểu diễn trên mặt phẳng phức.
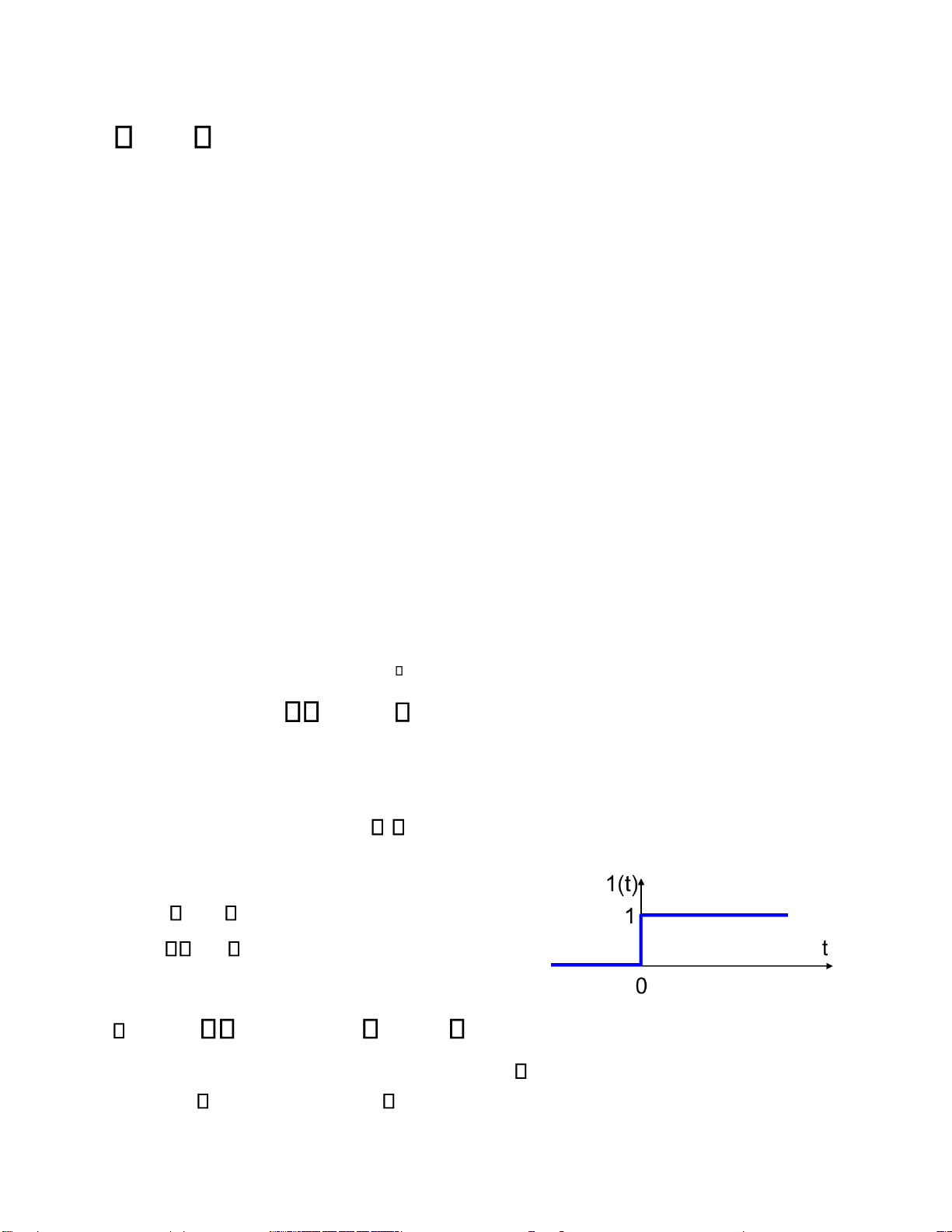
Hàm ơn vị ược ịnh nghĩa: 1: t 0 1(t )= 0: t 0 LT f (t ) = LT f (t ). (t ) 1
3.2.2. Các tính chất biến ổi LT một phía f (t ) ⎯→LT F( s ), f (t ) ⎯→LT ⎯→LT 1
F( s ),1 f (t )2 F ( s )2 lOMoARcPSD| 37054152
+ Tính tuyến tính: a f (t ) + ⎯→LT + 1 1 a f (t )2 2 a F( s )1 1 a F ( s )2 2 + Dịch
theo thời gian: f (t − a ). (t1 − a ) ⎯→LT e−asF( s ) chú ý rằng không có kết
quả cho trường hợp dịch trái trong miền thời gian. +Nhân với hàm mũ:
e−at f (t ) ⎯→LT F( s + a ) d
LT sF(s)− f (0+ )
+ Đạo hàm theo thời gian: f (t ) ⎯→ dt t LT 1F(s) + Tích phân: 0 f ( )d ⎯→s + Đạo hàm của F(s): t.f (t ) ⎯→−LT d F(s) ds
3.2.3. Biến ổi Laplace ngược
Đáp ứng trong mạch [U(s) hay I(s)] có dạng: A s( ) a + + + m 0 a s1 ...a sm Y s( ) = = n B s( ) b + + + 0 bs1 ... b sn
a. Mẫu thức B(s) có các nghiệm ơn: A s( ) A s( ) K n 1 K2 Kn Ki
Y s( ) = B s( ) = b sn ( −s1)(s −s2)...(s −sn ) = (s −s1) + (s −s2) + +...(s −sn) = i=1 (s −si ) K = i A s( )(s s− i ) B s( )s s= i lOMoARcPSD| 37054152
y t( ) = n K e s ti i .1( )t i=1 =
b. Mẫu thức B(s) có nghiệm s1 bội r: Y s( ) = B sA s( )( )
b sn ( −s1) (r sA s−( )sr+1)...(s − + s + + n
n ) = (sK−1s1) + (s −Ks21)2 ...
(s −Ksr 1)r l r 1 (sK−lsl ) = + = + i=r1
(s −Ksi 1)i l r = +n 1 (sK−lsl ) Vôùi
Ki (r −1i ds)! d(r i− ) Y s s( )( −s1)r s = s1
⎯⎯⎯→LT−1 y t( ) = (r i− ) K = l
B sA s( )( )(s−sl ) s = sl
c. Mẫu thức B(s) có nghiệm phức liên hiệp:
Y s( ) = B sA s( )( ) = b s = +
n ( − s1)(sA s−( )s1*)...(s − sn K1 1 K(2s
(−=sK1*)1*) + in3 (sK−isi ) ) (s − s ) = s = + = 1 1 j 1 , K1 K e1 j 1 y t( ) = K e + + 1 s t1 K e1* s t1*
i=n3 K ei s ti .1( )t = 2Re(K e1 s t1 )+ )+
i=n3 K ei s ti .1( )t y t( ) =
2 K e1 1t.cos( 1t + 1 i=n3 K ei s ti .1( )t lOMoARcPSD| 37054152
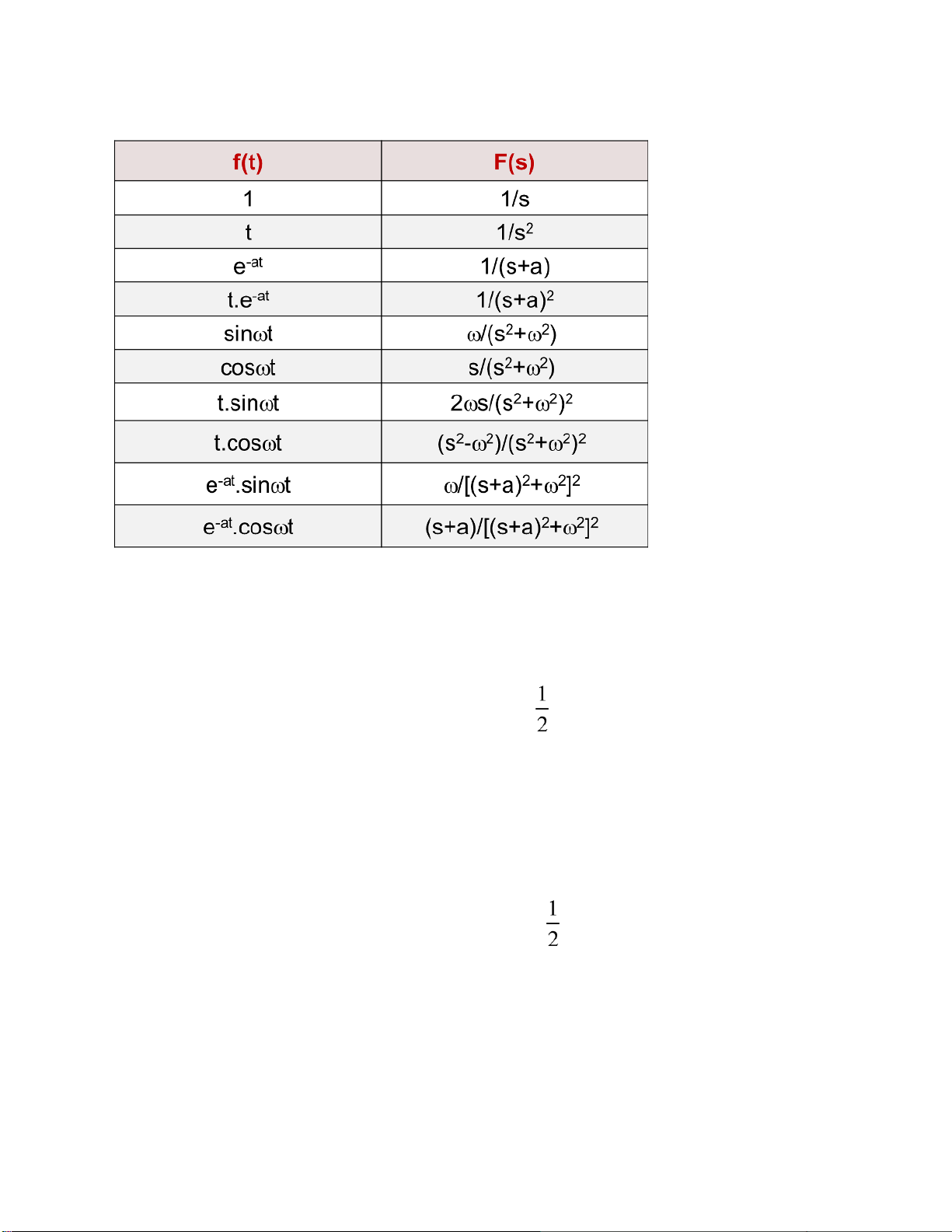
3.2.4. Bảng biến ổi LT một số hàm thông dụng
3.3. Tính liên tục của dòng iện qua L và iện áp trên C
Tính liên tục của dòng iện trên L:
- Tại thời iểm t=0 trong mạch có ột biến
- Năng lượng từ trường tích lũy trên L: W tL ( ) = Li t. ( )2
- Do năng lượng từ trường liên tục nên dòng iện qua cuộn dây cũng liên tục tại thời
iểm t=0: iL (0 )− =iL (0 )+ =iL(0)
Tính liên tục của iện áp trên C:
- Tại thời iểm t=0 trong mạch có ột biến
- Năng lượng iện trường tích lũy trên C: W tC ( ) = C u t. 2( )
- Do năng lượng iện trường liên tục -> iện áp trên tụ iện cũng liên tục tại thời iểm
t=0: uC (0 )− =uC (0 )+ =uC (0)
“Dòng iện qua cuộn dây và iện áp trên tụ cũng liên tục tại các thời iểm có ột biến trong mạch” lOMoARcPSD| 37054152
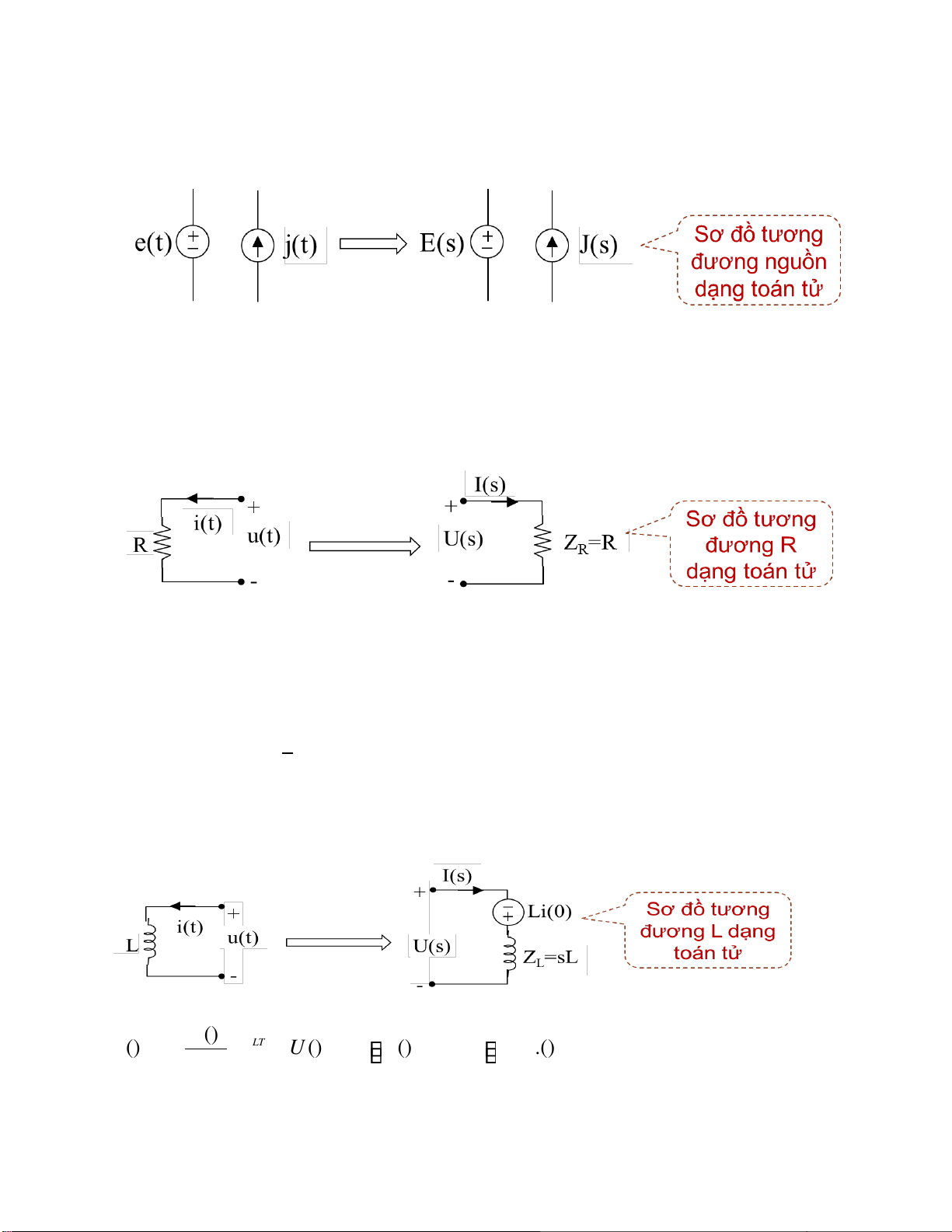
3.4. Sơ ồ tương ương của các phần tử MĐ dưới dạng toán tử Nguồn tác ộng
e t( )⎯⎯→LT E s( ) LT
j t( )⎯⎯→J s( )
Phần tử iện trở: Laplace hóa phương trình từ miền thời gian:
u t( ) = Ri t. ( )⎯⎯→LT
U s( ) = R I s. ( )
Trở kháng và dẫn nạp của iện trở trong miền p có dạng:
Z sR( )=R,Y ( )R s = R1
Ph ầ n t ử cu ộ n dây di() t () ut + + LT =L ⎯⎯→ () Us = Ls Is () −i (0 ) = s .() LIs −Li (0 ) dt lOMoARcPSD| 37054152
Trong ó i(0+) là dòng iện tại thời iểm ban ầu và gọi là iều kiện ầu, còn thành phần
L.i(0+) óng vai trò là một nguồn s ược sinh ra do iều kiện ầu của phần
t ử thu ầ n c ảm, ngượ c chi ề u U(s).
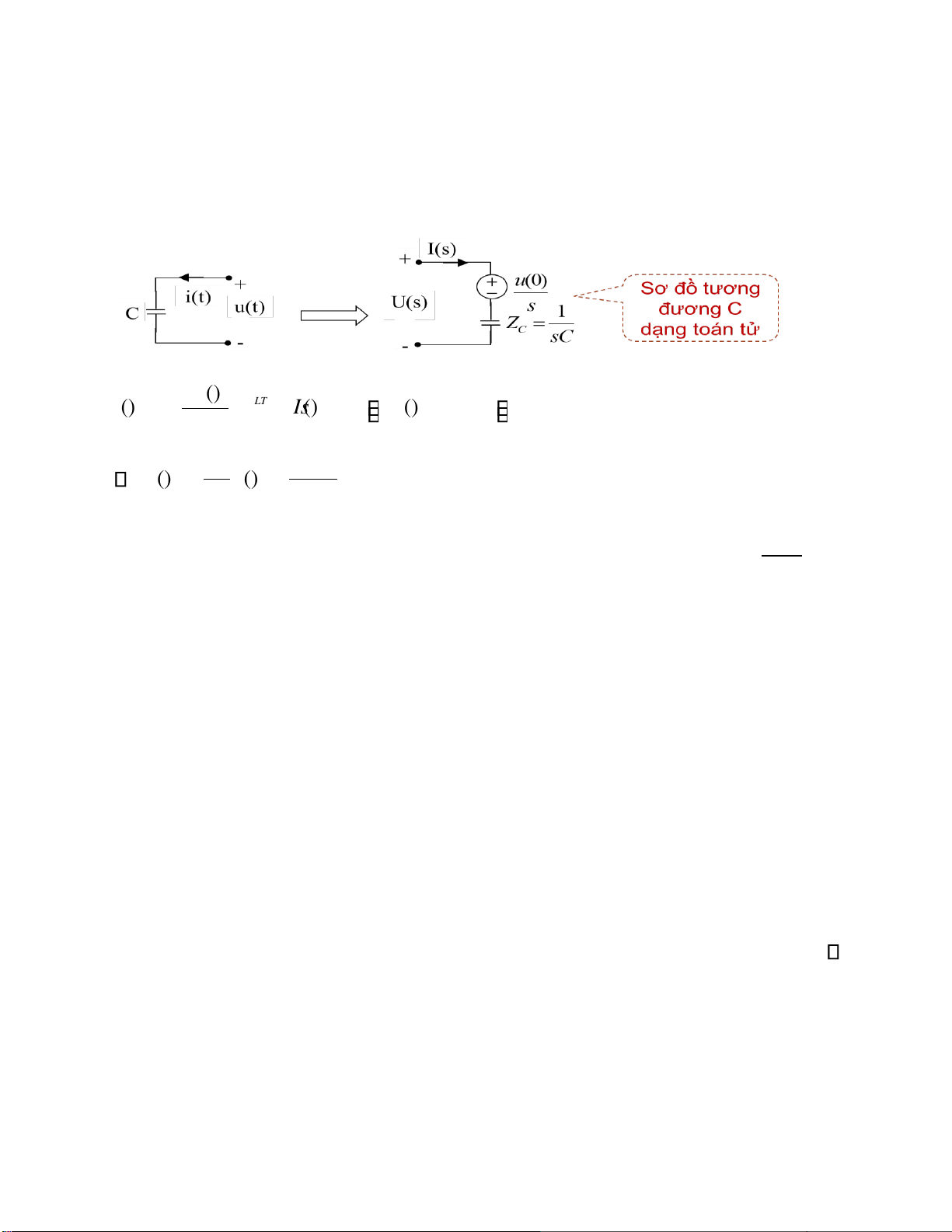
Ph ầ n t ử t ụ iệ n du() t () it + LT =C ⎯⎯→ () Is =Cs
U s () −u (0 ) dt 1 + u(0 ) () Us = () Is + sC s
Trong ó u(0+) là iện áp tại thời iểm ban ầu và gọi là iều kiện ầu, còn thành u(0 )+
phần óng vai trò là một nguồn s
ược sinh ra do iều kiện ầu của phần s
tử thuần dung, cùng chiều U(s) .
3.4. Phân tích mạch quá ộ dùng biến ổi laplace
Các bước tiến hành phân tích MĐ dùng biến ổi LT:
+ Xác ịnh iều kiện ầu của bài toán (chính là xác ịnh gốc thời gian, cùng với các giá
trị ban ầu của các phần tử quán tính).
- Dòng iện qua cuộn dây iL(0-) -
Điện áp trên tụ uC(0-)
+ Lập sơ ồ tương ương toán tử cho các phần tử của mạch iện (t >0).
+ Lập hệ phương trình cho áp ứng mạch dùng các Định luật, Phương pháp phân tích
mạch…, giải ra tìm Y(s)
+ Biến ổi Laplace ngược ể tìm hàm gốc y(t) của áp ứng trong miền thời gian: Y(s) y(t).
Cách nhận biết MĐ ở trạng thái quá ô
Thông thường loại bài toán này gắn liền với một khoá óng ngắt các nhánh mạch
hoặc là nguồn tác ộng làm việc ở chế ộ ột biến. Thời iểm trong mạch xảy ra ột
biến thường ược quy ước làm gốc (t=0). lOMoARcPSD| 37054152
CHƯƠNG 4: LÝ THUYẾT MẠNG BỐN CỰC (M4C)
4.1. Các hệ phương trình ặc tính của M4C: Z, Y, A
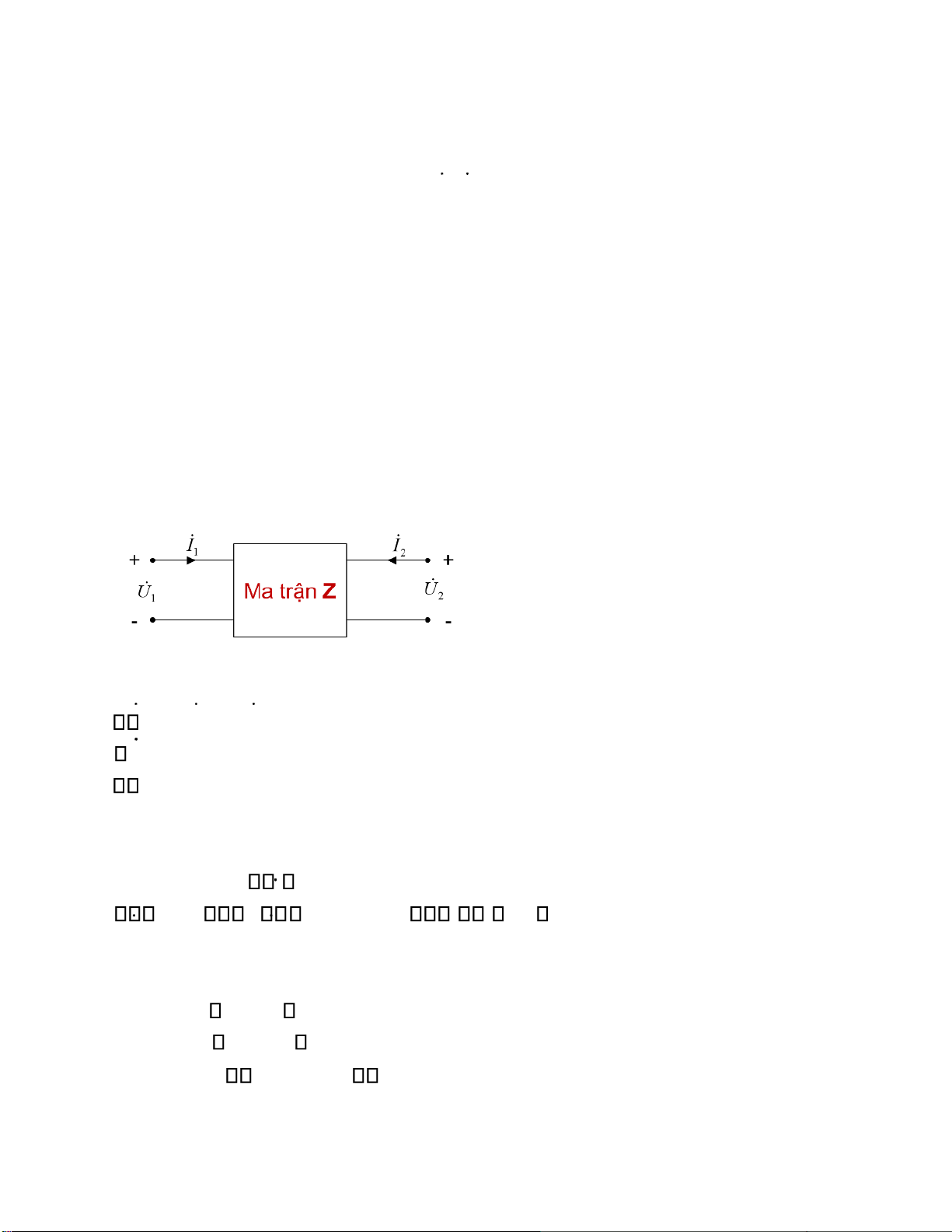
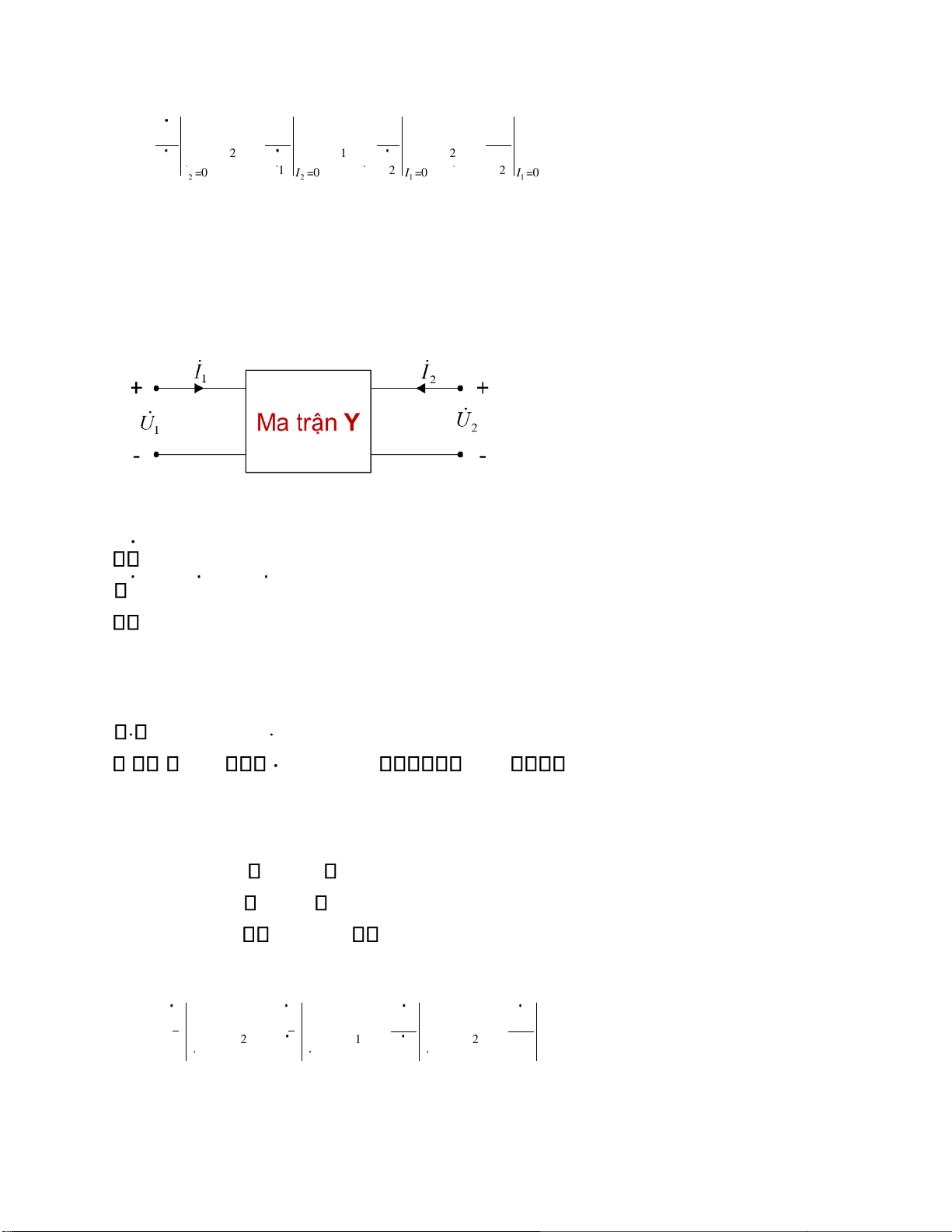
Mạng 4 cực có 4 thông số ặc trưng U I U1 1, , 2,I2 trên 2 cửa: Biểu diễn 2 thông số
bất kỳ theo 2 thông số còn lại -> 6 cách biểu diễn, tương ứng với 6 hệ phương trình ặc tính:
+ Hệ phương trình ặc tính trở kháng
+ Hệ phương trình ặc tính dẫn nạp
+ Hệ phương trình ặc tính truyền ạt
+ Hệ phương trình ặc tính truyền ạt ngược
+ Hệ phương trình ặc tính hỗn hợp
+ Hệ phương trình ặc tính hỗn hợp ngược
4.1.1. Hệ phương trình ặc tính trở kháng
Dưới dạng hệ phương trình U = + 1 z I11 1 z I12 2 U = + 2 z I21 1 z I22 2 Dưới dạng ma trận UU = 12 zz1121 zz1222
II12 U = Z.I
z z11 12 goïi laø ma traän trôû khaùng M4C Trong óZ = z z21 22
Các hệ số ược tính theo các công thức: lOMoARcPSD| 37054152 U U U U 1 2 1 2 ;z = ;z = ;z = 21 12 22 I I I I z = 1 = 1 I 0 = 2 I 0 = 2 I 0 I 0 = 11 2 2 1 1
Đối với trường hợp mạng bốn cực tương hỗ ta có: z = 12 z21
Đối với trường hợp mạng bốn cực ối xứng ta có: z = = 12 z21 ; z11
z22 4.1.2.
Hệ phương trình ặc tính dẫn nạp
Dưới dạng hệ phương trình: I = + 1 y U111 y U12 2 I = + 2 y U211 y U22 2 Dưới dạng ma trận: II = = 12 yy1121 yy1222 UU12 I Y.U
y y11 12 goïi laø ma traän daãn naïp cuûa M4C Trong ñoù: Y = y y21 22
Các hệ số ược tính theo các công thức: y11 I I I I 1 2 1 2 = = = = ;y ;y ;y 21 12 22 U U U 1 = 1 U 0 = 2 U 0 = 2 U 0 U 0 = 2 2 1 1 U lOMoARcPSD| 37054152
Đối với trường hợp mạng bốn cực tương hỗ ta có: y = 12 y21
Đối với trường hợp mạng bốn cực ối xứng ta có: y = = 12 y21 ; y11
y22 4.1.3.
Hệ phương trình ặc tính truyền ạt
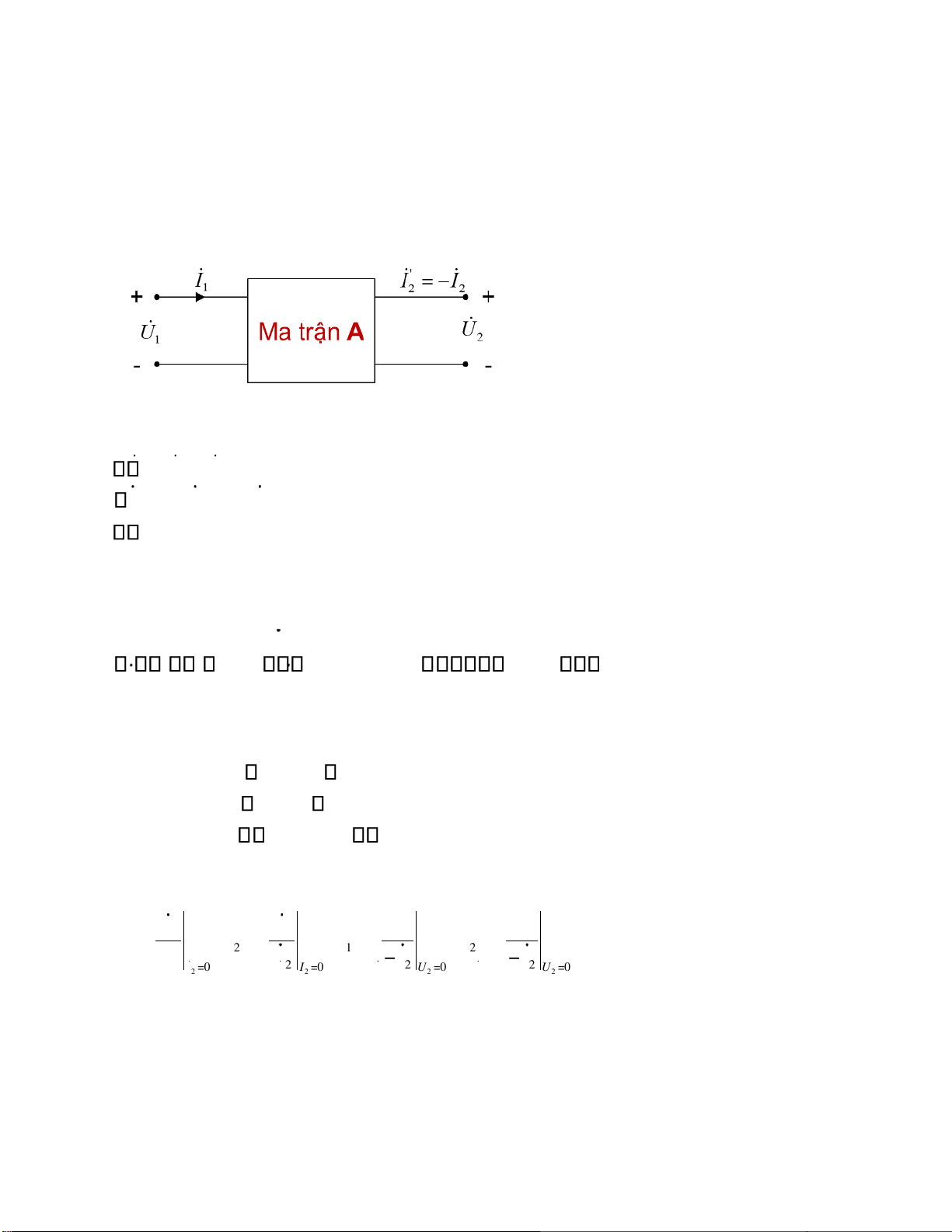
Dưới dạng hệ phương trình: U = − 1 a U112 a I12 2 I = − 1 a U212 a I22 2 Dưới dạng ma trận: U = 11 aa1121 aa1222 U−I22 I
a a11 12 goïi laø ma traän truyeàn ñaït cuûa M4C Trong ñoù: A= a a21 22
Các hệ số ược tính theo các công thức: U I U I 1 1 1 1 ;a = ;a = ;a = 21 12 22 U U I − I − a = 2 = 2 I 0 = 2 I 0 = 2 U 0 U 0 = 11 2 2 2 2
Đối với trường hợp mạng bốn cực tương hỗ ta có: det A= a a − = 11 22 a a12 21 1
Đối với trường hợp mạng bốn cực ối xứng ta có: det A=1 ; a = 11 a22 lOMoARcPSD| 37054152
4.2. Các sơ ồ tương ương của M4C
4.2.1. Khi nào cần tìm sơ ồ tương ương của M4C
Khi gặp M4C phức tạp ta có thể tách thành các M4C ơn giản
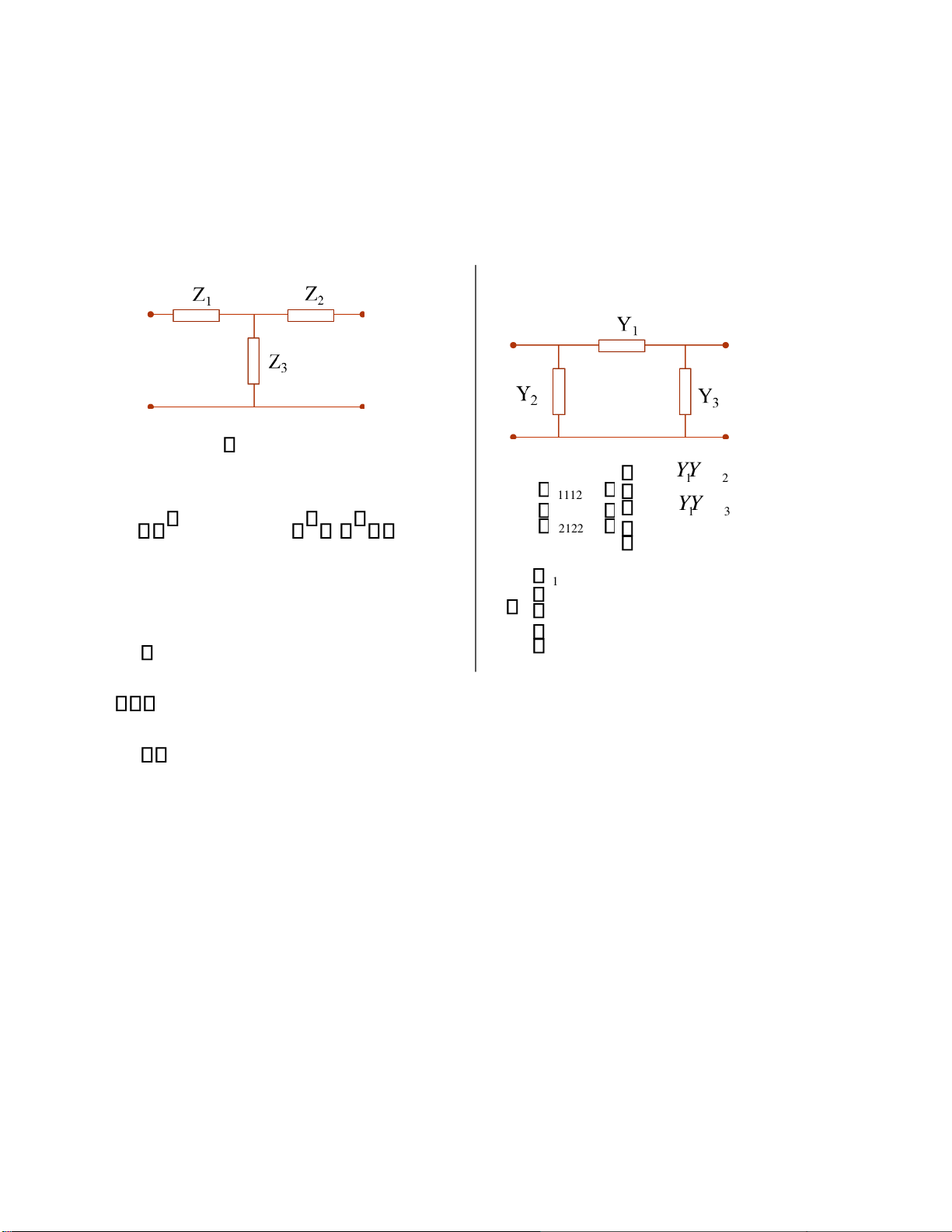
4.2.2. Sơ ồ tương ương hình T và hình π của M4C Sơ ồ
tương ương hình T:
Sơ ồ tương ương hình π : z = + 11 Z1 Z3 y YY =+ 11 1 2 yy 1112 Y= : y YY =+ z 22 1 3 yy Z= z zz z 2122 == 11 1221 22 : z1222 zZ212 y = y Y =− 12 21 +=Z Z =− =− 33 1 Y y y 1 21 12 Y = y + y 2 11 12 Y = y + y Z = − 3 22 12 1 z11 z12 Z = − 2 z22 z12 Z = = 3 z12 z21
4.3. Ghép nối các M4C
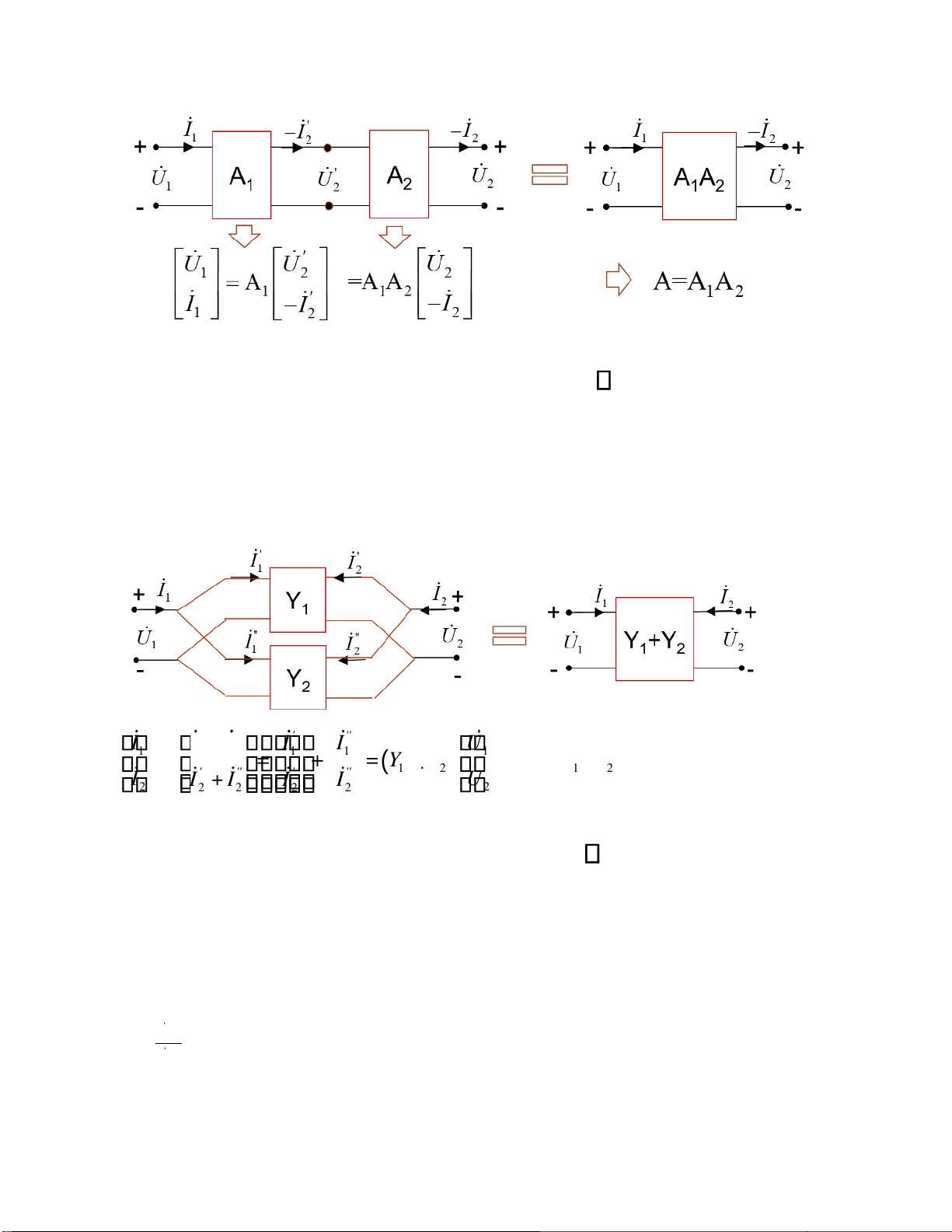
4.3.1. Ghép dây chuyền
Các bốn cực ược gọi là mắc theo kiểu dây chuyền với nhau nếu cửa ra của bốn cực
này ược nối với cửa vào của bốn cực kia theo thứ tự liên tiếp
Hệ phương trình thích hợp nhất ặc trưng cho ặc iểm của cách nối ghép này là hệ
phương trình truyền ạt. lOMoARcPSD| 37054152 n =
Tổng quát có n M4C ghép dây chuyền: A=A A1 2...An Ai i=1
4.3.2. Ghép song song – song song
Các bốn cực ược gọi là mắc theo kiểu S-S với nhau nếu ối với mỗi cửa có iện áp là
chung, còn dòng iện là tổng của các dòng iện thành phần. Hệ phương trình thích hợp
nhất ặc trưng cho ặc iểm của cách nối này là hệ phương trình dẫn nạp. ' '' ' '' I I + I I I U 1 1 1 1 1 = = + = ( 1 Y +Y → Y=Y+Y 1 2 ) 1 2 ' '' ' '' I I +I I I U 2 2 2 2 2 2
Tổng quát có n M4C ghép song song – song song: Y= n Yi i=1
4.4. Hàm truyền ạt iện áp (Ku): Biểu diễn Ku theo các phần tử ma trận Z, Y, A
4.4.1. Biểu diễn Ku theo các phần tử ma trận Z, Y, A U2 Ku = U1 lOMoARcPSD| 37054152
Biểu diễn Ku theo ma trận Z: UU == ++ =− → 12 z Iz I11 121 1 z Iz I1222 22 Z It 2 K = + u
z Z11 z Z21t t Z , U2 Z = z z − 11 22 z z12 21
Biểu diễn Ku theo ma trận Y: −y21 K = u y + 22 1/ Zt
Biểu diễn Ku theo ma trận A: K = + u 1 1 a a11 12 Zt
4.4.2. Cách vẽ ịnh tính ặc tuyến biên ộ |Ku| và ặc tuyến pha Ku
- Tìm giá trị biên ộ K ( ju )
- Tìm giá trị pha arg K( j ) - Xét = = 0
0tìm giá trị biên ộ và pha, 0
tìm giá trị biên ộ và pha.
Trường hợp bài toán yêu cầu, tiếp tục xét ω theo yêu cầu của bài toán 0
- Vẽ ịnh tính ặc tuyến biên ộ và ặc tuyến pha