Đề Cương Ôn Tập Xác Suất Thống Kê | Đại học Y Dược Thành phố Hồ Chí Minh

lOMoAR cPSD| 45470709
NỘI DUNG ÔN TẬP I. Xác suất:
+ Xác suất có điều kiện
+ Độ nhạy, Độ đặc hiệu, Giá trị tiên đoán II. Thống kê
1. Các khái niệm: Tổng thể và Mẫu; Tham số và Thống kê; Biến số ngẫu nhiên Biến số Định tính Định lượng Định danh Thứ bậc Rời rạc Liên tục ( D anh nghĩa) Chú ý:
+ Biến loại định tính hay định lượng được quyết định bởi dữ liệu của nó chứ không phải tên
biến. + Có thể chuyển đổi biến định tính sang biến định lượng (dùng trong mô hình hồi quy) bằng
kỹ thuật tạo biến giả (dummy variable) .
2 Thống kê mô tả
a. B iến định tính
Biến định tính 1 b iến định tính: 2 b iến định tính: + Bảng tóm tắt + Bảng tiếp liên +
Biểu đồ tròn (pie charts) + Biểu đồ cột so sánh hoặc cột (bar charts)
b. B iến định lượng lOMoAR cPSD| 45470709
Biến định lượng :
Tổ chức số liệu:
Các phân phối thường gặp: +
+ Sắp thứ tự/Biểu đồ cành lá Phân phối chuẩn + B
ảng phân phối tần số (tần suất) + P
hân phối chuẩn tắc (Gauss )
ghép lớp/Đa giác tần số (tần suất) + P hân phối Student + + B
ảng phân phối tích lũy/Đa
Phân phối Chi bình phương
giác tần số tích lũy
Các thống kê thường dùng :
+ Số đo giá trị trung tâm: Trung bình, trung vị, yếu vị
+ Số đo sự phân tán: Khoảng phân tán (Range), phương sai,
độ lệch chuẩn , h ệ số biên thiên (CV)…
+ Hình dạng phân phối : Độ nhọn, Độ lệch, T ứ phân vị, Biểu đồ hộp + Xác
định giá trị ngoại vi (outliers) bằng Zscore và Khoảng tứ phân vị IQR 3. Thống kê suy luận
a. Ước lượng: Ước lượng trung bình, ước lượng tỷ lệ, bài toán tìm cỡ mẫu b. Kiểm định:
+ So sánh trung bình: Z- Test, T-test, ANOVA
+ So sánh tỷ lệ, kiểm định sự phù hợp của quy luật xác suất, kiểm định sự độc lập của các
biến định tính: Z- Test, Chi bình phương χ2, chính xác Fisher c. Tương quan - Hồi quy tuyến tính
+ Hệ số tương quan Pearson
+ Mô hình hồi quy tuyến tính
Một số câu hỏi tham khảo
1. Biến định tính, Biến định lượng, Biến định danh, Biến thứ bậc? Cho ví dụ
Ví dụ: Phân loại các biến: nhóm máu, chiều cao, nồng độ ion Na+, hàm lượng acid, huyết áp.
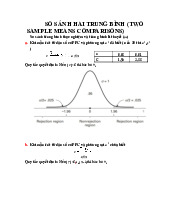
2. Phân biệt: Mẫu? Tổng thể? Tham số? Thống kê? Các ký hiệu thường dùng µ, σ, σ2, , SX, S2X Ví
dụ: Một trị số tóm tắt dữ liệu mẫu, ví dụ như phương sai mẫu, được gọi là gì? (Thống kê mẫu)
3. Số đo giá trị trung tâm? Số đo độ phân tán của số liệu? Tứ phân vị? Giá trị ngoại vi?
Ví dụ 1. Một trị số tóm tắt dữ liệu mẫu, ví dụ như phương sai mẫu, được gọi là A. Thống kê mẫu B. Tham số mẫu
C. Tham số tổng thể
D. Trung bình tổng thể
Ví dụ 2. Chọn số đo mô tả xu hướng trung tâm của số liệu lOMoAR cPSD| 45470709 A. Trung bình B. Phương sai
C. Khoảng phân tán D. Độ lệch chuẩn
Ví dụ 3. Trong các biến sau đây, biến nào là biến định lượng? A. Nhịp tim B. Tôn giáo C. Mức độ bệnh D. Nhóm máu
Ví dụ 4. Số đo nào sau đây cho biết mức độ biến động của số liệu xung quanh trung tâm của nó? A. Phương sai B. Trung bình C. Yếu vị D. Trung vị
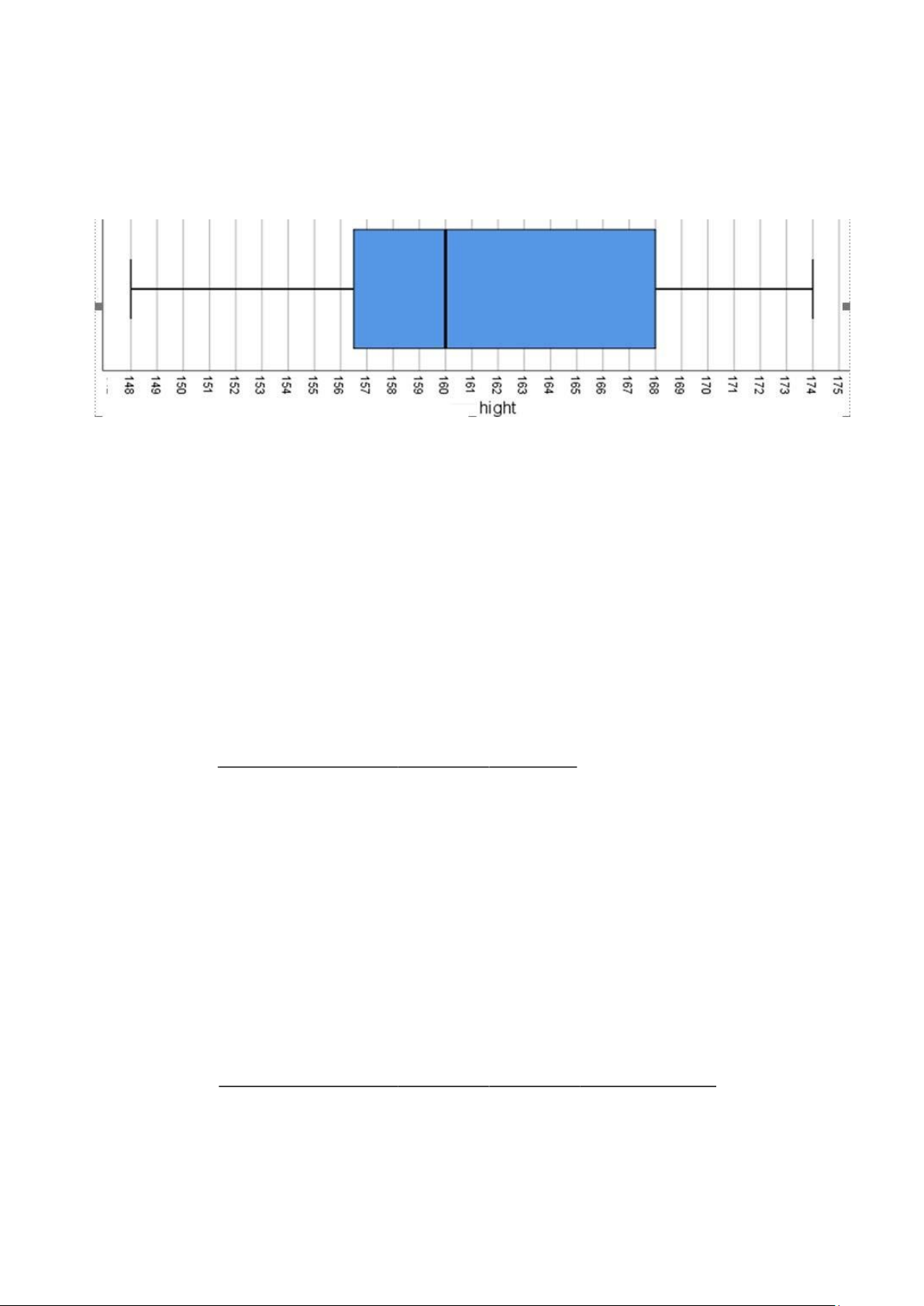
4. Biểu đồ hộp. Một khảo sát của sinh viên về chiều cao sinh SV có kết quả như biểu đồ hộp sau Hãy cho biết
+ ? % các bạn có chiều cao bé hơn 156.5 (cm)?
+ ? % các bạn có chiều cao lớn hơn 156.5 (cm)?
+ ? % các bạn có chiều cao lớn hơn 168 (cm)?
+ ? % các bạn có chiều cao bé hơn 168 (cm)?
+ Phân phối có bị lệch không?
5. Thăm dò tỷ lệ thuốc ngoại tại 11 điểm phân phối thuốc sỉ cho biết số liệu số loại thuốc bán ra: 13,
16, 17, 17, 17, 18, 18, 22, 22, 22, 28
a. Trung vị bảng số liệu?
b. Yếu vị bảng số liệu?
c. Khoảng phân tán (Range)?
d. Các điểm tứ phân vị?
e. Khoảng tứ phân vị?
6. Một khảo sát về tuổi, chiều cao và cân nặng của các học viên một câu lạc bộ tại nhà văn hóa thanh
niên có kết quả như sau
Tuổi, chiều cao và cân nặng ề Tuổi Chicao u nCânặng Sample size 54 54 54 Cho biết các thông tin sau về biến Mean (Xtb) 18.70 165.39 59.50 Chiều cao Std. Deviation (Sx) 0.54 8.22 13.39 + Cỡ mẫu, trung bình mẫu, Độ lệch Minimum 18.00 150.00 40.00 chuẩn mẫu? + Tứ Maximum 22.00 183.00 100.00 phân vị? 25th percentile 18.00 160.00 50.00 Khoảng 50th percentile 19.00 165.00 57.00 tứ phân 75th percentile 21.00 170.00 67.00 vị? Khoảng
phân tán? + Hệ số biến thiên của chiều cao?
+ Chiều Cao = 190cm có ngoại vi theo Zscore không?
+ Chiều Cao = 190cm có ngoại vi theo khoảng giới hạn tứ phân vị không?
+ Khoảng ước lượng trung bình về chiều cao ở độ tin cậy 95%. Muốn sai số ước lượng không
quá 1.5 cm thì cần quan sát ít nhất bao nhiêu người? lOMoAR cPSD| 45470709
7. Một nghiên cứu về sự liên quan giữa nhóm máu và tình trạng nhiễm Covid. Kết quả như sau: Nhóm máu Covid A B O AB Nhiễm 10 20 60 10 Không nhiễm 500 700 900 100
a. Hãy cho biết tỷ lệ nhiễm covid trong nhóm máu nào cao nhất?
b. Từ bảng quan sát trên, tỉ lệ người thuộc nhóm máu A và bị nhiễm là bao nhiêu?
c. Trong số những người bị nhiễm, tỷ lệ nhóm máu A, B, O, AB là ?
d. Trong số người có nhóm máu O, tỷ lệ nhiễm là?
f. Tỷ lệ bị nhiễm theo bảng khảo sát trên là?100/2300
8. Chiều cao (X) có phân phối chuẩn với trung bình là 1.65 m và độ lệch chuẩn là 0.1 m. Tính
a. Tỷ lệ người có chiều cao từ 1.6m đến 1.7m
b. Tỉ lệ người có chiều cao lớn hơn 1.5m
9. Một test trên 100 người trong đó có 20 bệnh nhân bị bệnh B. Sử dụng test này cho kết quả dương
tính trên 30 người, tuy nhiên trong số dương tính chỉ có 16 người ở nhóm bị bệnh B.
a. Tính độ nhạy, độ đặc hiệu của test
b. Kiểm tra 1 người, có kết quả dương tính. Tính xác xuất bị bệnh B.
10. Nghiên cứu tỉ lệ bệnh B ở một địa phương.
a. Muốn sai số cho ước lượng tỉ lệ không quá 0.02 thì cần quan sát ít nhất mấy người (γ=95%)?
b. Khám 150 người, thấy có 18 người bị bệnh B.
+ Tính khoảng tin cậy 95% cho tỉ lệ bệnh.
+ Muốn sai số ước lượng không quá 0.02 thì quan sát ít nhất mấy người (γ=95%)?
11. (Xem ví dụ 4.1/112) Quan sát 100 người bị tâm thần phân liệt 4 mùa trong năm. Kết quả: Mùa Xuân Hạ Thu Đông Số người 20 25 20 35
Hỏi: Bệnh tâm thần phân liệt có phụ thuộc theo mùa không?
12. (Xem ví dụ 4.2/116) Nhóm máu của 500 người trong một dân số D như sau: Nhóm máu A B AB O Số người 75 150 15 260
Cho biết tỷ lệ nhóm máu theo hằng số sinh học lần lượt là: A:B:AB:O = 0.18: 0.28: 0.05: 0.49.
Hỏi: Nhóm máu của dân số D có phù hợp quy luật trên không?
13. (Xem ví dụ 4.5/128) Một nghiên cứu nhằm đánh giá hiệu quả điều trị bệnh B trên 2 nhóm bệnh
nhân: nhóm 1 được điều trị bằng phương pháp mới, nhóm 2 được điều trị bằng phương pháp
thường quy (nhóm đối chứng). Sau 12 tuần điều trị, kết quả: Kết quả Nhóm Tổng Khỏi bệnh Không khỏi bệnh Nhóm 1 80 40 120 Nhóm 2 50 60 110 Tổng 130 100 230
Hỏi kết quả điều trị ở 2 nhóm có như nhau không?
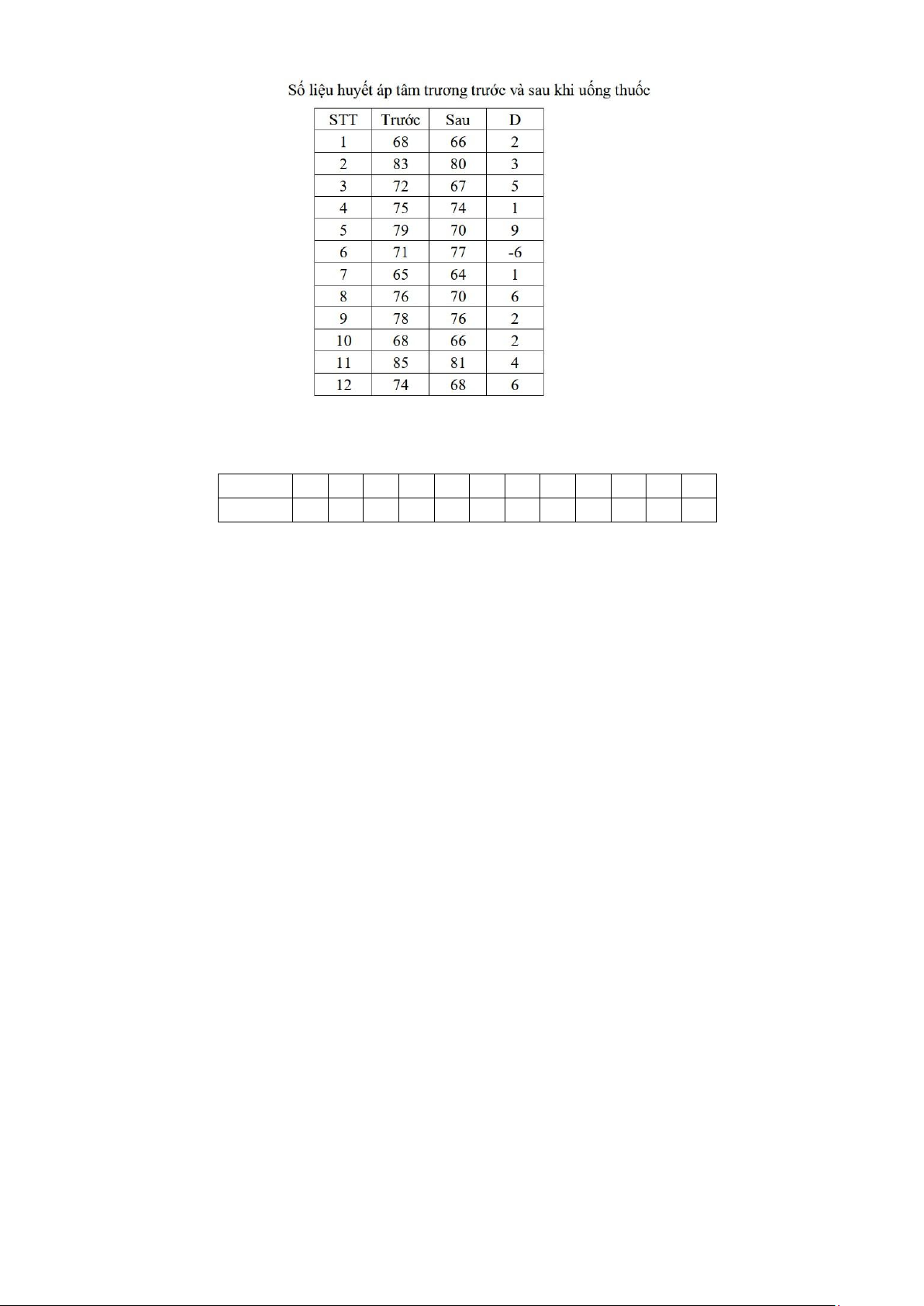
14. (Xem ví dụ 4.14/170) Một nghiên cứu đã được tiến hành trên 12 người để xác định xem liệu một
loại thuốc hạ huyết áp mới có thể làm giảm huyết áp tâm trương ở những người bình thường hay
không. Huyết áp được đo trước và sau khi uống thuốc. Kết quả (mmHg) được trình bày trong lOMoAR cPSD| 45470709
bảng sau. (Ghi chú: cột D = Trước - Sau là do tác giả thêm vào để thực hiện các tính toán tiếp theo)
Hỏi thuốc có tác dụng làm giảm huyết áp không?
15. Một mẫu chiều cao (X, Y) gồm 12 cặp cha và con trai trưởng thành
X(inch) 65 63 67 64 68 62 70 66 68 69 69 71
Y(inch) 68 66 69 67 72 64 75 65 71 73 71 75
+ Hệ số tương quan? (X, Y) có tương quan không? Phương trình hồi quy?
+ Chiều cao của con trai trưởng thành được giải thích bao nhiêu % theo chiều cao của người cha ở mẫu quan sát trên?
+ Nếu chiều cao của người cha là 70 inch thì chiều cao của người con có thể dự đoán là bao nhiêu?
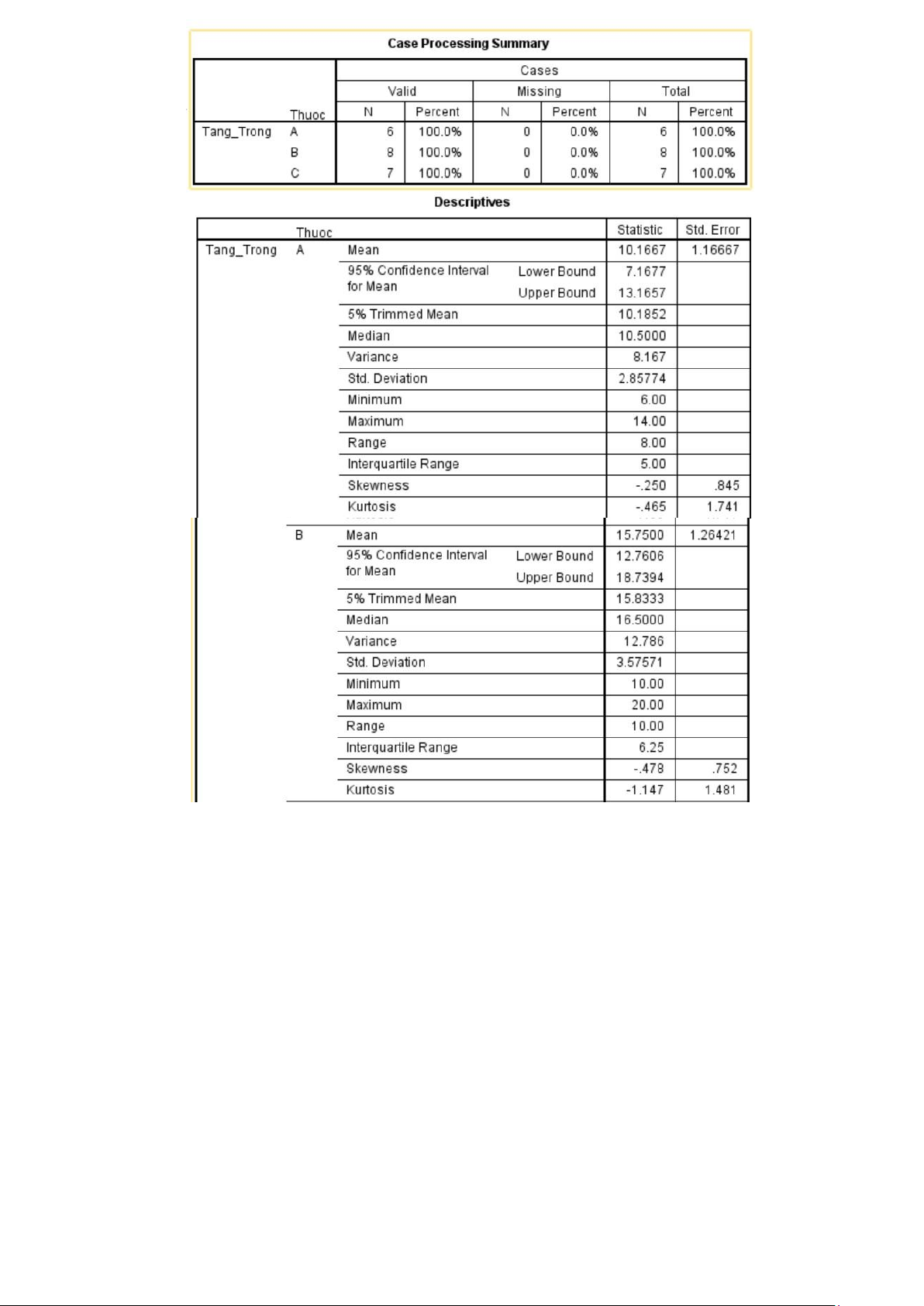
16. Thử nghiệm 3 loại thuốc bổ A, B, C trên 3 nhóm người, sau một thời gian đo độ tăng trọng (kg)
được kết quả như sau: A 10 12 14 11 8 6 B 20 18 19 12 14 10 15 18 C 4 6 7 2 3 1 2
Kết quả xử lý SPSS như sau lOMoAR cPSD| 45470709 lOMoAR cPSD| 45470709
Trả lời các câu hỏi sau
a. Mô tả dữ liệu của A, B, C (Phân phối chuẩn, lệch, nhọn, outliers, tứ phân vị, trung bình, độ lệch chuẩn,…)
b. Kết luận rằng độ tăng trọng trung bình của thuốc A là 12 kg có đáng tin không (α=0.05)?
c. Tác dụng của A và B có như nhau không?
d. Tác dụng của 3 loại thuốc A, B, C có như nhau không?