Tóm Tắt Lí Thuyết & Công Thức Môn Xác suất thống kê | Đại học Y Dược Thành phố Hồ Chí Minh

lOMoAR cPSD| 45470709
TÓMTẮTLÍTHUYẾT+CÔNGTHỨC
MÔNXÁCSUẤTTHỐNGKÊ I.
Mở ầu: thuật ngữ và khái niệm cơ bản 1. Thống kê
- Khái niệm: thống kê học là sự thu thập, quan sát, úc kết thông tin từ số liệu - Phân loại: + Thống kê mô tả + Thống kê suy luận Thống kê mô tả Thống kê suy luận Phương pháp
Thu thập, tóm tắt, trình bày, Dùng thông tin thu ược phân tích
từ mẫu rút ra kết luận về ặc iểm tổng thể Mẫu kết quả Biểu ồ, ồ thị, bảng Xác suất Mục ích
Rút ra thông tin về ặc
iểm Rút ra kết luận về
của một nhóm nhỏ ại diện
nhóm lớn dựa trên thông
cho nhóm lớn ang ược quan tin thu ược từ một nhóm tâm nhỏ Ví dụ
Thu thập cân nặng và chiều - Ước lượng: trung cao của 200 sinh viên bình mẫu bằng 75 kg, DCQ2023 trung bình tổng thể khoảng bao nhiêu? - Kiểm ịnh giả
thuyết: phát biểu “Cân nặng trung bình của dân số Việt Nam là 75 kg.” có cơ sở hay không?
2. Thuật ngữ cơ bản
- Tổng thể: nhóm lớn, bao gồm tất cả cá thể ược nghiên cứu quan tâm
- Tham số: trị số nói lên ặc trưng của tổng thể
- Mẫu: nhóm nhỏ, là một phần của tổng thể ược chọn ể phân tích
- Thống kê: trị số nói lên ặc trưng của mẫu lOMoAR cPSD| 45470709
- Biến số: ặc iểm của cá thể hay hạng ược phân tích, ví dụ: chiều cao, cân nặng…
- Số liệu: giá trị khác nhau của biến số ược thu thập, quan sát; thang o
phân loại các giá trị số liệu
3. Phân loại biến số
a. Phân loại theo thang o BIẾN SỐ ĐỊNH TÍNH ĐỊNH LƯỢNG Định danh Thứ bậc Khoảng Tỷ số (Ratio) (Nominal) (Ordinal) (Interval) Để phân biệt Để phân biệt và Khoảng chia có
Có số 0 tuyệt ối. tính chất. VD: -
sắp xếp thứ tự.
ý nghĩa, không có VD: - Cân nặng: Biến giới tính: VD: số 0 tuyệt ối → có thể nói 0 kg; nam, nữ - Biến - Biến kết không thể nói có thể nói 75 kg nhóm quả rèn luyện: gấp ôi, gấp ba gấp ba lần 25kg. máu: O, A, B,
Kém, Trung bình, hay chia ôi, chia AB Khá, Giỏi ba. - Điểm môn VD: học: - Nhiệt ộ: 0 A, B, C, D, F ộ C không phải là không có nhiệt ộ, mà là nhiệt ộ mà nước chuyển từ trạng thái rắn sang lỏng. - Năm: Không thể nói năm 2020 gấp ôi năm 1010 “=” hoặc “≠” “>” hoặc “<” “+” hoặc “-” “x” hoặc “÷” Biến rời rạc Biến rời rạc
Biến rời rạc hoặc Biến rời rạc hoặc liên tục liên tục
Chú ý: Phân loại biến rời rạc và liên tục Biến liên tục Biến rời rạc lOMoAR cPSD| 45470709
Giữa hai giá trị ã biết có thể có bất kỳ Giữa hai giá trị có thể không có bất giá trị nào. kỳ giá trị nào khác.
b. Phân loại theo vai trò BIẾN PHỤ THUỘC
BIẾN ĐỘC LẬP (biến dự oán) (biến kết quả) Định tính Định lượng Định tính So sánh tỷ lệ Chẩn oán Quyết ịnh Định lượng So sánh trung bình Dự báo
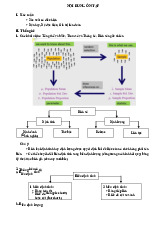
II. Quy trình khám phá số liệu
Quy trình khám phá số liệu: Đ4T - Định nghĩa - Thu thập - Tổ chức - Trực quan hóa - Phân Tích
1. Định nghĩa số liệu
a. Phân loại nguồn số liệu
- Cách phân loại 1: gồm 2 loại nguồn số liệu: Nguồn sơ cấp Nguồn thứ cấp
Người phân Là người thu thập số liệu Là người dùng số liệu ã có tích số liệu Ví dụ -
Số liệu iều tra thống - Phân tích số liệu iều tra/
kê - Số liệu thu thập trong từ Internet/ từ bài báo khoa thí nghiệm học… - Số liệu quan sát thực ịa
- Cách phân loại 2: gồm 4 loại nguồn số liệu Loại nguồn số liệu Ví dụ lOMoAR cPSD| 45470709
Do cá nhân, tổ chức
- Số liệu nghiên cứu ở phòng xét nghiệm
- Số liệu thống kê trên báo chuyên ngành
Điều tra (tổng thể)
- Điều tra xu hướng phát triển, sự hài lòng của nhân viên
- Điều tra mức ộ hài lòng của khách hàng
với sản phẩm, dịch vụ
Nghiên cứu thử nghiệm - Tính năng của phần mềm hỗ trợ iều trị
- Chất liệu chế tạo áo bảo hộ sinh học
Nghiên cứu quan sát
- Thời gian bệnh nhân ợi khám - Thông
lượng di chuyển trong hành lang hội nghị khoa học
b. Phân loại kiểu số liệu 2 kiểu số liệu: - Chi tiết cá nhân - Tổng hợp rút gọn
2. Thu thập số liệu
a. Một số tình huống cần thu thập số liệu
- Khi cần ánh giá tác dụng của một loại thuốc mới so với loại thuốc ang lưu hành.
- Khi cần tổng kết tình hình hoạt ộng, giao dịch của một ơn vị tư vấn, khám chữa bệnh. b. Lý do lấy mẫu
- Hạn chế về nguồn lực: không thể bao quát hết tổng thể lớn, nguồn lực nghiên cứu hạn hẹp…
- Suy luận về tổng thể: kết quả suy rộng từ mẫu có thể áp dụng trên tổng thể dân số c. Cách lấy mẫu lOMoAR cPSD| 45470709
Lưu ý: λ viết tắt cho chữ “người”
3. Tổ chức số liệu
a. Tổ chức số liệu ịnh tính
b. Tổ chức số liệu ịnh lượng lOMoAR cPSD| 45470709
4. Trực quan hóa số liệu
5. Phân tích số liệu
Không nằm trong nội dung kiểm tra giữa kỳ và cuối kỳ.
III. Công cụ mô tả
1. Thống kê vị trí trung tâm
- Số o vị trí trung tâm là xu hướng tụ tập của số liệu quanh một vị trí. lOMoAR cPSD| 45470709 Trung bình cộng Trung vị Yếu vị Đặc
- Dễ tính toán và diễn giải -
Số liệu ã ược sắp xếp -
Trị số có tần số iểm
- Dễ bị ảnh hưởng bởi giá thứ tự cao nhất trong dãy trị ngoại vi -
Là số “ ứng giữa” dãy số liệu số - Không bị ảnh -
Điểm chia 50% trên và hưởng của trị số 50% dưới ngoại vi -
Không bị ảnh hưởng bởi - Có thể không giá trị ngoại vi tồn tại, hoặc không duy nhất Công
Trước hết, sắp xếp các giá thức 𝑛
trị theo thứ tự thấp ến cao -
Nếu n lẻ, trung vị là trị số ∑ 𝑋 𝑋 + 𝑋 +𝑋 nằm 𝑖 𝑖=1 1 2 𝑛
giữa 𝑀𝑒𝑑𝑖𝑎𝑛 = 𝑋 𝑛+12 𝑋 = 𝑛 = 𝑛 dãy số liệu
- Nếu n chẵn, trung vị là
trung bình hai trị số nằm giữa 𝑀𝑒𝑑𝑖𝑎𝑛 = (𝑋 𝑛 + 𝑋 𝑛 ) +1 2 2 )
Sử dụng Thường dùng nhất, trừ
Thường dùng vì không chịu khi có số ngoại vi ảnh hưởng ngoại vi
Một số trường hợp cần báo cáo cả trung bình và trung vị
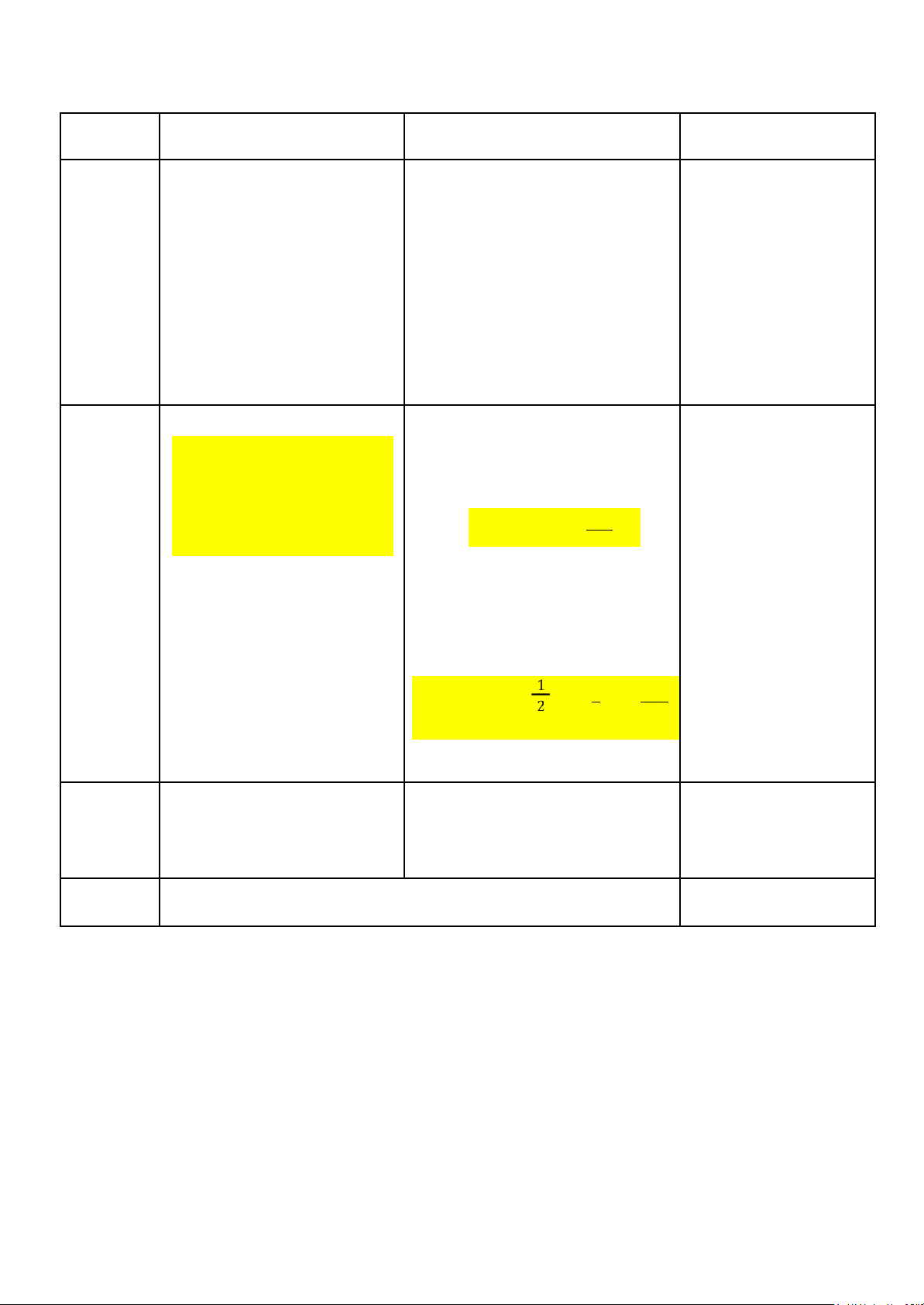
2. Thống kê phân tán quanh trung tâm
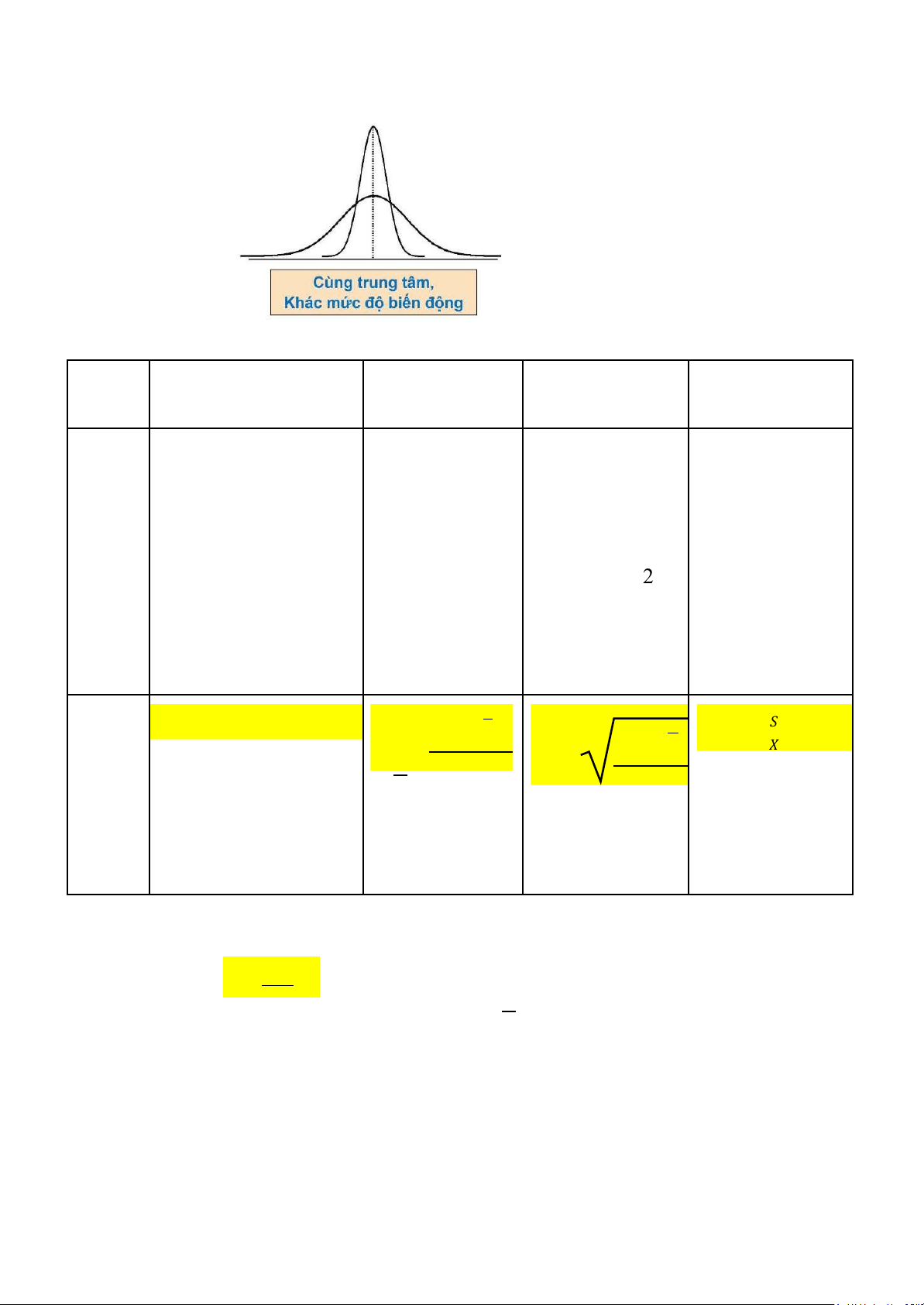
- Thể hiện mức ộ biến ộng của số liệu quanh trung tâm. lOMoAR cPSD| 45470709 Biên ộ Phươngsai Độlệchchuẩn Hệsốbiến thiên Đặc - Đơngiảnnhất - Xấpxỉtrung - Đượcdùng - Số obiến iểm - Không phảnánh bìnhcủabình rộngrãinhất ộngtươngối phânphốicủasốliệu phươngộlệch - Thểhiệnmức - L uônlàtỷlệ - Chịuảnhhưởngcủa cáctrịsốsovới ộbiếnộng ( % ) giátrịngoạivi trungbình quanhtrungbình - T hểhiệnbiến + - Làcănbậc 2 ộngtươngối củaphươngsai sovớitrung mẫu bình - Cù ngơnvị vớisốliệugốc
Công 𝑅𝑎𝑛𝑔𝑒 = 𝑋 𝑛 𝑛 thức 𝑚𝑎𝑥 + 𝑋 𝑚𝑖 ∑(𝑋 𝐶𝑉= 𝑆 𝑖 − 𝑋 )2 𝑆 2 = 𝑖=1 ∑(𝑋 − ) 2 𝑋 () .100 % 𝑖 𝑋 𝑛−1 𝑆= 𝑖=1 𝑛−1
𝑋 : 𝑡𝑟𝑢𝑛𝑔 𝑏ì𝑛ℎ n:cỡmẫu 𝑋 : t rịsốthứi 𝑖 củabiếnX
*Xác ịnh trị số ngoại vi (tính Z)
- Z là số lần ộ lệch chuẩn mà một trị số lệch khỏi trung bình. 𝑍 = 𝑋−𝑋𝑆
Với X: trị số thu thập ược
𝑋: 𝑡𝑟𝑢𝑛𝑔 𝑏ì𝑛ℎ 𝑐ỡ 𝑚ẫ𝑢
S: ộ lệch chuẩn mẫu
- Nếu: Z < -3 hoặc Z > 3: ó là giá trị ngoại vi
-3 ≤ Z ≤ 3: giá trị ó không phải ngoại vi lOMoAR cPSD| 45470709
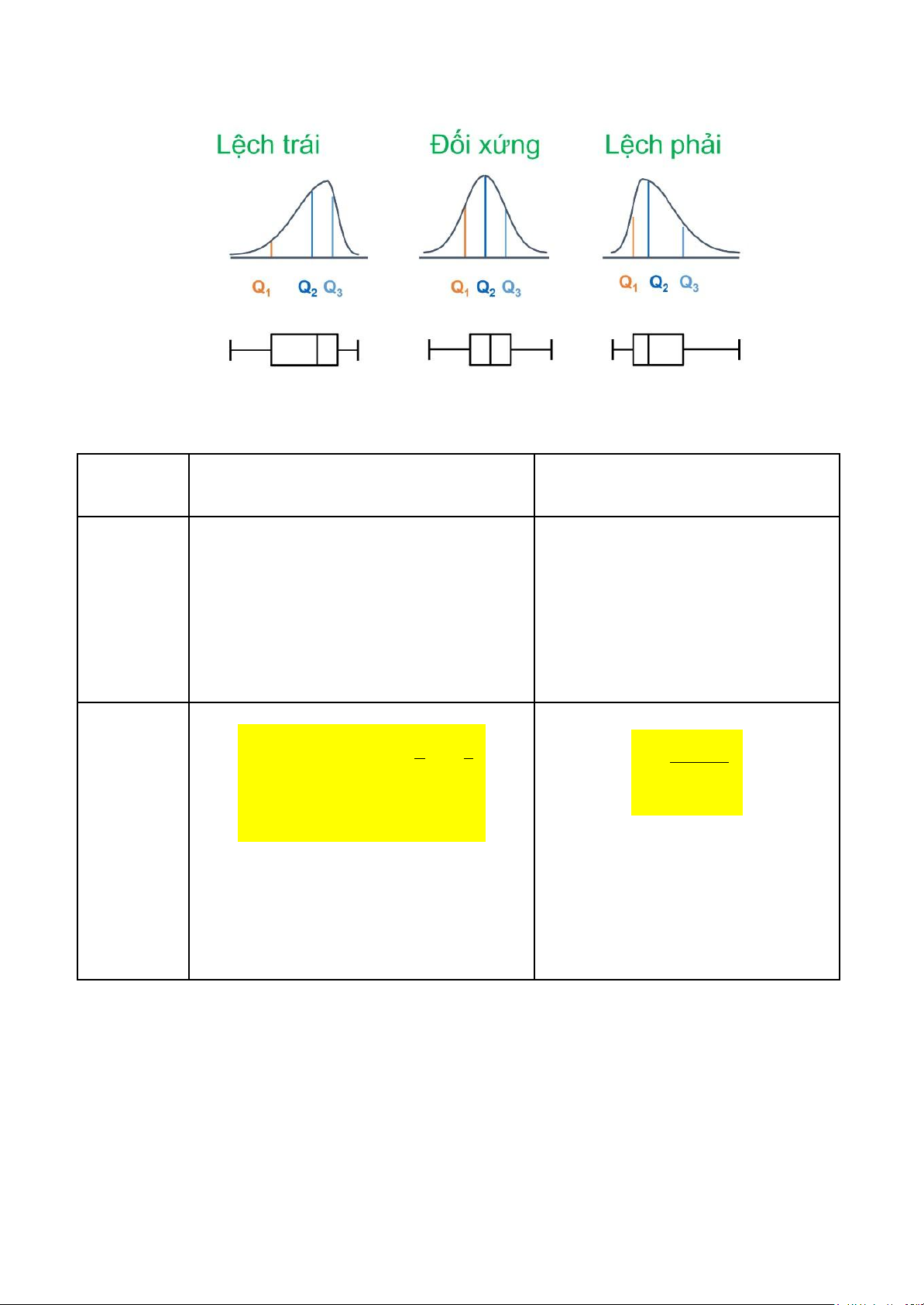
3. Thống kê hình dạng phân phối
- Thể hiện mức ộ khác biệt hình dạng phân phối so với phân phối chuẩn.
a. Độ lệch: o mức ộ không ối xứng của một phân phối
b. Độ nhọn: o mức ộ tập trung số liệu tại trung tâm so với tại uôi phân phối
c. Bộ 5 số phân vị: cho thấy trung tâm, phân tán, hình dạng phân phối số liệu - Xmin
- Tứ phân vị thứ nhất (Q1)
- Tứ phân vị thứ hai, trung vị (Q2)
- Tứ phân vị thứ ba (Q3) - Xmax Lệch trái Đối xứng Lệch phải Median – Xmin Median – Xmin Median – Xmin > ≈ < Xmax – Median Xmax – Median Xmax– Median Q1 – Xmin Q – X Q1 – Xmin > < X Xmax – Q3 max – Q3 Xmax – Q3 lOMoAR cPSD| 45470709 Median – Q1 Median – Q Median – Q 1 > 1 ≈ < Q Q 3 – Median 3 – Median Q3 – Median
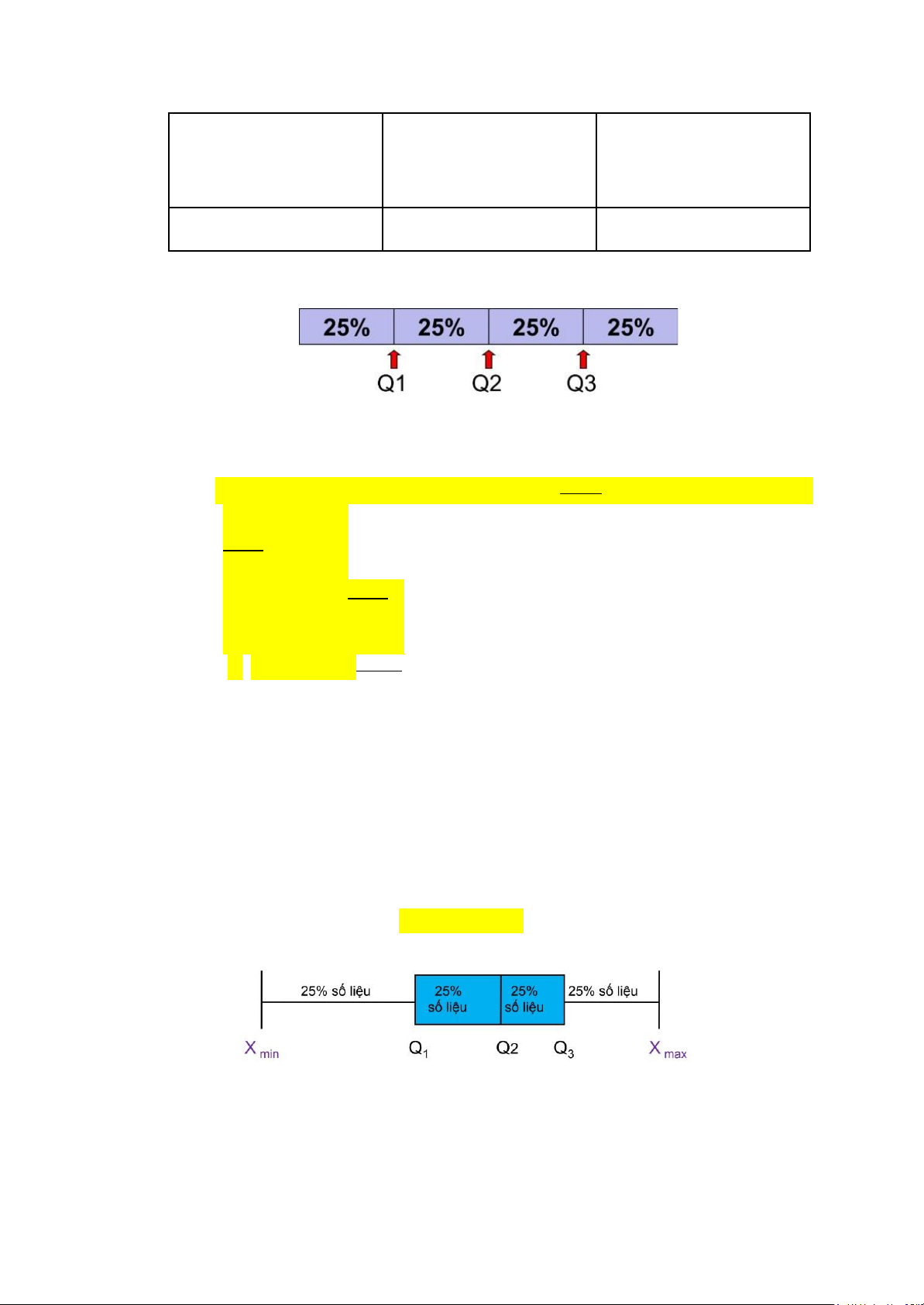
d. Số o tứ phân vị: là các iểm chia ều dãy số liệu sắp thứ tự thành
4 oạn có số lượng các trị số bằng nhau
Cách xác ịnh: Sắp xếp số liệu theo thứ tự → Tứ phân vị thứ i:
𝑄𝑖 = 𝑡𝑟ị 𝑠ố 𝑡ℎứ 𝑖(𝑛+1)4
𝑄 : 𝑡𝑟ị 𝑠ố 𝑡ℎứ 𝑛+14 1
𝑄 : 𝑡𝑟ị 𝑠ố 𝑡ℎứ 𝑛+12
(𝑡𝑟𝑢𝑛𝑔 𝑣ị) 2
𝑄3: 𝑡𝑟ị 𝑠ố 𝑡ℎứ 3(𝑛+1)4 Nếu kết quả là:
- Số nguyên: giữ nguyên kết quả
- Số lẻ 0.5: lấy TB giá trị ở 2 vị trí gần nhất xung quanh
- Số lẻ không phải 0.5: làm tròn kết quả ến số nguyên gần nhất
e. Khoảng tứ phân vị: là ộ rộng khoảng chứa 50% số liệu ở giữa,
không chịu ảnh hưởng của trị số ngoại vi → Q1, Q2, Q3, IQR
ược gọi là các thống kê bền vững IQR = Q3 – Q1
f. Biểu ồ hộp: cho thấy phân phối của số liệu
Các dạng biểu ồ hộp: lOMoAR cPSD| 45470709
4. Thống kê quan hệ tuyến tính
- Thể hiện sự liên quan của hai dãy số liệu với nhau Hiệp phương sai Hệ số tương quan Đặc iểm -
Số o quan hệ giữa hai biến
- Số o mức ộ tương quan -
Không phản ánh quan hệ nhân tuyến tính giữa hai biến
quả - Chỉ nói lên chiều hướng của
quan hệ, không thể o mức ộ mạnh yếu của mối quan hệ Công thức 𝑛
𝑟 = 𝑐𝑜𝑣(𝑋,𝑌)𝑆
∑ (𝑋 −𝑋)(𝑌 −𝑌) 𝑖 𝑖 𝑆 𝑖=1 𝑋 𝑌 𝑐𝑜𝑣 (𝑋, 𝑌) = 𝑛−1 - r càng gần 1: tương quan - cov(X,Y) > 0 X và Y có thuận càng mạnh khuynh hướng ồng biến -
r càng gần -1: tương quan - cov(X,Y) < 0 X và Y có nghịch càng mạnh
khuynh hướng nghịch biến - r càng gần 0: tương quan -
cov(X,Y) = 0 X và Y ộc lập tuyến tính càng mạnh
5. Phân phối chuẩn
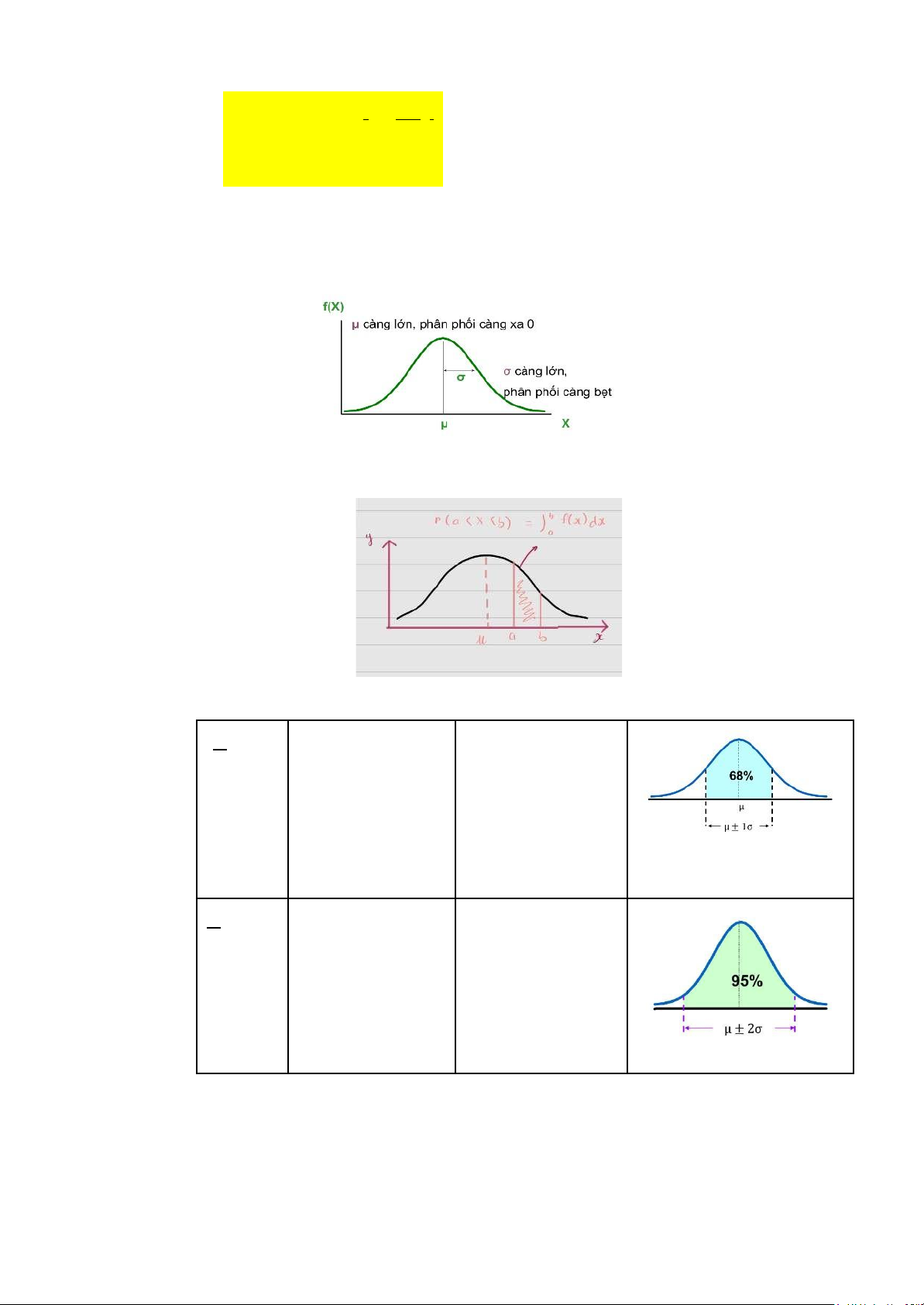
- Mỗi phân phối chuẩn có μ và σ cụ thể
+ Số o trung tâm = trung bình= μ
+ Số o phân tán = ộ lệch chuẩn = σ
- Phương trình ường cong lOMoAR cPSD| 45470709 𝑓(𝑥) = 1 𝑒− 12 ( (𝑋−µσ ) Với e = xấp xỉ 2,71828 )2 π = xấp xỉ 3,14159 μ = σ 2𝑥
trung bình tổng thể σ = ộ lệch chuẩn tổng thể X = trị số quan sát - Hình dạng ồ thị
- Diện tích dưới ường cong
- Quy tắc kinh nghiệm 1-2-3
Chiếm 68,8% số Do xấp xỉ 68,8% 𝑋 ± 𝑆 liệu giá trị của biến nằm trong khoảng μ ± 1σ Chiếm 95% số Do 95% giá trị 𝑋 ± 2𝑆 liệu của biến nằm trong khoảng μ ± 2σ lOMoAR cPSD| 45470709
Chiếm 97,7% số Do 97,7% giá 𝑋 ± 3𝑆 liệu trị của biến nằm trong khoảng μ ± 3σ - Quy tắc Chebyshev
Không liên quan ến số liệu có phân phối như thế nào ít nhất ( 1 − 1 ) 2 100% 𝑘
các giá trị nằm trong khoảng TB ± kĐLC, với k > 1. Ví dụ: Ít nhất Trong khoảng ( k=2 (μ ± 2σ) 1 − ) 212 100% = 75% ( k=3 (μ ± 3σ) 1 − ) 312 100% = 89% lOMoAR cPSD| 45470709 IV. Công cụ suy luận
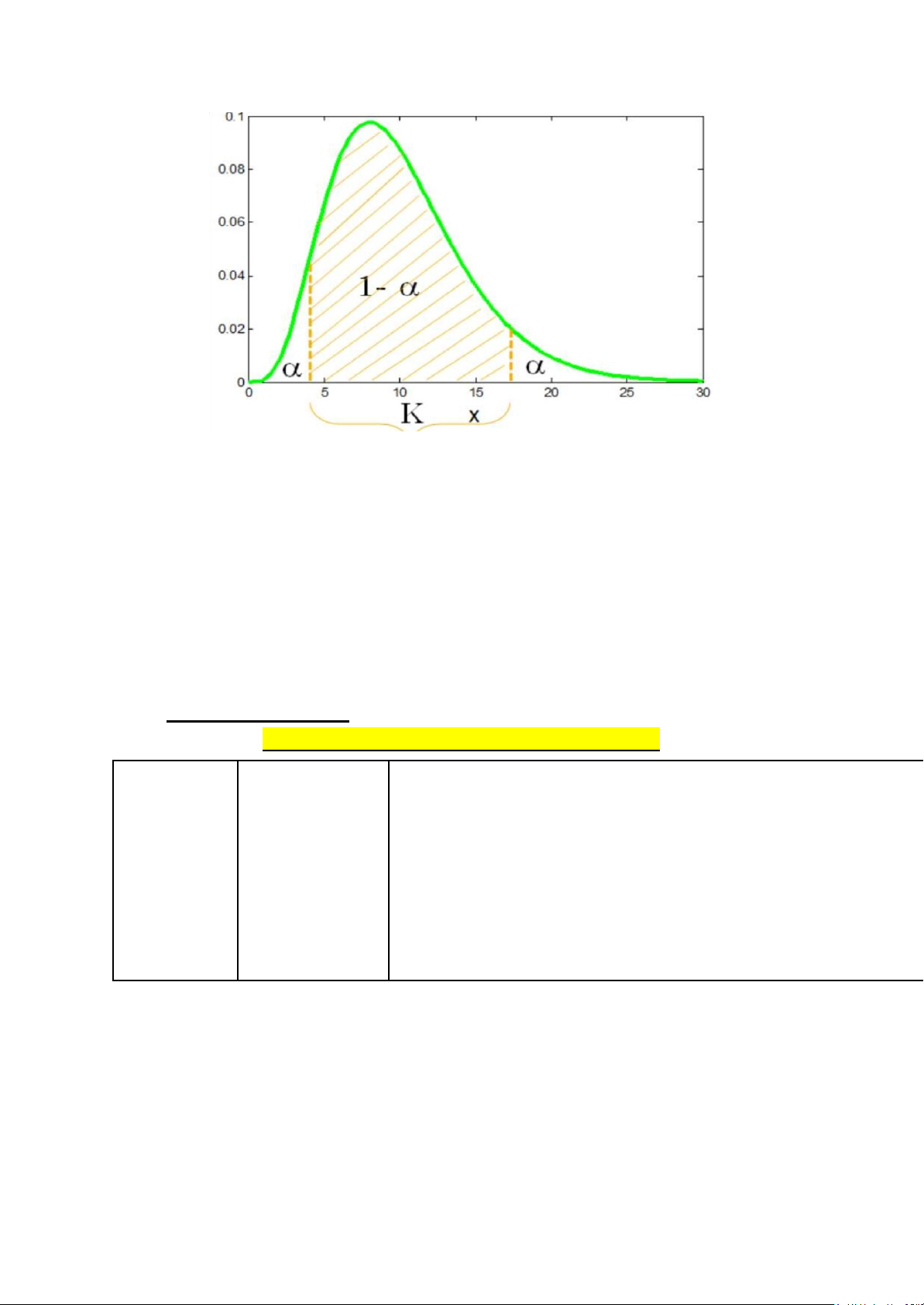
1. Nguyên lý ước lượng (Ước lượng khoảng tin cậy -KTC)
- Khi ta ước lượng X thuộc khoảng giá trị K nào ó, thì xác suất ể X
thuộc khoảng giá trị ấy ược gọi là ộ tin cậy của ước lượng. - Ký hiệu: γ= 1-𝛼 lOMoAR cPSD| 45470709
- Có các dạng ước lượng KTC thường gặp, ó là ước lượng: trung bình,
tỉ lệ, cỡ mẫu (cho trung bình hoặc tỉ lệ) - Ý nghĩa:
+ Ước lượng trung bình cho biết trung bình của mẫu có bằng/lớn/bé
hơn trung bình tổng thể hay không.
+ Ước lượng tỉ lệ cho biết tỉ lệ của mẫu có bằng/lớn/bé hơn tỉ lệ tổng thể hay không.
+ Ước lượng cỡ mẫu cho biết cần lấy bao nhiêu mẫu là vừa ủ ể sai số
cho trung bình hoặc tỉ lệ không vượt quá phần trăm ề cho.
2. Ba dạng ước lượng:
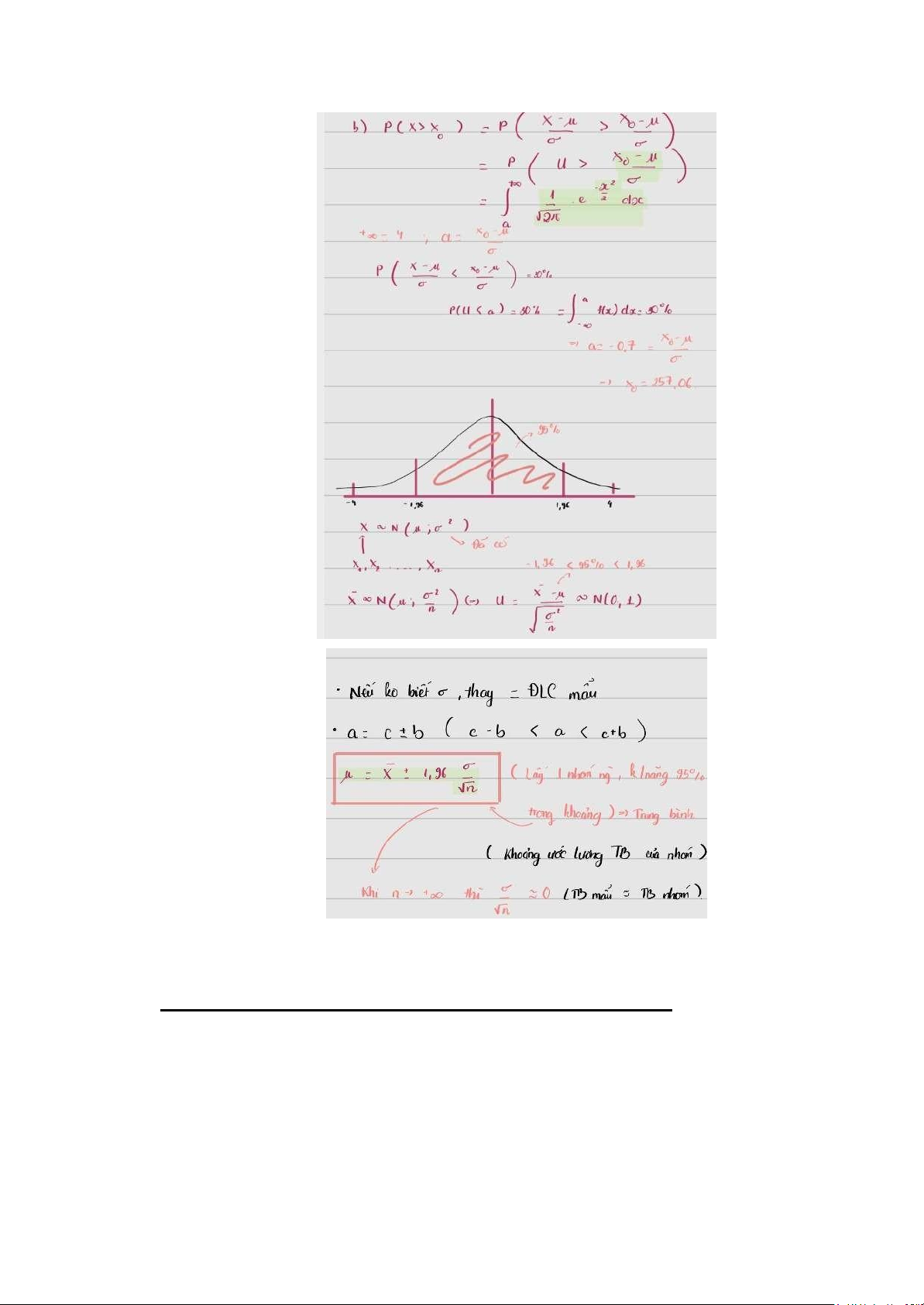
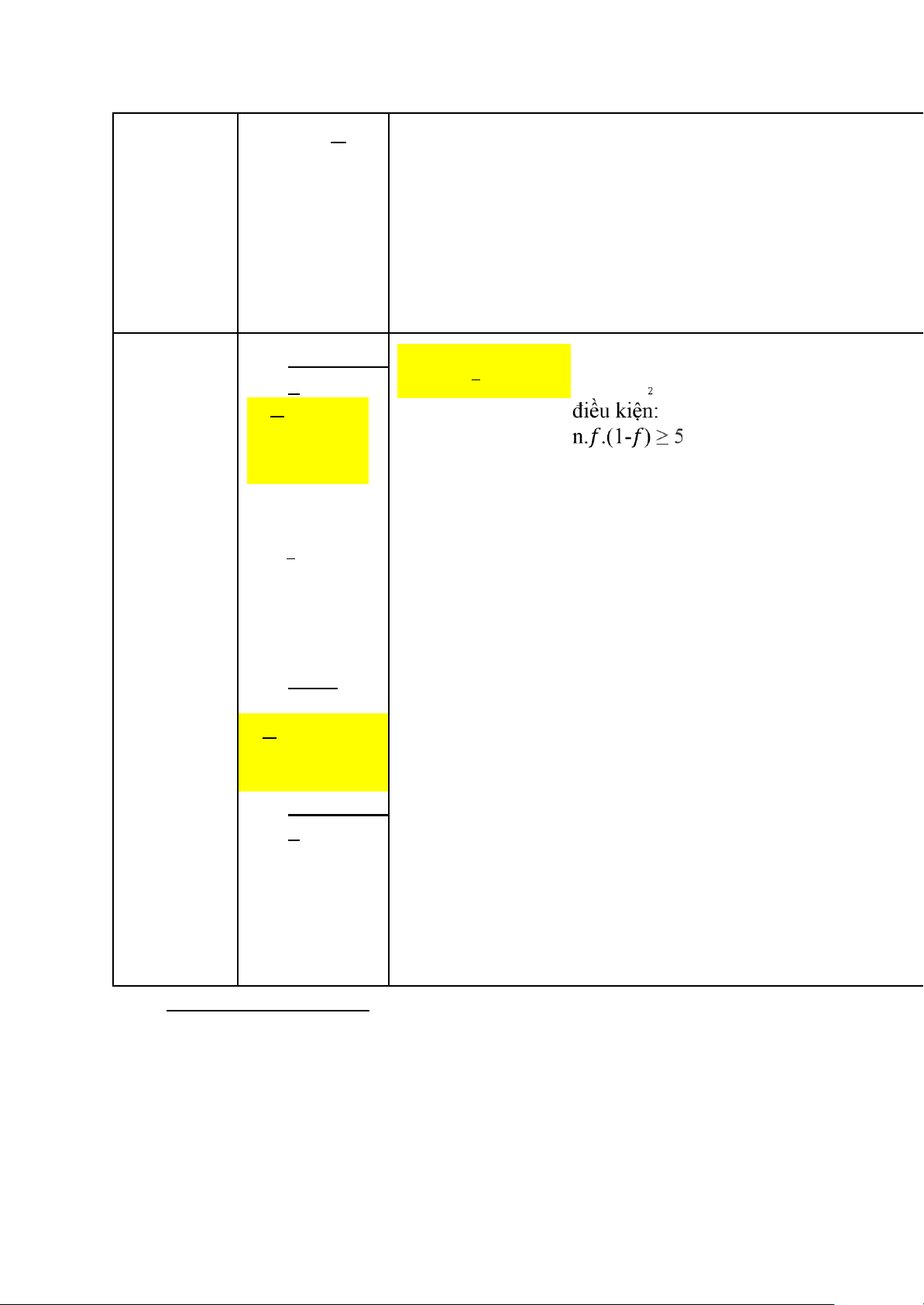
BẢNG SO SÁNH 3 DẠNG ƯỚC LƯỢNG: ƯỚC TRUNG BÌNH TỈ LỆ p LƯỢNG μ lOMoAR cPSD| 45470709 ƯỚC 𝑓 LƯỢNG 𝑋 ĐIỂM ƯỚC ● TH1: biết p= . LƯỢNG σ 𝑓± 𝑍 𝛼 KHOẢNG
γ= 1-𝛼 μ=𝑋± 𝑍 . σ 𝛼 𝑛 2 BÌNH: Độ tin cậy: 1- 𝛼=95% ● CHO TỈ LỆ: →𝑍 =1,96 𝛼 2 1-𝛼=99% → 𝑍 =2,58 𝛼 2 ● TH2:
(nếu không có mẫu thử) μ=𝑋±𝑡 (n-1). 𝑆 𝛼 𝑛 không biết σ 𝑡 (n-1): giá trị 𝛼 ngưỡng → Tra bảng pp student
3. Nguyên lý kiểm ịnh:
3.1. Khái niệm kiểm ịnh:
Trong thống kê, ta có hai dạng giả thuyết, là giả thuyết không, (null hypothesis),
ký hiệu là H0; loại giả thuyết ối của H0 là giả thuyết khả dụng, kí hiệu là H𝛼.
- H0: cái không mong muốn, bắt buộc có dấu =
- H𝛼: cái mong muốn, có dấu <, >, hoặc ≠ lOMoAR cPSD| 45470709
● Ví dụ 1: H0 =60, H𝛼: μ≠60 → kiểm ịnh 2 uôi (<60 và >60)
● Ví dụ 2: H0 μ≤60 (thỏa iều kiện có dấu =), H𝛼: μ>60 → kiểm ịnh 1 uôi (>60)
3.2. Các bước kiểm ịnh:
Ví dụ: Tỉ lệ nữ có phải là 48% hay không?
→ Thống kê dùng là tỉ lệ.
- Bước 1: Đặt giả thuyết H0: p=48% và H𝛼: p≠48% → Bài toán 2 uôi.
- Bước 2: Chọn 𝛼, n: 𝛼=5%, n=...
- Bước 3: Xác ịnh phép kiểm phù hợp và phương pháp kiểm ịnh: Z-test hay Chi-square test?
- Bước 4: Xác ịnh giá trị ngưỡng và vùng bác bỏ:
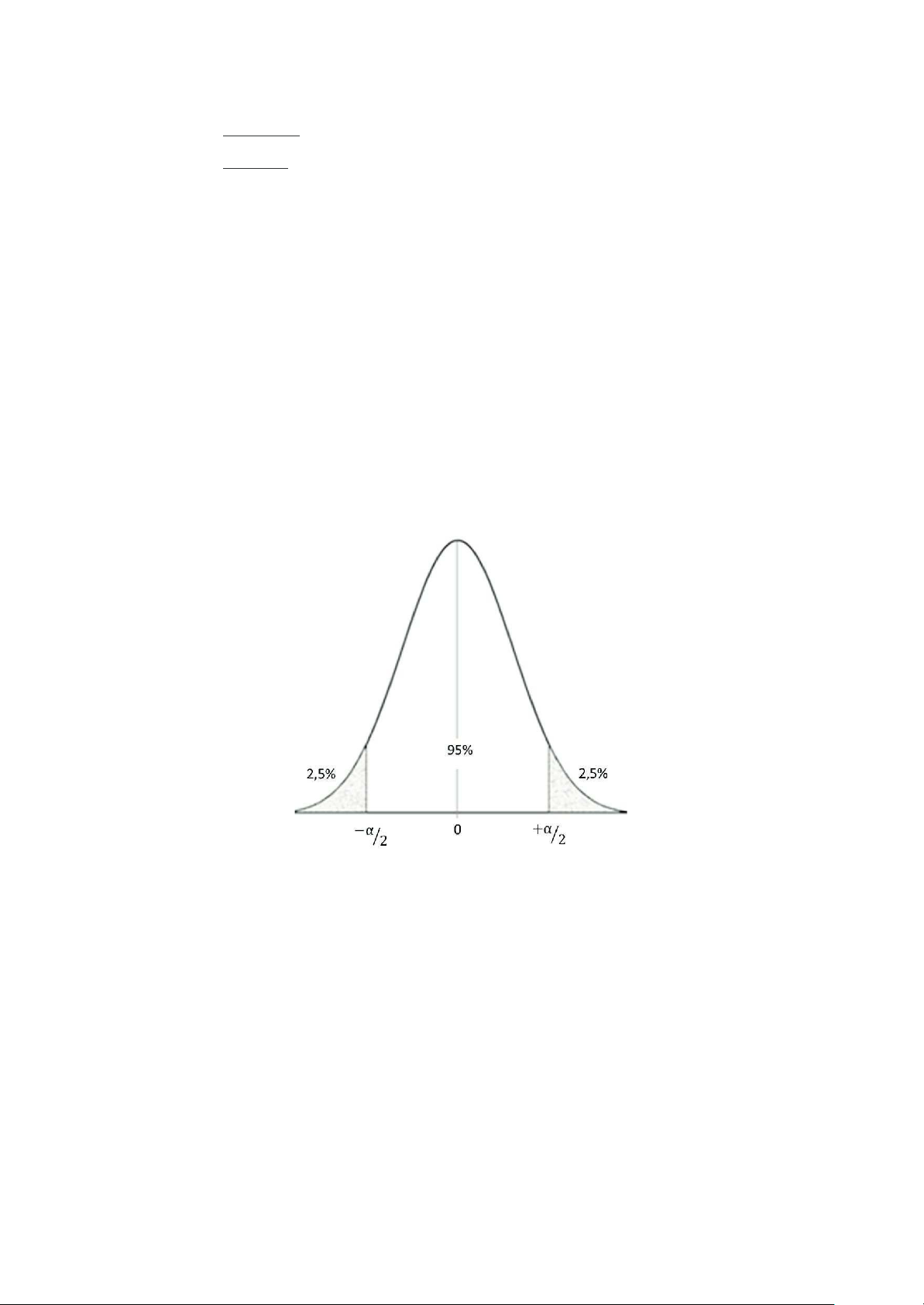
+ Đối với Z-test: [-1,96; +1,96]: vùng không bác bỏ, ối với ộ tin cậy=95%.
+ Đối với Chi-square test (phép kiểm Chi bình phương):
[0; 𝒳0,05(số cột - 1)]: không bác bỏ. lOMoAR cPSD| 45470709
(𝒳0,05 (số cột - 1) ; +∞): bác bỏ → Tra
bảng phân phối Chi bình phương
- Bước 5: Thu thập số liệu và tính trị số kiểm ịnh:
Đối với Z-test: Z = 𝑓−𝑝 . 𝑛 𝑝(1−𝑝)
Đối với Chi-square test (phép kiểm Chi bình phương):
Q (trị số kiểm ịnh) = Σ (𝑛𝑖 − 𝑛𝑖'𝑛𝑖' )2 *Chú thích:
- f: tần suất (trong thống kê)
- p: tỉ lệ cần kiểm ịnh (giả thiết)
- ni’: tần số kỳ vọng - n1’=n.p - n2’=n.(1-p)
- Bước 6: Ra quyết ịnh và kết luận.
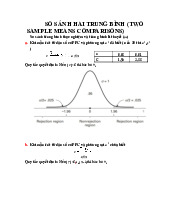
4. So sánh dựa vào 1 mẫu
Nếu thỏa iều kiện có phân phối chuẩn thì sử dụng phân phối Student, nếu không
thỏa iều kiện thì dùng Wilcoxon test. Trong chương trình học a số là phân phối chuẩn.
5. So sánh dựa vào 2 mẫu (dùng Independent T-test hay Paired T-test)
ĐK1: có phân phối chuẩn
ĐK2: có phương sai bằng nhau
- Nếu phương sai =, ộ lệch chuẩn xấp xỉ → Dùng Student’s T-test
- Nếu có phân phối chuẩn, phương sai không xấp xỉ (khác biệt nhiều):
dùng Welch’s T-test (ít gặp)
- Nếu không có phân phối chuẩn: dùng Mann-Whitney U-test (Có thể
dùng cho mọi trường hợp)
*Đọc thêm: Kiểm ịnh 3 mẫu: ANOVA
Bước 1: Đặt giả thuyết Bước 2: Chọn 𝛼, n
Bước 3: Có 𝛼, xác ịnh miền bác bỏ, miền không bác bỏ lOMoAR cPSD| 45470709
Bước 4: Lấy mẫu và tính giá trị kiểm ịnh
Bước 5: Ra quyết ịnh Bước 6: Kết luận.
6. Hồi quy tuyến tính ơn biến
6.1. Phương trình hồi quy tuyến tính ơn biến: 𝑛 2
𝑓(𝑎, 𝑏) = ∑ (𝑎 + 𝑏𝑥𝑖 − 𝑦𝑖) 𝑖=1
Tính chất hệ số tương quan (R):
- R nằm trong khoảng -1 ến 1
- R>0: tỉ lệ thuận (CÙNG TĂNG) - R<0: tỉ lệ nghịch (CÙNG GIẢM) -
4 mức ộ liên quan của R:
-0,25-0,5-0,75-1Hệ số xác ịnh R2: là một biến ộc lập giải thích sự phụ thuộc bao nhiêu phần
trăm vào phương trình hồi quy tuyến tính.
- Giá trị R2 dao ộng từ 0 ến 1.
- R2 càng gần 1 thì mô hình ã xây dựng càng phù hợp với bộ dữ liệu dùng chạy hồi quy.
- R2 càng gần 0 thì mô hình ã xây dựng càng kém phù hợp với bộ dữ
liệu dùng chạy hồi quy.
- Trong phương trình hồi quy ơn biến (chỉ có 1 biến ộc lập) thì R2
chính là bình phương của hệ số tương quan R giữa hai biến ó.
- Ý nghĩa cụ thể: giả sử R2 là 0,60 thì mô hình hồi quy tuyến tính này
phù hợp với tập dữ liệu ở mức 60%. Nói cách khác, 60% biến thiên
của biến phụ thuộc ược giải thích bởi các biến ộc lập.
7. Phân biệt các phép kiểm ịnh ã học:
- T-test: kiểm tra sự sai khác giá trị trung bình (mà không có ộ lệch chuẩn σ)
+ Independent t-test: 2 mẫu không liên quan, ộ lệch chuẩn không khác
biệt nhiều, ví dụ: giữa phụ nữ và nam giới, giữa có thai và không có thai,... lOMoAR cPSD| 45470709
+ Paired t-test: 2 mẫu có liên quan, ví dụ: việc bổ sung sắt và cân nặng trẻ sơ sinh,...
- Z-test: kiểm tra sự sai khác giá trị trung bình (có ộ lệch chuẩn σ)
- ANOVA test: 3 mẫu trở lên
- Chi-square test (Pearson’s chi-square test): kiểm ịnh sự khác biệt
giữa các tỉ lệ (dữ liệu ở dạng tần số), tần số kỳ vọng>5
- Fisher exact test: tương tự Chi-square test nhưng ộ chính xác cao
hơn, tần số kỳ vọng <2 (Bảng 2x2)