Đề cương ôn thi học kỳ 2 Toán 10 – Nguyễn Quốc Hiệp

Tài liệu gồm 40 trang tuyển tập bài tập trắc nghiệm và tự luận các chủ đề trong chương trình học kỳ 2 môn Toán lớp 10. Tài liệu do thầy Nguyễn Quốc Hiệp biên soạn.

81 41 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

TAM KỲ 4/2017

ĐỀ CƢƠNG ÔN THI

HỌC KỲ II

TOÁN 10

BIÊN SOẠN: GV NGUYỄN QUỐC HIỆP

NGHỊ LỰC VÀ BỀN BỈ CÓ THỂ CHINH PHỤC MỌI THỨ

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 1

ĐỀ CƢƠNG ÔN TẬP HỌC KỲ II TOÁN 10

BIÊN SOẠN VÀ GIẢNG DẠY GV NGUYỄN QUỐC HIỆP

A/ ĐẠI SỐ.

 CHƢƠNG IV: BẤT ĐẲNG THỨC BẤT PHƢƠNG TRÌNH.

BẤT PHƢƠNG TRÌNH- HỆ BẤT PHƢƠNG TRÌNH MỘT ẨN.

I/BÀI TẬP TỰ LUẬN

1) Tìm điều kiện của các bất phƣơng trình sau:







2 5 1 0x x x     



  



2) Xem xét cặp bất phƣơng trình nào là tƣơng đƣơng?

xx

và

1x 

xx

và

1x 



và

1x 

3) Giải các bất phƣơng trình- hệ bất phƣơng trình sau?

3 1 2 1 2

2 3 4

x x x  



     

1 2 2 2 1 2x x x x x      

   

4 1 0xx  

   

3 1 0xx  

3 7 2

4 4 6 1

  





  



II/BÀI TẬP TRẮC NGHIỆM

Câu 1. Tập xác định của bất phương trình

x x x

    



là:

 

 

3;6 \ 1D 



  

3; \ 1D   



  

3;6 \ 1D 





 

;6 \ 1D  

Câu 2. Tập nghiệm của bất phương trình

   

6 5 2 10 8x x x x x     

là:

S 

S 

 

;5S  

 

5;S  

Câu 3.

2x 

là nghiệm của bất phương trình nào sau đây:

2x 

  

1 2 0xx  

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 2







3xx

Câu 4. Bất phương trình

2 2 2x x x    

có tập nghiệm:

S 





;2S  

 

2S 





2;S  

Câu 5: Chọn khẳng định đúng trong các khẳng định sau:

33x x x  

11x

  

0 1 0



   

0x x x x   

Câu 6 : Cho các cặp bất phương trình sau:

10x

và

 

10xx

II.

10x 

và

 





III.

10x 

và

 

10xx

IV.

10x 

và

 

10xx

Số cặp bất phương trình tương đương là:

A. 1 B. 2 C. 3 D. 4

Câu 7: Hệ bất phương trình

2 1 3 4

5 3 8 9

  





  



có tập nghiệm là:

S 

 

;3S   





;4S  

 

3;4S 

Câu 8. Hệ bất phương trình

15 2 2

3 14

2( 4)



  















có tập nghiệm nguyên là:

 

1;2



 

1

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 3

Câu 9. Cho hệ bất phương trình

2 4 0

mx m









  





. Giá trị của

để hệ bất phương

trình vô nghiệm là:

m

m 

0m 

 0m

Câu 10. Với giá trị nào của

thì hệ bất phương trình









  





có nghiệm duy

nhất?

 

1; 3

 

1; 3

 

4; 3



DẤU CỦA NHỊ THỨC BẬC NHẤT- HỆ BẤT BẬC NHẤT HAI ẨN

I/BÀI TẬP TỰ LUẬN.

1) Xét dấu các biểu thức sau:

    

12f x x x  

 

  







 

2 1 2





2) Giải các bất phƣơng trình sau:

 

1 3 0xx  

  







1 2 4xx





5 8 11x

5 8 2xx  

2 1 2x x x    

II/BÀI TẬP TRẮC NGHIỆM.

Câu 1. Nhị thức

24f x x

luôn âm trong khoảng nào sau đây:

Câu 2. Cho biểu thức

12f x x x

Khẳng định nào sau đây đúng:

0, 1;f x x

0, ;2f x x

0,f x x

0, 1;2f x x

Câu 3. Nhị thức nào sau đây dương với mọi

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 4

3f x x

26f x x

39f x x

3f x x

Câu 4. Bất phương trình

1 1 0mx

có nghiệm với mọi

khi

Câu 5. Cho bảng xét dấu:





 





Hàm số có bảng xét dấu như trên là:

 

2f x x

 

2f x x  

 

16 8f x x

 

24f x x

Câu 6. Tập nghiệm của bất phương trình

  

3 2 6 0xx  

là :

 

3;3

   

; 3 3;   

3;3







\ 3;3

Câu 7. Tập nghiệm của bất phương trình

  

3 2 2 7 0xx  

;









;









;;

   

   

   

   

;







Câu 8. Hàm số có kết quả xét dấu



-1 2



 







là hàm số

    

12f x x x  

 







 







    

12f x x x  

Câu 9. Hàm số có kết quả xét dấu

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 5



1



 





là hàm số

 

1f x x

 







 







 

1f x x  

Câu 10. Hàm số có kết quả xét dấu





 







là hàm số

   

2f x x x

 

2f x x

 





   

2f x x x

Câu 11. Tập nghiệm của bất phương trình







1;2







 

1;2

   

; 1 2;   



1;2







Câu 12. Tập nghiệm của bất phương trình

















;

















;











Câu 13. Điều kiện

để bất phương trình

 

1 2 0m x m   

vô nghiệm là

m 

 

1;m   

 

2;m  

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 6

Câu 14. Điều kiện

để bất phương trình

 

1 2 0m x m   

có nghiệm với mọi

giá trị của

là

m 

 

1;m   

 

2;m  

Câu 15. Tập nghiệm của bất phương trình





là

1;2







1;2





 

;1









Câu 16. Cho

0 ab

, Tập nghiệm của bất phương trình

  

0x a a x b  

là:

   

;;ab  

 

;;



   





   

; b a;   

 

;;



  





Câu 17. Tìm

để bất phương trình

1xm

có tập nghiệm



3;S



  



3m 

4m 

2m 

1m 

Câu 18. Tìm m để bất phương trình

 

3 5 1x m x  

có tập nghiệm

 

2;S  

là

2m 

3m 

9m 

5m 

Câu 19. Điều kiện của tham số

để bất phương trình

1m x mx

có tập nghiệm là

là:

01mm   

0m 

1m 

1m

Câu 20. Tập nghiệm của bất phương trình

4 3 8x

là

;



 

























; 4;





   









Câu 21. Tập nghiệm của bất phương trình

2 3 12xx









;15







3;15





 



 



   



; 3 15;

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 7

Câu 22. Tập nghiệm của bất phương trình

là

; 1;

;

Câu 23. Tập nghiệm của bất phương trình

15 3x

là

C. D.

Câu 24. Tập nghiệm của bất phương trình

21xx

A. B.

;

Câu 25. Tập nghiệm

của bất phương trình

4 2 3 2x x x   

là:

 

7;S  

 

;7S   





;7S   





7;S  

Câu 26. Miền không bị gạch chéo (không kể đường thẳng d) là miền nghiệm của bất

phương trình nào? y

1 2 3 4 5-1-2-3-4-5

-1

-2

-3

-4

-5

2 2 0xy  

2 2 0xy

22xy  

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 8

Câu 27. Miền không bị gạch chéo (kể cả đường thẳng d1 và d2) là miền nghiệm của

hệ bất phương trình nào?

1 2 3 4 5-1-2-3-4-5

-1

-2

-3

-4

-5

2 4 0

  





  



2 4 0

  





  



2 4 0

  





  



2 4 0

  





  



Câu 28. Cặp số

 

1; 1

là nghiệm của bất phương trình

20xy

0xy  

41xy

3 1 0xy   

Câu 29. Điểm

 

0; 3M 

thuộc miền nghiệm của hệ bất phương trình:

2 5 12 8

x y x









  





2 5 12 8

x y x













  

2 5 12 8

x y x













  

2 5 12 8

x y x













  

Câu 30. Miền nghiệm của hệ bất phương trình :

3 4 12 0



  













Là miền chứa điểm nào trong các điểm sau?

 

1; 3M 

 

4; 3N 

 

1;5P 

 

2; 3Q 

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 9

DẤU CỦA TAM THỨC BẬC HAI

I/ BÀI TẬP TỰ LUẬN

Câu 1: Lập bảng xét dấu các biểu thức sau:

 

43f x x x  

 

  

2 1 3 4g x x x x x   

 

  

1 3 2h x x x x x    

 

  

4 4 5 4

x x x x

   





Câu 2: Giải các bất phương trình sau:

2017 2016 0xx  

6 9 0xx  

  

3 2 1 2 4 0x x x x   

4 3 4x x x



  

Câu 3: Cho phương trình:

 

2 1 4 1 0mx m x m    

, tìm tất các các giá trị của tham

số

để phương trình có

a) Hai nghiệm trái dấu.

b) Hai nghiệm phân biệt

c) Các nghiệm dương

d) Các nghiệm âm

Câu 4: Tìm tất các các giá trị của tham số

để các bất phương trình sau có nghiệm

đúng với mọi

50x x m  

 

2 2 2 0m m x mx   

x mx







Câu 5: Tìm tất các các giá trị của tham số

để các biểu thức sau luôn dương

x x m

10 5mx x

Câu 6: Giải các bất phương trình sau:

31xx  

2 5 4xx  

35xx  

II/ BÀI TẬP TRẮC NGHIỆM

Câu 1. Hàm số có kết quả xét dấu

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 10





 







là hàm số

 

32f x x x  

 

32f x x x  

    

12f x x x   

 

32f x x x   

Câu 2. Hàm số có kết quả xét dấu





 









là hàm số

   

 

3 3 2f x x x x   

   

 

1 5 6f x x x x   

   

 

2 4 3f x x x x    

     

1 2 3f x x x x   

Câu 3. Hàm số có kết quả xét dấu





 









là hàm số

   

 

   

2 4 3f x x x x

   

 

    

1 5 6f x x x x

     

   1 3 2f x x x x

   

 

   

3 3 2f x x x x

Câu 4. Cho bảng xét dấu

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 11





 



 





 









 







 







 

  

f x x x







 

  





Câu 5. Cho các mệnh đề

 

Với mọi

1;4x







 

4 5 0f x x x   

 

Với mọi

   

;4 5;10x   

 

9 10 0g x x x   

 

III

 

5 6 0h x x x   

Với mọi

2;3x







A. Chỉ mệnh đề

 

III

đúng B. Chỉ mệnh đề

 

và

 

đúng

C. Cả ba mệnh đề điều sai D. Cả ba mệnh đề điều đúng

Câu 6. Khi xét dấu biểu thức

 

3 10







ta có

 

0fx 

khi

51x   

hay

12x

 

0fx 

khi

5x 

hay

11x  

hay

2x 

 

0fx 

khi

52x  

 

0fx 

khi

1x 

Câu 7. Tập nghiệm của bất phương trình

4 3 0xx  

là

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 12

 

; 3 1;



    



 

3; 1

 

; 1 3;



    



3; 1







Câu 8. Tập nghiệm của bất phương trình

60xx   

là

 

; 2 3;



   





 

; 1 6;



    



2;3







Câu 9. Bất phương trình có tập nghiệm

2;10

là

12 20 0xx

3 2 0xx

12 20 0xx

2 10 0xx

Câu 10. Tìm

để

   

2 8 1f x x m x m    

luôn luôn dương

 

 0;28m

   

   ;0 28;m

 



   



;0 28;m







0;28m

Câu 11. Tìm

để

   

2 1 4f x mx m x m   

luôn luôn dương









 

; 1 ;



   





 

0; 

;









Câu 12.Tìm

để

   

2 2 2 2f x x m x m     

luôn luôn âm

 

0;2

   

;0 2;  

 

;0 2;



  



0;2





Câu 13. Tìm

để

   

2 1 4f x mx m x m   

luôn luôn âm









 



    





; 1 ;

 

  ;1m



 





;

Câu 14. Tìm

để

30x mx m   

có tập nghiệm là

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 13

 

6;2

   

; 6 2;   

6;2







 

; 6 2;



   



Câu 15. Tìm

để

 

4 1 5 0mx m x m    

vô nghiệm



  







  





 

 ;0m







     









; 1 ;

Câu 16. Tìm

để

 

2 2 2 2 0x m x m     

có hai nghiệm phân biệt









 



   





;0 ;















   









;0 ;

Câu 17. Tập nghiệm

của hệ

7 6 0

8 15 0



  





  





là







1;3S







5;6S

   



   

1;3 5;6S

S

Câu 18. Để phương trình

 

1 2 3 5 0x m x m m     

có hai nghiệm trái dấu

thì

thuộc





































Câu 19. Với giá trị nào của m để bất phương trình

x mx

  





nghiệm đúng với

mọi







2;2m

 

2;2m

 



    



; 2 2;m

m

Câu 20. Để giải bất phương trình

4 3 2

3 2 0x x x  

, một học sinh lập luận ba giai

đoạn như sau:

 

Ta có:

4 3 2 2 2

3 2 0 ( 3 2) 0x x x x x x      

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 14

 

2 2 2 2

0 ( 3 2) 0 3 2 0x x x x x x        neân

 

3 2 0 3 2 0 1 2

x x x x x





         









Suy ra

Vậy: Tập nghiệm của bất phương trình là:

 

1;2

Hỏi: Lập luận trên đúng hay sai? Nếu sai thì sai từ giai đoạn nào?

A. Sai từ

 

B. Lập luận đúng C. Sai từ

 

D. Sai từ

 

Câu 21. Cho phương trình bậc hai

2 2 0x mx m   

. Phát biểu nào sau đây là

đúng?

A. Phương trình luôn có hai nghiệm phân biệt.

B. Phương trình luôn vô nghiệm.

C. Phương trình chỉ có nghiệm khi m > 2.

D. Tồn tại một giá trị m để phương trình có nghiệm kép.

Câu 22. Tìm

để hệ bất phương trình

5 4 0

( 1) 0

x m x m



   





   





có nghiệm duy nhất

1m 

2m 

1m 

4m 

Câu 23. Cho hệ bất phương trình

7 12 0



  







. Hệ có nghiệm khi và chỉ khi giá trị

của

là

3m 

4m 

4m 

34m

Câu 24. Với giá trị nào của

để hai bất phương trình

4 3 0x m m   

và

2 3 3x m x  

tương đương?

7m 

hoặc

0m 

1m 

hoặc

3m 

m 

mR

Câu 25. Tập nghiệm

của bất phương trình

6 5 8 2x x x    

là:

   

   ;3 5;S

 

 ;3S

 

 5;S

 

 3;5S

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 15

 CHƢƠNG IV: CUNG VÀ GÓC LƢỢNG GIÁC- CÔNG THỨC LƢỢNG

GIÁC

CUNG VÀ GÓC LƢỢNG GIÁC

I/ BÀI TẬP TỰ LUẬN.

Câu 1:

a) Cho

sin





và







,tính các giá trị lượng giác còn lại của góc



b) Cho

tan





và





  

, tính các giá trị lượng giác còn lại của góc



Câu 2: Rút gọn các biểu thức sau:

     

sin sin sin cos



     



       





     

tan tan 2cot cot cot



      

   

         

   

   

       

sin 2016 cos 2017 tan 2019 cot cos



        



         





 

sin( ) cos( ) cot 2 tan

A x x x x





       





3 3 3 3

cos sin cos sin

2 2 2 2

A a a a a

   

       

       

       

       

Câu 3: Chứng minh các đẳng thức sau:

4 4 2

sin cos 1 2sin

  

  

sin 2cos 1

sin

cot









1 sin cos

cos tan

cos









sin tan

tan

cos cot













   

1 cot sin 1 tan cos sin cos

     

    

 

sin cos 1

2tan

cot sin cos





  







Câu 4:

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 16

a) Cho

sin cos





. Tính

sin .cosA





sin cosB





sin cosC





b) Cho

tan cot m





. Tính theo

giá trị của các biểu thức

tan cotD





tan cotE





c) Cho

tan





, tính giá trị của các biểu thức sau:



sin cos











3sin 12sin cos cos

sin sin cos 2cos

   







Câu 5: Tính giá trị của biểu thức:

cos cos ... cos

9 9 9

  

   

2 2 2 2

sin sin sin sin

3 9 18 6

   

   

sin sin ... sin

5 5 5

  

   

0 0 0 0

tan1 tan2 tan3 ....tan89D 

2222

sin sin sin sin tan cot

6 3 4 4 6 6

     

    

2 0 2 0 2 0 2 0 2 0 2 0 2 0

cos 15 cos 25 cos 35 cos 45 cos 105 cos 115 cos 125F      

II/ BÀI TẬP TRẮC NGHIỆM.

Câu 1: Chọn khẳng định sai trong các khẳng định sau:





230





150





145





Câu 2: Đường tròn có bán kính

20R cm

. Độ dài của cung tròn có số đo



là:





l cm





l cm





5l cm





Câu 3: Chọn khẳng định sai trong các khẳng định sau?

1 sin 1



  

sin

tan ( , )

cos 2

k k Z



  



   

 

cos 2 cos ,k k Z

  

  

cos

cot ( , )

sin

k k Z



  



   

Câu 4: Chọn khẳng định sai trong các khẳng định sau:

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 17

sin cos 1





1 tan (cos 0)

cos





  

1 cot (sin 0)

sin





  

tan .cot 1 ( , )

k k Z



  

   

Câu 5: Chọn khẳng định đúng trong các khẳng định sau?

sin 0

cos 0











  







sin 0

cos 0













  







sin 0

cos 0













  







sin 0

cos 0













  







Câu 6: Chọn khẳng định đúng trong các khẳng định sau?

 

sin sin





cos sin







  





 

cos cos

  



 

tan tan

  



Câu 7. Trong các khẳng định sau khẳng định nào sai?

tan( ) tan

  

  

tan( ) tan



  

tan( ) tan

  

  

tan( ) cot







Câu 8. Trong các khẳng định sau khẳng định nào đúng?

cos( ) sin( )



  

  

cos( ) cos( )

  

  



cos)2cos( 

cos( ) cos( )



  

  

Câu 9. Trong các khẳng định sau khẳng định nào đúng?

)tan()

cot(







tan( ) tan( )



  

  

tan( ) tan( )





  

tan( ) tan( )



  

  

Câu 10. Cho sinx =

và

27090  x

thì

A. cotx =



B. cotx =

3

C. cotx =

D. cotx =

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 18

Câu 11: Cho

cosx , .





   





Khi đó

tan x

bằng



Câu 12. Cho







. Trong các khẳng định sau khẳng định nào đúng?

sin( ) 0







sin( ) 0







sin( ) 0







sin( ) 0







Câu 13: Cho

tan





. Khẳng định nào sau đây đúng ?

cot 5





cot





cot





cot 2





Câu 14: Cặp đẳng thức nào sau đây không thể đồng thời xảy ra ?

sin 0,6 va cos 0,8





sin 0,2 va cos



  

sin 0,2 va cos 0,8





sin 0,2 va cos



   

Câu 15: Trên đường tròn lượng giác như hình vẽ bên, cho

sd AM





. Tìm vị trí

điểm M.

A. M là trung điểm của cung nhỏ

B. M là trung điểm của cung nhỏ

C. M là trung điểm của cung nhỏ

D. M là trung điểm của cung nhỏ

Câu 16: Đổi 294

30’ sang radian. Chọn đáp án đúng trong các đáp án sau.

294 30' 5,14

294 30' 4,14

294 30' 4,41

294 30' 5,41

Câu 17: Cho





  

. Khẳng định nào sau đây đúng ?

cos 0





sin 0





cot 0





tan 0





ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 19

Câu 18: Trên đường tròn lượng giác, điểm

;









là điểm cuối của cung lượng

giác α có điểm đầu A. Tìm α, biết rằng α là một trong bốn số đo cho dưới đây.

210





210













Câu 19: Đẳng thức nào sau đây có thể xảy ra ?

cos 1,1





cos





cos 0,1





cos





Câu 20: Tìm α, biết

cos 0





,k k Z





2,k k Z





k k Z





  

,k k Z

  

  

CÔNG THỨC LƢỢNG GIÁC

I/ BÀI TẬP TỰ LUẬN.

Câu 1: Chứng minh rằng:

cos cos cos cos3

3 3 4

x x x x



   

  

   

   

 

sin5 2sin cos4 cos2 sinx x x x x  

   

sin 45 cos 45

tan

sin 45 cos 45







  



  

Câu 2: Rút gọn các biểu thức sau:

sin2 sin

1 cos2 cos









4sin

1 cos







1 cos sin









1 sin 2sin 45

4cos





  







II/ BÀI TẬP TRẮC NGHIỆM

Câu 1: Giả sử

tan .tan tan

( ) ( )



  A x x x

được rút gọn thành

tan A nx

. Khi đó

n bằng :

A. 2. B. 1. C. 4. D. 3.

Câu 2: Nếu sinx = 3cosx thì sinx.cosx bằng:

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 20

Câu 3: Giá trị của biểu thức

0 0 0 0 0 0

tan110 .tan340 sin160 .cos110 sin250 .cos340

bằng

. B.

. C.

1

. D.

Câu 4: Cho

sin

a

. Tính

cos2 sinaa

17 5



Câu 5: Biết

sin

cot cot

sin sin



x kx

, với mọi x để các biểu thức có nghĩa. Lúc đó giá

trị của k là:

Câu 6: Nếu

cos sin 2 0



  



   





thì



bằng:



Câu 7: Nếu a =20

và b =25

thì giá trị của (1+tana)(1+tanb) là:

B.2 C.

D. 1 +

Câu 8: Tính

1 5cos

3 2cos









, biết

tan 2







Câu 9: Giá trị của

tan













bằng bao nhiêu khi



  



  





sin

38 25 3



. B.

8 5 3



. C.



. D.

38 25 3

Câu 10: Giá trị của biểu thức

sin18 sin54



bằng

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 21



. B.

. C.

2



Câu 11: Biểu thức tan30

+ tan40

+ tan50

+ tan60

bằng:









cos 20

C. 2 D.

sin 70

Câu 12: Nếu  là góc nhọn và sin2 = a thì sin + cos bằng:

 

2 1 1a

1  a a a

1a

1a a a  

Câu 13: Giá trị biểu thức

0 0 0 0

cos80 cos20

sin40 .cos10 sin10 .cos40





bằng

1

C. 1 D.

sin( )ab

Câu 14: Giá trị biểu thức

sin cos sin cos

15 10 10 15

cos cos sin sin

15 5 5 5

   





bằng:

1

Câu 15: Cho





, tính

tan tan





Câu 16: Đơn giản biểu thức

sin10 cos10

C

4sin 20

4cos20

8cos20

8sin 20

Câu 17: Cho

sin





. Khi đó

cos2



bằng:

. B.

. C.



. D.



ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 22

Câu 18: Giá trị biểu thức

sin .cos sin cos

15 10 10 15

cos cos sin .sin

15 5 15 5

   





là



1

C. 1 D.

Câu 19: Đẳng thức nào trong các đẳng thức sau là đồng nhất thức?

1) sin2x = 2sinxcosx 2) 1–sin2x = (sinx–cosx)

3) sin2x = (sinx+cosx+1)(sinx+cosx–1) 4) sin2x = 2cosxcos(



–x)

A. Chỉ có 1) B. 1) và 2) C. Tất cả trừ 3) D. Tất cả

Câu 20: Biết

sin ; cos ( ; 0 )

13 5 2 2





     a b a b

Hãy tính

sin( )ab



B/ HÌNH HỌC



CHƢƠNG II: TÍCH VÔ HƢỚNG CỦA HAI VECTO- ỨNG DỤNG

HỆ THỨC LƢỢNG TRONG TAM GIÁC- GIẢI TAM GIÁC

I/BÀI TẬP TỰ LUẬN

Câu 1: Cho



ABC có

20 , 35 , 60b cm c cm A  

a)Tính BC b) Tính diện tích



ABC c) Xét xem góc B tù hay nhọn?

d) Tính độ dài đường cao AH e) Tính bán kính đường tròn

nội tiếp

?r 

và ngoại tiếp

?R 

của tam giác trên

Câu 2: Cho



ABC có

ˆˆ

7 , 60 , 32b cm A C  

a) Tính diện tích



ABC b) Góc B tù hay nhọn? Tính B

c) Tính bánh kính

, , ?

h R r 

d) Tính độ dài đường trung

tuyến

Câu 3:

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 23

30 m

Giả sử chúng ta cần đo chiều cao

của một cái tháp với

là chân tháp,

là đỉnh

tháp. Vì không thể đến chân tháp được nên từ hai điểm

,AB

có khoảng cách

30AB m

sao cho ba điểm

,,A B C

thẳng hàng, người ta đo được các góc

43 , 67CAD CBD   

(như hình vẽ trên). Hãy tính chiều cao

của tháp?

Câu 4: Cho một tam giác

ABC

, chứng minh rằng

a) Nếu có

2b c a

thì

2sin sin sinA B C

b) Nếu có

bc a

thì

sin sin sinA B C

II/BÀI TẬP TRẮC NGHIỆM.

Câu 1. Tam giác

ABC

có

2 , 1 , 60AB cm AC cm A   

. Khi đó độ dài cạnh

là:

1 cm

2 cm

3 cm

5 cm

Câu 2. Tam giác

ABC

có

5 , 3 , 5a cm b cm c cm  

. Khi đó số đo của góc

là:

45A

90A 

30A 

120A 

Câu 3. Tam giác

ABC

có

8 , 10 , 6AB cm BC cm CA cm  

. Đường trung tuyến

của tam giác đó có độ dài bằng:

4 cm

5 cm

6 cm

7 cm

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 24

Câu 4. Tam giác

ABC

vuông tại

có

6 , 10AB cm BC cm

. Đường tròn nội tiếp

tam giác đó có bán kính

bằng:

1 cm

2 cm

3 cm

Câu 5. Tam giác đều nội tiếp đường tròn bán kính

4R cm

có diện tích là:

13 cm

13 2 cm

12 3 cm

15 cm

Câu 6. Tam giác

ABC

vuông và cân tại

có

AB a

. Đường tròn nội tiếp tam giác

ABC

có bán kính

bằng:



Câu 7: Tam giác

ABC

có các cạnh

,,abc

thỏa mãn điều kiện:

  

3a b c a b c ab    

. Khi đó số đo của góc

bằng:

45

120

60

30

Câu 8. Hình bình hành

ABCD

có

,2AB a BC a

và

45BAD 

. Khi đó hình bình

hành có diện tích bằng:

Câu 9: Tam giác đều cạnh

nội tiếp đường tròn bán kính

. Khi đó bán kính

bằng:

Câu 10. Cho tam giác

ABC

có diện tích

. Nếu tăng độ dài mỗi cạnh

và

lên

hai lần đồng thời giữ nguyên độ lớn của góc

thì diện tích tam giác

ABC

mới

được tạo nên bằng:

Câu 11: Cho tam giác

ABC

có

4, 3ab

và

6c 

và

là trọng tâm tam giác . Khi

đó , giá trị của tổng

2 2 2

GA GB GC

là bao nhiêu ?

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 25

Câu 12: Cho tam giác

ABC

có

60 , 45 , 5B C AB  

. Hỏi độ dài cạnh

bằng bao

nhiêu ?

Câu 13: Cho tam giác

ABC

có ba cạnh là

6,8,10

. Bán kính đường tròn nội tiếp tam

giác

ABC

là :

Câu 14: Cho tam giác

ABC

có ba cạnh là

5,12,13

có diện tích là :

20 2

10 3

Câu 15: Cho tam giác

ABC

có

30 , 10A BC

. Bán kính đường tròn nội tiếp tam

giác

ABC

là :

10 3

Câu1 6: Cho góc

30xOy 

. Gọi

, BA

lần lượt nằm trên

, Ox Oy

sao cho

2AB 

. Độ

dài lớn nhất của đoạn

là :

Câu 17: Cho tam giác

ABC

có diện tích

. Nếu tăng độ dài mỗi cạnh

, BCAC

lên

hai lần và giữ nguyên độ lớn của góc

thì diện tích của tam giác mới sẽ là :

Câu 18 : Cho tam giác

ABC

có

, CA= bBC a

. Tam giác

ABC

có diện tích lớn nhất

khi góc

đạt giá trị :

150

120

Câu 19: Tam giác

ABC

đều , cạnh

, ngoại tiếp đường tròn bán kính

. Khi đó

bán kính đường tròn nội tiếp tam giác

ABC

là :

Câu 20: Tam giác

ABC

đều , cạnh

, nội tiếp đường tròn bán kính

. Khi đó bán

kính đường tròn ngoại tiếp tam giác

ABC

là :

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 26

Câu 21: Tam giác

ABC

vuông cân tại

, A 2A B a

. Đường trung tuyến

có độ dài

là :

22a

23a

Câu 22 : Cho hình bình hành

ABCD

có

, B 2AB a C a

và góc

45BAD 

. Diện

tích của hình bình hành

ABCD

là :

Câu 23 : Tam giác

ABC

vuông cân tại

, A 2A B a

. Độ dài bán kính đường tròn nội

tiếp tam giác là :

 

22a 

Câu 24 : Cho tam giác

ABC

có

2 3, 2 2ab

và

2c 

. Kết quả nào trong các kết

quả sau là độ dài của trung tuyến

?AM

Câu 25 : Tam giác

ABC

đều nội tiếp đường tròn bán kính

8R 

. Diện tích của tam

giác

ABC

là :

48 3

24 3

Câu 26 : Tam giác

ABC

vuông tại

có

A 12, BC = 20B 

. Bán kính

của đường

tròn nội tiếp tam giác

ABC

có độ dài bằng :

Câu 27 : Cho tam giác

ABC

có

2, 1ab

và góc

60C 

. Độ dài cạnh

là bao

nhiêu ?

Câu 28: Cho tam giác

ABC

có

7 cm, c = 5 cmb 

và

cos

A 

. Tính

a, sin A

và diện

tích

của tam giác

ABC

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 27

= 4 2 cm, sinA= , S=14 cm

= 4 2 cm, sinA=- , S=14 cm

= 4 3 cm, sinA= , S=14 cm

= 4 5 cm, sinA= , S=14 cm

Câu 29 : Cho tam giác

ABC

có

7 cm, c = 5 cmb 

và

cos

A 

. Tính đường cao

xuất phát từ đỉnh

và bán kính

của đường tròn ngoại tiếp tam giác

ABC

7 5 2

cm, R = cm

h 

7 2 5 3

cm, R = cm

h 

7 2 5 2

cm, R = cm

h 

7 3 5 2

cm, R = cm

h 

Câu 30 : Cho tam giác

ABC

có

là trọng tâm , gọi

, c = AB, a = BCb CA

. Đẳng

thức nào sau đây là sai ?

2 2 2

2 cosa b c bc A  

sin

S ab C

2 2 2

b c a





 

2 2 2 2 2 2

GA GB GC a b c    



CHƢƠNG III: PHƢƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

PHƢƠNG TRÌNH ĐƢỜNG THẲNG

I/ BÀI TẬP TỰ LUẬN.

Câu 1: Lập phương trình tham số và tổng quát của đường thẳng

 



biết:

 



qua

 

2; 3M 

và có vecto pháp tuyến

 

1; 3n 

 



qua

 

1;3N 

và có vecto chỉ phương

( 3;4)u 

Câu 2: Lập phương trình tổng quát của đường thẳng

 



trong các trường hợp sau:

 



qua

 

2;3M 

và có hệ số góc

2k 

 



qua

 

2; 5N 

và song song với đường thẳng

2 3 2017 0xy  

 



qua

 

2; 5N 

và vuông góc với đường thẳng

4 3 2017 0xy  

Câu 3: Cho ba điểm

     

2;0 , 4;1 , 1;2A B C

lập thành ba đỉnh của tam giác.

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 28

a) Viết phương trình tham số của đường thẳng AB.

b) Viết phương trình tổng quát của đường thẳng BC

c) Viết phương trình đường trung tuyến AM của tam giác.

d) Viết phương trình tổng quát của các đường cao AH, BH, từ đó tìm tọa độ trực

tâm của tam giác.

e) Viết phương trình tổng quát đường trung bình MN của tam giác ABC với M

là trung điểm của AB, N là trung điểm của AC.

f) Viết phương trình đường trung trực của cạnh AB,AC từ đó tìm tọa độ tâm

đường tròn ngoại tiếp tam giác ABC

g) Tính khoảng cách từ C đến đường thẳng AB

h) Tính góc B của tam giác ABC

i) Tính diện tích của tam giác ABC.

Câu 4: Trong mặt phẳng toạ độ Oxy cho



ABC có đỉnh

 

1;2A

, đường trung tuyến

BM:

2 1 0xy  

và phân giác trong CD :

10xy  

. Viết phương trình đường

thẳng BC

Câu 5: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có phương trình cạnh

AB:

20xy  

, phương trình cạnh AC:

2 5 0xy  

. Biết trọng tâm của tam giác

 

3;2G

Viết phương trình cạnh BC.

Câu 6. Cho tam giác ABC có phương trình cạnh BC là

2 5 0xy  

các đường trung

tuyến BM và CN lần lượt có phương trình

3 7 0xy  

và

50xy  

. Viết phương

trình đường thẳng chứa các cạnh AB, AC ?

Câu 7. Trong mặt phẳng Oxy, cho tam giác ABC có AB:

3 5 33 0xy  

; đừơng cao

AH:

7 13 0xy  

; trung tuyến BM:

6 24 0xy  

(M là trung điểm AC). Tìm

phương trình các đừơng thẳng AC và BC

II/ BÀI TẬP TRẮC NGHIỆM

Câu 1: cho phương trình:

 

01ax by c  

với

0ab

. Mệnh đề nào sau đây sai?

A. (1) là phương trình tổng quát của đường thẳng có vectơ pháp tuyến là

 

;n a b

0a 

(1) là phương trình đường thẳng song song hoặc trùng với trục

0b 

(1) là phương trình đường thẳng song song hoặc trùng với trục

D. Điểm

 

0 0 0

;M x y

thuộc đường thẳng (1) khi và chỉ khi

0ax by c  

Câu 2: Mệnh đề nào sau đây sai? Đường thẳng (d) được xác định khi biết.

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 29

A. Một vecto pháp tuyến hoặc một vec tơ chỉ phương.

B. Hệ số góc và một điểm thuộc đường thẳng.

C. Một điểm thuộc (d) và biết (d) song song với một đường thẳng cho trước.

D. Hai điểm phân biệt thuộc (d).

Câu 3: Cho tam giác ABC. Hỏi mệnh đề nào sau đây sai?

là một vecto pháp tuyến của đường cao AH.

là một vecto chỉ phương của đường thẳng BC.

C. Các đường thẳng AB, BC, CA đều có hệ số góc.

D. Đường trung trực của AB có

là vecto pháp tuyến.

Câu 4: Đường thẳng (d) có vecto pháp tuyến

 

;n a b

. Mệnh đề nào sau đây sai ?

 

;u b a

là vecto chỉ phương của (d).

 

;u b a

là vecto chỉ phương của (d).

 

;n ka kb k R





là vecto pháp tuyến của (d).

D. (d) có hệ số góc

 





Câu 5: Cho đường thẳng (d):

2 3 4 0xy  

. Vecto nào sau đây là vecto pháp tuyến

của (d)?

 

3;2n 

 

4; 6n   

 

2; 3n 

 

2;3n 

Câu 6: Cho đường thẳng (d):

3 7 15 0xy  

. Mệnh đề nào sau đây sai ?

 

7;3u 

là vecto chỉ phương của (d). B. (d) có hệ số góc

k 

C. (d) không đi qua góc tọa độ. D. (d) đi qua hai điểm









và

 

5;0N

Câu 7: Cho đường thẳng (d):

3 5 15 0xy  

. Phương trình nào sau đây không phải

là một dạng

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 30

khác của (d)?



. B.

yx  

. C.

 













. D.

 

















Câu 8: Mệnh đề nào sau đây đúng? Đường thẳng (d):

2 5 0xy  

A. Đi qua

 

1; 2A 

. B.Có phương trình tham số:

 













C. (d) có hệ số góc

k 

. D. (d) cắt

 



có phương trình:

20xy

Câu 9: Cho đường thẳng(d):

2 1 0xy  

. Nếu đường thẳng

 



đi qua

 

1; 1M 

và

song song với (d) thì

 



có phương trình :

2 3 0xy  

. B.

2 5 0xy  

. C.

2 3 0xy  

. D.

2 1 0xy  

Câu 10: Cho ba điểm

     

1; 2 , 5; 4 , 1;4A B C  

. Đường cao



của tam giác ABC

có phương trình:

3 4 8 0xy  

. B.

3 4 11 0xy  

. C.

6 8 11 0xy   

. D.

8 6 13 0xy  

Câu 11: Đường thẳng

 



3 2 7 0xy  

cắt đường thẳng nào sau đây?

 

:3 2 0d x y

. B.

 

:3 2 0d x y

 

: 3 2 7 0.d x y   

 

:6 4 14 0.d x y  

Câu 12: Cho đường thẳng (d):

4 3 5 0xy  

. Nếu đường thẳng

 



đi qua góc tọa

độ và vuông góc với (d) thì

 



có phương trình :

4 3 0xy

. B.

3 4 0xy

. C.

3 4 0xy

. D.

4 3 0xy

Câu 13: Cho tam giác ABC có

     

4;1 2; 7 5; 6A B C  

và đường thẳng

(d):

3 11 0xy  

. Quan hệ giữa (d) và tam giác ABC là:

A. Đường cao vẽ từ A. B. Đường cao vẽ từ B.

C. Đường trung tuyến vẽ từ A. D. Đường phân giác góc

.BAC

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 31

Câu 14: Gọi H là trực tâm của tam giác ABC. Phương trình các cạnh và đường cao

của tam giác

là:

:7 4 0; :2 4 0; : 2 0AB x y BH x y AH x y        

Phương trình đường cao CH của tam giác ABC là:

7 2 0.xy  

7 0.xy

7 2 0.xy  

7 2 0.xy  

Câu 15: Phương trình đường thẳng đi qua hai điểm

   

2;4 ; 6;1AB

là:

3 4 10 0.xy  

3 4 22 0.xy  

3 4 8 0.xy  

3 4 10 0.xy  

Câu 16: Cho hai điểm

   

2;3 ; 4; 1 .AB

viết phương trình trung trực đoạn AB.

1 0.xy  

2 3 1 0.xy  

2 3 5 0.xy  

3 2 1 0.xy  

Câu 17: Cho đường thẳng

 







  



và điểm

; 2 .









Điểm

 

Ad

ứng với giá trị nào của t?

t 

t 

0t 

Câu 18: Phương trình tham số của đường thẳng (d) đi qua điểm

 

2;3M 

và vuông

góc với đường thẳng

 

:3 4 1 0d x y



  

là:

  









  









  



















Câu 19: Cho

 











. Điểm nào sau đây không thuộc

 

5;3 .A

 

2;5 .B

 

1;9 .C 

 

8; 3 .D 

Câu 20: Cho

 











Tìm điểm

 

Md

cách A một đoạn bằng 5.

8 10







 

44 32

4;4 , ; .







ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 32

 

24 2

4;4 ; ; .











 

24 2

4;4 ; ; .











Câu 21: Giao điểm M của

 







  



và

 

:3 2 1 0d x y



  

là:

2; .









0; .







0; .

















Câu 22: Phương trình nào sau đây biểu diển đường thẳng không song song với

đường thẳng

 

: 2 1?d y x

2 5 0.xy  

2 5 0.xy  

2 0.xy  

2 5 0.xy  

Câu 23: Cho hai đường thẳng

   

: 1 , : 2d mx y m d x my    

cắt nhau khi và chỉ

khi:

2.m 

1.m 

1.m 

1.m 

Câu 24: Cho hai đường thẳng

   

: 1 , : 2d mx y m d x my    

song song nhau khi

và chỉ khi:

2.m 

1.m 

1.m 

1.m 

Câu 25. Cho hai đường thẳng song song

:5 7 4 0; :5 7 6 0d x y d x y     

. Phương

trình đường thẳng song song và cách đều

và

5 7 2 0xy  

5 7 3 0xy  

5 7 3 0xy  

5 7 5 0xy  

Câu 26. Gọi

;I a b

là giao điểm của hai đường thẳng

: 4 0d x y

và

' : 3 5 0d x y

. Tính

. B.

. C.

. D.

Câu 27. Cho đường thẳng d:

3 3 0xy   

và điểm N(-2;4). Tọa độ hình chiếu

vuông góc của N trên d là:

 

3; 6

1 11

;









2 21

;







1 33

;

10 10







Câu 28. Cho ba điểm A(1;1), B(2;0), C(3;4). Viết phương trình đường thẳng đi qua A

và cách đều hai điểm B, C.

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 33

4 3 0; 2 3 1 0x y x y     

4 3 0; 2 3 1 0x y x y     

4 3 0; 2 3 1 0x y x y     

0; 2 3 1 0x y x y    

Câu 29. Cho đường thẳng

  











và điểm M(3;1). Tọa độ điểm A thuộc

đường thẳng



sao cho A cách M một khoảng bằng

   

0; 1 ; 1; 2

   

0;1 ; 1; 2

   

0; 1 ; 1;2

   

2; 1 ; 1; 2

Câu 30: Khoảng cách từ điểm

 

0;1M

đến đường thẳng



5 12 1 0xy  

bằng

C. 1 D.

Câu 31: Cho 2 điểm

   

2;3 , 1;4AB

. Đường thẳng nào sau đây cách đều 2 điểm A, B ?

10xy  

20xy

2 2 10 0xy  

100 0xy  

Câu 32: Khoảng cách giữa 2 đường thẳng 1 :

7 3 0xy  

và 2 :

7 12 0xy  

bằng

B. 9 C.

. D. 15

Câu 33: Cho ABC với

     

1;2 , 0;3 , 4;0A B C

Chiều cao tam giác ứng với cạnh BC bằng :

A. 3 B.

Câu 34: Khoảng cách từ điểm O(0 ; 0) tới đường thẳng  :



bằng

Câu 35: Diện tích ABC biết

     

3;2 , 0;1 , 1;5A B C

. C. 11 D.

Câu 36: Tìm côsin góc giữa 2 đường thẳng 1 :

10 5 1 0xy  

và 2 :











ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 34

. B.

3 10

Câu 37: Tìm côsin góc giữa 2 đường thẳng 1 :

2 2 0xy  

và 2 :

0xy

Câu 38: Góc giữa 2 đường thẳng 1 :

2 2 3 5 0xy  

và 2 :

60y 

có số đo

bằng:

A. 60

B. 125

. C. 145

D. 30

Câu 39: Góc giữa hai đường thẳng 1 :

30xy

và ø 2 :

10 0x 

có số đo bằng:

A. 45

B. 125

. C. 30

D. 60

Câu 40: Góc giữa 2 đường thẳng 1 :

6 5 15 0xy  

và 2 :

10 6

1 5 .











có số đo bằng

A. 90

B. 60

C. 0

D. 45

PHƢƠNG TRÌNH ĐƢỜNG TRÒN-TIẾP TUYẾN VỚI ĐƢỜNG TRÒN

I/ BÀI TẬP TỰ LUẬN.

Câu 1: Lập phương trình đường tròn

 

trong các trường hợp sau:

 

có tâm

 

1; 2I 

có bán kính

6R 

 

có tâm

 

5; 2I 

có đường kính

8d 

c )

 

có tâm

 

1;2I

và đi qua

 

4;6M

 

có đường kính

với

   

3; 5 , 3;3AB

 

đi qua ba điểm

     

1;2 , 5;2 , 1; 3A B C 

 

có tâm

 

3; 4I 

tiếp xúc với đường thẳng

4 3 15 0xy  

 

tiếp xúc với hai trục tọa độ

Ox,Oy

và đi qua điểm

 

2;1M

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 35

Câu 2: Cho đường tròn

 

có phương trình:

4 8 5 0x y x y    

a) Tìm tọa độ tâm và bán kính của đường tròn

 

b) Viết phương trình tiếp tuyến của

 

tại điểm

 

1;0M 

c) Viết phương trình tiếp tuyến với

 

biết tiếp tuyến vuông góc với đường thẳng

3 4 5 0xy  

II/ BÀI TẬP TRẮC NGHIỆM

Câu 1: Tâm

và bán kính

của đường tròn

   

2 3 16xy   

là:

 

2; 3 , 4IR

 

2;3 , 4IR

 

2; 3 , 16IR

 

2;3 , 16IR

Câu 2: Tâm

và bán kính

của đường tròn

2 8 8 0x y x y    

là:

 

1;4 , 5IR

 

1; 4 , 5IR

 

2;8 , 5IR

 

1; 4 , 8IR  

Câu 3: Với tất cả các giá trị nào của

thì phương trình

2 4 6 1 0x y mx my m     

là phương trình đường tròn?

 

; 1;



   





   

;1 3;m   

1; ;

   

   

   

   

 

; 2 ;



    





Câu 4: Đường tròn

2 10 1 0x y x y    

đi qua điểm nào trong các điểm dưới đây ?

A. (2 ; 1) B. (3 ; 2) C. (1 ; 3) D. (4 ; 1)

Câu 5: Tìm tọa độ giao điểm của đường thẳng  :

yx

và đường tròn (C) :

20x y x  

A. ( 0 ; 0) B. ( 0 ; 0) và (1 ; 1). C. ( 2 ; 0) D. (1 ; 1)

Câu 4: Tìm tọa độ tâm

đường tròn đi qua ba điểm

     

0;4 , 2;4 , 4;0A B C

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 36

 

0;0I

 

1;0I

 

3;2I

 

1;1I

Câu 5: Tìm bán kính

đường tròn đi qua ba điểm

     

0;4 , 3;4 , 3;0A B C

5R 

3R 

R 

Câu 6: Một đường tròn có tâm

 

3; 2I 

tiếp xúc với đường thẳng  :

5 1 0xy  

. Hỏi bán

kính đường tròn bằng bao nhiêu ?

A. 6 B.

Câu 7: Đường tròn nào sau đây tiếp xúc với trục Ox ?

2 10 0x y x y   

. B.

6 5 9 0x y x y    

10 1 0x y y   

50xy  

Câu 8: Đường tròn nào sau đây tiếp xúc với trục Oy ?

10 1 0x y y   

6 5 1 0x y x y    

20x y x  

. D.

50xy  

Câu 9: Tâm đường tròn

10 1 0x y x   

cách trục Oy bao nhiêu ?

A.  5 B. 0 C. 10. D. 5

Câu 10: Đường tròn

2 2 23 0x y x y    

cắt đường thẳng x  y + 2 = 0 theo một dây

cung có độ dài bằng bao nhiêu ?

A. 5 B.

2 23

C. 10 D.

PHƢƠNG TRÌNH ĐƢỜNG ELIP

BÀI TẬP TRẮC NGHIỆM.

Câu 1: Đường Elip



có 1 tiêu điểm là :

A. (0 ; 3) B.

(0 ; 3)

C. (

3

; 0) D. (3 ; 0)

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 37

Câu 2: Đường Elip

16 7



có tiêu cự bằng :

A. 18 B. 6 C. 9 D. 3

Câu 3: Phương trình của Elip có độ dài trục lớn bằng 8, độ dài trục nhỏ bằng 6 là:

9 16 144xy

9 16



9 16 1xy

64 36



Câu 5: Tâm sai của Elip



bằng :

C. 4 D.

Câu 6: Tìm phương trình chính tắc của Elip có tiêu cự bằng 6 và trục lớn bằng 10

25 9



100 81



25 16



25 16



Câu 7 Tìm phương trình chính tắc của Elip có tâm sai bằng

và trục lớn bằng 6



Câu 8: Tìm phương trình chính tắc của Elip có tiêu cự bằng 6 và đi qua điểm A(0; 5)

100 81



15 16



25 9



25 16



ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 38

Câu 9: Tìm phương trình chính tắc của Elip có trục lớn gấp đôi trục bé và có tiêu cự bằng

36 9



36 24



24 6



16 4



Câu 10: Tìm phương trình chính tắc của Elip có trục lớn gấp đôi trục bé và đi qua điểm

 

2; 2A 

24 6



36 9



16 4



20 5



Câu 11: Một elip có trục lớn bằng 26, tâm sai

e 

. Trục nhỏ của elip có độ dài bằng bao

nhiêu?

A. 10 B. 12 C. 24 D. 5

Câu 12: Cho Elip có phương trình :

9 25 225xy

. Lúc đó hình chữ nhật cơ sở có diện

tích bằng:

A. 15 B. 40 C. 60 D. 30

Câu 13: Tìm phương trình chính tắc của Elip có một đỉnh của hình chữ nhật cơ sở là M(4; 3)

16 9



16 9



16 4



Câu 14: Biết Elip(E) có các tiêu điểm F1(-

; 0), F2(

;0) và đi qua M( -

;

). Gọi N là

điểm đối xứng với M qua gốc toạ độ . Khi đó:

ĐỀ CƯƠNG TOÁN 10 HKII

GV: NGUYỄN QUỐC HIỆP Page 39

A. NF1+ MF2 =

B. NF2 + MF1 =

Câu 15: Cho Elip (E) có các tiêu điểm F1( - 4; 0 ), F2( 4; 0 ) và một điểm M nằm trên (E) biết

rằng chu vi của tam giác MF1F2 bằng 18. Lúc đó tâm sai của (E) là:

e 

e 

Bấm Tải xuống để xem toàn bộ.

| 1/40

| | Tải xuống

Preview text:

TAM KỲ 4/2017 ĐỀ CƢƠNG ÔN THI HỌC KỲ II TOÁN 10
BIÊN SOẠN: GV NGUYỄN QUỐC HIỆP
NGHỊ LỰC VÀ BỀN BỈ CÓ THỂ CHINH PHỤC MỌI THỨ ĐỀ CƯƠNG TOÁN 10 HKII
ĐỀ CƢƠNG ÔN TẬP HỌC KỲ II TOÁN 10
BIÊN SOẠN VÀ GIẢNG DẠY GV NGUYỄN QUỐC HIỆP A/ ĐẠI SỐ.
 CHƢƠNG IV: BẤT ĐẲNG THỨC BẤT PHƢƠNG TRÌNH.
BẤT PHƢƠNG TRÌNH- HỆ BẤT PHƢƠNG TRÌNH MỘT ẨN.
I/BÀI TẬP TỰ LUẬN
1) Tìm điều kiện của các bất phƣơng trình sau: x 1 x 1 a)  0
 x  x   x   c)  x  2  0 x  b) 2 5 1 0 3 2  x
2) Xem xét cặp bất phƣơng trình nào là tƣơng đƣơng? 1 a) 2
x  x và x 1 b) 4 2 x  x và 2 x  1 c)  1 và x 1 x
3) Giải các bất phƣơng trình- hệ bất phƣơng trình sau? 3x 1 x  2 1 2x a)  
b)  x   x   2 1 2
2  2  x   x   1  x  2 2 3 4     2 2 x 3 7 2x
c)  x  4  x   1  0
d)  x  3  x   1  0 e) 
4  4x  6x 1
II/BÀI TẬP TRẮC NGHIỆM 1
Câu 1. Tập xác định của bất phương trình
 x  3  x  6  x 2x  là: 2 A. D   3  ;6\  1 B. D   3  ; \  1 C. D   3  ;6 \  1 D. D   ;  6\  1
Câu 2. Tập nghiệm của bất phương trình x x  6  5  2x  10  x x  8 là: A. S   B. S  C. S   ;5  
D. S  5; Câu 3. x  2
 là nghiệm của bất phương trình nào sau đây: A. x  2 B.  x   1  x  2  0 GV: NGUYỄN QUỐC HIỆP Page 1 ĐỀ CƯƠNG TOÁN 10 HKII x 1 x C.   0
D. x  3  x 1 x x
Câu 4. Bất phương trình x  x  2  2  x  2 có tập nghiệm: A. S   B. S   ;  2 C. S    2
D. S  2;
Câu 5: Chọn khẳng định đúng trong các khẳng định sau: 1 A. 2
x  3x  x  3 B.  1  x  1 x x 1 C.  0  x 1  0
D. x  x  x  x  0 3 x
Câu 6 : Cho các cặp bất phương trình sau: I. x 1  0 và 2 x  x   1  0 1 II. x 1 0 và x   1  0 2 x  1 III. x 1 0 và 2 x  x   1  0 IV. x 1 0 và 2 x  x   1  0
Số cặp bất phương trình tương đương là: A. 1 B. 2 C. 3 D. 4
2x 1  3x  4
Câu 7: Hệ bất phương trình  có tập nghiệm là: 5
 x  3  8x  9 A. S   B. S   ;  3   C. S   ;  4 D. S   3  ;4  1
15x  2  2x  
Câu 8. Hệ bất phương trình 3 
có tập nghiệm nguyên là: 3x  14 2  (x  4)   2 A.  1 B.1;  2 C.  D.  1 GV: NGUYỄN QUỐC HIỆP Page 2 ĐỀ CƯƠNG TOÁN 10 HKII 2  x  4  0
Câu 9. Cho hệ bất phương trình 
. Giá trị của m để hệ bất phương
mx  m  2  0  trình vô nghiệm là: 2 2 A. 0  m  B.m  C.m  0 D. m  0 3 3 x   2m  2 
Câu 10. Với giá trị nào của m thì hệ bất phương trình  có nghiệm duy 2 x  m  1   nhất? A.1;  3 B. 1;   3 C.4;   3 D. 
DẤU CỦA NHỊ THỨC BẬC NHẤT- HỆ BẤT BẬC NHẤT HAI ẨN
I/BÀI TẬP TỰ LUẬN.
1) Xét dấu các biểu thức sau: x  2 x 1
a) f  x   x   1 2  x
b) g  x     c) h x 3 1   4  x 2x 1 x  2
2) Giải các bất phƣơng trình sau: x   1  x  5 1 3 a)  x   1  3  x  0 b)  0   0 6  c) 2x 1 2x x  4 d) 5  8x  11
e) 5  8x  x  2
f) x  2  1 x  x  2
II/BÀI TẬP TRẮC NGHIỆM.
Câu 1. Nhị thức f x 2x
4 luôn âm trong khoảng nào sau đây: A. ;0 B. 2; C. ;2 D. 0;
Câu 2. Cho biểu thức f x x 1 x
2 Khẳng định nào sau đây đúng: A. f x 0, x 1; B. f x 0, x ;2 C. f x 0, x C. f x 0, x 1;2
Câu 3. Nhị thức nào sau đây dương với mọi x 3 GV: NGUYỄN QUỐC HIỆP Page 3 ĐỀ CƯƠNG TOÁN 10 HKII A. f x 3 x B. f x 2x 6 C. f x 3x 9 D. f x x 3
Câu 4. Bất phương trình m 1 x 1
0 có nghiệm với mọi x khi A. m 1 B. m 1 C.m 1 D.m 1
Câu 5. Cho bảng xét dấu: x  2  f x   0 
Hàm số có bảng xét dấu như trên là:
A. f x   x  2
B. f x   x
  2 C. f x   16  8x
D. f x   2  4x
Câu 6. Tập nghiệm của bất phương trình x  3 2x  6  0 là : A. 3;3 B.  ;
 3  3; C.  3  ;3   D. \ 3;3
Câu 7. Tập nghiệm của bất phương trình 3  2x  2x  7  0  7 3  7 2   7   3  2 7  A.  ;   B.   ;  C.   ;
     ; D. ;   2 2   2 3   2 2     3 2  
Câu 8. Hàm số có kết quả xét dấu x  -1 2  f x   0   là hàm số x 
A. f x   x  1 x  2 B. f x  1  x  2 x  C. f x  1 
D. f x   x  1 x  2 x  2
Câu 9. Hàm số có kết quả xét dấu GV: NGUYỄN QUỐC HIỆP Page 4 ĐỀ CƯƠNG TOÁN 10 HKII x  1   f x   0  là hàm số x  1
A. f x   x  1
B. f x    x  12  C. f x  10 
D. f x   x   1 x  1
Câu 10. Hàm số có kết quả xét dấu x  0 2  f x   0  0  là hàm số
A. f x   x x  2
B. f x   x  2 x
C. f x  
D. f x   x 2  x  x  2 x  1
Câu 11. Tập nghiệm của bất phương trình  0 2  x A.  1  ;2   B. 1;2 C.  ;  1    2; D. 1;2   2x  1
Câu 12. Tập nghiệm của bất phương trình  0 2 3x  6  1   1   1   1  A.  ;  B.   ;2 C.  ;   D. 2;    2  2    2  2  
Câu 13. Điều kiện m để bất phương trình m  1x  m  2  0 vô nghiệm là A. m B. m  
C. m  1; 
D. m  2;  GV: NGUYỄN QUỐC HIỆP Page 5 ĐỀ CƯƠNG TOÁN 10 HKII
Câu 14. Điều kiện m để bất phương trình  2
m  1x  m  2  0 có nghiệm với mọi
giá trị của x là A. m B. m  
C. m  1; 
D. m  2;  1
Câu 15. Tập nghiệm của bất phương trình  1 là x  1 A. 1  ;2   B. 1;2 C.  ;1   D.  ;1  
Câu 16. Cho 0  a  b , Tập nghiệm của bất phương trình x  a  ax  b  0 là:  b  A.  ;
 a    ;b B.   ;
    a; a    b  C.  ;
  b  a; D.  ;
 a    ; a  
Câu 17. Tìm m để bất phương trình x  m  1 có tập nghiệm S  3;    A.m  3  B. m  4 C. m  2  D. m  1
Câu 18. Tìm m để bất phương trình 3x  m  5 x  1 có tập nghiệm S  2;  là A. m  2  B. m  3  C. m  9  D. m  5 
Câu 19. Điều kiện của tham số m để bất phương trình 2
m x  mx  1 có tập nghiệm là là:
A. m  0 m  1  B. m  0 C. m 1 D. m  1 
Câu 20. Tập nghiệm của bất phương trình 4  3x  8 là  4   4   4  A.  ;    B.  ; 4   C.  ;  4   ;    4;   3  D.     3   3  
Câu 21. Tập nghiệm của bất phương trình 2x 3 x 12 A. ;15 B. 3;15   C. ; 3
D. ; 3  15;     GV: NGUYỄN QUỐC HIỆP Page 6 ĐỀ CƯƠNG TOÁN 10 HKII 2x 1
Câu 22. Tập nghiệm của bất phương trình 2 là x 1 3 3 3 A. 1; B. ; 1; C. ; D. ;1 4 4 4
Câu 23. Tập nghiệm của bất phương trình x 15 3 là A. 6; B. ;4 C. D.
Câu 24. Tập nghiệm của bất phương trình x 2 x 1 1 1 1 A. B. 0; C. ; D. ; 2 2 2
Câu 25. Tập nghiệm S của bất phương trình 4  2x  3  x  2x là:
A. S  7; B. S   ;  7 C. S   ;  7  
D. S  7;
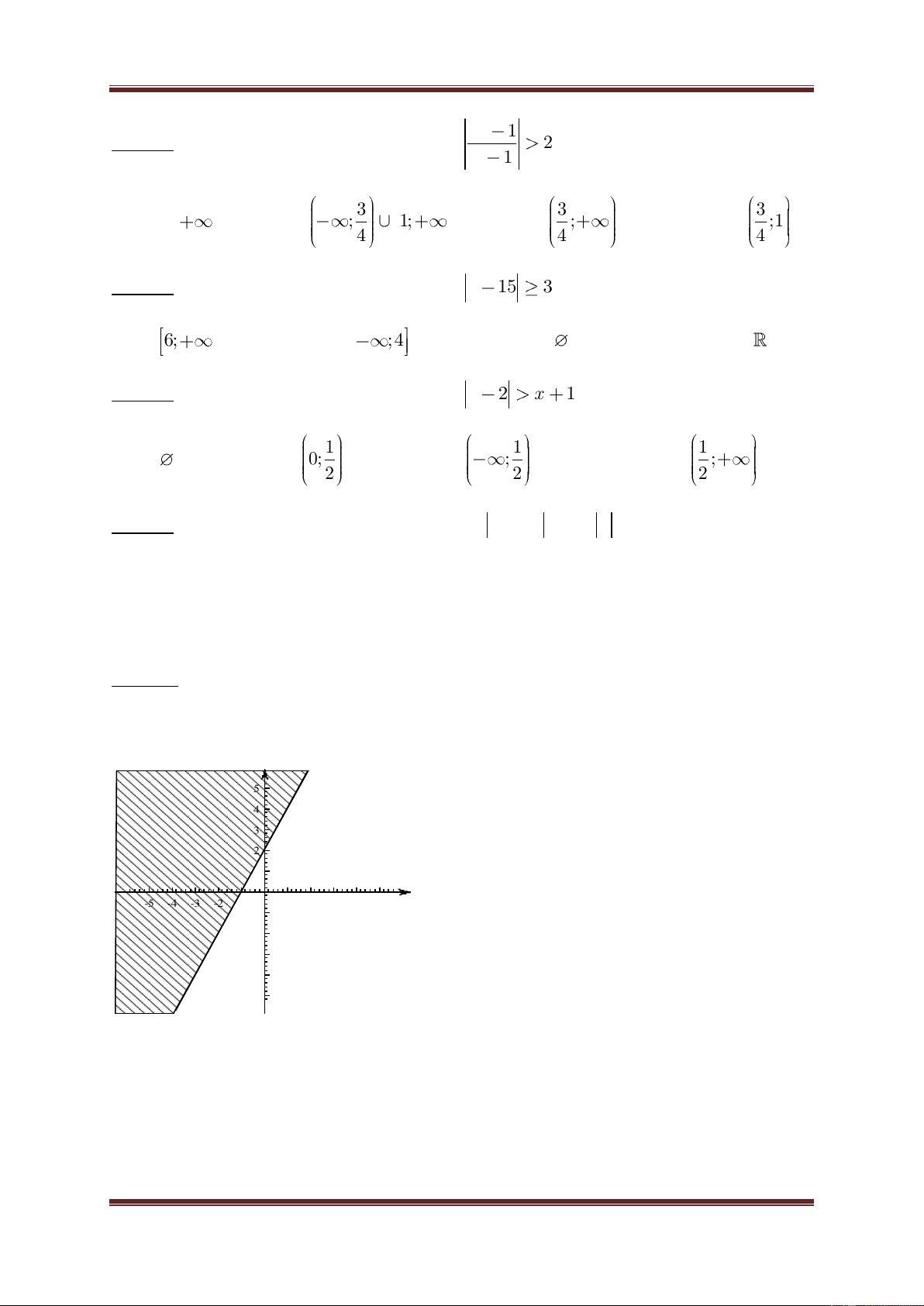
Câu 26. Miền không bị gạch chéo (không kể đường thẳng d) là miền nghiệm của bất phương trình nào? y 5 4 3 2 1 x -5 -4 -3 -2 -1 1 2 3 4 5 -1 -2 -3 -4 -5
A. x  2 y  2  0
B. 2x  y  2  0
C. 2x  y  2 
D. x  2 y  2  GV: NGUYỄN QUỐC HIỆP Page 7 ĐỀ CƯƠNG TOÁN 10 HKII
Câu 27. Miền không bị gạch chéo (kể cả đường thẳng d1 và d2) là miền nghiệm của
hệ bất phương trình nào? 5 4 3 2 1 -5 -4 -3 -2 -1 1 2 3 4 5 -1 -2 -3 -4 -5
x  y 1 0
x  y 1 0 A.  B. 
2x  y  4  0
2x  y  4  0
x  y 1 0
x  y 1 0 C.  D. 
2x  y  4  0
x  2y  4  0
Câu 28. Cặp số 1; 1 là nghiệm của bất phương trình
A. x  y  2  0 B. x   y  0
C. x  4y  1 D. x   3y  1  0
Câu 29. Điểm M 0; 3
 thuộc miền nghiệm của hệ bất phương trình: 0   2
 x  y  3 2
 x  y  3 A.  B.
2x  5y  12x  8  
2x  5y  12x  8  2
 x  y  3 2
 x  y  3 C. 2
 x  5y  12x  8 D.  
2x  5y  12x  8 
3x  4y  12  0 
Câu 30. Miền nghiệm của hệ bất phương trình :  x  y  5  0  x  1  0 
Là miền chứa điểm nào trong các điểm sau? A. M 1; 3 B. N 4;3 C. P 1;5 D. Q 2; 3 GV: NGUYỄN QUỐC HIỆP Page 8 ĐỀ CƯƠNG TOÁN 10 HKII
DẤU CỦA TAM THỨC BẬC HAI
I/ BÀI TẬP TỰ LUẬN
Câu 1: Lập bảng xét dấu các biểu thức sau: a) f  x 2
 x  4x  3
b) g  x   2
x  x   2 2 1 3x  4x
 2x 4x4 2x 5x4
c) h x   2
x  x   2
1 x  3x  2
d) k  x  2 4x  x  3
Câu 2: Giải các bất phương trình sau: a) 2
x  2017x  2016  0 b) 2
x  6x  9  0 1 3 c)  2
x  x   2 3 2
1 2x  4x  0 d)  2 2 x  4 3x  x  4
Câu 3: Cho phương trình: 2
mx  2m  
1 x  4m 1  0 , tìm tất các các giá trị của tham
số m để phương trình có a) Hai nghiệm trái dấu. b) Hai nghiệm phân biệt c) Các nghiệm dương d) Các nghiệm âm
Câu 4: Tìm tất các các giá trị của tham số m để các bất phương trình sau có nghiệm đúng với mọi x 2 x  mx  2 a) 2
5x  x  m  0
b) mm   2
2 x  2mx  2  0 c)  1  2 x  3x  4
Câu 5: Tìm tất các các giá trị của tham số m để các biểu thức sau luôn dương a) 2
x  x  m b) 2 mx 10x  5
Câu 6: Giải các bất phương trình sau:
a) x  3  1 x
b) x  2  5  4x
c) 3  x  5  x
II/ BÀI TẬP TRẮC NGHIỆM
Câu 1. Hàm số có kết quả xét dấu GV: NGUYỄN QUỐC HIỆP Page 9 ĐỀ CƯƠNG TOÁN 10 HKII x  1 2  f x   0  0  là hàm số
A. f x  2
 x  3x  2 B. f x  2
 x  3x  2
C. f x   x  1  x   2
D. f x  2  x   3x  2
Câu 2. Hàm số có kết quả xét dấu x  1 2 3  f x   0  0  0  là hàm số
A. f x   x    2
3 x  3x  2
B. f x     x   2 1
x  5x  6
C. f x   x    2 2 x   4x  3
D. f x   1  x  2  x  3  x 
Câu 3. Hàm số có kết quả xét dấu x  1 2 3  f x   0  0  0  là hàm số
A. f x   x    2
2 x  4x  3
B. f x   x    2 1
x  5x  6
C. f x   x  1 3  x  2  x 
D. f x     x   2 3
x  3x  2
Câu 4. Cho bảng xét dấu GV: NGUYỄN QUỐC HIỆP Page 10 ĐỀ CƯƠNG TOÁN 10 HKII x  1 2 3 
f x  + 0   0 +
g x    0  
f x   0   0  g x  f x  2 x  4x  3 f x  2 x  4x  3 A.  B.  g x  2 x  4x  4 g x  x  2
f x  x  2x  1 f x  2 x   4x  3 C.   g x  x  D. 3 g x  2  x
Câu 5. Cho các mệnh đề
I Với mọi x   1  ;4   , f x  2
 x  4x  5  0
II Với mọi x  ;
 4  5;10 ,g x  2
 x  9x  10  0
III h x 2
 x  5x  6  0 Với mọi x  2  ;3  
A. Chỉ mệnh đề III đúng
B. Chỉ mệnh đề I vàII đúng
C. Cả ba mệnh đề điều sai
D. Cả ba mệnh đề điều đúng x  3x  10
Câu 6. Khi xét dấu biểu thức f x  2  ta có 2 x  1
A. f x   0 khi 5   x  1  hay 1  x  2
B. f x   0 khi x  5  hay 1
  x  1 hay x  2
C. f x   0 khi 5   x  2
D. f x   0 khi x  1 
Câu 7. Tập nghiệm của bất phương trình 2
x  4x  3  0 là GV: NGUYỄN QUỐC HIỆP Page 11 ĐỀ CƯƠNG TOÁN 10 HKII A.  ;
 3  1;     B. 3;   1 C.  ;
 1  3;     D.  3  ; 1    
Câu 8. Tập nghiệm của bất phương trình 2 x
  x  6  0 là A.  ;
 2  3;     B.  C.  ;
 1  6;     D.  2  ;3  
Câu 9. Bất phương trình có tập nghiệm 2;10 là A. 2 x 12x 20 0 B. 2 x 3x 2 0 2 C. 2 x 12x 20 0 D. x 2 10 x 0
Câu 10. Tìm m để f x  2
 x  m  2x  8m  1 luôn luôn dương A.m  0;28
B.m  ;0  28; 
C. m  ;0  28;    
D. m  0;28  
Câu 11. Tìm m để f x  2
 mx  2 m  1x  4m luôn luôn dương  1     1  A.  1;  B.    1 ; 1   ; C. 0; 
D.  ;   3   3   3  
Câu 12.Tìm m để f x  2
 2x  2 m  2x  m  2 luôn luôn âm A. 0;2 B.  ;  0  2; C.  ;  0  2;     D. 0;2  
Câu 13. Tìm m để f x  2
 mx  2 m  1x  4m luôn luôn âm  1  1
A. m   1;  B.m  ;   
  1   ;  3   3   1 
C. m  ; 1
D. m   ;    3 
Câu 14. Tìm m để 2
x  mx  m  3  0 có tập nghiệm là R GV: NGUYỄN QUỐC HIỆP Page 12 ĐỀ CƯƠNG TOÁN 10 HKII A. 6;2 B.  ;
 6  2; C.  6  ;2   D.  ;  6    2  ;    
Câu 15. Tìm m để 2
mx  4 m  1x  m  5  0 vô nghiệm  1   1 
A. m   1;   B. m  1;     3   3  1
C. m  ;0 D.m     ;   1   ;      3 
Câu 16. Tìm m để 2
2x  2 m  2x  m  2  0 có hai nghiệm phân biệt  1  1 A.m   0;  B. m  ;0       ;  2   2   1 1 C. m  0;  D. m     ;0  ;      2 2  2 x
  7x  6  0
Câu 17. Tập nghiệm S của hệ  là 2
x  8x  15  0  A.S  1; 3   B.S  5;6  
C.S  1;3  5;6    
D. S  
Câu 18. Để phương trình 2
x  m   2
1 x  2m  3m  5  0 có hai nghiệm trái dấu thì m thuộc  5   5   5   5  A. 1;   B. 1;  C. 1;   D. 1;     2   2   2   2  2 x   2x  5
Câu 19. Với giá trị nào của m để bất phương trình  0 nghiệm đúng với 2 x  mx  1 mọi x ? A. m  2;2   B. m  2;2
C. m  ; 2  2;     D. m 
Câu 20. Để giải bất phương trình 4 3 2
x  3x  2x  0 , một học sinh lập luận ba giai đoạn như sau: 1 Ta có: 4 3 2 2 2
x  3x  2x  0  x (x  3x  2)  0 GV: NGUYỄN QUỐC HIỆP Page 13 ĐỀ CƯƠNG TOÁN 10 HKII 2 Do 2 2 2 2 x  0 neân x
(x  3x  2)  0  x  3x  2  0 x   1 3 2 2
x  3x  2  0   Suy rax
 3x  2  0  1  x  2 x  2 
Vậy: Tập nghiệm của bất phương trình là: 1;2
Hỏi: Lập luận trên đúng hay sai? Nếu sai thì sai từ giai đoạn nào? A. Sai từ 3 B. Lập luận đúng C. Sai từ 2 D. Sai từ 1 2
Câu 21. Cho phương trình bậc hai x  2mx  m  2  0 . Phát biểu nào sau đây là đúng?
A. Phương trình luôn có hai nghiệm phân biệt.
B. Phương trình luôn vô nghiệm.
C. Phương trình chỉ có nghiệm khi m > 2.
D. Tồn tại một giá trị m để phương trình có nghiệm kép. 2  x   5x  4  0
Câu 22. Tìm m để hệ bất phương trình  có nghiệm duy nhất 2
x  (m  1)x  m  0  A. m  1 B. m  2 C. m  1 
D. m  4 2
x  7x 12  0
Câu 23. Cho hệ bất phương trình 
. Hệ có nghiệm khi và chỉ khi giá trị x  m  0 của m là A. m  3 B.m  4 C.m  4 D. 3  m  4
Câu 24. Với giá trị nào của m để hai bất phương trình 2
x  m  4m  3  0 và
2x  3m  x  3 tương đương?
A. m  7 hoặc m  0 B. m  1 hoặc m  3 C. m   D. m R
Câu 25. Tập nghiệm S của bất phương trình 2
x  6x 5  8  2x là:
A. S  ;3  5; 
B. S  ;3
C. S  5;  D. S  3;5 GV: NGUYỄN QUỐC HIỆP Page 14 ĐỀ CƯƠNG TOÁN 10 HKII
 CHƢƠNG IV: CUNG VÀ GÓC LƢỢNG GIÁC- CÔNG THỨC LƢỢNG GIÁC
CUNG VÀ GÓC LƢỢNG GIÁC
I/ BÀI TẬP TỰ LUẬN. Câu 1: 2  a) Cho sin  và
    ,tính các giá trị lượng giác còn lại của góc  5 2 13  b) Cho tan   và 
   0 , tính các giá trị lượng giác còn lại của góc  8 2
Câu 2: Rút gọn các biểu thức sau:    a) M  sin      sin   sin  
   cos    2        b) N  tan  
   tan     2cot
  cot    cot        2   2   3 
c) P  sin   2016   cos 2017    tan   2019  cot  cos       2    d) A  x x           x 3 sin( ) cos( ) cot 2  tan  x   2  2   3   3   3   3  e) A  cos  a  sin  a  cos  a  sin  a          2   2   2   2 
Câu 3: Chứng minh các đẳng thức sau: 2 2 sin   2cos  1 a) 4 4 2
sin   cos  1  2sin  b) 2  sin  2  cot 2 2 1 sin  cos  2 2 sin   tan  c) 2 2  cos   tan  d) 6  tan  2 cos  2 2 cos   cot  e)     3     3 1 cot sin 1 tan cos   sin  cos sin cos2 1 f) 2  2tan  cot  sin cos Câu 4: GV: NGUYỄN QUỐC HIỆP Page 15 ĐỀ CƯƠNG TOÁN 10 HKII 5 a) Cho sin  cos 
. Tính A  sin.cos 3 3
, B  sin cos , C  sin   cos  ? 4
b) Cho tan  cot  m . Tính theo m giá trị của các biểu thức 2 2
D  tan   cot  3 3
, E  tan   cot  ? 3 c) Cho tan 
, tính giá trị của các biểu thức sau: 5     sin cos A  sin  cos 2 2        3sin 12sin cos cos B  2 2
sin   sin cos  2cos 
Câu 5: Tính giá trị của biểu thức:  2 8 a) A  cos  cos  ... cos 9 9 9   7  b) 2 2 2 2 B  sin  sin  sin  sin 3 9 18 6  2 9 c) C  sin  sin ... sin 5 5 5 d) 0 0 0 0
D  tan1 tan 2 tan 3 ....tan89    9   e) 2 2 2 2 E  sin  sin  sin  sin  tan cot 6 3 4 4 6 6 f) 2 0 2 0 2 0 2 0 2 0 2 0 2 0
F  cos 15  cos 25  cos 35  cos 45  cos 105  cos 115  cos 125
II/ BÀI TẬP TRẮC NGHIỆM.
Câu 1: Chọn khẳng định sai trong các khẳng định sau:  23 5 3 A. 60  B. 230  C. 150 D.  145 3 18 6 4 
Câu 2: Đường tròn có bán kính R  20cm . Độ dài của cung tròn có số đo là: 4    A. l  m B. l  cm C. l  cm D. l  5cm 5 4 5
Câu 3: Chọn khẳng định sai trong các khẳng định sau? sin  A. 1   sin 1 B. tan  ( 
 k ,k  Z) cos 2 cos
C. cos  k2   cos ,k  Z D. cot  
(  k , k  Z ) sin
Câu 4: Chọn khẳng định sai trong các khẳng định sau: GV: NGUYỄN QUỐC HIỆP Page 16 ĐỀ CƯƠNG TOÁN 10 HKII 1 A. 2 2 sin   cos   1 B. 2 1 tan   (cos  0) 2 cos  1  C. 2 1 cot   (sin  0) D. tan.cot  1
 (  k ,k  Z) 2 sin  2
Câu 5: Chọn khẳng định đúng trong các khẳng định sau?  sin  0  sin  0 A. 0      B.       2 cos  0 2 cos  0 3 sin  0 3 sin  0 C.       D.       2 cos  0 2 cos  0
Câu 6: Chọn khẳng định đúng trong các khẳng định sau?    A. sin      sin B. cos   sin    2 
C. cos    cos
D. tan     tan
Câu 7. Trong các khẳng định sau khẳng định nào sai?
A. tan(  )   tan B. tan(   )   tan 
C. tan(   )   tan D. tan(   )  cot  2
Câu 8. Trong các khẳng định sau khẳng định nào đúng? 
A. cos(   )  sin(  )
B. cos(  )  cos(   ) 2  C. cos(  2   )  co  s
D. cos(  )  cos(   ) 2
Câu 9. Trong các khẳng định sau khẳng định nào đúng?  
A. cot(   )  tan(   )
B. tan(  )  tan(   ) 2 2   C. tan(  )  tan(   )
D. tan(  )  tan(  ) 2 2 1
Câu 10. Cho sinx = và 0 0 90  x  270 thì 2 3 A. cotx =  B. cotx =  3 3 3 C. cotx = D. cotx = 3 3 GV: NGUYỄN QUỐC HIỆP Page 17 ĐỀ CƯƠNG TOÁN 10 HKII 2  3 
Câu 11: Cho cosx   ,   x  . 
 Khi đó tan x bằng 5  2  21 21 21 21 A. B. C.  D.  5 2 5 5 3
Câu 12. Cho    
. Trong các khẳng định sau khẳng định nào đúng? 2 7 7 A. sin( )  0 B. sin( )  0 2 2 7 7 C. sin( )  0 D. sin( )  0 2 2 2
Câu 13: Cho tan 
. Khẳng định nào sau đây đúng ? 5 5 2 A. cot  5 B. cot  C. cot  D. cot  2 2 5
Câu 14: Cặp đẳng thức nào sau đây không thể đồng thời xảy ra ? 2 6
A. sin  0,6 va cos  0,8
B. sin  0, 2 va cos   5 2 6
C. sin  0, 2 va cos  0,8 D. sin  0  , 2 va cos   5 13
Câu 15: Trên đường tròn lượng giác như hình vẽ bên, cho sd AM  . Tìm vị trí 4 điểm M.
A. M là trung điểm của cung nhỏ BC
B. M là trung điểm của cung nhỏ CD
C. M là trung điểm của cung nhỏ AD
D. M là trung điểm của cung nhỏ AB
Câu 16: Đổi 294030’ sang radian. Chọn đáp án đúng trong các đáp án sau. A. 0 294 30 '  5,14 B. 0 294 30 '  4,14 C. 0 294 30 '  4, 41 D. 0 294 30 '  5, 41  Câu 17: Cho 
   0 . Khẳng định nào sau đây đúng ? 2 A. cos  0 B. sin  0 C. cot  0 D. tan  0 GV: NGUYỄN QUỐC HIỆP Page 18 ĐỀ CƯƠNG TOÁN 10 HKII  3 1 
Câu 18: Trên đường tròn lượng giác, điểm N   ;  
 là điểm cuối của cung lượng 2 2  
giác α có điểm đầu A. Tìm α, biết rằng α là một trong bốn số đo cho dưới đây. A. 0   210  B. 0   210 C. 0   30  D. 0   30
Câu 19: Đẳng thức nào sau đây có thể xảy ra ? 7 3 A. cos  1,1 B. cos  C. cos  0  ,1 D. cos   2 7
Câu 20: Tìm α, biết cos  0 .
A.   k , k  Z
B.   k 2 , k  Z  C.  
 k ,k  Z
D.    k , k  Z 2
CÔNG THỨC LƢỢNG GIÁC
I/ BÀI TẬP TỰ LUẬN.
Câu 1: Chứng minh rằng:       1 a) cos x cos  x cos  x  cos3x      3   3  4
b) sin 5x  2sin xcos 4x  cos 2x  sin x
sin 45    cos45   c)       tan sin 45 cos 45
Câu 2: Rút gọn các biểu thức sau: 2    4sin   a) sin 2 sin B A  b)  1 cos 2  cos 2 1 cos 2    2         1 sin 2sin 45   c) 1 cos sin  2  C  d) D  1 cos  sin  4cos 2
II/ BÀI TẬP TRẮC NGHIỆM  
Câu 1: Giả sử A  tan . x tan (
 x)tan (  x) được rút gọn thành A  tan nx . Khi đó 3 3 n bằng : A. 2. B. 1. C. 4. D. 3.
Câu 2: Nếu sinx = 3cosx thì sinx.cosx bằng: GV: NGUYỄN QUỐC HIỆP Page 19 ĐỀ CƯƠNG TOÁN 10 HKII 3 2 1 1 A. B. C. D. 10 9 4 6
Câu 3: Giá trị của biểu thức 0 0 0 0 0 0
tan110 .tan 340 sin160 .cos110 sin 250 .cos340 bằng A. 0 . B. 1 . C. 1. D. 2 . 5
Câu 4: Cho sin a 
. Tính cos 2asin a 3 17 5 5 5 5 A. B.  C. D.  27 9 27 27 x sin kx
Câu 5: Biết cot  cot x 
, với mọi x để các biểu thức có nghĩa. Lúc đó giá 4 x sin sin x 4 trị của k là: 5 3 5 3 A. B. C. D. 4 4 8 8   
Câu 6: Nếu cos  sin   2 0      thì  bằng:  2      A. B. C. D. 6 3 4 8
Câu 7: Nếu a =200 và b =250 thì giá trị của (1+tana)(1+tanb) là: A. 2 B.2 C. 3 D. 1 + 2 1 5 cos 
Câu 8: Tính B   . 3  , biết tan 2 2 cos 2 2 20 2 10 A.  B. C. D.  21 9 21 21    3   
Câu 9: Giá trị của tan    sin         3  bằng bao nhiêu khi 5  2 .  38  25 3 8  5 3 8  3 38  25 3 A. . B. . C. . D. 11 11 11 11 . 1 1
Câu 10: Giá trị của biểu thức  bằng 0 0 sin18 sin 54 GV: NGUYỄN QUỐC HIỆP Page 20 ĐỀ CƯƠNG TOÁN 10 HKII 1  2 1  2 . B. 2 . C. 2  . . A. 2 D. 2
Câu 11: Biểu thức tan300 + tan400 + tan500 + tan600 bằng:  3  8 3 4 3 A. 41    B. 0 cos 20 C. 2 D. 0 sin 70 3   3 3
Câu 12: Nếu  là góc nhọn và sin2 = a thì sin + cos bằng:
A.  2 1 a 1 B. 2
a 1  a  a C. a 1 D. 2
a  1  a  a 0 0 cos80  cos 20
Câu 13: Giá trị biểu thức bằng 0 0 0 0
sin 40 .cos10  sin10 .cos 40 3 A. B. 1 C. 1
D. sin(a  b) 2     sin cos  sin cos
Câu 14: Giá trị biểu thức 15 10 10 15 bằng: 2  2  cos cos  sin sin 15 5 5 5 1 A. 1 B. 3 C. 1 D. 2  Câu 15: Cho 0
  60 , tính E  tan  tan 4 1 A. 1 B. 2 C. 3 D. 2 1 3
Câu 16: Đơn giản biểu thức C   0 0 sin10 cos10 A. 0 4 sin 20 B. 0 4cos 20 C. 0 8cos 20 D. 0 8sin 20 3
Câu 17: Cho sin  . Khi đó cos 2 bằng: 4 1 7 7 1 A. . B. . C.  . D.  . 8 4 4 8 GV: NGUYỄN QUỐC HIỆP Page 21 ĐỀ CƯƠNG TOÁN 10 HKII     sin .cos  sin cos
Câu 18: Giá trị biểu thức 15 10 10 15 là 2  2  cos cos  sin .sin 15 5 15 5 3 3 A.  B. 1  C. 1 D. 2 2
Câu 19: Đẳng thức nào trong các đẳng thức sau là đồng nhất thức?
1) sin2x = 2sinxcosx
2) 1–sin2x = (sinx–cosx)2 
3) sin2x = (sinx+cosx+1)(sinx+cosx–1)
4) sin2x = 2cosxcos( –x) 2 A. Chỉ có 1) B. 1) và 2) C. Tất cả trừ 3) D. Tất cả 5 3  
Câu 20: Biết sin a  ; cos b  (
 a  ; 0  b  ) Hãy tính sin(a  b) . 13 5 2 2 3 63 56 33 A. B. C. D.  2 65 65 65 B/ HÌNH HỌC
 CHƢƠNG II: TÍCH VÔ HƢỚNG CỦA HAI VECTO- ỨNG DỤNG
HỆ THỨC LƢỢNG TRONG TAM GIÁC- GIẢI TAM GIÁC
I/BÀI TẬP TỰ LUẬN
Câu 1: Cho  ABC có ˆ b  20c , m c  35c , m A  60 a)Tính BC
b) Tính diện tích  ABC
c) Xét xem góc B tù hay nhọn?
d) Tính độ dài đường cao AH
e) Tính bán kính đường tròn
nội tiếp r  ? và ngoại tiếp R  ? của tam giác trên
Câu 2: Cho  ABC có ˆ ˆ b  7c ,
m A  60 ,C  32
a) Tính diện tích  ABC
b) Góc B tù hay nhọn? Tính B
c) Tính bánh kính h , R, r  ?
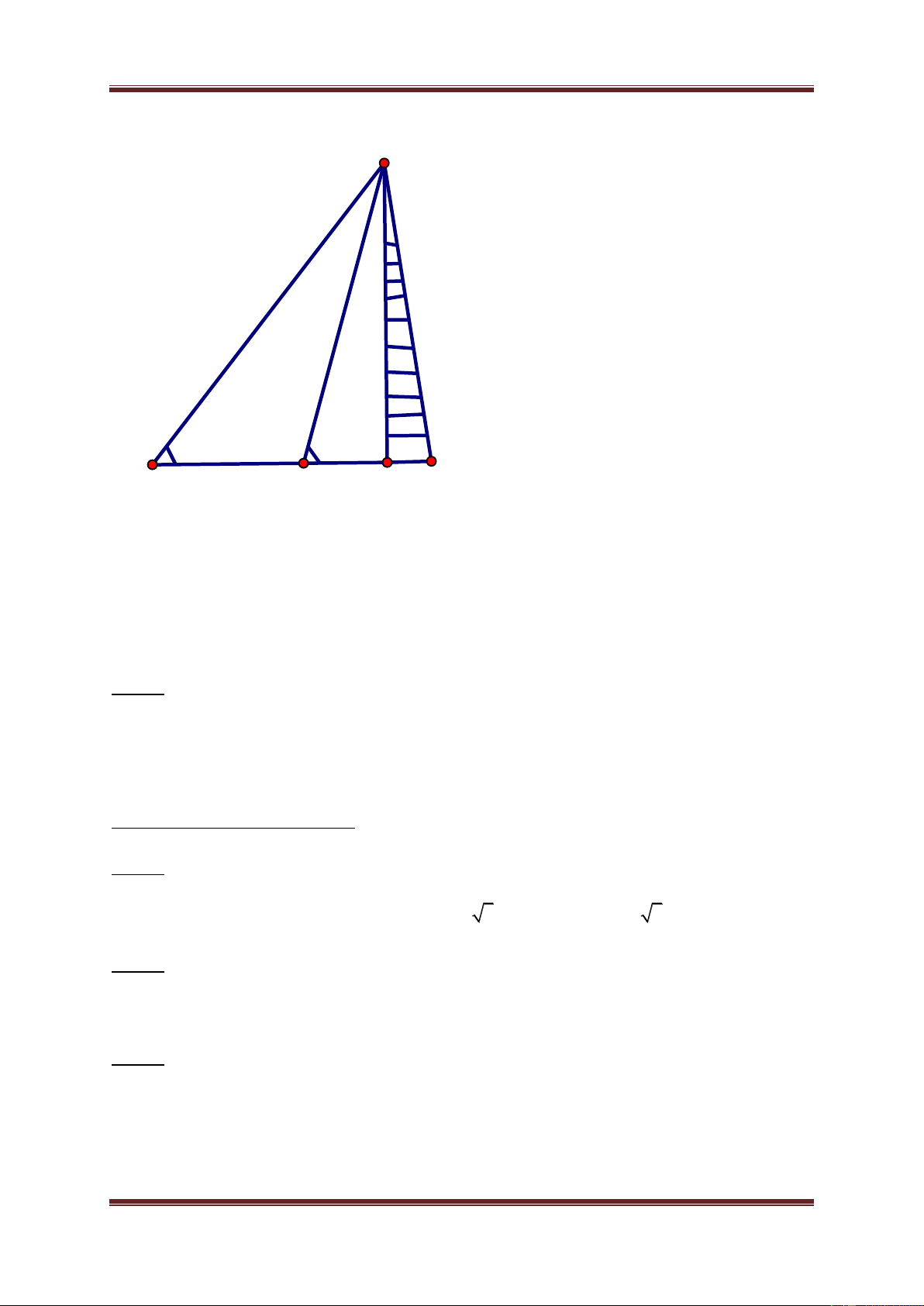
d) Tính độ dài đường trung a tuyến m b Câu 3: GV: NGUYỄN QUỐC HIỆP Page 22 ĐỀ CƯƠNG TOÁN 10 HKII D 43° 67° A 30 m B C
Giả sử chúng ta cần đo chiều cao CD của một cái tháp với C là chân tháp, D là đỉnh
tháp. Vì không thể đến chân tháp được nên từ hai điểm ,
A B có khoảng cách
AB  30 m sao cho ba điểm ,
A B,C thẳng hàng, người ta đo được các góc ˆ ˆ CAD  43 ,
 CBD  67 (như hình vẽ trên). Hãy tính chiều cao CD của tháp?
Câu 4: Cho một tam giác ABC , chứng minh rằng
a) Nếu có b  c  2a thì 2sin A  sin B  sinC b) Nếu có 2 bc  a thì 2
sin A  sin B sin C
II/BÀI TẬP TRẮC NGHIỆM.
Câu 1. Tam giác ABC có ˆ AB  2 c , m AC 1 c ,
m A  60 . Khi đó độ dài cạnh BC là: A. 1 cm B. 2 cm C. 3 cm D. 5 cm
Câu 2. Tam giác ABC có a  5 c , m b  3 c ,
m c  5 cm . Khi đó số đo của góc ˆA là: A. ˆ A  45 B. ˆ A  90 C. ˆ A  30 D. ˆ A  120
Câu 3. Tam giác ABC có AB  8 c , m BC  10 c ,
m CA  6 cm . Đường trung tuyến
AM của tam giác đó có độ dài bằng: A. 4 cm B. 5 cm C. 6 cm D. 7 cm GV: NGUYỄN QUỐC HIỆP Page 23 ĐỀ CƯƠNG TOÁN 10 HKII
Câu 4. Tam giác ABC vuông tại A có AB  6 c ,
m BC  10 cm . Đường tròn nội tiếp
tam giác đó có bán kính r bằng: A. 1 cm B. 2 cm C. 2 cm D. 3 cm
Câu 5. Tam giác đều nội tiếp đường tròn bán kính R  4 cm có diện tích là: A. 2 13 cm B. 2 13 2 cm C. 2 12 3 cm D. 2 15 cm
Câu 6. Tam giác ABC vuông và cân tại A có AB  a . Đường tròn nội tiếp tam giác
ABC có bán kính r bằng: a a a a A. B. C. D. 2 2 2  2 3
Câu 7: Tam giác ABC có các cạnh a,b,c thỏa mãn điều kiện:
a bca bc  3ab . Khi đó số đo của góc ˆC bằng: A. 45 B. 120 C. 60 D. 30
Câu 8. Hình bình hành ABCD có AB  ,
a BC  a 2 và ˆ
BAD  45 . Khi đó hình bình
hành có diện tích bằng: A. 2 2a B. 2 a 2 C. 2 a D. 2 a 3
Câu 9: Tam giác đều cạnh a nội tiếp đường tròn bán kính R . Khi đó bán kính R bằng: a 3 a 2 a 3 a 3 A. B. C. D. 2 3 3 4
Câu 10. Cho tam giác ABC có diện tích S . Nếu tăng độ dài mỗi cạnh BC và AC lên
hai lần đồng thời giữ nguyên độ lớn của góc ˆ
C thì diện tích tam giác ABC mới được tạo nên bằng: A. 2S B. 3S C. 4S D. 5S
Câu 11: Cho tam giác ABC có a  4,b  3 và c  6 và G là trọng tâm tam giác . Khi
đó , giá trị của tổng 2 2 2
GA  GB  GC là bao nhiêu ? 61 61 A. 62 B. 61 C. D. 2 3 GV: NGUYỄN QUỐC HIỆP Page 24 ĐỀ CƯƠNG TOÁN 10 HKII
Câu 12: Cho tam giác ABC có 0 0
B  60 ,C  45 , AB  5 . Hỏi độ dài cạnh AC bằng bao nhiêu ? 5 6 A. 5 3 B. 5 2 C. D. 10 2
Câu 13: Cho tam giác ABC có ba cạnh là 6,8,10 . Bán kính đường tròn nội tiếp tam giác ABC là : A. 3 B. 4 C. 2 D. 1
Câu 14: Cho tam giác ABC có ba cạnh là 5,12,13 có diện tích là : A. 30 B. 20 2 C. 10 3 D. 20
Câu 15: Cho tam giác ABC có 0
A  30 , BC  10 . Bán kính đường tròn nội tiếp tam giác ABC là : 10 A. 5 B. 10 C. D. 10 3 3 Câu1 6: Cho góc 0 xOy  30 . Gọi ,
A B lần lượt nằm trên Ox, Oy sao cho AB  2 . Độ
dài lớn nhất của đoạn OB là : A. 2 B. 3 C. 4 D. 5
Câu 17: Cho tam giác ABC có diện tích S . Nếu tăng độ dài mỗi cạnh AC, BC lên
hai lần và giữ nguyên độ lớn của góc C thì diện tích của tam giác mới sẽ là : A. 2S B. 3S C. 4S D. 5S
Câu 18 : Cho tam giác ABC có BC  a , CA= b . Tam giác ABC có diện tích lớn nhất
khi góc C đạt giá trị : A. 0 60 B. 0 90 C. 0 150 D. 0 120
Câu 19: Tam giác ABC đều , cạnh 2a , ngoại tiếp đường tròn bán kính R . Khi đó
bán kính đường tròn nội tiếp tam giác ABC là : a 3 2a 2 a 3 2a 3 A. B. C. D. 2 5 3 7
Câu 20: Tam giác ABC đều , cạnh 2a , nội tiếp đường tròn bán kính R . Khi đó bán
kính đường tròn ngoại tiếp tam giác ABC là : GV: NGUYỄN QUỐC HIỆP Page 25 ĐỀ CƯƠNG TOÁN 10 HKII 2a 2 2a 3 a 3 A. a 3 B. C. D. 3 3 2
Câu 21: Tam giác ABC vuông cân tại ,
A AB  2a . Đường trung tuyến BM có độ dài là : A. 3a B. 2a 2 C. 2a 3 D. a 5
Câu 22 : Cho hình bình hành ABCD có AB  ,
a BC  a 2 và góc 0 BAD  45 . Diện
tích của hình bình hành ABCD là : A. 2 2a B. 2 2a C. 2 a D. 2 3a
Câu 23 : Tam giác ABC vuông cân tại ,
A AB  2a . Độ dài bán kính đường tròn nội tiếp tam giác là : 4a A. a B. a 2 C. a 2  2  D. 3
Câu 24 : Cho tam giác ABC có a  2 3,b  2 2 và c  2 . Kết quả nào trong các kết
quả sau là độ dài của trung tuyến AM ? A. 2 B. 3 C. 3 D. 5
Câu 25 : Tam giác ABC đều nội tiếp đường tròn bán kính R  8 . Diện tích của tam giác ABC là : A. 26 B. 48 3 C. 24 3 D. 30
Câu 26 : Tam giác ABC vuông tại A có AB  12, BC = 20 . Bán kính r của đường
tròn nội tiếp tam giác ABC có độ dài bằng : A. 2 B. 2 2 C. 4 D. 6
Câu 27 : Cho tam giác ABC có a  2,b  1 và góc 0
C  60 . Độ dài cạnh AB là bao nhiêu ? A. 1 B. 3 C. 3 D. 5 3
Câu 28: Cho tam giác ABC có b  7 cm, c = 5 cm và cos A  . Tính a, sin A và diện 5
tích S của tam giác ABC . GV: NGUYỄN QUỐC HIỆP Page 26 ĐỀ CƯƠNG TOÁN 10 HKII 4 4 A. 2
a = 4 2 cm, sinA= , S=14 cm B. 2
a = 4 2 cm, sinA=- , S=14 cm 5 5 4 4 C. 2
a = 4 3 cm, sinA= , S=14 cm D. 2
a = 4 5 cm, sinA= , S=14 cm 5 5 3
Câu 29 : Cho tam giác ABC có b  7 cm, c = 5 cm và cos A  . Tính đường cao h 5 a
xuất phát từ đỉnh A và bán kính R của đường tròn ngoại tiếp tam giác ABC . 7 5 2 7 2 5 3 A. h  cm, R = cm B. h  cm, R = cm a 2 2 a 2 2 7 2 5 2 7 3 5 2 C. h  cm, R = cm D. h  cm, R = cm a 2 2 a 2 2
Câu 30 : Cho tam giác ABC có G là trọng tâm , gọi b  ,
CA c = AB, a = BC . Đẳng
thức nào sau đây là sai ? 1 A. 2 2 2
a  b  c  2bc cos A
B. S  absin C 2 2 2 2 b  c a 1 C. 2 m   D. 2 2 2
GA  GB  GC   2 2 2
a  b  c  a 2 4 4
 CHƢƠNG III: PHƢƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG
PHƢƠNG TRÌNH ĐƢỜNG THẲNG
I/ BÀI TẬP TỰ LUẬN.
Câu 1: Lập phương trình tham số và tổng quát của đường thẳng  biết:
a)  qua M 2; 3
  và có vecto pháp tuyến n  1; 3  
b)  qua N  1
 ;3và có vecto chỉ phương u  (3;4)
Câu 2: Lập phương trình tổng quát của đường thẳng  trong các trường hợp sau:
a)  qua M  2
 ;3và có hệ số góc k  2 
b)  qua N  2  ; 5
  và song song với đường thẳng 2x 3y  2017  0
c)  qua N  2  ; 5
  và vuông góc với đường thẳng 4x 3y  2017  0
Câu 3: Cho ba điểm A2;0, B4; 
1 ,C 1;2 lập thành ba đỉnh của tam giác. GV: NGUYỄN QUỐC HIỆP Page 27 ĐỀ CƯƠNG TOÁN 10 HKII
a) Viết phương trình tham số của đường thẳng AB.
b) Viết phương trình tổng quát của đường thẳng BC
c) Viết phương trình đường trung tuyến AM của tam giác.
d) Viết phương trình tổng quát của các đường cao AH, BH, từ đó tìm tọa độ trực tâm của tam giác.
e) Viết phương trình tổng quát đường trung bình MN của tam giác ABC với M
là trung điểm của AB, N là trung điểm của AC.
f) Viết phương trình đường trung trực của cạnh AB,AC từ đó tìm tọa độ tâm
đường tròn ngoại tiếp tam giác ABC
g) Tính khoảng cách từ C đến đường thẳng AB
h) Tính góc B của tam giác ABC
i) Tính diện tích của tam giác ABC.
Câu 4: Trong mặt phẳng toạ độ Oxy cho  ABC có đỉnh A1;2 , đường trung tuyến
BM: 2x  y 1  0 và phân giác trong CD : x  y 1  0 . Viết phương trình đường thẳng BC
Câu 5: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có phương trình cạnh
AB: x  y  2  0 , phương trình cạnh AC: x  2 y  5  0 . Biết trọng tâm của tam giác
G 3;2 Viết phương trình cạnh BC.
Câu 6. Cho tam giác ABC có phương trình cạnh BC là 2x  y  5  0 các đường trung
tuyến BM và CN lần lượt có phương trình 3x  y  7  0 và x  y  5  0 . Viết phương
trình đường thẳng chứa các cạnh AB, AC ?
Câu 7. Trong mặt phẳng Oxy, cho tam giác ABC có AB: 3x  5y  33  0 ; đừơng cao
AH: 7x  y 13  0 ; trung tuyến BM: x  6 y  24  0 (M là trung điểm AC). Tìm
phương trình các đừơng thẳng AC và BC
II/ BÀI TẬP TRẮC NGHIỆM
Câu 1: cho phương trình: ax  by  c  0  1 với 2 2
a  b  0 . Mệnh đề nào sau đây sai?
A. (1) là phương trình tổng quát của đường thẳng có vectơ pháp tuyến là n  a;b .
B. a  0 (1) là phương trình đường thẳng song song hoặc trùng với trục ox .
C. b  0 (1) là phương trình đường thẳng song song hoặc trùng với trục oy . D. Điểm M x ; y
thuộc đường thẳng (1) khi và chỉ khi ax  by  c  0 . 0  0 0  0 0
Câu 2: Mệnh đề nào sau đây sai? Đường thẳng (d) được xác định khi biết. GV: NGUYỄN QUỐC HIỆP Page 28 ĐỀ CƯƠNG TOÁN 10 HKII
A. Một vecto pháp tuyến hoặc một vec tơ chỉ phương.
B. Hệ số góc và một điểm thuộc đường thẳng.
C. Một điểm thuộc (d) và biết (d) song song với một đường thẳng cho trước.
D. Hai điểm phân biệt thuộc (d).
Câu 3: Cho tam giác ABC. Hỏi mệnh đề nào sau đây sai?
A. BC là một vecto pháp tuyến của đường cao AH.
B. BC là một vecto chỉ phương của đường thẳng BC.
C. Các đường thẳng AB, BC, CA đều có hệ số góc.
D. Đường trung trực của AB có AB là vecto pháp tuyến.
Câu 4: Đường thẳng (d) có vecto pháp tuyến n  a;b . Mệnh đề nào sau đây sai ? A. u   1
 ;b a là vecto chỉ phương của (d). B. u   2
 ;ba là vecto chỉ phương của (d).
C. n  k ;
a kb k  R là vecto pháp tuyến của (d). b 
D. (d) có hệ số góc k  b  0 . a
Câu 5: Cho đường thẳng (d): 2x  3y  4  0 . Vecto nào sau đây là vecto pháp tuyến của (d)? A. n  3; 2 B. n  4  ; 6  C. n  2; 3  D. n  2  ;3 . 4   3   2   1  
Câu 6: Cho đường thẳng (d): 3x  7 y 15  0 . Mệnh đề nào sau đây sai ? 3
A. u  7;3 là vecto chỉ phương của (d). B. (d) có hệ số góc k  . 7  1 
C. (d) không đi qua góc tọa độ.
D. (d) đi qua hai điểm M  ; 2   và N 5;0 .  3 
Câu 7: Cho đường thẳng (d): 3x  5y 15  0 . Phương trình nào sau đây không phải là một dạng GV: NGUYỄN QUỐC HIỆP Page 29 ĐỀ CƯƠNG TOÁN 10 HKII khác của (d)?  5 x y 3 x  t x  5  t A.   1.
B. y   x  3 . C. 
t  R . D. 
3 t  R . 5 3 5 y  5 y  t
Câu 8: Mệnh đề nào sau đây đúng? Đường thẳng (d): x  2 y  5  0 : x  t A. Đi qua A1; 2   .
B.Có phương trình tham số:  t  R .  y  2t 1
C. (d) có hệ số góc k  .
D. (d) cắt d có phương trình: x  2y  0 . 2
Câu 9: Cho đường thẳng(d): x  2 y 1  0 . Nếu đường thẳng  đi qua M 1;  1 và
song song với (d) thì  có phương trình :
A. x  2 y  3  0 .
B. x  2 y  5  0 .
C. x  2 y  3  0 .
D. x  2 y 1  0 .
Câu 10: Cho ba điểm A1; 2  , B5; 4  ,C  1
 ;4 . Đường cao AA của tam giác ABC có phương trình:
A. 3x  4 y  8  0 .
B. 3x  4 y 11  0 . C. 6
 x  8y 11  0 . D. 8x  6y 13  0 .
Câu 11: Đường thẳng  : 3x  2y  7  0 cắt đường thẳng nào sau đây?
A. d : 3x  2y  0 .
B. d : 3x  2y  0 . 2  1  C. d : 3
 x  2y  7  0.
D. d : 6x  4y 14  0. 4  3 
Câu 12: Cho đường thẳng (d): 4x  3y  5  0 . Nếu đường thẳng  đi qua góc tọa
độ và vuông góc với (d) thì  có phương trình :
A. 4x  3y  0 .
B. 3x  4 y  0 .
C. 3x  4 y  0 .
D. 4x  3y  0 .
Câu 13: Cho tam giác ABC có A 4  ;  1 B 2; 7  C 5; 6   và đường thẳng
(d): 3x  y 11  0 . Quan hệ giữa (d) và tam giác ABC là: A. Đường cao vẽ từ A. B. Đường cao vẽ từ B.
C. Đường trung tuyến vẽ từ A.
D. Đường phân giác góc BAC. GV: NGUYỄN QUỐC HIỆP Page 30 ĐỀ CƯƠNG TOÁN 10 HKII
Câu 14: Gọi H là trực tâm của tam giác ABC. Phương trình các cạnh và đường cao của tam giác
là: AB : 7x  y  4  0; BH :2x  y  4  0; AH : x  y  2  0 .
Phương trình đường cao CH của tam giác ABC là:
A. 7x  y  2  0.
B. 7x  y  0.
C. x  7 y  2  0.
D. x  7 y  2  0.
Câu 15: Phương trình đường thẳng đi qua hai điểm A 2  ;4; B 6  ;  1 là:
A. 3x  4 y 10  0. B. 3x  4 y  22  0. C. 3x  4 y  8  0. D.    3x 4 y 10 0.
Câu 16: Cho hai điểm A 2
 ;3; B4; 
1 . viết phương trình trung trực đoạn AB.
A. x  y 1  0. B. 2x  3y 1  0. C. 2x  3y  5  0. D. 3x  2 y 1  0. x   t  7 
Câu 17: Cho đường thẳng d  2 3 :  và điểm A ; 2 .  
 y  1 2t  2 
Điểm Ad  ứng với giá trị nào của t? 3 1 1
A. t  . B. t  . C. t   . D. t  0. 2 2 2
Câu 18: Phương trình tham số của đường thẳng (d) đi qua điểm M  2  ;3 và vuông
góc với đường thẳng d : 3x  4y 1  0 là: x  2   4t x  2   3t x  2   3t
x  5  4t A.  B.  C.  D.  y  3 3t y  3 4t y  3 4t
 y  6  3t x   t
Câu 19: Cho d  2 3 : 
. Điểm nào sau đây không thuộc d ?
y  5  4t A. A5;3. B. B 2;5. C. C  1  ;9. D. D 8; 3  . x   t
Câu 20: Cho d  2 3 : 
Tìm điểm M d  cách A một đoạn bằng 5.
 y  3  t.  8 10   44 32  A. M ; .   B. M 4; 4 , M ; . 1      3 3  2  5 5  GV: NGUYỄN QUỐC HIỆP Page 31 ĐỀ CƯƠNG TOÁN 10 HKII  24 2   24 2  C. M 4; 4 ; M ;  . D. M 4;4 ; M ; . 1   1   1      5 5  1  5 5  x   t
Câu 21: Giao điểm M của d  1 2 : 
và d : 3x  2y 1  0 là:
 y  3  5t  11   1   1   1 1  A. M 2;  .   B. M 0; .   C. M 0;  .   D. M ;  .    2   2   2   2 2 
Câu 22: Phương trình nào sau đây biểu diển đường thẳng không song song với
đường thẳng d  : y  2x 1?
A. 2x  y  5  0.
B. 2x  y  5  0.       C. 2x y 0. D. 2x y 5 0.
Câu 23: Cho hai đường thẳng d : mx  y  m 1 , d : x  my  2 cắt nhau khi và chỉ 1   2 khi: A. m  2. B. m  1.  C. m  1. D. m  1. 
Câu 24: Cho hai đường thẳng d : mx  y  m 1 , d : x  my  2 song song nhau khi 1   2 và chỉ khi: A. m  2. B. m  1.  C. m 1. D. m  1. 
Câu 25. Cho hai đường thẳng song song d : 5x  7 y  4  0; d : 5x  7 y  6  0 . Phương 1 2
trình đường thẳng song song và cách đều d và d 1 2
A. 5x  7 y  2  0          B. 5x 7 y 3 0 C. 5x 7 y 3 0 D. 5x 7 y 5 0
Câu 26. Gọi I a;b là giao điểm của hai đường thẳng d : x y 4 0 và d ' : 3x y 5 0 . Tính a b . 7 5 3 9 A. a b . B. a b . C. a b . D. a b . 2 2 2 2
Câu 27. Cho đường thẳng d: 3
 x  y  3  0 và điểm N(-2;4). Tọa độ hình chiếu
vuông góc của N trên d là:  1 11  2 21  1 33  A.  3  ; 6   B.  ; C. ; D. ;        3 3   5 5  10 10 
Câu 28. Cho ba điểm A(1;1), B(2;0), C(3;4). Viết phương trình đường thẳng đi qua A
và cách đều hai điểm B, C. GV: NGUYỄN QUỐC HIỆP Page 32 ĐỀ CƯƠNG TOÁN 10 HKII
A. 4x  y  3  0; 2x  3y 1  0
B. 4x  y  3  0; 2x  3y 1  0
C. 4x  y  3  0; 2x  3y 1  0
D. x  y  0; 2x  3y 1  0 x  2   2t
Câu 29. Cho đường thẳng  : 
và điểm M(3;1). Tọa độ điểm A thuộc  y 1 2t
đường thẳng  sao cho A cách M một khoảng bằng 13 . A. 0;  1 ;1; 2   B. 0;  1 ;1; 2   C. 0;   1 ;1; 2 D. 2;  1 ;1; 2  
Câu 30: Khoảng cách từ điểm M 0; 
1 đến đường thẳng  : 5x 12 y 1  0 bằng 11 13 A. B. C. 1 D. 13 13 17
Câu 31: Cho 2 điểm A2;3, B1;4 . Đường thẳng nào sau đây cách đều 2 điểm A, B ?
A. x  y 1  0
B. x  2 y  0
C. 2x  2 y 10  0
D. x  y 100  0
Câu 32: Khoảng cách giữa 2 đường thẳng        1 : 7 x y 3 0 và 2 : 7x y 12 0 bằng 9 3 2 A. B. 9 C. . D. 15 50 2
Câu 33: Cho ABC với A1;2, B0; 
3 ,C 4;0 Chiều cao tam giác ứng với cạnh BC bằng : 1 1 3 A. 3 B. C. D. . 5 25 5 x y
Câu 34: Khoảng cách từ điểm O(0 ; 0) tới đường thẳng  :   1 bằng 6 8 1 1 48 1 A. B. C. D. 8 10 14 6
Câu 35: Diện tích ABC biết A3;2, B0;  1 ,C 1;5 11 11 A. B. 17 . C. 11 D. 17 2 x  2  t
Câu 36: Tìm côsin góc giữa 2 đường thẳng     1 : 10 x 5 y 1 0 và 2 :  .  y  1 t GV: NGUYỄN QUỐC HIỆP Page 33 ĐỀ CƯƠNG TOÁN 10 HKII 3 10 3 10 3 A. . B. C. D. 10 10 10 5
Câu 37: Tìm côsin góc giữa 2 đường thẳng       1 : x 2 y 2 0 và 2 : x y 0 . 10 2 3 A. B. 2 C. D. . 10 3 3
Câu 38: Góc giữa 2 đường thẳng      1 : 2x 2 3y 5 0 và 2 : y  6 0 có số đo bằng: A. 600 B. 1250. C. 1450 D. 300
Câu 39: Góc giữa hai đường thẳng     1 : x 3y
0 và ø 2 : x  10 0 có số đo bằng: A. 450 B. 1250. C. 300 D. 600
x 10  6t
Câu 40: Góc giữa 2 đường thẳng     1 : 6x 5y 15 0 và 2 : 
có số đo bằng
y 1 5t . A. 900 B. 600 C. 00 D. 450.
PHƢƠNG TRÌNH ĐƢỜNG TRÒN-TIẾP TUYẾN VỚI ĐƢỜNG TRÒN
I/ BÀI TẬP TỰ LUẬN.
Câu 1: Lập phương trình đường tròn C trong các trường hợp sau:
a) C có tâm I 1; 2
  có bán kính R  6
b) C có tâm I 5; 2
  có đường kính d  8
c ) C có tâm I 1;2 và đi qua M 4;6
d) C có đường kính AB với A 3  ; 5  , B3;3
e) C đi qua ba điểm A1;2, B5;2,C 1; 3  
f) C có tâm I 3; 4
  tiếp xúc với đường thẳng 4x  3y 15  0
g) C tiếp xúc với hai trục tọa độ Ox,Oy và đi qua điểm M 2;  1 GV: NGUYỄN QUỐC HIỆP Page 34 ĐỀ CƯƠNG TOÁN 10 HKII
Câu 2: Cho đường tròn C có phương trình: 2 2
x  y  4x  8y  5  0
a) Tìm tọa độ tâm và bán kính của đường tròn C ?
b) Viết phương trình tiếp tuyến của C tại điểm M  1  ;0
c) Viết phương trình tiếp tuyến với C biết tiếp tuyến vuông góc với đường thẳng
3x  4 y  5  0
II/ BÀI TẬP TRẮC NGHIỆM 2 2
Câu 1: Tâm I và bán kính R của đường tròn  x  2   y   3 16 là: A. I 2; 3  , R  4 B. I  2  ;3,R  4 C. I 2; 3  ,R 16 D. I  2  ;3,R 16
Câu 2: Tâm I và bán kính R của đường tròn 2 2
x  y  2x  8y  8  0 là: A. I  1  ;4,R  5 B. I 1; 4  ,R  5 C. I  2  ;8,R  5 D. I  1  ; 4  , R  8
Câu 3: Với tất cả các giá trị nào của m thì phương trình 2 2
x  y  2mx  4my  6m 1  0
là phương trình đường tròn?  1  A. m  ;   1;    B. m  ;   1  3;  5   1   3    C. m  1;  ;     
D. m     1 ; 2  ;     5   4   5 
Câu 4: Đường tròn 2 2
x  y  2x 10y 1  0 đi qua điểm nào trong các điểm dưới đây ? A. (2 ; 1) B. (3 ; 2) C. (1 ; 3) D. (4 ; 1)
Câu 5: Tìm tọa độ giao điểm của đường thẳng  : y  x và đường tròn (C) : 2 2
x  y  2x  0 . A. ( 0 ; 0) B. ( 0 ; 0) và (1 ; 1). C. ( 2 ; 0) D. (1 ; 1)
Câu 4: Tìm tọa độ tâm I đường tròn đi qua ba điểm A0;4, B2;4,C 4;0 GV: NGUYỄN QUỐC HIỆP Page 35 ĐỀ CƯƠNG TOÁN 10 HKII A. I 0;0 B. I 1;0 C. I 3;2 D. I 1;  1
Câu 5: Tìm bán kính R đường tròn đi qua ba điểm A0;4, B3;4,C 3;0 10 5 A. R  5 B. R  3 C. R  D. R  . 2 2
Câu 6: Một đường tròn có tâm I 3; 2
  tiếp xúc với đường thẳng  : x  5y 1  0 . Hỏi bán
kính đường tròn bằng bao nhiêu ? 14 7 A. 6 B. 26 C. D. 26 13
Câu 7: Đường tròn nào sau đây tiếp xúc với trục Ox ? A. 2 2
x  y  2x 10y  0 . B. 2 2
x  y  6x  5y  9  0 C. 2 2
x  y 10 y 1  0 D. 2 2
x  y  5  0 .
Câu 8: Đường tròn nào sau đây tiếp xúc với trục Oy ? 2 2 A. 2 2
x  y 10 y 1  0
B. x  y  6x  5y 1  0 C. 2 2
x  y  2x  0 . D. 2 2
x  y  5  0 . 2 2
Câu 9: Tâm đường tròn x  y 10x 1  0 cách trục Oy bao nhiêu ? A.  5 B. 0 C. 10. D. 5
Câu 10: Đường tròn 2 2
x  y  2x  2 y  23  0 cắt đường thẳng x  y + 2 = 0 theo một dây
cung có độ dài bằng bao nhiêu ? A. 5 B. 2 23 C. 10 D. 5 2
PHƢƠNG TRÌNH ĐƢỜNG ELIP
BÀI TẬP TRẮC NGHIỆM. 2 2 x y Câu 1: Đường Elip 
 1 có 1 tiêu điểm là : 9 6 A. (0 ; 3) B. (0 ; 3) C. (  3 ; 0) D. (3 ; 0) GV: NGUYỄN QUỐC HIỆP Page 36 ĐỀ CƯƠNG TOÁN 10 HKII 2 2 x y Câu 2: Đường Elip   1 có tiêu cự bằng : 16 7 A. 18 B. 6 C. 9 D. 3
Câu 3: Phương trình của Elip có độ dài trục lớn bằng 8, độ dài trục nhỏ bằng 6 là: 2 2 2 2 x y
A. 9x 16 y  144 B.   1 9 16 2 2 x y C. 2 2
9x 16 y  1 D.   1 64 36 2 2 x y
Câu 5: Tâm sai của Elip   1 bằng : 5 4 5 2 1 A. B. C. 4 D. 4 5 5
Câu 6: Tìm phương trình chính tắc của Elip có tiêu cự bằng 6 và trục lớn bằng 10 2 2 x y 2 2 x y A.   1 B.   1 25 9 100 81 2 2 x y 2 2 x y C.   1 D.   1 25 16 25 16 1
Câu 7 Tìm phương trình chính tắc của Elip có tâm sai bằng và trục lớn bằng 6 3 2 2 x y 2 2 x y A.   1 B.   1 9 3 9 8 2 2 x y 2 2 x y C.   1 D.   1 9 5 6 5
Câu 8: Tìm phương trình chính tắc của Elip có tiêu cự bằng 6 và đi qua điểm A(0; 5) 2 2 x y 2 2 x y A.   1 B.   1 100 81 15 16 2 2 x y 2 2 x y C.   1 D.   1 25 9 25 16 GV: NGUYỄN QUỐC HIỆP Page 37 ĐỀ CƯƠNG TOÁN 10 HKII
Câu 9: Tìm phương trình chính tắc của Elip có trục lớn gấp đôi trục bé và có tiêu cự bằng 4 3 2 2 x y 2 2 x y A.   1 B.   1 36 9 36 24 2 2 x y 2 2 x y C.  1 D.   1 24 6 16 4
Câu 10: Tìm phương trình chính tắc của Elip có trục lớn gấp đôi trục bé và đi qua điểm A2; 2   2 2 x y 2 2 x y A.  1 B.   1 24 6 36 9 2 2 x y 2 2 x y C.   1 D.  1 16 4 20 5 12
Câu 11: Một elip có trục lớn bằng 26, tâm sai e 
. Trục nhỏ của elip có độ dài bằng bao 13 nhiêu? A. 10 B. 12 C. 24 D. 5 2 2
Câu 12: Cho Elip có phương trình : 9x  25y  225 . Lúc đó hình chữ nhật cơ sở có diện tích bằng: A. 15 B. 40 C. 60 D. 30
Câu 13: Tìm phương trình chính tắc của Elip có một đỉnh của hình chữ nhật cơ sở là M(4; 3) 2 2 x y 2 2 x y A.   1 B.   1 16 9 16 9 2 2 x y 2 2 x y C.   1 D.   1 16 4 4 3 9
Câu 14: Biết Elip(E) có các tiêu điểm F1(- 7 ; 0), F2( 7 ;0) và đi qua M( - 7 ; ). Gọi N là 4
điểm đối xứng với M qua gốc toạ độ . Khi đó: GV: NGUYỄN QUỐC HIỆP Page 38 ĐỀ CƯƠNG TOÁN 10 HKII 9 23 A. NF1+ MF2 = B. NF2 + MF1 = 2 2
Câu 15: Cho Elip (E) có các tiêu điểm F1( - 4; 0 ), F2( 4; 0 ) và một điểm M nằm trên (E) biết
rằng chu vi của tam giác MF1F2 bằng 18. Lúc đó tâm sai của (E) là: 4 4 4 4 A. e   B. e  C. e  D. e  5 9 18 5 GV: NGUYỄN QUỐC HIỆP Page 39

Đề cương ôn thi học kỳ 2 Toán 10 – Nguyễn Quốc Hiệp

Thông tin :

Tài liệu liên quan:

Chuyên đề một số phương pháp đếm trong các bài toán tổ hợp

Các dạng toán vectơ Toán 10 thường gặp

Các dạng toán mệnh đề và tập hợp Toán 10 thường gặp

Đề cương giữa học kỳ 1 Toán 10 năm 2024 – 2025 trường THPT Hoàng Văn Thụ – Hà Nội

Đề cương giữa học kỳ 1 Toán 10 năm 2024 – 2025 trường THPT Xuân Đỉnh – Hà Nội