Đề đề nghị cuối kì 2 Toán 8 năm 2022 – 2023 trường THCS Đống Đa – TP HCM
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 8 đề đề nghị kiểm tra cuối học kì 2 môn Toán 8 năm học 2022 – 2023 trường THCS Đống Đa, quận Bình Thạnh, thành phố Hồ Chí Minh; đề thi có đáp án và hướng dẫn chấm điểm.
Preview text:
UNBD QUẬN BÌNH THẠNH ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 NĂM HỌC 2022-2023
TRƯỜNG THCS ĐỐNG ĐA MÔN TOÁN LỚP 8
ĐỀ ĐỀ NGHỊ
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Bài 1 (3 điểm). Giải các phương trình sau:
a) 2x2 - 3x – 5(2x – 3) = 0 b) x − 4 x 3x −14 − = 2
x + 4 x − 4 x −16
c) 2x − 4 = x − 2
Bài 2 (2 điểm). Giải các bất phương trình sau rồi biểu diễn tập nghiệm lên trục
số a) 3(x – 2) + 7x ≤ 4(x + 1) + 14
b) x −1 x − 2 x − 3 − ≤ x − 2 3 4
Bài 3 (1 điểm) Một mảnh đất hình chữ nhật có chiều rộng nhỏ hơn chiều dài
10m. Nếu tăng chiều dài 5m, giảm chiều rộng 4m thì diện tích giảm 50 m2. Tính
chiều dài, chiều rộng của mảnh đất.
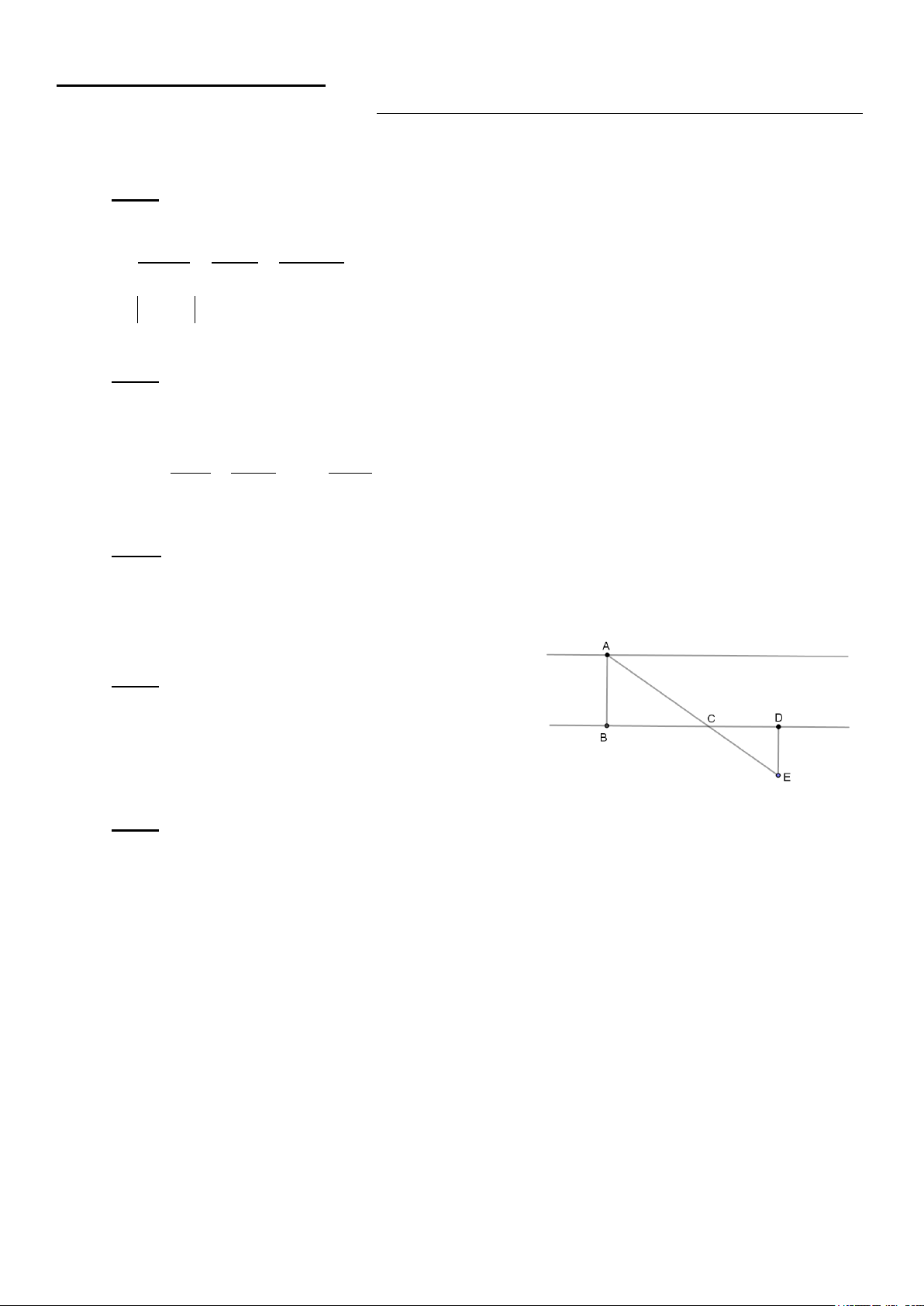
Bài 4 (1 điểm) Tính chiều rộng AB của con đường như hình vẽ.
Biết BC= 80m; CD = 40 m ; DE = 36m.
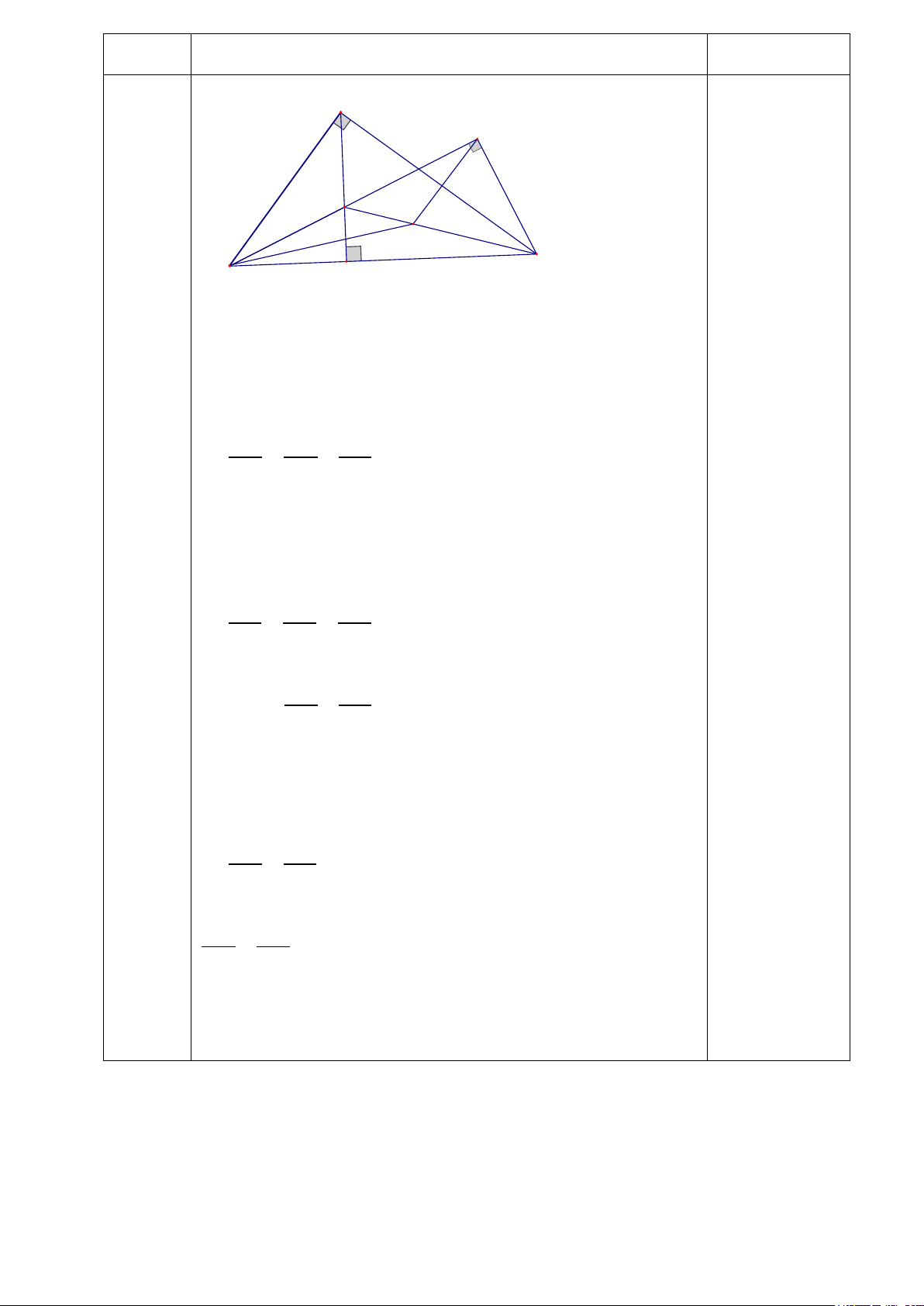
Bài 5 (3 điểm) Cho ∆ABC vuông tại A(AB < AC), với đường cao AD.
a) Chứng minh ∆ABC đồng dạng với ∆DBA .Viết tỉ số đồng dạng.
b) Trên đoạn AD lấy điểm E, gọi G là hình chiếu của C trên BE. Chứng minh BD.BC = BE.BG.
c) Trên đoạn CE lấy điểm F sao cho BF = BA. Chứng minh = BEF BFG .
--------------- HẾT ---------------
MA TRẬN ĐỀ KIỂM TRA CUỐI KỲ II NĂM HỌC 2022-2023 MÔN: TOÁN 8 Cấp độ Vận dụng Nhận biết Thông hiểu Tổng Chủ đề
Cấp độ thấp Cấp độ cao 1. Giải Phương trình rút Phương Phương trình phương gọn đưa về trình chứa chứa dấu giá trình phương trình ẩn ở mẫu trị tuyệt đối
bậc nhất một ẩn Số câu 1 1 1 3 Số điểm 1,0 1,0 1,0 3,0 Tỉ lệ 10% 10% 10% 30%
2. Giải bất Dạng nhân đa Dạng quy phương thức đồng với trình mẫu là số Số câu 1 1 2 Số điểm 1,0 1,0 2,0 Tỉ lệ 10% 10% 15% 3. Giải bài Toán toán bằng chuyển cách lập động; Chu phương vi, diên tích trình hình chữ nhật. Số câu 1 1 Số điểm 1,0 1,0 Tỉ lệ 10% 10% 4. Bài Áp dụng toán thực định lí, hệ tế hình quả Thales, tính chất đường phân giác. Số câu 1 1 Số điểm 1,0 1,0 Tỉ lệ 10% 10% 5. Hình Chứng minh Chứng minh Chứng minh học tam giác đồng đẳng thức vuông góc, dạng góc bằng nhau, song song, trung điểm. . Số câu 1 1 1 3 Số điểm 1,0 1,0 1,0 3,0 Tỉ lệ 10% 10% 10% 30% Số câu 3 4 2 1 10 Số điểm 3,0 4,0 2,0 1,0 10 Tỉ lệ 30% 40% 20% 10% 100% ĐÁP ÁN Nội dung Điểm Bài 1
a) 2x2 - 3x – 5(2x – 3) = 0
⇔ x(2x – 3) – 5(2x – 3) = 0 0,25 đ ⇔ (2x – 3)( x – 5 ) = 0
⇔ 2x – 3 = 0 hoặc x – 5 = 0 ⇔ 2x = 3 hoặc x = 5 0,25 đ x 2 ⇔ x = 3 hoặc x = 5 2
Vậy tập nghiệm của phương trình S = 3;5 2 0,25 đ b) x − 4 x 3x −14 − = 2
x + 4 x − 4 x −16
Điều kiện xác định : x ≠ - 4 và x ≠ 4 0,25 đ ⇔ x − 4 x 3x −14 − =
x + 4 x − 4 (x − 4)(x + 4)
⇔ (x − 4)(x − 4) x(x + 4) 3x −14 − = 0, 25 đ
(x + 4)(x − 4) (x + 4)(x − 4) (x − 4)(x + 4)
⇔ (x − 4)(x − 4) − x(x + 4) = 3x −14 0,25 đ ⇔ 2 2
x − 4x − 4x + 16 − x − 4x = 3x −14 ⇔ 2 2
x - 4x - 4x + 16 - x − 4x − 3x +14 = 0 ⇔ 15 − x + 30 = 0 ⇔ 30 x − = 15 − ⇔ x = 2
Vậy tập nghiệm của phương trình S = { } 2 0,25 đ
c) 2x − 4 = x − 2 x − 2 ≥ 0 x − 2 < 0 ⇔ hoặc 0,25 đ
2x − 4 = x − 2
2x − 4 = −(x − 2) x ≥ 2 x < 2 0,25 đ ⇔ hoặc 2x − x = 2 − + 4
2x + x = 2 + 4 x ≥ 2 x < 2 ⇔ hoặc x = 2 3 x = 6 0,25 đ x ≥ 2 x < 2 ⇔ hoặc x = 2 x = 2
Vậy phương trình có 2 nghiệm phân biệt x = 2 0,25 đ Bài 2
a) 3(x – 2) + 7x ≤ 4(x + 1) + 14
⇔ 3x – 6 + 7x ≤ 4x + 4 + 14 0,25 đ
⇔ 3x + 7x – 4x ≤ + 4 + 14 + 6 ⇔ 6x ≤ 24 0,25 đ ⇔ x ≤ 4
Vậy tập nghiệm của bất phương trình là : S = {x, x ≤ 4} 0,25 đ Biểu diễn tập nghiệm 0,25 đ
b) x −1 x − 2 x − 3 − ≤ x − 2 3 4 − − − −
⇔ 6(x 1) 4(x 2) 12x 3(x 3) − ≤ 12 12 12 0,25 đ − − + − +
⇔ 6x 6 4x 8 12x 3x 9 ≤ 12 12
⇔ 6x − 6 − 4x + 8 ≤12x − 3x + 9 0,25 đ
⇔ 2x + 2 ≤ 9x + 9
⇔ 2x − 9x ≤ 9 − 2 ⇔ 7 − x ≤ 7 ⇔ x ≥ 1 −
Vậy tập nghiệm của bất phương trình là : S = {x, x≥-1 } 0,25 đ Biểu diễn tập nghiệm 0,25 đ Bài 3
Gọi x là chiều rộng lúc đầu của mảnh đất (x > 0, m). 0,25 đ
Chiều dài lúc đầu của mảnh đất là x + 10
Chiều rộng lúc sau của mảnh đất là x – 4.
Chiều dài lúc sau của mảnh đất là (x + 10) + 5
Do diện tích khu vườn lúc sau giảm 50m2, ta có phương
trình : (x + 15)(x – 4) = x(x + 10) – 50 0,25 đ Giải phương trình :
(x + 15)(x – 4) = x(x + 10) – 50
⇔ x2 – 4x + 15x – 60 = x2 + 10x – 50
⇔ – 4x + 15x –10x = – 50 + 60 ⇔ x = 10 0,25 đ
Vậy chiều rộng ban đầu : 10 m
Chiều dài ban đầu là : 10 + 10 = 20 m 0,25 đ Bài 4 Xét ∆ABC và ∆EDC: 0,25 đ =
ABC EDC ( cùng bằng 90 độ) =
ACB ECD ( đối đỉnh) 0,25 đ Vậy ∆ABC ∼ ∆EDC(g.g)
Ta có tỉ số đồng dạng là: AB BC 0,25 đ = ED DC AB 80 ⇒ = 36 40 0, 25 đ => AB = 72 m
Chiều rộng AB của con đường là 72m Bài 5 A G E F C B D 0,25 đ
a) Xét ∆DBA và ∆ABC có : 0,25 đ =
BDA BAC ( cùng bằng 90 độ) ˆB: góc chung 0,25 đ 0,25 đ Vậy ∆ DBA ~ ∆ABC (g.g) 0,25 đ ⇒ BD DA AB = = BA AC CB
b) Xét ∆BED và ∆BCG có : ˆ 0,25 đ B góc chung =
EDB BGC ( cùng bằng 90 độ) 0,25 đ
Vậy ∆ BED ∼ ∆ BCG (g.g) ⇒ BE ED BD = = 0,25 đ BC CG BG ⇒ BD.BC = BE.BG (đpcm) c)Ta có : BD AB = BA CB 0,25 đ ⇒ AB.AB = BD.BC và BD.BC = BE.BG 0,25 đ ⇒ AB.AB = BE.BG
Mà BF = AB nên BF.BF = BE.BG ⇒ BF BE = BG BF 0,25 đ Xét ∆BEF và ∆BFG có : BF BE = BG BF ˆB 0,25 đ : góc chung
Vậy ∆BEF ∼ ∆BFG (c.g.c) ⇒ = BEF BFG