Đề học sinh giỏi tỉnh Toán THCS năm 2020 – 2021 sở GD&ĐT Kiên Giang

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI VÒNG TỈNH THCS KIÊN GIANG NĂM HỌC 2020-2021 --------------
------------------------------
ĐỀ THI CHÍNH THỨC Môn: TOÁN
Thời gian: 150 phút (không kể thời gian giao đề) Ngày thi: 19/3/2021
(Đề thi có 02 trang, gồm 05 bài) Bài 1. (4 điểm)
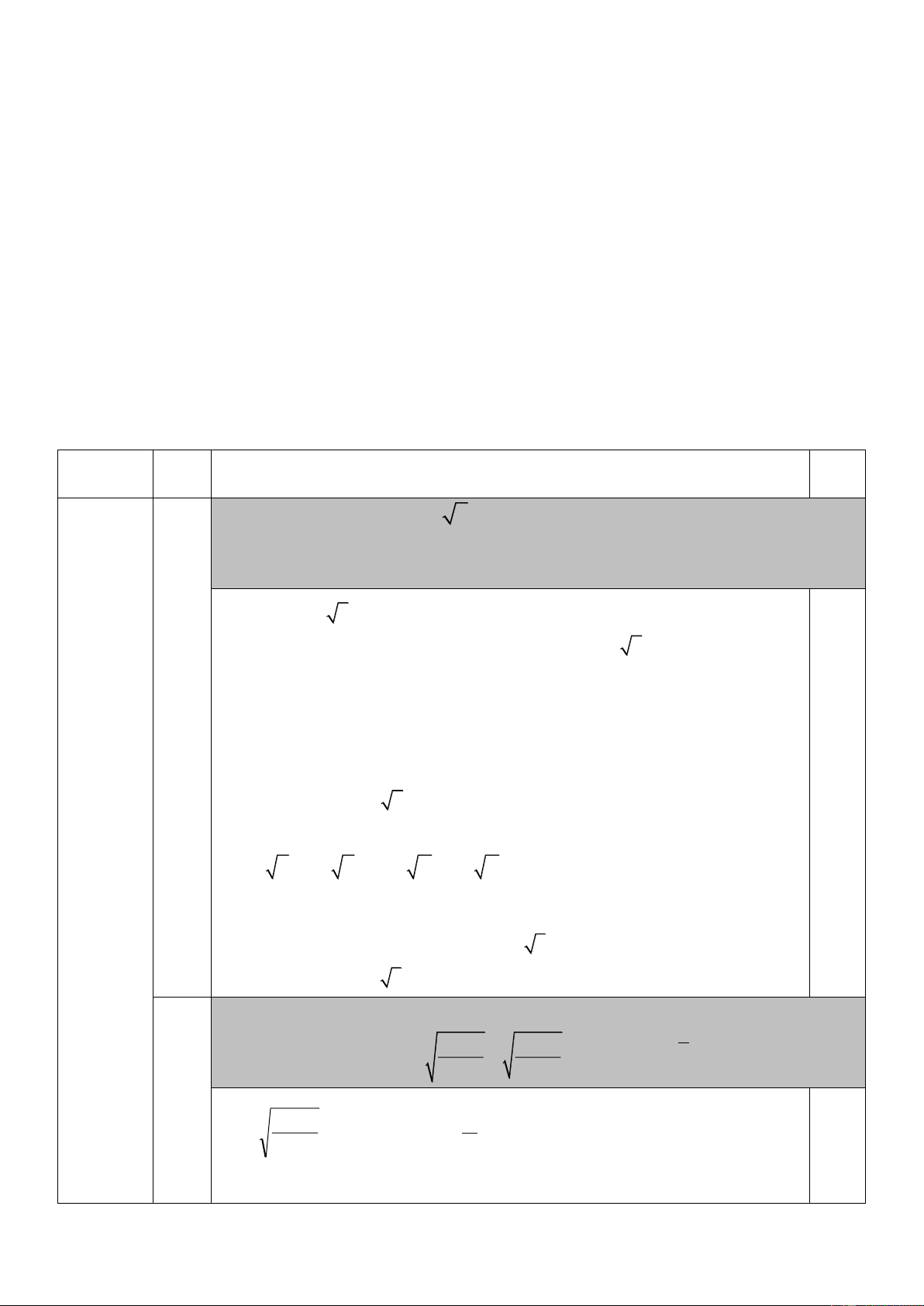
Câu 1. Cho phương trình: 4 2
x + 2 6mx + 24 = 0 ( m là tham số). Tìm giá trị của tham
số m để phương trình có 4 nghiệm x , x , x , x phân biệt thỏa mãn: 4 4 4 4
x + x + x + x = 144 1 2 3 4 1 2 3 4 3  x + 2y =19 
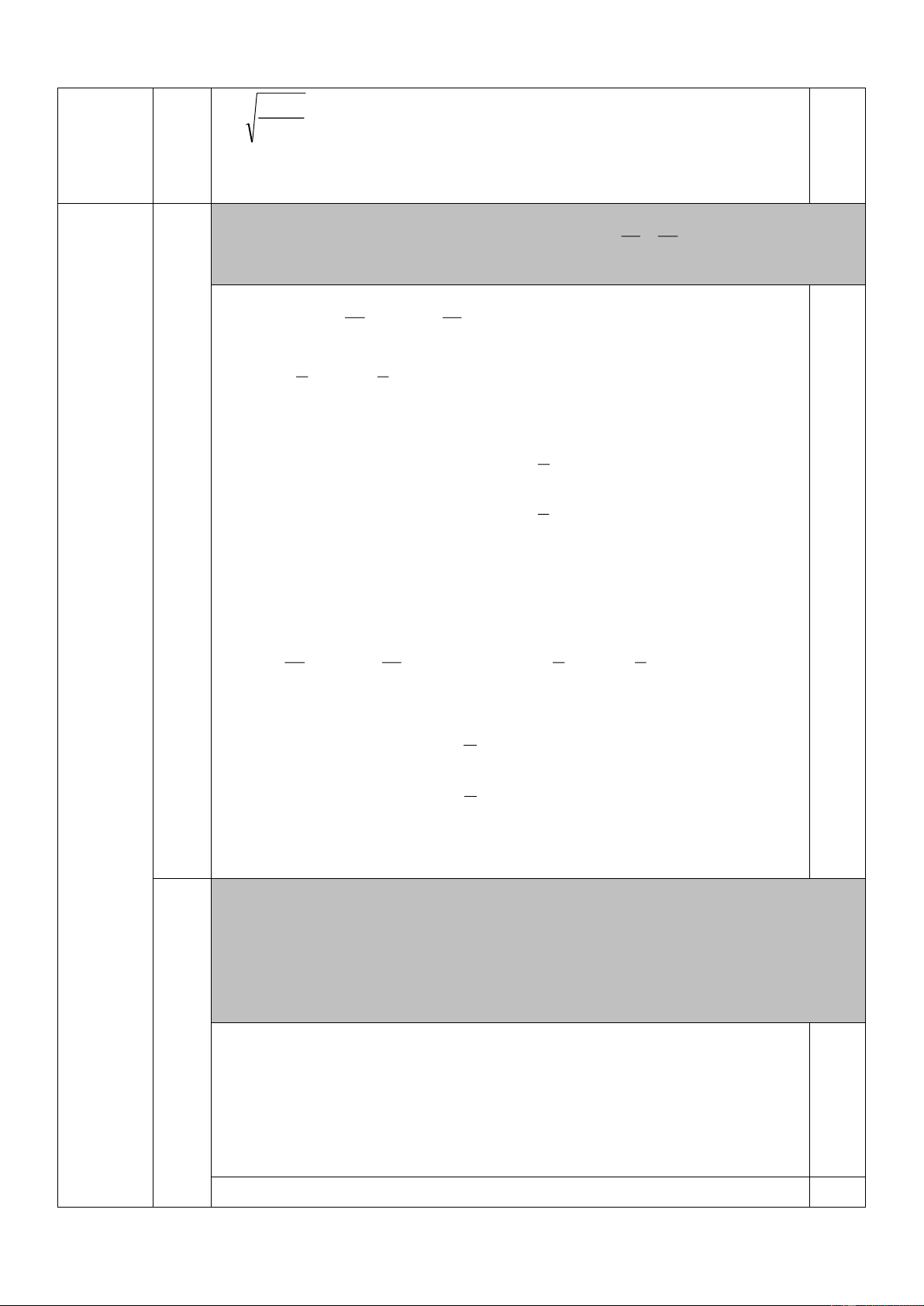
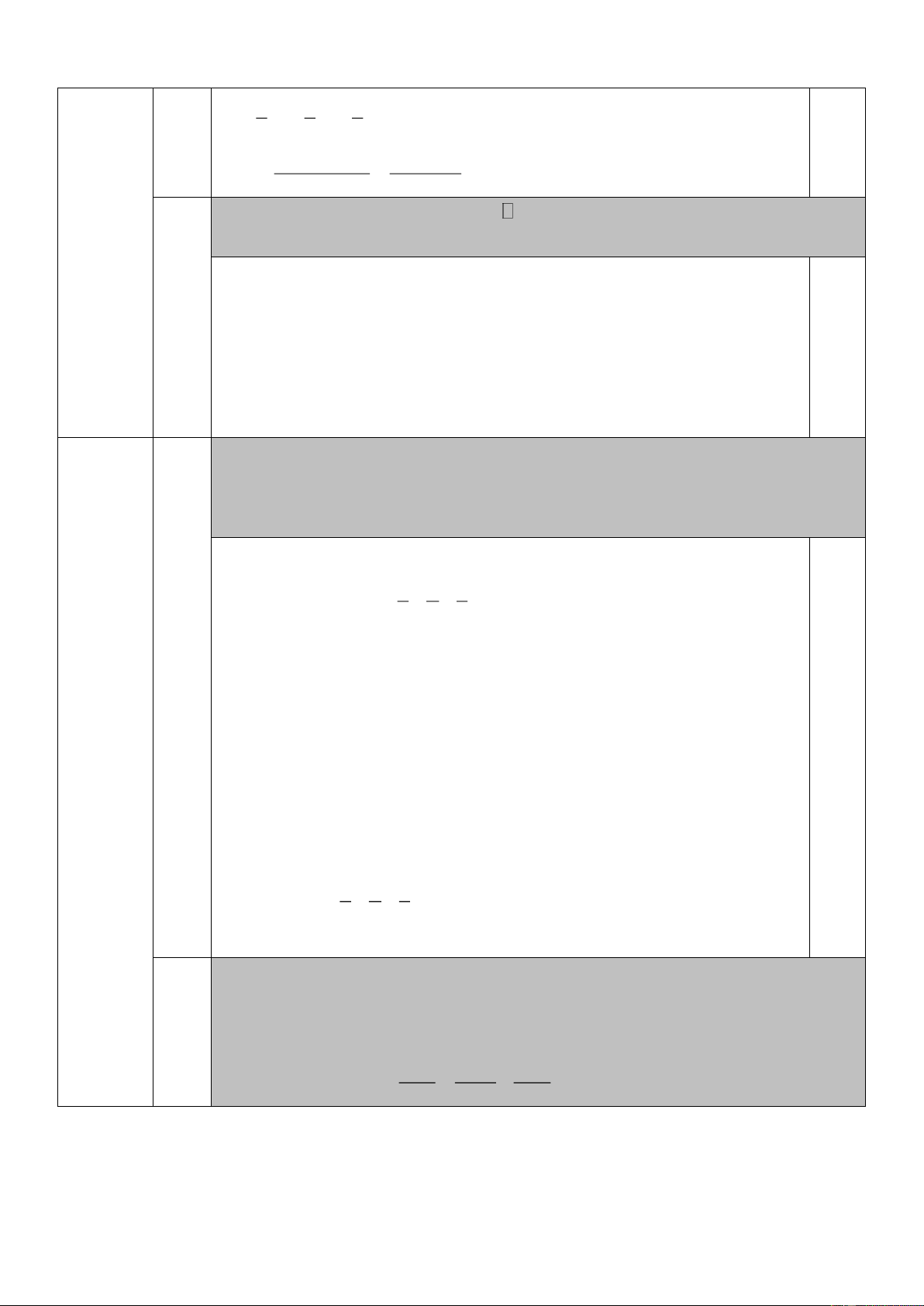
Câu 2. Giải hệ phương trình:  2x − 3 y + 5 (với 3 x  , y  5 − ) + = 2  2 y + 5 2x − 3  Bài 2. (4 điểm) 2 b 1
Câu 1. Cho hai số thực ,
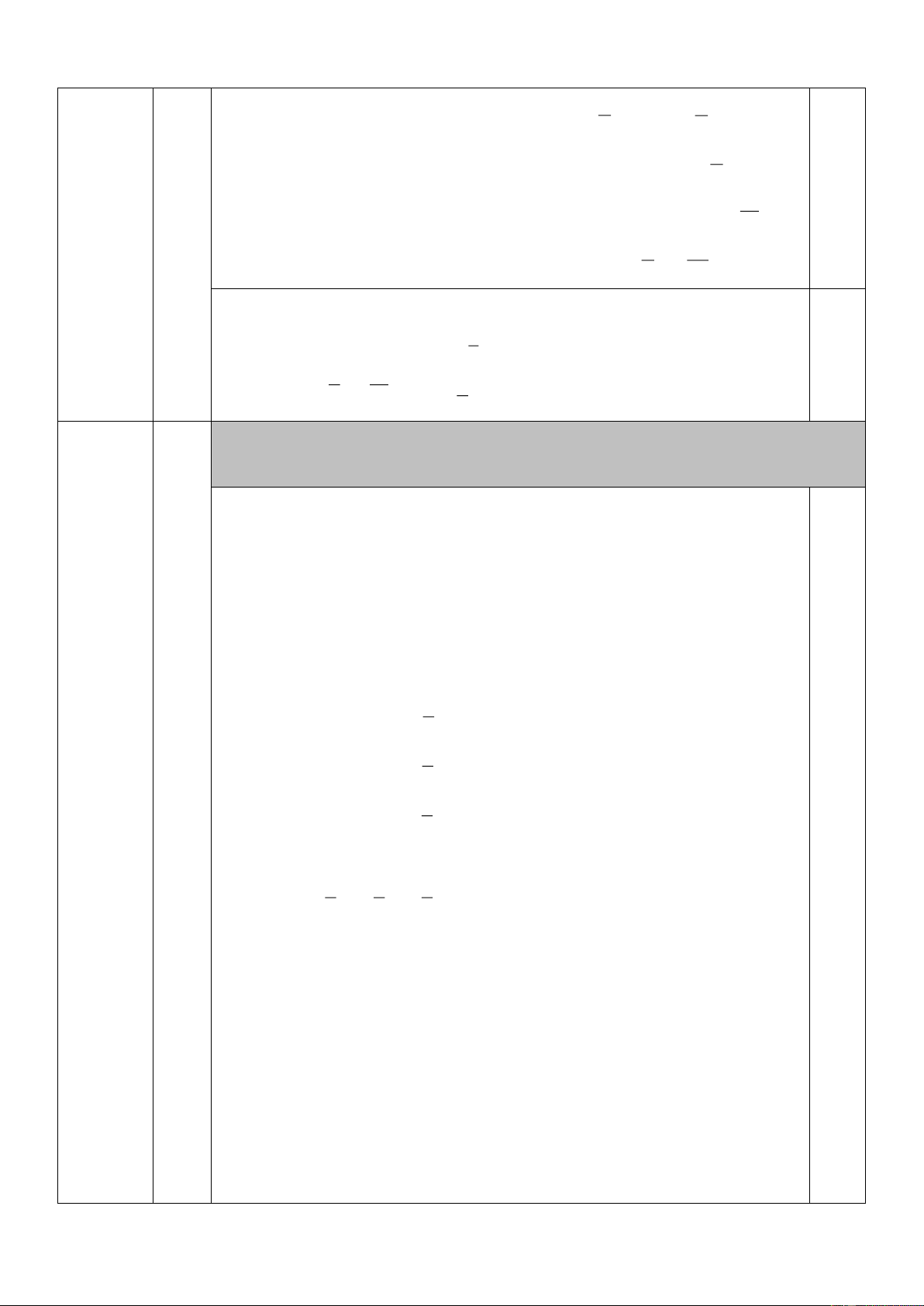
a b khác 0 thỏa mãn 2 2a + +
= 4 . Tìm giá trị lớn nhất 2 4 a
và giá trị nhỏ nhất của biểu thức: S = ab + 2019 .
Câu 2. Trong mặt phẳng Oxy cho Parabol 2
(P) : y = −x
a) Chứng minh rằng đường thẳng (d ) : y = 2x +1 tiếp xúc với parabol. Tìm tọa độ 1 của tiếp điểm.
b) Xác định tiếp tuyến d với parabol nói trên sao cho d ⊥ d . 2 2 1
c) Tìm tọa độ giao điểm của hai đường thẳng d và d . 1 2 Bài 3. (4 điểm) Câu 1. Cho 4 3 2
f (x) = ax + bx + cx + dx + e . Xác định các số hữu tỉ , a , b , c d,e sao cho 3
f (x) − f(x −1) = x . Từ đó tính 3 3 3 3
S =1 + 2 + 3 +... + n .
Câu 2. Chứng minh rằng với mọi , x y thì 4
A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y là số chính phương. Bài 4. (4 điểm)
Câu 1. Cho ba số thực dương thỏa mãn tích của chúng bằng một và tổng của chúng
luôn lớn hơn tổng nghịch đảo của chúng. Chứng minh rằng có một và chỉ một trong ba số lớn hơn một. 1
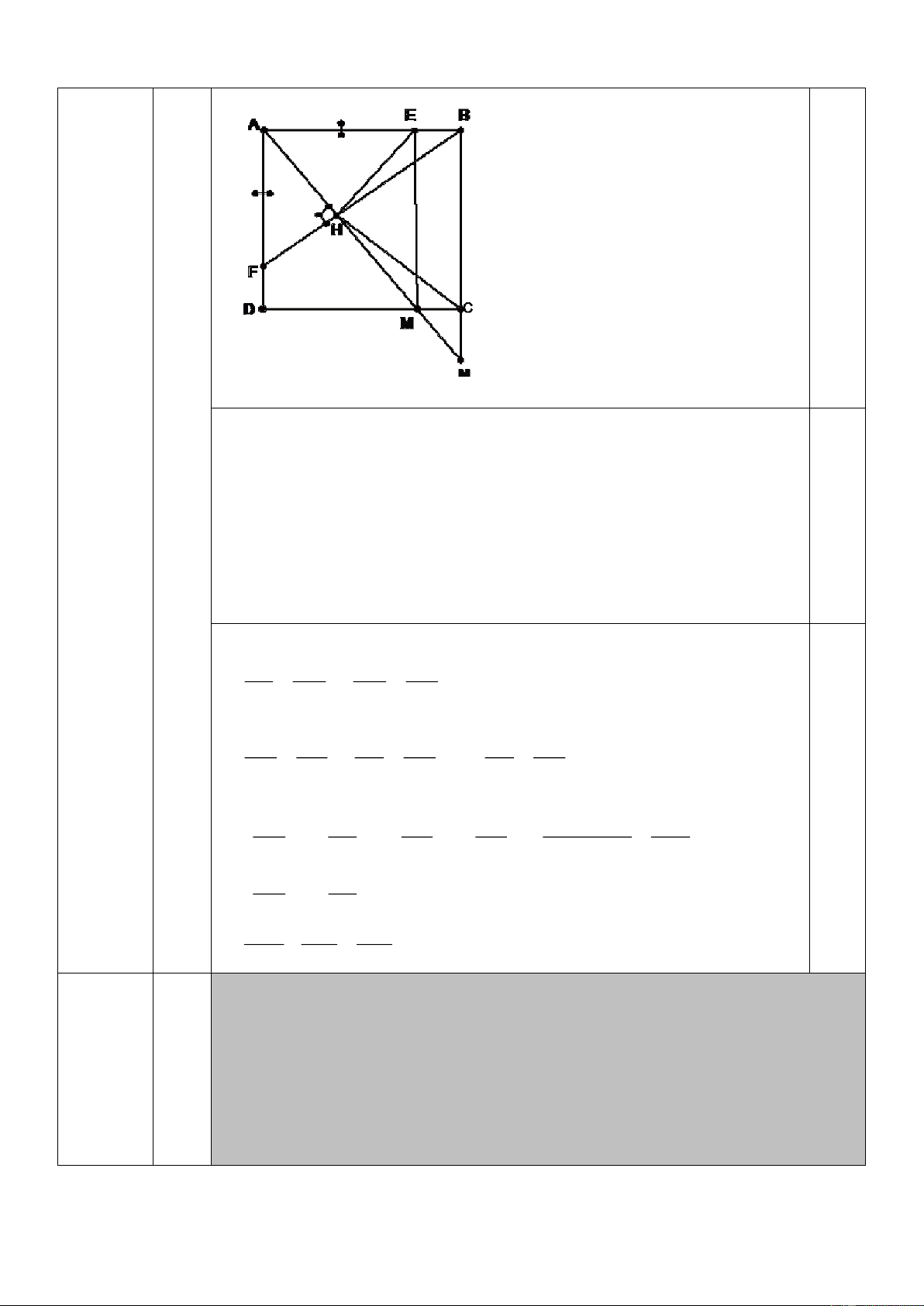
Câu 2. Cho hình vuông ABCD , trên cạnh AB lấy điểm E và trên cạnh AD lấy điểm
F sao cho AE = AF . Vẽ AH vuông góc với BF ( H thuộc BF ), AH cắt DC và BC lần lượt
tại hai điểm M , N .
a) Chứng minh tứ giác AEMD là hình chữ nhật. 1 1 1 b) Chứng minh rằng = + 2 2 2 AD AM AN
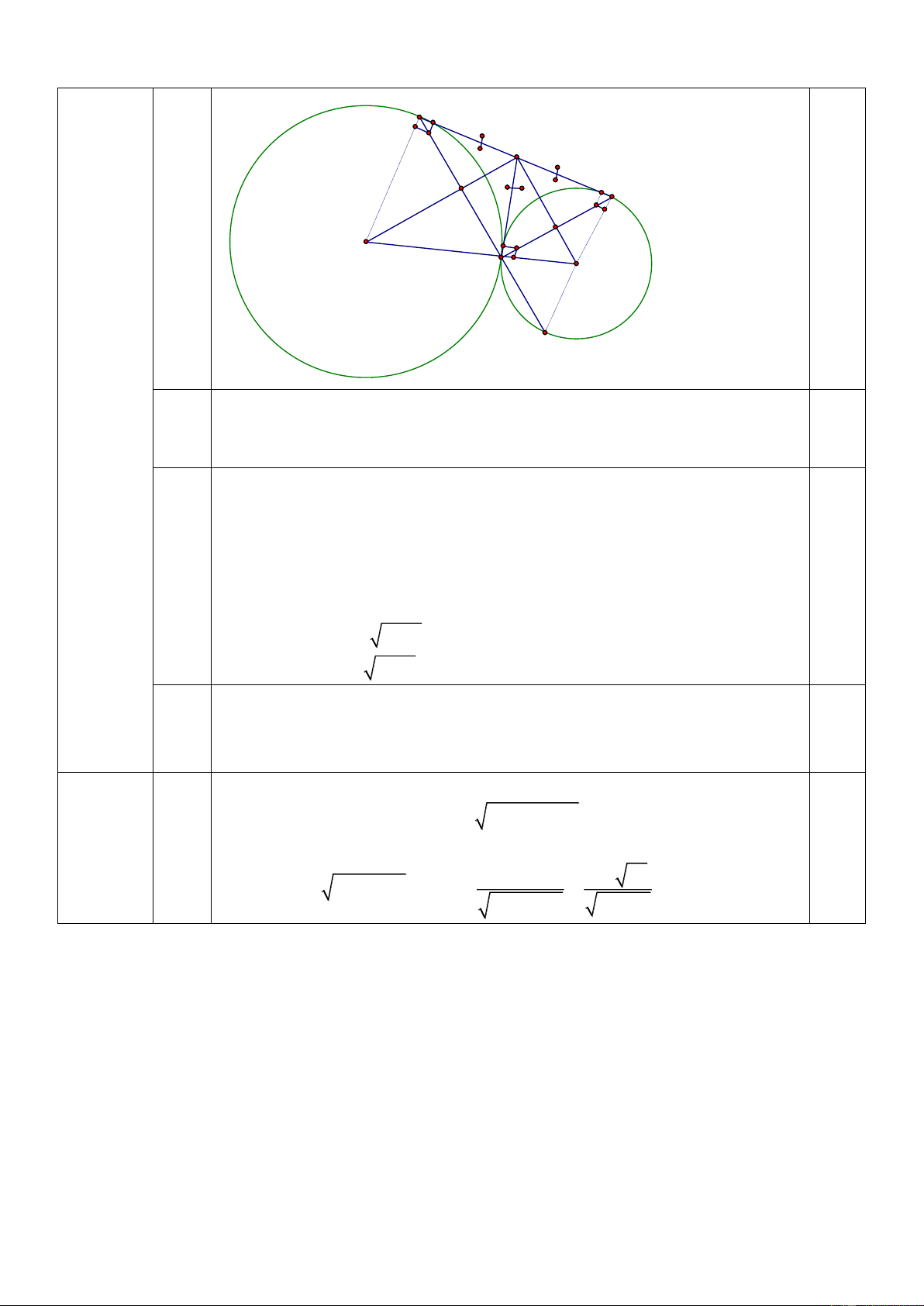
Bài 5. (4 điểm) Cho (O , R ) tiếp xúc ngoài với (O , R ) tại A. Kẻ tiếp tuyến chung 1 1 2 2
ngoài có BC , B(O ) , C(O ) . 1 2 a) Tính BAC .
b) Tính độ dài BC .
c) Gọi D là giao điểm của BA với (O ) . Chứng minh rằng ba điểm C, O , D thẳng 2 2 hàng.
d) Tính độ dài BA .
--------------------HẾT-------------------- Ghi chú:
• Thí sinh không được sử dụng tài liệu.
• Giám thị coi thi không giải thích gì thêm. 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI VÒNG TỈNH THCS KIÊN GIANG NĂM HỌC 2020-2021 -------------
------------------------------ HƯỚNG DẪN CHẤM Môn: TOÁN ĐỀ THI CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề) Ngày thi: 19/3/2021
(Hướng dẫn chấm có 05 trang)
A. HƯỚNG DẪN CHẤM
- Nếu thí sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì vẫn cho đủ
số điểm từng phần như hướng dẫn quy định;
- Việc chi tiết hóa (nếu có) thang điểm trong hướng dẫn chấm phải đảm bảo không
làm lệch hướng dẫn chấm;
- Sau khi cộng điểm toàn bài thi vẫn giữ nguyên số điểm, không được làm tròn.
B. ĐÁP ÁN – BIỂU ĐIỂM Biểu Bài Câu Nội dung điểm Cho phương trình: 4 2
x + 2 6mx + 24 = 0 ( m là tham số). Tìm giá trị của
tham số m để phương trình có 4 nghiệm x , x , x , x phân biệt thỏa mãn: 1 2 3 4 4 4 4 4
x + x + x + x = 144 1 2 3 4 Ta có: 4 2
x + 2 6mx + 24 = 0 Đặt: 2 0.25
t = x , t  0 , phương trình trở thành: 2
t + 2 6mt + 24 = 0(1)
Phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi (1) có 2
nghiệm dương phân biệt 0  t  t . 0.25 1 2 ' 2  = −  1 6m 24 0 2   Khi đó: m  4 t  .t = 24  0    m  2 − 0.5 1 2  m  0 t + t = 2 − 6m  0  1 2 Bài 1.
Với t ,t là hai nghiệm của (1) thì 1 2 0.25 (4 điểm)
x = − t , x = t , x = − t , x = t nên ta có: 1 1 2 1 3 2 4 2 0.25
x + x + x + x = 2(t + t ) = 2 (t + t )2 4 4 4 4 2 2 − 2t .t  1 2 3 4 1 2 1 2 1 2   0.25 2 2
= 2(24m − 48) =144  m = 5  m =  5
Từ đó suy ra m = − 5 0.25 3  x + 2y =19
Giải hệ phương trình:  2x −3 y + 5 (với 3 x  , y  5 − ) + = 2  2 y + 5 2x − 3  2 x − Đặt 2 3 = 1 m  0  m + = 2 0,5 y + 5 m 0,25
 m2 – 2m + 1 = 0  (m – 1)2 = 0  m = 1 (nhận). 0,5 3 x −  2
3 =1  2x - 3 = y + 5  2x – y = 8 y + 5 0,75 3x + 2y = 3x + 2y = x = Giải hệ 19 19 5      2x − y = 8
4x − 2y = 16 y = 2 2 Cho hai số thực b 1 ,
a b khác 0 thỏa mãn 2 2a + + = 4 . Tìm giá trị lớn 2 4 a
nhất và giá trị nhỏ nhất của biểu thức: S = ab + 2019. 2 1 b Ta có: 2 2 4 = a + − 2 + a + − ab + ab + 2 2 a 4 2 2  1   b  = a − + a −
+ ab + 2  ab + 2      a   2  0.25
Do đó: ab  2  S  2021 0.25  1 a − = 0   = − = −
Đẳng thức xảy ra khi và chỉ khi a 1, b 2 a    0.25 b  a =1,b = 2 a − = 0   2 1
Vì vậy giá trị lớn nhất của S là 2021, đạt được khi 0.25 ( , a ) b {  ( 1 − ; 2 − );(1;2)} Mặt khác ta cũng có: 2 2 2 1 b  1   b  2 2 4 = a + − 2 + a +
+ ab − ab + 2 = a − + a +
− ab + 2  −ab + 2     0.25 2 a 4  a   2  Bài 2. 0.25 Suy ra ab  2 −  S  2017 (4 điểm)  1 a − = 0  a =1,b = 2 0.25 a −
S = 2017 khi và chỉ khi    b  a = 1 − ,b = 2 a + = 0  2
Vì vậy giá trị nhỏ nhất của S là 2017 , đạt được khi 0.25 ( , a ) b {  (1; 2 − );( 1 − ;2)}
Trong mặt phẳng Oxy cho Parabol 2
(P) : y = −x
a) Chứng minh rằng đường thẳng y = 2x +1(d ) tiếp xúc với parabol. 1
Tìm tọa độ của tiếp điểm.
b) Xác định tiếp tuyến d với parabol nói trên sao cho d ⊥ d . 2 2 1
c) Tìm tọa độ giao điểm của hai đường thẳng d và d . 1 2 2 a) Parabol 2
(P) : y = −x và đường thẳng y = 2x +1(d ) tiếp xúc 1 Khi phương trình 2
−x = 2x+1 có nghiệm kép 2 2 2
−x = 2x +1 −x −2x 1
− = 0  x +2x+1= 0 0,25
 = 4 − 4 = 0 phương trình có nghiệm kép x = x = 1 − . 0,25 1 2
Tọa độ của tiếp điểm là ( 1 − ; 1 − ) 0,25
b) Gọi đường thẳng d là y = mx + n 2 4 Từ điều kiện 1 1
d ⊥ d ta có 2m = 1
−  m = −  y = − x + ( n d ) 2 1 2 2 2 0,25 Từ điều kiện 1 d tiếp xúc với 2 y = −x hay 2
 −x = − x + n có 2 2
nghiệm kép,  =1−16n để có nghiệm kép 1
1−16n = 0  n = 16 0,25
Vậy đường thẳng d có phương trình dạng 1 1 y = − x + 2 2 16 0,25
c) Tìm tọa độ giao điểm của hai đường thẳng d và d . 1 2  3 y = 2x +1 x = −    0,5 Ta có 8  1 1   y = − x + 1    2 16 y =  4 Cho 4 3 2
f (x) = ax + bx + cx + dx + e . Xác định các số hữu tỉ , a , b , c d,e sao cho 3
f (x) − f(x −1) = x . Từ đó tính 3 3 3 3
S =1 + 2 + 3 +... + n . 4 3 2
f (x) = ax + bx + cx + dx + ( e 1) 4 3 2
f (x −1) = a(x −1) + (
b x −1) + c(x −1) + d(x −1) + ( e 2)
Trừ từng vế (1) và (2) ta được: 0.25 3 2
f (x) − f(x−1) = 4ax + ( 6 − a +3 )
b x + (4a −3b + 2 )
c x − a + b − c + d = 0 Ta lại có: 3
f (x) − f(x −1) = x 0.25 Đồng nhất f ( ) x − f(x 1 − ) với 3 x ta sẽ được:  1 a =  4 4a =1   1   6 − a + 3b = 0 b  =    2 − + = Bài 3. 4a 3b 2c 0   1  0.25 − + − + =  = (4 điểm) 1 c a b c d 0 4   d = 0 Vậy 1 1 1 4 3 2
f (x) = x + x + x + e , với e bất kì. 0.25 4 2 4 Tính 3 3 3 3
S =1 + 2 + 3 +... + n . Trong đẳng thức 3
f (x) − f (x −1) = x , lần lượt cho x bằng 1, 2, 3, …, 0.25 n ta được: 3
f (1) − f (0) =1 3
f (2) − f (1) = 2 … 3
f (n) − f (n−1) = n
Cộng từng vế n đẳng thức trên rồi rút gọn ta được: 3 3 3 3
f (n) − f (0) =1 + 2 + 3 +... + n 0.25 5 1 1 1 4 3 2  0.25 ( n + n +
n + e) - e = 13 + 23 + 33 + … + n3 4 2 4 4 3 2 2 2
n + 2n + n n (n +1)  S = = 0,25 4 4
Chứng minh rằng với mọi , x y thì 4
A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y là số chính phương. 4
A = [(x + y)(x + 4y)][(x + 2y)(x + 3y)]+ y 0,25 2 2 2 2 4
A = (x + 5xy + 4y )(x + 5xy + 6y ) + y 0,25 2 2 2 2 2 2 4
A = (x + 5xy + 4y )[(x + 5xy + 4y ) + 2 y ]+ y 0,5 2 2 2 2 2 2 2 4
A = (x + 5xy + 4y )(x + 5xy + 4y ) + 2 y (x + 5xy + 4y ) + y 0,25 2 2 2 2 2 2 4
A = (x + 5xy + 4y ) + 2 y (x + 5xy + 4y ) + y 0,5 2 2 2 2 2 2 2
A = [(x + 5xy + 4y ) + y ] = (x + 5xy + 5y ) 0,25
Cho ba số thực dương thỏa mãn tích của chúng bằng một và tổng của
chúng luôn lớn hơn tổng nghịch đảo của chúng. Chứng minh rằng có một
và chỉ một trong ba số lớn hơn một.
Gọi x, y, z là ba số thỏa mãn điều kiện đề bài ta có: 1 1 1 . x .
y z =1; x + y + z  + + x y z 0,25 Ta xét các trường hợp:
Trường hợp 1: Nếu x, y, z đều nhỏ hơn 1 hoặc đều lơn hơn 1 thì 0,5 1 trái với giả thiết.
Trường hợp 2: Giả sử 2 trong ba số lớn hơn 1. Không làm mất tính Bài 4.
tổng quát, giả sử x 1, y 1. 0,25 (4 điểm) Vì . x .
y z =1 nên z 1, do đó: (x 1 − )(y 1 − )(z 1 − )  0
 xyz + x+ y + z − xy − xz − yz 1 −  0
 x + y + z  xy + yz + zx 1 1 1 0,25
 x + y + z  + + đều này trái với giả thiết. x y z
Vậy có một và chỉ một trong ba số lớn hơn một. 0,25
Cho hình vuông ABCD , trên cạnh AB lấy điểm E và trên cạnh AD lấy
điểm F sao cho AE = AF . Vẽ AH vuông góc với BF ( H thuộc BF ),
AH cắt DC và BC lần lượt tại hai điểm M , N . 2
a) Chứng minh rằng tứ giác AEMDlà hình chữ nhật. 1 1 1 b) Chứng minh rằng = + 2 2 2 AD AM AN 6
a) Ta có DAM = ABF (cùng phụ BAH ) AB = A ( D gt) 0
BAF = ADM = 90 (Tứ giác ABCD là hình vuông)  A  DM = B  AF(g.c.g) 0,5
 DM = AF , mà AF = AE(gt) nên AE = DM Lại có
AE / /DM (vì AB / /DC ) Suy ra tứ giác
AEMD là hình bình hành, mặt khác 0 DAE = 90 (gt) 0,5
Vậy tứ giác AEMD là hình chữ nhật.
b) Do AD / /CN(gt) , áp dụng hệ quả định lí Ta-lét ta có: AD AM AD CN  =  = (1) CN MN AM N M 0,25
Do MC/ / AB(gt) , áp dụng hệ quả định lí Ta-lét ta có: MN MC AB MC  =  = AD MC hay = (2) ( AB = AD ) 0,25 AN AB AN MN AN MN Từ (1) và (2) ta có 2 2 2 2 2 2 2  AD   AD   CN   CM  CN + CM MN  + = + = = =1         (Pytago) 0,5 2 2  AM   AN   MN   MN  MN MN 2 2  AD   AD   + =1     Chia hai vế cho 2 AD  0,25 AM   AN  1 1 1  + = (đpcm) 2 2 2 AM AN AD 0,25
Cho (O , R ) tiếp xúc ngoài với (O , R ) tại A . Kẻ tiếp tuyến chung ngoài 1 1 2 2
có BC , B(O ) , C(O ) . 1 2 Bài 5. a) Tính BAC . (4 điểm) b) Tính độ dài BC .
c) Gọi D là giao điểm của BA với (O ) . Chứng minh rằng C,O , D thẳng 2 2 hàng.
d) Tính độ dài BA . 7 B I H C K O1 A O2 D
a) Kẻ tiếp tuyến chung tại A, cắt BC tại I 0,25 5a
Theo tính chất của hai tiếp tuyến cắt nhau thì IA = IB = IC 0,5 Nên 0 BAC = 90 0,25
b) Vì IA = IB = IC và O A = O ; B O A = O C 1 1 2 2
Nên IO và IO lần lượt là trung trực của AB và AC 0,25 1 2 Do đó
IO ⊥ AB , IO ⊥ AC , suy ra tứ giác AHIK là hình chữ nhật vì 1 2 5b có ba góc vuông, nên 0 HIK = 90 hay O
 IO vuông tại I . 1 2 0,25
Áp dụng hệ thức về đường cao 2 , ,
h = b c , ta được 2 IA = O . A AO hay 1 2 2
IA = R .R  IA = R .R 1 2 1 2 0,25
Vậy BC = 2IA = 2 R .R 0,25 1 2
c) Vì CAD kề bù với 0 BAC = 90 nên 0 CAD = 90 0,25 5c Ta có C
 AD vuông tại A nội tiếp (O ) nên CD là đường kính. 0,5 2
Vậy C,O , D thẳng hàng. 0,25 2
d) Áp dụng Pytago vào B
 CD vuông tại C , ta có 2 2 2
BD = DC + CB 0,25 hay 2 2 2
BD = 4R + 4R R  BD = 4R + 4R R 0,25 2 1 2 2 1 2 5d
Áp dụng hệ thức về cạnh 2 , c = . a c ta được 2 BC = B . A BD hay 0,25 2R R 2R R 2 1 2 1 2 4R R = .2 BA
R + R R  BA = = 1 2 2 1 2 2 R + R R R + R 1 2 2 1 2 0,25
--------------------HẾT-------------------- 8