Đề học sinh giỏi Toán 11 năm 2020 – 2021 trường THPT Minh Châu – Hưng Yên

TRƯỜNG THPT MINH CHÂU
ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG TỔ TỰ NHIÊN NĂM HỌC 2020 - 2021 Môn: TOÁN - Lớp 11 ĐỀ CHÍNH THỨC
Thời gian: 120 phút (Không kể thời gian phát đề) Câu 1: (2 điểm)
a) Giải phương trình: sin 3x  3 cos3x  2sin 2x .
b) Tìm tất cả các nghiệm của phương trình cos 2x  7 cos x  3 sin 2x  7sin x  8 trên đoạn  2   ;2  Câu 2: (2 điểm) 9  1  a) Tìm số hạng chứa 3 x trong khai triển x  .    2x 
b) Đề thi THPT môn Toán gồm 50 câu trắc nghiệm khách quan, mỗi câu có 4 phương án trả lời và chỉ có 1
phương án đúng, mỗi câu trả lời đúng được cộng 0, 2 điểm, điểm tối đa là 10 điểm. Một học sinh có năng lực
trung bình đã làm đúng được 25 câu( từ câu 1 đến câu 25), các câu còn lại học sinh đó không biết cách giải
nên chọn phương án ngẫu nhiên cả 25 câu còn lại. Tính xác suất để điểm thi môn Toán của học sinh đó lớn
hơn 6 điểm nhưng không vượt quá 8 điểm( làm tròn đến hàng phần nghìn).
Câu 3:(1 điểm) Tìm tất cả các số thực x để ba số x, 2  x, 4
 theo thứ tự đó lập thành một cấp số nhân.
Câu 4: (2 điểm) Tính các giới hạn sau: 2 3 x  x  2  7x 1 a)  n 1 n n 1 lim 16 4 16 3n I        b) J  lim x 1  2  x   1 Câu 5: (1,5 điểm)
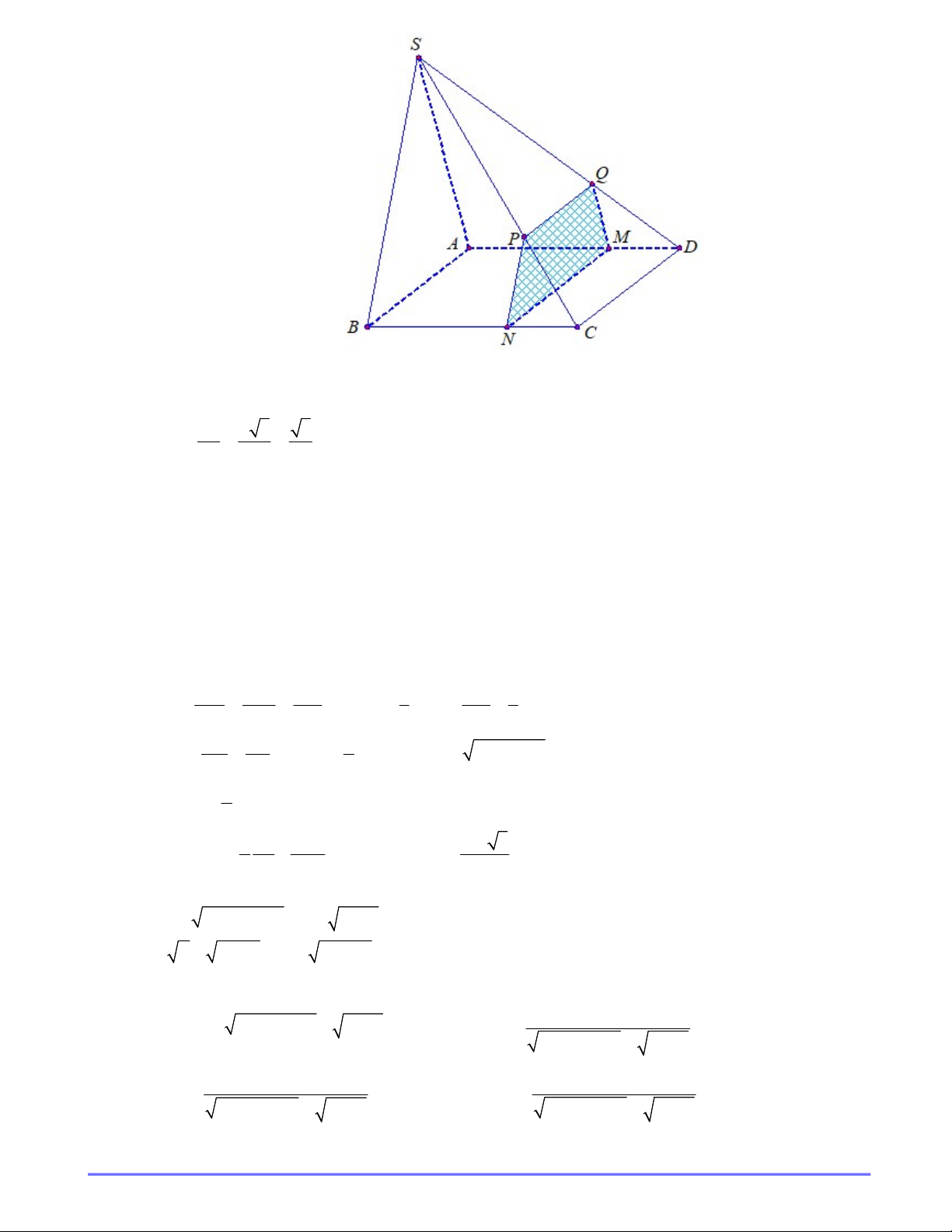
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, mặt bên SAB là tam giác vuông tại A ,
SA  a 3 , SB  2a . Điểm M nằm trên đoạn AD sao cho AM  2MD . Gọi P là mặt phẳng qua M và song song với SAB .
a) Tính góc giữa hai đường thẳng SB và CD.
b) Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng P . Câu 6: (1,5 điểm) 2 2
x  4  x 8x 17  y  y 1
a) Giải hệ phương trình  .
x  y  y  21 1  2 4y  3x  u   4  1
b) Cho dãy số u được xác định như sau *  , n   . n  9
 u  u  4  4 1 2u  n 1 n n
Tìm công thức số hạng tổng quát của dãy số u và tính limu n  n
----------------- Hết ----------------
(Giám thị coi thi không giải thích gì thêm)
Họ và tên thí sinh:...............................................
Chữ ký của giám thị:………………………
Số báo danh:……………….. Phòng thi số:……… TRƯỜNG THPT MINH CHÂU
HƯỚNG DẪN CHẤM ĐỀ THI HỌC SINH GIỎI TỔ TỰ NHIÊN NĂM HỌC 2020 - 2021 Môn: TOÁN – Khối 11 Câu 1:
a) Giải phương trình sau sin 3x  3 cos3x  2sin 2x . 1 3
Ta có : sin 3x  3 cos 3x  2sin 2x  sin 3x  cos 3x  sin 2x (0.25) 2 2     3x   2x  k2       x k2    3  sin 3x   sin 2x  3      k  (0.5)  3    2 k2 3x     2x  k2   x    3  15 5   2 k2 
Vậy phương trình đã cho có tập nghiệm S    k2;  k  . (0.25)  3 15 5  b) Ta có:
cos 2x  7 cos x  3 sin 2x  7sin x  8  cos 2x  3 sin 2x  7 cos x  3 sin x 8  0             2  cos 2x   7sin x   4  0  2sin x   7 sin x   3  0         (0.25)  3   6   6   6      1 sin x       6  2   (0.25)     sin x   3(VN )      6     x    k2 x  k2  1    Ta có: 6 6 sin x         2 (0.25)  6  2  5   x   k2 x    k2  3  6 6     Vì x     4 2 2 ; 2  x  2 ; ;0; ; 2  . (0.25)  3 3  Câu 2: 9  1  Câu 030. Tìm số hạng chứa 3 x trong khai triển x  .    2x  Lời giải
Theo khai triển nhị thức Niu-tơn, ta có 9 9  1  k  1 k k 9  x   C .x . 0.25   9    2x  k 0  2x  B1.X.T0 9  1 k k  92  C . . k x . 0.25 9   k 0  2  Hệ số của 3
x ứng với 9  2k  3  k  3 0.25 1 Vậy số hạng cần tìm 3 3 C x . 0.25 9 8
b) Gọi x là số câu học sinh đó trả lời đúng trong 25 câu còn lại.
Số điểm học sinh đó đạt được là 5  0, 2x . (0.25)
Theo yêu cầu đề bài 6  5  0, 2x  8  5  x  15, x  .
Như vậy, để điểm của học sinh đó lớn hơn 6 điểm nhưng không vượt quá 8 điểm thì học sinh đó phải trả lời
đúng từ 6 đến 15 câu và làm sai các câu còn lại.
Xác suất trả lời đúng 1 câu là 0,25; xác suất trả lời sai 1 câu là 0,75.
Xác suất trong mỗi trường hợp là 0.25x .0.7525 x x C
 với x   và 6  x  15 (0.25) 25 15
Suy ra xác suất cần tính là C 0.25x .0.7525x x  0,622 . (0.25) 25 x6  0,622 (0.25) Câu 3: x  0 Ta có 2x2 2  .
x 4  4x  4x  0   . (0.25) x 1 Với x  0 ta có 0; 0  ; 4
 không là cấp số nhân. (0.25) Với x 1 ta có 1; 2  ; 4
 là cấp số nhân có công bội q  2 . (0.25) Vậy x 1. (0.25) Câu 4:  4n  3n  a) Ta có  n 1 n n 1 lim 16 4 16 3n T         lim  (0.5) n 1  n n 1
 16  4  16   3n   3 n     1      4    1 lim    . (0.5)   1 n   3 n  8 16 16          4 16        b) Lời giải 2 3 2 3 x  x  2  7x 1
x  x  2  2  2  7x 1 Ta có lim  lim (0.25) x 1  2  x   x 1 1  2 x   1 2 3 x  x  2  2 2  7x 1  lim  lim  I  J . x 1  2  x   x 1 1  2  x   1 2 2 x  x  2  2 x  x  2  4 Tính I  lim  lim x 1  2  x   x 1 1  2  x   1  2x  x  2  2 x  1x  2 x  2 3  lim  lim  . (0.25) x 1  2  x  
1  2x  x  2  2 x 1 
2  2x  x  2  2 4 2 3 2  7x 1 8  7x 1 và J  lim  (0.25) x x   lim 2 1 x 2  x   1 4  2 7x 1    7x12 1 1 3 3    7  7  lim  . x   x    x   2 1 3 3  12 2 2 4 2 7 1 7 1   2 3 x  x  2  7x 1 2 Do đó lim  I  J  (0.25) x 1  2  x   1 12 Câu 5:
a) Ta có : AB//CD nên (SB,CD)=(SB,AB) (0.25)
Do tam giác SAB vuông tại A theo gt nên SB,CD   SBA (0.25) SA a Có :  3 3 sin SBA    SB 2a 2 Suy ra: SB CD 0 ,  60 (0.25)   P   // SAB   P    ABCD  MN b)    và MN // PQ // AB (1) M  AD, M   P   P   SCD  PQ   P   // SAB   P    SAD  MQ MQ // SA     và  M  AD, M   P   P    SBC  NP NP // SB
Mà tam giác SAB vuông tại A nên SA  AB  MN  MQ (2)
Từ (1) và (2) suy ra thiết diện là hình thang vuông tại M và Q . (0.25) MQ DM DQ 1 DQ 1 MQ // SA     MQ  SA và  . SA DA DS 3 DS 3 PQ SQ 2  PQ // CD    PQ  AB , với 2 2 AB  SB  SA  a (0.25) CD SD 3 1 Khi đó S  M . Q PQ  MN MNPQ   2 1 SA  2AB  2 5a 3  S  .  AB  S  . (0.25) MNPQ   2 3  3  MNPQ 18 2 2
x  4 x 8x 17  y  y 1  1 6. a) 
x  y  y  21 1  2 4y  3x  2
Điều kiện: y  0, 4y  3x  0 .   x  4  y  x  y   2 2 1
4  x  8x 17  y 1  0   x  y  4  2 2   0 2 2 x  8x 17  y 1  x  4  y    x   y x   y x  y  4  4  4    0   x  y  4   1   0 (0.25) 2 2 x  8x 17  y 1  2 2 x 8x 17 y 1         y  x  4 . x  4 y
x  42 1x  4 2  y 1  y (Vì: 1   0 x  , y ) (0.25) 2 2 2 2 x  8x 17  y 1 x  8x 17  y 1
Thay y  x  4 vào (2) ta được:
2  x  x  4  x  25 1 2 x 16
  x  4  2 x  25 5x 8 2 x 16  0  1 1 x 12   x    0    x  4  2
x  25  5 x  8  2 x 16  x  0  y  4 ( t/m)   1 1 x 12  . (0.25)    0 3  x  4  2
x  25  5 x  8  2 x 16
Do x  4  y  0  x  4  x  8  0 nên (3) vô nghiệm.
Vậy hệ phương trình đã cho có nghiệm  ; x y  0;4 . (0.25)
Chú ý: Ta có thể giải (1) như sau:    x    x   2 1 4 4 1  y  y 1 2 t t 1  t Xét hàm số f t 2
 t  t 1 có f t 1   0,t   . 2 2 t 1 t 1
Do đó f t đồng biến trên  nên  
1  f  x  4  f  y  x  4  y . Ta có * u  0, n
   và 9u  u  4  4 1 2u n n 1  n n
 18u  2u  8  8 1 2u n 1  n n 0,25  91 2u       1 2u 4 n n 2 1  3 1 2u  1 2u  4 n 1  n 0,25
 3 1 2u  2  1 2u  2 n 1   n Đặt *
v  1 2u  2, n   n n v  1 1  Ta có *  1 , n    6. b) v  v  n 1 n  3 (0.75đ) 1
 dãy số v là một cấp số nhân có công bội q  , số hạng đầu v  1. n  3 1 n 1  0,25  1   v  n    3  v  2    n 2 1 1 1 4  u     3 . n  2n2 n 1  2 2  3 3   1  1 4  Kết luận * u    3 , n    . Khi đó n  2n2 n 1  2  3 3   0,25 1  1 4  3 lim u  lim   3  . n  2n2 n 1  2  3 3   2 Hết