Đề khảo sát chất lượng Toán 9 năm 2021 – 2022 sở GD&ĐT Thanh Hóa

SỞ GD&ĐT THANH HOÁ
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 9 NĂM HỌC 2021 - 2022 ĐỀ CHÍNH THỨC MÔN: TOÁN
Thời gian làm bài: 120 phút.
(Không tính thời gian giao đề cho thí sinh)
Câu I (2,0 điểm). 2 x  x 2x  x 2 x   1 Cho biểu thức P   
, với x  0, x  1. x  x 1 x x 1
1. Rút gọn biểu thức P .
2. Tìm các giá trị của x để P  7 .
Câu II (2,0 điểm).
1. Trong mặt phẳng toạ độ Oxy , cho đường thẳng d  : y  3m  
1 x  2  m . Tìm
m để đường thẳng d  đi qua điểm A1; 3   .
2x  3y  7
2. Giải hệ phương trình:  .
x  4y  2 
Câu III (2,0 điểm). 1. Giải phương trình 2
x  9x  8  0 2. Cho phương trình 2
x  2x  m  3  0 (với m là tham số). Tìm m để phương trình
có hai nghiệm x , x thỏa mãn: 3 3 2 2 (
m x  x )  x x  9. 1 2 1 2 1 2
Câu IV (3,0 điểm). Từ điểm P nằm ngoài đường tròn O kẻ hai tiếp tuyến PQ , PR tới
đường tròn với Q và R là các tiếp điểm. Đường thẳng qua P cắt đường tròn O tại hai
điểm M và N ( M nằm giữa P , N và dây MN không qua tâm O ). Gọi I là trung điểm của đoạn MN .
1. Chứng minh rằng tứ giác PQOR nội tiếp đường tròn.
2. Chứng minh rằng IP là phân giác của QIR và PM .PN  P . Q PR .
3. Gọi K là giao điểm của PN và QR . Chứng minh: 2 1 1   . PK PM PN
Câu V (1,0 điểm).
Cho x, y, z là các số thực dương thay đổi thỏa mãn 3 3 3
x  y  z  8 . Tìm giá trị nhỏ nhất 2 2 2 2 2 2 x  y y  z z  x
của biểu thức A    . 3 3 3
xy(x  y)
yz(y  z ) zx(z  x )
-------------- Hết ------------
Thí sinh không được sử dụng tài liệu; cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:........................................................................ Số báo danh: .........................................................................
Chữ ký CBCT số 1:..................................................................... Chữ ký CBCT số 2: ........................................................
SỞ GD&ĐT THANH HOÁ
HƯỚNG DẪN CHẤM ĐỀ KHẢO SÁT MÔN TOÁN LỚP 9 ĐỀ CHÍNH THỨC
NĂM HỌC 2021 – 2022
(Hướng dẫn chấm gồm có: 04 trang) Hướng dẫn chung:
1) Nếu học sinh giải cách khác với cách nêu trong HDC này, mà đúng, thì vẫn được
điểm tối đa của phần (câu) tương ứng.
2) Trong câu hình, nếu học sinh không vẽ hình hoặc vẽ sai cơ bản thì không cho điểm câu đó. Câu Ý NỘI DUNG Điểm 2 x  x 2x  x 2 x   1
Cho biểu thức P   
, với x  0, x  1. x  x 1 x x 1
Rút gọn biểu thức P . x  3 x   1 x 2 x   1 2 x   1  x   1 Ta có P    0,25 1 x  x 1 x x 1 (1,0đ) x  x  
1 x  x   1 0,25   2 x   1  2 x   1 x  x 1 I  x  x   1 1 0,25 (2,0đ)  x  x  1 0,25
Tìm x để P  7 .
Do P  7 nên x  x 1  7  x  x  6  0 0,25 2
Đặt t  x t  0 ta được phương trình 2
t  t  6  0 (1) 0,25
(1,0đ) Phương trình (1) t  2t  
3  0 nên có nghiệm t  2  (loại), t  3 1 2 0,25 Với t  3 
x  3  x  9 . 0,25
Vậy với x  9 thì P  7 .
Trong mặt phẳng toạ độ Oxy , cho đường thẳng d  : y  3m  
1 x  2  m . 1
Tìm m để đường thẳng d  đi qua điểm A1;  3 .
(1,0đ) Vì d đi qua điểm A1; 
3 nên ta có: d  : 3   3m   1 .1 2  m . 0, 5  m  2  0,5    II 2x 3y 7
Giải hệ phương trình:  . (2,0đ)
x  4y  2  2
2x  3y  7
2x  3y  7 Hệ    0,5 (1,0đ)
x  4y  2 
2x  8y  4 
2x  3y  7    x 2    0,5 1  1y  11  y  1 1
Giải phương trình 2
x  9x  8  0 1
Ta có a  1,b  9
 ,c  8  a  b  c  0 0,5
(1,0đ) Nên phương trình có hai nghiệm x  1, x  8 1 2 0,5
Kết luận: phương trình có hai nghiệm x  1, x  8 1 2 Cho phương trình 2
x  2x  m  3  0 (với m là tham số). Tìm m để phương
trình có hai nghiệm x , x thỏa mãn: 3 3 2 2 (
m x  x )  x x  9. 1 2 1 2 1 2
Ta có điều kiện để phương trình có hai nghiệm là 0,25 III
'  4 m  0  m  4 (2,0đ) Giả thiết
m(x  x )  x x
 9  m  x  x
 3x x x  x   x x  9 1 2 1 2  1 23 3 3 2 2 1  1 2 2 2 2 1 2 2   (1) 0,25 (1,0đ)
x  x  2 Theo đị 1 2 nh lí Viet, ta có  x x  m  3  1 2 0,25 32 Thế vào (1), ta được 2
7m  32m  0  m  0; m  7
Kết hợp điều kiện, suy ra m  0. 0,25
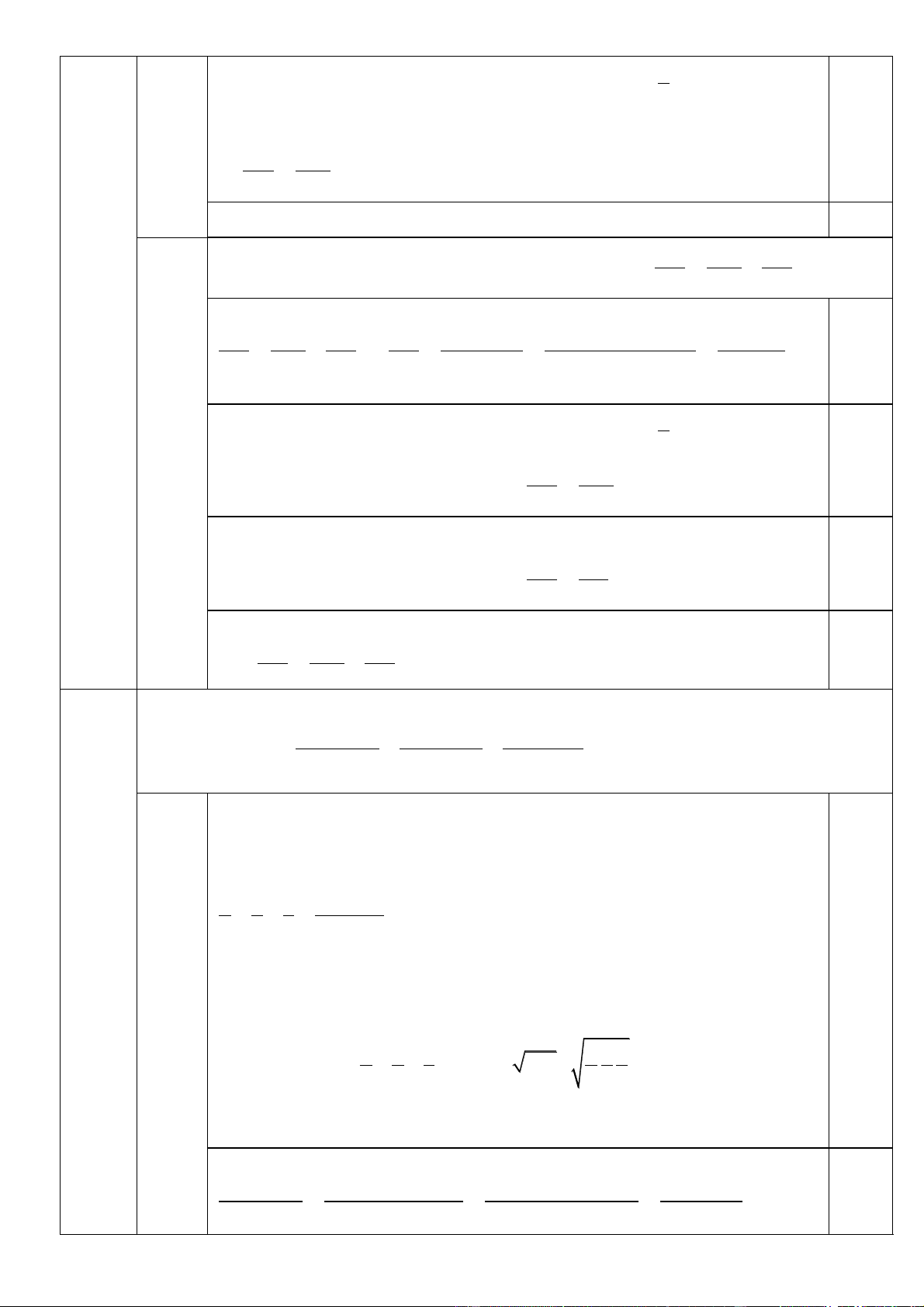
Từ điểm P nằm ngoài đường tròn O kẻ hai tiếp tuyến PQ , PR tới đường tròn với
Q và R là các tiếp điểm. Đường thẳng qua P cắt đường tròn O tại hai điểm M và
N ( M nằm giữa P , N và dây MN không qua tâm O ). Gọi I là trung điểm của đoạn MN . Q P O K M I N IV R (3,0đ)
Chứng minh rằng tứ giác PQOR nội tiếp đường tròn. 1 Ta có 0 PQO  90 , 0
PRO  90 (do PQ , PR là hai tiếp tuyến của O ). 0,5
(1,0đ) Suy ra bốn điểm P,Q,O,R cùng thuộc đường tròn đường kính PO . 0,5
Vậy tứ giác PQOR nội tiếp đường tròn.
Chứng minh rằng IP là phân giác của QIR và PM .PN  P . Q PR .
Ta có I là trung điểm của MN , suy ra 0
OI  MN  OIP  90 nên năm 0,25 2
điểm P,Q,O, I, R cùng thuộc đường tròn đường kính PO .
(1,0đ) Suy ra tứ giác PQIR nội tiếp, lại có PQ  PR (tính chất tiếp tuyến) nên
trong đường tròn đường kính PO thì sđ PQ = sđ PR  PIQ  PIR hay IP 0,25
là phân giác của QIR . 2 1
Xét ∆PQM và ∆PNQ có QPN chung PQM =PNQ (= sđ QM của đường 2
tròn O ), nên ∆PQM đồng dạng với ∆PNQ PQ PM 2  
 PQ  PM.PN 0,25 PN PQ
Mà PQ  PR  P .
Q PR  PM.PN 0,25 2 1 1
Gọi K là giao điểm của PN và QR . Chứng minh:   . PK PM PN Ta có: 2 1 1 2 PM  PN
PI  IM  PI  IN 2PI       0,25 PK PM PN PK PM .PN PM .PN PM .PN
 PM.PN  PK.PI 1
Xét ∆PQM và ∆PNQ có QPN chung PQM =PNQ (= sđ QM ), 3 2 0,25 (1,0đ) PQ PM
Nên ∆PQM đồng dạng với ∆PNQ 2  
 PQ  PM.PN (1) PN PQ
Xét ∆PQK và ∆PIQ có QPI chung PQK =PIQ (sđ PQ =sđ PR ), PK PQ 0,25
Nên ∆PQK đồng dạng với ∆PIQ 2  
 PQ  PK.PI (2) PQ PI
Từ (1) và (2) suy ra: PM.PN  PK.PI 2 1 1 0,25 Vậy   (đpcm). PK PM PN
Cho x, y, z là các số thực dương thay đổi thỏa mãn 3 3 3
x  y  z  8 . Tìm giá trị nhỏ nhất 2 2 2 2 2 2 x  y y  z z  x
của biểu thức A    3 3 3
xy(x  y)
yz( y  z) zx(z  x)  , a ,
b c  0 ta chứng minh được 3 3
ab(a  b)  a  b (1) 2 2 2
(a  b)  2(a  b ) (2) 1 1 1 9    a b c a  b  (3) c V Thật vậy (1,0đ) 0,25 3 3 2
(1)  a  b  ab(a  b)  0  (a  b)(a  b)  0 (1,0đ) 2 2 2 2
(2)  2(a  b )  (a  b)  0  (a  b)  0 1 1 1 1 1 1 3 3
(3)  (a  b  c)(   )  9  3 abc.3  9 a b c a b c
(1), (2) đẳng thức xảy ra khi a  . b
(3) đẳng thức xảy ra khi a  b  . c Áp dụng ta có: 2 2 2 2 2 2 x  y x  y x  y 1    0,25 3 2 3 3 2 2 3 3
xy(x  y)
xy(x  y)(x  y)
(x  y )2(x  y ) 2(x  y ) 3 2 2 y  z 1 2 2 z  x 1 Tương tự   3 3 3
yz( y  z) 2( y  ; z ) 3 3 3
zx(z  x) 2(z  0,25 x ) 1  1 1 1  1 9 9 Ta được A     .    3 3 3 3 3 3 3 3 3 2  x  y y  z
z  x  2 2(x  y  z ) 32 2
Dấu bằng xảy ra khi x  y  z  0,25 3 3 9
Vậy giá trị nhỏ nhất của A là 32
------------ Hết ------------ 4