Đề khảo sát chất lượng Toán 9 năm 2021 – 2022 trường THCS Lê Ngọc Hân – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp đề khảo sát chất lượng học sinh môn Toán 9 năm học 2021 – 2022 trường THCS Lê Ngọc Hân – Hà Nội giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.
Preview text:
TRƯỜNG THCS LÊ NGỌC HÂN
ĐỀ KHẢO SÁT CHẤT LƯỢNG
MÔN: TOÁN – LỚP 9 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút
Ngày kiểm tra: 12 tháng 02 năm 2022
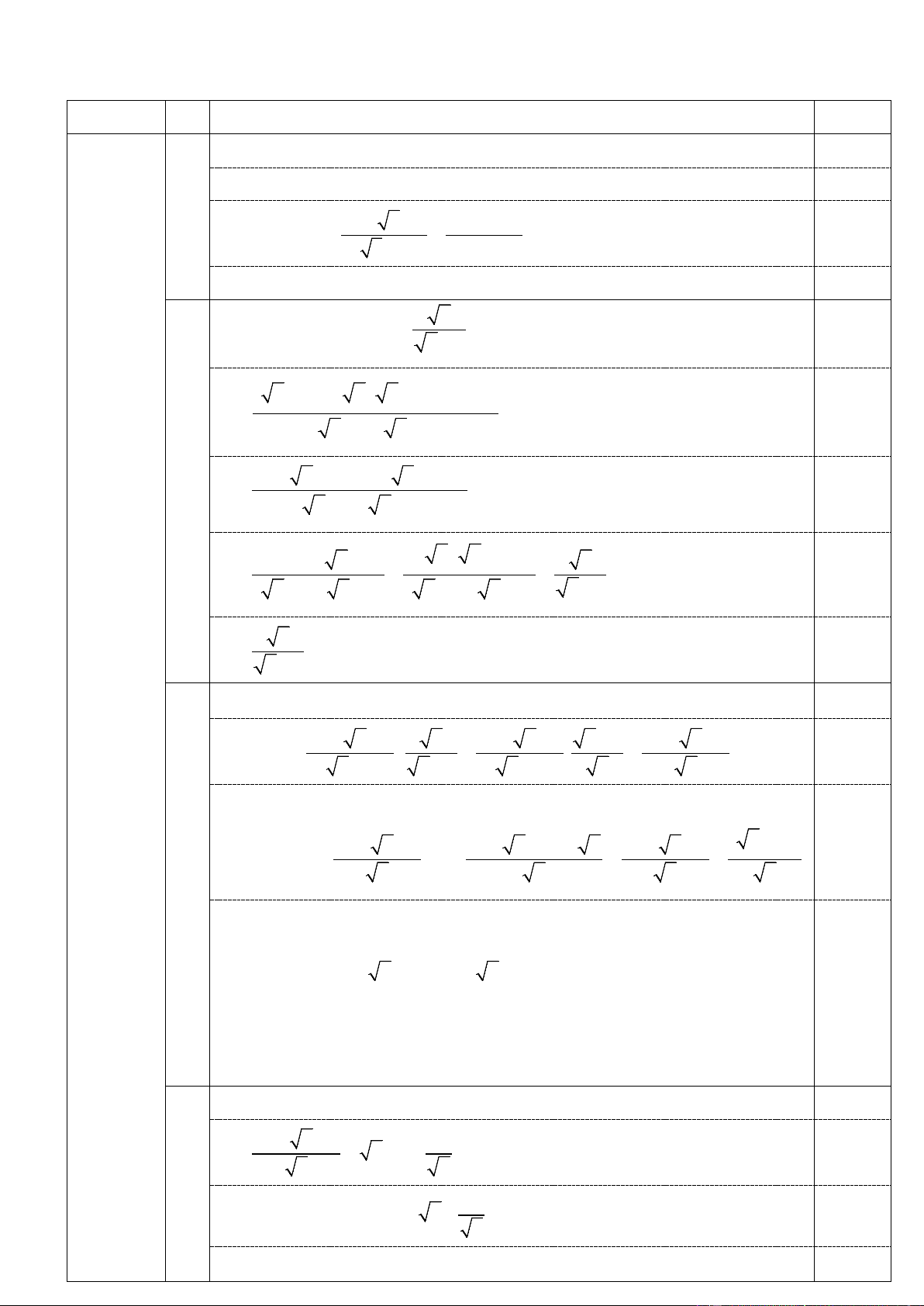
Bài I (3 điểm). Cho hai biểu thức: x − 2 x + 4 x + 2 x x + 4 A = và B = + −
với x > 0; x ≠ 4 x − 2 x − 2 x + 2 x − 4
1). Tính giá trị của biểu thức A khi x = 9 . x 2). Chứng minh: B = . x − 2
3). Đặt P = A : B . So sánh P và 2 .
4). Tìm giá trị nguyên dương nhỏ nhất của P.
Bài II (2,5 điểm). Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Để chuẩn bị cho công tác phòng chống dịch COVID – 19 khi học sinh quay trở lại
trường học trực tiếp, nhà trường dự định mua khẩu trang và dung dịch sát khuẩn với tổng số
tiền là 8 triệu đồng. Tuy nhiên, vì cửa hàng có chương trình ưu đãi dành cho trường học, giá
khẩu trang giảm 10%, giá dung dịch sát khuẩn giảm 15% nên nhà trường chỉ phải trả 7 triệu
đồng. Hỏi số tiền ban đầu dự định để mua khẩu trang là bao nhiêu? Bài III (4 điểm).
1). Giải hệ phương trình 1 1 − = 2 1 x + 1 + = 3 x y y a). b). 3 4 + = 1 10 − x + 1 = − 2 x y y
2). Trong mặt phẳng Oxy, cho đường thẳng (d): y = (m − 1) x + 2m (m ≠ 1)
a). Với m = 2, tìm giao điểm của (d) với đường thẳng (d1): y = 3x − 2.
b). Với giá trị nào của m để (d) song song với đường thẳng (d2): y = −x.
c). Đường thẳng (d) cắt trục Ox tại điểm B, cắt trục Oy tại điểm A.
Tìm m sao cho diện tích tam giác OAB bằng 1(đvdt).
Bài IV (0,5 điểm). Giải phương trình x + x + 1+ (2 5 −1) x = 3x − 2 x − 4 + 3
Chúc em làm bài tốt!
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM MÔN TOÁN 9 (12/02/2022) Bài Ý Đáp án Điểm
Tính giá trị của biểu thức A khi x = . 9 0,75
Thay x = 9 (TMĐK) vào biểu thức A. 0,25 1) Tính đượ 9 − 2 9 + 4 9 − 2.3 + 4 c A = = = 7 0,25 9 − 2 3 − 2 Kết luận 0,25 x
Chứng minh rằng B = 1,25 x − 2 ( x + )2 2
+ x ( x − 2)−(x + 4) B = ( 0,25 x − 2)( x + 2)
x + 4 x + 4 + x − 2 x − x − 4 2) B = ( 0,25 x − 2)( x + 2) x + x x ( x +2 2 ) = x B ( = = 0,25x2
x − 2)( x + 2) ( x − 2)( x + 2) x − 2 = x B (đpcm) 0,25 x − 2 Bài I
Cho S = A : B. So sánh P với 2. 0,5 (3 điểm) x − 2 x + 4 x x − 2 x + 4 x − 2 x − 2 x + 4
P = A : B = : = . = x − 2 x − 2 x − 2 x x Xét − + − + − − + ( x − x x x x x x x )2 2 2 4 2 4 2 4 4 0,25 P − 2 = − 2 = = = x x x x 3)
Theo ĐKXĐ: x > 0; x ≠ 4 Nhận xét: ( x − )2 2
> 0 ; x > 0 với mọi x > 0; x ≠ 4 0,25
Suy ra: P − 2 > 0 ⇔ P > 2 với mọi x > 0; x ≠ 4 Vậy P > 2
Tìm giá trị nguyên dương nhỏ nhất của P. 0,5 x − 2 x + = 4 = − + 4 P x 2 ( x ≥ 0 ; x ≠ 4) x x 4) 4
Áp dụng bđt Côsi ta có: x +
≥ 4 ⇒ P ≥ 4 − 2 = 2 0,25 x Dấu “=” xảy ra 0,25 Bài Ý Đáp án Điểm ⇔ 4 x =
⇔ x = 4( kot / m ) x
P > 2 mà P là số nguyên dương nhỏ nhất => P = 3 Khi đó x = 1 hoặc x = 16
Nếu thiếu điều kiện x ≠ 4 hoặc không so điều kiện thì trừ 0,25 điểm Số tiền mua khẩu
Số tiền mua dung dịch sát khuẩn trang (triệu đồng) (triệu đồng) Dự x 8 − x 0,25 x định
(0 < x < 8) 4 90%x 0,9 x
85% (8 − x) = 0,85 (8 − x) Bài II Thực tế = = 6,8 −0,85x (2,5 điểm)
Thực tế, tổng số tiền phải trả là 7 triệu đồng 0,25 x
⇒ 0,9x+6,8 − 0,85x =7 2
Giải phương trình, tìm được x = 4 0,25 x 2 Kiểm tra điều kiện. 0,25
Kết luận: Số tiền ban đầu dự định để mua khẩu trang là 4 triệu đồng. 0,25
Giải hệ phương trình 1
ĐK: x;y ≠ 0 0,25 1 1 − = 4 − 4 1 = 4 x y x y ⇔ 0,25 3 4 + = 3 + 4 10 = 1a) x y 10 x y
x = 1 / 2( t / m ) Giải ra 0,25
y = 1( t / m ) Bài III (4 điểm)
Kết luận: Vậy nghiệm của hệ là; ( ) 1 x; y = ;1 0,25 2 + + 2 x 1 = 3 y
Giải hệ phương trình 1
1 − x +1 = − 2 y 1b) ĐK: y > 0 3 Giải ra
= 1; x + 1 = 1 0,25 y Bài Ý Đáp án Điểm
Giải ra y = 9 ; = 4 x hoặc = − 10 x 0,25x2 3 3
So sánh điều kiện và kết luận:
4 10 0,25
Hệ có 2 nghiệm ( x; y) ∈ ;9 ; − ;9 3 3
Với m = 2, tìm giao điểm của đường thẳng (d): y = (m − 1) x + 2m với đườ 0,75
ng thẳng (d1): y = 3x − 2.
Với m = 2, xét phương trình hoành độ giao điểm của (d) và (d1): 2a) 0,25
x + 4 = 3x − 2.
Giải ra, tìm được x = 3.Tính được y = 7. 0,25
Kết luận: Giao điểm cần tìm là (3;7 ) . 0,25
2b) Với giá trị nào của m để (d) song song với đường thẳng (d2): y = −x. 0,5
m − 1 = −1
Để (d) song song với (d2) ⇔ 0,25 2m ≠ 0 Giải ra m ∈∅ 0,25
Vậy không có giá trị của m để (d) song song với (d2)
Đường thẳng (d) cắt trục Ox tại điểm B, cắt trục Oy tại điểm A. 2c) 0,75
Tìm m sao cho diện tích tam giác OAB bằng 1(đvdt). ( ) −2m 2m A 0;2m ; B
;0 ⇒ OA = 2m ; OB = m − 1 m − 1 0,25 2 OA.OB 2m Bài III
Tam giác OAB vuông tại O ⇒ S = = OAB 2 m − (3,5 1 điểm) 2 2m 2 2 Để S = 1 ⇔
= 1 ⇔ m − 1 = 2m ⇔ m − 1 = ±2m OAB m − 1 TH1: ( m < 1) m = −1 1 2 2 0,25 m 1 2m 2m m 1 0 (m 1) − = − ⇔ + − = ⇔ + m − = 0 ⇔ (TM) = 1 2 m 2 TH2: m ≥ 1 2 1 7 2 2 0,25
m − 1 = 2m ⇔ 2m − m + 1 = 0 ⇔ 2m −
+ = 0 ⇔ m∈∅ 2 2 8
(Nếu vừa thiếu so sánh điều kiện, vừa thiếu ý tam giác OAB vuông tại
O thì trừ 0,25 điểm)
Giải phương trình x + x + 1 + (2 5 − 1) x = 3x − 2 x − 4 + 3 0,5 Bài IV (0,5 ĐK: x ≥ 4 điểm) 2 2
2x − 2 5 . x − 2 x − 4 + 2 = 0 ⇔ ( x − 5) + ( x − 4 −1) = 0 0,25 Bài Ý Đáp án Điểm
Giải ra, tìm được x = 5. So sánh điề 0,25 u kiện và kết luận.