Đề khảo sát chất lượng Toán 9 năm 2023 – 2024 phòng GD&ĐT Hoàn Kiếm – Hà Nội

UBND QUẬN HOÀN KIẾM
ĐỀ KHẢO SÁT CHẤT LƯỢNG
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO Môn: Toán học, Lớp 9 Năm học 2023 – 2024 ĐỀ CHÍNH THỨC Ngày khảo sát: 15/5/2024 (Đề thi gồm 01 trang)
Thời gian làm bài: 120 phút (không kể thời gian phát đề) x  2 x 1 x x 1
Bài I. (2,0 điểm) Cho hai biểu thức A  và B    với x  0; x  1 x x 1 x 1 x 1
1) Tính giá trị của biểu thức A khi x 16 .
2) Rút gọn biểu thức B . 3) Xét biểu thức P  .
A B . Tìm tất cả giá trị của x sao cho P nhận giá trị nguyên. Bài II. (2,0 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Hai đội công nhân làm chung một công việc thì làm xong sau 20 ngày. Nếu mỗi đội làm riêng thì đội thứ hai
cần nhiều hơn đội thứ nhất 9 ngày thì mới xong công việc đó. Hỏi nếu làm riêng, mỗi đội làm xong công việc đó sau bao nhiêu ngày?
2) Một quả địa cầu hành chính có đường kính bằng 33cm. Tính thể tích của quả
địa cầu, lấy   3,14 . Bài III. (2,5 điểm)  2 x   5  y 1
1) Giải hệ phương trình:  1 3 x   1  y 1
2) Trong mặt phẳng tọa độ Oxy , cho parabol P 2
: y  x và đường thẳng d  : y  m  2 x  3m  3 ( m là tham số).
a) Với m  4 , chứng minh đường thẳng d  cắt parabol P tại hai điểm phân biệt có hoành độ x ; x . 1 2 13
b) Tìm tất cả giá trị của m để x ; x là độ dài hai đường chéo của một hình thoi có độ dài cạnh là 1 2 2 Bài IV. (3,0 điểm) Cho đường tròn  ;
O R và một điểm M nằm ngoài đường tròn. Kẻ tiếp tuyến M ,
A MB với đường tròn  ; O R ( ,
A B là các tiếp điểm). Vẽ đường kính AD , tiếp tuyến tại điểm D của  ;
O R cắt đường thẳng AB tại C .
1) Chứng minh bốn điểm M , ,
A O, B thuộc một đường tròn; 2) Chứng minh 2 AB.AC  4R ;
3) Đường thẳng MB cắt đường thẳng CD tại điểm I .
a) Chứng minh AD là tiếp tuyến của đường tròn ngoại tiếp tam giác MOI ; b) Chứng minh MD  OC .
Bài V. (0,5 điểm) Với các số thực dương , x y thỏa mãn 2 2
x  2y  2xy  6y  7 . 3 9
Tìm giá trị nhỏ nhất của biểu thức P  x  y   . x y
…………..……. Hết ………………… UBND QUẬN HOÀN KIẾM
HƯỚNG DẪN CHẤM KHẢO SÁT
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
MÔN TOÁN LỚP 9 NĂM HỌC 2023 - 2024 Ngày khảo sát: 15/5/2024 Bài Ý
Đáp án – Hướng dẫn chấm Điểm Bài I 1)
Tính giá trị của biểu thức A khi x 16 0,5 đ (2,0 điểm) 0,25
Thay x  16 (TMĐK) vào biểu thức A 16  2 1 A   16 2 0.25 2) x 1 x x 1 Rút gọn B    1,0 đ x 1 x 1 x 1 x 1 x x 1 B    x 1 x 1  0,25 x   1  x   1  x  2 1 x  x   1 x 1 B     0,25 x   1  x   1
 x  1 x  1  x  1 x  1 x  x B   0,25 x   1  x   1 x B  0,25 x 1 3) Xét biểu thức P  .
A B . Tìm tất cả giá trị của x sao cho P nhận giá trị nguyên. 0,5đ x  2 3 3 Ta có P  . A B  1 . Do x  0 nên  0  P 1 0,25 x 1 x 1 x 1 3 3 Do x  0  x 1  1  3  P  1  2 x 1 x 1  x  2  P  0   0  x  4tm Suy ra x 1 2 P 1, P Z       .  0,25 x  2 1 P  1   1  x  tm  x 1 4 1 Vậy x  4; . 4 Bài 1)
Giải bài toán bằng cách lập phương trình hoặc hệ phương trình: 1,5 đ II
Gọi thời gian đội thứ nhất làm một mình xong công việc là x ( * x  N , ngày) 0,25 (2,0 điểm)
Suy ra thời gian đội thứ hai làm một mình xong công việc là x  9 (ngày) 0,25 Trong một ngày 0,25 1
Đội thứ nhất làm được (công việc) x 1
Đội thứ hai làm được (công việc) x  9
Vì hai đội làm chung trong 20 ngày xong công việc nên ta có phương trình 1 1 1 0,25   x x  9 20 x  36tm
Giải phương trình ta được  (t/m) x  5   l 0,5
Vậy đội thứ nhất làm một mình xong công việc sau 36 ngày
Đội thứ hai làm một mình xong công việc sau 45 ngày
Tính thể tích của quả địa cầu 0,5 đ 2)
Bán kính của quả địa cầu là 33:2 = 16,5 (cm) 0,25
Tính được thể tích của quả địa cầu: 4 4 0,25 3 3
V   R  .3,14.16,5  18807,03 3 cm  3 3 Bài 1)  2 III x   5  y 1 2,5
Giải hệ phương trình:  1,0đ 1 điểm  3 x   1  y 1  2 x   5  y 1 
(điều kiện: x  0; y  1 1  ) 0,25 3 x   1  y 1  x 1  Giải được  1 0,5  2   y 1  x  1 
Giải được nghiệm của hệ là  1 0,25 y   2
a) Với m  4 , chứng minh đường thẳng d  luôn cắt parabol P tại hai điểm phân 0,75đ
biệt có hoành độ x ; x . 1 2
Xét phương trình hoành độ giao điểm của đường thẳng d  và parabol P là: 2a) 0,25 2 x  m   2
2 x  3m  3  x  m  2 x  3m  3  0*
Tính được   b  ac  m  m   m  2 2 2 4 8 16 4 0,25
Chứng minh được với m  4 thì phương trình (*) luôn có hai nghiệm phân biệt, 0,25
suy ra (d) cắt (P) tại hai điểm phân biệt
Tìm tất cả giá trị của m để x ; x là độ dài hai đường chéo của một hình thoi có 1 2 2b) 13 0,75đ độ dài cạnh là 2 x  x  m  2 Theo định lí vi –ét 1 2  x .x  3m  3  1 2
Do x ; x là độ dài hai đường chéo của một hình thoi nên x ; x dương do đó 1 2 1 2 0,25 x  x  m  2  0 1 2   m  1 x .x  3m  3  0  1 2 13
x ; x là độ dài hai đường chéo của một hình thoi có độ dài cạnh là nên 1 2 2 0,25 2 2  x   x  13 1 2    x  x  13  x  x
 2x x  13  m  2m  3  0     1 2  1 2 2 2 2 2 1 2  2   2  4
Giải được m  1l; m  3tm . Kết luận m = 3 thì thỏa mãn đề bài 0,25
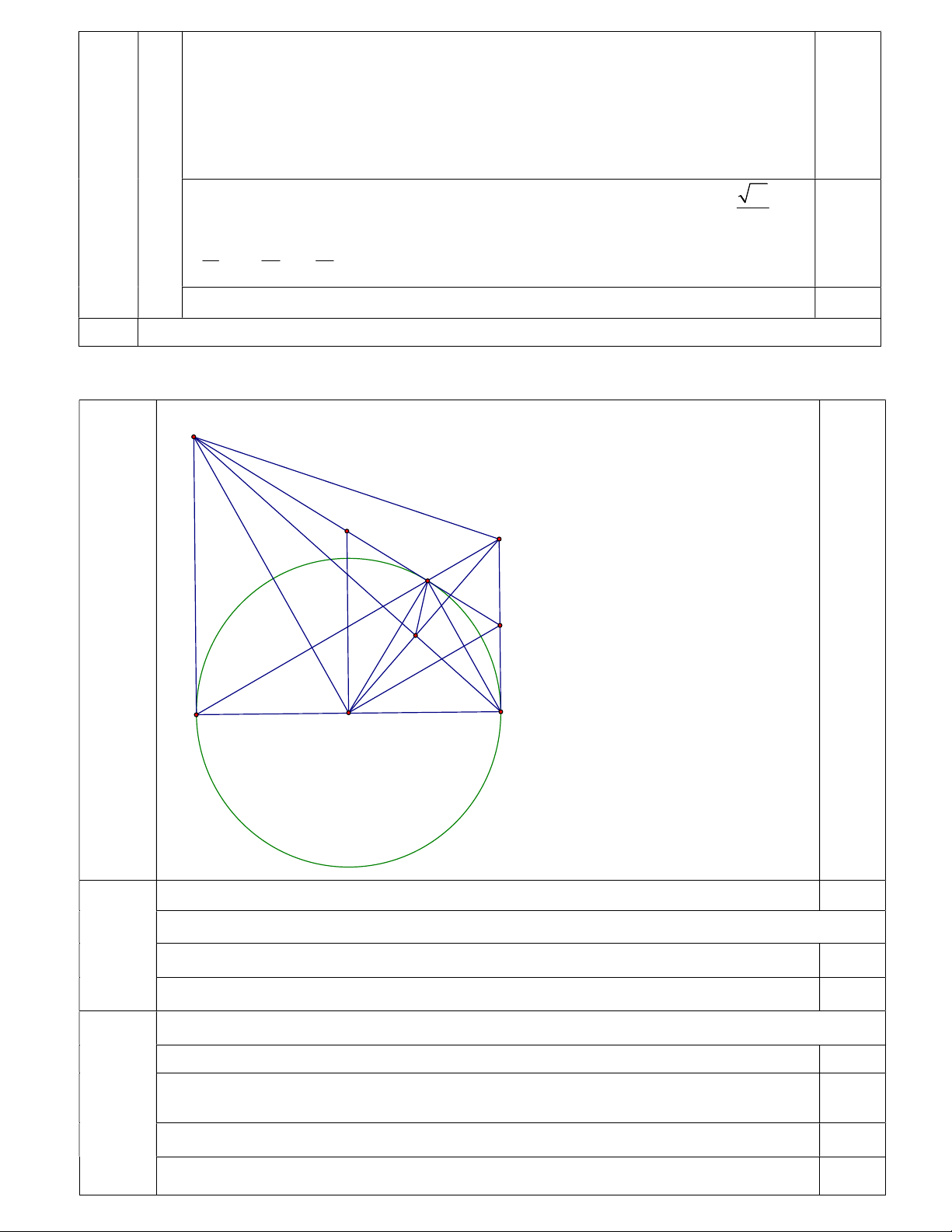
Lưu ý cách làm khác của học sinh Bài IV. M 3,0 điểm K C B I T A D O Vẽ hình đúng đến ý a 0,25
Chứng minh bốn điểm M , ,
A O, B thuộc một đường tròn 1)
c/m: góc MAO = góc MBO = 90 ; (mỗi góc vuông được 0,25 điểm) 0,5 Chứng minh được M , ,
A O, B nằm trên một đường tròn. 0,25 Chứng minh 2 AB.AC  4R ;
Chứng minh được góc ABD vuông từ đó suy ra DB vuông góc với AC 0,25
Chỉ ra CD là tiếp tuyến của đường tròn (O) nên CD vuông góc với AD suy ra tam giác 2) 0,25 ADC vuông tại D
Sử dụng hệ thức lượng trong tam giác vuông ADC suy ra 2 AD  A . B AC 0,25 Chứng minh được 2 AB.AC  4R 0,25
Chứng minh AD là tiếp tuyến của đường tròn ngoại tiếp tam giác MOI ;
Chứng minh được tam giác MOI vuông tại O 0,25
Gọi K là trung điểm của MI, chứng minh OK là đường trung bình của hình thang AMID
nên OK vuông góc với AD tại O. Từ đó chứng minh được AD là tiếp tuyến của đường 0,25
tròn ngoại tiếp tam giác MOI Chứng minh MD  OC . 3)
Gọi giao điểm của MD và OC là T BC BD
Chứng minh được BCD ∽ B  OM g.g    BO BM Có  0    0    0 OBC 180 ABO 180 OAB  180   IBD   MBD . Do đó M  BD ∽ O  BC  .cg.c 0,25 MBD ∽ O  BC   BMT  
BOT nên tứ giác MBTO nội tiếp 0,25   MTO   0
MBO  90  OC  MD tại T Bài V
Với các số thực dương , x y thỏa mãn 2 2
x  2y  2xy  6y  7 . 0,5điểm 3 9
Tìm giá trị nhỏ nhất của biểu thức P  x  y   . 0,5 x y Với , x y dương ta có
x  y  xy  y    x  y2   y  2 2 2 2 2 6 7 3 16  x  y  4 0,5 3 9 3 9
P  x  y    3x   y   2 x  y  6  6 8  4 x y x y
Vậy GTNN của P là 4. Dấu = xảy ra khi x = 1; y = 3.
Lưu ý: Học sinh có cách giải khác đúng, vẫn cho điểm tối đa