Đề khảo sát chất lượng Toán 9 năm 2023 – 2024 phòng GD&ĐT Thạch Thất – Hà Nội

UBND HUYỆN THẠCH THẤT
ĐỀ KHẢO SÁT CHẤT LƯỢNG LỚP 9
PHÒNG GD&ĐT THẠCH THẤT
Năm học: 2023 – 2024 MÔN: TOÁN
(Đề thi gồm 01 trang)
(Thời gian 120 phút, không
kể thời gian giao đề)
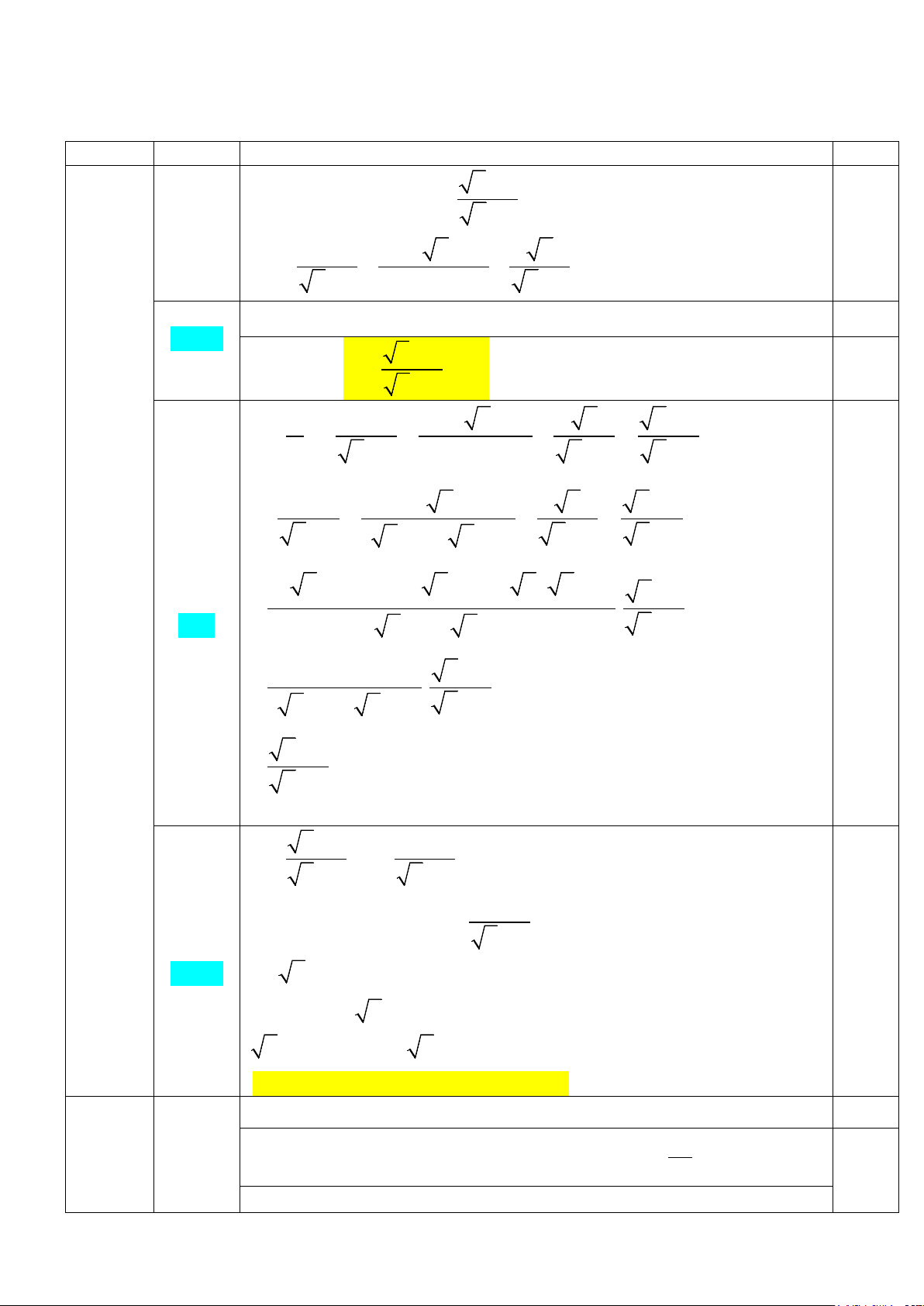
Bài I. (2,0 điểm): Cho hai biểu thức: x + 5 A x − x − = và 4 2 13 = + − x B
với x ≥ 0;x ≠ 9 x − 3 x + 3 x − 9 x − 3
1) Tính giá trị của biểu thức A khi x = 4 2) Đặt x − = B P . Chứng minh P = 5 A x + 3
3) Tìm giá trị nguyên nhỏ nhất của x để P nhận giá trị nguyên
Bài II. (2,0 điểm):
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một người đi xe đạp từ A đến B cách nhau 36 km. Khi đi từ B trở về A, người đó tăng vận
tốc thêm 3 km/h, vì vậy thời gian về ít hơn thời gian đi là 36 phút. Tính vận tốc của người
đi xe đạp khi đi từ A đến B.
2) Bóng đèn huỳnh quang dài 1,2 mét được xem như là một hình trụ với đường kính đáy
bằng 4 cm. Tính thể tích lượng khí chứa bên trong bóng đèn (độ dày của lớp vỏ thủy tinh
xem như không đáng kể, lấy π≈3,14).
Bài III. (2,0 điểm):  2 + 3. y + 3 =13 
1) Giải hệ phương trình sau:  x − 2  2  + y + 3 = 5  x − 2
2) Cho phương trình: 2
x + mx + m −1= 0 ( )
1 với x là ẩn, m là tham số.
a) Chứng tỏ phương trình (1) luôn có nghiệm với mọi giá trị của m.
b) Gọi x1, x2 là hai nghiệm của phương trình (1). Tính giá trị của biểu thức: A = (x + )2 1 (x + )2 1 + 2024 1 2
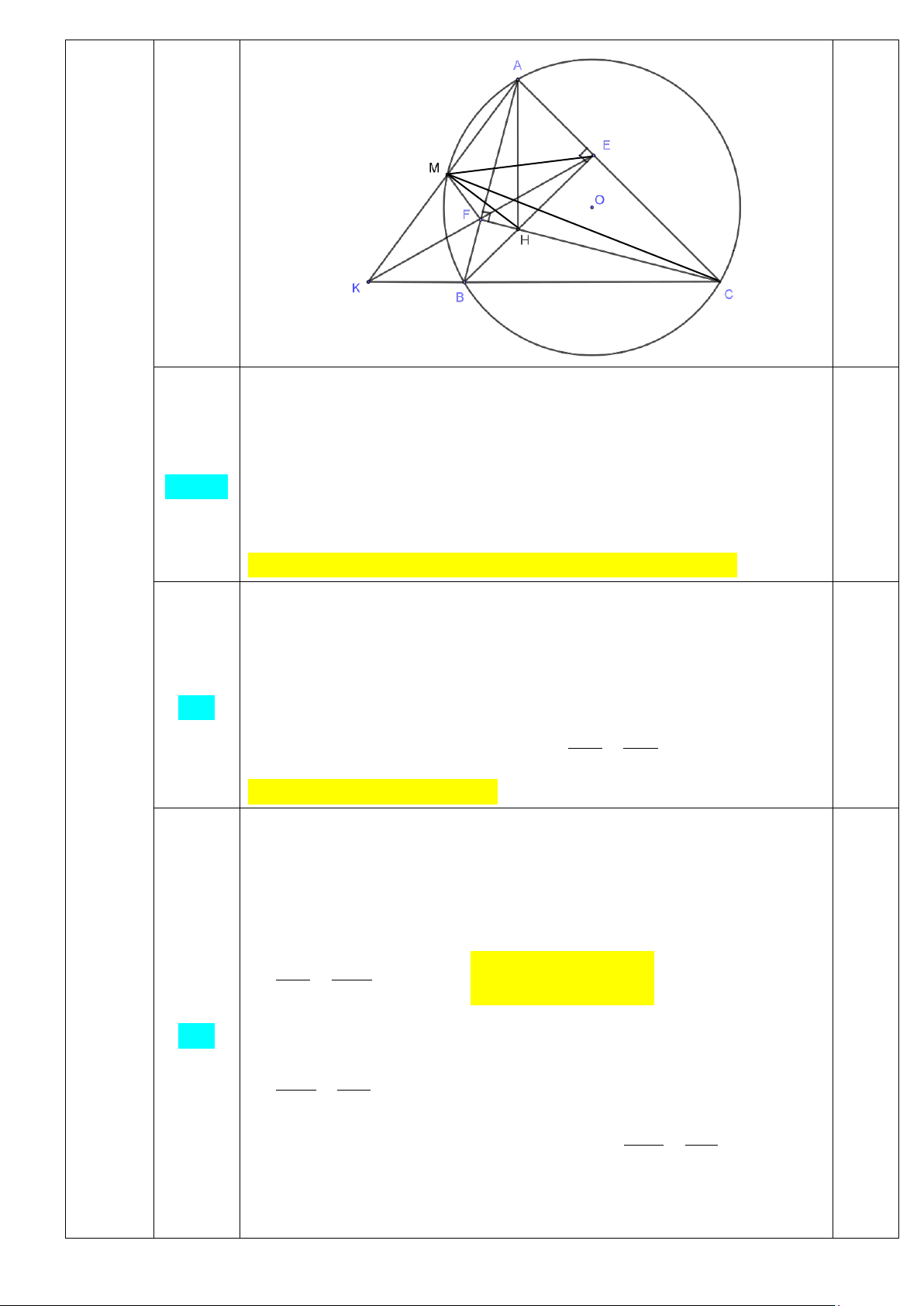
Bài IV. (3,5 điểm): Cho đường tròn (O) và dây cung BC cố định không đi qua O. Lấy điểm
A di động trên cung lớn BC sao cho AB < AC và ∆ABC nhọn. Các đường cao BE, CF của
∆ABC cắt nhau tại H. Gọi K là giao điểm của EF và BC.
1) Chứng minh tứ giác BCEF nội tiếp. 2) Chứng minh .
KB KC = KE.KF .
3) Gọi M là giao điểm của AK với đường tròn (O) (M khác A).
Chứng minh KE.KF = .
KA KM và MH vuông góc với AK.
Bài V. (0,5 điểm): Cho 2 số thực dương a,b.
Tìm giá trị nhỏ nhất của biểu thức: a + = b + ab P ab a + b
--------------------------------------------------------------
Giám thị không giải thích gì thêm
Họ và tên thí sinh ......................................... Số báo danh ............................
UBND HUYỆN THẠCH THẤT
ĐÁP ÁN ĐỀ KHẢO SÁT CHẤT LƯỢNG LỚP 9
PHÒNG GD&ĐT THẠCH THẤT
NĂM HỌC 2023 – 2024
(Đáp án gồm 04 trang) MÔN: TOÁN
Thời gian làm bài: 120 phút Bài ý NỘI DUNG Điểm Cho hai biểu thức: x + 5 A = và x − 3 4 2x − x −13 x B = + −
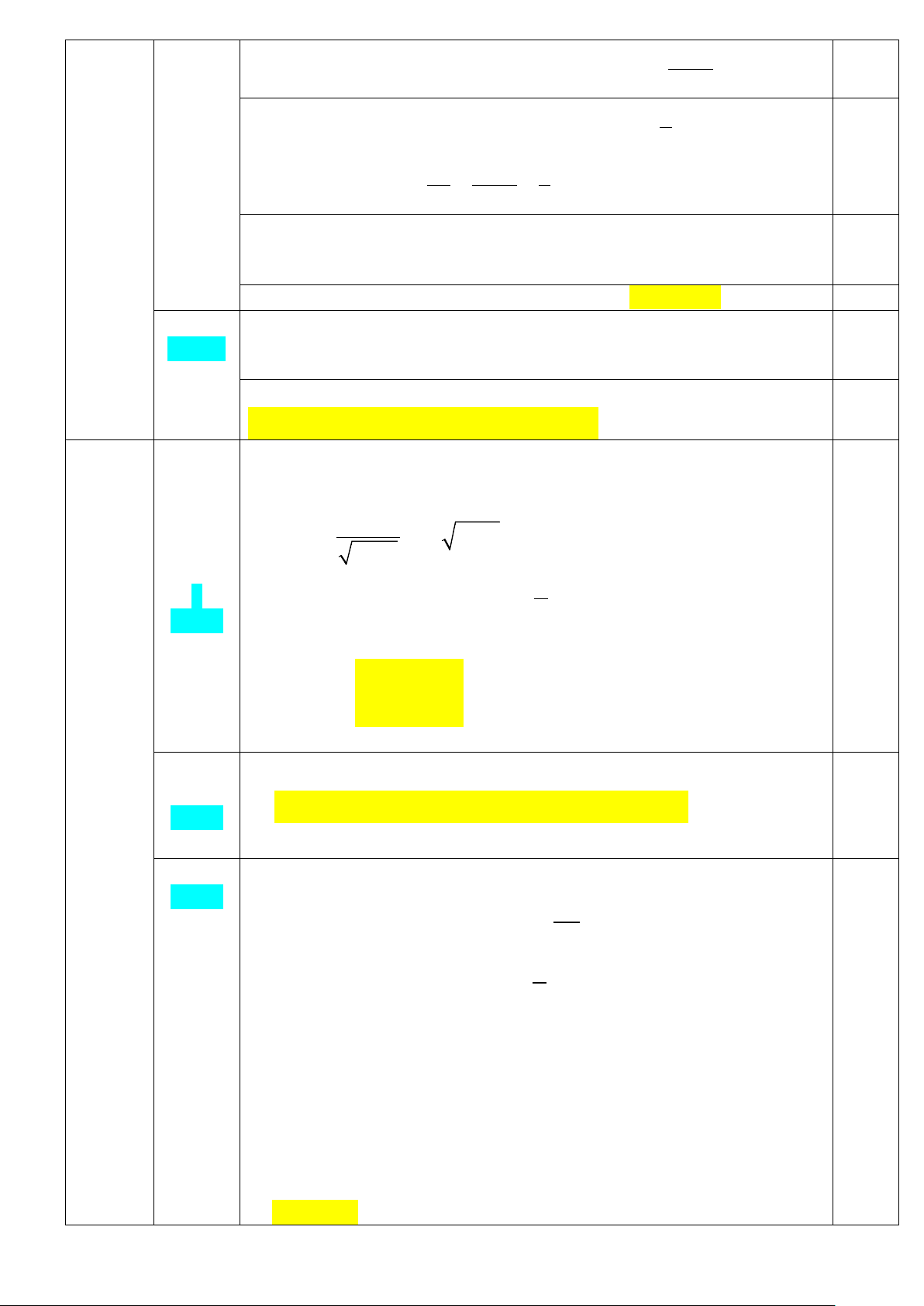
Với x ≥ 0;x ≠ 9 x + 3 x − 9 x − 3 1
Thay x = 4 ( TMĐKXĐ) vào biểu thức A 0,25 (0,5đ) Tính được 4 5 A + = = 7 − và kết luận 0,25 4 − 3 B  4 2x − x −13 x  x + 5 P = =  + −  : A  x + 3 x − 9
x − 3  x − 3  4 2x x 13 x  − − x + 5   = + − 0,25  x +  ( x −3)( x +3) : 3 x − 3  x − 3  Bài I
4( x − 3) + 2x − x −13 − x ( x + 3) 2 x − 3 (2đ) = . (1đ) ( 0,25 x − 3)( x + 3) x + 5 x − 25 x − 3 = (
x − 3)( x + 3). x + 5 0,25 x − 5 = x + 3 0,25 Kết luận :…. P = x − 5 8 =1− x + 3 x + 3 P nhận giá trị nguyên 8 ⇔ có giá trị nguyên 3 x + 3
(0,5đ) ⇔ x + 3∈U (8) = { 1 ± ; 2 ± ; 4 ± ;± } 8 0,25
Do x ≥ 0 ⇒ x + 3 ≥ 3 nên: x + 3∈{4; } 8 ⇔ x ∈{1; } 5 ⇔ x∈{1;2 } 5 0,25
Vì x là số nguyên nhỏ nhất ⇒ x =1
Gọi vận tốc của người đi xe đạp khi đi từ A đến B là x (km/h, x > 0) 0,25 1 36
(1,5đ) Thời gian của người đi xe đạp khi đi từ A đến B là (giờ) x 0,25
Vận tốc của người đi xe đạp khi đi từ B về A là x + 3 (km/h) 1 Bài II 36 (2,0 đ)
Thời gian của người đi xe đạp khi đi từ B đến A là (giờ) 0,25 x + 3
Vì thời gian về ít hơn thời gian đi là 36 phút 3 = (h) 5 36 36 3 0,25 Ta có phương trình: − = x x + 3 5 x =12 0,25
Giải phương trình này ra hai nghiệm  x = 15 −  (loai) 
Vậy vận tốc của người đi xe đạp đi từ A đến B là 12 km/h 0,25 2
Bán kính đáy của bóng đèn là: 4: 2 = 2 (cm)
(0,5 đ) Chiều cao của bóng đèn là:h =1,2
m =120 (cm) 0,25
⇒ Thể tích của lượng khí chứa bên trong bóng đèn là: 2 2 3
V = π R h ≈ 3,14.2 .120 =1507,2(cm ) 0,25 x > 2 * Điều kiện  0,25 y ≥ 3 − 1 0,25 * Đặt u =
;v = y + 3 , đk: u > 0;v ≥ 0 x − 2 1 2u + 3v =13  1 u = 0,25 (1,0đ) ta có hệ:  ⇔  2 (tm) 2u + v = 5 v = 4 x = 6 * Tìm được  (tm) y =13 * Kết luận 0,25 Cho phương trình 2
x + mx + m −1= 0 ( ) 1 với m tham số 2a 0,25
Bài III (0,5đ) a) 2 2 2
∆ = m − 4.(m −1) = m − 4m + 4 = (m − 2) ≥ 0 với mọi m . (2,0 đ) Vậy phương trình ( )
1 luôn có nghiệm với mọi m 0,25 2b
b) Với mọi m , phương trình ( )
1 có hai nghiệm x , x 1 2 (0,5đ)  b S = x + x − = = −m  1 2  Theo hệ thức Vi-ét: a  c
P = x x = = m −1 1 2  a 0,25
Ta có: A = (x + )2 1 (x + )2 1 + 2024 1 2
A = (x + )1(x + ) 2 1  + 2024 1 2 
A = (x x + x + x + )2 1 + 2024 1 2 1 2
A = (m − − m + )2 1 1 + 2024 2 A = 0 + 2024 A 0,25 = 2024 2 0,25
1) Chứng minh tứ giác BFEC nội tiếp. Trong tam giác A ∆ BC ta có:
BE ⊥ AC tại E (tính chất đường cao) ⇒  0 BEC = 90 0,25 1
CF ⊥ AB tại F (tính chất đường cao)⇒  0 BFC = 90 0,25
(1,25đ) Xét tứ giác BFEC có  =  0
BEC BFC = 90 và E,F là hai đỉnh kề 0,25
cùng nhìn cạnh BC dưới góc 0 90
⇒ Tứ giác BFEC nội tiếp đường tròn đường kính BC . 0,5 2) Chứng minh .
KB KC = KE.KF Bài IV Xét K ∆ BE và K ∆ FC có: (3,5 đ)  BKF chung 2  = 
KEB KCF (hai góc nội tiếp cùng chắn 
BF của đường tròn ngoại
(1đ) tiếp tứ giác BFEC ) 0,5 K
∆ BE đồng dạng K ∆ FC (g – g) KB KE ⇒ = (tính chất) KF KC 0,5 ⇒ .
KB KC = KE.KF (đpcm)
3) Chứng minh KE.KF = .
KA KM và MH ⊥ AK Xét KCM ∆ và K ∆ AB có:  BKM chung  = 
KCM KAB (hai góc nội tiếp cùng chắn 
BM của đường tròn (O)) ⇒ KCM ∆ đồng dạng K
∆ AB (g − g) KC KM ⇒ = (tính chất)⇒ . KB KC = . KA KM 0,25 KA KB 3 Mà .
KB KC = KE.KF (cmt b) (1đ) ⇒ KE.KF = . KA KM 0,25 KF KA ⇒ = KM KE xét K ∆ FA và K ∆ EM có: 
MKF chung và KF KA = KM KE K
∆ FA đồng dạng K
∆ ME (c − g − c) ⇒  =  KAF KEM (cặp góc
tương ứng) hoặc  =  MAF FEM 3
⇒ Tứ giác MAEF có hai đỉnh kề ,
A E cùng nhìn cạnh MF dưới
một góc bằng nhau ⇒ Tứ giác MAEF nội tiếp. (1)
Cũng có BE và CF cắt nhau tại H và: 0,25
BE ⊥ AC tại E (tính chất đường cao)⇒  0 HEA = 90
CF ⊥ AB tại F (tính chất đường cao) ⇒  0 HFA = 90
⇒ tứ giác AEHF có các đỉnh E , F cùng nhìn cạnh AH dưới một góc vuông.
⇒ Tứ giác AEHF nội tiếp đường tròn đường kính AH (2)
Từ (1) và (2) ⇒ Các điểm ,
A E,F,H,M cùng thuộc đường tròn đường kính AH . ⇒  0
AMH = 90 (góc nội tiếp chắn nửa đường tròn)
⇒ AM ⊥ MH hoặc AK ⊥ MH (đpcm). 0,25 a b ab
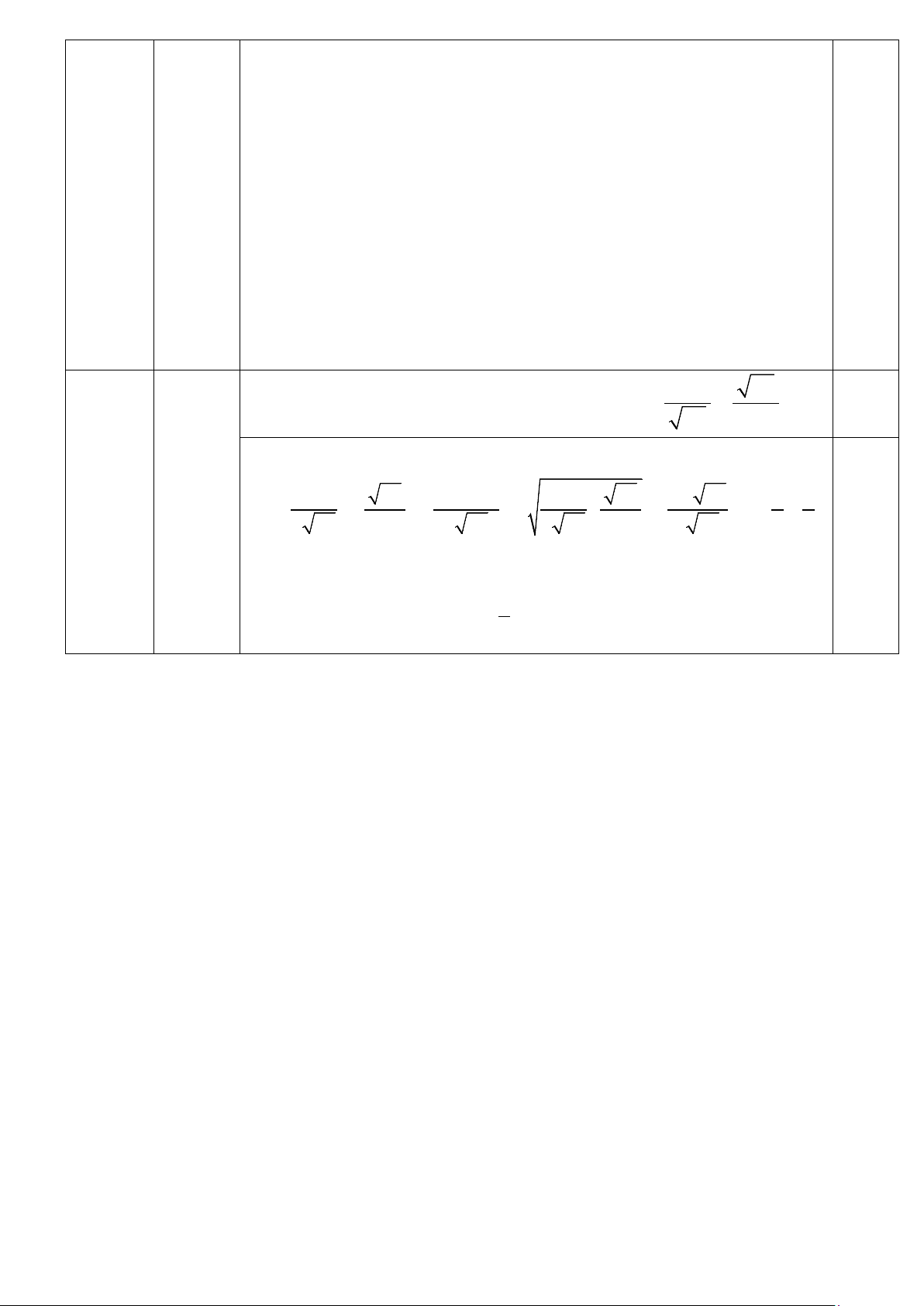
Cho 2 số thực dương a,b. Tìm GTNN của + P = + ab a + b Bài V Ta có: (0,5 đ)  a + b
ab  3(a + b) a + b ab 3.2 ab 3 5 P =  +  + ≥ 2 . + =1+ = 4 ab a + b 4 ab 4 ab a +   b 4 ab 2 2 0,5
Dấu “=” xảy ra ⇔ a = b
Vậy GTNN của P là 5 2
Lưu ý: HS làm cách khác đúng vẫn cho điểm tối đa. 4
Document Outline

• ĐỀ-KSCL-TOÁN-9-năm-2023-2024
• Hướng-dẫn-chấm-KSCL-Toán-9-2023-2024