SỞ GD&ĐT HÀ TĨNH
KỲ THI KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 9 NĂM HỌC 2023 - 2024
ĐỀ THI CHÍNH THỨC Môn thi: Toán
(Đề thi gồm 01 trang, 07 câu)
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Mã đề thi: 01
Câu 1. (2,0 điểm) Rút gọn các biểu thức sau a) = + ( − )2 A 2 12 3 1 − 27 +1. ( + )2 x 3 − 2 x − 5 b) x − 2 x B = − , với x > 0. x + 2 x
Câu 2. (2,0 điểm)
a) Cho đường thẳng d có phương trình = ( 2 y 2m − )
1 x + 3m − 2, với m là tham số. Tìm
tất cả các giá trị của tham số m để đường thẳng đã cho song song với đường thẳng ∆ có phương trình y = x -5.
b) Không dùng máy tính cầm tay, giải hệ phương trình sau  3x − + y = 6  . x + 2y = 5
Câu 3. (1,0 điểm) Cho phương trình bậc hai 2 x − 2(m − )
1 x + 4m −8 = 0 , với m là tham số.
Tìm tất cả các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt x ,x 1 2 x x 4 thỏa mãn 1 2 + = . x +1 x +1 3 2 1
Câu 4. (1,0 điểm) Một ca nô chạy xuôi theo dòng nước từ bến A đến bến B, cùng lúc đó có một
chiếc bè cũng trôi theo dòng nước từ A đến B, khoảng cách giữa hai bến là 30km. Khi ca nô đến
bến B và quay trở lại bến A (ca nô không dừng nghỉ) thì gặp chiếc bè tại vị trí C cách bến A 10km.
Hỏi vận tốc của ca nô khi nước đứng yên bằng bao nhiêu biết vận tốc dòng nước là 5km/h?
Câu 5. (1,0 điểm) Cho hình thang vuông ABCD , vuông tại A và D, CD là đáy lớn. Hai đường
chéo AC và BD vuông góc với nhau tại O, biết AB = 9cm , AD =12cm . Tính độ dài AO và CD.
Câu 6. (2,0 điểm) Cho nửa đường tròn đường kính AB , C là điểm thuộc nửa đường tròn (C
khác A và B, sđ  AC < sđ 
CB ). Đường phân giác trong của góc 
ACB cắt AB tại D, đường
thẳng vuông góc với AB tại D cắt đường thẳng AC tại M và cắt đường thẳng BC tại N.
a. Chứng minh tứ giác BDCM là tứ giác nội tiếp.
b. Gọi K là giao điểm của AN với nửa đường tròn, E là giao điểm của CK và tiếp tuyển
của nửa đường tròn tại A. Chứng minh ND = AD và tứ giác ADNE là hình vuông.
Câu 7. (1,0 điểm) Cho các số thực a,b,c thỏa mãn 2 2 2
a ≥ b ≥ c; a +b +c =1. Tìm giá trị nhỏ nhất
của biểu thức P = (a- b)(b-c)(c-a)(ab+ bc+ ca) . ------HẾT------
- Thí sinh không được sử dụng tài liệu.
- Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh .................................................................. Số báo danh ...................................
SỞ GD&ĐT HÀ TĨNH
KỲ THI KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 9 NĂM HỌC 2023 - 2024
ĐÁP ÁN CHÍNH THỨC Môn thi: Toán
(Đáp án gồm 03 trang, 07 câu)
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Mã đề thi: 01
Chú ý: - Mọi cách giải đúng, ngắn gọn đều cho điểm tương ứng.
- Điểm toàn bài không qui tròn.
- Ban chấm thi có thể thống nhất để chia các ý có điểm lớn hơn 0.25 thành các ý 0.25 điểm
(nếu thấy cần thiết). Câu Nội dung Điểm
Câu 1a A = 4 3 + 3 −1− 3 3 +1 = 2 3 1,0 đ 1,0 x ( x − + + − − 2 x 6 x 9 2 x 5 ) B = − 0,5 x + 2 x Câu 1b 1,0 đ ( + + + )2 x 2 x 4 x 4 = − x + 2 = − x + 2 0,25 x + 2 x + 2 = x + 2 − x + 2 = 4. 0,25 2  Ta có 2m −1 = 1
d  ∆ khi và chỉ khi  0,5 3m  − 2 ≠ 5 − 2 2 2m = 2 m =1 Câu 2a ⇔  ⇔  0,25 1,0đ 3  m ≠ 3 − m ≠ 1 − m = 1  ⇔ m = 1 − ⇔ m = 1. 0,25  m ≠ 1 − − + =
Hệ tương đương với 6x 2y 12  0,5 x + 2y = 5 Câu 2b 1,0 đ 7x = 7 −  x = 1 − ⇔  5 − x ⇔ . 0,5 y  = y = 3  2 Phương trình 2 x − 2(m − ) 1 x + 4m −8 = 0 Ta có ∆ = ( − )2 2 '
m 1 − 4m + 8 = m − 6m + 9 = (m − 3)2 0,25
Phương trình có hai nghiệm phân biệt khi ∆' > 0 ⇔ m ≠ 3 x + x = 2m - 2
Theo định lí Viet, ta có 1 2  0,25 x .x = 4m -8 Câu 3 1 2 1,0 đ 2 2 x x 4 x + x + x + x 4 (x + x − 2x x + x + x 1 2 )2 4 Khi đó 1 2 1 2 1 2 + = ⇔ = 1 2 1 2 ⇔ = x +1 x +1 3 x x + x + x +1 3 x x + x + x +1 3 2 1 1 2 1 2 1 2 1 2
Áp dụng định lí Viet ta được: 0,25 ( − )2 − ( − ) + − 4 ( − )2 2m 2 2 4m 8 2m 2 2m 2 − 6m +14 4 = ⇔ = 4m −8 + 2m − 2 +1 3 6m − 9 3 2 2m − 7m + 9 3 ⇔ = 2 ( m ≠ ) 2m − 3 2 m = 3 2 2m 11m 15 0  ⇔ − + = ⇔ 5  m =  2 5
Đối chiếu điều kiện thì m = thỏa mãn yêu cầu. 0,25 2 x = 2
Nhận xét: Bài toán này có thể tìm được hai nghiệm 
, sau đó xử lí yêu cầu của x = 2m − 4 bài toán.
Gọi x là vận tốc ca nô (x > 5), khi đó vận tốc ca nô xuôi dòng nước là (x + 5) km/h và vận
tốc ca nô ngược dòng nước là (x – 5)km/h. 0,25
Thời gian của bè trôi từ A đến C là 10 : 5 =2 giờ.
Câu 4 Quãng đường ca nô đi ngược dòng là 30 – 10 = 20 km. 0,25 1,0 đ
Thời gian ca nô đi từ bến A đến bến B và ngược lại gặp bè ở điểm C là: 30 20 + . 0,25 x + 5 x -5
Do ca nô gặp bè tại C nên thời gian ca nô đi bằng thời gian ca nô gặp bè, do đó ta có phương trình 30 20 +
= 2 ⇔ x = 25 , (Do x > 5). 0,25 x + 5 x -5
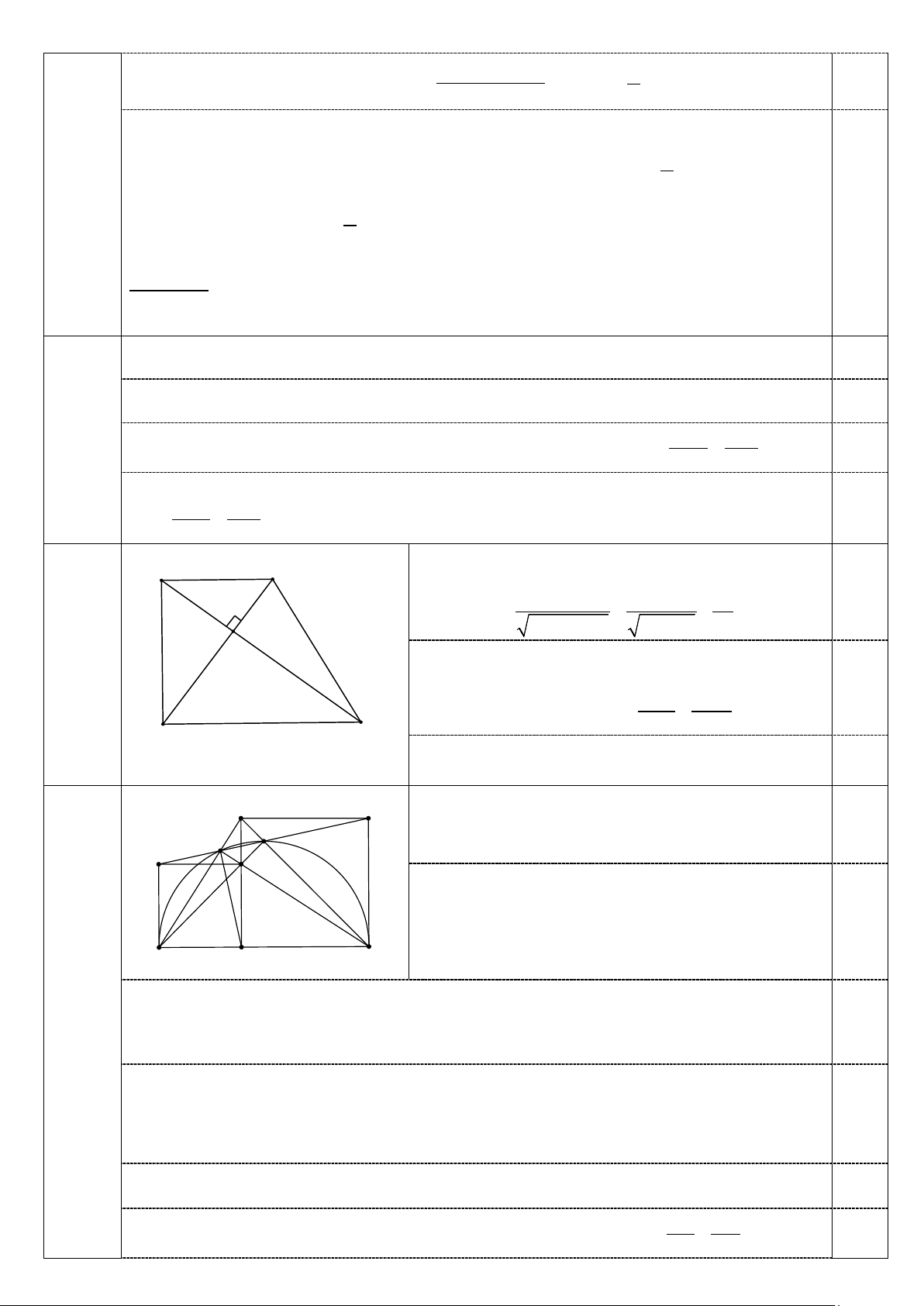
Áp dụng hệ thức lượng trong tam giác vuông ABD A 9 B với AO là đường cao: 0,5 AB.AD 9.12 36 AO= = = 2 2 2 2 AB +AD 9 +12 5 Câu 5 12 O
Áp dụng hệ thức lượng trong tam giác vuông ADC 1,0đ với DO là đường cao: 2 2 0,25 2 AD 12 .5 AD =AO.AC ⇒ AC= = =20 D C AO 36
Áp dụng định lí Pitago vào tam giác vuông ADC: 2 2 2 2 2
DC =AC - AD =20 - 12 =256 ⇒ DC=16cm 0,25
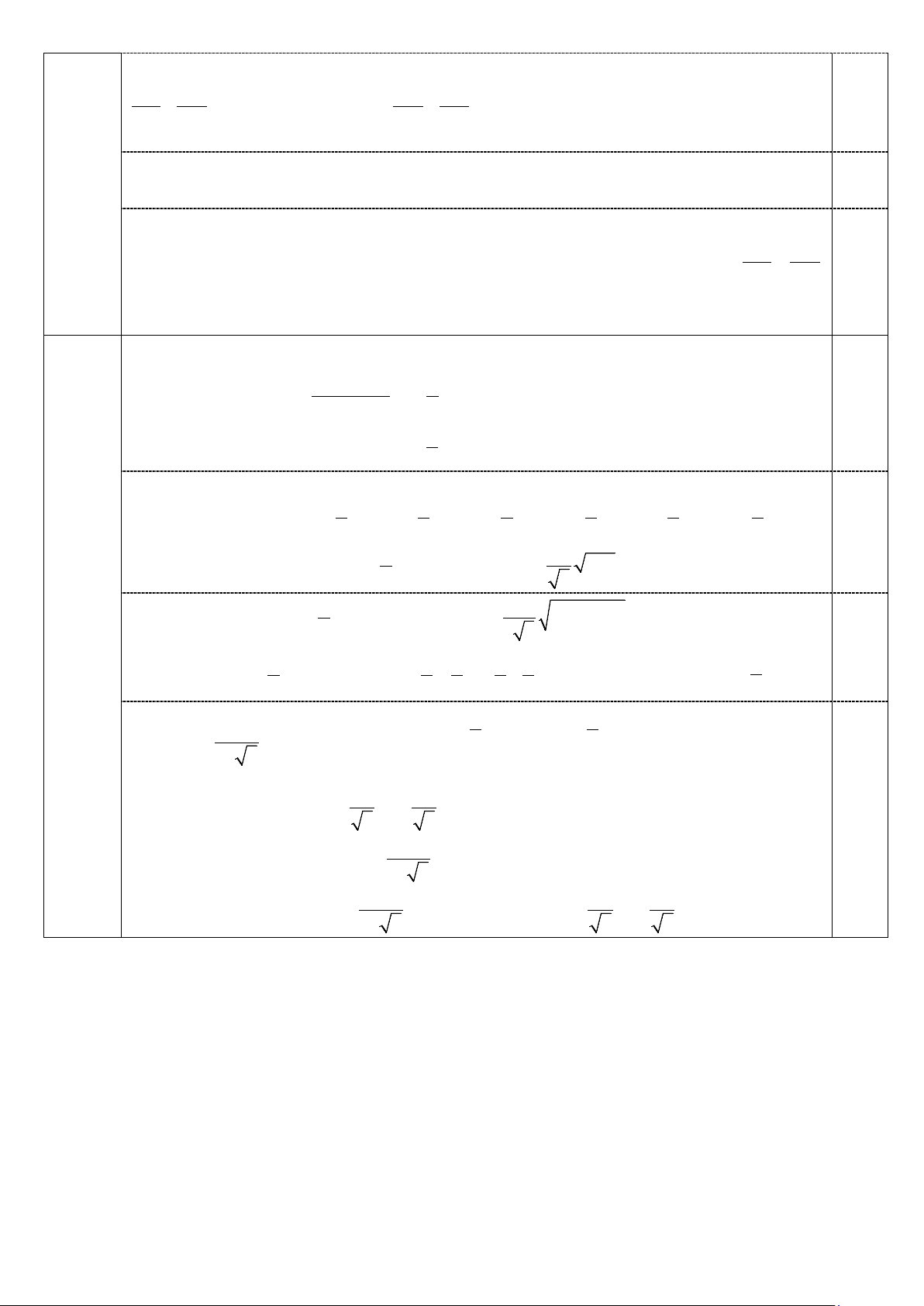
a. Ta có điểm C nhìn đường kính AB dưới một góc M F vuông nên  0 BCM=90 , lại có  0 MDB=90 , từ đó 1,0 C E K  
MDB=BCM , hay tứ giác BDCM nội tiếp. N b.Ta có  ACN =  0
NDA = 90 nên tứ giác ADNC nội tiếp Suy ra   0
ACD=AND = 45 (Phân giác góc vuông). 0,5 A B D
Do đó tam giác ADN vuông cân tại D nên DN = DA. Ta có  NAD =  KBA =  0 EAN = 45 .
Câu 6 Từ đó ⇒  0
MCK=45 (do tứ giác ABKC nội tiếp). 0,25 2,0 đ Mà  
ECA=MCK (đối đỉnh), do đó  0 ECA=45 , mặt khác  0 ACD=45 , do đó  0 ECD=90 . Mặt khác  0
EAD=90 (tính chất tiếp tuyến), suy ra tứ giác AECD nội tiếp với đường kính ED,
ta cũng có tứ giác ACND nội tiếp với đường kính AN, do đó 5 điểm A, E, C, N, D cùng thuộc 0,25
một đường tròn có các đường kính là AN, DE nên  0 AEN=90 .
Do đó tứ giác ADNE có ba góc vuông và DA = DN nên nó là hình vuông. Cách 2 của câu b
- Do CD là phân giác của góc ACB nên theo tính chất đường phân giác DB AD = (1). 0,25 CB AC
Xét ΔBCA và ΔBDN , có góc B chung,   0 BDN=BCA=90 , do đó BD ∆ N  ΔBCA . Suy ra: DB DN =
(2). Từ (1) và (2) ta có DN AD =
, suy ra DN=AD , khi đó tam giác AND vuông 0,25 CB AC AC AC cân tại D. Từ đó  0 NAD=45 nên  0 KBA=45 suy ra  0
MCK=45 (do tứ giác ABKC nội tiếp). 0,25 Mà  
ECA=MCK (đối đỉnh), do đó  0 ECA=45 , mặt khác  0 ACD=45 , do đó  0 ECD=90 . Mặt khác  0
EAD=90 (tính chất tiếp tuyến), suy ra tứ giác ADCE nội tiếp, do đó 5 điểm
A,D,N,C,E cùng thuộc một đường tròn có tâm là giao của ED và AN và bán kính ED = AN 2 2 0.25 nên  0 AEN=90 .
Vậy tứ giác ADNE có ba góc vuông và AD = DN nên là hình vuông.
Xét biểu thức Q = -P = (a - b)(b -c)(a -c)(ab+bc+ca) , ta sẽ tìm giá trị lớn nhất của Q. 2 + Ta có ( )( )  a -b + b-c  1 a - b b - c ≤   = (a - c)2 , suy ra  2  4 0,25 ( )( )( ) 1
a - b b - c a - c ≤ (a -c)3 , (Do a - b ≥ 0, a -c ≥ 0, b -c ≥ 0 ). 4 + Lại có 2 2 2 1 ( )2 1( )2 1( )2 1 ≥ ( )2 1 ( )2 3 a + b + c -ab - bc -ca = a -c + a - b + b -c a -c + a -c = (a -c)2 2 2 2 2 4 4 0,25
Đặt x = ab + bc + ca , ta có 3 ≥ ( )2 2 1- x a - c ≥ 0 ⇒ a - c ≤
1- x , (Do 1- x ≥ 0,a - c ≥ 0 ). 4 3 1 3 2 3 2
Câu 7 + Xét x ≥ 0 . Khi đó Q ≤ (a -c) (ab + bc + ca) ≤ (1- x) .x 4 3 3 1,0 đ 5 0,25 Ta có ( )3 2 4 ( )( )( ) 3 3 4  3 1- x x = 1- x 1- x 1- x . x. x .  ≤ . Dấu bằng xảy ra khi 2 x = . 9 2 2 9  5    5  2  2 x = x = Do đó 4 Q ≤
. Dấu bằng xảy ra khi  5 ⇔  5 . 25 5 a -b = b -c   a + c = 2b Khi đó ta tìm được 1 2 c = 0;b = ;a = . 5 5 0,25
Nếu x < 0 , thì hiển nhiên 4 Q ≤ 0 < . 25 5
Vậy P đạt giá trị nhỏ nhất là 4 − , đạt được khi 1 2 c = 0;b = ;a = . 25 5 5 5 HẾT.
SỞ GD&ĐT HÀ TĨNH
KỲ THI KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 9 NĂM HỌC 2023 - 2024
ĐỀ THI CHÍNH THỨC Môn thi: Toán
(Đề thi gồm 01 trang, 07 câu)
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Mã đề thi: 02
Câu 1. (2,0 điểm) Rút gọn các biểu thức sau a) ( − )2 A = 3 8 + 2 1 - 32 +1. ( )2 x + 2 + 2 x + 5 b) x+ 3 x B = - , với x > 0. x + 3 x
Câu 2. (2,0 điểm)
a) Cho đường thẳng d có phương trình = ( 2 y
m − 3)x + 3m − 2, với m là tham số. Tìm tất
cả các giá trị của tham số m để đường thẳng đã cho song song với đường thẳng ∆ có phương trình y = x -8.
b) Không dùng máy tính cầm tay, giải hệ phương trình sau 3x  + y = 3  . x − 2y = 8
Câu 3. (1,0 điểm) Cho phương trình bậc hai 2 x - 2(m + )
1 x - 4m -8 = 0, với m là tham số. Tìm
tất cả các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt x ,x 1 2 thỏa mãn x x 1 2 + = 4. x +1 x +1 2 1
Câu 4. (1,0 điểm) Một ca nô chạy xuôi theo dòng nước từ bến A đến bến B, cùng lúc đó có một
chiếc bè cũng trôi theo dòng nước từ A đến B, khoảng cách giữa hai bến A, B là 35km. Khi ca nô
đến bến B và quay trở lại bến A (ca nô không dừng nghỉ) thì gặp chiếc bè tại vị trí C cách bến A
10km. Hỏi vận tốc của ca nô khi nước đứng yên bằng bao nhiêu, biết vận tốc dòng nước là 5km/h?
Câu 5. (1,0 điểm) Cho hình thang vuông ABCD, vuông tại A và D, CD đáy lớn. Hai đường chéo
AC và BD vuông góc với nhau tại O, biết AB = 18 cm, AD = 24 cm. Tính độ dài AO và CD.
Câu 6. (2,0 điểm) Cho nửa đường tròn đường kính CD , E là điểm thuộc nửa đường tròn ( E
khác C và D, sđ  CE < sđ 
ED ). Đường phân giác trong của góc 
CED cắt CD tại F, đường thẳng
vuông góc với CD tại F cắt đường thẳng CE tại M và cắt đường thẳng DE tại N.
a. Chứng minh tứ giác DFEM là tứ giác nội tiếp.
b. Gọi K là giao điểm của CN với nửa đường tròn, H là giao điểm của EK và tiếp tuyển
của nửa đường tròn tại C. Chứng minh NF = CF và tứ giác CFNH là hình vuông.
Câu 7. (1,0 điểm) Cho các số thực a,b,c thỏa mãn 2 2 2
a ≥ b ≥ c; a +b +c =1. Tìm giá trị nhỏ nhất
của biểu thức P = (a- b)(b-c)(c-a)(ab+ bc+ ca) . ------HẾT------
- Thí sinh không được sử dụng tài liệu.
- Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh .................................................................. Số báo danh ...................................
SỞ GD&ĐT HÀ TĨNH
KỲ THI KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 9 NĂM HỌC 2023 - 2024
ĐÁP ÁN CHÍNH THỨC Môn thi: Toán
(Đáp án gồm 03 trang, 07 câu)
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Mã đề thi: 02
Chú ý: - Mọi cách giải đúng, ngắn gọn đều cho điểm tương ứng.
- Điểm toàn bài không qui tròn.
- Ban chấm thi có thể thống nhất để chia các ý có điểm lớn hơn 0.25 thành các ý 0.25 điểm (nếu thấy cần thiết). Câu Nội dung Điểm
Câu 1a A = 6 2 + 2 −1− 4 2 +1 = 3 2 1,0 đ 1,0 ( + )2 x 2 + 2 x + 5 x ( x + + + + 3 x 3 x x 6 x 9 ) B = − = − 0,5 x + 3 x x + 3 x Câu 1b 1,0 đ ( + )2 x 3 = − x − 3 0,25 x + 3 = x + 3 − x − 3 = 0 0,25 2  Ta có m − 3 = 1
d  ∆ khi và chỉ khi  0,5 3m  − 2 ≠ 8 − 2 m = 4 Câu 2a ⇔  0,25 1,0đ m ≠ 2 − m = 2  ⇔ m = 2 − ⇔ m = 2 0,25  m ≠ 2 − 6x + 2y = 6
Hệ phương trình tương đương với  0,5 x − 2y = 8 Câu 2b 1,0 đ 7x = 14   = x 2 ⇔  x − 8 ⇔ 0,5 y  = y = 3 −  2 Phương trình 2 x − 2(m + ) 1 x − 4m −8 = 0 Ta có ∆ = ( + )2 2 '
m 1 + 4m + 8 = m + 6m + 9 = (m + 3)2 0,25
Phương trình có hai nghiệm phân biệt khi ∆' > 0 ⇔ m ≠ 3 − x + x = 2m + 2
Theo định lí Viet, ta có 1 2  0,25 Câu 3 x .x = -4m -8 1 2 1,0 đ 2 2 x x x + x + x + x (x + x − 2x x + x + x 1 2 )2 Khi đó 1 2 1 2 1 2 + = 4 ⇔ = 4 1 2 1 2 ⇔ = 4 x +1 x +1 x x + x + x +1 x x + x + x +1 2 1 1 2 1 2 1 2 1 2 0,25 ( + )2 + ( + ) + + ( + )2 2m 2 2 4m 8 2m 2 2m 2 +10m +18 ⇔ = 4 ⇔ = 4 4m − − 8 + 2m + 2 +1 2m − − 5 2 4m +18m + 22  5  ⇔ = 4m ≠ − 2m 5 2  − −   m = 3 − 2 2m 13m 21 0  ⇔ + + = ⇔ 7  m = −  2 7
Đối chiếu điều kiện tìm được m = − thỏa mãn yêu cầu. 0,25 2 x = 2 −
Nhận xét: Bài toán này có thể tìm được hai nghiệm 
, sau đó xử lí yêu cầu của x = 2m + 4 bài toán.
Gọi x là vận tốc ca nô (x > 5), khi đó vận tốc ca nô xuôi dòng nước là (x + 5) km/h và vận tốc
ca nô ngược dòng nước là (x – 5) km/h. 0,25
Thời gian của bè trôi từ A đến C là 10 : 5 =2 giờ. Quãng đường ca nô đi ngược dòng là 35 – Câu 4 10 = 25 km. 0,25 1,0 đ
Thời gian ca nô đi từ bến A đến bến B và ngược lại gặp bè ở điểm C là: 35 25 + . 0,25 x + 5 x -5
Do ca nô gặp bè tại C nên thời gian ca nô đi bằng thời gian ca nô gặp bè, do đó ta có phương trình 35 25 +
= 2 ⇔ x = 30 , (Do x > 5). 0,25 x + 5 x -5
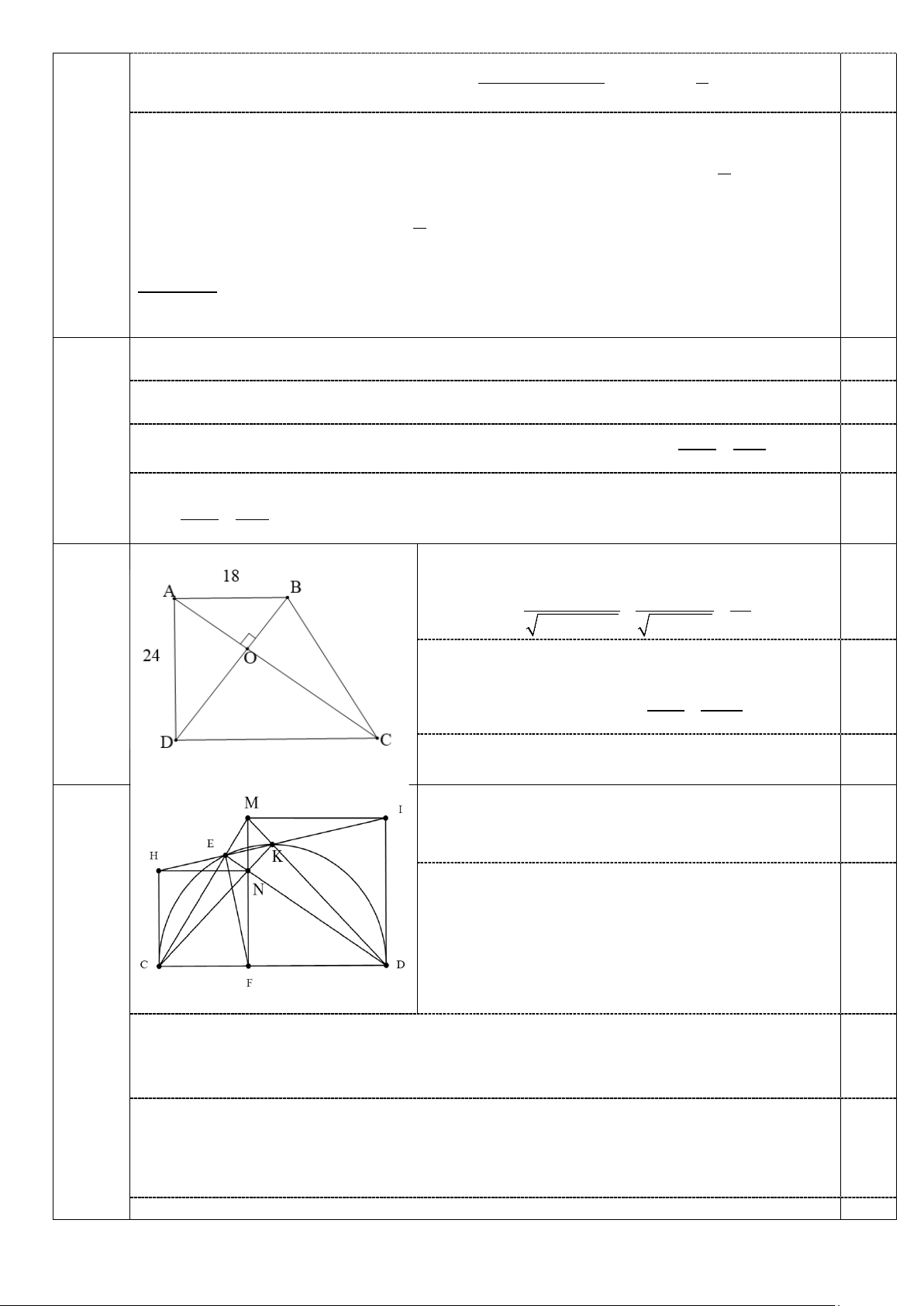
Áp dụng hệ thức lượng trong tam giác vuông ABD với AO là đường cao: 0,5 AB.AD 18.24 72 AO= = = 2 2 2 2 AB +AD 18 +24 5 Câu 5
Áp dụng hệ thức lượng trong tam giác vuông ADC với 1,0đ DO là đường cao: 2 2 0,25 2 AD 24 .5 AD =AO.AC ⇒ AC= = =40 AO 72
Áp dụng định lí Pitago vào tam giác vuông ADC: 2 2 2 2 2
DC =AC - AD =40 - 24 =1024 ⇒ DC=32cm 0,25
a. Ta thấy điểm E nhìn đường kính CD dưới một góc vuông nên  0 DEM=90 , lại có  0 MFD=90 , từ đó 1,0  
DEM =MFD , hay tứ giác DFEM nội tiếp. b. Ta có  CEN =  0
CFN = 90 nên tứ giác CENF nội tiếp. Suy ra   0
CEF=CNF = 45 (Phân giác góc vuông).
Do đó tam giác CFN vuông cân tại F nên NF = CF . 0,5 Câu 6 2,0 đ Ta có  NCF =  KDC =  0 HCN = 45 . Từ đó ⇒  0
MEK=45 (do tứ giác CDKE nội tiếp). 0,25 Mà  
HEC=MEK (đối đỉnh), do đó  0 HEC=45 , mặt khác  0 CEF=45 , do đó  0 HEF=90 . Mặt khác  0
HCF=90 (tính chất tiếp tuyến), nên tứ giác CFEH nội tiếp với đường kính HF, ta
cũng có tứ giác CENF nội tiếp với đường kính CN do đó 5 điểm C, F, N, E, H cùng thuộc một 0,25
đường tròn có các đường kính là HF, CN nên  0 CHN=90 .
Do đó tứ giác CFNH có ba góc vuông và CF = FN nên nó là hình vuông. Cách 2 của câu b
- Do EF là phân giác của góc 
CED nên theo tính chất đường phân giác FD CF = (1). 0,25 DE EC
Xét ΔDEC và ΔDFN , có góc D chung,   0 DEC=DEN=90 , do đó DE ∆ C  ΔDFN . Suy ra DF FN = (2). DE EC 0,25 Từ (1) và (2), ta có FN CF =
, suy ra FN=CF, khi đó tam giác CNF vuông cân tại F. EC CE Từ đó  0 NCF=45 nên  0 KDC=45 suy ra  0
MEK=45 (do tứ giác CDKE nội tiếp). 0,25 Mà  
HEC=MEK (đối đỉnh), do đó  0 HEC=45 , mặt khác  0 CEF=45 , do đó  0 HEF=90 . Mặt khác  0
HCF=90 (tính chất tiếp tuyến), suy ra tứ giác CFEH nội tiếp, do đó 5 điểm C, F,
N, E, H cùng thuộc một đường tròn có tâm là giao của HF và CN và bán kính HF = CN nên 2 2 0.25  0 CHN=90 .
Do đó tứ giác CFNH có ba góc vuông và CF = FN nên nó là hình vuông.
Xét biểu thức Q = -P = (a - b)(b -c)(a -c)(ab+bc+ca) , ta sẽ tìm giá trị lớn nhất của Q. 2 + Ta có ( )( )  a -b + b-c  1 a - b b - c ≤   = (a - c)2 , suy ra  2  4 0,25 ( )( )( ) 1
a - b b - c a - c ≤ (a -c)3 , (Do a - b ≥ 0, a -c ≥ 0, b -c ≥ 0 ). 4 + Lại có 2 2 2 1 ( )2 1( )2 1( )2 1 ≥ ( )2 1 ( )2 3 a + b + c -ab - bc -ca = a -c + a - b + b -c a -c + a -c = (a -c)2 2 2 2 2 4 4 0,25
Đặt x = ab + bc + ca , ta có 3 ≥ ( )2 2 1- x a - c ≥ 0 ⇒ a - c ≤
1- x , (Do 1- x ≥ 0,a - c ≥ 0 ). 4 3
Câu 7 + Xét x ≥ 0 . Khi đó 1 ≤ ( )3 ( ) 2 Q a - c ab + bc + ca ≤ (1- x)3 2 .x 1,0 đ 4 3 3 5 0,25 Ta có ( )3 2 4 ( )( )( ) 3 3 4  3 1- x x = 1- x 1- x 1- x . x. x .  ≤ . Dấu bằng xảy ra khi 2 x = . 9 2 2 9  5    5  2  2 x = x = Do đó 4 Q ≤
. Dấu bằng xảy ra khi  5 ⇔  5 . 25 5 a -b = b -c   a + c = 2b Khi đó ta tìm được 1 2 c = 0;b = ;a = . 5 5 0,25
Nếu x < 0 , thì hiển nhiên 4 Q ≤ 0 < . 25 5
Vậy P đạt giá trị nhỏ nhất là 4 − , đạt được khi 1 2 c = 0;b = ;a = . 25 5 5 5 HẾT.
Document Outline

• DAP AN KSCL TOAN 9 NAM HOC 2023-2024 (MD 01)
• DAP AN KSCL TOAN 9 NAM HOC 2023-2024 (MD 02)