

Preview text:
UBND HUYỆN NAM SÁCH
ĐỀ KHẢO SÁT CHẤT LƯỢNG
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2024 - 2025 MÔN: TOÁN 9
Thời gian làm bài 120 phút
(Không kể thời gian giao đề)
Phần I. Trắc nghiệm nhiều phương án lựa chọn (2,0 điểm)
Thí sinh trả lời từ câu 1 đến câu 8. Mỗi câu thí sinh chỉ chọn một phương án
và ghi vào giấy thi (Ví dụ: Câu 1. A,…)
Câu 1. Phương trình nào sau đây không phải là phương trình bậc nhất hai ẩn? A. x + y = 3
B. 2x − 5y = 0
C. 7x − 3y −11 = 0 D. 2 x − y = 3 x − y = 2
Câu 2. Cặp số nào sau đây là nghiệm của hệ phương trình 2x + y = 7 A. (1; 3) B. (3;1) C. (1;-3) D. (-3; 1)
Câu 3. Bạn My có các tấm thẻ, mỗi tấm thẻ ghi một chữ cái trong từ
MATHEMATIC. Bạn My rút ngẫu nhiên một tấm thẻ. Xác suất để rút được tấm thẻ ghi chữ T là: A. 1 B. 0,1 C. 0,2 D. 0,3
Câu 4. Cặp số nào sau đây là một nghiệm của phương trình x − 3y = 1? A. (4; ) 1 B. (2;0) C. (1;2) D.(2;− ) 1
Câu 5. Giá trị của a để phương trình ax − 3y = 6 có nghiệm (1;−2) là
A. a = 3 B. a = 2 C. a = 0 D. a = −3
Câu 6. Hàm số nào dưới đây không phải hàm số bậc nhất − 3 A. y = x −3
B. y = 3x + 5 C. = x y D. 2 y = x − 3 2
Câu 7. Tam giác ABC vuông tại A, tan C bằng: AB AB AC AC A. B. C. D. AC BC AB BC
Câu 8. Giá trị sin 300 bằng: 3 1 2 A. B. 0,5 C. D. 2 3 2
Phần II. Tự luận (8,0 điểm) Câu 9 (2,0 điểm).
1) Giải phương trình hệ phương trình 2x + 3y = 5 4x = y + 3
2) Tìm a, b để đường thẳng y = ax + b đi qua điểm A (3; 2) và song song với
đường thẳng y = –2x + 3. Câu 10 (2,0 điểm). x + 2 5 2
1) Rút gọn biểu thức: A = − + x ≠ − x ≠ 2 với 3; 2
x + 3 x + x − 6 2 − x
2) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình.
Trên quãng đường AB dài 150 km, một người đi xe ô tô từ A và một người
đi xe máy từ B. Hai xe xuất phát cùng một lúc và sau 1 giờ 30 phút thì gặp nhau.
Biết rằng vận tốc xe ô tô lớn hơn vận tốc xe máy là 20km/h. Tính vận tốc mỗi xe. Câu 11 (3,0 điểm).
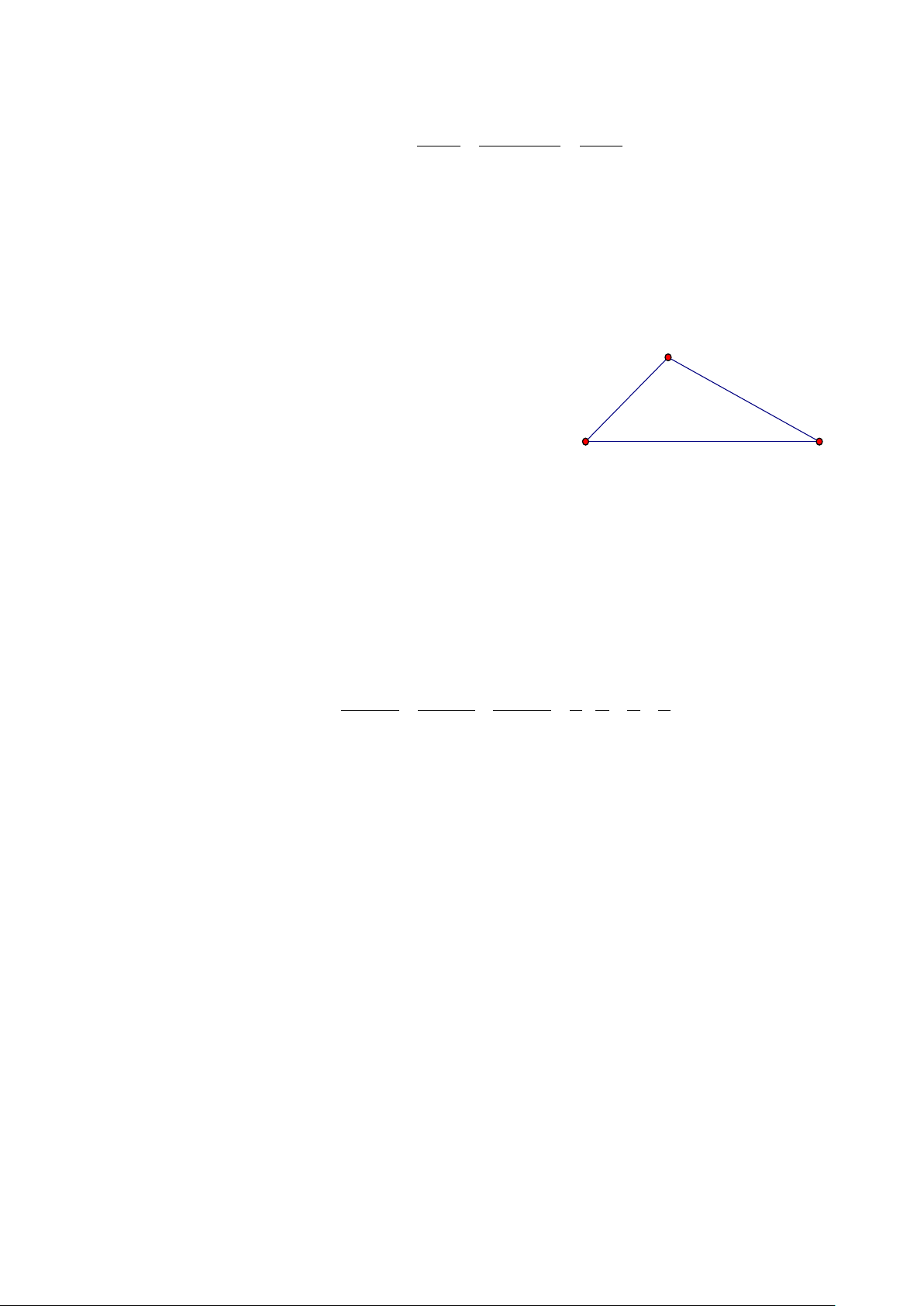
1) Hai bạn An và Bình đứng ở hai vị trí C
A, B cách nhau 100m cùng quan sát một chiếc
diều tại vị trí C. Biết rằng tại thời điểm đó góc
nâng tại vị trí A và B lần lượt là 400 và 300.
Hỏi độ cao của diều tại thời điểm đó là bao
nhiêu mét (làm tròn đến hàng phần mười). A B
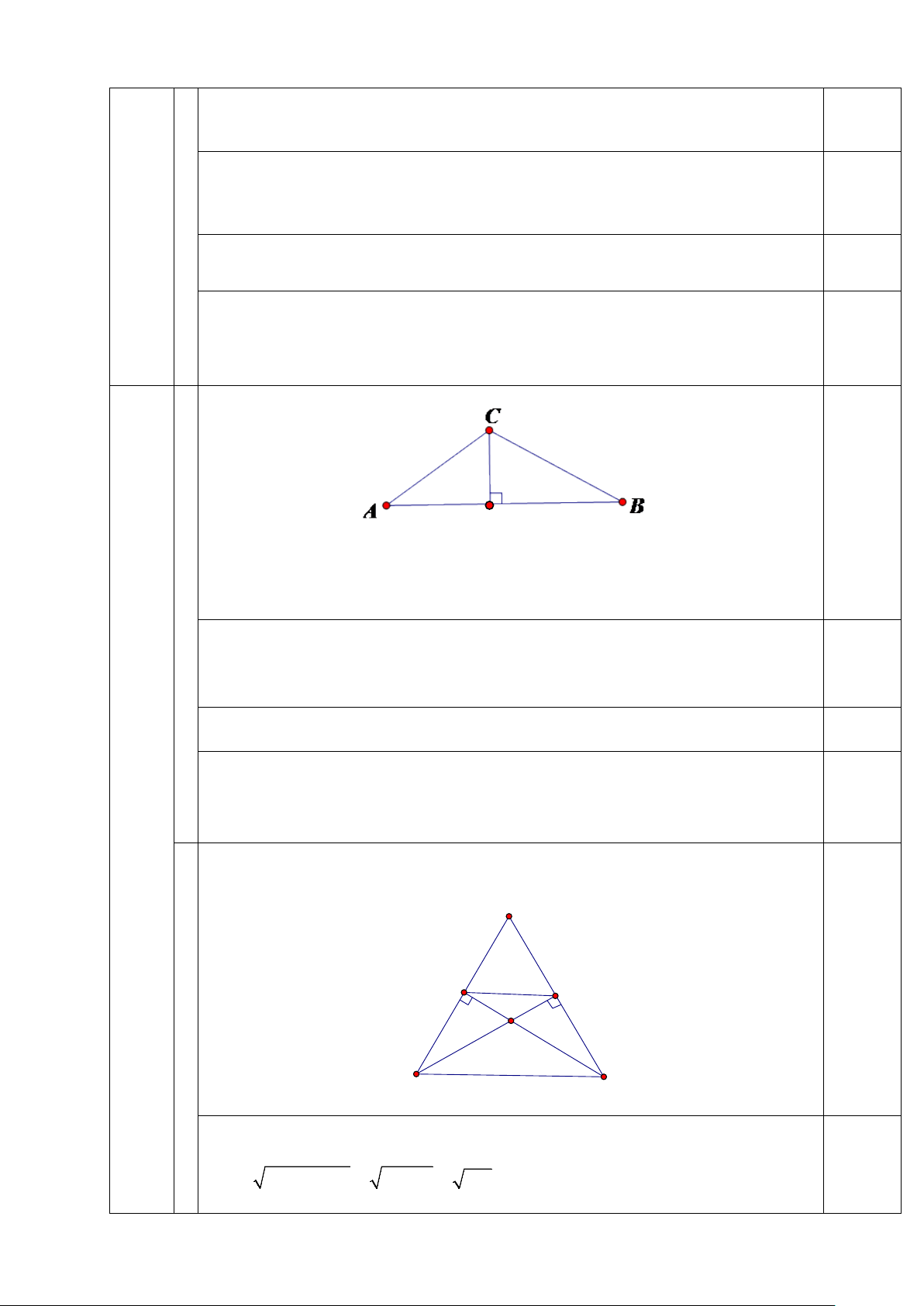
2) Cho ∆ ABC vuông tại A biết AB = 6cm và AC = 8cm.
a) Tính cạnh BC, góc B, góc C (làm tròn đến độ).
b) Phân giác góc ABC cắt cạnh AC tại E. Qua C kẻ đường thẳng d vuông
góc với đường thẳng BE tại D và đường thẳng d cắt tia BA tại I. Chứng minh: IA.IB = ID.IC và 2 I . A AB = 2 . AD ID − AI
Câu 12 (1,0 điểm). Cho a, b, c là ba số thực dương thỏa mãn: a + b + c =1.
Tìm giá trị nhỏ nhất của biểu thức: ab bc ca 1 1 1 1 S = + + + + + 2 2 2 2 2 2 a b b c c a 4 a b c + + +
………………HẾT………………
HƯỚNG DẪN CHẤM ĐỀ KHẢO SÁT NĂM HỌC 2024 -2025 MÔN: TOÁN 9
Phần I. Trắc nghiệm nhiều phương án lựa chọn (2,0 điểm)
Mỗi câu đúng 0,25 điểm Câu 1 2 3 4 5 6 7 8 Đáp án D B C A C D A B
Phần II. Tự luận (8,0 điểm) Câu Ý Nội dung Điểm
2x + 3y = 5
4x = y +3
2x + 3y = 5 (1)
4x − y = 3 (2)
Nhân vào 2 vế của phương trình (2) với 3 ta được hệ phương trình 9 x + y = 2,0 đ 1 mới: 2 3 5 0,25 12 x − 3y = 9
Cộng từng vế hai phương trình của hệ phương trình mới ta được: 14x = 14 suy ra x = 1 0,25
Thay x = 1 vào phương trình (2) ta được:4.1 – y = 3 suy ra y = 1 0,25
Vậy hệ phương trình có nghiệm (x;y) = (1; 1) 0,25
Do đường thẳng y = ax + b song song với đường thẳng y = –2x + 3
nên a = – 2 và b ≠ 3. Ta được phương trình đường thẳng y = –2x + b 0,25
Vì đường thẳng y = –2x + b đi qua điểm A (3; 2) nên ta có: 2 2 = –2.3 + b 0,25 Suy ra b = 8 0,25
Giá trị b = 8 có thỏa mãn khác 3. Vậy a = -2 , b = 8 0,25 x + 2 5 2 A = − + 2
x + 3 x + x − 6 2 − x x + 2 5 2 1 A = − −
x + 3 (x + 3)(x − 2) x − 2 0,25
(x + 2)(x − 2) − 5 − 2(x + 3) 0,25 10 A = ( x + 3)(x − 2) 2,0 đ 2 x − 2x −15
A = (x+3)(x−2) 0,25
(x + 3)(x − 5) x − 5 A = = 0,25 x ≠ − x ≠ ( với 3; 2
x + 3)(x − 2) x − 2
Gọi vận tốc của xe máy là x(km/h) với x > 0
Vận tốc của ô tô là x + 20 (km/h) 0,25
Đổi 1 giờ 30 phút = 1,5 giờ
2 Quãng đường xe máy và ô tô lần lượt đi được đến chỗ gặp nhau là: 1,5x (km); 1,5(x+20) km 0,25
Tổng quãng đường hai xe đi đến chỗ gặp nhau là quãng đường AB. 0,25
Ta có phương trình: 1,5x + 1,5(x+20) = 150 1,5x + 1,5x + 30 = 150 3x = 120 suy ra x = 40 0,25
Vậy vận tốc của xe máy là 40 km/h; vận tốc của ô tô là 60 km/h H
1 Kẻ CH ⊥ AB ; CH là độ cao đạt được của chiếc diều. 0,25
Tam giác AHC vuông tại H nên: AH = CH.cot A 0,25
Tam giác BHC vuông tại H nên: HB = CH.cot B
Mà AH + HB = AB nên CH.cot A + CH.cot B = BC 0,25
CH (cot 400 + cot 300 ) = 100 Suy ra CH ≈ 34,2m 0,25 11 3,0 đ
Vậy tại thời điểm đó diều đạt độ cao khoảng 34,2 mét.
Vẽ đúng hình đến ý a I A D 0,25 E 2 B C
a Trong tam giác ABC vuông tại A nên BC2 = 2 2
AB + AC (Pythagore) 2 2 2 2
BC = AB + AC = 6 + 8 = 100 =10cm 0,25 sin B = AC 8 = = 0,8 . Suy ra 0 B ≈ 53 0,25 BC 10 Ta có: 0 C = − 0 0 0
90 B ≈ 90 − 53 = 37 0,25
Hai tam giác IAC và IDB có: góc I chung; IAC = 0 IDB (= 90 ) 0,25 IA IC
Vậy ∆IAC ∆IDB (g – g) suy ra = ⇒ . IA IB = . ID IC 0,25 ID IB 2
b Tam giác BIC có BD là đường phân giác đồng thời là đường cao nên
tam giác BIC cân tại B nên ID = DC
Tam giác ACI vuông tại A có AD là trung tuyến nên IC = 2AD 0,25 Vậy .2 ID AD = . ID IC = . IA IB = .
IA (IA + AB) 0,25 Suy ra 2 2 2A . D ID = IA + . IA IB ⇒ 2A . D ID − IA = . IA IB (đpcm) ab bc ca 1 1 1 1 S = + + + ( + + ) 2 2 2 2 2 2 a + b b + c c + a 4 a b c 1 1 1 1 = + +
+ (a + b + c a + b + c a + b + c + + ) a b b c c a 4 a b c + + + 0,25 b a c b a c 1 1 1 1 = + + + (1 b c + + +1 a c + + +1 a b + + ) a b b c c a 4 a a b b c c + + + b a c b a c 12 b c c a 1,0 đ Đặt a b + = x + = y + = z 0,25 b a c b a c
1 x 1 y 1 z 3 3 15 S = + + + + + + ≥ 1+1+1+ = 0,25
x 4 y 4 z 4 4 4 4 Dấu “=” khi 2 2 2
x = 4, y = 4, z = 4 suy ra x = y = z = 2 (Vì x,y,z > 0) Khi đó a=b=c= 1 . 3 0,25
Ghi chú: - Học sinh làm bài cách khác đúng vẫn cho điểm tối đa.
- Bài hình nếu học sinh không vẽ hình hoặc hình sai cơ bản thì không
chấm điểm bài hình.
Xem thêm: KHẢO SÁT CHẤT LƯỢNG TOÁN 9
https://thcs.toanmath.com/khao-sat-chat-luong-toan-9
Document Outline
- TOAN 9
- New Microsoft Word Document





