Đề khảo sát cuối năm Toán 9 năm 2022 – 2023 trường THCS Nguyễn Trãi – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp đề khảo sát chất lượng học sinh môn Toán 9 năm học 2022 – 2023 trường THCS Nguyễn Trãi – Hà Nội giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.
Preview text:
https://thcs.toanmath.com/khao-sat-chat-luong-toan-9
TRƯỜNG THCS NGUYỄN TRÃI
ĐỀ KIỂM TRA KHẢO SÁT THÁNG 5
NĂM HỌC 2022 – 2023 ĐỀ MÔN: TOÁN 9 CHÍNH THỨC
Ngày kiểm tra: 06/ 5 /2023
(Thời gian làm bài: 120 phút) HƯỚNG DẪN CHUNG
+) Điểm toàn bài để lẻ đến 0,25.
+) Các cách làm khác nếu đúng vẫn cho điểm tương ứng với biểu điểm của hướng dẫn chấm.
+) Các tình huống phát sinh trong quá trình chấm do Hội đồng chấm thi quy định, thống nhất bằng biên bản.
+) Hướng dẫn chấm gồm 03 trang.
HƯỚNG DẪN CHẤM (ĐỀ CHÍNH THỨC) Bài Ý Đáp án Điểm
Tính giá trị của biểu thức A khi x = 9. 0,5
Thay x = 9 (TMĐK) vào biểu thức . A 0,25 1) 9 3 Tính được A = = . 0,25 9 + 2 5 1
Chứng minh B = . 1,0 x + 2 3 8 + = − 2 x B 0,25
x − 2 ( x − 2)( x + 2) 3 ( x + 2) 8 + 2 x 2) B = − 0,25 Bài I
( x −2)( x +2) ( x −2)( x +2) 2,0 điểm x − = 2 ( 0,25 x − 2)( x + 2) B = 1 . 0,25 x + 2
Tìm tất cả giá trị của x để biểu thức P = 3A + 2B đạt giá trị nhỏ nhất. 0,5 3√𝑥 2 3√𝑥 + 6 − 4 4 𝑃 = 3𝐴 + 2𝐵 = + = = 3 − . 3) 0,25 √𝑥 + 2 √𝑥 + 2 √𝑥 + 2 √𝑥 + 2 4 x 0 x 2 2 2 P 3 2 1 Vì + − = x + 2 0,25
Dấu bằng xảy ra khi x = 0.
Vậy với x = 0 thì giá trị nhỏ nhất của P = 1.
Tính vận tốc ô tô, xe máy. 1,5
Gọi vận tốc của xe máy là x (đơn vị :km/h, x 0 ); 0,25
Vận tốc của ô tô là x + 10 (km/h) Bài II 1) 60 2,0 điểm
Thời gian xe máy đi hết quãng đường AB là (h) x 0,25 60
Thời gian ô tô đi hết quãng đường AB là (h) x + 10 1 1 60 60 1 0,25 12 phút =
giờ , Lập luận để có PT: − = . 5 x x +10 5 2 0,25 x +1 0x – 3000 = 0
Giải phương trình được 2 nghiệm: x = 50 ; x 6 =− 0 0,25 1 2
Đối chiếu điều kiện và thử lại: 0,25
Vận tốc của xe máy là 50 km/h, vận tốc của ô tô là 60 km/h
Tính thể tích của bóng đèn huỳnh quang. 0,5 2 2 2)
Tính thể tích của bóng đèn bằng: S = R h 3,14 2 120 0,25 = 1507,2 (cm3). 0,25
2x + 3 y −1 = 5
Giải hệ phương trình . ĐK: y≥ 1 1,0
3x − 2 y − 1 = 1
2x + 3b = 5. 1)
Đặt y − 1 = b (b 0), ta có hệ 3x − 2b = 1 0,25 x = 1 Giải hệ được . 0,25 b = 1(tm)
y − 1 = 1⇔ y = 2 (tmđk) 0,25
Vậy hệ phương trình có nghiệm duy nhất là (1;2). 0,25
Chứng minh (d) luôn đi qua điểm A(0;4) … 0,5
Thay tọa độ điểm A(0;4) vào phương trình đường thẳng d ta có: 0,25 2a) 4 = .
m 0 + 4 đúng với mọi m Bài III
Vậy đường thẳng d luôn đi qua điểm A(0;4) với mọi giá trị của m. 2,5 điểm 0,25
Tìm tất cả giá trị của m để … 1,0
Xét phương trình hoành độ giao điểm của đường thẳng (d) và parabol (P) : 2 x = mx + 4 2
x − mx − 4 = 0 (1). (d) 0,25
cắt (P) tại hai điểm phân biệt phương trình (1) có 2 nghiệm phân biệt 2 0
m + 16 0,m
Gọi x , x là hai nghiệm của phương trình (1). 1 2 2b)
x + x = m 0,25 Theo đị 1 2
nh lý Vi-et ta có: x x = − 4 1 2 Ta có 2 2 2
(x + 2x )(x + 2x ) = 14 2x + 2x + 5x x = 14 2(x + x ) + x x = 14 0,25 1 2 2 1 1 2 1 2 1 2 1 2 2
2m − 4 = 14 m = 3. 0,25 Vậy m = 3. Bài IV
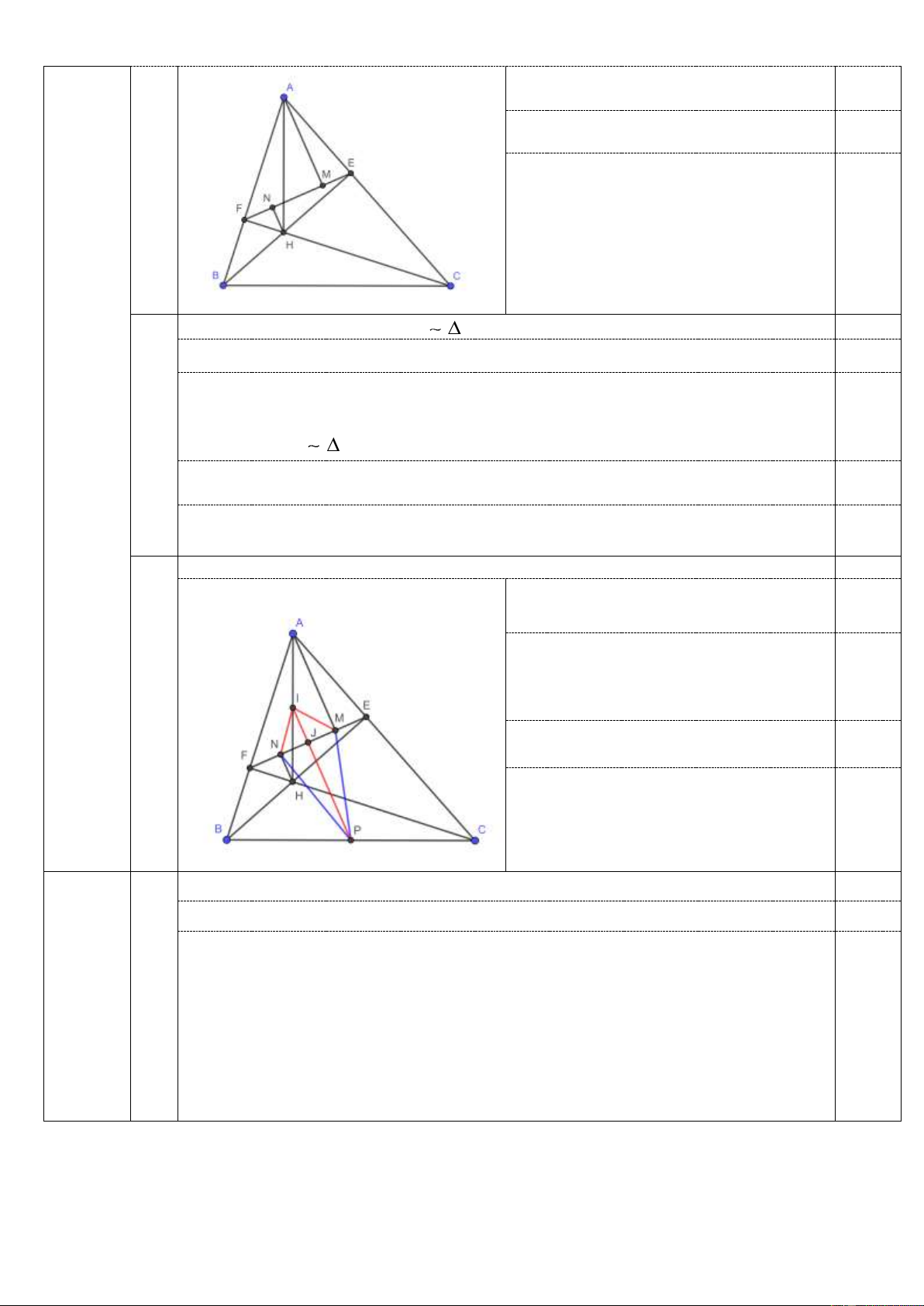
Chứng minh 4 điểm B, C, E và F cùng thuộc một đường tròn. 3,0 điểm 1) 1,0 2
Vẽ đúng hình đến ý 1). 0,25 Chỉ ra được BEC = 0 90 BFC = 0 , 90 0,5
Suy ra bốn điểm B, C, E và F cùng
thuộc một đường tròn đường kính BC. 0,25
Chứng minh tam giác AEH
FNH và AF.HE + AE.HF = AH.EF … 1,0
Chứng minh tứ giác AEHF nội tiếp suy ra HFN = HAE 0,25
Xét FNH và AEH Có FNH = AEH = o
( 90 ) và HFN = HAE (cm trên) 0,25 2) Suy ra AEH
FNH(g − g)
Suy ra AE.FH = AH.FN 0,25
Chứng minh tương tự ta có : AF.EH = AH.EN
Vậy AF.HE + AE.HF = AH.EN + AH.FN = AH.EF 0,25
Chứng minh tam giác PMN cân… 1,0
Gọi I là trung điểm AH. Chứng minh IP 0,25
là trung trực EF IP ⊥ EF.
Gọi J là trung điểm của MN. Xét hình
thang ANHM có I, J là trung điểm 2 đườ 0,25 ng chéo 3)
Suy ra IJ // AM IJ ⊥ EF.
Từ đó suy ra P,I,J là ba điểm thẳng 0,25 hàng.
Suy ra PJ vừa là đường cao vừa là
đường trung tuyến của tam giác PMN 0,25
Vậy tam giác PMN cân tại P.
Tìm giá trị lớn nhất của biểu thức P = (x + 2)(y + 1). 0,5
Vì x,y không âm ta có P = (x + 2)(y + 1) = xy + 2y + x + 2 x + y + 2 0,25 2 2 2
Vì x + y + xy = 4 (x + y) = 4 + xy 4 x + y 2.
Suy ra P x + y + 2 4. Bài V 0,5 điểm x = 2
Dấu '' = " xảy ra y = 0,25 0 x = 2
Vậy giá trị nhỏ nhất của P = 4 khi y = 0 3
Document Outline
- https
- HDC chuan đề thi thử THCS Nguyễn Trãi (1)