Đề khảo sát HSG Toán 7 năm 2023 – 2024 phòng GD&ĐT Gia Viễn – Ninh Bình

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 HUYỆN GIA VIỄN
NĂM HỌC 2023 – 2024 MÔN: TOÁN (ĐỀ CHÍNH THỨC)
Thời gian: 150 phút (không kể thời gian giao đề)
(Đề này gồm 05 câu, 01 trang) Câu 1: (5,0 điểm) 0
a) Tính giá trị biểu thức: 1 7  2022 A 0,2 : 15 9  = + ⋅ − + − . 121 3  2023   b) Rút gọn biểu thức: 1  1  1  1   1 B .1 1 1 .....1  = + + + + . 2 1.3 2.4 3.5 2021.2023       
c) Tính giá trị của biểu thức 2023 2023
A = 2022x + y + z Với y + z + x + z + x + y −
x, y, z là các số thực thỏa mãn 1 2 3 1 = = = x y z x + y + z Câu 2: (4,0 điểm)
1) Tìm ba số x, y, z thỏa mãn: 4x  3y ; x z = và 2 2 2
2x + 2y − 3z = 100 − . 3 5
2) Nhà trường dự định chia vở viết cho 3 lớp 7A, 7B, 7C tỉ lệ theo số học sinh
là7 : 6 : 5. Nhưng sau đó vì có học sinh thuyên chuyển giữa ba lớp nên phải chia lại
theo tỉ lệ 6 : 5 : 4. Do đó có lớp đã nhận được ít hơn dự định là 12 quyển. Tính số
vở mà mỗi lớp thực tế đã nhận được.
3) Cho hai đa thức: f (x) = (x − ) 1 (x + 3) và ( ) 3 2 g x = x − ax + bx − 3
Xác định hệ số a,b của đa thức g (x) biết nghiệm của đa thức f (x) cũng là nghiệm
của đa thức g (x) Câu 3: (4,0 điểm) 1) Tìm x, biết: a) 2
7x − 35x + 42 = 0 b) x + 2 + x + 3 = 4(x − ) 1 − x −1
2) Cho a, b là các số nguyên thỏa mãn  7a  5 – 21b  a  1  3b  7
Chứng minh rằng: 11b  15  43a  7. 3) Cho biểu thức 3− 2x P =
với x là số nguyên. Tìm giá trị lớn nhất của P 2 − x
Câu 4: (6,0 điểm)
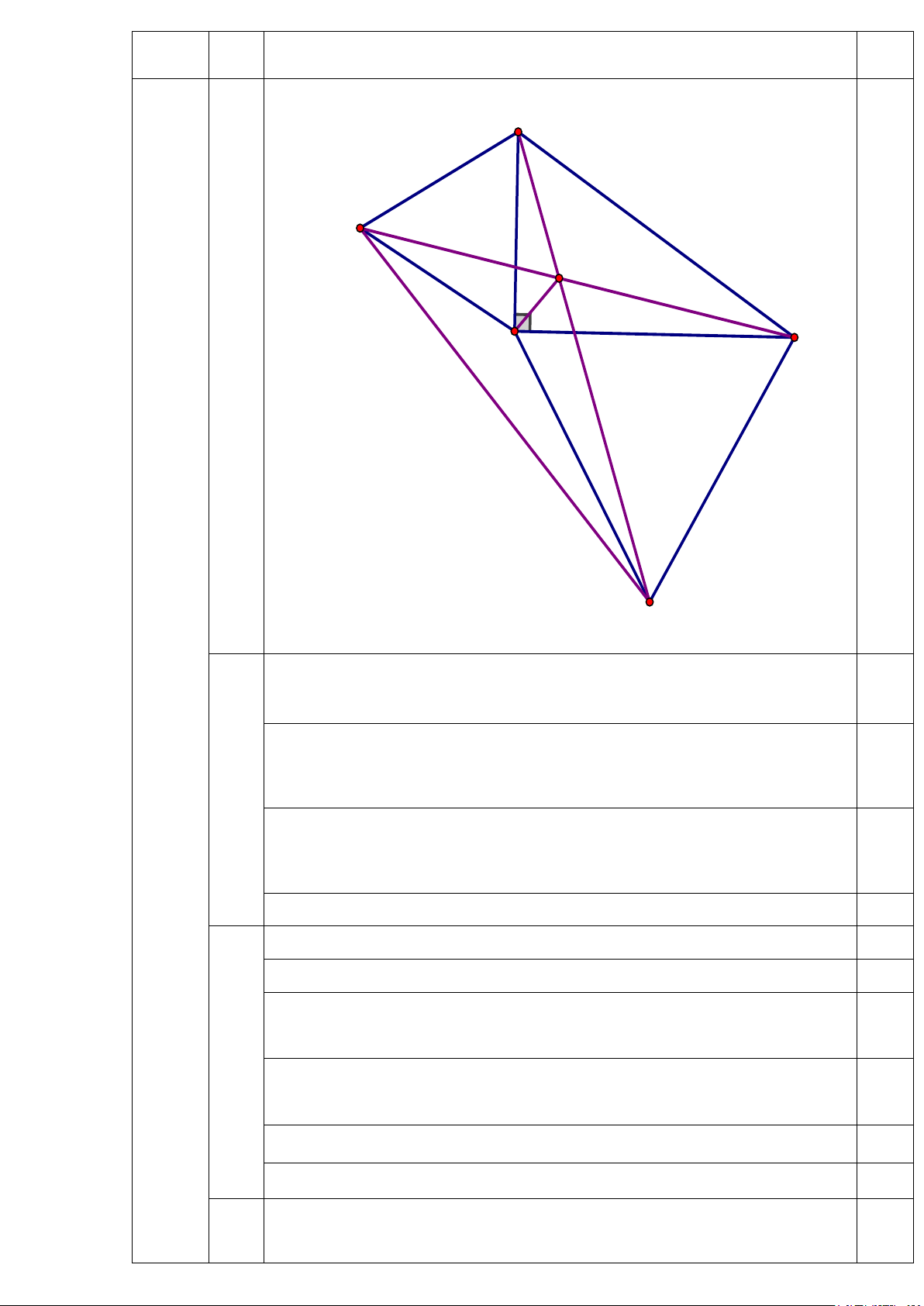
Cho tam giác ABC vuông tại A. Vẽ về phía ngoài tam giác ABC các tam giác
đều ABD và ACE . Gọi I là giao điểm BE và CD. Chứng minh rằng: 1) A  BE  A  DC 2) DE  BE 3)  0
EIC = 60 và IA là tia phân giác của  EID .
Câu 5: (1,0 điểm)
1) Một hộp chứa bốn cái thẻ được đánh số 1; 2; 3; 4, hai thẻ khác nhau thì ghi hai
số khác nhau. Lấy ngẫu nhiên hai thẻ cùng một lúc. Tính xác xuất của các biến cố sau:
a) A : “Tổng các số trên hai thẻ là số chẵn”.
b) B : “Tích các số trên hai thẻ là số chẵn”.
2) Tìm các số nguyên m để (m + )( 2
1 m + 2m) là một số chính phương.
…………………………Hết………………………..
UBND HUYỆN GIA VIỄN
HƯỚNG DẪN CHẤM KSCL HỌC SINH GIỎI
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
Năm học 2023 – 2024 MÔN: TOÁN 7 ĐỀ CHÍNH THỨC
HƯỚNG DẪN CHẤM GỒM 07 TRANG Câu Ý Nội dung Điể m Câu 1 1 0 1 7  2022  1 1 7 (5,0
a) A = 0,2 : + ⋅ 15 − + 9 − = : + ⋅6 −   1 121 3  2023  5 11 3 1,0 điểm) 11 76 = +14 −1 = 5 5 0,5 2 1  1  1  1   1 B . 1 1 1 .....1  = + + + + 2 1.3 2.4 3.5 2021.2023       
1 2 23 34 4 2022 2022 B   .     .      . ...     . 
2 1 3 1 43 5  2021 2023 0,5 1 2 2 3 3 4 4 2022 2022
B  . . . . . . ....... . 2 1 3 2 4 3 5 2021 2023 0,5 2022 B  2023 0,5 3
Áp dụng tính chất dãy tỉ số bằng nhau ta có: 0,5
y + z +1 x + z + 2 x + y − 3 1 = = = x y z x + y + z ( y + z + )
1 + (x + z + 2) + (x + y − 3) 2(x + y + z) = = = 2 x + y + z x + y + z Khi đó: 0,5
y + z +1 x + z + 2 x + y − 3 1 = = = = 2 x y z x + y + z  1 0,5
x + y + z =   1  1 2  1  x
x + y + z = x + y + z = =   1  2 2 2 +1 = 3x      2  5
⇒ y + z +1 = 2x ⇒ x + y + z +1 = 3x ⇒  ⇒ y = 1 6
x + z + 2 = 2y x + z + y + 2 = 3y  + 2 = 3y    2  5 −
x + y − 3 = 2z
x + y + z − 3 = 3z z = 1  6  − 3 = 3z 2 Thay 1 5 5 0,5 x ; y ; z − = = = vào biểu thức 2023 2023
A = 2022x + y + z ta 2 6 6 2023 2023 được: 1  5   5 A 2022. −  = + + =     1011 2  6   6  Câu 2: 1. Từ 4x x z x y z
 3y ; = ⇒ = = ta có : 0,5 (4,0 3 5 3 4 5 điểm) 2 2 2 2 2 2 2 2 2 x y z 2x 2y 3z
2x + 2y − 3z 100 − = = = = = = = = 4 0,5 9 16 25 18 32 75 25 − 25 − 2 x = 36 x = 6 x = 6 − 0,5  2  
y = 64 ⇔ y −8 hoặc y = 8
− ( vì x, y, z cùng dấu)  2 z =100    z =  10 z = 10 −  2.
Gọi tổng số vở 3 lớp đã nhận được là x (quyển) ( x là số tự nhiên 0,25 khác 0).
Gọi số vở dự định chia cho 3 lớp 7 A,7 B,7C lúc đầu lần lượt là:
a,b,c (quyển) ; a,b,c là các số tự nhiên khác 0.
Ta có: a b c a +b + c x 7x x 5x = = = = ⇒ a = ;b = ;c = ( ) 1 0,25 7 6 5 18 18 18 3 18
Gọi số vở sau đó chia cho 3 lớp lần lượt là a', b', c' (quyển); 0,25
a', b', c' là các số tự nhiên khác 0, ta có:
a′ b′ c′ a′ + b′ + c′ x 2x x 4x = = = = ⇒ a′ = ;b′ = ;c′ = (2) 6 5 4 15 15 5 3 15 So sánh ( ) 1 và (2) ta có: a
′ ′ = b ;′c>c′ ' nên lớp 7C nhận ít hơn 0,25 dự định Do đó: x x x
c − c′ =12 hay 5 4 − =12 ⇔ =12 ⇒ x =1080. 0,25 18 15 90
Vậy số vở 3 lớp 7 A,7 B,7C nhận được lần lượt là: 0,25 2 1080 4
⇒ a′ = ⋅1080 = 432;b′ = = 360;c′ = ⋅1080 = 288 quyển 5 3 15 3.
Ta có: f (x) = 0 ⇔ (x − )
1 (x + 3) = 0 ⇔ x∈{1;− } 3 0,25
Do nghiệm của đa thức f (x)cũng là nghiệm của đa thức g (x)nên 0,25 g ( ) 1 = 0 1
 − a + b − 3 = 0 0,25  ⇔  g  ( 3 − ) = 0  27
− − 9a − 3b − 3 = 0
−a +b = 2 a = 3 − ⇔  ⇔ 0,25 4a 12 b  = −  = 1 − Câu 3 1 a) 2 − + = 0,25 (4,0 7x 35x 42 0 điểm) ( 2
7 x − 5x + 6) = 0 2
x − 5x + 6 = 0 2
(x − 3x) − (2x − 6) = 0 (x − ) 3 (x − 2) = 0 0,25 * TH1: x −3 = 0 x = 3 * TH2: x − 2 = 0 0,25 x = 2 Vậy x∈{2; } 3
b) x + 2 + x +3 = 4(x − ) 1 − x −1 0,25
x + 2 + x +3 + x −1 = 4(x − ) 1
Do vế trái luôn lớn hơn hoặc bằng 0 nên vế phải cũng phải lớn hơn
hoặc bằng 0 nên x −1≥ 0 ⇒ x ≥1
Với x ≥1⇒ x + 2 > 0; x +3 > 0; x −1≥ 0 nên ta có: 0,25
x + 2 + x +3+ x −1= 4(x − ) 1 ⇒ x = 8( t/m) 0,25 Vậy x = 8 2
Ta có với mọi số nguyên a; b thì: 0,25
7a7; 21b7 ⇒ 7a − 21b + 5 không chi hết cho 7 (vì 5 không chia hết cho 7).
Mà  7a  5 – 21b  a  1  3b  7 , và 7 là số nguyên tố . 0,25
 a – 3b   1 7
Lại có 42a14b14  7 do 42a7;14b7 0,25
 42a 14b 14 
 a3b  1 7
Hay 11b1543a 7  đpcm  0,25 3 Ta có:
3− 2x 2x − 3 2x − 4 +1 2(x − 2) 1 1 0,25 P = = = = + = 2 + 2 − x x − 2 x − 2 x − 2 x − 2 x − 2
P đạt GTLN khi và chỉ khi 1 có giá trị lớn nhất. 0,25 x − 2 + Với 1
x < 2 ⇒ x − 2 < 0 ⇒ < 0 (1) x − 2 + Với 1
x = 2 ⇒ x − 2 = 0 ⇒ không có nghĩa (2) 0,25 x − 2 + Với 1
x > 2 ⇒ x − 2 > 0 ⇒ > 0 x − 2
Phân số 1 có tử và mẫu đều dương và tử không đổi nên đạt 0,25 x − 2 GTLN khi mẫu đạt GTNN
Vì x∈Z nên x − 2∈Z và x − 2 > 0 nên x − 2 có GTNN khi 0,25
x − 2 =1⇒ x = 3 khi đó 1 =1 (3) x − 2 Từ (1), (2), (3) 3− 2x P =
đạt GTLN là 3 khi x = 3. 0,25 2 − x 0,5 B Câu 4: (6,0 điểm) D 1 I 2 1 1 3 1 2 2 A C 1 2 E 1   =  0 0 0 0 0,25
Ta có: DAC A +90 = 60 +90 =150 1  ⇒  =  DAC BAE   =  0 0 0 0
BAE A + 90 = 60 + 90 =150 2 Xét A  DC và A  BE có: 0,25 DA  BA  gt  = 
DAC BAE (Chứng minh trên) 0,25 AC  AE  gt  A  DC  A
 BE c g c 0,25 2 Ta có:  +  +  +  0 = ⇔  0 0 0 0 A A BAC A 360 A + 60 + 90 + 60 = 360 0,25 3 1 2 3 ⇔  0 = ⇔  =  0 A 150 A BAE =150 0,25 3 3 Xét DAE và BAE có: 0,25 DA  BA  gt   0,25 3
A  BAE ( Chứng minh trên) AE : Cạnh chung
DAE  BAE c – g – c 0,25  DE
 BE (hai cạnh tương ứng) 0,25 3
Ta có: DAC  BAE (CM câu a)  
 E C (hai góc tương ứng) 0,25 1 1
Lại có: I + E +  0 0,25 1 2
ICE = 180 (Tổng 3 góc trongICE )      0  I 0,25
1  ( AEC  E )  (C  C )  180 1 1 2  0   0 0  I 0,25
1  60  E  C  60  180 1 1  0 0    I 0,25
1 120  180 (E  C ) 1 1  0  I  60 , hay  0 EIC = 60 0,25 1 * Vì DAE
 BAE (chứng minh câu b) ⇒  
E  DEA ( hai góc 0,25 1 tương ứng)
 EA là tia phân giác của  DEI 0,25
 EAlà tđường phân giác trong của E  ID (1) 0,25
Vì DACBAE  DAC  DAE DAE   BAE   
 D  D (Hai góc tương ứng) 0,25 1 2
 DA là tia phân giác của  EDC
 DA là đường phân giác trong của E  ID (2)
Từ (1) và (2) ⇒ IAlà đường phân giác thứ ba trong EID . 0,25
Hay IAlà tia phân giác của  EID 0,25 Câu 5 1
Khi lấy ngẫu nhiên hai thẻ cùng một lúc, tập hợp các kết quả có 0,25 (1,0
thể xảy ra đối với số ghi trên hai thẻ là: điểm)
({1;2),(1;3),(1;4),(2;3),(2;4),(3;4)}.
a) Có 2 kết quả thuận lợi cho biến cố A là: (1;3), (2;4). 0,25
Do đó, xác suất của biến cố A là 2 1 = . 6 3
b) Có 5 kết quả thuận lợi cho biến cố B là:
(1;2),(1;4),(2;3),(2;4),(3;4).
Do đó, xác suất của biến cố B là 5 . 6 2 Ta có (m + )( 2
1 m + 2m) là một số chính phương với m là số nguyên. 0,25 Suy ra (m + )( 2 m + m) 2 1 2 = k (k ∈) Vì 2
k ≥ 0 ⇒ (m + )( 2 1 m + 2m) ≥ 0 Với m < 2 − ⇒ (m + )( 2
1 m + 2m) < 0 (loại) Với m∈{ 2 − ; 1; − } 0 ta đều có 2 k = 0 (thoả mãn). Với m > 0 ta có 2 k = (m + )( 2 1 m + 2m) 0,25
Gọi d là một ước chung nguyên tố của m +1 và 2 m + 2m (  m + ) 1 d 2 Suy ra 
m + md m +1d ( ⇒  ⇒ 
⇒ 1d ⇒ d = 1 ± 2 m +  2m 2  )d
m + 2md md Nên (m + )( 2
1 m + 2m) là một số chính phương khi m +1 và 2 m + 2m
đều là số chính phương. Để 2
m + 2m là số chính phương thì 2 2
m + 2m = a (a∈) . Suy ra (m + )2 2
1 −1 = a ⇒ (m +1+ a)(m +1− a) =1 ⇒ m +1+ a = m +1− a ⇒ a = 0 ⇒ m = 0  (không thoả mãn) m = 2 − Vậy m∈{ 2 − ; 1; − } 0 thì (m + )( 2
1 m + 2m) là một số chính phương.
Document Outline