PHÒNG GIÁO DỤC VÀ ĐÀO TẠO ĐỀ KHẢO SÁT HỌC SINH GIỎI CẤP THÀNH PHỐ
THÀNH PHỐ THÁI BÌNH NĂM HỌC 2023- 2024 MÔN TOÁN 7
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
Bài 1. (4,0 điểm) 16 4 6 7 1. Tính 3 .5 3 .5 100 3 49 1 A + + − = + 14 3 4 8 3 .5 + 3 .5 3 + 2 36 − 25
2. Cho a, b, c là 3 số thực thỏa mãn b + c +1 a + c + 2 a + b − 3 1 = = = a b c a + b + c Tính 3 M = (2a + 8b − 4c −13) .
Bài 2. (4,0 điểm)
1. Tìm cặp số nguyên (a, b) thỏa mãn 2 3 2 (a + b + 2)a +1 = a + b . 2. Tìm x, y, z biết 2 2
2023 x − 2 + 2024 y + 3 + (6xy + z ) = 0 .
Bài 3. (4,0 điểm) 1. Tìm x + ≥ 0 để biểu thức x 7 K = nhận giá trị nguyên. x + 2
2. Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng biểu thức a b c P = + +
không thể nhận giá trị nguyên. b + c c + a a + b
Bài 4. (6,0 điểm)
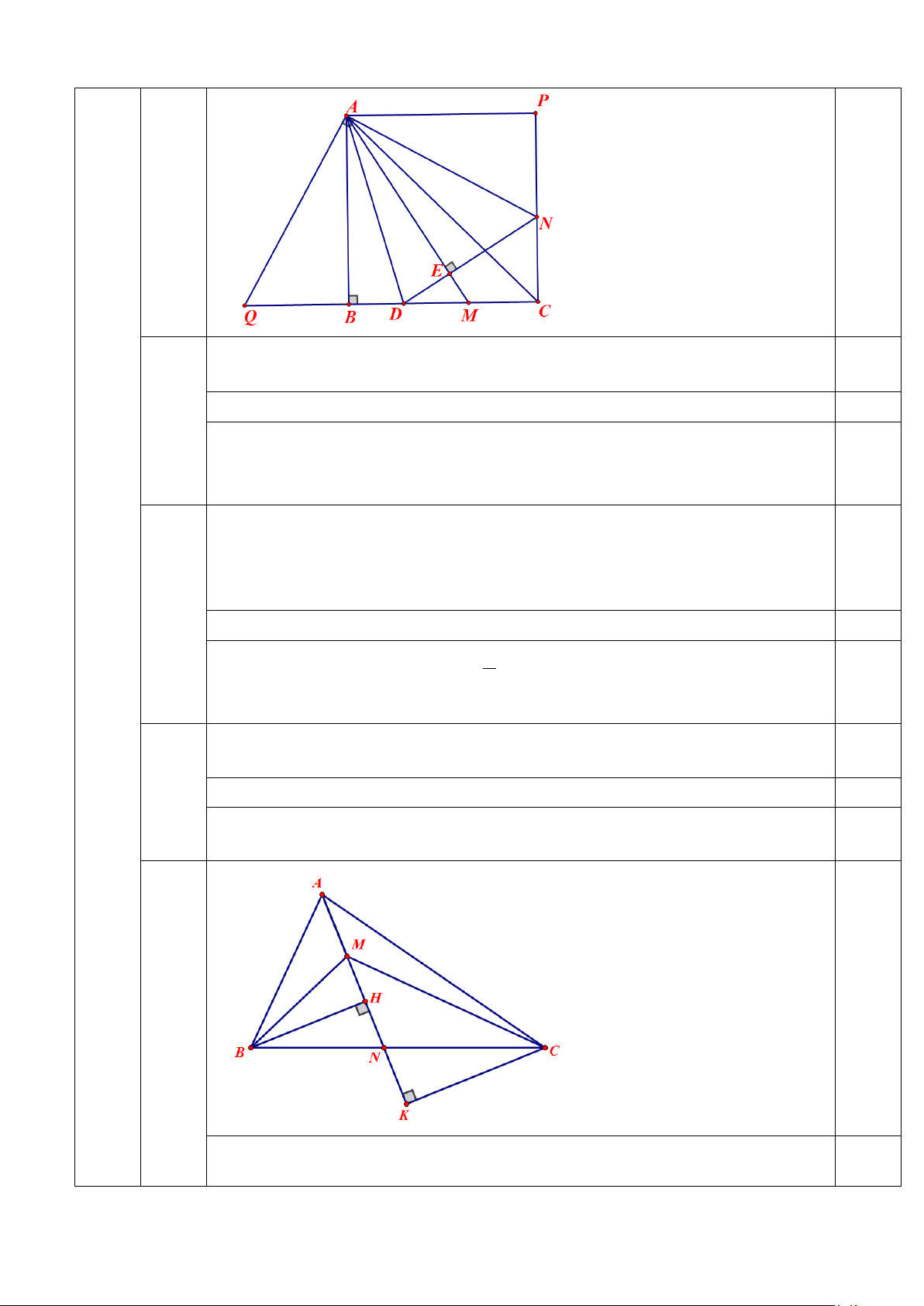
1. Cho tam giác ABC vuông tại B có AB = BC. Trên cạnh BC lấy điểm M
khác B và C, tia phân giác của góc BAM cắt BC ở D. Đường thẳng qua D
vuông góc với AM tại E cắt đường thẳng qua C vuông góc với BC tại N.
a) Chứng minh rằng AB = AE. b) Tính  DAN .
c) Đặt AB = a. Chứng minh rằng chu vi tam giác DCN bằng 2a.
2. Cho tam giác ABC có diện tích bằng 1, M là điểm tùy ý trong trong tam giác.
Chứng minh rằng MA.BC + MB.AC + MC.AB ≥ 4.
Bài 5. (2,0 điểm)
Tìm bộ 3 số tự nhiên x, y, z thỏa mãn đồng thời các điều kiện sau: a) 2 2 2 3x + 54 = 2y + 4z b) 2 2 2 5x + 74 = 3y + 7z
c) Q = x + y + z đạt giá trị nhỏ nhất. ----- HẾT-----
Họ và tên thí sinh:………………………………………Số báo danh:……………….
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM
THÀNH PHỐ THÁI BÌNH
ĐỀ KHẢO SÁT HỌC SINH GIỎI CẤP THÀNH PHỐ NĂM HỌC 2023- 2024 MÔN TOÁN 7
Bài Câu Néi dung §iÓm 16 4 6 7 100 + 3 49 −1 A 3 .5 3 .5 = + 14 3 4 8 + 3 .5 + 3 .5 3 + 2 36 − 25 1,0 1 6 4 3 .5 ( 10 3 3 + 5 ) 10 + 3.7 −1 A = + (2,0) 4 3 3 .5 ( 10 5 3 + 5 ) 3+ 2.6 −5 10 3 10 3 3 + 5 10 + 21−1 3 + 5 1424676 A = 45. + = 45. + 3 = . 1,0 10 5 10 5 3 + 5 3 +12 − 5 3 + 5 31087
Điều kiện abc ≠ 0;a + b + c ≠ 0 (*) 0,25 + + + + + − 1
Xét giả thiết b c 1 a c 2 a b 3 1 = = = a b c a + b + c (4,0) 0,5 1
b + c +1+ a + c + 2 + a + b − 3 2(a + b + c) ⇒ = = = 2 a + b + c a + b + c a + b + c 2  1 a + b + c =  2 (2,0)  ⇒ b + c +1 = 2a 0,5 a + c + 2 = 2b   Ta tìm được 1 5 5 a ;b ;c − = = = (thỏa mãn (*)) 0,5 2 6 6
Khi đó thay vào biểu thức ta có 1 5 5 3 M = (2. +8. + 4. −13) = 8 − . Vậy M = -8 0,25 2 6 6 Xét 2 3 2 (a + b + 2)a +1 = a + b 2 ⇔ (b + 2)a = b −1 (1) 0,25
Nếu b= - 2 thay vào (1) ta có: 0=3 (vô lý) 2 2 Nếu b − − + ≠ 2 − ta có b 1 (b 4) 3 3 ⇔ a = = = b − 2 + (2) 0,5 b + 2 b + 2 b + 2
Do a, b là hai số nguyên nên b − 2;b + 2 là các số nguyên ⇒ 3(b + 2). 2 0,5 Vậy b + 2∈{ 1; − 1; 3 − ; } 3 ⇒ b∈{ 3 − ; 1; − 5 − ; } 1 (4,0) 1
Với b= -3 thay vào (2) ta có a = 8 − (thỏa mãn)
(2,0) Với b= -1 thay vào (2) ta có a =0(thỏa mãn)
Với b= -5 thay vào (2) ta có a = 8 − (thỏa mãn)
Với b= 1 thay vào (2) ta có 0,5 a = 0(thỏa mãn)
Vậy (a;b)=(-8;-3); (0;-1) ;(-8;-5);(0;1)là cặp số nguyên cần tìm 0,25 1 Điều kiện: y ≥ 3 − 2 2
x − 2 ≥ 0; y + 3 ≥ 0;(6xy + z ) ≥ 0 x ∀ , y,z Tacó 0,5 2 2
⇒ 2023 x − 2 + 2024 y + 3 + (6xy + z ) ≥ 0 x − 2 = 0 x = 2 2 Dấu bằng xảy ra  y 3 0  ⇔ + = ⇔ y = 3 − 0,5 (2,0)  2  2 6xy + z = 0 z = 36 x = 2 x = 2  ⇔  y = 3 − hoặc y = 3 − 0,5 z =   6 z = 6 − 
Đối chiếu điều kiện ta có: x=2; y=-3; z=6 hoặc x=2; y=-3; z=-6 0,5 Với x + ≥ 0 ta có x 7 5 K = = 1+ 0,5 x + 2 x + 2 Do 5 5 7
5 > 0; x + 2 ≥ 2 ⇒ 0 < ≤ ⇒ 1 < K ≤ 0,5 x + 2 2 2
Mặt khác K là số nguyên nên K = 2 hoặc K = 3 0,25 1 Nếu K =2 (2,0) x + 7 ⇒
= 2 ⇒ x + 7 = 2( x + 2) ⇒ x = 3 ⇒ x = 9 (tm x ≥ 0) 0,25 x + 2 Nếu K = 3 x + 7 1 1 ⇒
= 3 ⇒ x + 7 = 3( x + 2) ⇒ x = ⇒ x = (tm x ≥ 0) 0,25 x + 2 2 4
Vậy giá trị cần tìm của x là: x = 9; 1 x = 0,25 4 3
Do a, b, c là ba cạnh của tam giác nên a,b,c > 0 (4,0) a a b b c c ⇒ > ; > ; > 0,25
b + c a + b + c c + a a + b + c a + b a + b + c + + ⇒ a b c a b c P = + + > = 1. Vậy P >1 (1) 0,5 b + c c + a a + b a + b + c Ta có 2a a 2a(b + c) − a(a + b + c) a(b + c − a) − = = a + b + c b + c (a + b + c)(b + c) (a + b + c)(b + c) 2
Cũng do a, b, c là ba cạnh của tam giác nên a,b,c>0 và (2,0) b + c − a > 0 + − ⇒ a(b c a) > 0 vậy 2a a > 0,5 (a + b + c)(b + c) a + b + c b + c
Chứng minh tương tự ta có: 2b b > ; 2c c >
a + b + c c + a a + b + c a + b 0,5 Vậy 2a 2b 2c 2(a + b + c) + + = = 2 > P (2) a + b + c a + b + c a + b + c a + b + c
Từ (1) và (2) ⇒1< P < 2. Do đó P không thể nhận giá trị nguyên 0,25 2 Do tam giác ABC vuông ở B 0.5 ⇒  0 ABC = 90 . Theo giả thiết ⊥ ⇒  0 DE AM AED = 90
1a Mặt khác AD là phân giác của  ⇒ = BAM BAD EAD 0.25 (1,5) Xét AB  D và AE  Dcó  =  0 =  = 
ABD AED 90 ;BAD EAD;ADlà cạnh chung 0,75 ⇒ AB  D = AE
 D (Cạnh huyền - góc nhọn) ⇒AB=AE
Gọi P là hình chiếu của A trên đường thẳng CN ⇒ AP ⊥ CP mà ⊥ ⇒ ⇒  =  BC CP AP / /BC ACB PAC
Từ đó khẳng định được AB  C = C  PA ⇒ AP = BC = AB 0.5 4 1b ⇒AK=AB=BE
(6,0) (1,5) Chứng minh được  = ⇒  =  AEN APN EAN PAN 0,5 Ta có ⇒  =  +  1 =  DAN DAE NAE BAP 2 0,5 Mặt khác  0 = ⇒  0 BAP 90 DAN = 45
Qua A vẽ đường thẳng vuông góc với AN cắt đường thẳng BC ở Q. Chứng minh được P  AN = B  AQ ⇒ PN = BQ 0,25 1c  =
(1,0) Chứng minh được AQD AND ⇒ QD = DN 0,25 P
= DN + CD + CN = QD + DC + CN = (BD + CD) + (PN + CN) CDN 0,5 = BC + CP = a + a = 2a 2 (2,0)
Gọi H và K lần lượt là hình chiếu của B và C trên đường thẳng AM,
N là giao điểm AK với BC, ta có 1,0 3 1 1 1 S + S = BH.AM + CK.AM = AM(BH + CK) ABM ACM 2 2 2 1 1 ≤ AM(BN + CN) = AM.BC. 2 2 Vậy AM.BC ≥ 2(S + S ) (1) ABM ACM
Chứng minh tương tự ta có BM.AC ≥ 2(S + S ) (2) ABM BCM CM.AB ≥ 2(S + S ) (3) 0,5 BCM ACM Từ (1), (2), (3) ta có AM.BC + BM.AC + CM.AB ≥ 4(S + S + S ) = 4S = 4 0,5 ABM ACM BCM ABC Từ giả thiết ta có 2 2 2
5(3x + 54) = 5(2y + 4z ) (1) 2 2 2
3(5x + 74) = 3(3y + 7z ) (2) 0,5
Trừ từng vế (1) cho (2) ta được 2 2 48 = y − z
⇔ (y − z)(y + z) = 48 (*)
Do y, z là 2 số tự nhiên nên từ (*) suy ra y - z và y + z cùng tính chẵn
đồng thời y-z < y+z vậy ta có các trường hợp sau y − z = 2  − =  − = hoặc y z 4 hoặc y z 6    0,5 y + z = 24 y + z = 12 y + z = 8 Trường hợp 1:  − =  = Nếu y z 2 y 13  ⇔
từ đó tìm được x = 16. Vậy Q = 40 0,25 y z 24  + = z = 11 Trường hợp 2:  − =  = Nếu y z 4 y 8  ⇔ Từ đó ta tính được 2 x = 46 (loại) 0,25 y z 12  + = z = 4 Trường hợp 3: 5  − =  = (2,0) Nếu y z 6 y 7  ⇔
từ đó tính được x = 4. Vậy Q =12 0,25 y z 8  + = z = 1
Từ các trường hợp trên suy ra Q đạt giá trị nhỏ nhất bằng 12 khi x = 4; y = 7; z =1 0,25
Hướng dẫn chung:
- Trên đây là các bước giải bắt buộc và biểu điểm tương ứng, thí sinh phải
có lời giải chặt chẽ, chính xác mới công nhận cho điểm.
- Mọi cách giải khác mà đúng vẫn cho điểm tối đa.
- Chấm từng phần. Điểm bài thi là tổng các điểm thành phần không làm
tròn, tính đến 0,25. 4