Đề khảo sát HSG Toán 7 năm 2023 – 2024 trường THCS Quảng Chính – Thanh Hóa

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 7 đề khảo sát học sinh giỏi cấp huyện môn Toán 7 năm học 2023 – 2024 trường THCS Quảng Chính, huyện Quảng Xương, tỉnh Thanh Hóa; đề thi có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem!

34 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 7

Môn: Toán 7

Thông tin:

6 trang 6 tháng trước

Tác giả:

Profile M. Hậu
UBND HUYỆN QUẢNG XƯƠNG
TRƯỜNG THCS QUẢNG CHÍNH
ĐỀ KHẢO SÁT HỌC SINH GIỎI CẤP HUYỆN
NĂM HỌC 2023 - 2024
Môn: Toán 7
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
Bài 1.(4.0điểm)
1) Thực hiện phép tính:
a)
− −− −

=+ ++


59 3 48 3
A :( ) :( )
9 15 2 9 20 2
b)
−
=
−
84 5 4
3 4 9 13
6 .2 4 .18
B
27 .8 3 .2
2) Tính giá trị biểu thức
333
abc
Q
abc
++
=
với a, b, c thỏa mãn:
( )
2
32 43 0ab bc− +−≤
Bài 2. (4,0điểm)
1) Tìm x biết:
(
)
14 2
3, 2
35 5
x −+=− +
2)
Tìm
, , xyz
biết
3) Tìm x; y; z biết
= =
x yy z
;
4 75 6
và
+−=
x y z 39
4) Ba thửa ruộng hình chữ nhật A, B , C có cùng diện tích. Chiều rộng các thửa ruộng A;
B; C lần lượt tỉ lệ thuận với 4; 5; 6. Chiều dài của thửa ruộng A nhỏ hơn tổng chiều dài của
thửa ruộng B và C là 42 m. Tính chiều dài mỗi thửa ruộng?
Bài 3 (4,0điểm)
1) Chứng minh rằng :
17101723 baba +⇔+
(a, b ∈ Z )
2)Tìm cặp số (x, y) nguyên thỏa mãn:
( )
2
5 49x xy y− +=−−
Bài 4 (6,0 điểm)
1) Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D (D khác B, C). Trên tia đối của tia
CB, lấy điểm E sao cho CE = BD. Đường vuông góc với BC kẻ từ D cắt AB tại M. Đường vuông
góc với BC kẻ từ E cắt đường thẳng AC tại N, MN cắt BC tại I.
1. Chứng minh DM = EN.
2. Chứng minh IM = IN, BC < MN.
3. Gọi O là giao của đường phân giác góc A và đường thẳng vuông góc với MN tại I. Chứng
minh rằng
BMO CNO∆=∆
. Từ đó suy ra điểm O cố định.
2) Bác Long có một căn phòng hình hộp chữ
nhật có một cửa ra vào và một cửa sổ hình
vuông với các kích thước như hình bên. Hỏi
bác Long cần trả bao nhiêu chi phí để sơn bốn
bức tường xung quanh của căn phòng này
(không sơn cửa)? Biết rằng để sơn mỗi mét
vuông tốn 30 nghìn đồng.
Bài 5.(1,0điểm)
Cho
,,abc
là độ dài ba cạnh của tam giác. Chứng minh rằng:
( )
222
2ab bc ca a b c ab bc ca++≤++< ++
…….Hết…….
Họ và tên thí sinh……………………………………. Số báo danh…………………
UBND HUYỆN QUẢNG XƯƠNG
TRƯỜNG THCS QUẢNG CHÍNH
HƯỚNG DẪN CHẤM ĐỀ KHẢO SÁT HỌC SINH GIỎI
NĂM HỌC 2023 - 2024
MÔN TOÁN 7
(Gồm 05 trang)
HƯỚNG DẪN CHẤM
Điểm
Bài 1.(4.0điểm)
1) Thực hiện phép tính:
a)
− −− −

=+ ++


59 3 48 3
A :( ) :( )
9 15 2 9 20 2
b)
−
=
−
84 5 4
3 4 9 13
6 .2 4 .18
B
27 .8 3 .2
2) Tính giá trị
333
abc
Q
abc
++
=
với a, b, c thỏa mãn:
( )
2
32 43 0ab bc− +−≤
1(a)
1,0đ
− −− −

=+ ++


53 2 42 2
A .( ) .( )
95 3 95 3
0,25
−− −

= ++ +


2 53 42
A( )
3 9595
0,25

− −−

= + ++




2 5 4 32
A ( ). ( )
3 9 9 55
0,25
[ ]
−−
= −+ = =
22
A ( ). ( 1) 1 .0 0
33
0,25
1(b)
1,0đ
−− −
= = =
− −−
84 5 4 8 4 25 24 884 1048
3 4 9 13 3 3 3 4 9 13 9 12 9 13
6 .2 4 .18 (2.3) .2 (2 ) (2.3 ) 2 .3 .2 2 .2 .3
B
27 .8 3 .2 (3 ) .(2 ) 3 .2 3 .2 3 .2
0,25
−
=
−
12 8 14 8
9 12 9 13
2 .3 2 .3
B
3 .2 3 .2
0,25
−−
= =
−−
12 8 2 12 8
9 12 9 12
2 .3 (1 2 ) 2 .3 .( 3)
B
3 .2 (1 2) 3 .2 .( 1)
0,25
Rút gọn đúng được kết quả B = 1
0,25
2
2,0đ
Vì
( )
2
3 2 0; 4 3 0ab bc− ≥ −≥
nên để
( )
2
32 43 0ab bc− +−≤
thì:
( )
2
32 0
32
43
234
43 0
ab
ab
abc
bc
bc
−=
=
⇒ ⇒==

=
−=
1,0
Đặt
2;3;4
234
abc
k a kb kc k===⇒= = =
Thay vào Q ta có:
( ) ( ) ( )
( )
333
33 3 3
333
3
234
234
33
2 .3 .4 24 8
k
kkk
abc
Q
abc k k k k
++
++
++
= = = =
1,0
Bài 2. (4,0điểm)
1) Tìm x biết:
(
)
14 2
3, 2
35 5
x
−+=− +
2)
Tìm
, , xyz
biết
( )

− + − + +−≤


2022
2020
2
2x 3 y x y z 0
5
3) Tìm x; y; z biết
= =
x yy z
;
4 75 6
và
+−=x y z 39
4) Ba thửa ruộng hình chữ nhật A, B , C có cùng diện tích. Chiều rộng các thửa
ruộng A; B; C lần lượt tỉ lệ thuận với 4; 5; 6. Chiều dài của thửa ruộng A nhỏ hơn tổng
chiều dài của thửa ruộng B và C là 42 m. Tính chiều dài mỗi thửa ruộng?
1(a)
1,0đ
( )
17
2
33
5
1
2
3
3
14 2 14 162
3, 2
35 5 35 5 5
1 4 14
355
1
2
3
xx
x
x
xx
x
x
−= =
=−
−=−
−
−+=− + ⇔−+= +
⇔−+=
⇔−=⇔
⇔
0,25
0,25
0,5
1(b)
1,0đ
Vì
( )

− ≥ − ≥ +− ≥


2022
2020
2
2x 3 0; y 0; x y z 0
5
với mọi
,,xyz
Nên :
( )

− + − + +− ≥


2022
2020
2
2x 3 y x y z 0
5
với mọi
,,xyz
Do đó (1) xảy ra khi và chỉ khi
( )
−=

−=


+− =
2020
2022
2x 3 0
2
y0
5
xyz 0
=
⇔=
=
3
x
2
2
y
5
19
z
10
0,25
0,75
2)
1,0đ
Vì
= =⇒= =
x yy z x y y z
;;
4 7 5 6 20 35 35 42
0,25
⇒==
xyz
20 35 42
0,25
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
+−
= = = = =
+−
x y z x y z 39
3
20 35 42 20 35 42 13
0,25
Suy ra được: x = 60; y = 105; z =126
0,25
3)
1,0đ
Gọi chiều rộng các thửa ruộng hình chữ nhật A; B ; C lần lượt là: a; b; c
(m)
chiều dài các thửa ruộng hình chữ nhật A; B ; C lần lượt là: x; y; z (m)
( Điều kiện: 0 < a < x; 0 < b < y; 0 < c < z)
Chiều rộng các thửa ruộng A; B; C lần lượt tỉ lệ thuận với 4; 5; 6 nên
0,25
= =
abc
456
Vì chiều dài thửa ruộng A nhỏ hơn tổng chiều dài thửa ruộng B và C là
42m nên ta có:
+−=y z x 42
Vì ba thửa ruộng cùng diện tích nên: ax = by = cz
= = ⇒==
a bc
4.x. 5.y. 6.z. 4x 5y 6z
4 56
0,25
Suy ra:
==⇒ ==⇒==
4x 5y 6z x y z
4x 5y 6z
60 60 60 15 12 10
0,25
Áp dụng tính chất dãy tỉ số bằng nhau suy ra x = 90; y = 72; z = 60
Vậy chiều dài của các thửa ruộng A; B; C lần lượt là: 90 m; 72m; 60m
0,25
1) Chứng minh rằng :
17101723 baba +⇔+
(a, b ∈ Z )
2)Tìm cặp số (x, y) nguyên thỏa mãn:
( )
2
5 49x xy y− +=−−
1
2,0đ
* 3a + 2b
17
⇒
10a + b
17
Ta có : 3a + 2b
17
⇒
9 ( 3a + 2b )
17
⇒
27a + 18 b
17
⇒
( 17a + 17b) + ( 10a + b )
17
⇒
10a + b
17
1,0
* 10a + b
17
⇒
3a + 2b
17
Ta có : 10a + b
17
⇒
2 ( 10a + b )
17
⇒
20a + 2b
17
⇒
17a + 3a + 2b
17
⇒
3a + 2b
17
1,0
2
2,0đ
Ta có:
( )
2
5 49x xy y− +=−−
( )
2
2
59 4
59 4
x x xy y
x x yx
− += −
⇒ − += −
0,25
( ) ( )
{ } { }
2
59 4
4 45454
4 1; 5 1;3;5;9
⇒−+ −
⇒ −−−+ −⇒ −
⇒ − ∈± ± ⇒ ∈−

xxx
xx x x x
xx
0,25
0,5
Với
1x = −
thì
3y = −
Với
3x =
thì
3
y = −
Với
5x =
thì
9y
=
Với
9x =
thì
9
y
=
Vậy
( )
( ) ( )
( ) (
)
{ }
, 1; 3,3; 3,5;9,9;9xy∈−− −
1,0
Bài 4 (6,0 điểm)
1) Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D (D khác B, C). Trên tia đối
của tia CB, lấy điểm E sao cho CE = BD. Đường vuông góc với BC kẻ từ D cắt AB
tại M. Đường vuông góc với BC kẻ từ E cắt đường thẳng AC tại N, MN cắt BC tại I.
1. Chứng minh DM = EN.
2. Chứng minh IM = IN, BC < MN.
3. Gọi O là giao của đường phân giác góc A và đường thẳng vuông góc với MN tại
I. Chứng minh rằng
BMO CNO∆=∆
. Từ đó suy ra điểm O cố định.
2) Bác Long có một căn phòng hình hộp
chữ nhật có một cửa ra vào và một cửa sổ
hình vuông với các kích thước như hình
bên. Hỏi bác Long cần trả bao nhiêu chi
phí để sơn bốn bức tường xung quanh của
căn phòng này (không sơn cửa)? Biết rằng
để sơn mỗi mét vuông tốn 30 nghìn đồng.
1
5,0đ
1.
M
D
I
C
E
N
O
B
A
Tam giác ABC cân tại A nên
; ;ABC ACB NCE ACB= =
(đối đỉnh)
Do đó:
( .. )MDB NEC g c g DM EN∆ =∆ ⇒=
.
0,75
0,75
2. Ta có
( .. )MDI NEI g c g MI NI∆ =∆ ⇒=
Vì BD = CE nên BC = DE .
Lại có DI < MI, IE < IN nên DE = DI + IE < MI + IN = MN
Suy ra BC < MN.
0,5
0,75
0,25
3) Ta chứng minh được:
(..) , .ABO ACO c g c OC OB ABO ACO∆ =∆ ⇒= =
(..) .MIO NIO c g c OM ON∆=∆ ⇒=
Ta lại có: BM = CN. Do đó
(..)BMO CNO c c c∆=∆
MBO NCO⇒=
, Mà:
MBO ACO
=
suy ra
NCO ACO=
, mà đây là hai góc
kề bù nên CO
⊥
AN.
Vì tam giác ABC cho trước, O là giao của phân giác góc A và đường
vuông góc với AC tại C nên O cố dịnh.
0,75
0,5
0,5
0,25
2
Diện tích xung quanh của căn phòng là:
S
xq
= 2. (5 + 6) . 3 = 66 (m
2
).
0,25
1,0đ
Diện tích phần cửa lớn và cửa sổ là:
1,2 . 2 + 1 . 1 = 3,4 (m
2
)
0,25
Diện tích phần cần sơn là:
66 – 3,4 = 62,6 (m
2
).
0,25
Tổng chi phí cần để sơn là:
62,6. 30 000 = 1 878 000 (đồng).
Vậy bác Long cần 1 878 000 đồng để sơn bốn bức tường xung quanh
của căn phòng này.
0,25
Bài 5 (2,0 điểm) Cho
,,abc
là độ dài ba cạnh của tam giác. Chứng minh rằng:
( )
222
2ab bc ca a b c ab bc ca++≤++< ++
2,0đ
Ta có:
( )
2
2 2 22
02 0 2
a b a ab b a b ab− ≥⇒− +≥⇔+≥
Tương tự ta cũng có:
22 22
2; 2
b c bc c a ac
+≥ +≥
(
)
( )
222
222
22
(1)
a b c ab ac bc
ab ac bc a b c
⇒ ++ ≥ ++
⇒++≤++
Dấu
""=
xảy ra
a b c ABC⇔ = = ⇔∆
đều
0,5
0,25
0,25
Áp dụng bất đẳng thức tam giác, ta có:
( )
2
2 222
2
2 (2)
a b c ac bc c
a c b ab bc b a b c ab ac bc
b c a ab ac a
+>⇒ + >
+>⇒ + > ⇒ + + < + +
+>⇒ + >
Từ (1) và (2) ta có:
( )
222
2ab ac bc a b c ab ac bc++≤++< ++
0,5
0,5
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

UBND HUYỆN QUẢNG XƯƠNG
ĐỀ KHẢO SÁT HỌC SINH GIỎI CẤP HUYỆN
TRƯỜNG THCS QUẢNG CHÍNH NĂM HỌC 2023 - 2024 Môn: Toán 7
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
Bài 1.(4.0điểm) 1) Thực hiện phép tính: a)  −5 9  −3  −4 8  − = + : ( ) + + 3 A     : ( )  9 15  2  9 20  2 8 4 5 4 b) 6 .2 − = 4 .18 B 3 4 27 .8 − 9 13 3 .2 3 3 3
2) Tính giá trị biểu thức a + b + c Q =
với a, b, c thỏa mãn:( a − b)2 3 2
+ 4b − 3c ≤ 0 abc
Bài 2. (4,0điểm) 1 4 2
1) Tìm x biết: x − + = ( 3, − 2) + 3 5 5 2022
2) Tìm x, y, z biết (2x 3)2020  2  − + y − + x + y − z ≤   0  5 
3) Tìm x; y; z biết x = y y = z ; và x + y − z = 39 4 7 5 6
4) Ba thửa ruộng hình chữ nhật A, B , C có cùng diện tích. Chiều rộng các thửa ruộng A;
B; C lần lượt tỉ lệ thuận với 4; 5; 6. Chiều dài của thửa ruộng A nhỏ hơn tổng chiều dài của
thửa ruộng B và C là 42 m. Tính chiều dài mỗi thửa ruộng?
Bài 3 (4,0điểm)
1) Chứng minh rằng : 3a + 2b 17 ⇔ 10a + b 17 (a, b ∈ Z )
2)Tìm cặp số (x, y) nguyên thỏa mãn: 2
x − x( y + 5) = 4 − y − 9
Bài 4 (6,0 điểm)
1) Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D (D khác B, C). Trên tia đối của tia
CB, lấy điểm E sao cho CE = BD. Đường vuông góc với BC kẻ từ D cắt AB tại M. Đường vuông
góc với BC kẻ từ E cắt đường thẳng AC tại N, MN cắt BC tại I.
1. Chứng minh DM = EN.
2. Chứng minh IM = IN, BC < MN.
3. Gọi O là giao của đường phân giác góc A và đường thẳng vuông góc với MN tại I. Chứng minh rằng B ∆ MO = CNO ∆
. Từ đó suy ra điểm O cố định.
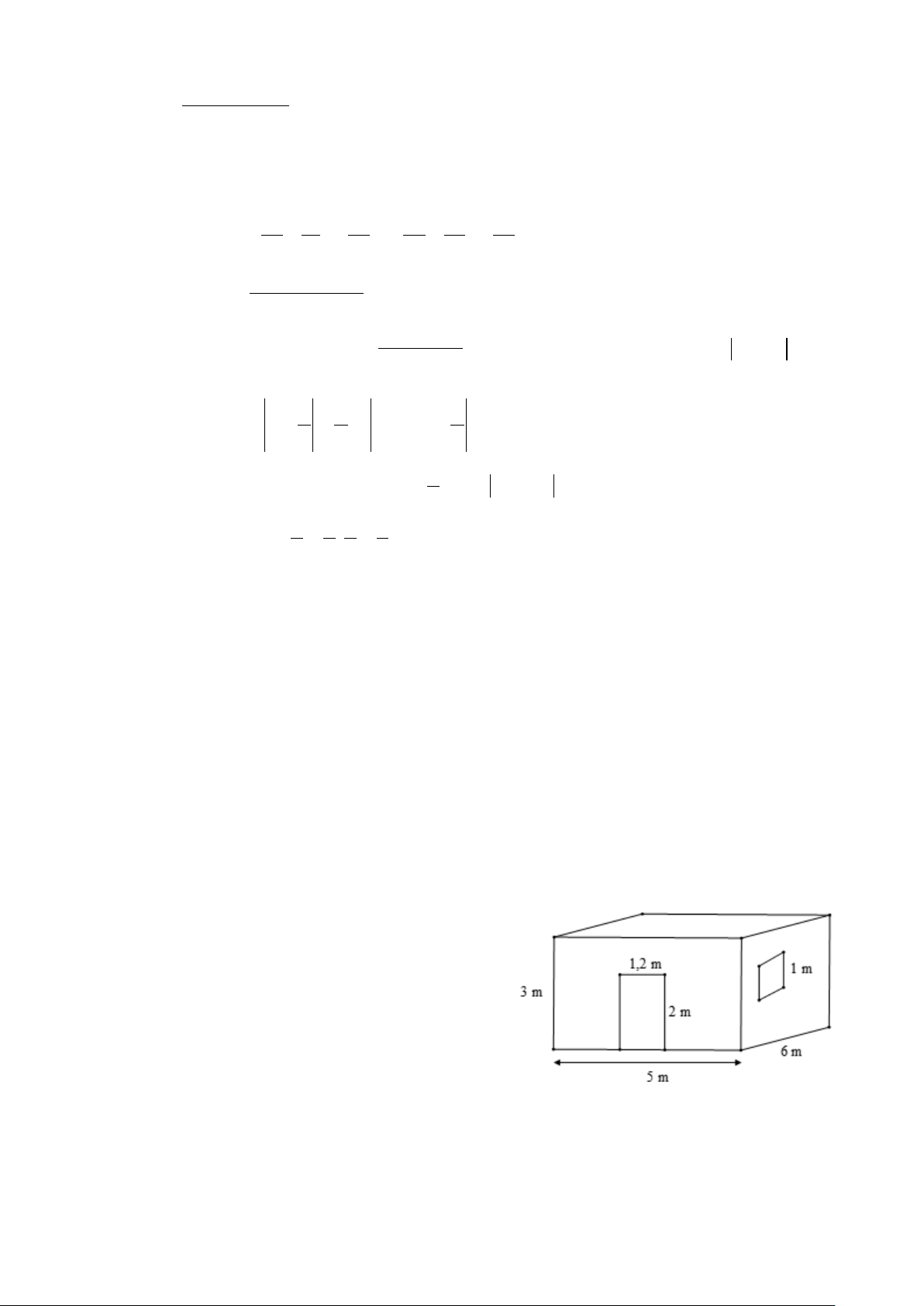
2) Bác Long có một căn phòng hình hộp chữ
nhật có một cửa ra vào và một cửa sổ hình
vuông với các kích thước như hình bên. Hỏi
bác Long cần trả bao nhiêu chi phí để sơn bốn
bức tường xung quanh của căn phòng này
(không sơn cửa)? Biết rằng để sơn mỗi mét
vuông tốn 30 nghìn đồng.
Bài 5.(1,0điểm) Cho a, ,
b clà độ dài ba cạnh của tam giác. Chứng minh rằng: 2 2 2
ab + bc + ca ≤ a + b + c < 2(ab + bc + ca)
…….Hết…….
Họ và tên thí sinh……………………………………. Số báo danh…………………
UBND HUYỆN QUẢNG XƯƠNG
HƯỚNG DẪN CHẤM ĐỀ KHẢO SÁT HỌC SINH GIỎI
TRƯỜNG THCS QUẢNG CHÍNH NĂM HỌC 2023 - 2024 MÔN TOÁN 7
(Gồm 05 trang) HƯỚNG DẪN CHẤM Điểm
Bài 1.(4.0điểm) 1) Thực hiện phép tính: a)  −5 9  −3  −4 8  − = + : ( ) + + 3 A     : ( )  9 15  2  9 20  2 8 4 5 4 b) 6 .2 − = 4 .18 B 3 4 27 .8 − 9 13 3 .2 3 3 3 2) Tính giá trị a + b + c Q =
với a, b, c thỏa mãn: ( a − b)2 3 2
+ 4b − 3c ≤ 0 abc  −5 3  −2  −4 2  − = + .( ) + + 2 A    .( )  9 5  3  9 5  3 0,25 −2  −5 3 −4 2  1(a) A = ( ) + + +   0,25 3  9 5 9 5  1,0đ −2  −5 −4  3 2  A = ( ). + + ( +   ) 0,25 3  9 9  5 5  −2 [ ] − = − + = 2 A ( ). ( 1) 1 .0 = 0 0,25 3 3 8 4 6 .2 − 5 4 8 4 4 .18 (2.3) .2 − 2 5 2 4 8 8 4 (2 ) (2.3 ) 2 .3 .2 − 10 4 8 2 .2 .3 B = = = 0,25 3 4 27 .8 − 9 13 3 3 3 4 3 .2 (3 ) .(2 ) − 9 13 9 12 3 .2 3 .2 − 9 13 3 .2 12 8 14 8 2 .3 − = 2 .3 B 0,25 1(b) 9 12 3 .2 − 9 13 3 .2 12 8 2 .3 (1 − 2 12 8 2 ) 2 .3 .(−3) 1,0đ B = = 0,25 9 12 9 12 3 .2 (1 − 2) 3 .2 .(−1)
Rút gọn đúng được kết quả B = 1 0,25 2 Vì ( a − b)2 3 2
≥ 0; 4b − 3c ≥ 0 nên để ( a − b)2 3 2
+ 4b − 3c ≤ 0 thì: 2,0đ (  a − b)2 3 2 = 0 3  a = 2b a b c  ⇒  ⇒ = = 1,0
 4b − 3c = 0 4b = 3c 2 3 4  Đặt a b c
= = = k ⇒ a = 2k;b = 3k;c = 4k Thay vào Q ta có: 2 3 4 1,0 a + b + c
(2k)3 +(3k)3 +(4k)3 3 k ( 3 3 3 3 3 3 2 + 3 + 4 ) 33 Q = = = = 3 abc 2k.3k.4k 24k 8
Bài 2. (4,0điểm) 1) Tìm x biết: 1 4 x − + = (− ) 2 3,2 + 3 5 5 2022
2) Tìm x, y, z biết (2x 3)2020  2  − + y − + x + y − z ≤   0  5 
3) Tìm x; y; z biết x = y y = z ; và x + y − z = 39 4 7 5 6
4) Ba thửa ruộng hình chữ nhật A, B , C có cùng diện tích. Chiều rộng các thửa
ruộng A; B; C lần lượt tỉ lệ thuận với 4; 5; 6. Chiều dài của thửa ruộng A nhỏ hơn tổng
chiều dài của thửa ruộng B và C là 42 m. Tính chiều dài mỗi thửa ruộng? 1 4 x − + = (− ) 2 1 4 1 − 6 2 3,2 + ⇔ x − + = + 3 5 5 3 5 5 5 0,25 1 4 14
1(a) ⇔ x − + = 3 5 5 0,25 1,0đ  1  7 x− =2 1  3 x= ⇔  3 ⇔ x − = 2 ⇔  1  5 3 0,5 x− = 2  3 − x=−  3 2022 Vì (2x 3)2020  2  − ≥ 0; y − ≥ 0; x + y − z ≥  
0 với mọi x, y, z  5  2022 Nên : ( 0,25 2x 3)2020  2  − + y − + x + y − z ≥  
0 với mọi x, y, z  5  1(b) 1,0đ (  3 2x − 3)2020 = 0 x =   2 0,75  2022 
Do đó (1) xảy ra khi và chỉ khi  2   2  y − =   0 ⇔ y =   5   5  x + y − z =  19  0  z =  10 x y y z x y y z Vì = ; = ⇒ = ; = 0,25 4 7 5 6 20 35 35 42 2) x y z 1,0đ ⇒ = = 0,25 20 35 42
Áp dụng tính chất dãy tỉ số bằng nhau ta có: x y z x + y − = = = z = 39 = 0,25 3 20 35 42 20 + 35 − 42 13
Suy ra được: x = 60; y = 105; z =126 0,25
Gọi chiều rộng các thửa ruộng hình chữ nhật A; B ; C lần lượt là: a; b; c 3) (m)
1,0đ chiều dài các thửa ruộng hình chữ nhật A; B ; C lần lượt là: x; y; z (m) 0,25
( Điều kiện: 0 < a < x; 0 < b < y; 0 < c < z)
Chiều rộng các thửa ruộng A; B; C lần lượt tỉ lệ thuận với 4; 5; 6 nên a = b = c 4 5 6
Vì chiều dài thửa ruộng A nhỏ hơn tổng chiều dài thửa ruộng B và C là
42m nên ta có: y + z − x = 42
Vì ba thửa ruộng cùng diện tích nên: ax = by = cz a = b = c 4.x. 5.y. 6.z. ⇒ 4x = 5y = 6z 0,25 4 5 6
Suy ra: = = ⇒ 4x = 5y = 6z ⇒ x = y = z 4x 5y 6z 0,25 60 60 60 15 12 10
Áp dụng tính chất dãy tỉ số bằng nhau suy ra x = 90; y = 72; z = 60
Vậy chiều dài của các thửa ruộng A; B; C lần lượt là: 90 m; 72m; 60m 0,25
1) Chứng minh rằng : 3a + 2b 17 ⇔ 10a + b 17 (a, b ∈ Z )
2)Tìm cặp số (x, y) nguyên thỏa mãn: 2
x − x( y + 5) = 4 − y − 9
* 3a + 2b  17 ⇒ 10a + b  17 Ta có : 3a + 2b  17 ⇒ 9 ( 3a + 2b )  17 1,0 ⇒ 27a + 18 b  17
⇒( 17a + 17b) + ( 10a + b )  17 1 ⇒ 10a + b  17
2,0đ * 10a + b  17 ⇒ 3a + 2b  17 Ta có : 10a + b  17 ⇒ 2 ( 10a + b )  17 1,0 ⇒ 20a + 2b  17 ⇒ 17a + 3a + 2b  17 ⇒ 3a + 2b  17 Ta có: 2
x − x( y + 5) = 4 − y − 9 2
x − 5x + 9 = xy − 4y 2
⇒ x − 5x + 9 = y (x − 4) 0,25 2
⇒ x − 5x + 9x − 4
⇒ x(x − 4) − (x − 4) + 5x − 4 ⇒ 5x − 4 0,25 2
2,0đ ⇒ x − 4∈{ 1 ± ;± } 5 ⇒ x∈{ 1 − ;3;5; } 9 0,5 Với x = 1 − thì y = 3 −
Với x = 3 thì y = 3 −
Với x = 5 thì y = 9
Với x = 9 thì y = 9
Vậy (x, y)∈ ({ 1 − ; 3 − ),(3; 3 − ),(5;9),(9;9)} 1,0
Bài 4 (6,0 điểm)
1) Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D (D khác B, C). Trên tia đối
của tia CB, lấy điểm E sao cho CE = BD. Đường vuông góc với BC kẻ từ D cắt AB
tại M. Đường vuông góc với BC kẻ từ E cắt đường thẳng AC tại N, MN cắt BC tại I.
1. Chứng minh DM = EN.
2. Chứng minh IM = IN, BC < MN.
3. Gọi O là giao của đường phân giác góc A và đường thẳng vuông góc với MN tại
I. Chứng minh rằng B ∆ MO = CNO ∆
. Từ đó suy ra điểm O cố định.
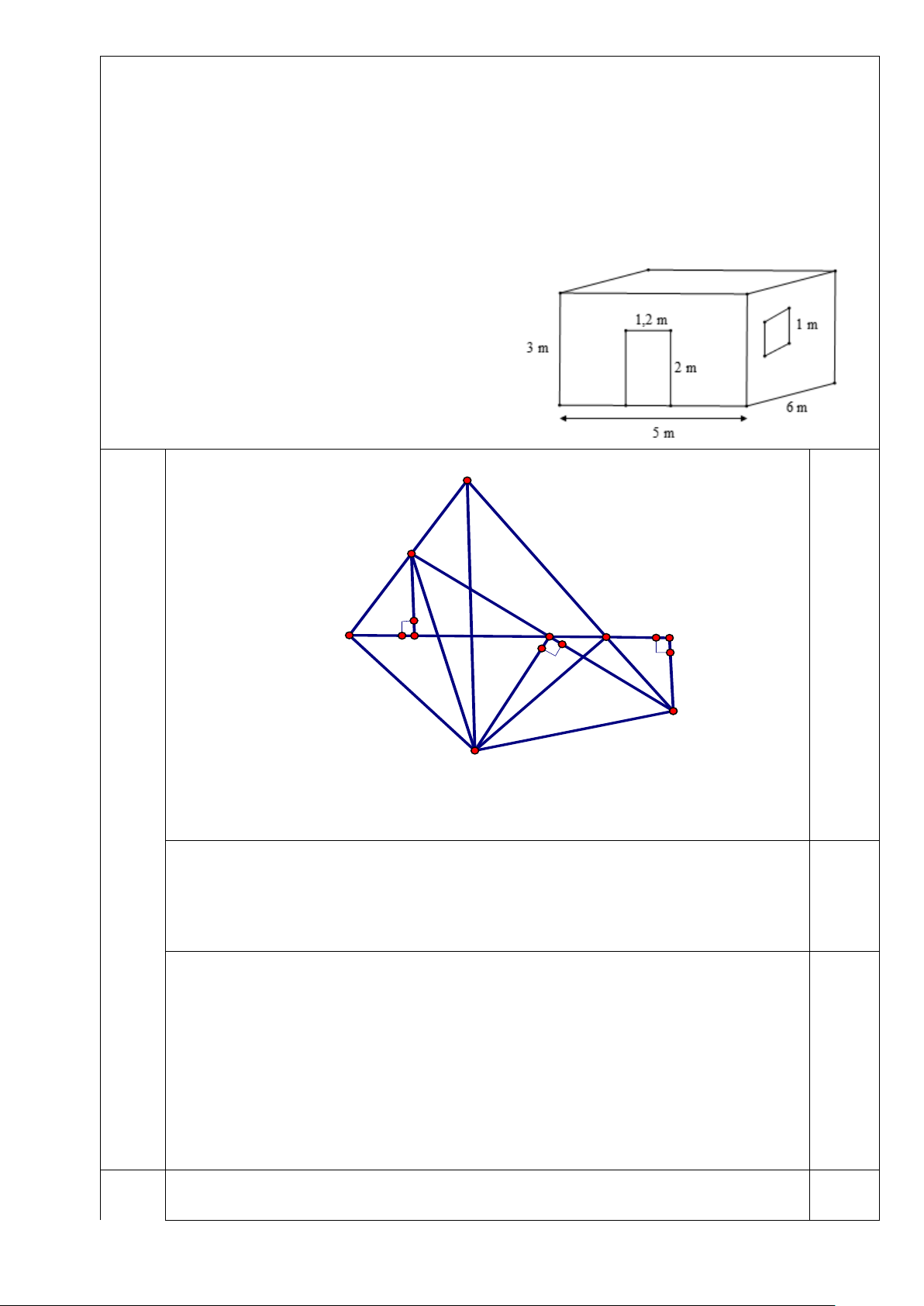
2) Bác Long có một căn phòng hình hộp
chữ nhật có một cửa ra vào và một cửa sổ
hình vuông với các kích thước như hình
bên. Hỏi bác Long cần trả bao nhiêu chi
phí để sơn bốn bức tường xung quanh của
căn phòng này (không sơn cửa)? Biết rằng
để sơn mỗi mét vuông tốn 30 nghìn đồng. 1 A 5,0đ M B I C E D N 1. O
Tam giác ABC cân tại A nên  =   =  ABC AC ; B NCE AC ; B (đối đỉnh) 0,75 Do đó: M ∆ DB = N ∆ EC(g. .
c g) ⇒ DM = EN . 0,75 2. Ta có MD ∆ I = N ∆ EI(g. .
c g) ⇒ MI = NI 0,5 Vì BD = CE nên BC = DE .
Lại có DI < MI, IE < IN nên DE = DI + IE < MI + IN = MN 0,75 Suy ra BC < MN. 0,25 3) Ta chứng minh được: ∆ = ∆ ⇒ =  =  ABO ACO( . c g.c) OC OB, ABO AC . O MIO ∆ = N ∆ IO( .
c g.c) ⇒ OM = ON. 0,75
Ta lại có: BM = CN. Do đó B ∆ MO = CNO ∆ ( .c .cc) 0,5 ⇒  = 
MBO NCO , Mà:  = 
MBO ACO suy ra  = 
NCO ACO , mà đây là hai góc kề bù nên CO ⊥ AN. 0,5
Vì tam giác ABC cho trước, O là giao của phân giác góc A và đường
vuông góc với AC tại C nên O cố dịnh. 0,25 2
Diện tích xung quanh của căn phòng là:
Sxq = 2. (5 + 6) . 3 = 66 (m2). 0,25
1,0đ Diện tích phần cửa lớn và cửa sổ là: 1,2 . 2 + 1 . 1 = 3,4 (m2) 0,25
Diện tích phần cần sơn là: 66 – 3,4 = 62,6 (m2). 0,25
Tổng chi phí cần để sơn là:
62,6. 30 000 = 1 878 000 (đồng).
Vậy bác Long cần 1 878 000 đồng để sơn bốn bức tường xung quanh 0,25 của căn phòng này.
Bài 5 (2,0 điểm) Cho a, ,
b clà độ dài ba cạnh của tam giác. Chứng minh rằng: 2 2 2
ab + bc + ca ≤ a + b + c < 2(ab + bc + ca)
Ta có: (a − b)2 2 2 2 2
≥ 0 ⇒ a − 2ab + b ≥ 0 ⇔ a + b ≥ 2ab Tương tự ta cũng có: 2 2 2 2 b + c ≥ 2 ; bc
c + a ≥ 2ac 0,5 2 2 2
⇒ 2(a + b + c ) ≥ 2(ab + ac + bc) 2,0đ 2 2 2
⇒ ab + ac + bc ≤ a + b + c (1) 0,25
Dấu " = "xảy ra ⇔ a = b = c ⇔ A ∆ BC đều 0,25
Áp dụng bất đẳng thức tam giác, ta có: 2
a + b > c ⇒ ac + bc > c   2 2 2 2
a + c > b ⇒ ab + bc > b  ⇒ a + b + c < 2(ab + ac + bc) (2) 0,5 2 b c a ab ac a  + > ⇒ + >  Từ (1) và (2) ta có: 2 2 2
ab + ac + bc ≤ a + b + c < 2(ab + ac + bc) 0,5