Đề khảo sát lần 1 Toán 9 năm 2023 – 2024 phòng GD&ĐT Cẩm Giàng – Hải Dương
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp đề khảo sát chất lượng học sinh môn Toán 9 năm học 2023 – 2024 phòng GD&ĐT Cẩm Giàng – Hải Dương giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.
Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG LẦN 1 CẨM GIÀNG NĂM HỌC 2023 - 2024 MÔN: TOÁN - LỚP 9
Thời gian làm bài: 120 phút
(Đề bài gồm 01 trang)
Câu 1 (2,0 điểm). Tính giá trị các biểu thức sau: a) 81 49 16 b) 3 5 3 5 c) 2 7 4 7 d) 8 18 2: 2
Câu 2 (2,0 điểm). Giải các phương trình sau:
a) 2x 3 6 x b) 2
x 6x 9 5 0 2 x 2 x c) 2 x 3 3 x x 9 Câu 3 (2,0 điểm). 3 x 1 x 3 x 8
a) Rút gọn biểu thức A với x 0 ; x 4 x 2 x 2 x 4
b) Một người đi từ A đến B với vận tốc 30 km/h. Khi về người đó đi đường khác
dài hơn đường cũ 30 km nhưng với vận tốc lớn hơn vận tốc lúc đi là 20 km/h. Tính
quãng đường lúc đi biết thời gian đi nhiều hơn thời gian về là 1 giờ. Câu 4 (3,0 điểm).
Cho tam giác ABC vuông tại A có AB AC , đường cao AH (H BC) .
a) Cho BH 1c ;
m HC 4cm , tính AH; AC
b) Gọi M, N là hình chiếu của H trên AB, AC; K là giao của AH và MN. Chứng 1 4 4
minh: ANM và ABC đồng dạng và 2 2 2 MK AB AC
c) Phân giác góc ABC cắt cạnh AC tại E. Đường thẳng qua C vuông góc với
đường thẳng BE cắt BE tại D và cắt tia BA tại I. Chứng minh: 2 I . A AB 2A . D ID AI Câu 5 (1,0 điểm). Cho các số thực dương 1 1 1 ,
x y, z thỏa mãn 2023. x y y z z Tìm giá trị nhỏ x 2 2 2 2 2 2 y 3x z 3y x 3z
nhất của biểu thức P . xy yz zx
-------------------- HẾT --------------------
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM CẨM GIÀNG
ĐỀ KHẢO SÁT CHẤT LƯỢNG LẦN 1 NĂM HỌC 2023-2024 MÔN : TOÁN 9
Hướng dẫn chấm gồm 04 trang Ghi chú:
- Học sinh làm cách khác đúng cho điểm tối đa. Điểm tổng toàn bài không làm tròn.
- Học sinh phải làm đủ nội dung của ô thì mới được điểm. Nếu học sinh làm chưa tới
dòng cuối nội dung của ô thì không được điểm của ô đó (trừ khi có hướng dẫn riêng).
- Ở câu hình, nếu học sinh vẽ hình không chính xác thì không cho điểm hình nhưng
vẫn chấm điểm, học sinh vẽ sai hình thì không chấm điểm. Câu Phần Nội dung Biểu điểm 1a
81 49 16 9 7 4 12 0,5 3 53 5 1b = 32 –( 5 )2 0,25
= 9 – 5 = 4 ( HS chỉ làm dòng này thì vẫn được 0,5) 0,25 1 2 7 4 7 = 7 4 7 0,25 1c 4 7
7 = 4 (HS chỉ làm dòng này thì vẫn được 0,5) 0,25
8 18 2: 2= 2 2 3 2 2: 2 1d 0,25 4 2 : 2 4 0,25 2
2x 3 6 x 3x 9 0,25 2a x 3
Vậy phương trình có nghiệm x = 3 0,25 2
x 6x 9 5 0 2
x 6x 9 5 2
(x 3) 5 x 3 5 0,25 x 3 5 x 8 x 3 5 x 2 2b
Vậy phương trình đã cho có nghiệm x = - 2; x = 8
(HS giải thiếu 1 TH cho 0,25 điểm 0,5
HS không ra giá trị tuyệt đối trừ 0,25 điểm
Học sinh đặt ĐK sai dẫn tới loại nghiệm thì trừ 0,25 điểm) 2 x 2 x
(ĐKXĐ: x 3; x 3 ) 2 x 3 3 x x 9
x x x 2 3 2 3 x
(HS có thể bỏ qua dòng này) 0, 25
x x 0 3 3 2 2 2c
x 3x 2x 6 x 0 5 x 6 0 0,25 6 x (thỏa mãn) 5 0,25
Vậy phương trình có nghiệm là 6 x 5
HS mắc một trong các lỗi không đặt ĐK, không xét thỏa mãn
ĐK, dùng dấu “” khi khử mẫu hoặc tất cả thì bị trừ 0,25 điểm. 3 3 x 1 x 3 x 8 A x 2 x 2 x 4 0,25 3x 6 x
x 2 x 2 x 3 x 6 x 8 x 2 x 2 3x 6 x 0,25 x 2 x 2 3a 3 x x 2 x 2 x 2 0,25
HS không tách để rút gọn không chấm điểm ô này nhưng chấm ô tiếp theo. 3 x Vậy A 3 x với x 0 ; x 4 0,25 x 2 x 2
Gọi quãng đường lúc đi là x (km) (x > 0) 0,25
Quãng đường lúc về là x + 30 (km)
Thời gian lúc đi là x (h) 30
Thời gian lúc về là x 30 (h) 0,25 50 3b
Theo bài ra ta có phương trình x x 30 - = 1 30 50
5x 3x 90 150 2x 240 x 120 0,25
x = 120 thỏa mãn điều kiện.
Vậy quãng đường lúc đi là 120 km.
Trong các yếu tố ĐK, đối chiếu ĐK, đơn vị nếu thiếu từ 2 lỗi 0,25
trở lên thì trừ 0,25đ
Nếu HS chỉ chọn ẩn và nêu phương trình ngay thì trừ 0,25đ 4 4.1 0,25
Vẽ hình đúng yêu cầu chung của đề bài Xét ABC
vuông tại A có AH là đường cao 2
AH HC.HB 0,25
Thay số ta được AH = 2cm 0,25 Mà 2
AC HC.BC 4.1a 2 AC 4.5 20
AC 2 5 cm (AC 4,472c ) m 0,25
- Một trong 2 đoạn AH, AC chỉ tính đúng được 1 đoạn thì chấm 0,5 điểm
- HS ra kết quả AC 20 cm cho điểm tối đa Xét ABH
vuông tại H có HM là đường cao AH2 = AM.AB (1) 0,25 Xét A
CH vuông tại H có HN là đường cao AH2 = AN.AC (2) AM AC Từ (1) và (2) AM.AB = AN.AC AN AB Mà BAC chung ANM ABC (c.g.c) 0,25
(Học sinh có thể chứng minh hai tam giác đồng dạng theo
trường hợp góc – góc trong đó chứng minh đúng 2 góc nhọn
bằng nhau được 0,25 điểm) 4.1b Tứ giác AMHN có AMH MAN ANH 90
Nên AMHN là hình chữ nhật, do K là giao 2 đường chéo 0,25 AH = MN = 2MK Xét ABC
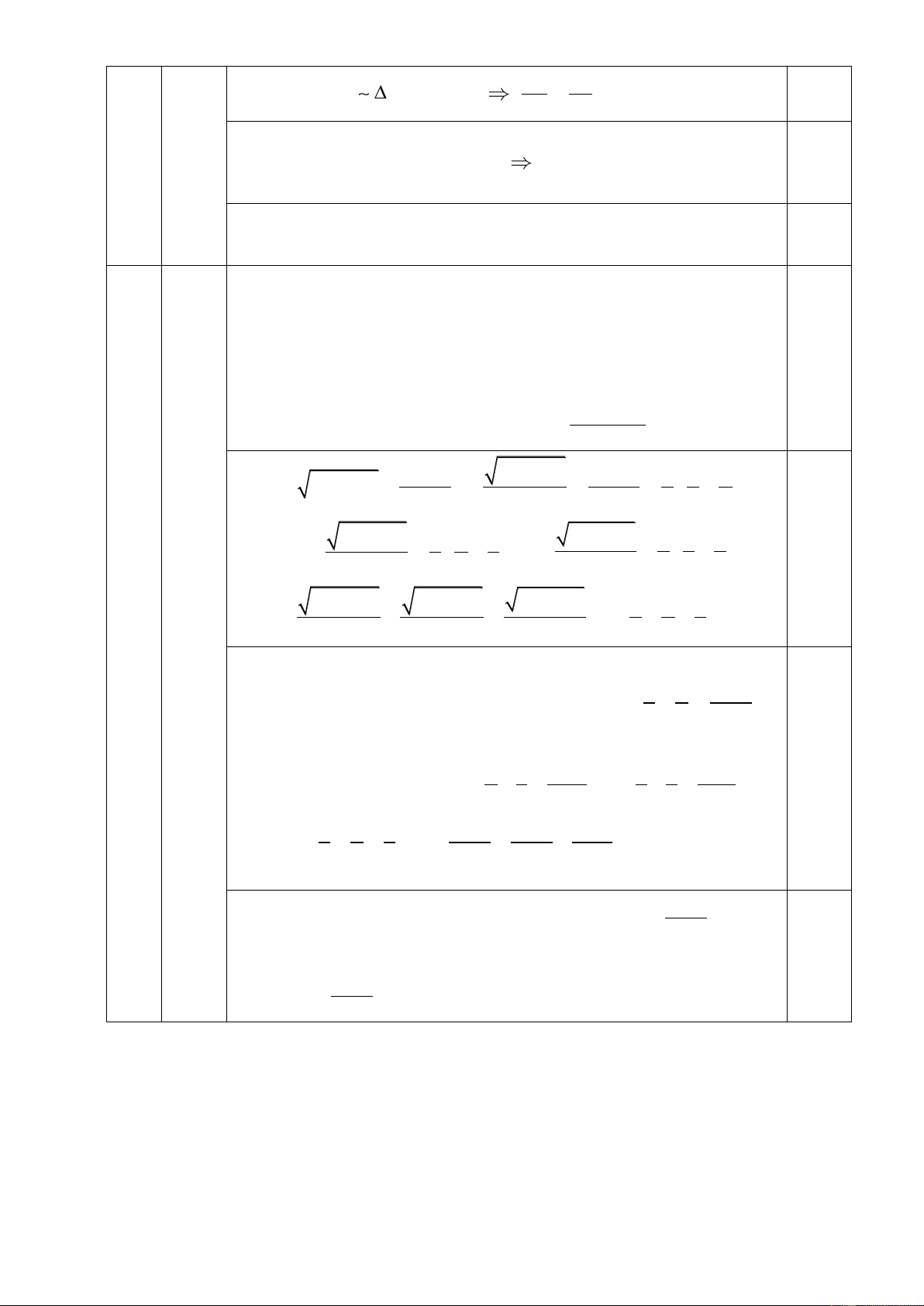
vuông tại A có AH là đường cao 1 1 1 2 2 2 AH AB AC 1 1 1 1 1 1 2 2 2 2 2 2 (2MK) AB AC 4MK AB AC 4 4 4 1 4 4 2 2 2 2 2 2 4MK AB AC MK AB AC 0,25 4.c AI IC C.minh IAC IDB (g – g) I .
A IB DI.IC 0,5 DI IB
Tam giác BIC có BD là đường phân giác đồng thời là đường
cao nên tam giác BIC cân tại B. ID DC 0,25
Tam giác ACI vuông tại A có AD là trung tuyến nên IC 2AD Vậy I .
D 2AD I . D IC I . A IB I .
A IA AB 0,25 Suy ra 2 2 2A .
D ID IA I . A IB 2A .
D ID IA I . A IB (đpcm)
Với hai số dương x, y ta có x y2 0, đẳng thức xảy ra khi x . y
Ta có x y2 2 2 3
0 3y 3x 6xy 0,25 2 2 2 2
4y 12x y 6xy 9x
4 3 3 3 2 2 2 2 2 2 3 y x y x y x y x 4 2 2 Do đó y 3x y 3x y 3x 1 1 3 2 2 y 3x 2 xy 2xy 2 x y 2 2 2 2 Tương tự z 3y 1 1 3 x 3z 1 1 3 và . yz 2 y z zx 2 z x 2 2 2 2 2 2 y 3x z 3y x 3z 1 1 1 P 2 0,25 5 xy yz zx x y z Với ,
x y, z 0 ta có
x y2 0 x y 2xy x y2 1 1 4 2 2 4xy x y x y
đẳng thức xảy ra khi x . y 1 1 4 1 1 4
Chứng minh tương tự ta có y z y z z x z x 1 1 1 1 1 1 P 2 4 4.2023 8092. x y z
x y y z z x 0,25
Suy ra P 8092, đẳng thức xảy ra khi 3
x y z . 4046
Vậy giá trị nhỏ nhất của P cần tìm là 8092 khi 3
x y z . 0,25 4046 --- Hết ---