Đề khảo sát lần 1 Toán 9 năm 2023 – 2024 trường THCS Tam Dương – Vĩnh Phúc
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp đề khảo sát chất lượng học sinh môn Toán 9 năm học 2023 – 2024 trường THCS Tam Dương – Vĩnh Phúc giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.
Preview text:
TRƯỜNG THCS TAM DƯƠNG
THI KHẢO SÁT CHẤT LƯỢNG LẦN 1 NĂM HỌC 2023-2024
ĐỀ THI MÔN: Toán lớp 9
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Đề thi này gồm 01 trang
I. PHẦN TRẮC NGHIỆM (2,0 đ)
Ghi vào bài làm chữ cái in hoa đứng trước kết quả đúng!
Câu 1. Điều kiện xác định của biểu thức 1012 − 2024x là A. 1 x ≥ B. 1 x ≤
C. x ≥ 2 D. 1 x − ≤ 2 2 2
Câu 2. Giá trị của biểu thức B = − (− )2 3 4 2 3 bằng A. 24 B. 3 C. 0 D.12
Câu 3. Điều kiện của tham số m để hàm số y = ( 2 m − )
1 x + m − 3 là hàm số bậc nhất là
A. m ≠ 0 B. m ≠ 1 −
C. m ≠ 1 D. m ≠ 1 ±
Câu 4. Cho tam giác MNP vuông ở M , MN = a ; MP = 3a . Khi đó, cos MNP bằng: A. 1 B. 3 10 C. 10 D. 10 3 10 3 10
II. PHẦN TỰ LUẬN (8,0 điểm)
Câu 5. (1,5 điểm) a) Rút gọn biểu thức 1 1 − b) Tìm x, biết 2
x − 8x +16 = 2x − 3 3 − 2 3 + 2
Câu 6. (1,5 điểm) Cho biểu thức: 1 1 x +1 x + 2 A = − : −
( x ≥ 0; x ≠ 1; x ≠ 4) x −1
x +1 x − 2 x −1
a) Rút gọn biểu thức A.
b) Tìm các giá trị của x để biểu thức A có giá trị âm.
c) Tìm các giá trị nguyên của x để A có giá trị nguyên.
Câu 7. (1,5 điểm) Cho hàm số y = (2m − 4) x + m − 3 ( m là tham số).
a) Tìm các giá trị của m để hàm số đi qua điểm (2; 3 − ) .
b) Tìm các giá trị của m để đồ thị của hàm số và đường thẳng y = 3x + 6 cắt nhau tại
một điểm trên trục hoành.
Câu 8. (2,5 điểm) Từ một điểm A ở ngoài đường tròn ( ;
O R), kẻ tiếp tuyến AB với đường
tròn ( B là tiếp điểm). Gọi I là trung điểm của đoạn thẳng AB , kẻ tiếp tuyến IM với
đường tròn (O) ( M là tiếp điểm).
a) Chứng minh rằng = IAM IMA.
b) Gọi K là giao điểm của OI và BM . Chứng minh rằng 2
MB = 2AM.KO
c) Biết AB = 2R . Tìm vị trí điểm Q trên cung nhỏ BM để diện tích tam giác BMQ
đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
Câu 9 (1,0 điểm). Giải phương trình 2 2 2
7x − 5x + 6 + x + 3 =11x x + 3
-------------HẾT------------
Cán bộ coi thi không giải thích gì thêm.
Họ tên thí sinh......................................................................SBD:.................phòng thi.............
TRƯỜNG THCS TAM DƯƠNG
HDC THI KHẢO SÁT CHẤT LƯỢNG LẦN 1 NĂM HỌC 2023-2024
ĐỀ THI MÔN: Toán lớp 9
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Đề thi này gồm 01 trang
I. PHẦN TRẮC NGHIỆM (2,0 đ)
Mỗi câu đúng được 0,5 điểm Câu 1 2 3 4 Đáp án B C D D
II. PHẦN TỰ LUẬN (8,0 điểm)
Câu 5. (1,5 điểm) Nội dung Điểm
a) (0,75 điểm) 1 1 3 + 2 3 − 2 − = − 3 − 2
3 + 2 ( 3 + 2)( 3 −2) ( 3 + 2)( 3 −2) 0,25 3 + 2 − ( 3 − 2) = ( 3 + 2)( 3 − 2) 0,25 3 + 2 − 3 + 2 = 3− 4 = 4 − 0,25 b) (0,75 điểm) 2
x 8x 16 2x3 ( x − )2 4 = 2x − 3
x − 4 = 2x − 3 ĐK: 3 x ≥ 0,25 2
TH1: x − 4 = 2x − 3 2x − x = 4 − + 3 x = 1 − (L) TH1: x − 4 = 2 − x + 3 0,25 2x + x = 3 + 4 7 x = (L) 3 0,25 Vậy 7 x = 3
Câu 6. (1,5 điểm) Nội dung Điểm + + a) (0,5 điểm) 1 1 x 1 x 2 A = − : − x 1 x 1 x 2 x 1 − + − −
x +1− ( x − ) 1 ( x + ) 1 ( x − )
1 − ( x + 2)( x − 2) = ( x + )( x − ) : 1 1
( x −2)( x − )1 2
x −1− (x − 4) = 0,25
( x + )( x − ) : 1
1 ( x − 2)( x − )1 2 3 = ( x + )( x − ) : 1
1 ( x − 2)( x − )1
( x −2)( x − )1 2( x −2 2 ) = ( ⋅ = x + ) 1 ( x − )1 3 3( x + )1 2( x − 2)
Vậy với x ≥ 0; x ≠ 1; x ≠ 4 thì A = . 3( x + )1 0,25
b) (0,5 điểm) Với x ≥ 0 thì 3( x + )1 > 0. 0,25
Do đó A < 0 ⇔ 2( x − 2) < 0 ⇔ 0 ≤ x < 4 và x ≠1
Vậy A < 0 khi 0 ≤ x < 4 và x ≠1 0,25
c) (0,5 điểm) Với x nguyên, A có giá trị nguyên khi 2( x −2)3( x + )1
mà 3( x + )13( x + )1 nên 2.3( x + )1−3.2( x −2) 3( x + )1 ⇒183( x + ) 1 0,25 ⇒ 6( x + ) 1
Do x +1 > 0 ⇒ x +1 là các ước dương của 6. x +1 1 2 3 6 x 0 (L) 1 (L) 4 (L) 25 (L )
Vậy không có giá trị x thỏa mãn. 0,25
Câu 7. (1,5 điểm) Nội dung Điểm
a) (0,75 điểm) Thay x = 2; y = 3
− vào hàm số đã cho ta được
3 2m42 m3 0,25
3 4m8 m3 5m 8 0,25 8 m = 5 Vậy 8 m = . 0,25 5
b) (0,75 điểm) Đồ thị hàm số đã cho và đường thẳng y = 3x + 6 cắt nhau khi 7
2m − 4 ≠ 3 ⇔ m ≠ 2
Gọi tọa độ giao điểm cắt nhau trên trục hoành là (x ;0 . 0,25 0 )
Thay x = x ; y = 0 và phương trình y = 3x + 6 ta được x = 2 − . 0 0 Thay x = 2
− và y = 0 vào hàm số đã cho ta được 0,25
0 2m42 m3 ⇔ 3m = 5 5 ⇔ m = (TM) 3 0,25 Vậy 5 m = . 3
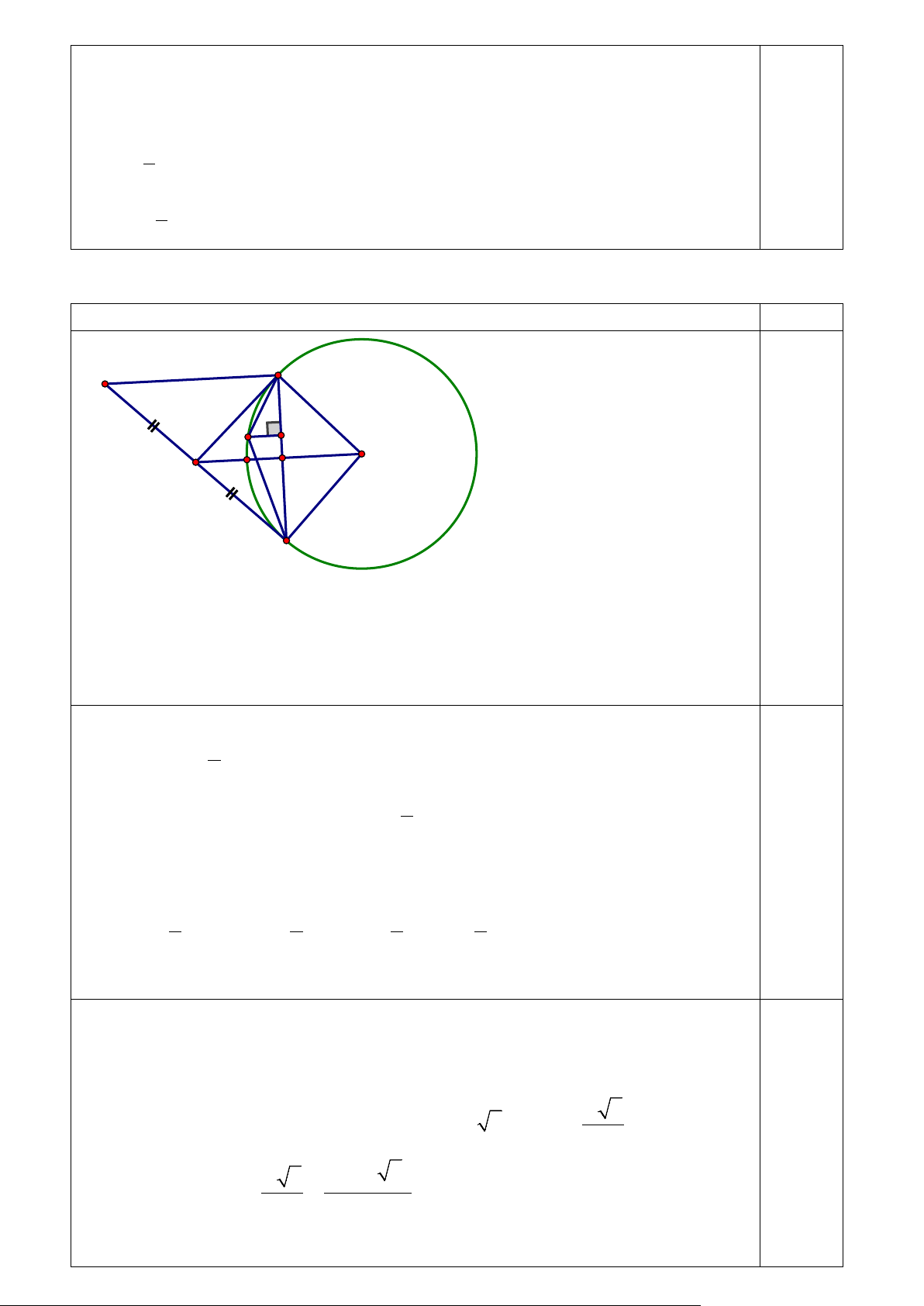
Câu 8. (2,5 điểm) Nội dung Điểm M A Q H O I N K B
a) (1,0 điểm) Theo tính chất tiếp tuyến cắt nhau ta có IM = IB
mà IB = IA (gt) nên IM = IA 0,25 ⇒ IA
∆ M cân tại I . 0,25 ⇒ = IAM IMA. 0,25 0,25
b) (1,0 điểm) Ta có OM = OB và IM = IB nên OI là đường trung trực của BM . 1
⇒ MK = BK = MB và OI ⊥ MB . 2 0,25 KI 1
là đường trung bình A
∆ MB ⇒ IK = AM . 2 IMO ∆
vuông tại M có MK là đường cao 0,25 2
⇒ MK = IK.KO (hệ thức về cạnh và đường cao) 1 1 2 1 1
Mà MK = MB và IK = AM nên MB = AM.KO 0,25 2 2 2 2 ⇒ 2
MB = 2.AM.KO 0,25
c) (0,5 điểm) Kẻ QH ⊥ MB tại H , gọi N là giao điểm của IO và (O) .
Ta có MI = MO = BO = IB = R ⇒ Tứ giác BOMI là hình thoi mà OBI = 90°
⇒ BOMI là hình vuông. 2 2 2
OI = IB + OB R 2
(định lý Pytago) ⇒ OI = MB = R 2 ⇒ OK = 2 R R (2− 2 2 ) 0,25
NK = ON − KO = R − = 2 2
Ta thấy QH ≤ NK . R( − ) 2 2 2 R ( 2 − ) 1 1 1 1 S
= QH MB ≤ NK MB = R = BMQ . . . . 2 2 2 2 2 2 0,25
Dấu " = " xảy ra khi Q trùng với N .
Câu 9 (1,0 điểm). Nội dung Điểm 2 2 2
7x − 5x + 6 + x + 3 =11x x + 3 ⇔ ( 2 2
x − x − x x + )+( 2x + −(x − ) 2 5 5 10 3 2 6 1 x + 3) = 0 ⇔ x ( 2 x − − x + ) 2 + x + ( 2 5 . 1 2 3
3. 2 x + 3 − x + )1 = 0 0,25 ⇔ ( 2
x −1− 2 x + 3)( 2
5x − x + 3) = 0 2 2 x + 3 = x −1 ⇔ 2 x +3 = 5x 0,25 x ≥1 +) 2
2 x + 3 = x −1 ⇔ ⇒ x ∈∅ 2 3
x + 2x +11 = 0 x ≥ 0 0,25 +) 2 2
x + 3 = 5x ⇔ ⇔ x = . 2 1 x = 4 8
Vậy phương trình có nghiệm 2 x = . 0,25 4