Đề khảo sát lần 1 Toán 9 năm 2024 – 2025 phòng GD&ĐT Hồng Bàng – Hải Phòng

UBND QUẬN HỒNG BÀNG
ĐỀ KHẢO SÁT CHẤT LƯỢNG LẦN 1
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
Năm học 2024 – 2025 MÔN: TOÁN 9
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
(Thí sinh trả lời từ Câu 1 đến Câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.)
Câu 1. Biểu thức nào sau đây không phải là phân thức đại số? x  2 1 3 A. 3x . B. . C. x 1. D. y 0 2 x  4
Câu 2. Phương trình nào sau đây là phương trình bậc nhất một ẩn? 1 5 A. 0x  3  0. B. 2 x  2  0. C. x  3  0. D. 1  0. 2 x
Câu 3. Đồ thị của hai hàm số y  2024x 1   và y
2025x 1 là hai đường thẳng có vị trí như thế nào? A. Trùng nhau. B. Song song.
C. Không cắt nhau. D. Cắt nhau.
Câu 4. Phương trình nào sau đây là phương trình bậc nhất hai ẩn? y A. 2
2x  2  0. B. 3y 1  5 y  2 . C. 2x   1. D. 2
3 x  y  0 . 2 S
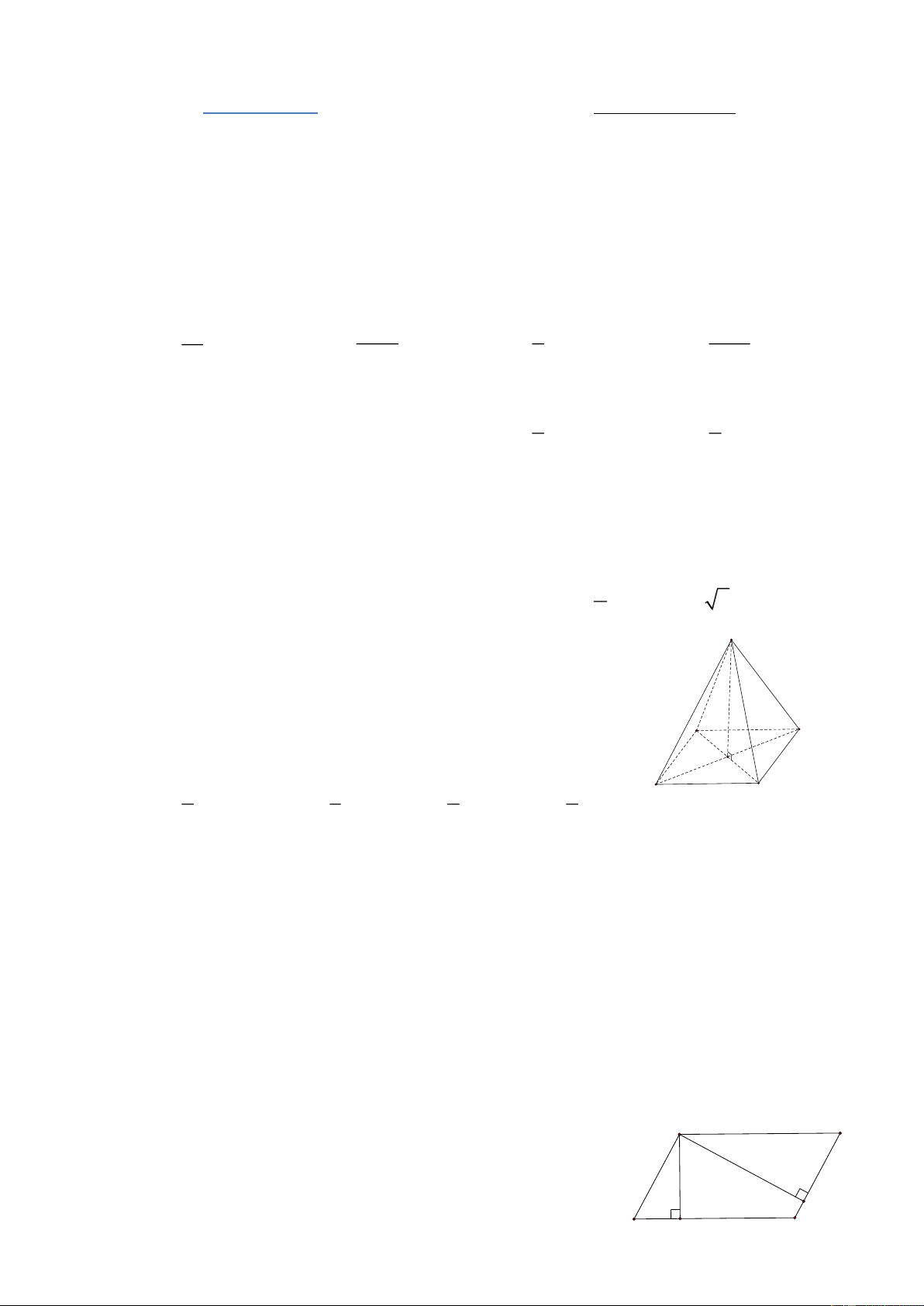
Câu 5. Cho hình chóp tứ giác đều S.ABCD (hình bên), SH được gọi là A. đường cao. B. cạnh bên. C. cạnh đáy. D. đường chéo. Câu 6. Cho ABC 
vuông tại A có AC  4c , m AB  3cm . A D Khi đó tan B bằng H 3 3 4 4 B C A. . B. . C. . D. . 4 5 5 3
Câu 7. Một hộp có 4 tấm thẻ cùng loại được đánh số lần lượt: 2; 3; 4; 5. Chọn ngẫu nhiên
một thẻ từ hộp, kết quả thuận lợi cho biến cố “Số ghi trên thẻ chia hết cho 2” là
A. Thẻ ghi số 2 và thẻ ghi số 3.
B. Thẻ ghi số 2 và thẻ ghi số 4.
C. Thẻ ghi số 2 và thẻ ghi số 5. D. Thẻ ghi số 3 và thẻ ghi số 4.
Câu 8. Cho tam giác ABC đồng dạng với tam giác MNP theo tỉ số 2 .
Khẳng định nào sau đây là đúng? A. MN  2AB. B. AC  2NP . C. MP  2BC . D. BC  2NP.
Câu 9. Cặp số  2  ;  
3 là nghiệm của hệ phương trình nào sau đây?
x  2y  3
2x  y  1 
2x  y  1 
4x  2y  0 A.  . B.  . C.  . D. 
2x  y  4
x  3y  8
x  3y  7
x  3y  5 A B
Câu 10. Cho hình bình hành ABCD , kẻ AH CD tại H ;
AK  BC tại K . Khẳng định nào sau đây là đúng? K D H C A. H  DA∽ K  A . B B. A  DH ∽ A  BK. C. K  AB∽ D  AH D. B  KA∽ A  H . D
Câu 11. Bạn An gieo một con xúc xắc 50 lần và thống kê lại kết quả các lần gieo ở bảng sau: Mặt 1 chấm 2 chấm 3 chấm 4 chấm 5 chấm 6 chấm
Số lần xuất hiện 8 9 9 5 6 13
Xác suất thực nghiệm của biến cố “Gieo được mặt có số chấm là số lẻ” sau 50 lần thử trên là: A. 0, 46 . B. 0,52 . C. 0,54 . D. 0, 48 . Câu 12. Cho ABC 
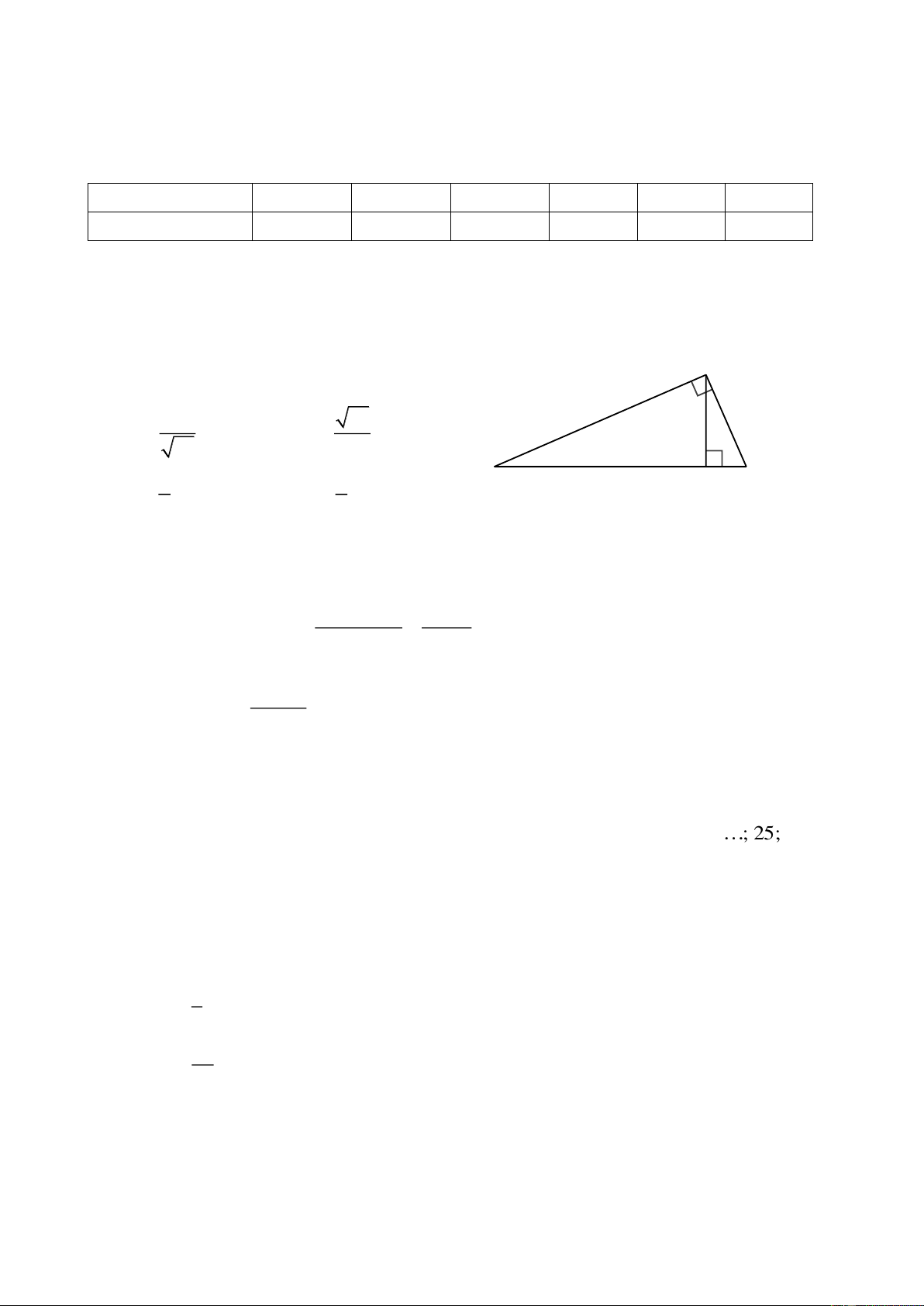
vuông tại A , đường cao AH có A
AC 15 cm , CH  6 cm . Tỉ số lượng giác cos B bằng 5 21 A. . B. . 21 5 5 2 B H C C. . D. . 2 5
PHẦN II. Câu trắc nghiệm đúng sai. (Thí sinh trả lời từ Câu 13 đến Câu 16. Trong
mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.) 2 x  6x  9 4x  8
Câu 13. Cho biểu thức P   2 9  x x  3
a) Điều kiện xác định của biểu thức P là x  3 3x 11
b) Rút gọn P  x  3
c) Giá trị của P tại x  2  là 5 d) x  2  ; 1  ; 
4 thì biểu thức P nhận giá trị nguyên. Câu 14.
Một hộp có 25 thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3; 4; 5; ; 25; hai
thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Gọi A là biến cố
“Số xuất hiện trên thẻ được rút ra là số chia hết cho 5 ” và B là biến cố “Số xuất hiện trên
thẻ được rút ra là số có hai chữ số và tổng các chữ số bằng 5 ”
a) Có 3 kết quả thuận lợi cho biến cố A
b) Có 2 kết quả thuận lợi cho biến cố B 1 c) P( ) A  5 2 d) P(B)  25
Câu 15. Cho phương trình x  2 y  3.
a) Phương trình đã cho là phương trình bậc nhất một ẩn. b) Cặp số 5;  
1 là một nghiệm của phương trình đã cho. 1
c) Tất cả nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng y  3  . x 2
d) Phương trình đã cho có vô số nghiệm, nghiệm tổng quát là 3 2 ;
y y với y  tùy ý.
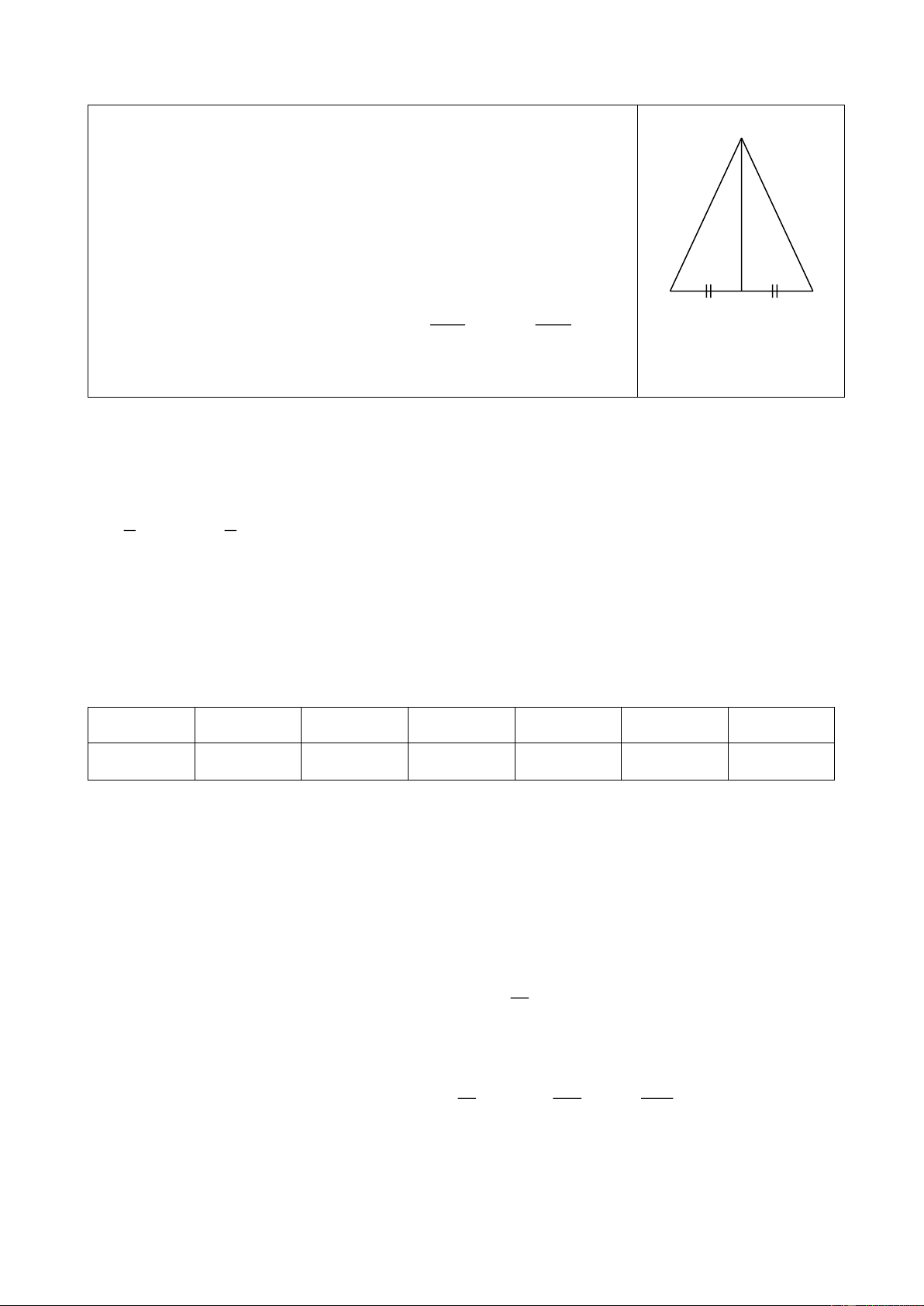
Câu 16. Cho tam giác ABC cân tại A có AB  2a và B   . Kẻ đường trung tuyến AM. Khi đó:
a) sin BAM  cos . b) BM  2 . a sin . c) AM  2 . a cos .
d) Diện tích tam giác ABC là: 2
S  4a sin.cos .
PHẦN III. Câu trắc nghiệm trả lời ngắn. (Thí sinh trả lời từ Câu 17 đến Câu 22.)
ax  6y  5
Câu 17. Cho hệ phương trình 
nhận cặp số 2;  
1 làm nghiệm. Tính tổng
5x  by  4
bình phương của a và b ( Làm tròn đến hàng phần mười)
Câu 18. Camera quan sát tại đường X trong 365 ngày liên tiếp ghi nhận 217 bị tắc đường
vào giờ cao điểm buổi sáng ( từ 7 giờ 30 phút đến 8 giờ). Từ số liệu thống kê đó, hãy dự
đoán xem trong 100 ngày có khoảng bao nhiêu ngày bị tắc đường vào giờ cao điểm buổi sáng tại đường X?
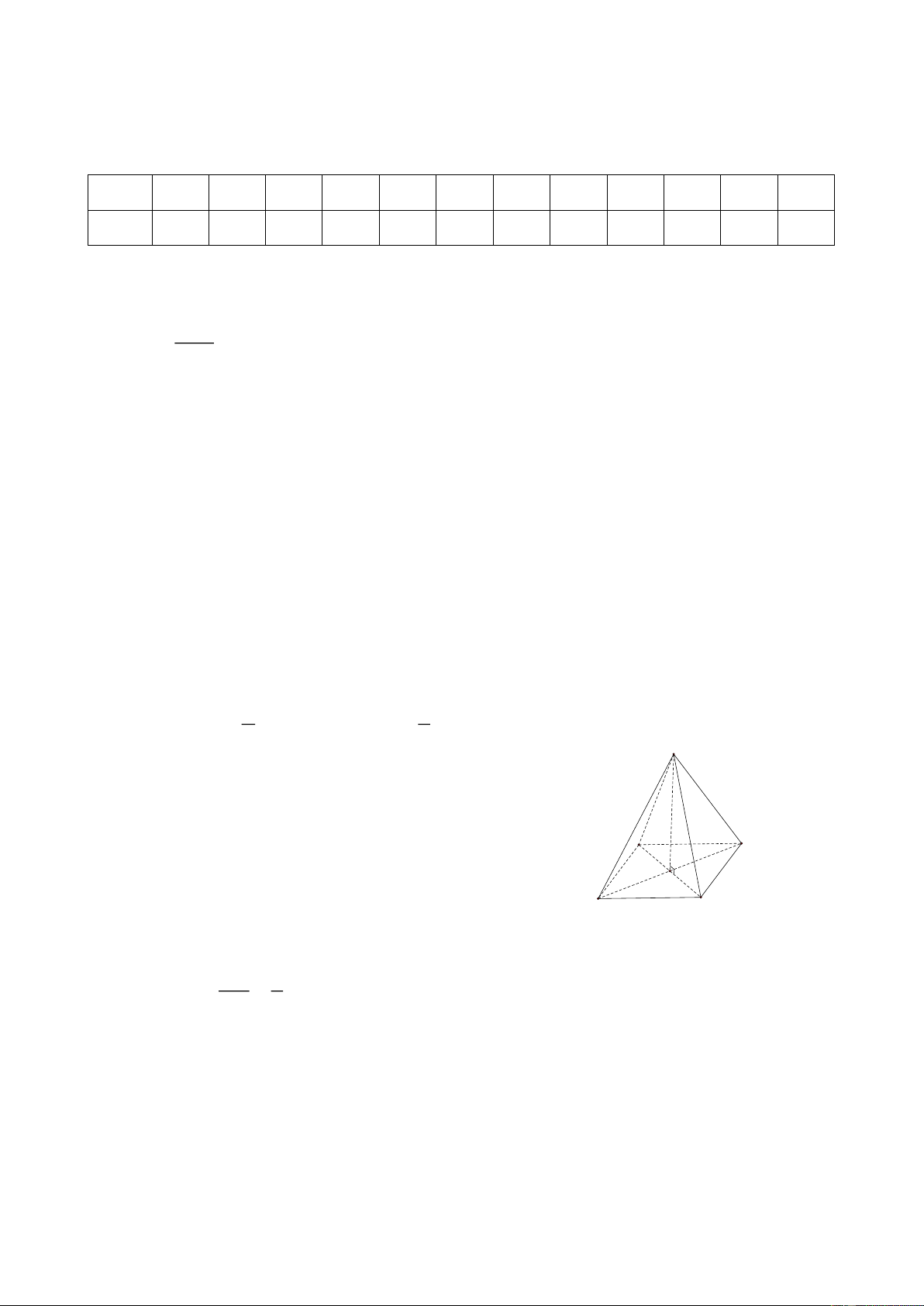
Câu 19. Một khối rubik có dạng hình chóp tam giác đều với diện tích đáy là 2
22, 45 cm và thể tích của khối đó là 3 44,002 cm . Tính chiều
cao của khối rubik đó. ( Đơn vị : cm )
Câu 20. Một người đi xe máy từ A đến B với vận tốc 40km / h . Lúc về người đó tăng vận
tốc thêm 5km / h , biết thời gian lúc về ít hơn thời gian lúc đi là 20 phút. Tính quãng đường
AB? ( Đơn vị: km )
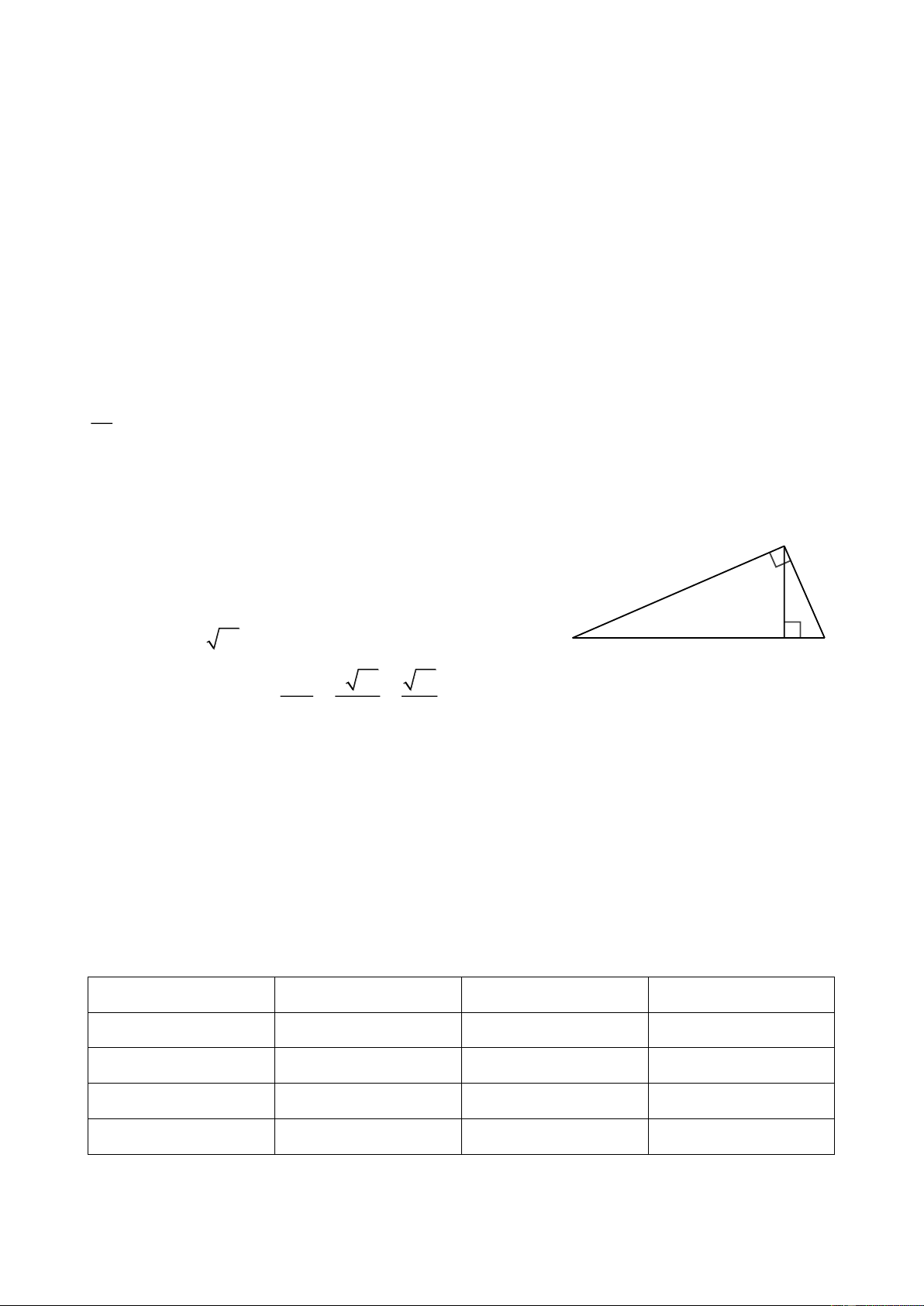
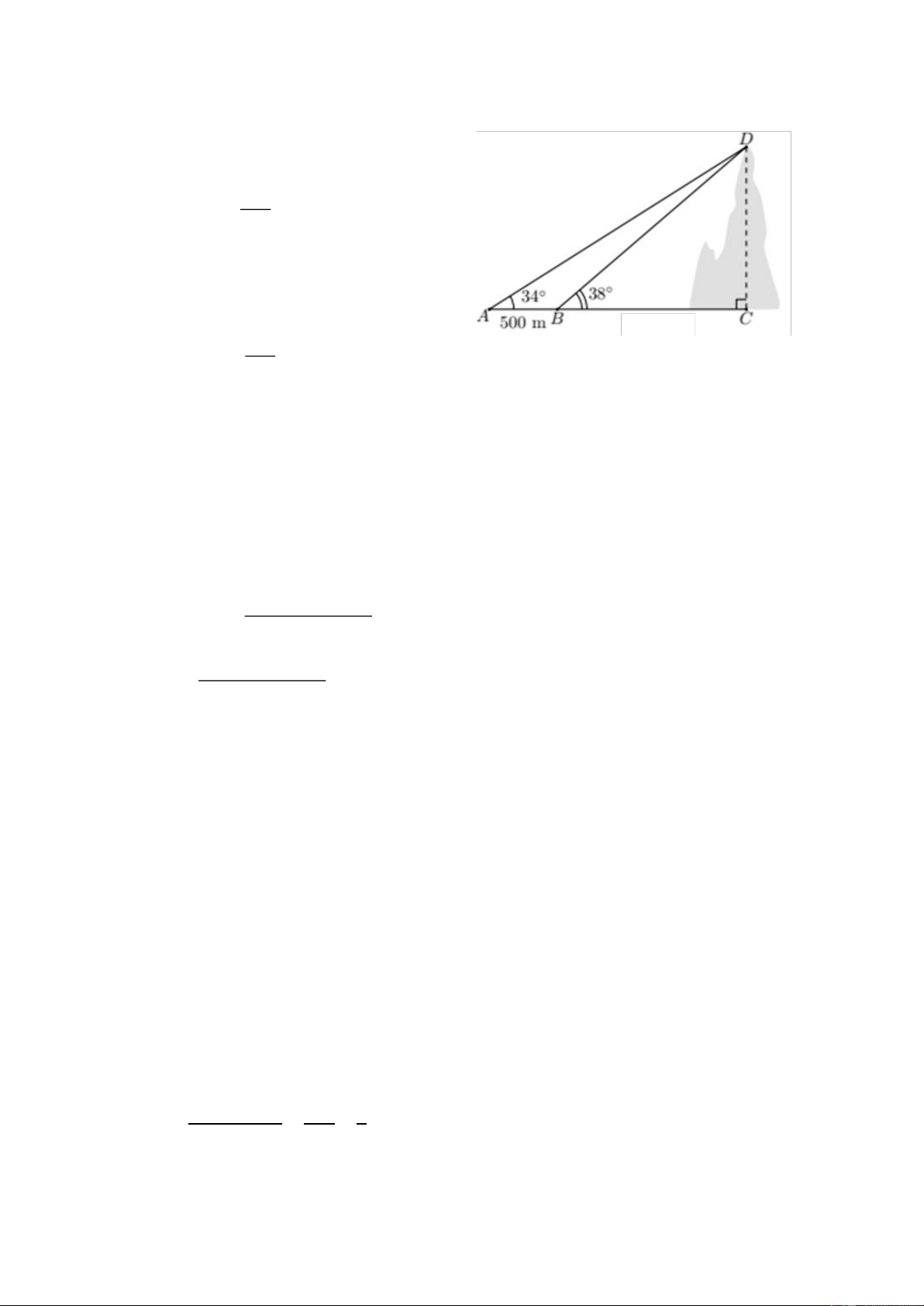
Câu 21. Tại hai điểm ,
A B cách nhau 500 m, người
ta nhìn thấy đỉnh núi với góc nâng lần lượt là 34
và 38. Tính chiều cao của ngọn núi.
( Đơn vị: m ; Kết quả làm tròn đến hàng đơn vị) Câu 22. 2 2 2
a  b  c Cho 3 3 3
a  b  c  3abc và a  b  c  0. Tính giá trị của biểu thức N  
a  b  c . 2
( Kết quả làm tròn đến hàng phần trăm)
Họ và tên thí sinh:...............................................Số báo danh:...............................................
Cán bộ coi thi 1:………………….…Cán bộ coi thi 2: .............................................. UBND QUẬN HỒNG BÀNG
ĐÁP ÁN ĐỀ KHẢO SÁT ĐẦU NĂM
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
Năm học 2024 – 2025 Môn: TOÁN 9
PHẦN I. ( Mỗi câu trả lời đúng thí sinh được 0,25 điểm) Câu 1 2 3 4 5 6 7 8 9 10 11 12 Chọn B C D C A D B D C B A B
PHẦN II. (Điểm tối đa của 01 câu hỏi là 1,0 điểm)
- Thí sinh chỉ lựa chọn chính xác 01 ý trong 1 câu hỏi được 0,1 điểm.
- Thí sinh chỉ lựa chọn chính xác 02 ý trong 1 câu hỏi được 0,25 điểm.
- Thí sinh chỉ lựa chọn chính xác 03 ý trong 1 câu hỏi được 0,5 điểm.
- Thí sinh chỉ lựa chọn chính xác 04 ý trong 1 câu hỏi được 1,0 điểm. Câu 13 Câu 14 Câu 15 Câu 16 a) S a) S a) S a) Đ b) Đ b) Đ b) Đ b) S c) Đ c) Đ c) S c) S d) S d) Đ d) Đ d) Đ
PHẦN III. (Mỗi câu trả lời đúng thí sinh được 0,5 điểm) Câu 17 18 19 20 21 22 Đáp án 66,3 59 5,88 120 2468 0,33 7 ĐÁP ÁN CHI TIẾT
PHẦN I. ( Mỗi câu trả lời đúng thí sinh được 0,25 điểm) Câu 1 2 3 4 5 6 7 8 9 10 11 12 Chọn B C D C A D B D C B A B
Câu 1. ( Đại số 8)
Biểu thức x  1 không phải là phân thức đại số vì có mẫu bằng 0. 0 Đáp án : B Câu 2. ( Đại số 8)
Phương trình bậc nhất một ẩn có dạng ax  b  0 với a  0. Đáp án : C Câu 3. ( Đại số 8)
Hệ số góc của đường thẳng y  2024x 1 là 2024 ;
Hệ số góc của đường thẳng y  2025x 1 là 2025.
Vì 2024  2025 nên đồ thị của hai hàm số y  2024x 1   và y
2025x 1 là hai đường thẳng cắt nhau. Đáp án: D Câu 4. ( Đại số 9)
Phương trình bậc nhất hai ẩn có dạng ax  by  c với a và b không đồng thời bằng 0. Phương trình y 2x   1 viết thành 1 2x 
y  1, là phương trình bậc nhất hai ẩn. 2 2 S Đáp án: C Câu 5. ( Hình 8)
Hình chóp tứ giác đều S.ABCD có SH được gọi là đường cao. Đáp án: A A D H Câu 6. ( Hình 9) B C ABC 
vuông tại A có AC  4c , m AB  3cm Khi đó, AC 4 tan B   . AB 3 Đáp án: D Câu 7. ( XSTK 8)
Trong các số 2; 3; 4; 5 thì có 2 và 4 chia hết cho 2
Do đó, kết quả thuận lợi cho biến cố “Số ghi trên thẻ chia hết cho 2 ” là thẻ ghi số 2 và thẻ ghi số 4 . Đáp án: B 8 Câu 8. ( Hình 8) BC Vì A  BC∽ M
 NP theo tỉ số 2 nên
 2 hay BC  2NP. NP Đáp án: D Câu 9. ( Đại 9)
Để kiểm tra xem cặp số  2  ;  
3 có là nghiệm của hệ phương trình nào, ta thay x  2  và
y  3 vào từng hệ phương trình:
x  2y  3 ⦁ Xét phương án A. 
2x  y  4  2   2   3    4  3 Thay x  2
 và y  3 vào hệ phương trình trên ta được:  2   2     3    7   4. Do đó cặp số  2  ;  
3 không phải là nghiệm của hệ phương trình ở phương án A.
2x  y  1  ⦁ Xét phương án B. 
x  3y  8 2   2     3    1  Thay x  2
 và y  3 vào hệ phương trình trên ta được:   2   3   3    7  8. Do đó cặp số  2  ;  
3 không phải là nghiệm của hệ phương trình ở phương án B.
2x  y  1  ⦁ Xét phương án C. 
x  3y  7 2   2     3    1  Thay x  2
 và y  3 vào hệ phương trình trên ta được:   2  3    3    7. Do đó cặp số  2  ;  
3 là nghiệm của hệ phương trình ở phương án C.
4x  2y  0 ⦁ Xét phương án D. 
x  3y  5 4   2    2 3    2   0 Thay x  2
 và y  3 vào hệ phương trình trên ta được:   2   3   3    7  5. Do đó cặp số  2  ;  
3 không phải là nghiệm của hệ phương trình ở phương án D. Vậy cặp số  2  ;  
3 là nghiệm của hệ phương trình ở phương án C. Đáp án : C
Câu 10. < TH> ( Hình 8) 9
Vì ABCD là hình bình hành (gt) nên B  D (hai góc đối của hình bình hành) Xét A
 DH và ABK có B  D (cmt)
AHD  AKB  90 Do đó A  DH ∽ A  BK (g.g) Đáp án: B
Câu 11. < TH> ( XSTT 8)
Trong 50 lần thử, số lần gieo được mặt có số chấm là số lẻ là: 8  9  6  23 (lần).
Xác suất thực nghiệm của biến cố “Gieo được mặt có số chấm là số lẻ” sau 50 lần thử trên là 23  0,46. 50 Đáp án: A Câu 12. ( Hình 9) Xét ABC 
vuông tại A , B và C phụ nhau, do đó cos B  sin C . A Xét A
 CH vuông tại H , theo định lí Pythagore, ta có: 2 2 2
AC  AH  CH , suy ra 2 2 2 2 2
AH  AC  CH 15  6 189.
Do đó AH  3 21 cm. B H C Khi đó, AH 3 21 21
cos B  sin C    . AC 15 5 Đáp án: B
PHẦN II. (Điểm tối đa của 01 câu hỏi là 1,0 điểm)
- Thí sinh chỉ lựa chọn chính xác 01 ý trong 1 câu hỏi được 0,1 điểm.
- Thí sinh chỉ lựa chọn chính xác 02 ý trong 1 câu hỏi được 0,25 điểm.
- Thí sinh chỉ lựa chọn chính xác 03 ý trong 1 câu hỏi được 0,5 điểm.
- Thí sinh chỉ lựa chọn chính xác 04 ý trong 1 câu hỏi được 1,0 điểm. Câu 13 Câu 14 Câu 15 Câu 16 a) S a) S a) S a) Đ b) Đ b) Đ b) Đ b) S c) Đ c) Đ c) S c) S d) S d) Đ d) Đ d) Đ
Câu 13. ( Đại số 8) 10 2 x  6x  9 4x  8 Cho biểu thức P   2 9  x x  3
a) Điều kiện xác định của biểu thức P là x  3; x  3  Do đó a) Sai 2 2 x  6x  9 4x  8 (3  x) 4x  8 3  x 4x  8 3x 11 b) Rút gọn P        2 9  x x  3
(3  x)(3  x) x  3 x  3 x  3 x  3 Do đó b) Đúng c) Với x  2
 thỏa mãn ĐK : x  3; x  3  3.( 2  ) 11 Nên P( 2  )   5
x   là 5 . Do đó c) Đúng 2  
Giá trị của P tại 2 3 3x 11 3(x  3)  2 2 d) P    3  x  3 x  3 x  3
Nếu x và P là những số nguyên thì 2
x  là ước nguyên của
x  là số nguyên, do đó 3 3
2 . Vì vậy x  31;2; 1  ;  2 hay x  2  ; 1  ; 4  ; 
5 ( Các giá trị này của x đều thỏa
mãn điều kiện xác định của P ). Do đó d) Sai Câu 14. ( XSTT 8)
a) Có 5 kết quả thuận lợi cho biến cố A là 5; 10; 15; 20; 25. Do đó a) Sai
b) Có 2 kết quả thuận lợi cho biến cố B là 14; 23.Do đó b) Đúng
c) Xác suất của biến cố A là 5 1 P( ) A   .Do đó c) Đúng 25 5
d) Xác suất của biến cố B là 2 P(B)  . Do đó d) Đúng 25 Đáp án: a) S. b) Đ. c) Đ. d) Đ.
Câu 15 . < Đại 9>
a) Phương trình x  2y  3 là phương trình bậc nhất hai ẩn. Do đó ý a) Sai.
b) Thay x  5 và y  1
 vào phương trình đã cho, ta được: 5  2.  1  3.
Suy ra cặp số 5;  
1 là một nghiệm của phương trình x  2 y  3. Do đó ý b) Đúng. 3 1
c) Viết lại phương trình x  2 y  3 thành y 
 x , khi đó tất cả các nghiệm của phương 2 2 trình đã cho đượ 3 1
c biểu diễn bởi đường thẳng y 
 x . Do đó ý c) Sai. 2 2
d) Phương trình x  2y  3 là phương trình bậc nhất hai ẩn, có vô số nghiệm.
Viết lại phương trình x  2 y  3 thành x  3  2 y .
Khi đó, nghiệm tổng quát của phương trình đó là: 3 2 ;
y y với y  tùy ý. Do đó ý d) Đúng. Đáp án: a) S. b) Đ. c) S. d) Đ. 11
Câu 16. < Hình 9> a) Xét ABC 
cân tại A có AM là đường trung tuyến nên đồng A
thời là đường phân giác và đường cao của tam giác. Xét ABM 
vuông tại M , khi đó BAM và B là hai góc phụ nhau,
nên sin BAM  cos B  cos . Do đó ý a) Đúng. b) và c) α B M C Xét BM AM ABM 
vuông tại M , ta có: cos B  ;sin B  AB AB
Suy ra BM  A . B cos B  2 .
a cos và AM  A . B sin B  2 . a sin.
Do đó ý b) và c) đều Sai.
d) Ta có BC  2BM  2.2 . a cos  4 . a cos .
Diện tích tam giác ABC là: 1 1 S  AM .BC  2 . a sin   4 . a cos  2  4a sin.cos . 2 2 Do đó ý d) Đúng. Đáp án:
a) Đ. b) S. c) S. d) Đ.
PHẦN III. (Mỗi câu trả lời đúng thí sinh được 0,5 điểm) Câu 17 18 19 20 21 22 Đáp án 66,3 59 5,88 120 2468 0,33 Câu 17. ( Đại 9) Vì cặp số 2;  
1 là nghiệm của hệ phương trình, ta thay x  2 và y  1  vào hệ phương  . a 2  6.  1  5 2a  6  5
trình đã cho, ta được:  hay  . 5.2  . b    1  4 1  0  b  4   11 2a  11 a 
Giải hệ phương trình ta được:  suy ra  2 b   6 b   6 2 11 121 265
Tổng bình phương của a và b là: 2 2 2 a  b   6   36   66,25  66,3    2  4 4
Đáp án: 66,3 Câu 18 ( XSTT 8) 12
Gọi k là số ngày trong 100 ngày ghi nhận tắc đường vào giờ cao điểm buổi sáng tại đường k 217 217 X . Ta có  , suy ra k  100.  59,452... 100 365 365
Vậy ta dự đoán trong 100 ngày tới có khoảng 59 ngày tắc đường trong giờ cao điểm tại đường X Đáp số : 59 Câu 19. ( Hình 8)
Thể tích hình chóp tam giác đều là: 1 V  S.h . 3 Suy ra 3.V h  S
Chiều cao của khối rubik là: 3.44,002  5,88 (cm) . 22, 45
Vậy chiều cao của khối rubik là 5,88 cm . Đáp án: 5,88
Câu 20. < VD> ( Đại 8) Đổi 1 20 phút  giờ. 3
Gọi quãng đường AB là x(k )
m  x  0. Thời gian đi từ x
A đến B là (giờ). 40
Lúc về người đó tăng vận tốc thêm 5 km/h nên vận tốc lúc về của người đó là 40  5  45 (km/h). Thời gian đi từ x B về A là (giờ). 45
Vì thời gian lúc về ít hơn thời gian lúc đi là 1 20 phút (
giờ) nên ta có phương trình: 3 x x 1   40 45 3 9x 8x 120   360 360 360
9x 8x 120
x 120 (thỏa mãn).
Vậy quãng đường AB là 120 km. Đáp án: 120 13 Câu 21.
Đặt: BC  x m; AC  AB  BC  500  x m .
Xét tam giác ACD vuông tại C , ta có: CD tan CAD  AC
Suy ra CD  A .
C tanCAD  500  x.tan34 . 
Xét tam giác BCD vuông tại C , ta có: CD tan CBD  BC
Suy ra CD  BC.tanCBD  . x tan38 .
Do đó, ta có:  500  x.tan34  . x tan38 500.tan34  . x tan34  . x tan38 . x tan38  .
x tan34  500.tan34 .
x tan38  tan34  500.tan34 500.tan34
x  tan38 tan34 500.tan34 Suy ra CD 
 tan38  2468(m) tan38  tan34
Vậy ngọn núi cao khoảng 2468 mét. Đáp án: 2468 Câu 22. ( Đại số 8) Ta có 3 3 3 3 3 3 3 3
a  b  c  3abc  (a  b )  c  3abc  (a  b)  3ab(a  b)  c  3abc
 a  b3  c   aba  b  c  a  b  ca  b2 3 2 3
 c(a  b)  c      3  a ( b a  b  ) c
 a  b  ca  b2  ca  b 2  c  3ab 2 2 2 
  a  b  ca  b  c  ab  bc  ac Vì 3 3 3
a  b  c  3abc và a  b  c  0 nên 2 2 2
a  b  c  ab  bc  ca  0. Lại có  2 2 2
2 a  b  c  ab  bc  ca   2 2
a  ab  b    2 2
b  bc  c    2 2 2 2
c  2ca  a 
   2    2    2 a b b c c a . Như vậy, từ 2 2 2
a  b  c  ab  bc  ca  0 suy ra a  b  . c 2 2 2 2   Do đó, a b c 3a 1 N     
a  b  c 0,33 2 2 9a 3 Đáp số: 0,33 14 15
Document Outline