Đề khảo sát Toán 9 đầu năm học 2022 – 2023 trường THCS Giảng Võ – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp đề khảo sát chất lượng học sinh môn Toán 9 năm học 2022 – 2023 trường THCS Giảng Võ – Hà Nội giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.
Preview text:
PHÒNG GD&ĐT QUẬN BA ĐÌNH
ĐỀ KHẢO SÁT CHẤT LƯỢNG ĐẦU NĂM
TRƯỜNG THCS GIẢNG VÕ HỌC
NĂM HỌC 2022 – 2023 ĐỀ CHÍNH THỨC Môn thi : TOÁN 9
Ngày thi : 29 tháng 9 năm 2022
Thời gian làm bài : 90 phút
Bài I (2,5 điểm)
1) Rút gọn các biểu thức sau :
a) (5 18 − 7 8 + 4 128). 2 . 2 5 b) + (2 − 3) . 2 − 3
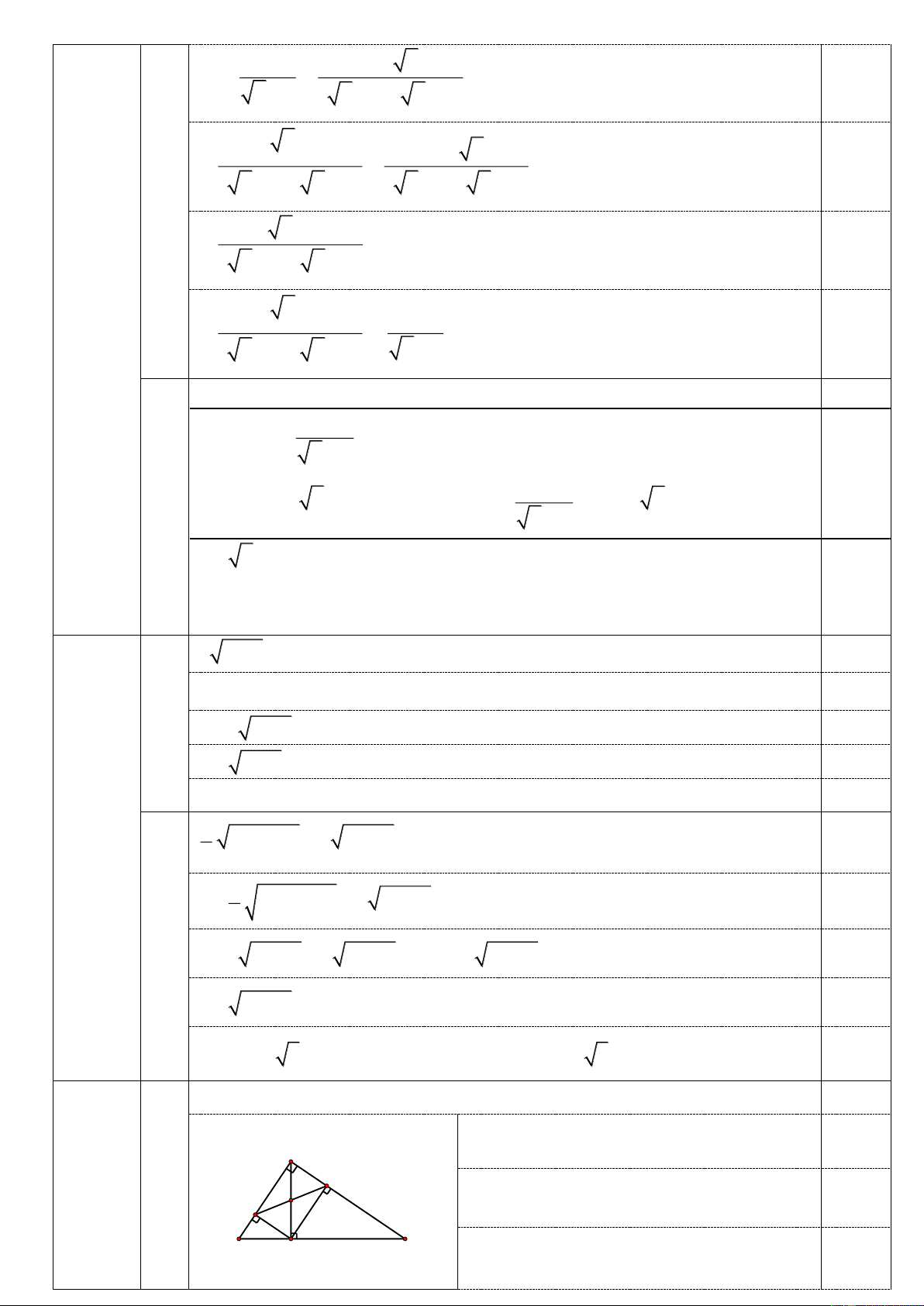
2) Mặt cắt của một ngôi nhà có phần mái có dạng tam A
giác ABC cân tại A . Biết CH = 4, 5 m và độ dốc của mái 25° là = 25o C
. Tính chiều cao AH của mái nhà (đơn vị: mét, B C H
làm tròn đến chữ số thập phân thứ nhất).
(Học sinh không phải vẽ lại hình).
Bài II (2,0 điểm) x − 1 5 9 − x
Cho hai biểu thức A = và B = +
với x 0, x 1. x + 2 x + 1 x − 1
1) Tính giá trị của biểu thức A khi x = 16 . 4 2) Chứng minh B = . x − 1 3) Cho P = .
AB . Tìm tất cả các giá trị nguyên của x để P 1 .
Bài III (2,0 điểm)
Giải các phương trình sau :
1) 2 x − 1 − 7 = 11. 5 2) 2 9x + 36 − 2 2 x + 4 = 9 . 3
Bài IV (3,0 điểm)
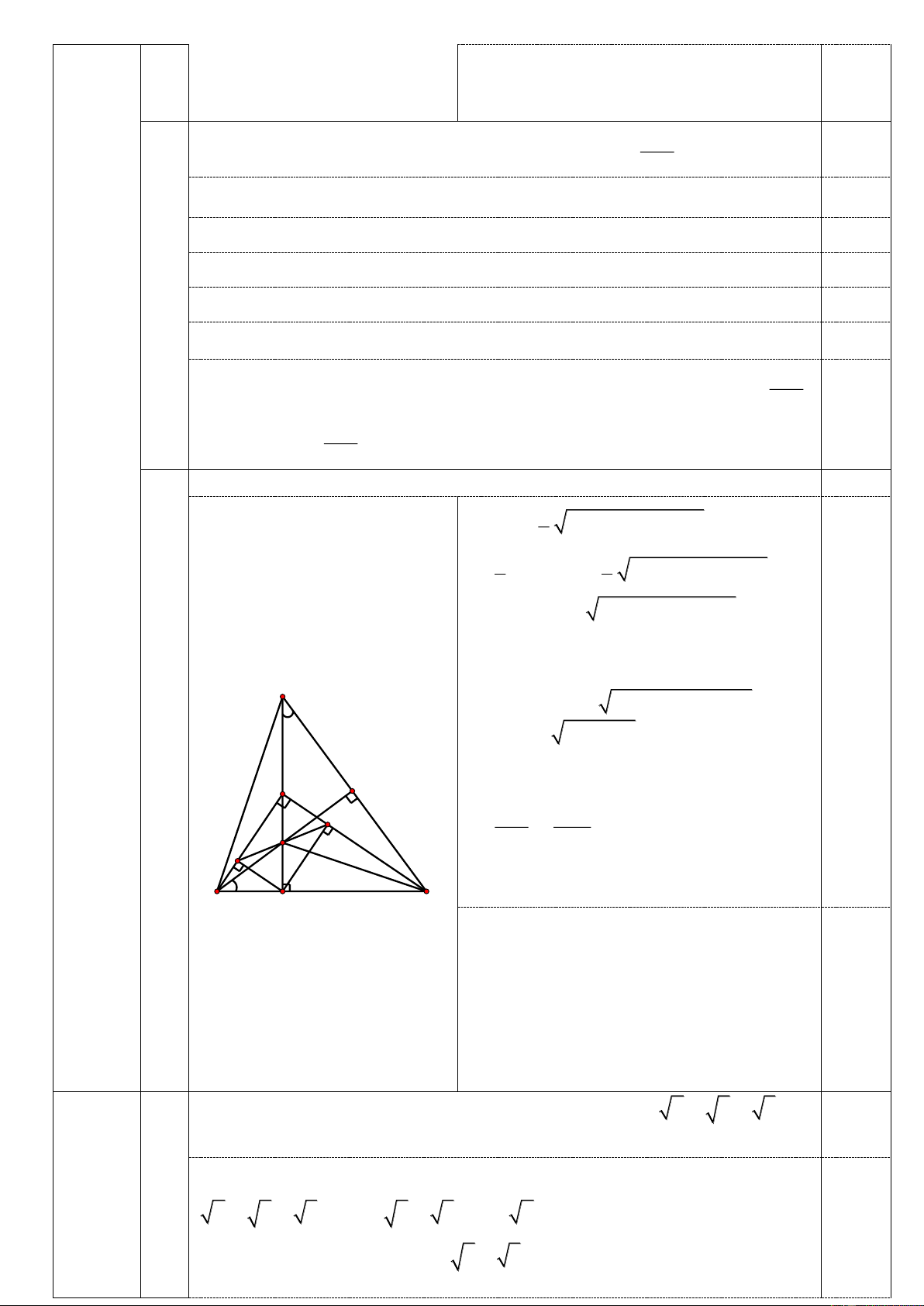
Cho ABC vuông tại A có AH là đường cao . Gọi E và F lần lượt là chân các đường vuông góc
kẻ từ điểm H đến các đường thẳng AB và AC .
1) Giả sử AB = 6 c ,
m BC = 10 cm
. Tính độ dài các đoạn thẳng BH, AH . AC
2) Chứng minh rằng AE.AB = AF.AC và cos AEF = . BC
3) Gọi O là giao điểm của AH và EF . Trên tia đối của tia AH lấy điểm M , kẻ BD vuông góc
với CM tại D . Biết rằng S = 1 B .
D BC.CM.OH . Chứng minh ba điểm , B ,
O D thẳng hàng. ABC 2
Bài V (0,5 điểm)
Cho các số thực x, ,
y z 0 thỏa mãn x + y + z = 19 và x + y + z = 5 . Tìm giá trị lớn nhất của x .
…………..……. Hết …………………
HƯỚNG DẪN CHẤM CHO ĐỀ CHÍNH THỨC (gồm 04 trang) HƯỚNG DẪN CHUNG
+) Điểm toàn bài để lẻ đến 0,25.
+) Các cách làm khác nếu đúng vẫn cho điểm tương ứng với biểu điểm của hướng dẫn chấm.
+) Các tình huống phát sinh trong quá trình chấm do Hội đồng chấm thi quy định, thống nhất bằng biên bản.
+) Bài hình vẽ hình sai thì không cho điểm. HƯỚNG DẪN CHẤM Bài Ý Đáp án Điểm 1a)
(5 18 −7 8 +4 128). 2. 1,0
= (5 9.2 − 7 4.2 + 4 64.2). 2 0,25 = (15 2 −14 2 + 32 2). 2 0,25 = 33 2. 2 0,25 = 66 . 0,25 1b) 2 5 + (2 − 3) . 1,0 2 − 3 5 (2 + 3) = + 2 − Bài I ( 3 0,25 2 − 3 )(2 + 3) 2,5 điểm = 5 (2 + 3) + 2 − 3 0,25 = 10 + 5 3 + 2 − 3 0,25 = 12 + 4 3 . 0,25 2)
Tính chiều cao AH của mái nhà (đơn vị: mét, làm tròn đến chữ số thập phân 0,5
thứ nhất). AH
Xét AHC vuông ở H , theo tỉ số lượng giác của góc nhọn: tanC = 0,25 CH = . tan = 4, 5. tan 25o AH CH C 2,1(m) . 0,25
Vậy chiều cao của mái nhà là AH 2,1 (m ) . 1)
Tính giá trị của biểu thức A khi x = 16 . 1,0 16 − 1
Thay x = 16 (TMĐK) vào biểu thức A có: A = 0,5 16 + 2 Bài II 2,0 điểm Tính được A = 1 . 0,5 2 2) 4 Chứng minh B = . 1,0 x − 1 5 9 − 0,25 = + x B x + 1
( x − )1( x + )1 5 ( x − ) 1 0,25 9 − = x ( x )1( x ) + − + 1
( x − )1( x +1) 4 x + 0,25 = 4 ( x − ) 1 ( x + ) 1 4 ( x + ) 1 0,25 = 4 ( (đpcm). x − ) 1 ( x + ) = 1 x − 1 3) Cho P = .
AB . Tìm tất cả các giá trị nguyên của x để P 1 . 0,5 4 0,25 P = . A B = x + 2 4
Vì x 0 x + 2 0 , vậy P 1
1 x + 2 4 . x + 2
x 2 x 4 . 0,25
Kết hợp với điều kiện x là số nguyên và x 0, x 1, ta tìm được x 0; 2; 3 . 1)
2 x − 1 − 7 = 11. 1,0 ĐK: x 1. 0,25 2 x − 1 = 18 0,25
x − 1 = 9
x − 1 = 81 0,25
x = 82 (TMĐK). Vậy phương trình có nghiệm duy nhất x = 82 . 0,25 2) 5 2 9x + 36 − 2 2 x + 4 = Bài III 9 . 3 1,0 2,0 điểm 5 9 ( 2 x + 4) − 2 2 x + 4 = 9 0,25 3 2 x + − 2 x + = 2 5 4 2 4 9 3 x + 4 = 9 0,25 2 x + = 2 x + = 2 4 3 4 9 x = 5 0,25
x = 5 . Vậy phương trình có nghiệm x = 5 . 0,25 1)
Giả sử AB = 6 c ,
m BC = 10 cm . Tính độ dài các đoạn thẳng BH, AH . 1,5
Vẽ đúng hình đến ý 1) (không cần chính xác A AB = 6 c ,
m BC = 10 cm 0,5 ). Bài IV F 3,0 điểm
Xét ABC vuông tại A , đường cao AH , 0,25 E theo hệ thức lượng: 2
AB = BH.BC B C H 2
6 = BH.10 BH = 3, 6 (cm) 0,25
CH = BC − BH = 6, 4 (cm) 0,25 2
AH = BH.CH AH = 4, 8 (cm) . 2) AC
Chứng minh rằng AE.AB = AF.AC và cos AEF = . 1,0 BC
Xét ABH vuông tại H , có đường cao HE nên 2
AH = AE.AB (htl).
Xét ACH vuông tại H , có đường cao HF nên 2
AH = AF.AB (htl). 0,25
Từ đó AE.AB = AF.AC . 0,25
Chứng minh AEF ∽ ACB (c.g.c) 0,25
Suy ra AEF = ACB (2 góc tương ứng). AC
Xét ABC vuông tại A , theo tỉ số lượng giác của góc nhọn: cos ACB = BC 0,25 AC cos AEF = . BC 3)
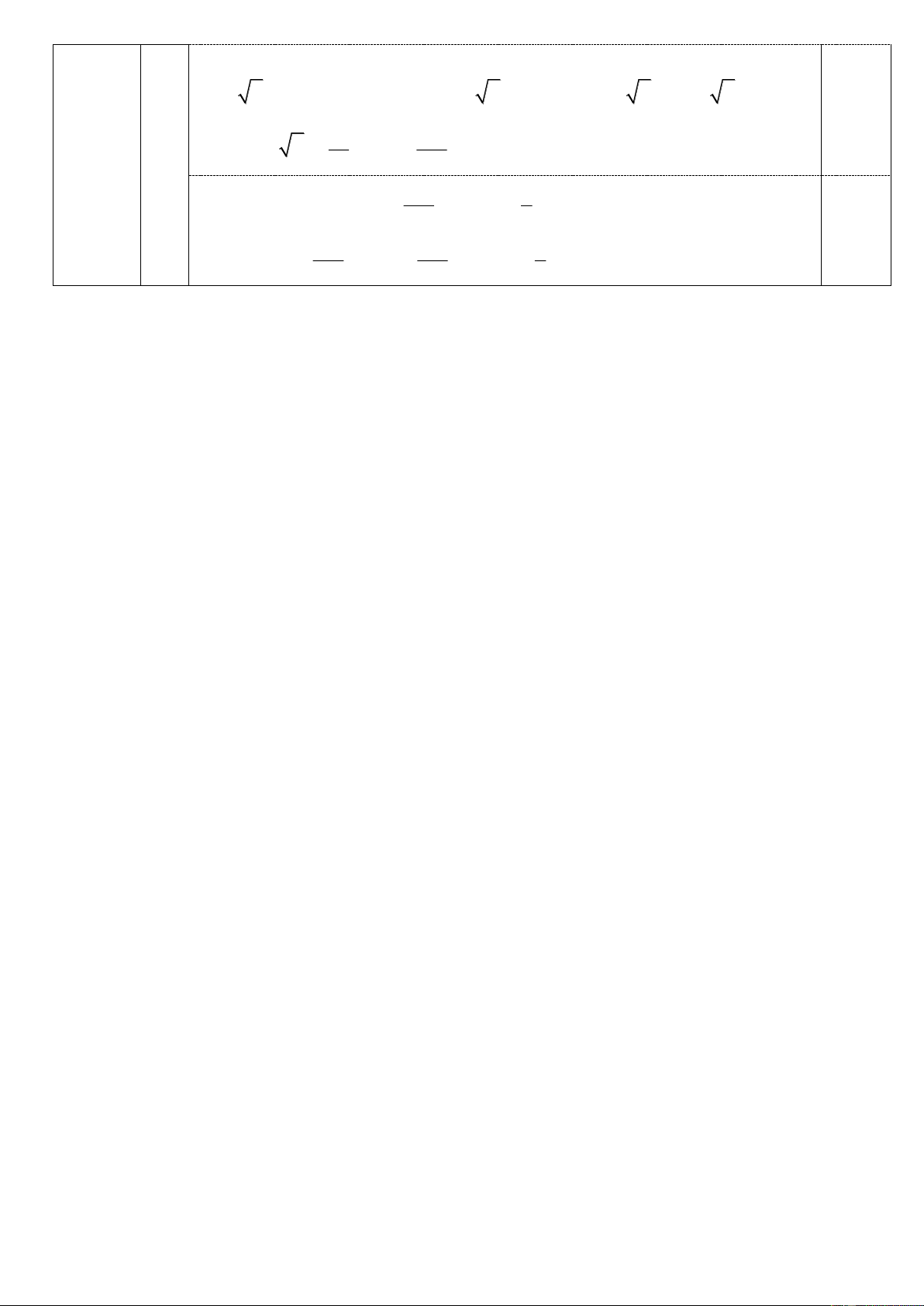
Chứng minh ba điểm , B ,
O D thẳng hàng. 0,5 S = 1 B .
D BC.CM.OH ABC 2 1 AH BC = 1 . B .
DCM.BC.OH 2 2
AH.BC = B . DCM.BC.OH
Vì BD ⊥ CM nên
BD.CM = MH.BC (= 2S MBC ) M Vậy AH.BC =
MH.BC.BC.OH 0,25
AH = MH OH 2 .
AH = MH.OH Mà D' 2 A D
AH = BH.CH BH.CH = MH.OH F
BH = MH BOH ∽ MCH O OH CH E (c.g.c) B C
Từ đó OBH = OMD (2 góc tương ứng). H
Gọi D ' là giao điểm của BO và CM .
Vì OBH = OMD ' và BOH = MOD ' (đối
đỉnh) nên BOH ∽ MOD ' (g.g) Suy ra MD = BHO = 0 'O 90 , từ đó 0,25
BO ⊥ MC tại D ' .
Mà BD ⊥ MC tại D , suy ra D ' trùng D . Vậy ba điểm , B ,
O D thẳng hàng.
Cho các số thực x, ,
y z 0 thỏa mãn x + y + z = 19 và x + y + z = 5 0,5
. Tìm giá trị lớn nhất của x . Bài V
x + y + z = 19 y + z = 19 − x 0,5 điểm
x + y + z = 5 y + z = 5 − x . 2
Chứng minh bất đẳng thức phụ: ( y + z ) 2(y + z ) Suy ra ( 2
5 − x ) 2(19 − x) 3x −10 x −13 0 (3 x −13)( x + ) 1 0 . 13 169 0,25 Tìm được x x . 3 9 169 1
Dấu bằng xảy ra khi x = ; y = z = . 9 9 169 1 0,25 Vậy x = 169 max khi x = ; y = z = . 9 9 9
……………………………………Hết…………………………….