Đề khảo sát Toán 9 lần 2 năm 2022 – 2023 trường THCS Nguyễn Trường Tộ – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp đề khảo sát chất lượng học sinh môn Toán 9 năm học 2022 – 2023 trường THCS Nguyễn Trường Tộ – Hà Nội giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.
Preview text:
PHÒNG GD & ĐT QUẬN ĐỐNG ĐA
KHẢO SÁT CHẤT LƯỢNG
THCS NGUYỄN TRƯỜNG TỘ
MÔN TOÁN 9 – LẦN 2
-----------o0o-----------
Năm học 2022 – 2023 Ngày 18/5/2023 ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút
(Không kể thời gian phát đề)
Bài 1. (2,0 điểm) Cho các biểu thức x 2 x A và 2 4 B
với x 0 và x 1. x 2 x 1 1 x x 1
1) Tính giá trị của A khi x = 9.
2) Rút gọn biểu thức B.
3) Đặt P AB. Tìm các giá trị nguyên của x để 7 P . 4
Bài 2. (2,0 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình. Một ca nô đi từ bến A đến bến B rồi
trở về A ngay. Hai bến sông cách nhau 40km và tổng thời gian cả đi và về của ca nô là 3 giờ 20
phút. Tính vận tốc riêng của ca nô biết vận tốc dòng nước là 5km/h.
2) Một cốc nước hình trụ có đường kính đáy là 10cm đang chứa nước nhưng chưa đầy. Người ta
thả vào cốc 6 viên bi hình cầu giống hệt nhau thì thấy mực nước trong cốc dâng lên 5cm (và nước
vẫn chưa đầy cốc). Tính bán kính của mỗi viên bi.
Bài 3. (2,5 điểm) 2 3 x 1 8
1) Giải hệ phương trình y 1 . 3 x 1 1 y 1
2) Trong mặt phẳng tọa độ Ox ,
y cho đường thẳng (d) : y = mx − 2m + 3 và parabol P y = 2 ( ) : x .
a) Với m = 2, tìm tọa độ giao điểm của (d) và (P).
b) Tìm m để (d) cắt (P) tại hai điểm phân biệt có hoành độ x ,x thỏa mãn 2
x + mx = 2m. 1 2 2 1
Bài 4. (3,0 điểm) Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau. Lấy điểm M
thuộc đoạn thẳng AC (M khác ,
A C ). Đường thẳng qua điểm O vuông góc với đường thẳng
OM cắt đường thẳng BC tại điểm N. Tia AN cắt tia DB tại điểm E. Gọi F là chân đường
vuông góc của B đến đường thẳng CE.
1) Chứng minh tứ giác MONC là tứ giác nội tiếp.
2) Chứng minh CO CD CF CE và AC là tiếp tuyến của đường tròn ngoại tiếp tam giác AFE.
3) Khi điểm M thay đổi vị trí trên đoạn thẳng AC, chứng minh đường thẳng NF luôn đi qua một điểm cố định.
Bài 5. (0,5 điểm) Cho các số thực không âm x,y thỏa mãn 2 x + 2 y + x − 2 (
y) = 8. Tìm giá trị lớn nhất và
nhỏ nhất của biểu thức T = x + y.
-----------HẾT-----------
Họ và tên thí sinh: ………………………………………………… Số báo danh: ……………….
ĐÁP ÁN - HƯỚNG DẪN CHẤM Bài Ý
Nội dung – Đáp án Điểm
1) Tính giá trị của A khi x = 9. 0,50
Với x = 9 (TMĐK) ⇒ A = 7 . 0,50 5
Rút gọn biểu thức B. 1,00 x 2 4 x 2 4 B 0,25 x 1 1 x x 1 x 1 x 1
x 1 x 1 x x 1 2 x 1 4 B 0,25 2) x 1 x x
x 1 x 2 2 Bài 1 B 0,25 (2,0đ)
x 1 x 1 x 1 x 1 x 2 B . 0,25 x 1
Tìm các giá trị nguyên của x để 7 P . 0,50 4 x 2 P AB . x 1 3) 0,25 7 x 2 7 P
4x 7 x 15 0 4 x 1 4
( x 3)(4 x 5) 0 x 9 (TMĐK) 0,25 Vậy x 9
Tính vận tốc riêng của ca nô biết vận tốc dòng nước là 5km/h. 1,50
Gọi vận tốc riêng của ca nô là x (km/h). Đk: x > 0. 0,25
Vận tốc ca nô khi đi xuôi dòng là x 5 (km/h)
Thời gian ca nô khi đi xuôi dòng là 40 (giờ) 0,25 x 5
Vận tốc ca nô khi đi xuôi dòng là x 5 (km/h) Bài 2
Thời gian ca nô khi đi xuôi dòng là 40 (2,0đ) 1) (giờ) 0,25 x 5
Đổi 3 giờ 20 phút = 10 (giờ). 3 0,25 Ta có phương trình 40 40 10 x 5 x 5 3
Giải phương trình ta được x 25 (TMĐK) hoặc x 1 (loại) 0,25
Vậy vận tốc riêng của ca nô là 25km/h. 0,25
Tính bán kính của mỗi viên bi. 0,50 2
Thể tích nước dâng lên là: 10 V .
.5 125 (cm3) 1 0,25 2
2) Gọi R là bán kính viên bi. Thể tích 6 viên bi là thể tích nước dâng lên trong
cốc. Khi đó thể tích 6 viên bi là 4 3 3 V 6. . R 8 . R 2 3 0,25 Từ đó: 3 5 8 .
R 125 R (cm) 2
Giải hệ phương trình 1,0 ĐK: y 1 1 3
a 2b 8 Đặt x 1 a, b . 0,25 y 1 a 3b 1
Giải hệ ta được a 2, b 1. 1) 0,25 x 3 Với a 2 x 1 2 x 1 0,25
Với b 1 y 2 (TMĐK)
Vậy x; y 3; 2 ; 1; 2 . 0,25
Với m = 2, tìm tọa độ giao điểm của (d) và (P). 0,75
Với m = 2, (d) : y = 2x − 1. 0,25
Phương trình hoành độ giao điểm: 2 2
x 2x 1 x 2x 1 0. 2a) Bài 3
x 1 y 1. 0,25 (2,5đ)
Tọa độ giao điểm (1;1). 0,25
Tìm m để 2
x + mx = 2m. 0,75 2 1
Xét phương trình hoành độ giao điểm của (d) và (P): 2 2
x mx 2m 3 x mx 2m 3 0 (1) Có 2 2
m 4(2m 3) m 8m 12. 0,25
Để (d) cắt (P) tại 2 điểm phân biệt thì (1) có 2 nghiệm phân biệt 0. 2
m 8m 12 0 (2) 2b) x + x = m Theo Vi-et, ta có: 1 2
x .x = 2m − 3 1 2 0,25 Khi đó 2
x + mx = 2m ⇔ mx − 2m + 3 + mx = 2m 2 1 2 1
⇔ m(x + x ) − 4m + 3 = 0 1 2 2
⇔ m − 4m + 3 = 0 ⇔ m = 1 hoặc m = 3. 0,25
Đối chiếu điều kiện ta được m = 1.
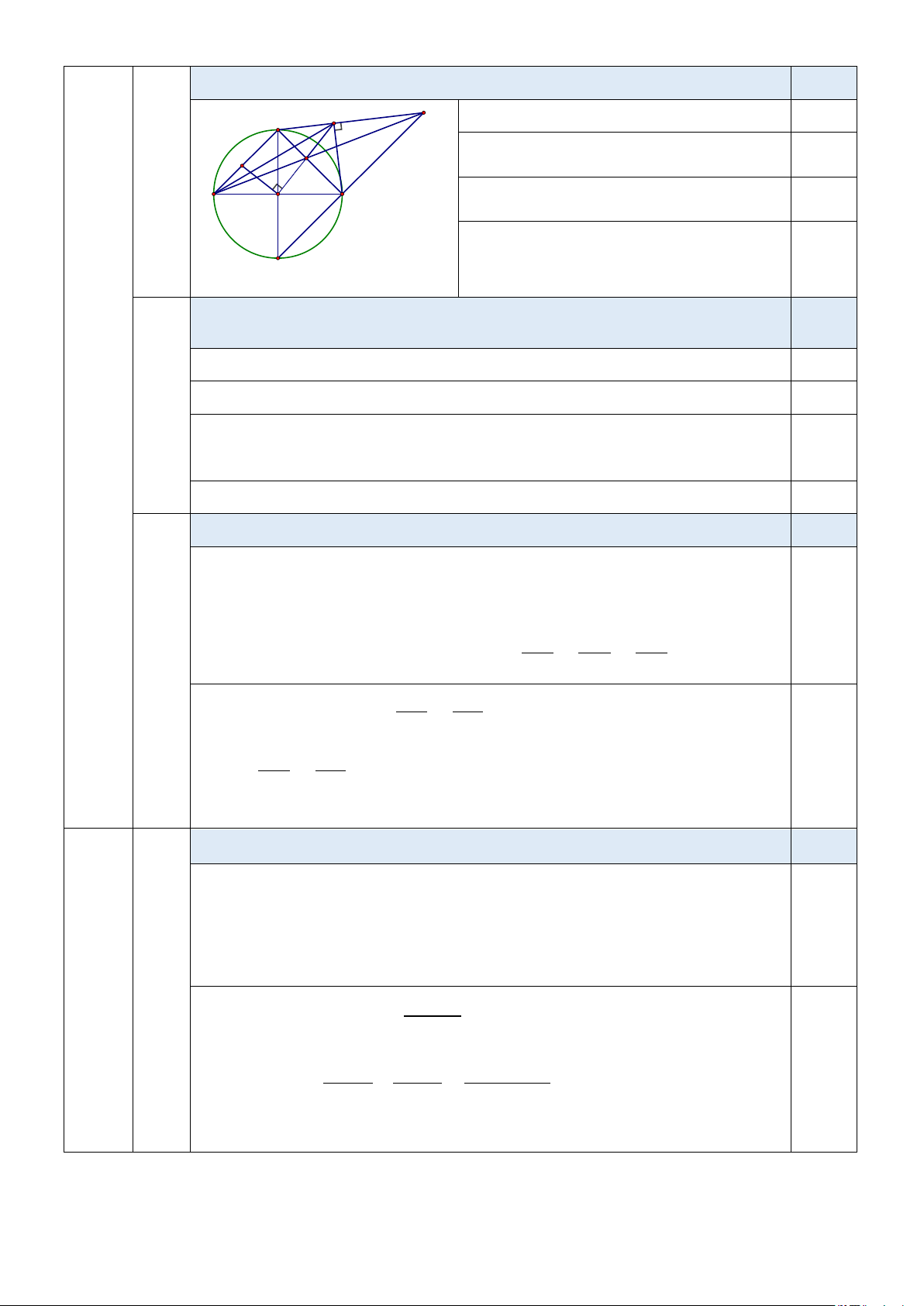
Chứng minh tứ giác MONC là tứ giác nội tiếp. 1,25 F E
Vẽ hình đúng hết câu a) 0,25 C M Chỉ ra MCN = 90° , MON = 90° 0,50 N 1) A B O Từ đó
MCN + MON = 180° 0,25
Mà hai góc này đối nhau nên tứ giác 0,25 D
MONC là tứ giác nội tiếp.
Chứng minh CO CD CF CE và AC là tiếp tuyến của đường tròn 1,25
ngoại tiếp tam giác Chứng minh 2
CO CD CB 0,50 2) Chứng minh 2
CB CF CE . Từ đó CO CD CF CE 0,25 Bài 4 Chứng minh 2
CA CF CE CA F# CE A . 0,25 (3,0đ) Từ đó suy ra CAF FEA
Lập luận CA là tiếp tuyến đường tròn ngoại tiếp tam giác AFE. 0,25
Chứng minh đường thẳng NF luôn đi qua một điểm cố định. 0,50
Tứ giác BFCO nội tiếp nên
BFO BCO 45.
Suy ra FO là phân giác BFC. 0,25 CN AC BC
ACBD là hình vuông AC / /BD 3) BN BE BE Mà BC FC BF C ~ E BC BE FB Suy ra CN FC 0,25
FN là phân giác BFC BN FB
Suy ra F,N,O thẳng hàng.
Tìm giá trị lớn nhất và nhỏ nhất của biểu thức T = x + y. 0,50 Từ giả thiết có 2 x + 2 y − xy = 4. 2 T = x + 2 y = 2 x + 2 ( )
y − xy + 3xy = 4 + 3xy ≥ 4 0,25
⇒ T ≥ 2 ⇒ T
= 2, dấu “=” xảy ra khi chẳng hạn x = 2, y = 0. Bài 5 min (0,5đ) 2 2 Có 2 2 x + + = + ≤ + y x y xy ⇒ 2 x + 2 4 4 y ≤ 8. 2 2 x + 2 y + 2 x + 2 4 4 y +
T = x + y ≤ + = 8 2 2 2 ≤ 8 2 2 2
⇒ T ≤ 4 ⇒ T
= 4 ⇒ T ≤ 4 ⇒ T
= 4, dấu “=” có khi x = y = 2. max max