Đề khảo sát Toán 9 năm 2018 – 2019 phòng GD&ĐT Phúc Yên – Vĩnh Phúc
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp đề khảo sát chất lượng học sinh môn Toán 9 năm học 2018 – 2019 phòng GD&ĐT Phúc Yên – Vĩnh Phúc giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.
Preview text:
PHÒNG GD&ĐT PHÚC YÊN
ĐỀ KHẢO SÁT LỚP 9 – LẦN 1 MÔN: TOÁN NĂM HỌC: 2018 – 2019
Thời gian: 120 phút (không kể thời gian giao đề)
I. PHẦN TRẮC NGHIỆM (2,0 điểm)
Câu 1. Rút gọn biểu thức 2
2 x y x y với x 0, y 0 ta được: A. 3x y B. C. D. 2 x y x y 3 x y 3x 5
Câu 2. Hệ số góc của đường thẳng y là: 2 5 3 A. 3 B. -5 C. D. 2 2
Câu 3. Tam giác ABC vuông tại A, đường cao AH. Biết AB = 4cm, AC = 3cm. Khi đó độ dài đoạn HC bằng: 4 9 16 3 A. cm B. cm C. cm D. cm 5 5 5 5
Câu 4. Cho đường tròn (O) đường kính bằng 6cm và dây MN bằng 2cm. Khoảng cách từ O đến dây MN bằng : A. 2 2cm B. 5cm C. 4 2cm D. 35cm
II PHẦN TỰ LUẬN. (8,0 điểm)
Câu 5. (2,0 điểm)
1) Rút gọn biểu thức: 72 98 0,5. 8 . x 2 x 1 1
2) Cho biểu thức: P . x x 1 x x 1 x 1
a) Rút gọn biểu thức P. 1 b) Tìm x để P . 3
Câu 6. (2,0 điểm)
x my 3m Cho hệ phương trình (I), m là tham số. 2
mx y m 2
a) Giải hệ phương trình (I) với m 2 .
b) Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn x 2018y 2017 .
Câu 7. (3,0 điểm)
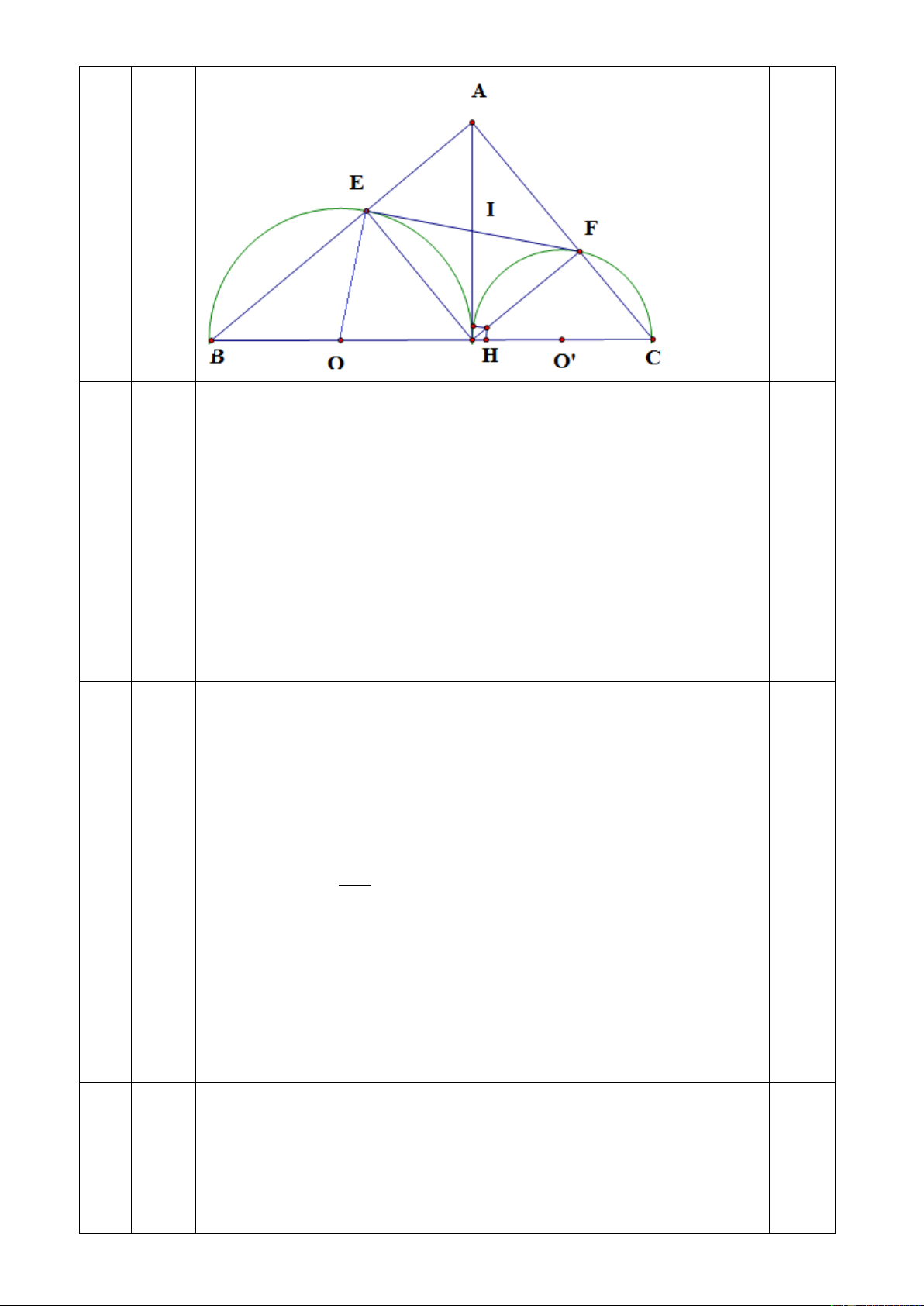
Cho tam giác ABC vuông ở A (AB > AC), đường cao AH. Trên nửa mặt phẳng bờ BC
có chứa điểm A, vẽ nửa đường tròn tâm O đường kính BH cắt AB tại E; vẽ nửa đường tròn
tâm O’ đường kính CH cắt AC tại F.Gọi I là giao điểm của AH và EF.
a) Chứng minh AE.AB = AF.AC.
b) Chứng minh EF là tiếp tuyến của đường tròn (O).
c) Chứng minh BI AO'.
Câu 8. (1,0 điểm)
Cho các số thực dương a, ,
b c thỏa mãn điều kiện a b c 3. Chứng minh rằng: 1 1 1 1. 2 2 2 2 a b 2 b c 2 c a ------ Hết ------
Họ và tên:……………………………………. SBD:……………….
PHÒNG GD&ĐT PHÚC YÊN
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm) Câu 1 2 3 4 Kết quả C D B A
PHẦN II: TỰ LUẬN (8,0 điểm) Câ ý Nội dung Điểm u 5
1) Rút gọn biểu thức 72 98 0,5. 8 . x 2 x 1 1
2) Cho biểu thức P . x x 1 x x 1 x 1
a) Rút gọn biểu thức P. 1 b) Tìm x để P . 3 1 +) Ta có: 0,5đ 72 98 0,5. 8 0,25đ 3 2 7 2 2 5 2 0,25đ 2 a) 0,25đ +) ĐK: 1,5đ x 0, x 1 +) x 2 x 1 x x 1 P x x 1 x x 1 x x 1 0,5đ x x x x x 1 x x 1 x Vậy P 0,25đ x x 1 1 0,25đ b) P 3 x 1 x x 1 3 x 2 1 0 x x 1 x 2 1 0 x 1 0 0,25đ
x 1(không thỏa mãn điều kiện).
Vậy không có giá trị nào của x thỏa mãn yêu cầu bài toán. 6
x my 3m Cho hệ phương trình (I), m là tham số. 2
mx y m 2
1) Giải hệ phương trình(I) với m 2 .
2) Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn
x 2018y 2017 . 1
x 2y 6 0,25đ
+) Với m 2 , hệ phương trình trở thành: 1,0đ
2x y 2
x 2y 6 5 x 10 0,25đ
4x 2y 4
2x y 2 x 2 . 0,25đ 4 y 2 x 2 y 2 0,25đ
Vậy với m = 2 hệ phương trình có nghiệm (x;y) = (2;2) 2
2) Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn 0,25đ 1,0đ x 2018y 2017 . +)
x my 3m 1
x 3m my 2 2 2
mx y m 2 2
m 1 y 2m 1 *
Xét phương trình (*) : 2
m y 2 1 2 m 1 . Ta có m2 +1 >0 , m
. Do đó, phương trình (*) có nghiệm duy nhất với mọi m. 2
m y 2 1 2 m 1 y 2 .
Thay y vào phương trình (1) ta được x = m.
Do vậy, với mọi m hệ phương trình (I) luôn có nghiệm duy nhất 0,25đ (x ;y) = (m ;2). 0,25đ m 2018.2 2017
+) Với nghiệm duy nhất (x ;y) = (m ;2) ta có 0,25đ m 2019
Vậy m = -2019 là số cần tìm. 7 3,0đ
Cho tam giác ABC vuông ở A (AB > AC), đường cao AH.
Trên nửa mặt phẳng bờ BC có chứa điểm A, vẽ nửa đường tròn tâm
(O) đường kính BH cắt AB tại E; vẽ nửa đường tròn tâm (O’)
đường kính CH cắt AC tại F. Gọi I là giao điểm của AH và EF.
1) Chứng minh AE.AB = AF.AC.
2) Chứng minh EF là tiếp tuyến của đường tròn (O).
3) Chứng minh BI AO'. 1,0 đ a) 0,25đ
+) Trong đường tròn (O), ta có 0
BEH 90 (góc nội tiếp chắn nửa
đường tròn), suy ra HE AB . Trong 0 A H ,
B H 90 , HE AB ta có: 2 AH E. A AB .(1)
+) Trong đường tròn (O’), ta có 0
CFH 90 (góc nội tiếp chắn nửa 0,25đ
đường tròn), suy ra HF AC . Trong 0 A
HC, H 90 , HF AC ta có: 2
AH AF.AC (2) 0,25đ
Từ (1) và (2) suy ra AE.AB = AF.AC. Vậy AE.AB = AF.AC. 0,25đ b)
+) Ta có HE AB (cmt) 0 HEA 90 , 0,25đ HF AC 0 A HF 90 Mà 0 BAC 90
Suy ra tứ giác AEHF là hình chữ nhật.
Do đó, IEH IHE (3). 0,25đ BH
Mà OE OH suy ra O
EH là tam giác cân tại O. Suy ra 2
OEH OHE (4).
Từ (3), (4) suy ra OEH IEH OHE IHE . Hay 0,25đ 0
OEI IHO 90 . 0,25đ
Ta có E thuộc (O), OE EF suy ra EF là tiếp tuyến của đường tròn (O).
Vậy EF là tiếp tuyến của đường tròn (O). c) BI AO' 0,5đ
+) Ta có I là trung điểm của AH (AEHF là hình chữ nhật)
O’ là trung điểm của HC.
Suy ra IO’ là đường trung bình của tam giác AHC. Do đó, IO’ // AC. 0,25đ
+) Mà AC AB . Suy ra IO’ AB. Mà AH BO’
Suy ra I là trực tâm của tam giác ABO’. Do vậy, BI AO’. 0,25đ Vậy BI AO’. 8 1,0đ
Áp dụng bất đẳng thức AM-GM, 0,25đ ta có 2 3 2
11 a b 3 a b và 3 2
3 ab a b b a 2 . b 2 2 1 a b 1 1 Suy ra 2 3 2 1 a b 1
1 a ab 1 a a 2b 2 2 3 2 2 a b 11 a b 3 9 3 a b 1 1 1 Suy ra 2 (a 2ab) (1) 2 2 a b 2 18 Tương tự, cũng có: 1 1 1 2 (b 2bc) (2) 0,25đ 2 2 b c 2 18 1 1 1 2 (c 2ca) (3) 2 2 c a 2 18
Cộng (1), (2), (3) vế đối vế, thu được 0,25đ 1 1 1 3 1 2
a b c
1. Điều phải chứng minh. 2 2 2 2 a b 2 b c 2 c a 2 18 0,25đ
Dấu đẳng thức xảy ra khi và chỉ khi a b c 1.